Abstract
In addressing the control of asynchronous motors in the remote conductivity of fertigation machines, this study proposes a joint control strategy based on the Fast Terminal Sliding Mode Control-Disturbance Observer (FTSMC-DO) system for asynchronous motors. The goal is to enhance the dynamic performance and disturbance resistance of asynchronous motors, particularly under low-speed operating conditions. The approach involves refining the two-degree-of-freedom internal model controller using fractional-order functions to explicitly separate the controller’s robustness and tracking capabilities. To mitigate the motor’s sensitivity to external disturbances during variable speed operations, a load disturbance observer is introduced, employing hyperbolic tangent and Fal functions for real-time monitoring and compensation, seamlessly integrated into the sliding mode controller. To address issues related to low-speed chattering typically associated with sliding mode controllers, this study introduces a revised non-singular fast terminal sliding mode surface. Additionally, guided by fuzzy control principles, the study enables real-time selection of sliding mode approaching law parameters. Experimental results from the asynchronous motor control platform demonstrate that FTSMC-DO control significantly reduces adjustment time and speed fluctuations during operation, minimizing the impact of load disturbances on the system. The system exhibits robust disturbance rejection, improved robustness, and enhanced control capability. Furthermore, field tests validate the effectiveness of the FTSMC-DO system in regulating remote electrical conductivity (EC) levels. The control time is observed to be less than 120 s, overshoot less than 16.1%, and EC regulation within 0.2 mS·cm−1 over a pipeline distance of 120 m. The FTSMC-DO control consistently achieves the desired EC levels with minimal fluctuation and overshoot, outperforming traditional PID and SMC methods. This high level of precision is crucial for ensuring optimal nutrient delivery and efficient water usage in agricultural irrigation systems, highlighting the system’s potential as a valuable tool in modern, sustainable farming practices.
1. Introduction
The integration of advanced control systems into agricultural machinery, especially in fertigation equipment, has become imperative to address the increasing complexities associated with managing water and nutrient supplies in modern agriculture [1,2]. A critical focus in this domain is the optimization of asynchronous motors, pivotal components in fertigation machines, to enhance their dynamic performance and disturbance resistance [3,4]. These machines play a vital role in delivering precise quantities of water and nutrients, crucial for sustainable agricultural practices [5,6]. However, the operation of these machines is often complicated by remote nonlinear and irregular electrical conductivity (EC) disturbances, leading to inefficiencies and inconsistencies in resource distribution [7]. This not only impacts crop yield and quality but also raises concerns about resource conservation and environmental sustainability [8].
In the context of agricultural machinery, particularly in fertigation equipment, addressing challenges associated with asynchronous motors is paramount due to their central role in the precise delivery of water and nutrients [9]. While research in fertigation control has made significant strides in understanding parameters such as pH and EC [10], a notable gap persists in existing control methods, such as PID and SMC, in effectively managing the specific challenges posed by the non-linear and dynamic nature of remote electrical conductivity control [11].
The pH value of the soil and water solution is vital for agriculture, influencing nutrient availability and plant uptake [12,13]. Optimal pH ensures nutrient solubility and accessibility, directly impacting crop health and productivity [14]. Similarly, EC is a critical parameter in fertigation, indicating the concentration of soluble salts (nutrients) in irrigation water [15]. Precise control of EC is essential for maintaining the correct nutrient balance [16]. Over or under-concentration can lead to nutrient-related issues, adversely affecting crop health and yield [12]. Accurate control and adjustment of EC are key factors in precision agriculture [17,18].
Existing research has predominantly focused on developing control methods like PID and SMC to enhance system performances [19,20]. However, these traditional approaches fall short in addressing the challenges of remote electrical conductivity control’s non-linear and dynamic nature, especially in dealing with irregular fluctuations [21]. The complexity arises from continuous variations in moisture levels, soil characteristics, and environmental factors [22]. Consequently, there remains a gap in developing a control system that effectively integrates robustness, precision, and adaptability, particularly under variable and unpredictable agricultural conditions [23]. Fuzzy PID algorithms were used to detect concentrations and compare them with set concentrations, and the effects of fertilizer flow rate and water flow rate on fertilizer concentration were determined using the control variable experimental method [24]. Based on single-chip microcomputers and fuzzy control, a water and fertilizer control system was designed and introduced into the fertigation device. The control system calculates and adjusts the fertilizer flow rate based on input and feedback information, enabling the automatic operation of the fertigation device [25]. NB-IoT technology was employed for remote control of fertigation machines [26].
This study bridges the identified gap by proposing a novel joint control strategy, integrating an improved internal model control with Fast Terminal Sliding Mode Control-Disturbance Observer (FTSMC-DO). The research aims to enhance the dynamic performance and disturbance resistance of asynchronous motors in fertigation machines, contributing to the advancement of precision agriculture practices. This strategy is expected to broaden the capabilities of existing control systems by improving the dynamic performance and disturbance resistance of asynchronous motors in fertigation machines. The objectives include developing and experimentally validating the FTSMC-DO control system to achieve enhanced speed and torque control for asynchronous motors. Additionally, the research aims to demonstrate the effectiveness of the FTSMC-DO system in managing electrical conductivity (EC) levels in fertigation scenarios, especially under conditions of remote, nonlinear, and irregular conductivity fluctuations. This involves minimizing fluctuations and overshoot in EC levels to ensure precise nutrient delivery and efficient water usage in agricultural irrigation systems.
The structure of the paper includes a detailed discussion of materials and methods in Section 2, presenting the technical framework and setup of the proposed control system. Section 3 provides results from experimental evaluations and field tests, comparing the FTSMC-DO system with traditional control methods. Finally, Section 4 concludes with a discussion on the implications of the findings and their potential impact on advancing fertigation technologies in sustainable agriculture.
2. Materials and Methods
2.1. Description of the Remote Conductivity Control System for the Fertigation Machine
As shown in Figure 1, the remote conductivity control system of the fertigation machine comprises four main components: the water supply component, the fertilization component, the drip irrigation component, and the monitoring component. The water supply component comprises primarily a storage tank and a water pump. The fertilization component includes elements such as a fertilizer storage tank and a fertilizer pump. The drip irrigation component is made up of a filter, drip irrigation tapes, and wireless electronic control valves, while the monitoring component consists of a remote monitoring system and remote conductivity sensors.

Figure 1.
The remote conductivity control system of the fertigation machine.
This study primarily concentrates on the asynchronous motor control system in fertigation machines, introducing an enhanced control strategy that integrates internal model control with FTSMC-DO. This approach aims to enhance the dynamic performance and disturbance resistance of asynchronous motors under remote, nonlinear, and irregular conductivity disturbances.
The fertilization liquid mixing model employs a typical first-order lag model. The approximate transfer function of the remote conductivity (EC) after Laplace transformation is:
In this equation, VT represents the volume of fertilizer liquid stored in the pipeline, in liters (L). The flow rate in the main drip irrigation pipe, qm, and the maximum fertilizer absorption rate of the fertigation machine, qw, are measured in liters per hour (L/h). The flow rate at the end of the drip irrigation tape, q2, is also in L/h. E1 denotes the EC of the fertilizer solution in the tank, while E0 represents the EC of the clean water in the inlet pipe.
2.2. Asynchronous Motor Mathematical Model
The actuating component of the fertigation machine is an asynchronous motor. The asynchronous motor used in this study has a rated power of 3 kW, a rated speed of 1400 r/min, a rated current of 6.7 A, a rated torque of 20.3 N/m, and a pole pair number of 2. The pump used is a peristaltic pump, with a starting torque of 230 N/m, a maximum flow rate of 5310 L/h, and a maximum operating pressure of 8 Pa. It is known that the mathematical model of an asynchronous motor is multivariable and nonlinear [27,28]. By performing a coordinate transformation, the three-phase stationary coordinate system is equivalently converted into a two-phase rotating coordinate system. This enables the decoupling and order reduction of the asynchronous motor, allowing the control strategies of DC motors to be applied to asynchronous motor control, making the control both simple and efficient. The equations of the asynchronous motor in the two-phase rotating dq coordinate system are as follows:
Current equation:
Flux linkage equation:
Speed equation:
Motion equation:
In the above equations, isd, isq, usd, and usq represent the current and voltage in the dq axis, respectively; Lm is the mutual inductance between the stator and rotor windings in the dq axis; Ls, Lr, are the self-inductances of the stator and rotor windings in the dq axis, respectively; Rs, Rr are the resistances of the stator and rotor, respectively; σ is the motor’s leakage magnetic coefficient, and σ = (Lm2/LsLr); Tr is the rotor electromagnetic time constant, Tr = (Lr/R); ω1, ω are the stator frequency synchronous speed and the rotor speed, respectively; and ωm is the mechanical speed.
2.3. Internal Model Controller Design
The two-degree-of-freedom internal model control and the equivalent internal model control are illustrated in Figure 2 and Figure 3.

Figure 2.
The two-degree-of-freedom internal model control.
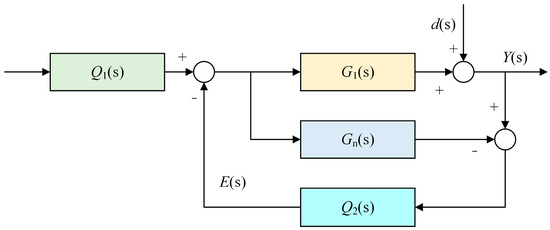
Figure 3.
The equivalent internal model control.
In the figures, Q1(s) and Q2(s) represent the two-degree-of-freedom internal model controllers, while G(s) and Gn(s) are the controlled object and the reference model of the controlled object, respectively. A comparison between Figure 2 and Figure 3 yields:
When designing the internal model controller, a low-pass filter is generally introduced, which can be represented as:
where f1(s) and f2(s) are the introduced low-pass filters.
Fractional-order controllers are used for their flexibility and precise control of the model, with the transfer function of the fractional-order controller being:
Following the principles of fractional-order controllers, the designed low-pass filters in this study are:
where γ is the fractional order of integration, 1 < γ < 2, and λ1 and λ2 are the adjustable time constants of the filter.
2.4. Fuzzy Sliding Mode Speed Regulator Design
Due to the rotor short circuit in the asynchronous motor [29], the rotor dq axis voltage equals zero, and the rotor magnetic chain orientation Ψrq = 0. By combining the voltage equation and magnetic chain equation in the dq coordinate system, we get:
From Equation (10), it is evident that coupling issues still exist in the dq axis. Therefore, to decouple the rotor magnetic chain and after applying the Laplace transform, we obtain:
Consequently, the internal model controller is derived as:
This study improves the disturbance rejection capability of the controller by adopting a two-degree-of-freedom fractional-order internal model control, effectively separating disturbance rejection and tracking. Its structure is shown in Figure 4.
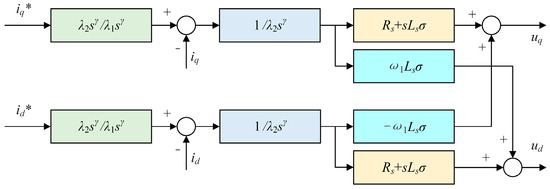
Figure 4.
Equivalent internal model control.
2.5. Fast Terminal Sliding Mode Control Method Based on Asynchronous Motor Disturbance Observer
2.5.1. Load Disturbance Observer Design
In order to enhance the disturbance rejection capability of the speed controller, a load disturbance observer based on the hyperbolic tangent function (tanh) and the Fal function is designed in this paper. It identifies and compensates in real time for load disturbances in the speed controller. The rotor mechanical angular velocity ωm and load disturbance d(t) are chosen as the state variables for the load disturbance observer, where d(t) = (np/J)TL.
Due to the high switching frequency of the motor controller and the mechanical time constant being much larger than the electrical time constant, it can be assumed that the load disturbance remains constant within one sampling period, TL = 0, d(t) = 0. Combining this with Equation (5), the state equation is given as follows:
Here, , , , , u = Te.
Designing the disturbance observer based on Equation (13), the expression for the disturbance observer is given by:
Here, = , and are their respective estimated values, is a constant with 0 < < 1, and is the filtering constant.
The hyperbolic tangent function, tanh, is a type of hyperbolic function known for its smooth continuity and convergence properties. Its formula is given by:
The Fal function is commonly employed in Extended State Observers within the framework of active disturbance rejection control. It is known for its rapid convergence and good robustness. The formula is:
The Fal function varies with the change in |eω|. As indicated by Equations (15) and (16), when |eω| > δ, tanh|eω|μsgn(eω) enables the system to rapidly approach the actual values, leading eω to converge to δ. On the other hand, when |eω| < δ, tanh(eω/δ1−μ) acts like a low-pass filter. Therefore, the proposed tanhFal(eω, μ, δ) function possesses fast convergence characteristics, facilitating the convergence of observation errors.
2.5.2. Fuzzy Sliding Mode Speed Controller Design
Considering the practical requirements of the speed regulator, the state variables for the sliding mode controller are selected as:
Here, x1 represents the motor speed error, with ω* and ω being the set speed and actual speed of the motor, respectively.
In order to further alleviate the chattering phenomenon in Sliding Mode Control (SMC), this paper references methods proven effective in overcoming chattering issues with sliding mode controllers at low speeds [30]. The designed nonsingular fast terminal sliding surface is:
where c1, c2 > 0, 1 < p/q < 2 and p, q are positive odd integers.
The Fal function, as shown in Equation (16), speeds up the error convergence to the sliding mode surface when |x1| > δ, and the terms and |x1|μsgn(x1) work together to accelerate the error’s convergence toward the sliding mode surface. As the error approaches the equilibrium point along the sliding surface, the convergence speed is determined by the introduced term x1/1−μ. This design ensures that the error moves towards the sliding surface more efficiently, especially as it nears the equilibrium point.
This study employs rotor magnetic chain-oriented vector control, where Ψrq = Ψr, and Ψrq = 0. From Equation (2), we obtain:
Deriving Equation (18) yields:
Combined with the exponential approaching law = −μsgn(s) − ks, we get:
where , is the real-time observation value of the load disturbance observer.
To verify the stability of the proposed sliding mode controller, the Lyapunov function V = s2/2 is chosen, and its derivative is:
Combining Equations (20) and (21) yields:
From this, we obtain:
In the above equation, c1 > 0, 0 < (p/q) – 1 < 1, and p, q are positive odd integers, η > 0. Therefore, it can be concluded:
From the above equation, it can be observed that the designed sliding mode controller satisfies the general sliding mode conditions, aligning with stability theory.
This paper, leveraging the characteristics of fuzzy control, extends the sliding mode control by incorporating fuzzy control to construct a dynamic sliding surface. The selection of control index approaching law parameters k ensures that the asynchronous motor maintains more accurate dynamic performance under different operating conditions.
Based on the design of the sliding mode controller, fuzzy control takes the actual motor speed and the load estimate from the load disturbance observer as inputs, with = (J/np).The sliding mode control parameter k is then produced as the output. The schematic diagram of the fuzzy sliding mode control is illustrated in Figure 5.
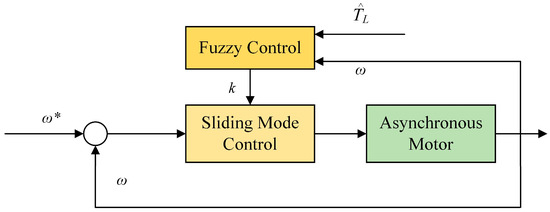
Figure 5.
Fuzzy sliding mode control schematic.
The fuzzy inference rule table is presented in Table 1. The actual speed , load estimate , and sliding mode control parameter k employ triangular membership functions and are divided into 5 fuzzy sets: Negative Big (NB), Negative Small (NS), Zero (Z0), Positive Small (PS), and Positive Big (PB). The domains for actual speed , load estimate , and parameter k are [150, 1000], [5, 35], and [150, 350], respectively.

Table 1.
Fuzzy control inference rules table.
The selection of parameter k influences the convergence speed of the system. When k is smaller, the convergence speed is slower. Therefore, according to Table 1, it can be inferred that when the actual motor speed is high and the load estimate is too low, the parameter value should be increased to ensure rapid convergence and improve stability. Conversely, when the actual speed is low and the load estimate is high, the parameter value should be decreased to enhance the system’s disturbance rejection capability.
The parameters for the PID speed controller are set as kp = 8, ki = 0.6, for the traditional SMC η = 10, k = 200, and for the fuzzy sliding mode-internal model control p = 15, q = 11, c1 = 12, c2 = 0.5. The FTSMC-DO is depicted in Figure 6.
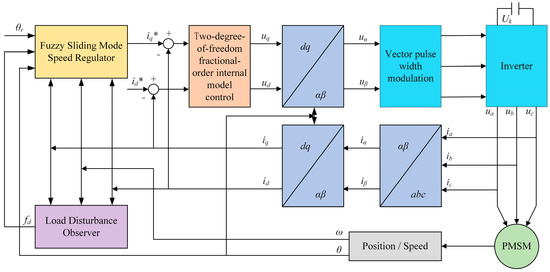
Figure 6.
The fast terminal sliding mode control based on the asynchronous motor disturbance observer.
2.6. Test Platform
The experimental validation of the control method in this study is conducted using a fast terminal SMCl platform equipped with an asynchronous motor disturbance observer. The test platform for assessing the control outcomes of the asynchronous motor is shown in Figure 7 and Figure 8, where the control system layout is also depicted. The experimental setup comprises an asynchronous motor coupled with a load motor, a computer, drivers, an adapter box, sensors, brake resistors, and other integral components. For field testing, the study employs the remote conductivity control system of the fertigation machine, as illustrated in Figure 1, to demonstrate the practical applicability and efficacy of the developed control strategy in real-world agricultural scenarios.

Figure 7.
The layout of the test platform.

Figure 8.
The control system.
3. Results and Discussion
3.1. Control Results of the Asynchronous Motor
The study initially evaluates the effectiveness of the FTSMC-DO developed with the constructed disturbance observer, comparing it with traditional SMC and PID control methods. The tests assess motor speed and torque control performance.
3.1.1. Motor Speed Control
The first test examines the start-up and sudden load response of the three control methods. The initial pump start-up load is set at 200 N·m with a set speed of 1400 r/min. At 25 s, the fertigation valve is abruptly turned off for an instantaneous unload. The results are illustrated in Figure 9.
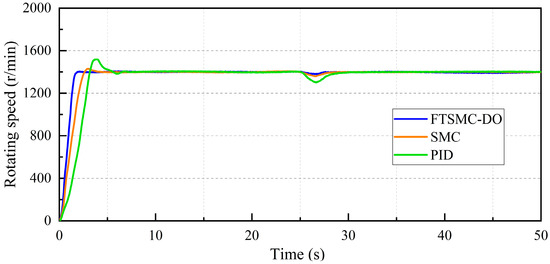
Figure 9.
Start-up and sudden load speed response of the three control methods.
The study also tests the speed response of the three control methods during acceleration, deceleration, and sudden unload experiments. In Figure 10, the experiment starts with an initial pump load of 200 N·m and a set speed of 1400 r/min, decelerates to 600 r/min at 0.2 s, accelerates to 1200 r/min at 25 s, and then undergoes an instantaneous unload by turning off the fertigation valve at 0.5 s.
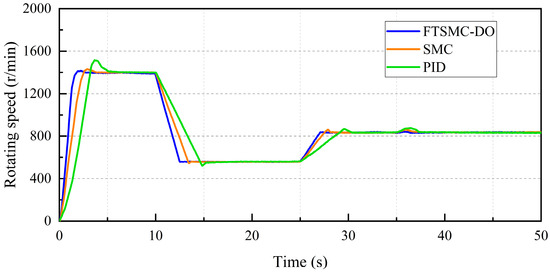
Figure 10.
Acceleration, deceleration, and sudden unload speed response of the three control methods.
Comparative analysis of the test results reveals:
- During the start-up phase of the asynchronous motor, FTSMC-DO control reaches the set speed faster than PID and SMC controls, with virtually no overshoot.
- Under sudden load conditions, the speed under PID control significantly drops, while the FTSMC-DO control demonstrates enhanced speed regulation capability, maintaining the set speed effectively.
- During acceleration and deceleration, PID and SMC controls show noticeable delays in adjustment time, whereas FTSMC-DO control exhibits rapid and accurate convergence speed.
3.1.2. Motor Torque Control
Using similar comparative methods, the torque response of the asynchronous motor under sudden load conditions is observed, as shown in Figure 11.

Figure 11.
Torque response of the three control methods under sudden load.
Comparative analysis of the test results shows:
- During steady operation, traditional PID control exhibits significant fluctuations, SMC control still shows noticeable fluctuations, while FTSMC-DO control has substantially less fluctuation.
- At 25 s under sudden load, traditional SMC control takes longer to stabilize and still displays some fluctuation. FTSMC-DO control smoothly transitions and quickly reaches a steady state with minimal fluctuation.
The test results indicate that the FTSMC-DO control proposed in this paper significantly reduces adjustment time and speed fluctuations during operation, minimizing the impact of load disturbances on the system. This demonstrates the system’s improved disturbance rejection, robustness, and overall control capability.
3.2. Experimental Validation
The experiment was conducted under the following conditions: main pipe pressure was maintained at 0.55 MPa, the end flow rate of the drip irrigation tape was 2 L/h, and the EC of the irrigation water was 1.0 mS/cm. The stock solution in the fertilizer tank, prepared using potassium nitrate fertilizer, had an EC of 10 mS/cm. The distance from the fertigation machine to the end of the pipeline was 120 m. The sampling period was set at 5 s, and measurements were continuously taken for 900 s. The experiment compared the performance of PID control, traditional SMC, and FTSMC-DO, each set to different EC levels. The results are shown in Table 2.

Table 2.
Statistics of nutrient contents in soil samples.
The performance of PID, SMC, and FTSMC-DO control methods in regulating different EC levels at remote endpoints is depicted in Figure 12, Figure 13, and Figure 14, respectively.
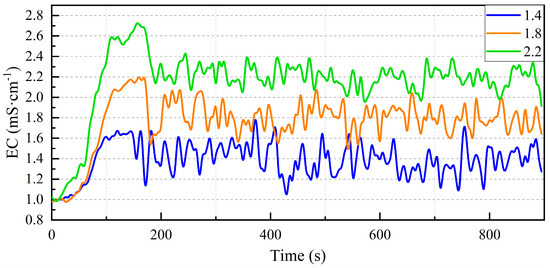
Figure 12.
PID control methods in regulating different EC levels at remote endpoints.
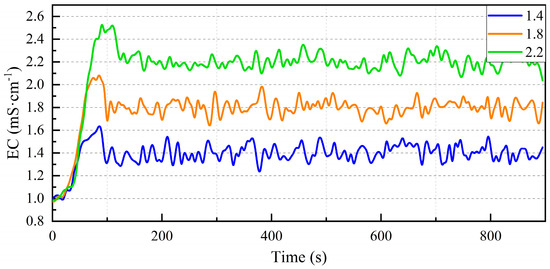
Figure 13.
SMC control methods in regulating different EC levels at remote endpoints.
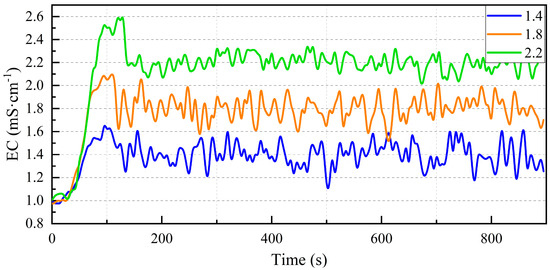
Figure 14.
FTSMC-DO control methods in regulating different EC levels at remote endpoints.
From the table and figures, it can be observed that all three control algorithms demonstrate that as the target EC increases, the fluctuation in EC decreases, and the steady-state EC becomes more precise, but both steady-state time and overshoot increase, indicating greater latency and enhanced stability.
At the same target EC, FTSMC-DO appears to be the most effective in terms of minimal fluctuation, fastest stabilization, and lowest overshoot. While PID is a commonly used control method, it tends to have higher fluctuations and overshoot, and it takes longer to stabilize. SMC falls between the two in terms of performance, exhibiting moderate results in all three criteria.
The FTSMC-DO control, in comparison to the other two algorithms, shows smaller EC fluctuations, faster response, and smaller overshoot; the time required to regulate water and fertilizer is less than 120 s. In the tested fertigation system, the time for water and fertilizer to travel from the outlet to the drip head is at least 2 min. Therefore, it can be concluded that the fast terminal SMC system based on the asynchronous motor disturbance observer developed in this study can meet the practical needs of fertigation.
To further elaborate on the above situation, the unloaded-locked rotor method was employed to compare the FTSMC-DO and SMC models. The comparison was conducted at low speed (600 r/min), medium speed (1000 r/min), and high speed (1400 r/min) under different torque conditions, as illustrated in Figure 15, Figure 16 and Figure 17. The results indicate that under the same torque and speed conditions, FTSMC-DO requires less current compared to the SMC method. This results in the asynchronous motor exhibiting superior torque-to-current ratio characteristics, achieving better control precision and corresponding performance.

Figure 15.
The isd and isq curves required for different torques under n = 600 r/min.
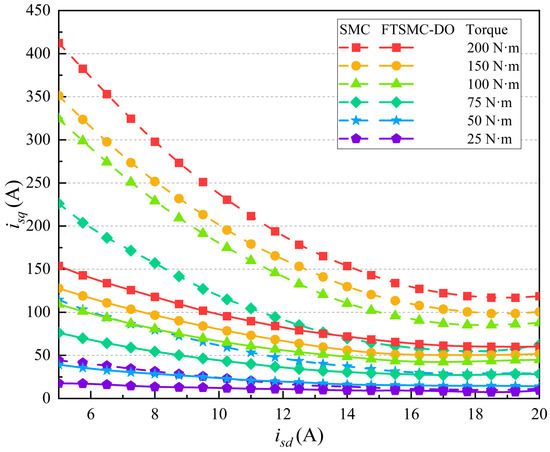
Figure 16.
The isd and isq curves required for different torques under n = 1000 r/min.
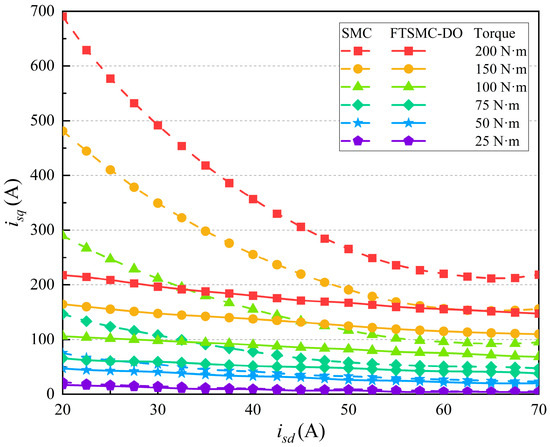
Figure 17.
The isd and isq curves required for different torques under n = 1400 r/min.
In summary, whether in terms of motor speed control or remote conductivity (EC) regulation, the FTSMC-DO model stands out as the optimal choice. This is attributed to its immunity to model errors and external disturbances, allowing for flexible adjustments of calibration parameters based on the motor’s operating states. The model enables the motor to output maximum torque under any given speed and current conditions, showcasing optimal torque-to-current ratio characteristics.
4. Conclusions
This study has successfully devised and validated a sophisticated control system tailored for asynchronous motors in fertigation machines. The primary focus was on enhancing dynamic performance and disturbance resistance, particularly in the face of remote, nonlinear conductivity disturbances. The proposed system seamlessly integrates an enhanced Internal Model Control with a Fractional-Order Sliding Mode Control with Disturbance Observer (FTSMC-DO), showcasing substantial advancements over conventional control methodologies such as PID and standard SMC.
The experimental findings underscore the superior performance of the FTSMC-DO approach in governing the speed and torque of asynchronous motors. Notably, it surpasses PID and SMC counterparts in achieving swift convergence to the set speed with minimal overshoot, particularly during start-up and sudden load changes. The adept handling of speed and load variations accentuates the control system’s viability for practical applications in agricultural irrigation systems.
Moreover, field tests conducted under diverse conditions validate the effectiveness of the FTSMC-DO system in regulating Electrical Conductivity (EC) levels in fertigation. The system exhibits remarkable precision in maintaining desired EC levels, minimizing fluctuations and overshoot, thus proving more efficient than traditional PID and SMC methods. This efficiency is paramount in ensuring optimal nutrient delivery and water usage in fertigation systems.
In conclusion, the FTSMC-DO control system, as developed in this research, represents a noteworthy advancement in agricultural automation. Its capacity to effectively navigate the intricacies of fertigation systems under diverse conditions underscores its potential for enhancing sustainable agricultural practices. The system’s robustness, precision, and adaptability position it as a valuable tool for farmers and agronomists striving to optimize irrigation and fertilization processes, ultimately contributing to increased crop yields and resource conservation. Furthermore, future research endeavors will focus on refining and expanding the application of the FTSMC-DO system to address evolving challenges in agricultural automation.
Author Contributions
Conceptualization, H.W., J.Z. and L.Z.; methodology, H.W.; software, J.Z. and L.Z.; validation, H.W., J.Z. and L.Z.; formal analysis, L.Z. and S.Y.; investigation, L.Z. and S.Y.; resources, L.Z. and S.Y.; data curation, H.W.; writing—original draft preparation, J.Z., H.W. and L.Z.; writing—review and editing, H.W. and L.Z.; visualization, H.W.; supervision, H.W.; project administration, L.Z.; funding acquisition, L.Z. and S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Major Science and Technology Special Projects in Xinjiang Uygur Autonomous Region, No. 2022A0201-4. This study was also supported by the National Natural Science Foundation of China, No. 52065055. This study was also supported by Xinjiang Agricultural Machinery R&D, Manufacturing, Promotion, and Application Integration Project, No. YTHSD2022 -03.
Data Availability Statement
All relevant data presented in the article are stored according to institutional requirements and, as such, are not available online. However, all data used in this manuscript can be made available upon request to the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fadiji, A.E.; Yadav, A.N.; Santoyo, G.; Babalola, O.O. Understanding the plant-microbe interactions in environments exposed to abiotic stresses: An overview. Microbiol. Res. 2023, 271, 127368. [Google Scholar] [CrossRef] [PubMed]
- Mainardis, M.; Cecconet, D.; Moretti, A.; Callegari, A.; Goi, D.; Freguia, S.; Capodaglio, A.G. Wastewater fertigation in agriculture: Issues and opportunities for improved water management and circular economy. Environ. Pollut. 2022, 296, 118755. [Google Scholar] [CrossRef] [PubMed]
- Li, H.R.; Mei, X.R.; Wang, J.D.; Huang, F.; Hao, W.P.; Li, B.G. Drip fertigation significantly increased crop yield, water productivity and nitrogen use efficiency with respect to traditional irrigation and fertilization practices: A meta-analysis in China. Agric. Water Manag. 2021, 244, 106534. [Google Scholar] [CrossRef]
- Anas, M.; Liao, F.; Verma, K.K.; Sarwar, M.A.; Mahmood, A.; Chen, Z.L.; Li, Q.; Zeng, X.P.; Liu, Y.; Li, Y.R. Fate of nitrogen in agriculture and environment: Agronomic, eco-physiological and molecular approaches to improve nitrogen use efficiency. Biol. Res. 2020, 53, 47. [Google Scholar] [CrossRef] [PubMed]
- Yue, H.; Meng, F.; An, S.; Hu, X.; Wang, Z.; Niu, M.; Beijing Agric Techn Extension Station (Beij-Non-Standard); Hebei Shuirun Jiahe Modern Agric Technol (HEBE-Non-Standard). Light Intelligent Water and Fertilizer Integrated Machine Fertilization Process Based on Machine Learning Includes Establishing Crop Parameter Model, Performing Machine Learning Parameter Control and Establishing Irrigation Decision. Patent CN112731994-A; CN214474676-U, 22 October 2021. [Google Scholar]
- Seokmin; Han, K.D.; Kwon, D.; SEVEN TREE CO LTD. (SEVE-Non-standard), assignee. Unmanned Irrigation and Fertilization System for Automatically Supplying Water and Fertilizer to Soil, Has Control Unit That Con-trols Irrigation Unit and Fertilizer Unit to Perform Irrigation and Fertilizer When Predicted Value of Vegetation Index Is Lower. Patent KR2350450-B1, 25 May 2000. [Google Scholar]
- Darrhal, N.; Houssa, A.A.; Dhassi, K.; Amlal, F.; Ouichou, A.; Mounsif, M.; Drissi, S. Nutrient Status of Forage Corn (Zea mays L.) and Fodder Beet (Beta vulgaris L.) Irrigated with Saline Water. Commun. Soil Sci. Plant Anal. 2022, 53, 2734–2748. [Google Scholar] [CrossRef]
- Colque, R.; Romaniuk, R.; Arias, P.; Castiglioni, M. Rotación de cultivos en la producción de tabaco: Efecto sobre algunas propiedades edáficas. Cienc. Del Suelo 2021, 39, 127–143. [Google Scholar]
- Chernykh, A.G.; IOP. Use of centrifugal pumps with canned asynchronous motors in irrigation systems. In Proceedings of the International Conference on Engineering Studies and Cooperation in Global Agricultural Production, Azov Black Sea Engn Inst Zernograd, Zernograd, Russia, 27–28 August 2020. [Google Scholar]
- Yang, Y.; Xiao, C.; Zhang, Y.; Zhang, R.; Ji, L.; Li, P.; Zhangjiakou Acad Agric Sci Hebei Res Ins (Zhan-Non-Standard); Zhangjiakou Sansheng Intelligent Agric (Zhan-Non-Standard), assignee. Intelligent Irrigation and Fertilization Decision System Based on Soil Moisture Content Monitoring, Has Soil Ec Sensor That Monitor Soluble Salt Concentration of Soil, Where Soil Nitrogen-Phosphorus-Potassium Sensor Monitors Nitro-gen-Phosphorus-Potassium Content of the Soil. Patent CN117016358-A, 10 November 2023. [Google Scholar]
- Niedda, M.; Pirastru, M. Field investigation and modelling of coupled stream discharge and shallow water-table dynamics in a small Mediterranean catchment (Sardinia). Hydrol. Process. 2014, 28, 5423–5435. [Google Scholar] [CrossRef]
- Wu, H.; Gao, F.; Niu, M.; Li, J.; Xue, G.; Gu, C.; Wu, H.; Modern Agric Equip Co Ltd. (Mode-Non-Standard); Chinese Acad Agric Mechanization Sci (Chnm-C), assignee. Method for Adjusting Ec-Ph Balance of Fertilizing Machine in Water-Saving Irrigation Field, Involves Injecting Mother Liquid According to Acid Liquid Amount or Alkali Liquid Amount and Mixing with Raw Water to Obtain Balanced and Adjusted Fertilizer Water to Output Continuously. Patent CN115500133-A; CN115500133-B, 23 December 2022. [Google Scholar]
- Yang, G.; He, N.; Dalian Lingkong Data Technology Co Ltd. (DALI-Non-standard); SUZHOU DATATELLIT INFORMATION TECHNOLOGY (SUZH-Non-standard), assignee. Ph-Ec Sensor for Use in Water Culture System for Monitoring Ph Value and Ec Value of Water Quality of Plant, Water Storage Part Set in Shell, Measuring Part, Cleaning Part and Drying Part, and Control Part for Controlling Matching Action of Them Sequentially. Patent CN116087292-A, 9 May 2023. [Google Scholar]
- Mabitazan, M.B.; Mabitazan, R.C.; Univ Saint Louis Inc. (UYSL-Non-standard), assignee. Automated Closed Hydroponic System for Monitoring Ph and Electrical Conductivity (Ec) of Nutrient Solution for Plant Cultivation, Has Nutrient Uptake Analysis Conducted to Determine Plant Nutritional Status to Make Sure That Plants Are Taking up Nutrient Balance They Require. Patent PH12021050463-A1, 17 January 2020. [Google Scholar]
- Wang, H.; Zhang, L.X.; Zhao, J.W.; Hu, X.; Ma, X. Application of Hyperspectral Technology Combined with Genetic Algorithm to Optimize Convolution Long- and Short-Memory Hybrid Neural Network Model in Soil Moisture and Organic Matter. Appl. Sci. 2022, 12, 10333. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, R.; Fan, J.; Univ Shihezi (Ushz-C), assignee. Cotton Field Drip Irrigation Water Fertilizer Electrical Conductivity (Ec) Value Adjusting and Fertilizing Control System, Has Ec Sensor That Is Installed on Outer Pipeline of Mixing Tank for Measuring Ec Value Mass Concentration, and Control Cabinet Power Switch That Is In-stalled in Control Cabinet. Patent CN113366957-A, 10 September 2021. [Google Scholar]
- Zhang, W.; Li, L.; Hu, J.; Kexin Tianjin Ecological Agric Technolog (KEXI-Non-standard), assignee. System for Controlling Water Fertilizer Machine, Has Fertilizer Proportioning Module for Proportioning Mul-tiple Fertilizers, and Irrigation Plan Module for Selecting Irrigation Mode and Irrigation Type According to Partition. Patent CN115525083-A, 29 September 2022. [Google Scholar]
- Ahmad, I.; Yan, Z.A.; Kamran, M.; Ikram, K.; Ghani, M.U.; Hou, F.J. Nitrogen management and supplemental irrigation affected greenhouse gas emissions, yield and nutritional quality of fodder maize in an arid region. Agric. Water Manag. 2022, 269, 107650. [Google Scholar] [CrossRef]
- Zhu, F.L.; Zhang, L.X.; Hu, X.; Zhao, J.W.; Meng, Z.H.; Zheng, Y. Research and Design of Hybrid Optimized Backpropagation (BP) Neural Network PID Algorithm for Integrated Water and Fertilizer Precision Fertilization Control System for Field Crops. Agronomy 2023, 13, 1423. [Google Scholar] [CrossRef]
- Ali, K.; Cao, Z.W.; Rsetam, K.; Man, Z.H. Practical Adaptive Fast Terminal Sliding Mode Control for Servo Motors. Actuators 2023, 12, 433. [Google Scholar] [CrossRef]
- Maraveas, C.; Karavas, C.S.; Loukatos, D.; Bartzanas, T.; Arvanitis, K.G.; Symeonaki, E. Agricultural Greenhouses: Resource Management Technologies and Perspectives for Zero Greenhouse Gas Emissions. Agriculture 2023, 13, 1464. [Google Scholar] [CrossRef]
- Glaser, D.R.; Barrowes, B.E.; Shubitidze, F.; Slater, L.D. Laboratory investigation of high-frequency electromagnetic induction measurements for macro-scale relaxation signatures. Geophys. J. Int. 2023, 235, 1274–1291. [Google Scholar] [CrossRef]
- Kataria, N.; Singh, N. Role of Potassium on Growth, Nitrogen Fixation and Biochemical Traits in Vigna radiata Wilczek under Water Stress. Legume Res. 2022, 45, 719–726. [Google Scholar] [CrossRef]
- Song, X.H.; Li, H.; Chen, C.; Xia, H.M.; Zhang, Z.Y.; Tang, P. Design and Experimental Testing of a Control System for a Solid-Fertilizer-Dissolving Device Based on Fuzzy PID. Agriculture 2022, 12, 1382. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Chen, C.; Li, H.; Xia, H.M. Design and Evaluation of A Control System for The Fertigation Device. J. Asabe 2022, 65, 1293–1302. [Google Scholar] [CrossRef]
- Jia, Z.F.; Zhuang, P.D. IntelligentWater and Fertilizer System Based on NB-IoT. In Proceedings of the 10th International Conference on Communications, Signal Processing, and Systems, Electr Network, Chang Bai Shan, China, 21–22 August 2021; pp. 533–540. [Google Scholar]
- Gao, P.C.; Yang, P.H. Research on Speed Control of Three-Phase Alternating Current Asynchronous Motor Based on Back Propagation Neural Network Tuning Proportion Integration Differentiation Control. J. Nanoelectron. Optoelectron. 2022, 17, 958–966. [Google Scholar] [CrossRef]
- Novotnak, J.; Oravec, M.; Hijj, J.; Jurc, D.; IEEE. Slip Control by Identifying the Magnetic Field of the Elements of an Asynchronous Motor. In Proceedings of the 19th IEEE World Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 21–23 January 2021; pp. 273–277. [Google Scholar]
- Rybak, T.Y.; Solovyev, D.S.; Popov, E.A.; Tyagovye Komponenty Llc. (Tyag-Non-Standard); Russian Electric Motors Stock Co. (RUEL-Non-standard), assignee. Rotor for an Asynchronous Traction Motor, Com-Prises a Winding of Short-Circuited Single-Turn Coils of Copper Tape That Includes a Core with Ventilation Channels, and the Shaft of Landing Cones for Installing Small Gear Wheels. Patent RU203517-U1, 30 December 2020. [Google Scholar]
- Wentao, S.; Kun, L. SMC-FUZZY Joint Vector Control of Built-in Permanent Magnet Synchronous Motorized Spindle. J. Mech. Eng. 2022, 58, 177–185. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).