Modeling and Application of Temporal Correlation of Grain Temperature during Grain Storage
Abstract
1. Introduction
2. Data and Methods
2.1. Grain Temperature Data Collection and Processing
2.1.1. Data Collection
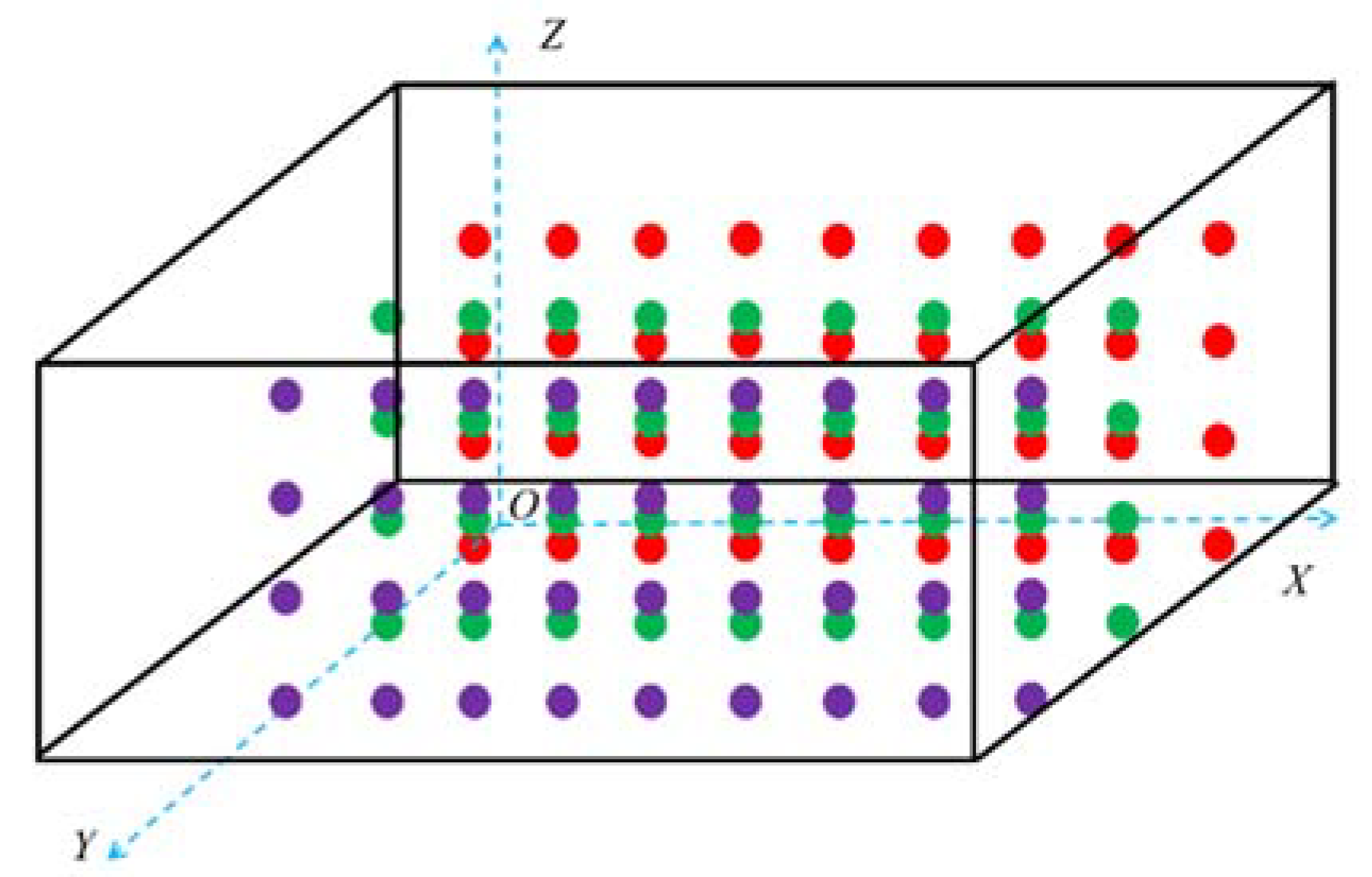
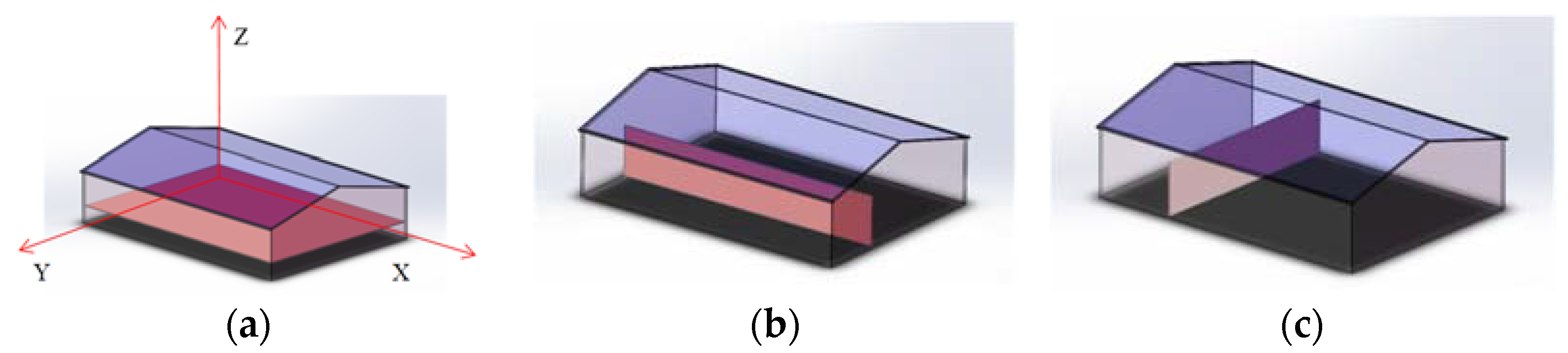
2.1.2. Grain Temperature Plane Composition
2.1.3. Grain Temperature Data Preprocessing
2.2. Research Methods
2.2.1. Time Correlation Calculation Method for Plane Grain Temperature
2.2.2. Correlation Coefficient Preprocessing
2.2.3. Threshold Setting Method
- (1)
- Threshold Setting Method Based on DBSCAN Clustering
- (2)
- 3σ-Threshold-Based Setting Method
2.2.4. Model Building Method and Environment
2.2.5. Relevance Rating
2.2.6. Evaluation of the Model Index
3. Results and Discussion
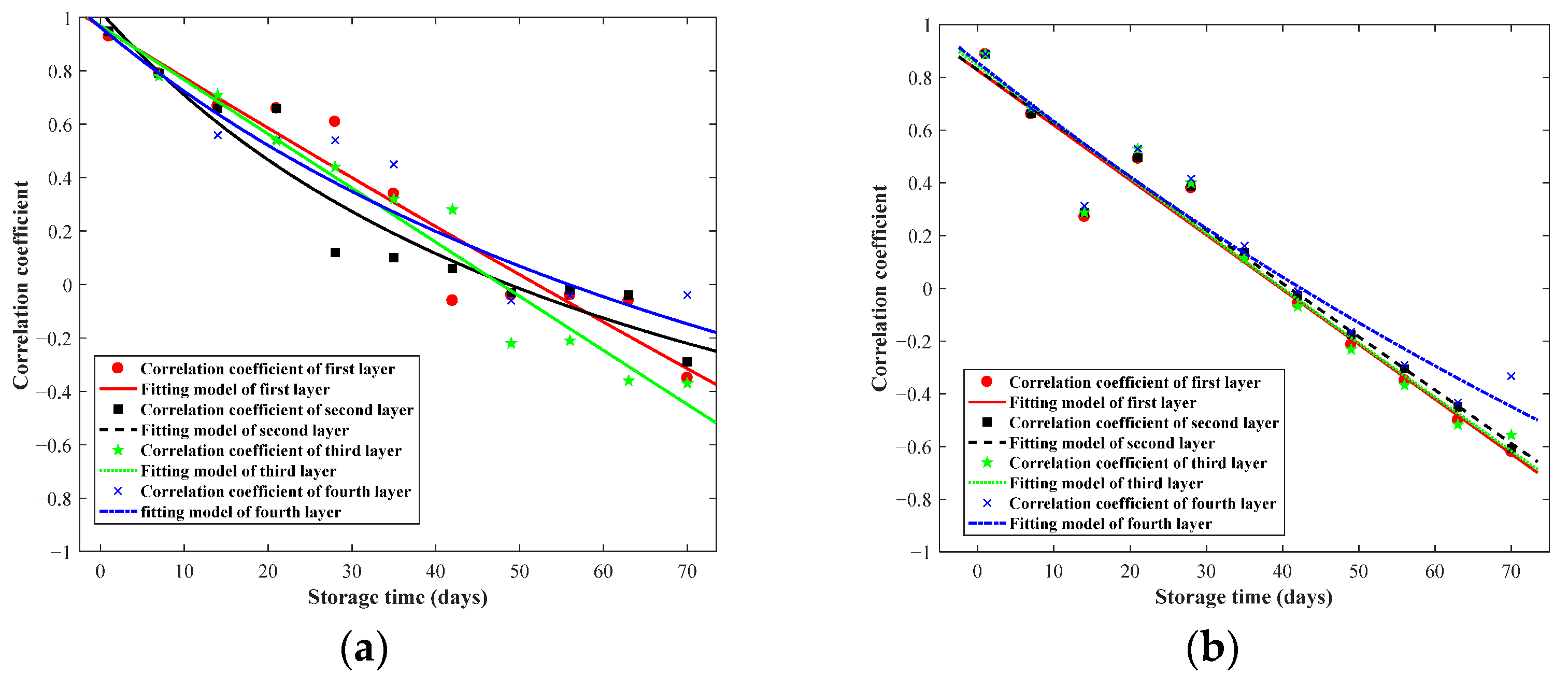
3.1. Mode of Correlation Coefficient Threshold
3.1.1. Models of Grain Temperature Correlation Coefficient Threshold on the XOY Plane
3.1.2. Models of Grain Temperature Correlation Coefficient Threshold on the XOZ Plane
3.1.3. Models of Grain Temperature Correlation Coefficient Threshold on the YOZ Plane
3.1.4. Evaluation of Threshold Setting Method
3.2. Discussion
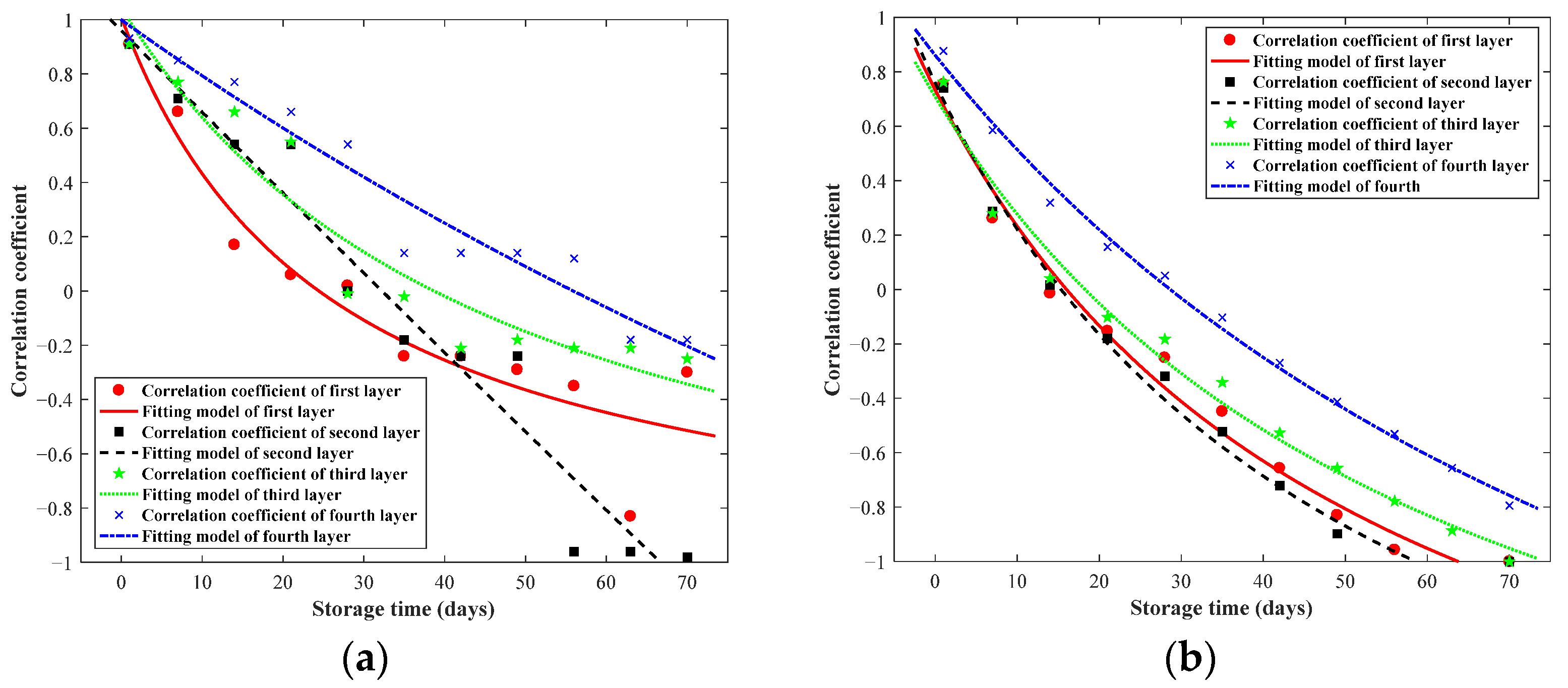
3.2.1. Influence of Empty Warehouse on Temperature Correlation
3.2.2. Influence of New Grain on Temperature Correlation
3.2.3. Influence of Aeration Operation on Temperature Correlation
3.2.4. Influence of Self-Heating on Temperature Correlation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wenhao, L. Research on Key Technologies of Internet of Things for Grain Monitoring and Control Based on Wireless Communication. Ph.D. Thesis, Henan University of Technology, Zhengzhou, China, 2017. [Google Scholar]
- Jingjing, B. Remote Monitoring and Early Warning of Fungus in Granary. Ph.D. Thesis, Henan University of Technology, Zhengzhou, China, 2019. [Google Scholar]
- Xiaomeng, W.; Wenfu, W.; Jun, Y.; ZhongJie, Z.; Zidan, W.; Qu, Y. Analysis of wheat bulk mould and temperature-humidity coupling based on temperature and humidity field cloud map. Trans. Chin. Soc. Agric. Eng. 2018, 34, 260–266. [Google Scholar]
- Xiaomeng, W.; Wenfu, W.; Jun, Y.; Zhongjie, Z.; Zidan, W.; Hongqing, Z. Research on temperature and humidity field change during corn bulk microbiological heating. Trans. Chin. Soc. Agric. Eng. 2019, 35, 268–273. [Google Scholar]
- Hongyang, G.; Xiaoping, H. Regional layout of China’s government grain reserves: Present situation, impact and optimization path. J. Huazhong Agric. Univ. 2021, 6, 27–34+187. [Google Scholar]
- Pingyuan, L.; Hong, J.; Qingfeng, F.; Weike, L. Discussion on the monitoring method of grain quality and safety and its effectiveness and timeliness. Grain Sci. Technol. Econ. 2017, 42, 18–20. [Google Scholar]
- Ling, L. Legislative proposals on improving the supervision & management mechanism of China grain reserves. J. Henan Univ. Technol. 2015, 11, 49–52. [Google Scholar]
- Xuecang, Z.; Pingfei, G.; Tong, Z.; Jianjun, W. Development and prospect of multifunctional grain condition measurement and control system. Grain Process. 2018, 43, 68–71. [Google Scholar]
- Panigrahi, S.S.; Singh, C.B.; Fielke, J.; Dariush, Z. Modeling of heat and mass transfer within the grain storage ecosystem using numerical methods: A review. Dry. Technol. 2019, 38, 1677–1697. [Google Scholar] [CrossRef]
- Quemada-Villagómez, L.I.; Molina-Herrera, F.I.; Carrera-Rodríguez, M.; Calderón-Ramírez, M.; Martínez-González, G.M.; Navarrete-Bolaños, J.L.; Jiménez-Islas, H. Numerical study to predict temperature and moisture profiles in unventilated grain silos at prolonged time periods. Int. J. Thermophys. 2020, 41, 52. [Google Scholar] [CrossRef]
- Novoa-Muñoz, F. Simulation of the temperature of barley during its storage in cylindrical silos. Math. Comput. Simul. 2018, 157, 1–14. [Google Scholar] [CrossRef]
- Qinqin, C.; Yang, L.; Xiaoliang, L.; Wangbao, W.; Hui, P.; Rong, J.; Qingye, S. Variation in paddy microbial communities under different storage temperatures and relative humidity. Food Res. Int. 2019, 126, 108581. [Google Scholar]
- Libing, J.; Yaqi, X.; Xinya, L.; Zhen, W. Numerical simulation and experimental study on temperature field of underground grain storage bin. J. Henan Univ. Technol. 2019, 40, 120–125. [Google Scholar]
- Mengmeng, G.; Guixiang, C.; Wenlei, L.; Chaosai, L. Simulation of Temperature Field of Paddy Grain Pile in Static Storage Based on COMSOL. J. Henan Univ. Technol. 2020, 41, 101–105. [Google Scholar]
- Chunyun, M. Study on the Numerical Simulation and Regularity of the Heat and Humidity Field of Corn Grain Piles without Artificial Intervention; Shenyang Normal University: Shenyang, China, 2017. [Google Scholar]
- Xiangxiang, Z.; Hao, Z.; Zhenqing, W.; Xi, C.; Yan, C. Study on temperature field of grain piles in underground grain silos lined with plastic. Trans. Chin. Soc. Agric. Eng. 2021, 37, 8–14, (Chinese with English Abstract). [Google Scholar]
- Mengmeng, G. Study on the Coupled Law of Heat and Moisture in the Ventilation Process of Bulk Wheat Grain Pile. Ph.D. Thesis, Henan University of Technology, Zhengzhou, China, 2021. [Google Scholar]
- Dexian, Z.; Miao, Z.; Qinghui, Z.; Yuan, Z. Granary storage quantity detection method based on bottom pressure estimation. Trans. Chin. Soc. Agric. Eng. 2017, 33, 287–294, (In Chinese with English Abstract). [Google Scholar]
- Zidan, W.; Qiang, Z.; Jun, Y.; Xiaomeng, W.; Zhongjie, Z.; Wenfu, W.; Fujun, L. Interactions of multiple biological fields in stored grain ecosystems. Sci. Rep. 2020, 10, 9302. [Google Scholar]
- Hongwei, C.; Wenfu, W.; Zidan, W.; Feng, H.; Jianpeng, D.; Yujia, W. Monitoring method of stored grain quantity based on temperature field cloud maps. Trans. Chin. Soc. Agric. Eng. 2019, 35, 296–298. [Google Scholar]
- Hongwei, C.; Wenfu, W.; Zidan, W.; Feng, H.; Haotian, Z.; Xiao, Q. Reserves monitoring method for grain storage based on temporal and spatial correlation of grain temperature. Trans. Chin. Soc. Agric. Mach. 2019, 50, 321–330. [Google Scholar]
- Xiao, Q. Research on the Strategies and Methods of Storing Grain Digital Supervision. Ph.D. Thesis, Jilin University, Changchun, China, 2018. [Google Scholar]
- Haotian, Z. Feature Extraction of Storage Grain Nephogram and Application of Supervision Method. Ph.D. Thesis, Jilin University, Changchun, China, 2019. [Google Scholar]
- Hongwei, C.; Wenfu, W.; Zidan, W.; Tianyi, L.; Jianpeng, D. Method to detect granary state based on statistical characteristics of grain temperature. Trans. Chin. Soc. Agric. Eng. 2020, 36, 320–330. [Google Scholar]
- Zhenfang, H.; Yuxia, Z.; Yang, C.; Dongfang, L.; Tong, Z.; Pengcheng, F.; Jianjun, W. Statistical character on temporal and spatial distributing of grain temperature in warehouse. Grain Storage 2010, 39, 15–20. [Google Scholar]
- Zhenqing, W.; Dongjie, T.; Haiyan, L. Experimental study on temperature field of underground reinforced concrete circular granary. J. Henan Univ. Technol. 2018, 39, 99–102, 126. [Google Scholar]
- Ruonan, L.; Yizhong, X.; Yan, L. Dynamic signature verification method based on Pearson correlation coefficient. J. Instrum. 2022, 43, 279–287. [Google Scholar]
- Akoglu, H. User’s guide to correlation coefficients. Turk. J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef] [PubMed]
- Martin, E.; Hans-Peter, K.; Sander, J.; Xiaowei, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96), Portland, OR, USA, 2–4 August 1996; AAAI Press: Santa Clara, CA, USA; pp. 226–231. [Google Scholar]
- Weitun, W.; Yileh, W.; Chengyuan, T.; Mawkae, H. Adaptive density-based spatial clustering of applications with noise (DBSCAN) according to data. In Proceedings of the 2015 International Conference on Machine Learning and Cybernetics (ICMLC), Guangzhou, China, 12–15 July 2015; IEEE: Piscataway Township, NJ, USA; Volume 1, pp. 445–451. [Google Scholar]
- Xu, R.; Wunsch, D. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef] [PubMed]
- Jianbin, H.; Jianmei, K.; Junjie, Q.; Heli, S. A hierarchical clustering method based on a dynamic synchronization model. Inf. Sci. 2013, 43, 599–610. [Google Scholar]
- Jing, L.; Jinqiu, H. A study of adaptive composite-indicator alarm threshold optimization of chemical process parameters. Pet. Sci. Bull. 2016, 1, 407–416. [Google Scholar]
- Hongwei, C.; Wenfu, W.; Zhongjie, Z.; Feng, H.; Zhe, L. Clustering and application of grain temperature statistical parameters based on the DBSCAN algorithm. J. Stored Prod. Res. 2021, 93, 101819. [Google Scholar]




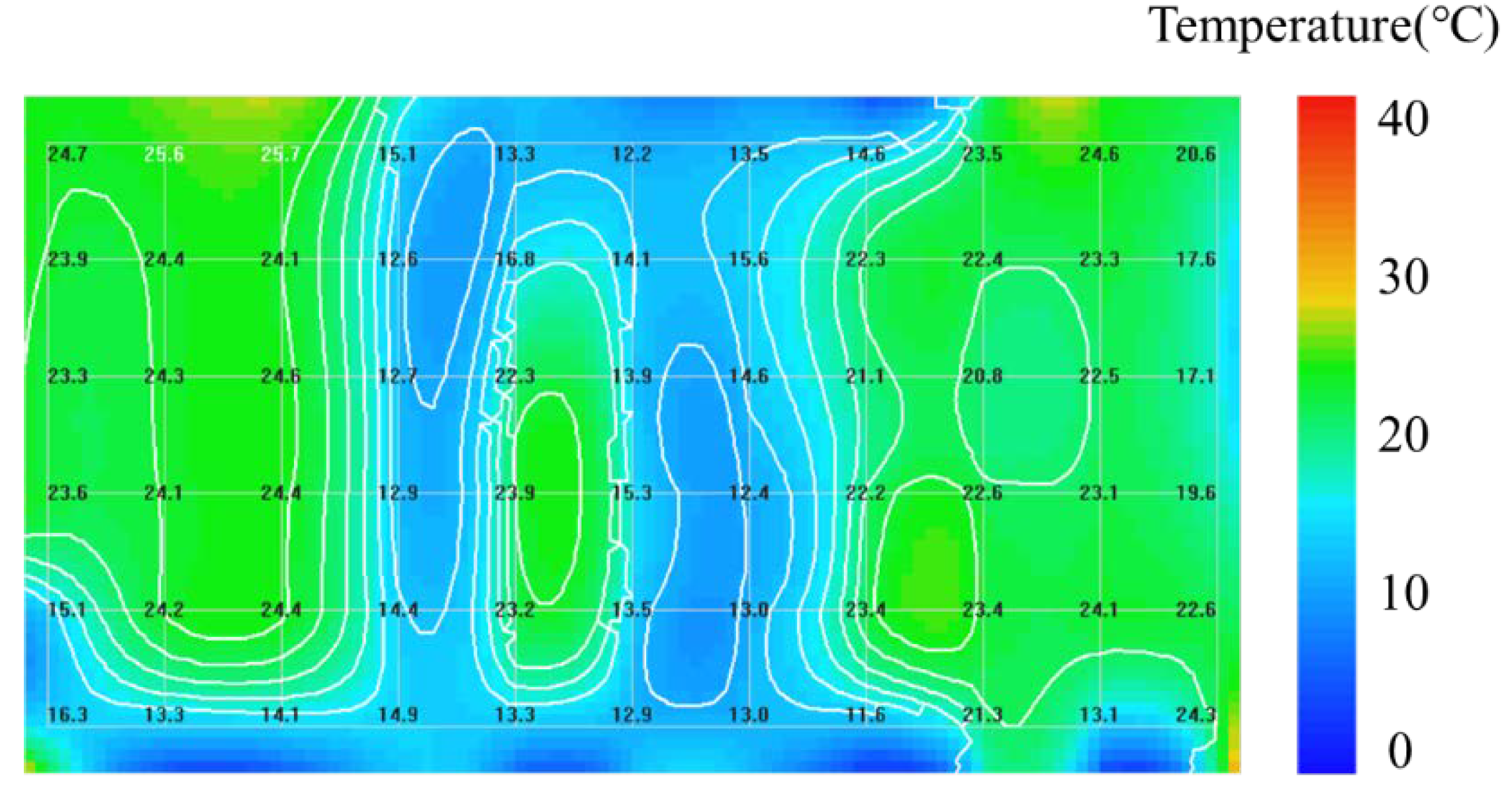
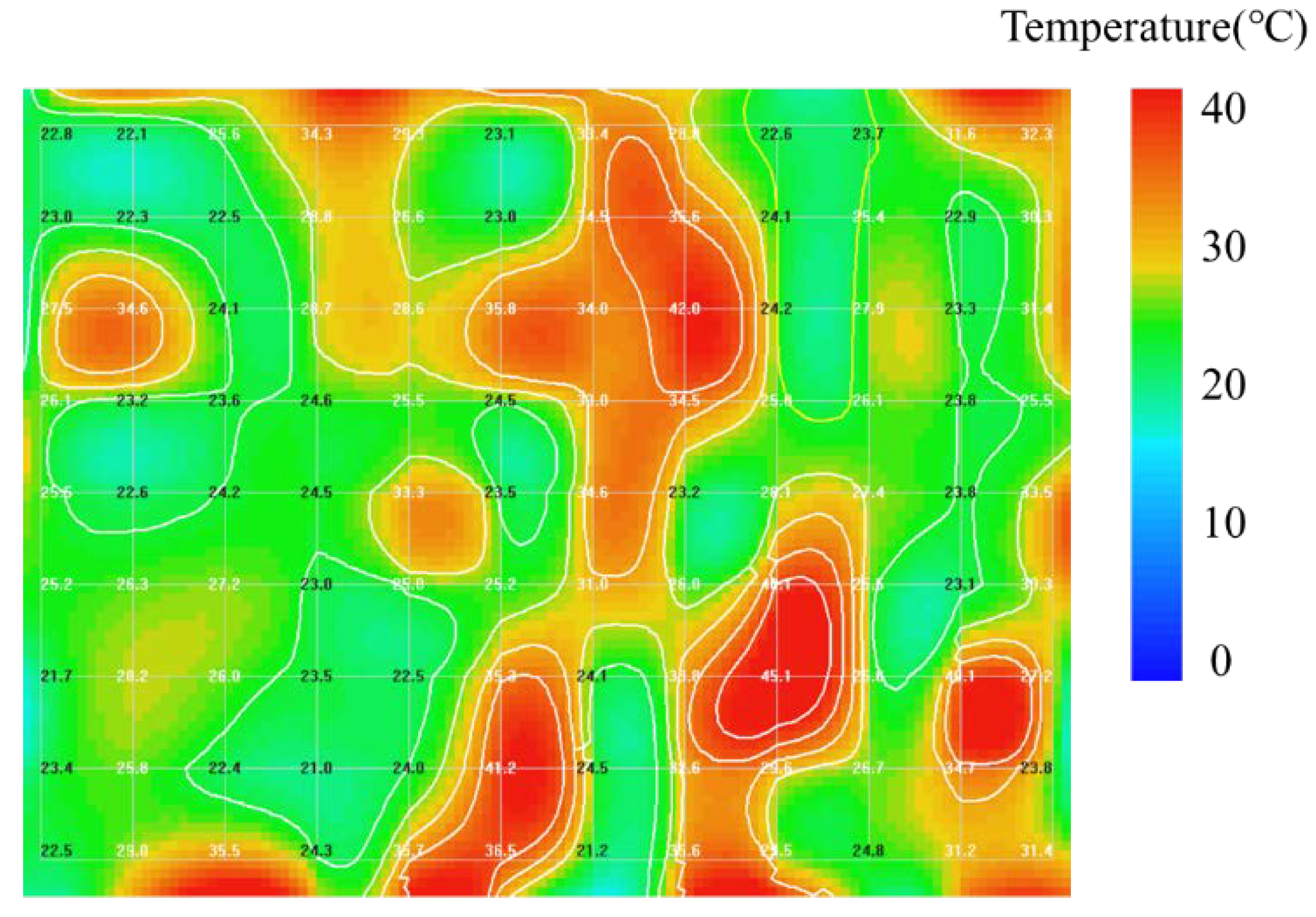
| Ranges | Levels |
|---|---|
| 0.8~1.0 | Extremely strong correlation |
| 0.6~0.8 | Strong correlation |
| <0.6 | Weak correlation or no correlation |
| Layers | DBSCAN | 3σ | ||||
|---|---|---|---|---|---|---|
| p1 | P2 | q1 | p1 | P2 | q1 | |
| First Layer | −780.2 | 39,970 | 39,860 | −44.64 | 1784 | 2188 |
| Second Layer | −17.46 | 840.4 | 849.6 | −120.3 | 5012 | 5715 |
| Third Layer | −23.89 | 1163 | 1190 | −309.1 | 13,260 | 15,480 |
| Fourth Layer | −0.74 | 37.27 | 35.14 | −4.34 | 201.9 | 232.7 |
| Planes | DBSCAN | 3 | ||||
|---|---|---|---|---|---|---|
| p1 | P2 | q1 | p1 | P2 | q1 | |
| First Layer | −23.15 | 1206 | 1247 | −984.3 | 39,150 | 47,330 |
| Second Layer | −1.44 | 69.99 | 68.37 | −1038 | 42,470 | 51,250 |
| Third Layer | −893 | 42,710 | 44,040 | −49.98 | 1998 | 2362 |
| Fourth Layer | −1.85 | 103.1 | 106.9 | −5.81 | 246.5 | 287.5 |
| Planes | DBSCAN | 3 | ||||
|---|---|---|---|---|---|---|
| p1 | P2 | q1 | p1 | P2 | q1 | |
| First Layer | −1.09 | 26.58 | 26.36 | −2.46 | 39.27 | 53.48 |
| Second Layer | −75.52 | 2435 | 2538 | −2.55 | 39.08 | 51.47 |
| Third Layer | −1.29 | 49.85 | 47.75 | −2.45 | 44.66 | 63.06 |
| Fourth Layer | −5.22 | 291.8 | 292.2 | −3.28 | 93.95 | 109.1 |
| Planes | DBSCAN | 3 | ||||
|---|---|---|---|---|---|---|
| SSE | R2 | RMSE | SSE | R2 | RMSE | |
| XOY Planes | 0.1282 | 0.9323 | 0.1223 | 0.0080 | 0.9961 | 0.0314 |
| XOZ Planes | 0.1209 | 0.9306 | 0.1222 | 0.1132 | 0.9496 | 0.1188 |
| YOZ Planes | 0.1723 | 0.9332 | 0.1444 | 0.0467 | 0.9857 | 0.0742 |
| Means | 0.1405 | 0.9320 | 0.1296 | 0.0560 | 0.9771 | 0.0748 |
| XOY Planes | 20 March 2017 and 20 April 2017 | 20 March 2017 and 20 May 2017 |
|---|---|---|
| First Layer | 0.133 | −0.184 |
| Second Layer | 0.001 | −0.193 |
| Third Layer | −0.086 | −0.257 |
| Fourth Layer | −0.113 | 0.322 |
| XOY Planes | 17 July 2017 and 17 August 2017 | 17 July 2017 and 28 September 2017 |
|---|---|---|
| First Layer | −0.216 | 0.095 |
| Second Layer | −0.147 | −0.324 |
| Third Layer | −0.067 | −0.113 |
| Fourth Layer | 0.334 | 0.357 |
| XOY Planes | 21 September 2017 and 20 October 2017 | 21 September 2017 and 31 October 2017 |
|---|---|---|
| First Layer | 0.176 | 0.711 |
| Second Layer | −0.007 | 0.068 |
| Third Layer | 0.048 | 0.067 |
| Fourth Layer | −0.015 | 0.064 |
| XOY Planes | 20 July 2018 and 20 August 2018 | 20 July 2018 and 20 September 2018 |
|---|---|---|
| First Layer | 0.234 | 0.574 |
| Second Layer | 0.149 | 0.186 |
| Third Layer | 0.974 | 0.911 |
| Fourth Layer | 0.975 | 0.946 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, H.; Zhang, Q.; Wu, W.; Zhang, H.; Ji, J.; Ma, H. Modeling and Application of Temporal Correlation of Grain Temperature during Grain Storage. Agriculture 2022, 12, 1883. https://doi.org/10.3390/agriculture12111883
Cui H, Zhang Q, Wu W, Zhang H, Ji J, Ma H. Modeling and Application of Temporal Correlation of Grain Temperature during Grain Storage. Agriculture. 2022; 12(11):1883. https://doi.org/10.3390/agriculture12111883
Chicago/Turabian StyleCui, Hongwei, Qu Zhang, Wenfu Wu, Haolei Zhang, Jiangtao Ji, and Hao Ma. 2022. "Modeling and Application of Temporal Correlation of Grain Temperature during Grain Storage" Agriculture 12, no. 11: 1883. https://doi.org/10.3390/agriculture12111883
APA StyleCui, H., Zhang, Q., Wu, W., Zhang, H., Ji, J., & Ma, H. (2022). Modeling and Application of Temporal Correlation of Grain Temperature during Grain Storage. Agriculture, 12(11), 1883. https://doi.org/10.3390/agriculture12111883







