Abstract
In this paper, we extend the analysis of farm structural change with respect to farm specialisation, size and exit in Norway by, first, explicitly incorporating the location information of farms generating a number of neighbouring farms within a certain range and, second, by predicting farm numbers in addition to farm group shares, which allows for consideration of the exit farm group. We use Norwegian single-farm full census data for the period 1996–2015. Four production specialisations and seven size classes represent farm groups, as well as a residual and an exit farm group at the regional level. The estimates indicate the explanatory power and importance of aggregated farm location information in the model. Simulation analysis showed that the farm groups develop differently, given a change in the number of neighbouring farms with respect to the farm numbers and farm group shares.
1. Introduction
(This article is based on two conference papers. First, by Neuenfeldt, S., Rieger, J., Heckelei, T, Gocht, A. Ciaian, P. and Tetteh, G. (2018): A multiplicative competitive interaction model to explain structural change along farm specialisation, size and exit/entry using Norwegian farm census data. Paper for IAAE Conference 2018, Vancouver, 28 July–2 August 2018. Vancouver: IAAE, 20p. doi:10.22004/ag.econ.277090). Second, a thus far unpublished paper by Neuenfeldt, S., Gocht, A., Heckelei, T. and Ciaian, P. (2021): Using Aggregated Farm Location Information to Predict Regional Structural Change Of Farm Specialization, Size And Ex-it/Entry in Norway Agriculture. Paper for EAAE Conference 2021, Prague).
Norway, as with many other industrialised countries, went through substantial structural changes in the agricultural sector, reflected in the declining number of farms, farm size growth and production re-specialisation over time. A better understanding of the drivers of these past structural changes, particularly of the farmers’ exit decisions, will help in projecting future developments and has significant policy implications on the national and international levels.
Today, agriculture in Norway is dominated by grass-based dairy farming, beef and sheep production and, to some extent, spring and winter cereals for bread or animal feed, mainly in the southern regions [1]. The agricultural structure is rather small-scale, with a total number of 42,018 farms in 2015, with an average farm size of 23.5 ha [2]. The total agricultural area in 2015 was 0.986 million hectares, which corresponds to 2.7% of the country’s total land area. Norwegian agriculture is, hence, dominated by very small farms, compared to the rest of Europe where farming has been rationalised into much larger units, thereby, improving the structural efficiency of agriculture. This structural development partly results from one of the most strongly state regulated agricultural sectors in Europe [3].
Compared to other countries, the Norwegian farming sector is heavily dependent on governmental support measures, as more than the half of farm income is related to market price support and subsidies [4]. Agricultural policy measures are negotiated between the Norwegian government and the farmers’ organisations on a yearly basis. Therefore, the payment rates that differ by region and farm size can change every year, potentially affecting the structure of the Norwegian agricultural sector over time [1].
The literature offers a multitude of additional determinants to explain structural changes in Norway, which are also in line with findings in other countries, including technology (economies of scale, productivity growth, farm household and path dependency), input and output prices and macroeconomic conditions (e.g., the unemployment rate), regional characteristics, agricultural policies and competitive pressures from non-agricultural sectors for resources (e.g., [5,6,7,8,9,10,11]).
Natural and climate conditions are important determinants of agricultural specialisation across regions. For instance, the growing degree days and altitude are related to land-use changes [12] and elevation and steepness [13]. Mandryk et al. [14] gave a short overview of the literature that indicated climate change as a cause of structural changes. Climate change refers to changes in the climatic conditions or climate variability that affects crop productivity, yields, farmer income and land use [15,16,17,18,19,20].
Important drivers in Norway include techno-economic development (economies of scale) and a reduced compensation to smaller farmers since the 1990s [3], as well as the fact that farm types are differently affected, such that farms with breeding stock, primarily sheep and dairy cattle, are more likely to continue farming [21].
The importance of incorporating spatial patterns or neighbouring effects has become apparent in recent years. Storm et al. [22] showed the importance of direct payments and of farm size for structural change in Norway and highlighted the importance of farm interaction for strategic farm decisions due to the competition over land causing regional specific patterns and spatial dependencies. Additional recent work using a spatial framework highlighted the spill-over effects in farm specification activities and indicated cooperation and competition between farms that affects the adoption of diversification activities [23] in Europe.
Vroege et al. [23] also concluded that spatially proximate farms are not independent of each other and that different degrees of proximity matter. Similarly, Saint-Cyr et al. [24] highlighted the substantial variation between farm types with respect to neighbouring effects and spatial patterns in Brittany. Neighbouring effects have often been analysed based on farm characteristics of farmer decisions [25,26,27]. Adoption decisions as social norms and attitudes [28] and access to information—direct and through the neighbourhood—and social conformity [29] show the importance of farmer interactions. Roberts et al. [30] showed that transactions between farm households also depended on their local economies.
Even though farm activity diversification related to off-farm or non-agricultural activities is difficult to quantify with the available statistics, some work on this topic has also incorporated spatial patterns and neighbouring effects. Among others, a case study in Eastern Germany revealed that diversification in terms of touristic development was more prone to farms in rural areas, and the continuation of farming increased with closer proximity to urban consumer markets [31]. Such income diversification strategies appear to be a possible direction for farms in the future as a survival strategy [32]. Focusing on efficiency, Schneider et al. [33] and Skevas and Lansink [34] also indicated the existence of neighbouring effects on arable and dairy farms in Dutch agriculture.
Studies focused on the relevant determinants for exit decisions have shown that smaller farms [35,36,37,38], lower profitability [39,40] and older farmers or farms with no successor are associated with a higher likelihood of exit [35,40,41,42,43,44,45] as are spatial effects. In addition, a high population density can either increase [37] or decrease [46] the exit rates for farmers. The decoupling of subsidies from production seemed to accelerate the exit of livestock production farms and of farms that were already in the process of leaving the sector [47].
Recent research also highlighted the fact that exit rates appear to be differently influenced by the farm size or farm holder’s age with regard to different farm types [24]. Breustedt and Glauben [36] and Goetz and Debertin [48] argued that farm profitability is increased by farm support and that this reduces farm exits. Among other determinants, Foltz [49] demonstrated that, for the Connecticut dairy industry, higher prices, lower lending rates, higher unemployment and lower population density increased the probability to stay in business.
Rather than being a result, structural change (i.e., change in the type of farming) is also seen as a driver that influences farm income distribution [50]. Most of the studies thus far reviewed have focused either on a subpopulation of farms or on a specific set of determinants to explain structural change. A comprehensive theoretical framework accounting for all major drivers of structural adjustment in agriculture, including farmers’ exit decisions and accounting for all specialisation and spill-over effects between the farm population, has not been considered.
A promising strand of analysing farm structural change has been developed by using Multiplicative Competitive Interaction (MCI) models, which analyse the heterogeneous economic and social behaviour of farm groups at the regional level [51]. The models have been applied to the farm accountancy data network (FADN) in Europe to analyse structural change with respect to the development of farm group shares, i.e., farm specialisations and size classes as farm typology, over time at the NUTS2 regional level. (The NUTS classification subdivides the economic territory of the EU Member States into territorial units (regions) […]. The classification is made up of three hierarchical levels: each Member State is divided into so-called NUTS 1 regions, which in turn are subdivided into NUTS 2 regions and then divided further into NUTS 3 regions. (European Union, 2015: 4–5)).
This farm typology was representative of the FADN regions, usually in a similar manner to that of the NUTS2 regions in the EU. The approach has major drawbacks, which make direct use of the results for policy assessment on determinants of structural change and the use for EU impact assessment models, such as CAPRI [52] or IFM-CAP [53], difficult. The evolution of the total number of farms, required to identify the actual number of farms in a farm group, affected by structural change is missing.
The MCI approach operates on shares of farm groups over time and does not provide estimates on the total farm number of each group. In addition, an exit group (share of inactive farmers over time) was not considered, as this would also require knowing the evolution of the total active farm population over time. Although the missing total numbers of farms can be solved by using additional observations from regional farm structure survey (FSS) time to capture the general trend of total farm numbers in a region, it would result into two different approaches and, hence, is prone to inconsistencies.
The disadvantage of this work is mainly in the missing incorporation of the absolute number of farms and, consequently, the missing exit class. In addition, the data quality of the regional representative farm groups over time was of concern when using FADN. Changes in the methodology, due to a change in the sampling plan, or a change in the classification scheme, i.e., the standard gross margin (SGM) versus standard output (SO), seriously affected the data quality and, hence, the estimation results.
Given this background, the aim of this paper is twofold. First, we extend the approach of Neuenfeldt et al. [51] such that it accounts for entering and exiting farms in the MCI framework, which allows for quantification of the absolute numbers of all active and inactive groups. The proposed extension of the MCI is an important step in applying the concept for quantitative simulation models and in accounting endogenously for farm structural change. The second aim of the paper is to make use of spatial information by fully exploiting the location information of the Norwegian dataset, i.e., to estimate the neighbouring effects, indicated recently in the literature as an important driver for structural change.
Our paper, therefore, contributes to the existing literature on farm structural change in several ways. First, we apply and extend the MCI approach by using FSS data to incorporate farm entry/exit decisions and, second, we explicitly incorporate the location information of farms by using indicators to account for the number of neighbouring farms within a certain radius, which has not previously been used in this strand of analysis. We investigate whether and how a farm group is affected by the density of neighbouring farms. In other words, we analyse which farm group and region shrink due to competition effects and which grow due to positive externalities deriving from agglomeration economies.
The paper is structured as follows. The next section introduces the MCI approach with a short explanation and relevant references. In the third section, we explain the construction of farm groups at the regional level, including the definition of the exit class, and the choice of explanatory variables is justified. In Section 4, the model results are presented. A simulation experiment with the incorporated locational variable is presented in Section 5. The final section concludes the research described in the paper.
2. Methods
We use the Multiplicative Competitive Interaction (MCI) proposed by Neuenfeldt et al. [51] for explaining farm structural change, which is originally based on the theoretical framework developed for the estimation of market share attractions in the marketing literature [54]. Generally, MCI are also applied in the marketing literature to explain market shares of brands or products to investigate how they are affected by firm’s own actions (e.g., marketing instruments and management choices), actions of competitors and other factors, such general economic development or policy changes [54,55].
They rely on two fundamental hypotheses: (i) the market share of a brand or product is proportional to the marketing effort applied by the firm [56] and (ii) consumers are attracted to different brands/products, and the most attractive one gains the largest market share [57]. The MCI approach is also applied in other fields than marketing, such as hospital services [58] and the financial sector [59,60,61].
This theoretical framework has been extended to agricultural farm groups distinguished by production specialisation and farm size. According to Gocht et al. [62] and Neuenfeldt et al. [51], the farmers’ choices on production activities determine the share of different farm groups in a region. Analogous to the market share hypotheses of Cooper and Nakanishi [54], in which brands and products compete for shares of a limited market, the different farm groups compete for their share over limited agricultural resources (e.g., land, labour). Hence, each farm group share depends on the resources allocated and their efficient use in the production process.
According to Neuenfeldt et al. [51] the model does not need to impose constraints on parameters to ensure that the shares sum up to one, because subsequent normalisation accounts for this. A further advantage is that farm group specific sets of explanatory variables can be used to specify the estimation equations. This is particularly important in the presence of heterogeneous farm groups, because farm group shares (e.g., dairy farms versus cereal farms) may be affected by different drivers. For example, payments coupled to production activities are specifically relevant only for certain farm groups.
The observed farm group shares can be seen as the result of the utility-maximising behaviour of each farm, given all the information and circumstances it faces. Depending on the production decisions, a farm represents a specific farm group. Therefore, the farm group share in a region is defined by the aggregated utility generated from farming activities by the farm group relative to the total utility obtained by all farm groups:
where and are farm group indices, is the time, is the utility of farm group in , is the share of farm group in all farm groups in , and is the number of farm groups considered at the regional level.
The utility of specific farm activities is formulated as a multiplicative function:
where is the number of explanatory variables, is the k-th explanatory variable explaining the utility of farm group in , is the coefficient measuring the influence of the k-th explanatory variable on the utility of farm group in , is a farm group-specific parameter, is the positive, monotone transformation of and is the error term.
Each farm group is estimated separately, and the variables with the most predictive power are selected via a forward selection based on the Bayesian information criterion. The estimation equation for each farm group i across the regions reads as follows: (for a detailed discussion and why the model is applicable we refer the reader to Neuenfeldt [51])
where variable is the share of farm group in year for farm groups. is the farm group specific intercept, is the farm group specific coefficient for each explanatory variable of all explanatory variables and is the lag, which can be for time-independent variables or between and for time-dependent variables. is the k-th explanatory variable explaining the farm group share in for different lags and the lagged farm group shares of group are also part of the set of explanatory variables.
To ensure that the estimated farm group shares are summing up to 1, the shares of the farm groups are calculated by using the normalisation procedure [63]. This means that, if is the estimate of the dependent variable in the equation above, the estimated farm group share, , is given as follows:
where the farm group share is calculated as the ratio of the inverse logarithm of the estimate divided by the sum of all the inverse logarithm estimates of the dependent variable over all farm groups.
We refrain from presenting all the estimated coefficients for each farm group and rather report some statistics of the fit of the estimated regressions and the summary of the decomposition results of the drivers of farm structural change and compare them with Neuenfeldt et al. [51].
To elaborate the fit of the estimated regressions, we take a closer look at the coefficient of determination for each estimated regression. The farm group-specific coefficient of determination is calculated as follows:
where is the average farm group share of farm group at time , and is the total number of available years.
3. Data
3.1. Farm Group Construction
We follow the farm typology of the European Union to construct farm groups. This typology is also applied to FSS and FADN. The advantage is that, later, we can compare our results with the findings of Neuenfeldt et al. [51], who used the same rules of constructing farm groups. Official European data, as FSS or FADN, classifies farms by production specialisation (principal type of farming) and farm size (economic size class). Each farm group in our paper is a combination of farm specialisation and size class.
We consider four farm specialisations and seven size classes, as provided in Table 1. Specialist cereals oilseeds and protein crops, various field crops combined, specialist dairying and sheep, goats and other grazing livestock farm are the farm types of our choice. We further define size classes ranging from below 4000 standard output (SO), between 4000 SO and 8000 SO, up to above 100,000 SO, as depicted in Table 1. The standard output of an agricultural product (crop or livestock) is the average monetary value of the agricultural output at farm-gate price, in euro per hectare or per head of livestock.

Table 1.
Selected stratification of farm type and size class.
For the crop activities, only the smaller size classes are considered; for animal grazing activities, the larger size classes are considered. The principal type of farming (farm specialisation) is defined in terms of the dominant farm activity of the farm calculated as the relative share of SO of the dominant activity in the total farm SO (European Commission, 2010). The selected farm groups are chosen based on their relative importance in terms of the SO for Norwegian agriculture.
For our analysis, we further group the remaining farms into the residual farm group (all remaining combinations of farm specialisation and size class) when they are still active. Finally, and to contribute to another part of structural change—entry or exit—we construct an exit farm group, which is derived as the difference of the maximum number of active farms over the whole period deducted by the active farms in each period.
3.2. Model Variable Construction
For the whole dataset over the period from 1996 to 2015, we have 84,901 unique farms. After deselecting regions with low numbers of farms, our dataset still has 82,641 unique farms in 51 regions. After the selection procedure is done and the relevant regions and farm groups are chosen, the farm group shares () are calculated in the following form:
with being the number of farms belonging to farm group in year and being the total number of farms in year . The construction of the exit farm group is achieved by finding the year with the maximum number of farms () for the whole dataset and setting the number of farms in this group as the difference of all active farms and the maximum number of farms, as follows:
Figure 1 presents the development of the farm group shares from 2000 to 2015. There were roughly 69,000 farms in 1996, declining to roughly 38,000 farms in 2015 (−45%). Grazing and various field crops activities were predominant in Norway in terms of SO. It is also apparent that the larger-size class farms of specialist cereals oilseeds and protein crops, various field crops combined and specialist dairying farms were increasing, whereas the smaller-size classes were decreasing over time. The exit farm group was increasing over time but at a diminishing rate.
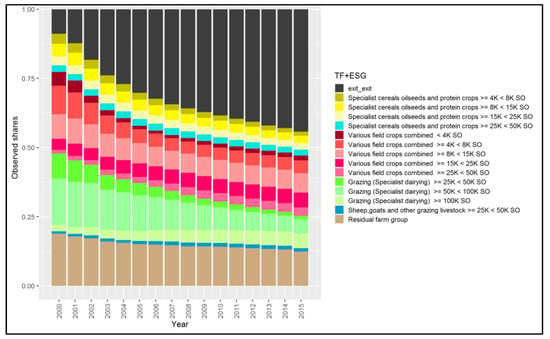
Figure 1.
Development of the chosen farm typology in Norway. Source: Own contribution.
Figure 2 shows the evolution of the farm groups of three regions: NO012003, which is the intersection of NUTS3 region NO012 and the agricultural region 3; NO012002, which is the intersection of NUTS3 region NO012 and the agricultural region 2; and, finally, NO012003, which is the intersection of NUTS3 region NO061 and the agricultural region 4. All regions contain different farm groups, and the data suggest that the inactive farm group was increasing.
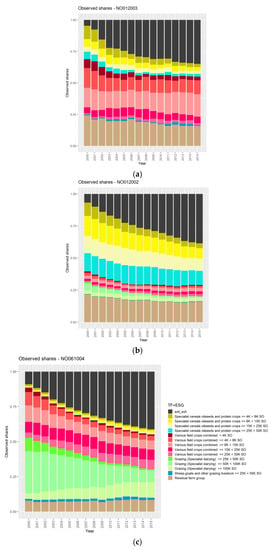
Figure 2.
Development of the chosen farm typology in the example regions (a) NO012003, (b) NO012002 and (c) NO061004. Source: Own contribution.
3.3. Choice of Explanatory Variables
We used six sets of explanatory variables (see Table 2), in our analysis, which have been used thoroughly in the literature to analyse farm structural change in terms of farm entry or exit, and change in farm specialisation and size: (i) prices (input and output prices), (ii) population and age, (iii) subsidies, (iv) macroeconomic variables, (v) natural conditions and (vi) locational information. Variables containing information about the location of farms are discussed below in more detail.

Table 2.
Summary statistics of the explanatory variables in each variable category.
Table 2 provides the mean, standard deviation and median as well as the spatial and temporal resolution. The sources of the explanatory variables are Norwegian census farm data (subsidies, age of the farm holder and number of neighbouring farms), EUROSTAT (interest rate and unemployment rate), the World Bank (GDP growth rate), CAPRI (prices), CORINE land cover (arable land, artificial surface, heterogeneous agricultural areas, pastures and permanent crops) and EUGIS (slope and elevation), as well as the CRU TS 4.01 database (See https://crudata.uea.ac.uk/cru/data/hrg/cru_ts_4.01/ge/ (accessed on 1 July 2021) for a description) (temperature, precipitation and potential evapotranspiration to calculate the mean and standard deviation for the growing degree days and vegetation period for the thresholds of 5 and 10 degrees Celsius).
The farm group specific explanatory variables for the exit farm group are constructed in two ways. First, country and regional data are the same as for the active farm groups. Second, the farm group specific variables are constructed by averaging over all the active farm groups in each region. For instance, the price of cereals is the same for all inactive and active farm groups regardless of the regions. The regional level variables, such as population density, are the same in each region for all farm groups.
The variables that are farm group-specific at the regional level are different for each active farm group and region. This means that, for the inactive (exit) farm group, these variables are calculated as the regional average over all active farm groups. For instance, the total subsidies are farm group- and region-specific for each active farm group, and thus, for the exit farm group, an average of the active farm group values is used.
We added three variables for location information (see Table 2 and for a more detailed discussion Table 3), namely, the average number of neighbouring farms of a farm group. These annual variables were calculated at the regional level. For this, we counted the number of farms within a 10, 20 or 50 km radius of each farm in the data set. Afterward, the farm level data was averaged to the regional level. With increasing farm size in terms of SO, the average number of neighbouring farms was increasing. On average, the farm specialisation, various field crops combined, and other grazing livestock faced fewer neighbouring farms, whereas grazing and specialised cereals farms were surrounded by more neighbouring farms. For all farm groups, one can see that there was a huge variation over region and time for the number of neighbouring farms.

Table 3.
Summary of the number of neighbouring farms per farm group.
The existing literature distinguishes between two types of effects of neighbouring farm size. First, neighbours are seen as competitors, especially regarding the acquisition of agricultural land [41]. In this case, a farmer who is surrounded by larger farms may stop farming if these larger farms introduce new technologies more quickly, as they are likely to have better access to information and financial resources [64]. A higher willingness to pay for the land of the neighbouring farms results in a negative impact on the probability to continue with the farm under consideration. Further, Storm et al. [22] showed the importance of farm interactions for strategic farm decisions due to the competition over land causing regional specific patterns and spatial dependencies.
On the other hand, neighbours can be seen as a source of motivation and a model for the introduction of new technologies [25,26,27]. In this case, the size of neighbouring farms has a positive effect on the survival of the farm concerned, as a farmer surrounded by larger farms is more likely to adopt the innovative technologies they use [9]. Vroege et al. [23] suggested, in their analysis, that locally proximate farms seemed to cooperate and that competitive effects may occur at higher spatial levels. As neighbouring effects can be very heterogenous between farm types [24], we attempted to reflect this by our farm group-specific analysis.
As we estimate regional farm group models, the question arises regarding how the aforementioned aspects of neighbouring effects, which are derived from farm level interaction, are transmitted and interpreted to our regional case. Therefore, we aimed to analyse the farm structure (how the farm groups are evolving over time), given that there were different trends in the number of neighbouring farms within a certain range, and how these lead to different states of farm structure. Figure 3 presents the regional resolution chosen on which the farm structural change was analysed.
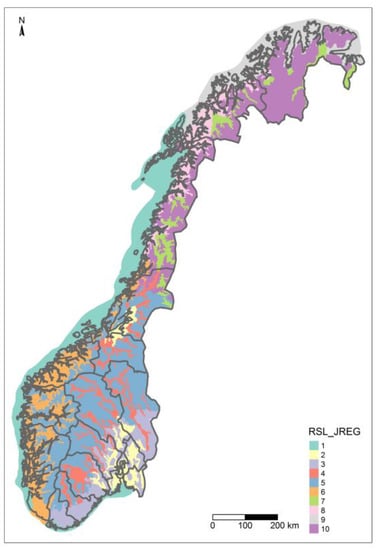
Figure 3.
Regional aggregation of NUTS3 and agricultural regions in Norway. Source: Own contribution.
The borders of administrative zones (NUTS3) are in black, and the agricultural regions are marked in 10 colours. (The geo reference file comes from https://kart8.nibio.no/uttak_Download/landskap/0000_32632_Jordbruksregioner_SHAPE.zip (accessed on 1 July 2021), and the agricultural regions are made available from NIBIO https://kartkatalog.geonorge.no/metadata/landscape-agricultural-regions/ea46cdee-fbe8-4dd4-9017-c8f85ebe2253 (accessed on 1 July 2021). Further information on the specific regions can be found at https://kart13.nibio.no/landskap/10_jordbruksregioner/Jordbruksregioner_kart/ (accessed on 1 July 2021) and https://www.nibio.no/tema/landskap/landskapskart/nasjonalt-referansesystem-for-landskap/jordbruksregioner (accessed on 1 July 2021)) For instance, in one NUTS3 region, there can be several agricultural regions. The intersection gives us the opportunity to capture heterogenous effects coming from administrative or natural units.
4. Results
4.1. Coefficient of Determination
The coefficient of determination of the estimated farm group equations ranged from 86.7% to 98.8% with a mean of 95.5%. This shows the overall high fit of the estimated models. The variable average number of neighbouring farms was selected to be a contributor to explain the shares of the smallest and largest specialist cereals, oilseeds and protein crops, the largest grazing and the exit farm group.
Three location information variables were generated as an additional set of explanatory variables. After the forward selection, the ‘average number of neighbouring farms within 10 km’ was selected for four farm groups, as indicated in the last column in Table 4.

Table 4.
Farm group-specific estimation results.
4.2. Comparison of Observed and Estimated Shares
To further elaborate upon the fit of the estimated models, Figure 4 shows the absolute difference of the observed and estimated farm group shares aggregated for all regions at the country level. The figure reveals that most of the differences were between −0.5 and 0.5 percentage points. The highest differences occurred for the exit farm group in 2012, with 1.5 percentage points difference. Overall, the errors were randomly distributed around a zero mean.
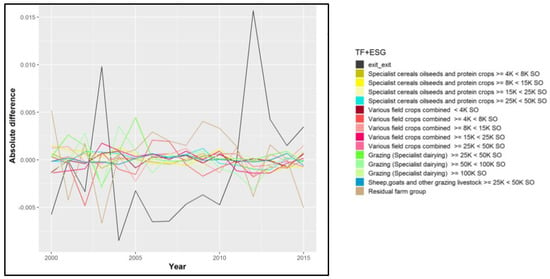
Figure 4.
Absolute difference of the observed and estimated farm group shares aggregated at the country level (The share values in the data set were between 0 and 1. Therefore, the absolute differences between observed and estimated shares were between −0.007 and 0.015, which translates into −0.7 and 1.5 percentage points. For better understanding, the observed and predicted values are presented in the annex aggregated for Norway.) Source: Own contribution.
4.3. Decomposition of the Estimated Effects
To better identify the importance of various drivers of farm structural change, we decompose the variance of the dependent variable—farm group shares—into relative contributions of each explanatory variable for all models [65,66]. The results are presented for the aforementioned variable sets and (past) farm structure (lags of dependent variables). Figure 5 presents the relative contribution of the explanatory variables to farm structural change in Norway. The past farm structure (the lagged farm group shares) itself explained most of the variance (87%), followed by natural conditions (4.1%) as well as subsidies (4.8%). The variables containing location information accounted for 2.6%; the macro variables and prices had nearly no explanatory value.
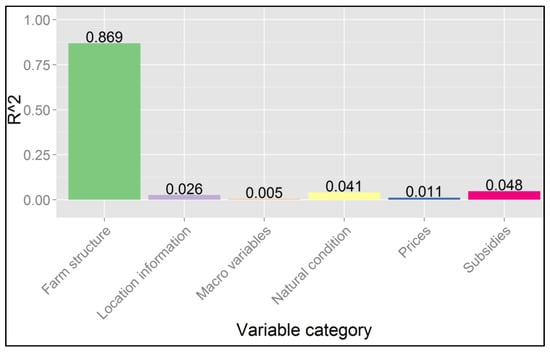
Figure 5.
Relative contributions of the variable categories to farm structural change. (The variables from category “age and population” were not selected in the forward selection based on the Bayesian information criterion.) Source: Own contribution.
When we look at the relative contributions of the variable categories across farm groups (see Figure 6), we can see that the historic farm structure contributed the most to the explanatory power. Specifically, for the exit farm group, historic farm structure showed the lowest contribution (62.8%), whereas, for specialist cereals, oilseeds and protein crops (≥15,000 <25,000 SO), it was the highest (99.8%). In particular, for the exit farm group (inactive farms), this low contribution seems to be reasonable, as this farm group is derived from exiting farms. Subsidies showed the highest contribution for the exit farm group (32%).
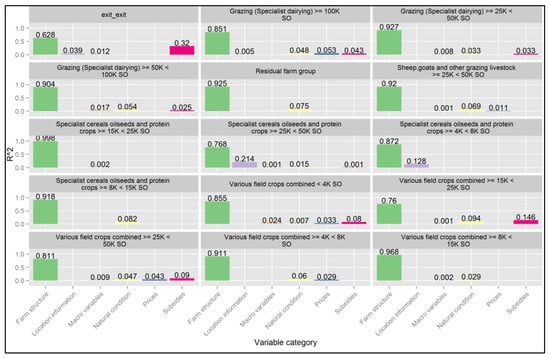
Figure 6.
Relative contribution of the variable categories to farm structural change across farm groups. Source: Own contribution.
Natural conditions explained the most for the various field crops combined (≥15,000 <25,000 SO), with 9.4%. The average number of farms explained the most for the largest specialist cereals, oilseeds and protein crops, with 21.4%. Prices explained the most for the largest grazing farm group (5.3%). The highest contribution from macro variables can be seen for the smallest various field crops combined farm group (2.4%). Most farm groups had more than two variable categories that contributed to the explanatory power, but no farm group contained all variable categories. These results contributed to the fact that several different determinants played a role in structural change, and these determinants correlated differently between farm specialisations and farm sizes.
5. Sensitivity of Location Information
The sensitivity analysis focused on the variable ‘Average number of neighbouring farms within 10 km’ (nobs10 km) in two ways. We tested two different scenarios: an increase by 100% and a decrease by 50%. For this, we increased (decreased) sequentially per year the variable until 2025, which then reached 200% (50%) of the value from 2015 (the last year of observation). The changes affected the variable at the farm group, at the region and in each year. The other explanatory variables in this sensitivity analysis remained constant to better eliminate the effect of the spatial location variable contribution to structural change. In Table 5, the results are presented by the predicted farm group shares in comparison to the baseline scenario.

Table 5.
Absolute number of farms and the percentage difference for an increase of 100% and a decrease of 50% of neighbouring farms within 10 km compared to the baseline at the country level.
The baseline scenario depicts the farm group shares that are predicted on a yearly basis until 2025 without changes. Due to the dynamic model (lags of the farm group shares) there was still progress for the farm group shares—the importance of past farm structure comes into play. The decreasing scenario may be understood as a continuation of increasing structural change (reducing the number of farms in a radius of 10 km), however, at an increasing rate, whereas the increasing scenario may be seen as a change in the direction of the ongoing trend of the declining number of farms.
We present the exit farm group, the smallest and largest specialist cereals farm group and the largest specialist dairying farm group, as they have the spatial location variable as explanatory in their farm group-specific estimation model. These farm groups have the strongest changes in their share; however, as all groups are linked in MCI to each other, the simulated variable also has an effect on the other farm groups. The estimated farm group shares are constructed through normalization of the estimated.
The Table 5 indicates that, if the number of neighbouring farms within 10 km of specialist dairying (100,000 SO) (no. 13) is decreasing (increasing) by 50% (100%) until 2025, the relative percentage change is 15% (5%), which is 5 (5) percentage points higher/lower than the baseline with a 10% relative change. The total number of farms is given in the third column for the year 2015. The absolute change in farm numbers is also presented.
Overall, a reduction in density of the surrounding farms (declining scenario) leads, in 12 active farm groups, to a further reduction compared to the baseline, even if they increase from 2015 onwards (farm groups with a positive sign of the fourth and fifth column). As we are comparing to the baseline in which the trend of a declining number of farms continues, the decreasing scenario describes an even higher exit of farms out of the sector.
The effects presented are an aggregated picture over all 51 regions, and the effects at the farm-group level might differ in a region. The sensitivity analysis reveals, however, that most farm groups are negatively affected (reducing the absolute and relative size), when the density of the surrounding farms declines, and spill-over effects and neighbouring cooperation become less possible (common use of machinery).
The analysis also revealed that the large farm groups, such as the farm group specialist dairying (100,000 SO), appeared to be less dependent on agglomeration effects and could even further increase their importance by almost 200 farms in the declining scenario. This may be the result of a strong competition position of the large farms, e.g., on the land market [22], which may lead to lower profitability and, thus, to other smaller farm groups exiting the sector [39,40]. In contrast, the farm group specialist cereals (25,000–50,000 SO) (no. 5) declined by about 290 farms, which is −21%.
For the scenario of increasing the density of surrounding farms, the results were almost mirrored. The increasing scenario describes the situation in which more farms have entered the farming sector compared to the baseline. This scenario can be interpreted as what would the farm structure look like if there would be more (neighbouring) farms. The ongoing trend of the declining number of farms in the sector is slowed down.
In this case, farms entering the sector would choose those production activities that are associated with those farm groups that experience an acceleration in their shares compared to the baseline. There must have been relatively low entry barriers due to sufficient profits, lower land rents and growth of the most preferable farm groups. An increasing number of neighbouring farms is most likely a reasonable scenario in terms of farm division, because new entrants must take non-occupied agricultural land or lend from active farmers.
The inactive (exit) farm group (no. 1) must be considered differently. This farm group reflects the ongoing structural change in terms of declining active farm numbers and, hence, increasing inactive farms. Structural change most often implies that smaller farms are exiting more frequently than larger farms. We predicted with the estimated model for the baseline development for most of the small farming groups a decline (specialist cereals (4000–8000 SO), crops combined (8000–15,000 SO), specialist dairying (25,000–50,000 SO) and the residual farm group).
Only the farm group crops combined could increase their shares for small size classes; this might be due to effects, such as part-time farming or off-farm employment. The specialist cereals (25,000–50,000 SO) farm group (no. 5) is the only farm group that changed its baseline prediction from decreasing to increasing, likely since the decline in the baseline was rather moderate (−2%), and, at the same time, the effects of the two scenarios were very profound (−21%; +20%).
6. Discussion and Conclusions
In this paper, we analyse the drivers of farm structural change in Norwegian agriculture with farm census data. We adopted the Multiplicative Competitive Interaction (MCI) model. We extended the MCI framework by accounting explicitly for the absolute farm numbers and, hence, a farm exit class, and, in addition, by considering farm locations with which to generate an aggregated variable—the number of neighbouring farms within a certain range.
We applied this approach to Norwegian farm census data for the period 1996 to 2015. Overall, we considered four production specialisations and seven size classes generating 15 farm groups, including a residual and an exit farm group in a region. This allowed us to simultaneously analyse farm structural changes in terms of changing production orientation as well as exit decisions. A simulation experiment of a changing number of neighbouring farms provided concrete advice as to how this variable influenced the farm structure.
The results showed that the relative importance of the different variable sets was comparable to that found by Neuenfeldt et al. [51]. Differences exist, however, in particular with regard to the explanatories of the farm manager age and population density, which were not selected when applying the dimension reduction forward selection, which indicates insignificancy. The impact of population density on farm structures might be captured by spatial variables and by the regional units, stratified by agrarian and administrative zones.
Further, at least for the exit rates of farms, population density had mixed effects with respect to farm exits [37,46,49]. That the age of a farmer was not selected as an explanatory variable can be explained due to its contrary effects [23] on farm exits. Farm managers who have been in the business for longer periods of time have more experience from which to react to changing conditions; however, of course, the probably increases when approaching retirement. To better account for this, farm succession is needed but was not available in this study.
In the Appendix A, Table A1 shows the heterogenous distribution of the farm groups among the agrarian zones in Norway. For clarity, we dropped the inactive and residual farm group from the Table. One can see that the specialist dairying farm groups and crops combined were almost always represented in all agrarian zones, whereas specialist cereals farms were mostly active in only a few agrarian zones. In correspondence to the high fit of the estimated farm group models, the strategy to intersect the administrative and agrarian zones in order to build the regional basis of the analysis showed the high interrelatedness between the development of farm groups among the regions and enabled concentration of the analysis and discussion on the farm groups.
Most of the structural change of the farms can be explained by the past farm structures and, to a smaller extent, by factors, such as subsidies, natural conditions, macro variables and prices. This is not surprising, as Norwegian agriculture is highly subsidised, and farm structural changes are less dynamic. This leads also to relatively stable shares for certain farm groups and, hence, a higher explanatory contribution from past farm structures in the model, even though the total farm number is declining.
The extension by considering the neighbouring effects gained additional explanatory power for the model. We tested three radius distances for deriving the spatial location indicator to describe the density of surrounding farms. The location variable with the radius of 10 km was selected in a forward selection of being significant for explaining structural change for four farms groups. A larger radius appeared to be less relevant.
When we used the model to project into the future of 2025 from 2015, we observed that larger farm groups (with respect to SO) were increasing their share relative to smaller ones, even if the number of total farms was declining. In the context of a sensitivity analysis with two scenarios, in varying the farm density, we found that most farm groups were negatively affected (reducing the absolute and relative size) when the density of the surrounding farms declined, and spill-over effects and neighbouring cooperation became less possible. For the scenario of increasing the density of surrounding farms, the results were almost mirrored.
Our results face certain limitations. Regarding the explanatory variables, one shortcoming is the missing information on farm income, as this was not collected in the census, and not available from other sources for long-time series, as with the census. Additionally, off-farm income, part-time farming or other gainful activities might increase the model quality to explain particular farm groups with a smaller farm size.
As in Neuenfeldt et al. [51], our estimates may be affected by regional heterogeneity in social capital as well as formal and informal land market institutions, which we were not able to fully control in our estimations, partially also due to the unavailability of data. We could derive other variables to count the number of neighbouring farms, distinguishing between nearby farms that have similar and different demands to their surrounding area; or we could count not only the numbers of neighbouring farms within a certain range but also another farm as a neighbour, when this farm is located within a certain commuting range.
Due to the proposed extension in this paper toward the absolute farm number and the exit group, we could now exploit the use of the estimated farm structural change model in the context of mathematical programming supply models for policy impact analyses, such as the Agrispace model [67].
Author Contributions
Conceptualisation, S.N., A.G., T.H. and P.C.; methodology, S.N., A.G., T.H.; formal analysis, S.N. and A.G.; Data Curation, S.N. and K.M.; writing—original draft preparation, S.N. and A.G.; writing—review and editing, S.N., A.G., P.C. and T.H.; visualisation, S.N.; supervision, A.G. All authors have read and agreed to the published version of the manuscript.
Funding
The study was developed as part of the H2020 MIND STEP project which received funding from the European Union’s Horizon 2020 research and innovation programme under Grant Agreement No. 817566.
Data Availability Statement
The regionalised data set finally used for the MCI approach can be provided. The single different data sources were obtained as follows. The Norwegian farm structure survey data and deducted subsidy payments were provided by Hugo Storm and Klaus Mittenzwei. Generally, the Norwegian farm structure survey data can be obtained from https://data.norge.no/datasets?opendata=true&theme=GOVE&losTheme=naring%2Flandbruk (accessed on 8 July 2021). Filter for Open data; Business—Agricultural sector; Government and public sector. The Norwegian name of the data sets is: ‘Produksjons- og avløsertilskudd til jordbruksforetak—søknadsomgang’. CAPRI database (2017). Database for prices—unit valued price (UVAP). COCO2: The Complete and Consistent Data Base (COCO) for the national scale. The finishing step estimates consumer prices, consumption losses and some supplementary data for the feed sector (by-products used as feedstuffs, animal requirements on the MS level, contents and yields of roughage). Both tasks run simultaneously for all countries and build on intermediate results from the main (COCO1) part of COCO, such as human consumption and processing quantities. https://www.capri-model.org/dokuwiki_help/doku.php?id=getting_started_with_capri (accessed on 8 July 2021). for data and https://www.capri-model.org/dokuwiki_help/doku.php?id=the_capri_data_base (accessed on 8 July 2021) for explanation. EUGIS data base: Osterburg, B., Nitsch, H., Laggner, A. and Wagner, S. (2008). Analysis of the policy measures for greenhouse gas abatement and compliance with the Convention on Biodiversity. Project MEACAP, Work package 6. Corine 2000 (CLC2000), 2006 (CLC2006), 2012 (CLC2012) land use classification. https://land.copernicus.eu/pan-european/corine-land-cover. accessed on 20 April 2021. EUROSTAT (2015). Population density by NUTS 3 region—inhabitants per km2. http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=demo_r_d3dens&lang=en (accessed on 19 October 2017). EUROSTAT (2017). EMU convergence criterion series—annual data. EMU convergence criterion bond yields. http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=irt_lt_mcby_a&lang=en (accessed on 18 October 2017). EUROSTAT (2017). Harmonised unemployment rates (%)—monthly data, seasonally adjusted, unemployment rate according to ILO definition. http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=ei_lmhr_m&lang=en (accessed on 18 October 2017). CRU TS Version 4.01. A comprehensive set of high-resolution grids of monthly climate data for Europe and the globe. https://crudata.uea.ac.uk/cru/data/hrg/cru_ts_4.01/ (accessed on 19 October 2017). Worldbank (2017). GDP growth (annual %)—World Bank national accounts data, and OECD National Accounts data files. https://data.worldbank.org/indicator/NY.GDP.MKTP.KD.ZG?cid=GPD_30 (accessed on 18 October 2017).
Acknowledgments
In developing the ideas presented here, we would like to thank Norbert Röder for introducing the idea of using MCI models in an agricultural economics context and methodological support in earlier stages. We also thank the three anonymous reviewers for their feedback and the editor for helpful comments. The authors are solely responsible for the content of the paper. The views expressed are purely those of the authors.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
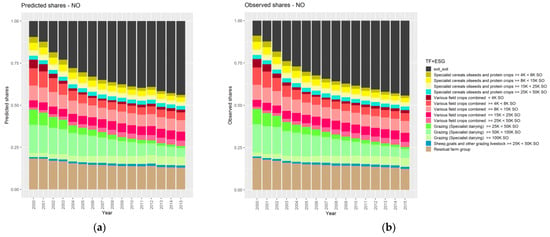
Figure A1.
Predicted (a) and observed (b) farm group shares for Norway. Source: Own contribution.

Table A1.
Average farm group shares for the agrarian zones in Norway.
Table A1.
Average farm group shares for the agrarian zones in Norway.
| Farm Group | Agrarian Zones | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 6 | 7 | 8 | 9 | |
| Specialist cereals (4000–8000 SO) | 0.5 | 4.1 | 1.6 | 1.1 | 0 | 0 | 0 | 0 |
| Specialist cereals (8000–15,000 SO) | 1.2 | 7.2 | 2.5 | 1.7 | 0.1 | 0 | 0 | 0 |
| Specialist cereals (15,000–25,000 SO) | 0.6 | 7.2 | 1.8 | 1.3 | 0.1 | 0 | 0 | 0 |
| Specialist cereals (25,000–50,000 SO) | 0.4 | 6.8 | 1.8 | 0.9 | 0 | 0 | 0 | 0 |
| Crops combined (less than 4000 SO) | 2.6 | 0.9 | 1.8 | 1.3 | 2.2 | 1.7 | 2.6 | 5.5 |
| Crops combined (4000–8000 SO) | 4.9 | 2.2 | 6.2 | 4.7 | 6.5 | 4.7 | 4.8 | 6.8 |
| Crops combined (8000–15,000 SO) | 6.6 | 3.7 | 7.7 | 8 | 9.4 | 9.1 | 7.1 | 11 |
| Crops combined (15,000–25,000 SO) | 5.2 | 2.9 | 4.6 | 7.3 | 6.4 | 7.4 | 5.8 | 4.6 |
| Crops combined (25,000–50,000 SO) | 3.3 | 2 | 2.2 | 4.7 | 3.6 | 0 | 2.4 | 6.3 |
| Specialist dairying (25,000–50,000 SO) | 0.7 | 0.2 | 0.9 | 1.4 | 2.4 | 1.6 | 0.8 | 0 |
| Specialist dairying (50,000–100,000 SO) | 5.2 | 1.6 | 3.2 | 7.7 | 7.2 | 6.4 | 5.7 | 4.6 |
| Specialist dairying (100,000 SO) | 8.5 | 3.4 | 3.2 | 6.6 | 5.4 | 4.6 | 4 | 4.6 |
| Other grazing livestock (25,000–50,000 SO) | 1.3 | 0.5 | 1.5 | 1.3 | 1.9 | 0.3 | 1.1 | 0 |
Source: Own contribution.
References
- Mittenzwei, K.; Persson, T.; Höglind, M.; Kværnø, S. Combined Effects of Climate Change and Policy Uncertainty on the Agricultural Sector in Norway. Agric. Syst. 2017, 153, 118–126. [Google Scholar] [CrossRef]
- Statistics Norway Agriculture, Forestry, Hunting and Fishing—Holdings, Agricultural Area and Livestock. Available online: https://www.ssb.no/en/statbank/list/stjord?rxid=8480068c-54d5-4265-a149-f3477ce65573 (accessed on 8 July 2021).
- Forbord, M.; Bjørkhaug, H.; Burton, R.J.F. Drivers of Change in Norwegian Agricultural Land Control and the Emergence of Rental Farming. J. Rural Stud. 2014, 33, 9–19. [Google Scholar] [CrossRef]
- Agricultural Policy Monitoring and Evaluation 2014: OECD Countries. Available online: https://www.oecd-ilibrary.org/agriculture-and-food/agricultural-policy-monitoring-and-evaluation-2014_agr_pol-2014-en (accessed on 19 May 2021).
- Cochrane, W.W. Farm Prices: Myth and Reality; University of Minnesota Press: Minneapolis, MN, USA, 1958; ISBN 978-0-8166-5732-2. [Google Scholar]
- Zimmermann, A.; Heckelei, T. Structural Change of European Dairy Farms—A Cross-Regional Analysis. J. Agric. Econ. 2012, 63, 576–603. [Google Scholar] [CrossRef]
- Balmann, A.; Dautzenberg, K.; Happe, K.; Kellermann, K. On the Dynamics of Structural Change in Agriculture: Internalc Frictions, Policy Threats and Vertical Integration. Outlook Agric. 2006, 35, 115–121. [Google Scholar] [CrossRef]
- Arfa, N.B.; Daniel, K.; Jacquet, F.; Karantininis, K. Agricultural Policies and Structural Change in French Dairy Farms: A Nonstationary Markov Model. Can. J. Agric. Econ. Can. Agroecon. 2015, 63, 19–42. [Google Scholar] [CrossRef]
- Harrington, D.H.; Reinsel, R.D.; Harrington, D.H. A Synthesis of Forces Driving Structural Change. Can. J. Agric. Econ. 1995, 1995, 3–14. [Google Scholar]
- Alvarez-Cuadrado, F.; Poschke, M. Structural Change Out of Agriculture: Labor Push versus Labor Pull. Am. Econ. J. Macroecon. 2011, 3, 127–158. [Google Scholar] [CrossRef]
- van Neuss, L. The Drivers of Structural Change. J. Econ. Surv. 2019, 33, 309–349. [Google Scholar] [CrossRef]
- Fezzi, C.; Bateman, I.J. Structural Agricultural Land Use Modeling for Spatial Agro-Environmental Policy Analysis. Am. J. Agric. Econ. 2011, 93, 1168–1188. [Google Scholar] [CrossRef]
- Müller, D.; Zeller, M. Land Use Dynamics in the Central Highlands of Vietnam: A Spatial Model Combining Village Survey Data with Satellite Imagery Interpretation. Agric. Econ. 2002, 27, 333–354. [Google Scholar] [CrossRef]
- Mandryk, M.; Reidsma, P.; van Ittersum, M.K. Scenarios of Long-Term Farm Structural Change for Application in Climate Change Impact Assessment. Landsc. Ecol. 2012, 27, 509–527. [Google Scholar] [CrossRef]
- Olesen, J.E.; Bindi, M. Consequences of Climate Change for European Agricultural Productivity, Land Use and Policy. Eur. J. Agron. 2002, 16, 239–262. [Google Scholar] [CrossRef]
- Bradshaw, B.; Dolan, H.; Smit, B. Farm-Level Adaptation to Climatic Variability and Change: Crop Diversification in the Canadian Prairies. Clim. Chang. 2004, 67, 119–141. [Google Scholar] [CrossRef]
- Berry, P.M.; Rounsevell, M.D.A.; Harrison, P.A.; Audsley, E. Assessing the Vulnerability of Agricultural Land Use and Species to Climate Change and the Role of Policy in Facilitating Adaptation. Environ. Sci. Policy 2006, 9, 189–204. [Google Scholar] [CrossRef]
- Reidsma, P.; Ewert, F.; Oude Lansink, A.; Leemans, R. Vulnerability and Adaptation of European Farmers: A Multi-Level Analysis of Yield and Income Responses to Climate Variability. Reg. Environ. Chang. 2008, 9, 25. [Google Scholar] [CrossRef]
- Bindi, M.; Olesen, J.E. The Responses of Agriculture in Europe to Climate Change. Reg. Environ. Chang. 2011, 11, 151–158. [Google Scholar] [CrossRef]
- Agovino, M.; Casaccia, M.; Ciommi, M.; Ferrara, M.; Marchesano, K. Agriculture, Climate Change and Sustainability: The Case of EU-28. Ecol. Indic. 2019, 105, 525–543. [Google Scholar] [CrossRef]
- Stokstad, G. Exit from Farming and Land Abandonment in Northern Norway. Available online: https://ageconsearch.umn.edu/record/95343 (accessed on 19 May 2021).
- Storm, H.; Mittenzwei, K.; Heckelei, T. Direct Payments, Spatial Competition, and Farm Survival in Norway. Am. J. Agric. Econ. 2015, 97, 1192–1205. [Google Scholar] [CrossRef]
- Vroege, W.; Meraner, M.; Polman, N.; Storm, H.; Heijman, W.; Finger, R. Beyond the Single Farm—A Spatial Econometric Analysis of Spill-Overs in Farm Diversification in the Netherlands. Land Use Policy 2020, 99, 105019. [Google Scholar] [CrossRef]
- Saint-Cyr, L.D.F.; Storm, H.; Heckelei, T.; Piet, L. Heterogeneous Impacts of Neighbouring Farm Size on the Decision to Exit: Evidence from Brittany. Eur. Rev. Agric. Econ. 2019, 46, 237–266. [Google Scholar] [CrossRef]
- Case, A. Neighborhood Influence and Technological Change. Reg. Sci. Urban Econ. 1992, 22, 491–508. [Google Scholar] [CrossRef]
- Holloway, G.; Shankar, B.; Rahman, S. Bayesian Spatial Probit Estimation: A Primer and an Application to HYV Rice Adoption. Agric. Econ. 2002, 27, 383–402. [Google Scholar] [CrossRef]
- Läpple, D.; Holloway, G.; Lacombe, D.J.; O’Donoghue, C. Sustainable Technology Adoption: A Spatial Analysis of the Irish Dairy Sector. Eur. Rev. Agric. Econ. 2017, 44, 810–835. [Google Scholar] [CrossRef]
- Läpple, D.; Kelley, H. Spatial Dependence in the Adoption of Organic Drystock Farming in Ireland. Eur. Rev. Agric. Econ. 2015, 42, 315–337. [Google Scholar] [CrossRef]
- Wollni, M.; Andersson, C. Spatial Patterns of Organic Agriculture Adoption: Evidence from Honduras. Ecol. Econ. 2014, 97, 120–128. [Google Scholar] [CrossRef]
- Roberts, D.; Majewski, E.; Sulewski, P. Farm Household Interactions with Local Economies: A Comparison of Two EU Case Study Areas. Land Use Policy 2013, 31, 156–165. [Google Scholar] [CrossRef]
- Lange, A.; Piorr, A.; Siebert, R.; Zasada, I. Spatial Differentiation of Farm Diversification: How Rural Attractiveness and Vicinity to Cities Determine Farm Households’ Response to the CAP. Land Use Policy 2013, 31, 136–144. [Google Scholar] [CrossRef]
- Weltin, M.; Zasada, I.; Franke, C.; Piorr, A.; Raggi, M.; Viaggi, D. Analysing Behavioural Differences of Farm Households: An Example of Income Diversification Strategies Based on European Farm Survey Data. Land Use Policy 2017, 62, 172–184. [Google Scholar] [CrossRef]
- Schneider, K.; Skevas, I.; Lansink, A.O. Spatial Spillovers on Input-Specific Inefficiency of Dutch Arable Farms. J. Agric. Econ. 2021, 72, 224–243. [Google Scholar] [CrossRef]
- Skevas, I.; Lansink, A.O. Dynamic Inefficiency and Spatial Spillovers in Dutch Dairy Farming. J. Agric. Econ. 2020, 71, 742–759. [Google Scholar] [CrossRef]
- Hoppe, R.A.; Korb, P.J. Understanding U.S. Farm Exits. Available online: https://ageconsearch.umn.edu/record/7212/ (accessed on 8 July 2021).
- Breustedt, G.; Glauben, T. Driving Forces behind Exiting from Farming in Western Europe. J. Agric. Econ. 2007, 58, 115–127. [Google Scholar] [CrossRef]
- Landi, C.; Stefani, G.; Rocchi, B.; Lombardi, G.V.; Giampaolo, S. Regional Differentiation and Farm Exit: A Hierarchical Model for Tuscany. J. Agric. Econ. 2016, 67, 208–230. [Google Scholar] [CrossRef]
- Thiermann, I.; Breustedt, G.; Rosenau, C. The Impact of Size on Exiting from Livestock Production—An Empirical Analysis of Dairy and Sow Farms in Germany—GJAE—German Journal of Agricultural Economics. GJAE Ger. J. Agric. Econ. 2019, 68, 139–155. [Google Scholar]
- Bragg, L.A.; Dalton, T.J. Factors Affecting the Decision to Exit Dairy Farming: A Two-Stage Regression Analysis. J. Dairy Sci. 2004, 87, 3092–3098. [Google Scholar] [CrossRef]
- Dong, F.; Hennessy, D.A.; Jensen, H.H.; Volpe, R.J. Technical Efficiency, Herd Size, and Exit Intentions in U.S. Dairy Farms. Agric. Econ. 2016, 47, 533–545. [Google Scholar] [CrossRef]
- Weiss, C.R. Farm Growth and Survival: Econometric Evidence for Individual Farms in Upper Austria. Am. J. Agric. Econ. 1999, 81, 103–116. [Google Scholar] [CrossRef]
- Gale, H.F. Age-Specific Patterns of Exit and Entry in U.S. Farming, 1978–1997. Appl. Econ. Perspect. Policy 2003, 25, 168–186. [Google Scholar] [CrossRef]
- Pietola, K.; Väre, M.; Lansink, A.O. Timing and Type of Exit from Farming: Farmers’ Early Retirement Programmes in Finland. Eur. Rev. Agric. Econ. 2003, 30, 99–116. [Google Scholar] [CrossRef]
- Mishra, A.K.; El-Osta, H.S.; Shaik, S. Succession Decisions in U.S. Family Farm Businesses. J. Agric. Resour. Econ. 2010, 35, 133–152. [Google Scholar]
- Corsi, A.; Frontuto, V.; Novelli, S. What Drives Farm Structural Change? An Analysis of Economic, Demographic and Succession Factors. Agriculture 2021, 11, 438. [Google Scholar] [CrossRef]
- Glauben, T.; Tietje, H.; Weiss, C. Agriculture on the Move: Exploring Regional Differences in Farm Exit Rates in Western Germany. Jahrb. Reg. 2006, 26, 103–118. [Google Scholar] [CrossRef]
- Kazukauskas, A.; Newman, C.; Clancy, D.; Sauer, J. Disinvestment, Farm Size, and Gradual Farm Exit: The Impact of Subsidy Decoupling in a European Context. Am. J. Agric. Econ. 2013, 95, 1068–1087. [Google Scholar] [CrossRef]
- Goetz, S.J.; Debertin, D.L. Why Farmers Quit: A County-Level Analysis. Am. J. Agric. Econ. 2001, 83, 1010–1023. [Google Scholar] [CrossRef]
- Foltz, J.D. Entry, Exit, and Farm Size: Assessing an Experiment in Dairy Price Policy. Am. J. Agric. Econ. 2004, 86, 594–604. [Google Scholar] [CrossRef]
- Piet, L.; Desjeux, Y. New Perspectives on the Distribution of Farm Incomes and the Redistributive Impact of CAP Payments. Eur. Rev. Agric. Econ. 2021, 48, 385–414. [Google Scholar] [CrossRef]
- Neuenfeldt, S.; Gocht, A.; Heckelei, T.; Ciaian, P. Explaining Farm Structural Change in the European Agriculture: A Novel Analytical Framework. Eur. Rev. Agric. Econ. 2019, 46, 713–768. [Google Scholar] [CrossRef]
- Gocht, A.; Britz, W. EU-Wide Farm Type Supply Models in CAPRI—How to Consistently Disaggregate Sector Models into Farm Type Models. J. Policy Model. 2011, 33, 146–167. [Google Scholar] [CrossRef]
- Louhichi, K.; Ciaian, P.; Espinosa, M.; Perni, A.; Gomez y Paloma, S. Economic Impacts of CAP Greening: Application of an EU-Wide Individual Farm Model for CAP Analysis (IFM-CAP). Eur. Rev. Agric. Econ. 2018, 45, 205–238. [Google Scholar] [CrossRef]
- Cooper, L.G.; Nakanishi, M. Market-Share Analysis: Evaluating Competitive Marketing Effectiveness; International Series in Quantitative Marketing; 6. Print; Kluwer: Boston, MA, USA, 1997; ISBN 978-0-89838-278-5. [Google Scholar]
- Fok, D.; Hans, F.P.; Paap, R. Econometric analysis of the market share attraction model. In Advances in Econometrics; Advances in Econometrics; Emerald Group Publishing Limited: Bingley, UK, 2002; Volume 16, pp. 223–256. ISBN 978-1-84950-142-2. [Google Scholar]
- Kotler, P. Marketing Management: Analysis, Planning, and Control; Prentice-Hall: Hoboken, NJ, USA, 1984; ISBN 978-0-13-557927-5. [Google Scholar]
- Bell, D.E.; Keeney, R.L.; Little, J.D.C. A Market Share Theorem. J. Mark. Res. 1975, 12, 136–141. [Google Scholar] [CrossRef]
- Erickson, G.M.; Finkler, S.A. Determinants of Market Share for a Hospital’s Services. Med. Care 1985, 23, 1003–1018. [Google Scholar] [CrossRef]
- Banker, R.D.; Kauffman, R.J. Strategic Contributions of Information Technology: An Empirical Study of Atm Networks; Social Science Research Network: Rochester, NY, USA, 1988. [Google Scholar]
- Banker, R.; Chen, P.Y.; Liu, F.C.; Ou, C.S. Complementarity of the Impact of Alternative Service Channels on Bank Performance. In Proceedings of the ICIS 2010 Proceedings—Thirty First International Conference on Information Systems, Saint Louis, MI, USA, 1 December 2010. [Google Scholar]
- Bod’a, M. Stochastic Sensitivity Analysis of Concentration Measures. Cent. Eur. J. Oper. Res. 2017, 25, 441–471. [Google Scholar] [CrossRef]
- Gocht, A.; Röder, N.; Neuenfeldt, S.; Storm, H.; Heckelei, T. Modelling Farm Structural Change: A Feasibility Study for Ex Post Modelling Utilizing FADN and FSS Data in Germany and Developing an ex Ante Forecast Module for the CAPRI Farm Type Layer Baseline; Publications Office: Luxembourg, 2012. [Google Scholar]
- Nakanishi, M.; Cooper, L.G. Technical Note—Simplified Estimation Procedures for MCI Models. Mark. Sci. 1982, 1, 314–322. [Google Scholar] [CrossRef][Green Version]
- Goddard, E.; Weersink, A.; Chen, K.; Turvey, C.G. Economics of Structural Change in Agriculture. Can. J. Agric. Econ. Can. Agroecon. 1993, 41, 475–489. [Google Scholar] [CrossRef]
- Fabbris, L. Measures of Predictor Variable Importance in Multiple Regression: An Additional Suggestion. Qual. Quant. 1980, 14, 787–792. [Google Scholar] [CrossRef]
- Grömping, U. Variable Importance in Regression Models. WIREs Comput. Stat. 2015, 7, 137–152. [Google Scholar] [CrossRef]
- Mittenzwei, K.; Britz, W. Analysing Farm-Specific Payments for Norway Using the Agrispace Model. J. Agric. Econ. 2018, 69, 777–793. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).