Bayesian Information-Theoretic Calibration of Radiotherapy Sensitivity Parameters for Informing Effective Scanning Protocols in Cancer
Abstract
1. Introduction
2. Mathematical Models Used for Testing
2.1. The One-Compartment Ode Model
2.2. The Two-Compartment Ode Model
2.3. The Cellular Automaton Model
2.4. Radiotherapy Treatment
3. Bayesian Information-Theoretic Methodology
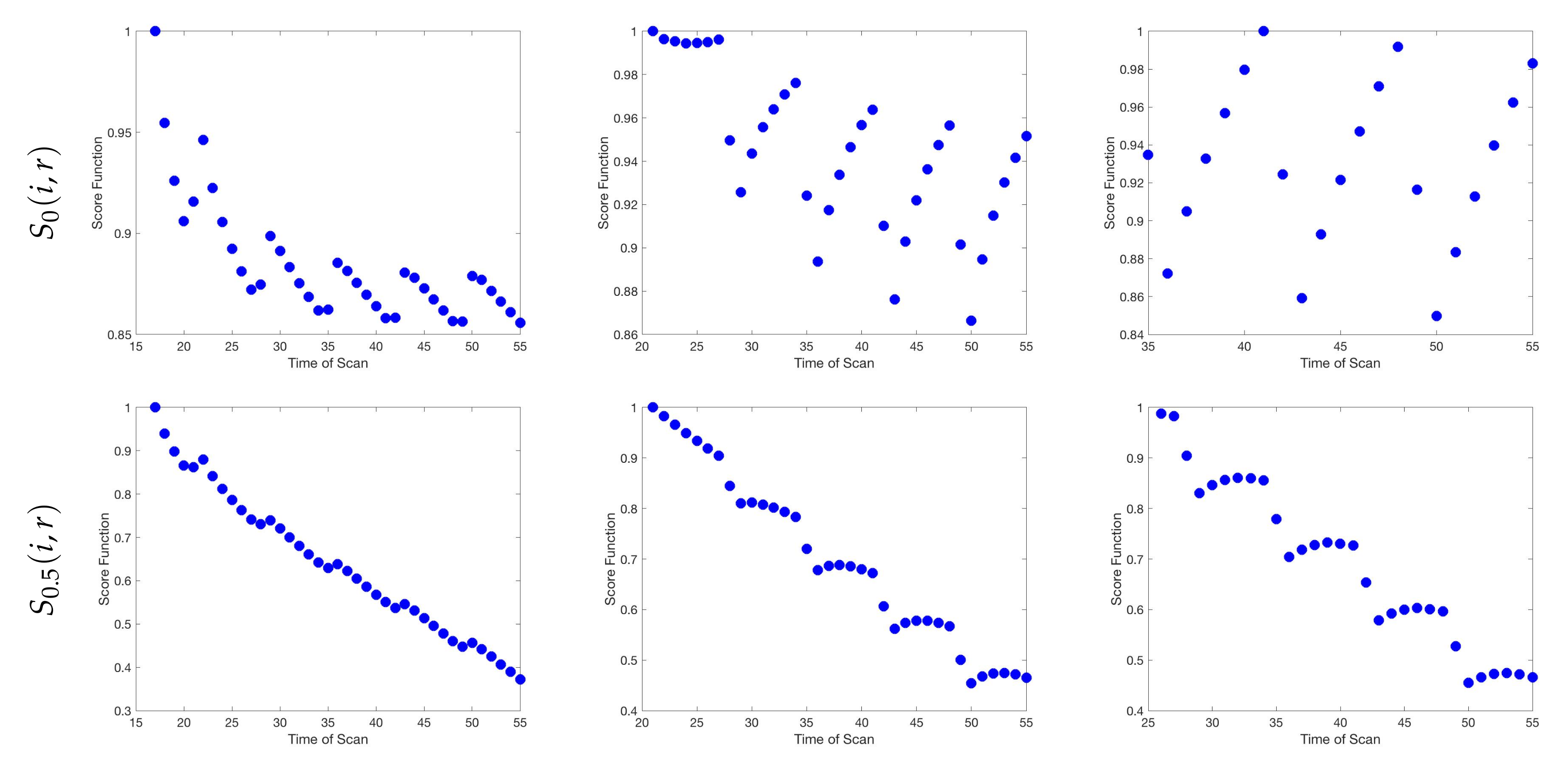
3.1. Experimental Design Framework Using Mutual Information
3.2. Modified Mutual Information for Time Series Data
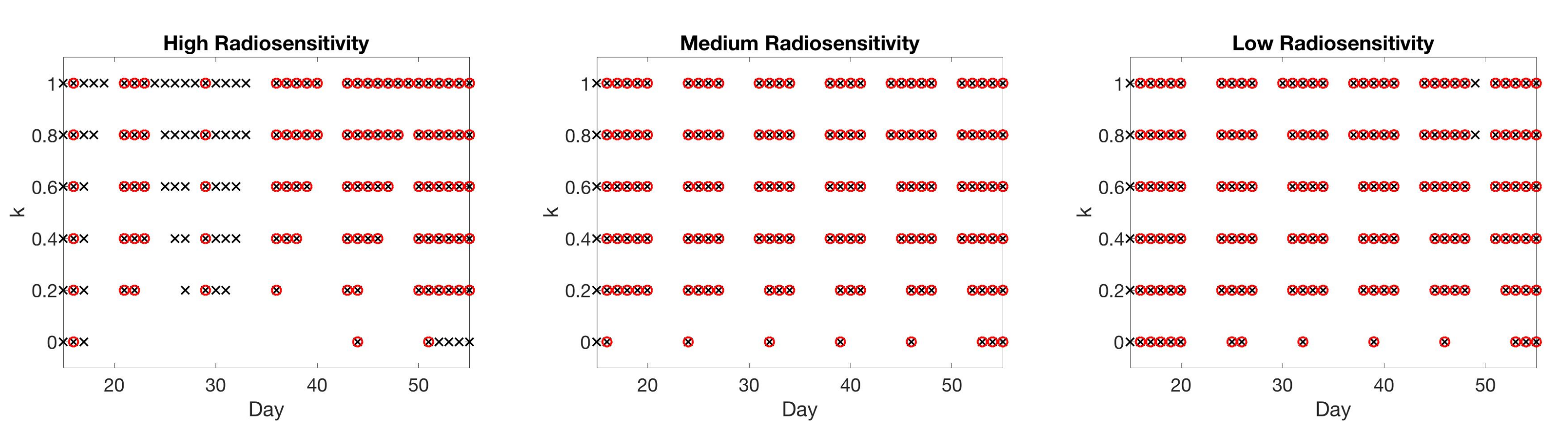
4. Simulation Results
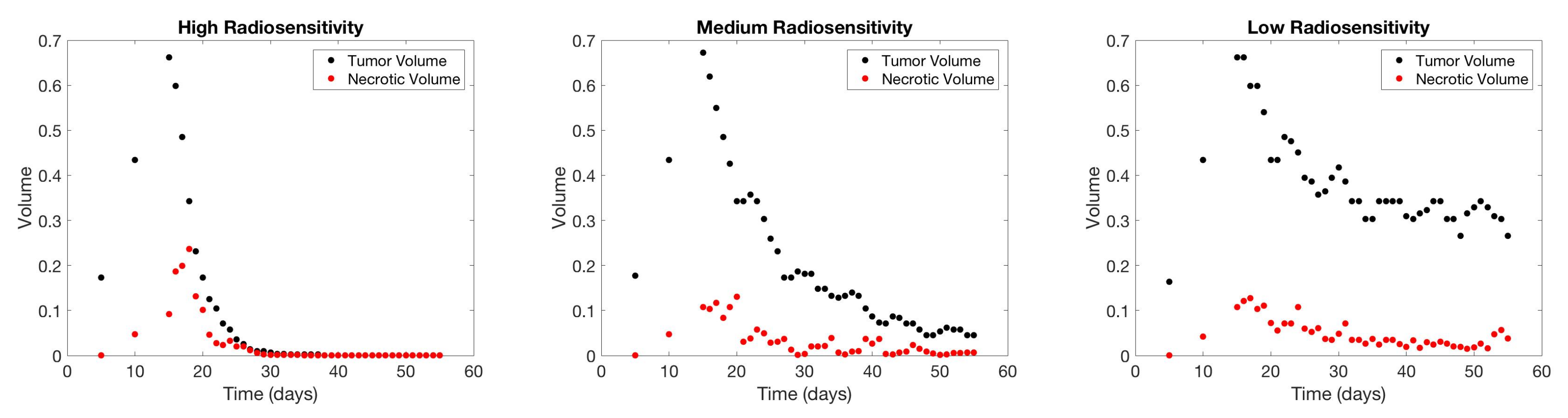
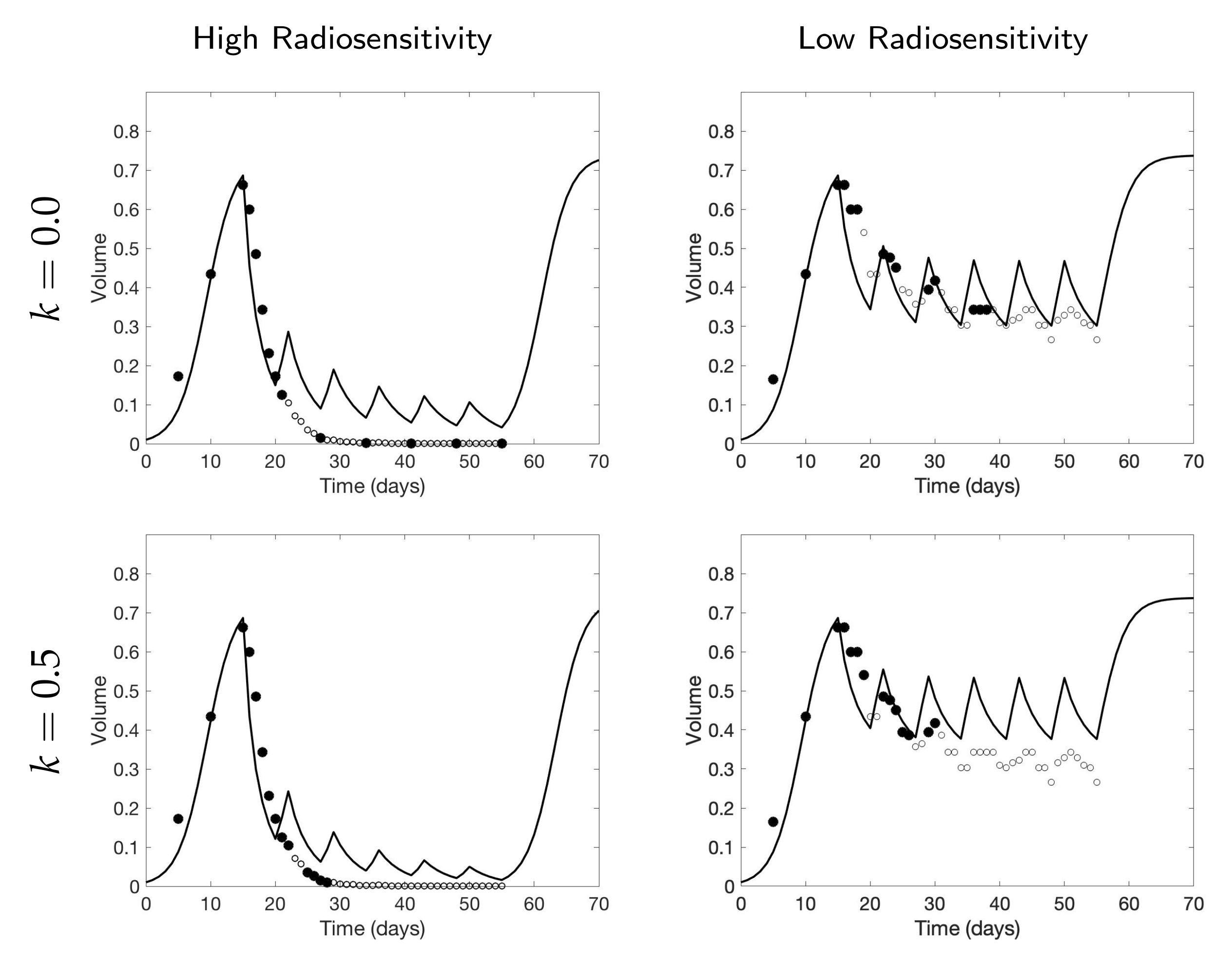
4.1. Scenario 1: Collecting One Scan Per Week
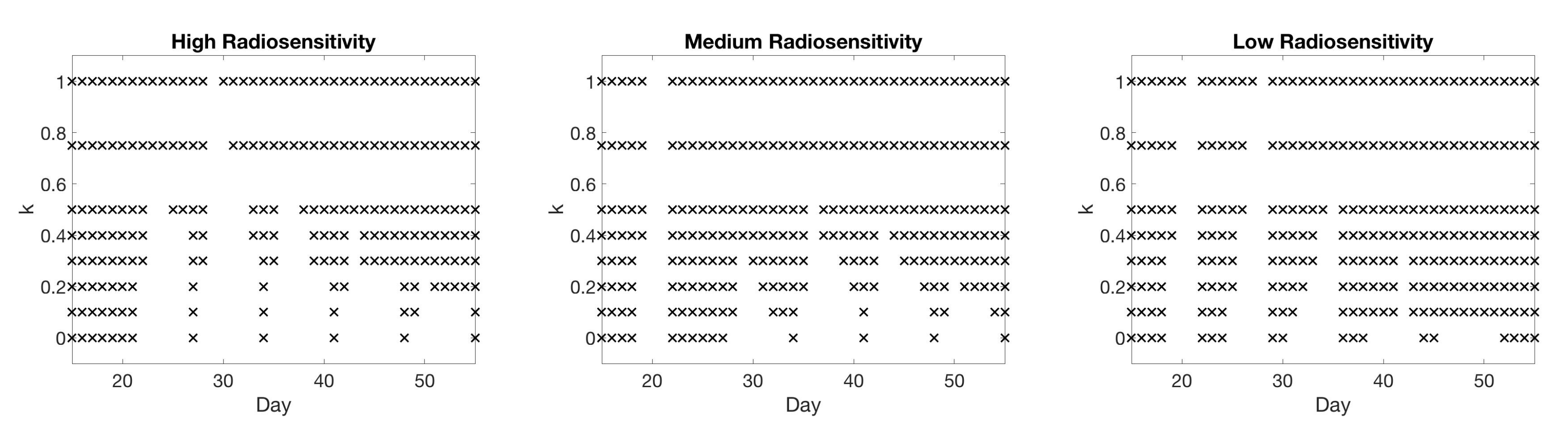
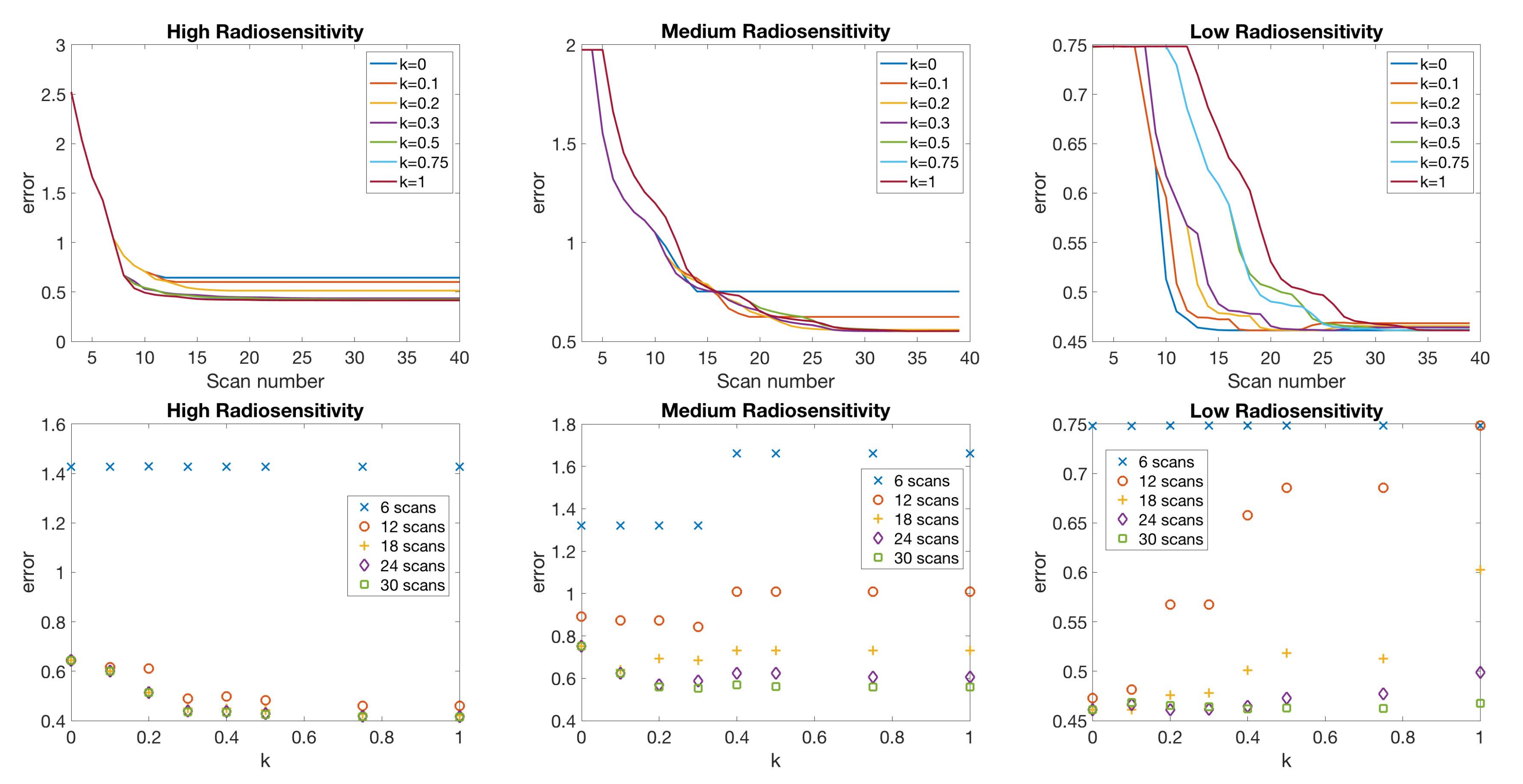
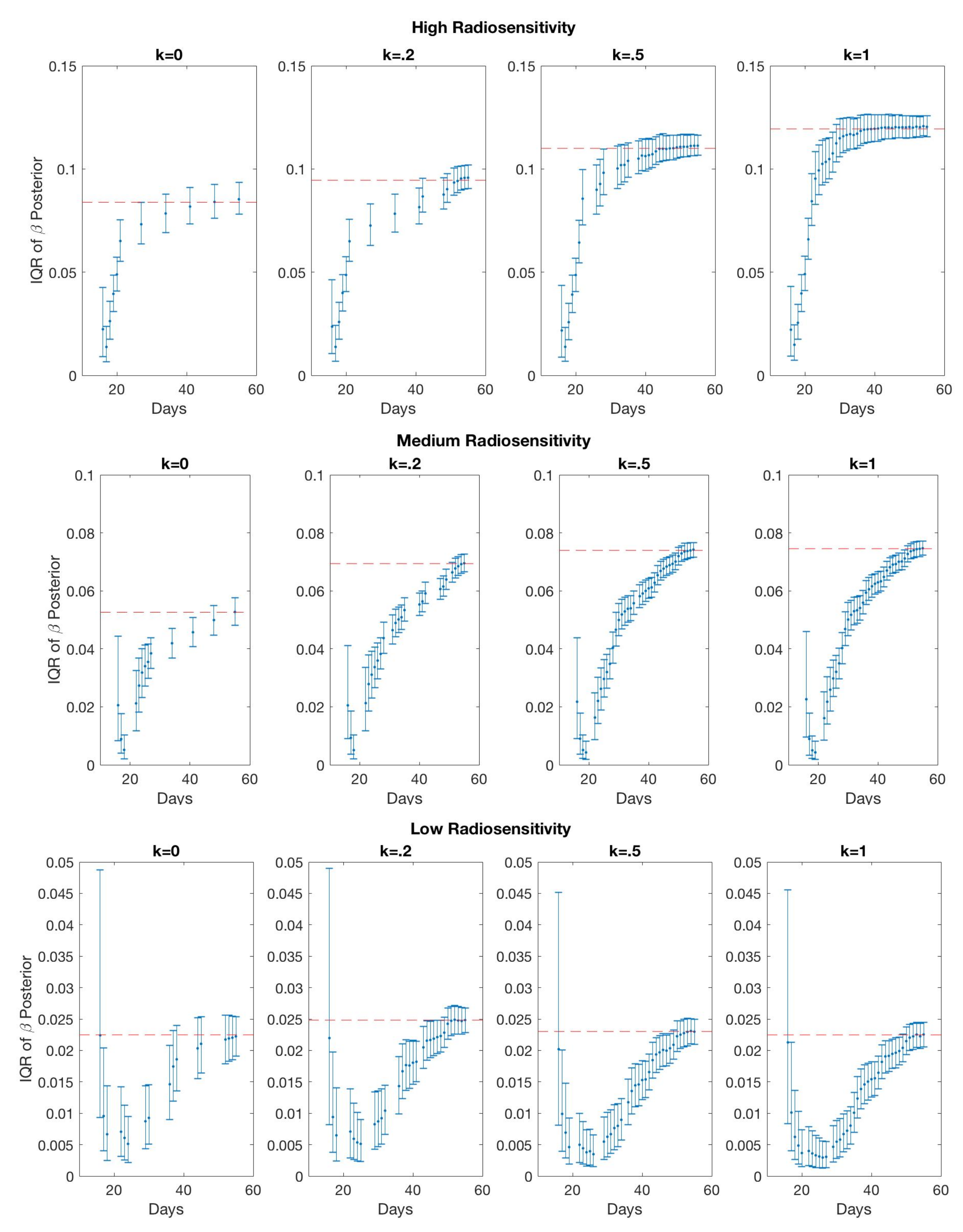
4.2. Scenario 2: One-Compartment Model with N Number of Scans
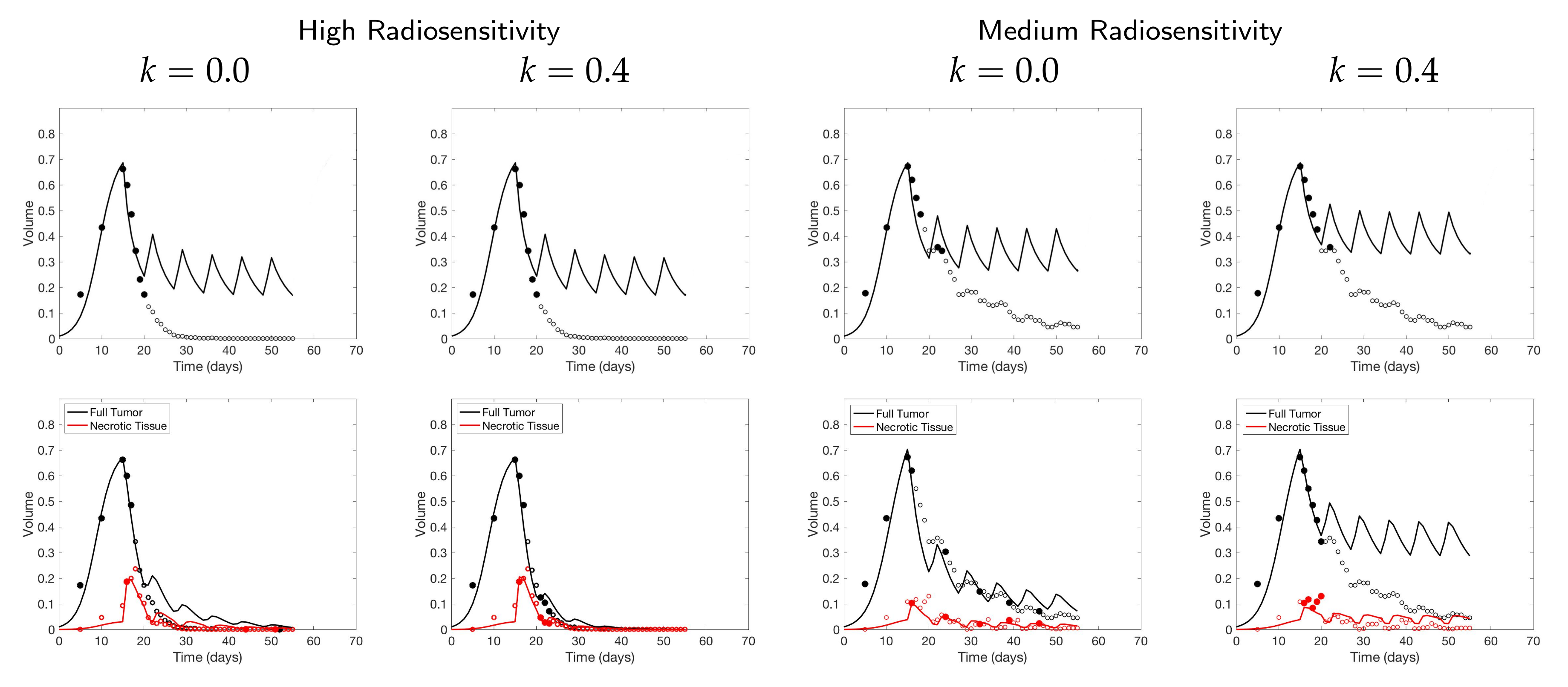
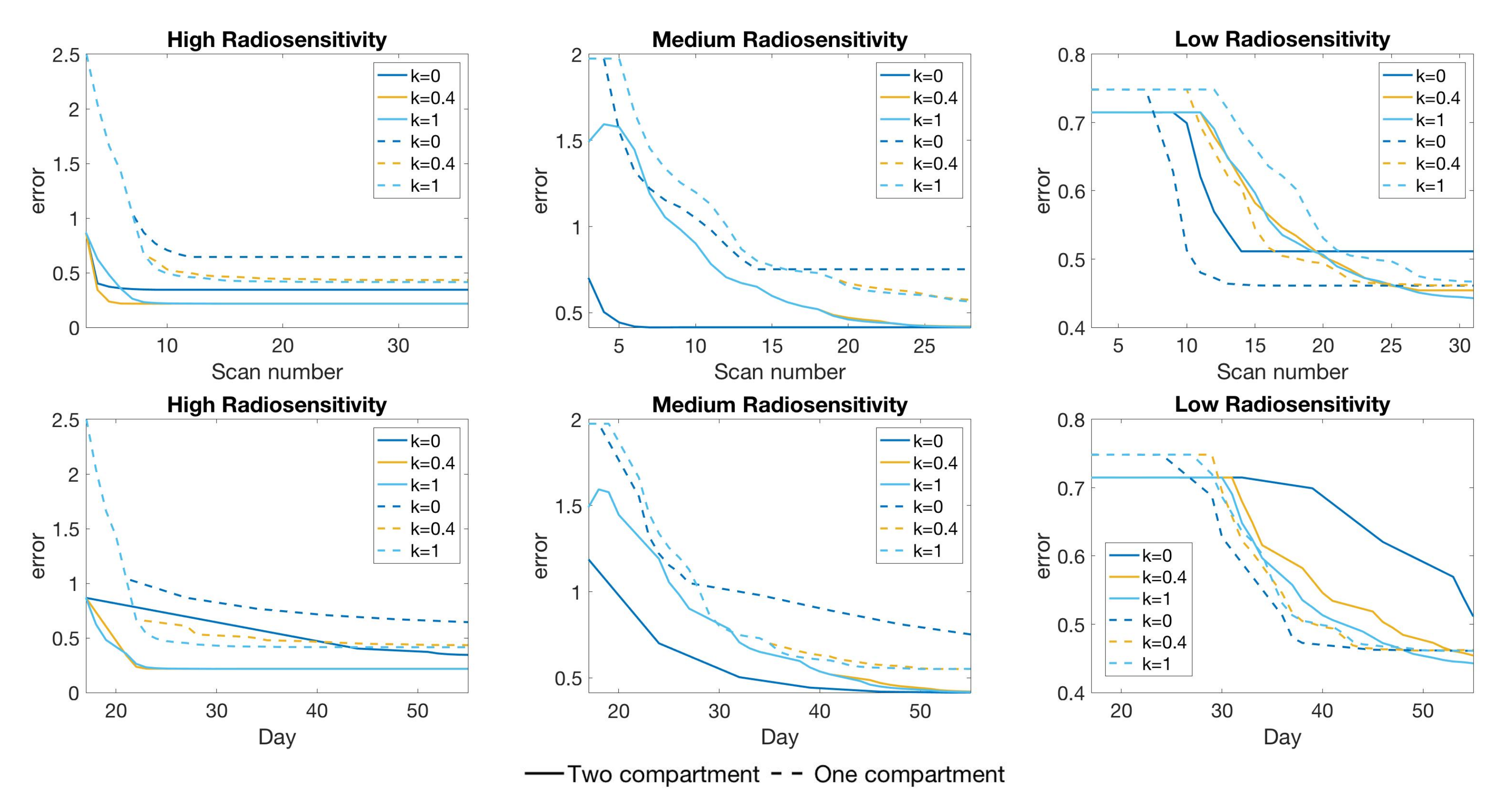
4.3. Scenario 3: Two-Compartment Model with N Number of Scans
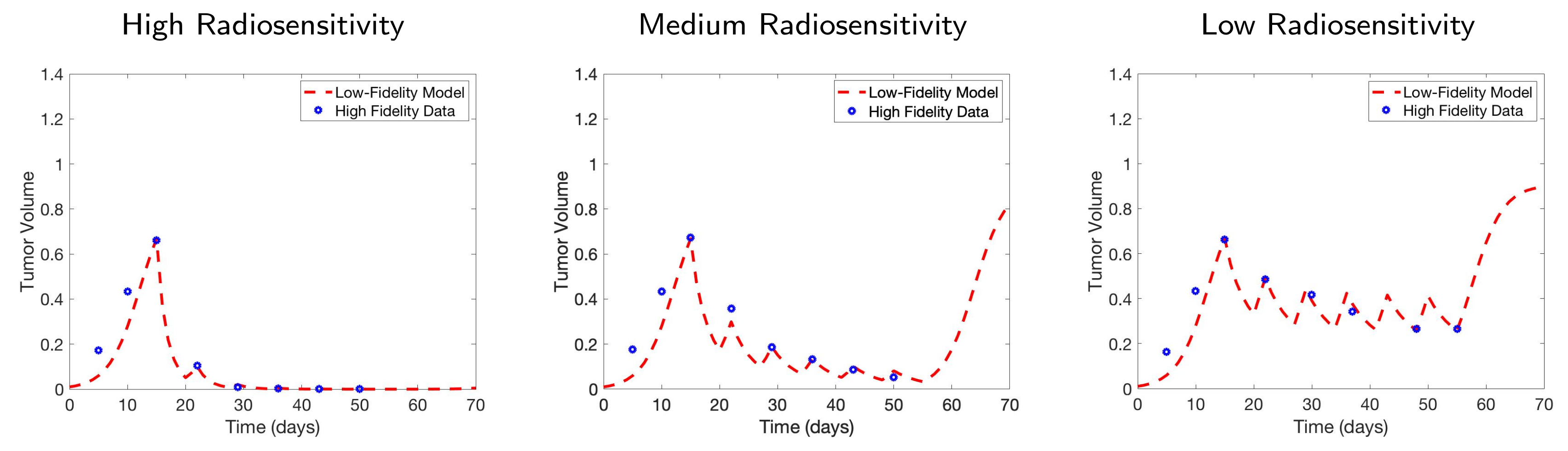
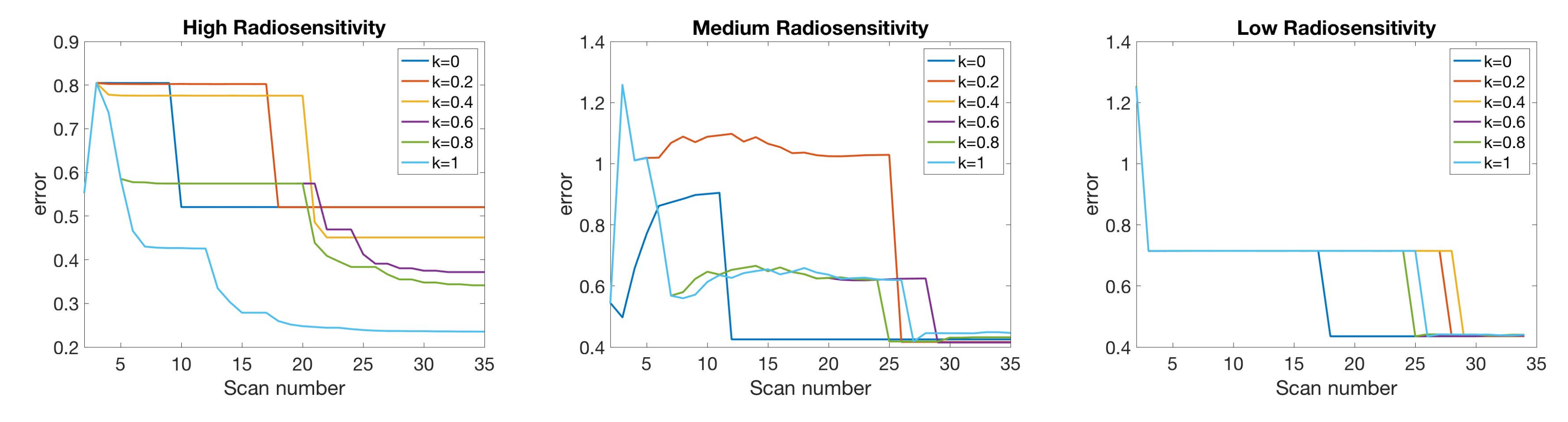
4.4. Scenario 4: Two-Compartment Model in Practical Setting
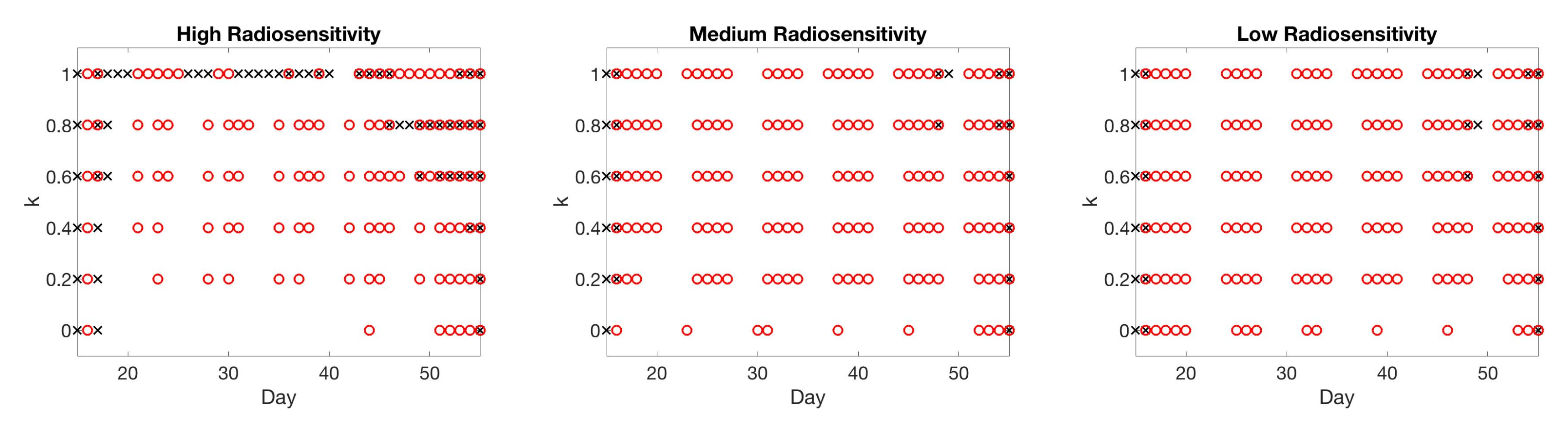
4.5. Summary of Scan Schedule Recommendations
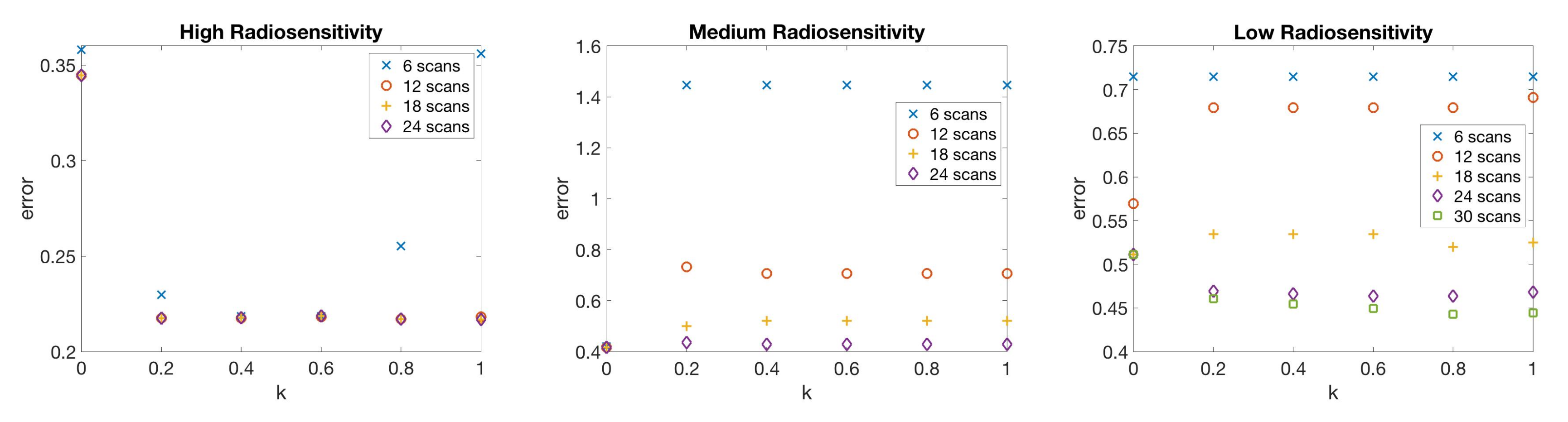
If only total tumor volume is measured, then for a small scan budget, our results recommend to start with a score function with small k, within . Then, if the patient is highly responsive to radiotherapy, increase , or if the patient is less responsive to radiotherapy, reduce to . When the budget of total scans is high (for example, more than 15), we suggest using large k in the range of , and then to increase k further if the patient is highly responsive to radiotherapy.
If both the tumor volume and necrotic volume can be measured, then for a small scan budget, our results suggest to start with a score function with parameter . Similarly to the one-compartment case, we might further recommend increasing k for highly responsive patients, or reducing k to for less responsive patients. For a scan budget at or above 15 scans, we suggest using a non-zero k, for instance, , in all scenarios.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ODE | Ordinary Differential Equation |
| L-Q | Linear-Quadratic |
| RT | Radiotherapy |
| CA | Cellular Automaton |
| kNN | kth-Nearest-Neighbor |
| DRAM | Delayed Rejection Adaptive Metropolis |
Appendix A. Parameter Values
| Parameter | Description | Value | Units |
|---|---|---|---|
| l | Cell size | 0.0018 | cm |
| L | Domain length | 0.36 | cm |
| Mean (standard deviation) cell cycle time | 18.3 (1.4) | h | |
| Background O concentration | mol cm | ||
| D | O diffusion constant | cms | |
| O concentration threshold for proliferating cells | mol cm | ||
| O concentration threshold for quiescent cells | mol cm | ||
| O consumption rate of proliferating cells | mol cms | ||
| O consumption rate of quiescent cells | mol cms | ||
| Rate of lysis of necrotic cells | 0.015 | hr |
| One-Compartment Model | Two-Compartment Model | |||||
|---|---|---|---|---|---|---|
| Parameter | High | Medium | Low | High | Medium | Low |
| A | 0.4584 | 0.4584 | 0.4584 | |||
| B | 0.6213 | 0.6213 | 0.6213 | |||
| 0.5193 | 0.4845 | 0.6236 | ||||
| k | 0.7201 | 0.9529 | 0.9031 | |||
| 0.0366 | 0.0828 | 0.1762 | ||||
| 0.7270 | 1.3476 | 1.6638 | ||||
Appendix B. KNn Estimate of Mutual Information
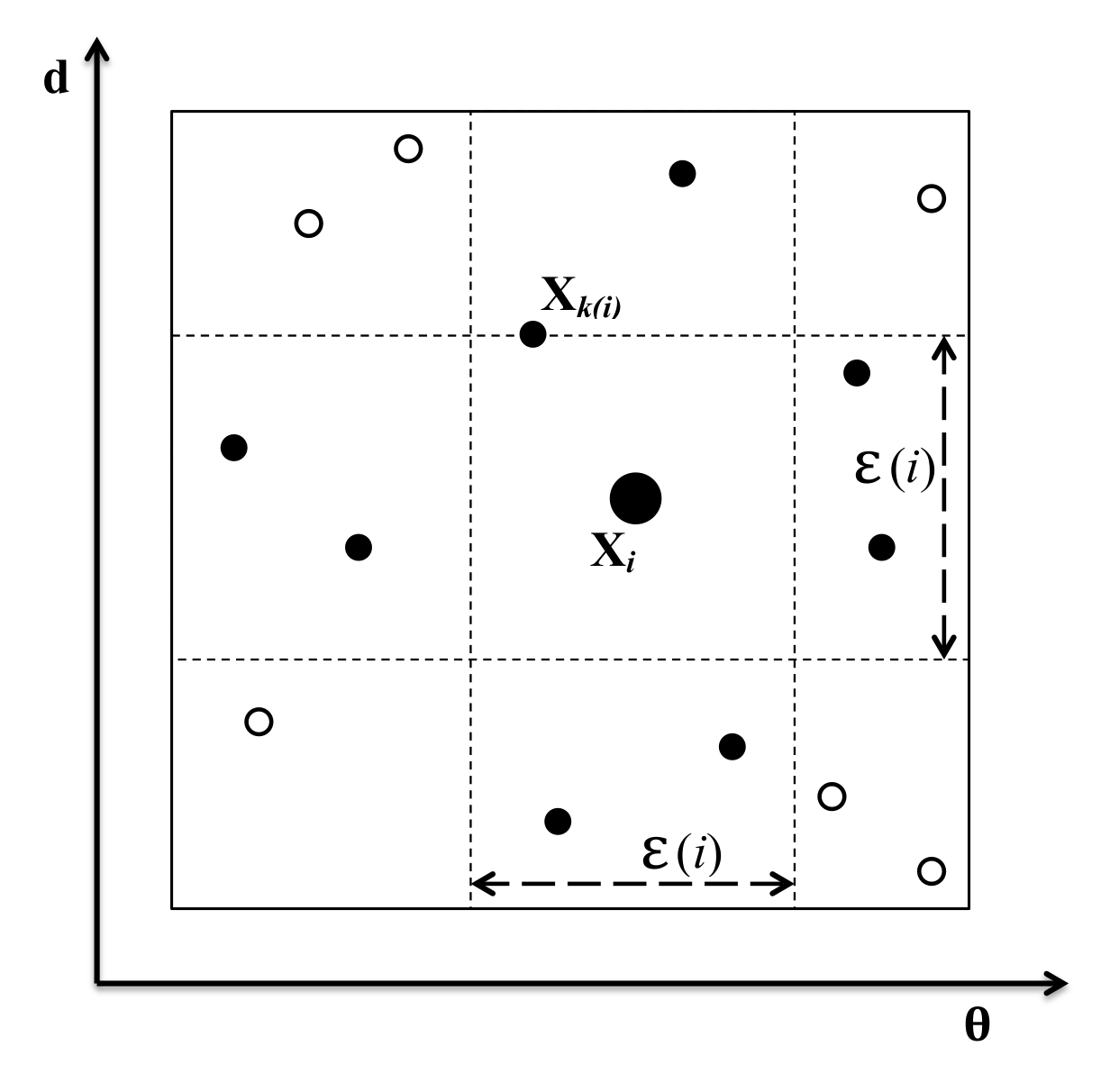
References
- Altrock, P.M.; Liu, L.L.; Michor, F. The mathematics of cancer: Integrating quantitative models. Nat. Rev. Cancer 2015, 15, 730–745. [Google Scholar] [CrossRef] [PubMed]
- Lavi, O.; Gottesman, M.M.; Levy, D. The dynamics of drug resistance: A mathematical perspective. Drug Resist. Updat. 2012, 15, 90–97. [Google Scholar] [CrossRef] [PubMed]
- Swierniak, A.; Kimmel, M.; Smieja, J. Mathematical modeling as a tool for planning anticancer therapy. Eur. J. Pharmacol. 2009, 625, 108–121. [Google Scholar] [CrossRef] [PubMed]
- Byrne, H.M. Dissecting cancer through mathematics: From the cell to the animal model. Nat. Rev. Cancer 2010, 10, 221–230. [Google Scholar] [CrossRef]
- Rockne, R.C.; Hawkins-Daarud, A.; Swanson, K.R.; Sluka, J.P.; Glazier, J.A.; Macklin, P.; Hormuth, D.A.; Jarrett, A.M.; Lima, E.A.; Tinsley Oden, J.; et al. The 2019 mathematical oncology roadmap. Phys. Biol. 2019, 16, 1–33. [Google Scholar] [CrossRef]
- Chambers, D.A.; Amir, E.; Saleh, R.R.; Rodin, D.; Keating, N.L.; Osterman, T.J.; Chen, J.L. The Impact of Big Data Research on Practice, Policy, and Cancer Care. Am. Soc. Clin. Oncol. Educ. Book 2019, 39, e167–e175. [Google Scholar] [CrossRef]
- Bibault, J.E.; Giraud, P.; Burgun, A. Big Data and machine learning in radiation oncology: State of the art and future prospects. Cancer Lett. 2016, 382, 110–117. [Google Scholar] [CrossRef]
- Murphy, H.; Jaafari, H.; Dobrovolny, H.M. Differences in predictions of ODE models of tumor growth: A cautionary example. BMC Cancer 2016, 16, 1–10. [Google Scholar] [CrossRef]
- Collis, J.; Connor, A.J.; Paczkowski, M.; Kannan, P.; Pitt-Francis, J.; Byrne, H.M.; Hubbard, M.E. Bayesian Calibration, Validation and Uncertainty Quantification for Predictive Modelling of Tumour Growth: A Tutorial. Bull. Math. Biol. 2017, 79, 939–974. [Google Scholar] [CrossRef]
- Koziol, J.A.; Falls, T.J.; Schnitzer, J.E. Different ODE models of tumor growth can deliver similar results. BMC Cancer 2020, 20, 1–10. [Google Scholar] [CrossRef]
- Liu, Y.; Purvis, J.; Shih, A.; Weinstein, J.; Agrawal, N.; Radhakrishnan, R. A multiscale computational approach to dissect early events in the erb family receptor mediated activation, differential signaling, and relevance to oncogenic transformations. Ann. Biomed. Eng. 2007, 35, 1012–1025. [Google Scholar] [CrossRef] [PubMed]
- Ramis-Conde, I.; Chaplain, M.A.; Anderson, A.R.; Drasdo, D. Multi-scale modelling of cancer cell intravasation: The role of cadherins in metastasis. Phys. Biol. 2009, 6. [Google Scholar] [CrossRef] [PubMed]
- Hawkins-Daarud, A.; Prudhomme, S.; van der Zee, K.G.; Oden, J.T. Bayesian calibration, validation, and uncertainty quantification of diffuse interface models of tumor growth. J. Math. Biol. 2013, 67, 1457–1485. [Google Scholar] [CrossRef] [PubMed]
- Kannan, P.; Paczkowski, M.; Miar, A.; Owen, J.; Kretzschmar, W.; Lucotti, S.; Kaeppler, J.; Chen, J.; Markelc, B.; Kunz-Schughart, L.; et al. Radiation resistant cancer cells enhance the survival and resistance of sensitive cells in prostate spheroids. bioRxiv 2019. [Google Scholar] [CrossRef]
- Cho, H.; Lewis, A.; Storey, K.; Jennings, R.; Shtylla, B.; Reynolds, A.; Byrne, H. A framework for performing data-driven modeling of tumor growth with radiotherapy treatment. In Springer Special Issue: Using Mathematics to Understand Biological Complexity, Women in Mathematical Biology; Springer: Berlin/Heidelberg, Germany, 2020; accepted. [Google Scholar]
- Thames, H.D.; Rodney Withers, H.; Peters, L.J.; Fletcher, G.H. Changes in early and late radiation responses with altered dose fractionation: Implications for dose-survival relationships. Int. J. Radiat. Oncol. Biol. Phys. 1982, 8, 219–226. [Google Scholar] [CrossRef]
- Fowler, J.F. The linear-quadratic formula and progress in fractionated radiotherapy. Br. J. Radiol. 1989, 62, 679–694. [Google Scholar] [CrossRef]
- Rockne, R.; Rockhill, J.K.; Mrugala, M.; Spence, A.M.; Kalet, I.; Hendrickson, K.; Lai, A.; Cloughesy, T.; Alvord, E.C.; Swanson, K.R. Predicting the efficacy of radiotherapy in individual glioblastoma patients in vivo: A mathematical modeling approach. Phys. Med. Biol. 2010, 55, 3271–3285. [Google Scholar] [CrossRef]
- Corwin, D.; Holdsworth, C.; Rockne, R.C.; Trister, A.D.; Mrugala, M.M.; Rockhill, J.K.; Stewart, R.D.; Phillips, M.; Swanson, K.R. Toward patient-specific, biologically optimized radiation therapy plans for the treatment of glioblastoma. PLoS ONE 2013, 8. [Google Scholar] [CrossRef]
- Sunassee, E.D.; Tan, D.; Ji, N.; Brady, R.; Moros, E.G.; Caudell, J.J.; Yartsev, S.; Enderling, H. Proliferation saturation index in an adaptive Bayesian approach to predict patient-specific radiotherapy responses. Int. J. Radiat. Biol. 2019, 95, 1421–1426. [Google Scholar] [CrossRef]
- Enderling, H.; Alfonso, J.C.L.; Moros, E.; Caudell, J.J.; Harrison, L.B. Integrating Mathematical Modeling into the Roadmap for Personalized Adaptive Radiation Therapy. Trends Cancer 2019, 5, 467–474. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Terejanu, G.; Upadhyay, R.R.; Miki, K. Bayesian experimental design for the active nitridation of graphite by atomic nitrogen. Exp. Therm. Fluid Sci. 2012, 36, 178–193. [Google Scholar] [CrossRef]
- Bryant, C.; Terejanu, G. An information-theoretic approach to optimally calibrate approximate models. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar] [CrossRef]
- Liepe, J.; Filippi, S.; Komorowski, M.; Stumpf, M.P. Maximizing the Information Content of Experiments in Systems Biology. PLoS Comput. Biol. 2013, 9, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Lewis, A.; Smith, R.; Williams, B.; Figueroa, V. An information theoretic approach to use high-fidelity codes to calibrate low-fidelity codes. J. Comput. Phys. 2016, 324, 24–43. [Google Scholar] [CrossRef]
- Lorenzo, G.; Pérez-García, V.M.; Mariño, A.; Pérez-Romasanta, L.A.; Reali, A.; Gomez, H. Mechanistic modelling of prostate-specific antigen dynamics shows potential for personalized prediction of radiation therapy outcome. J. R. Soc. Interface 2019, 16, 1–13. [Google Scholar] [CrossRef]
- Walker, A.J.; Ruzevick, J.; Malayeri, A.A.; Rigamonti, D.; Lim, M.; Redmond, K.J.; Kleinberg, L. Postradiation imaging changes in the CNS: How can we differentiate between treatment effect and disease progression? Future Oncol. 2014, 10, 1277–1297. [Google Scholar] [CrossRef]
- Ghaye, B.; Wanet, M.; El Hajjam, M. Imaging after radiation therapy of thoracic tumors. Diagn. Interv. Imaging 2016, 97, 1037–1052. [Google Scholar] [CrossRef]
- Rashidian, M.; Keliher, E.J.; Bilate, A.M.; Duarte, J.N.; Wojtkiewicz, G.R.; Jacobsen, J.T.; Cragnolini, J.; Swee, L.K.; Victora, G.D.; Weissleder, R.; et al. Noninvasive imaging of immune responses. Proc. Natl. Acad. Sci. USA 2015, 112, 6146–6151. [Google Scholar] [CrossRef]
- Shuhendler, A.J.; Ye, D.; Brewer, K.D.; Bazalova-Carter, M.; Lee, K.H.; Kempen, P.; Dane Wittrup, K.; Graves, E.E.; Rutt, B.; Rao, J. Molecular magnetic resonance imaging of tumor response to therapy. Sci. Rep. 2015, 5, 1–14. [Google Scholar] [CrossRef]
- Kasoji, S.K.; Rivera, J.N.; Gessner, R.C.; Chang, S.X.; Dayton, P.A. Early assessment of tumor response to radiation therapy using high-resolution quantitative microvascular ultrasound imaging. Theranostics 2018, 8, 156–168. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Deng, H.; Yang, W.; Wang, Z.; Lin, L.; Munasinghe, J.; Jacobson, O.; Liu, Y.; Tang, L.; Ni, Q.; et al. Early stratification of radiotherapy response by activatable inflammation magnetic resonance imaging. Nat. Commun. 2020, 11, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Hall, E.J. Radiobiology for the Radiologist; J.B. Lippincott: Philadelphia, PA, USA, 1994. [Google Scholar]
- Enderling, H.; Chaplain, M.A.; Hahnfeldt, P. Quantitative Modeling of Tumor Dynamics and Radiotherapy. Acta Biotheor. 2010, 58, 341–353. [Google Scholar] [CrossRef] [PubMed]
- Lewin, T.D. Modelling the Impact of Heterogeneity in Tumor Composition on the Response to Fractionated Radiotherapy. Ph.D. Thesis, University of Oxford, Oxford, UK, 2018. [Google Scholar]
- Lewin, T.D.; Byrne, H.M.; Maini, P.K.; Caudell, J.J.; Moros, E.G.; Enderling, H. The importance of dead material within a tumour on the dynamics in response to radiotherapy. Phys. Med. Biol. 2020, 65, 015007. [Google Scholar] [CrossRef] [PubMed]
- Lewin, T.D.; Maini, P.K.; Moros, E.G.; Enderling, H.; Byrne, H.M. A three phase model to investigate the effects of dead material on the growth of avascular tumours. Math. Model. Nat. Phenom. 2020, 15, 1–29. [Google Scholar] [CrossRef]
- Lea, D.E.; Catcheside, D.G. The mechanism of the induction by radiation of chromosome aberrations in Tradescantia. J. Genet. 1942, 44, 216–245. [Google Scholar] [CrossRef]
- Pérez-García, V.M.; Bogdanska, M.; Martínez-González, A.; Belmonte-Beitia, J.; Schucht, P.; Pérez-Romasanta, L.A. Delay effects in the response of low-grade gliomas to radiotherapy: A mathematical model and its therapeutical implications. Math. Med. Biol. 2015, 32, 307–329. [Google Scholar] [CrossRef]
- Prokopiou, S.; Moros, E.G.; Poleszczuk, J.; Caudell, J.; Torres-Roca, J.F.; Latifi, K.; Lee, J.K.; Myerson, R.; Harrison, L.B.; Enderling, H. A proliferation saturation index to predict radiation response and personalize radiotherapy fractionation. Radiat. Oncol. 2015, 10, 1–8. [Google Scholar] [CrossRef]
- Poleszczuk, J.; Walker, R.; Moros, E.G.; Latifi, K.; Caudell, J.J.; Enderling, H. Predicting Patient-Specific Radiotherapy Protocols Based on Mathematical Model Choice for Proliferation Saturation Index. Bull. Math. Biol. 2018, 80, 1195–1206. [Google Scholar] [CrossRef]
- Haario, H.; Laine, M.; Mira, A.; Saksman, E. DRAM: Efficient adaptive MCMC. Stat. Comput. 2006, 16, 339–354. [Google Scholar] [CrossRef]
- Smith, R. Uncertainty Quantification: Theory, Implementation, and Applications; SIAM: Philadelphia, PA, USA, 2014. [Google Scholar]
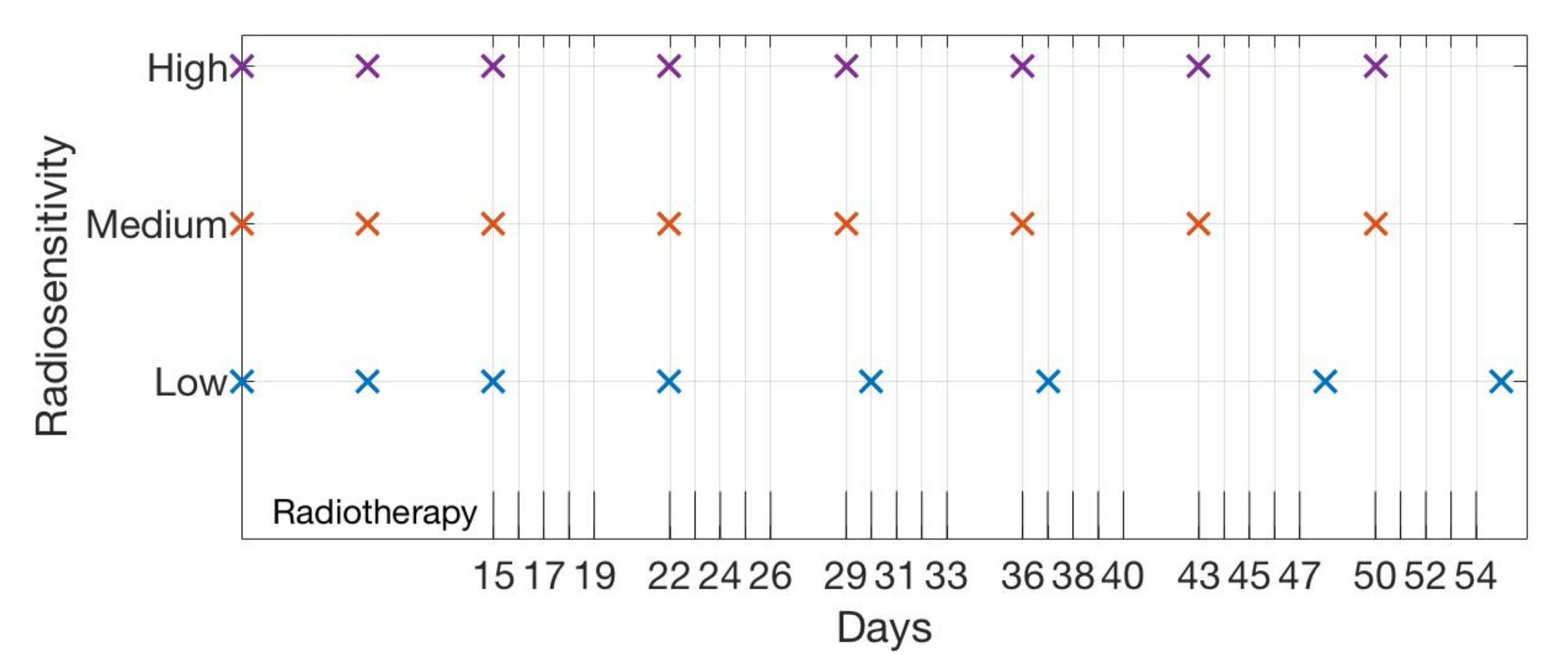
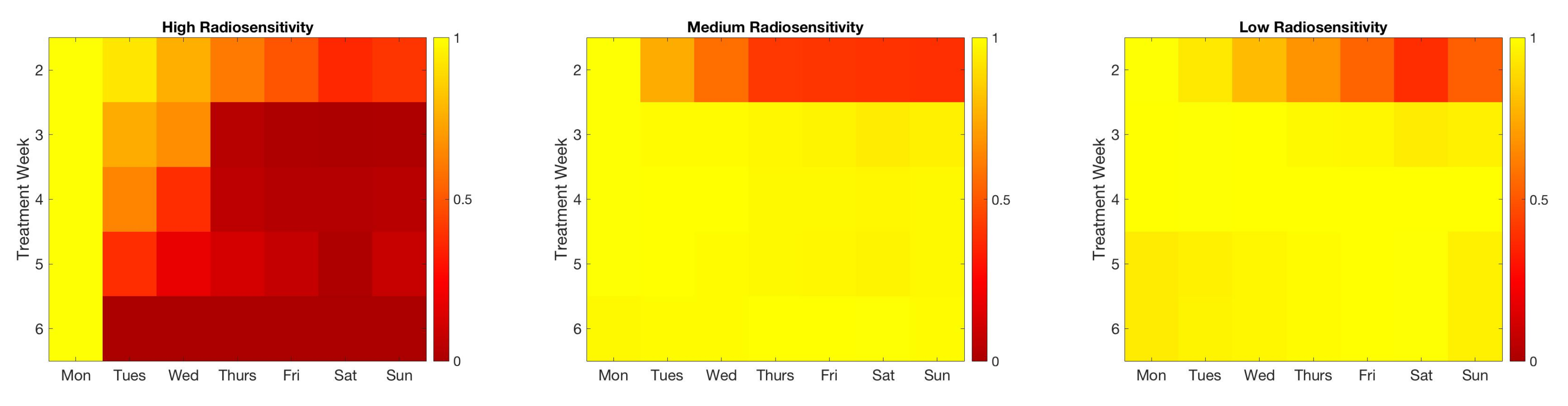
| Initial | Week 1 | Week 2 | Week 3 | Week 4 | Week 5 | Week 6 | |
|---|---|---|---|---|---|---|---|
| High | 5 10 | 15 | 22 (1) | 29 (1) | 36 (1) | 43 (1) | 50 (1) |
| Medium | 5 10 | 15 | 22 (1) | 29 (1) | 36 (1) | 43 (1) | 50 (1) |
| Low | 5 10 | 15 | 22 (1) | 30 (2) | 37 (2) | 48 (6) | 55 (6) |
| Radiosensitivity | ||||
|---|---|---|---|---|
| High | 0.0838 | 0.0945 | 0.1100 | 0.1194 |
| Medium | 0.0526 | 0.0694 | 0.0740 | 0.0745 |
| Low | 0.0225 | 0.0248 | 0.0239 | 0.0225 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, H.; Lewis, A.L.; Storey, K.M. Bayesian Information-Theoretic Calibration of Radiotherapy Sensitivity Parameters for Informing Effective Scanning Protocols in Cancer. J. Clin. Med. 2020, 9, 3208. https://doi.org/10.3390/jcm9103208
Cho H, Lewis AL, Storey KM. Bayesian Information-Theoretic Calibration of Radiotherapy Sensitivity Parameters for Informing Effective Scanning Protocols in Cancer. Journal of Clinical Medicine. 2020; 9(10):3208. https://doi.org/10.3390/jcm9103208
Chicago/Turabian StyleCho, Heyrim, Allison L. Lewis, and Kathleen M. Storey. 2020. "Bayesian Information-Theoretic Calibration of Radiotherapy Sensitivity Parameters for Informing Effective Scanning Protocols in Cancer" Journal of Clinical Medicine 9, no. 10: 3208. https://doi.org/10.3390/jcm9103208
APA StyleCho, H., Lewis, A. L., & Storey, K. M. (2020). Bayesian Information-Theoretic Calibration of Radiotherapy Sensitivity Parameters for Informing Effective Scanning Protocols in Cancer. Journal of Clinical Medicine, 9(10), 3208. https://doi.org/10.3390/jcm9103208






