Role of Additional Screws and Rod Fixation in Cage Loading During Oblique Lateral Interbody Fusion: A Finite Element Analysis
Abstract
1. Introduction
2. Materials and Methods
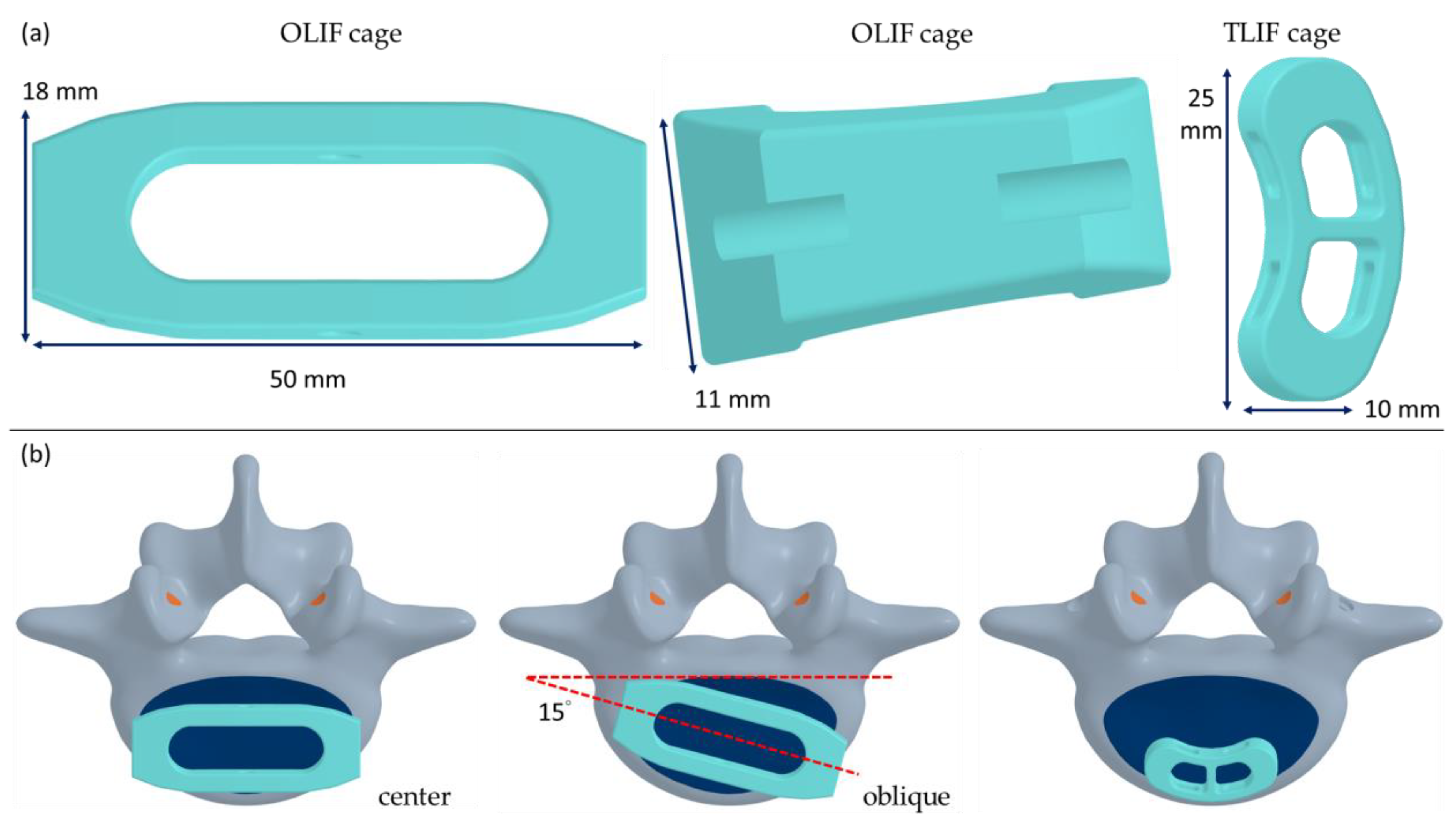
2.1. Solid Modeling
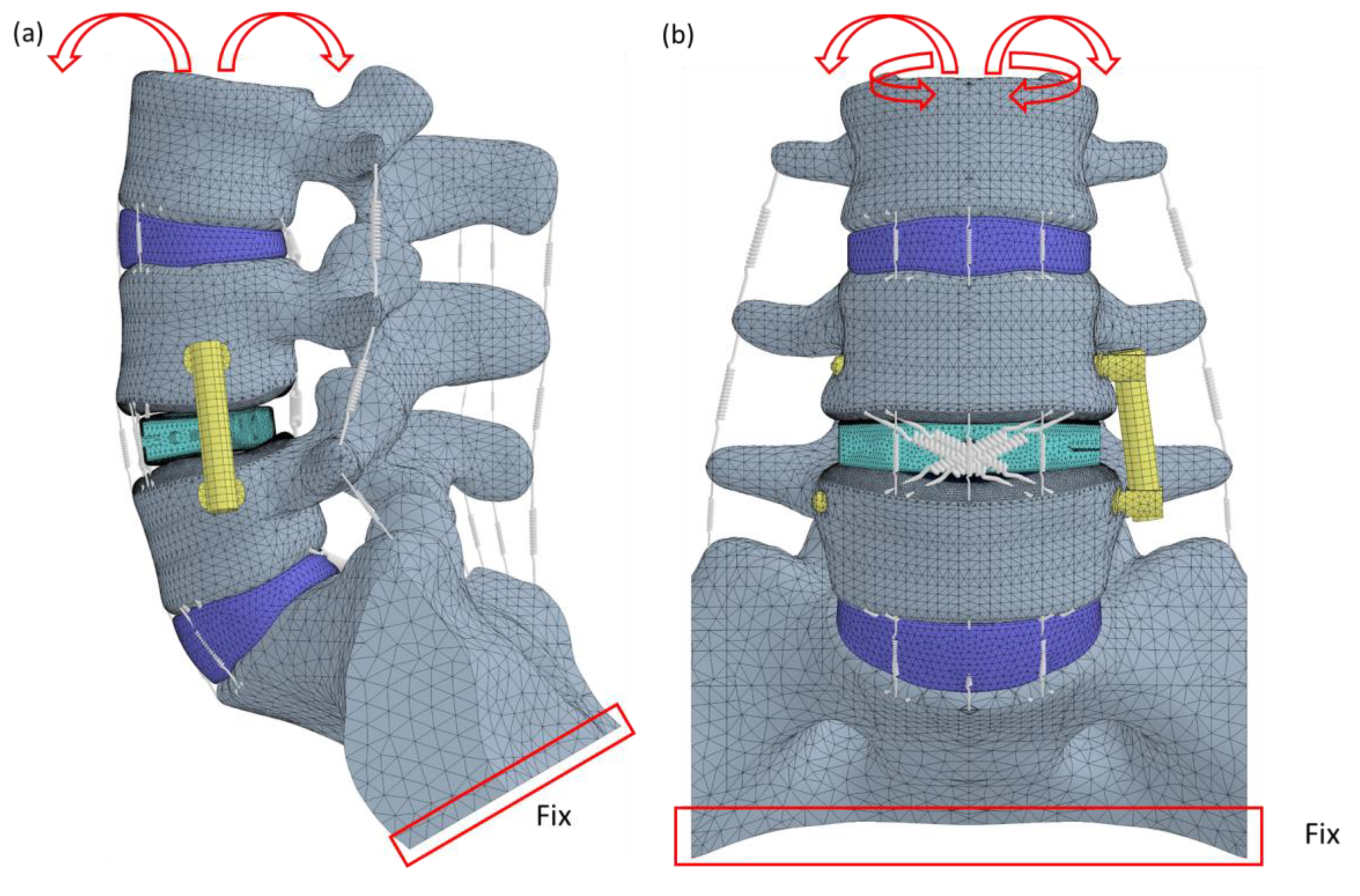
2.2. Finite Element Modeling
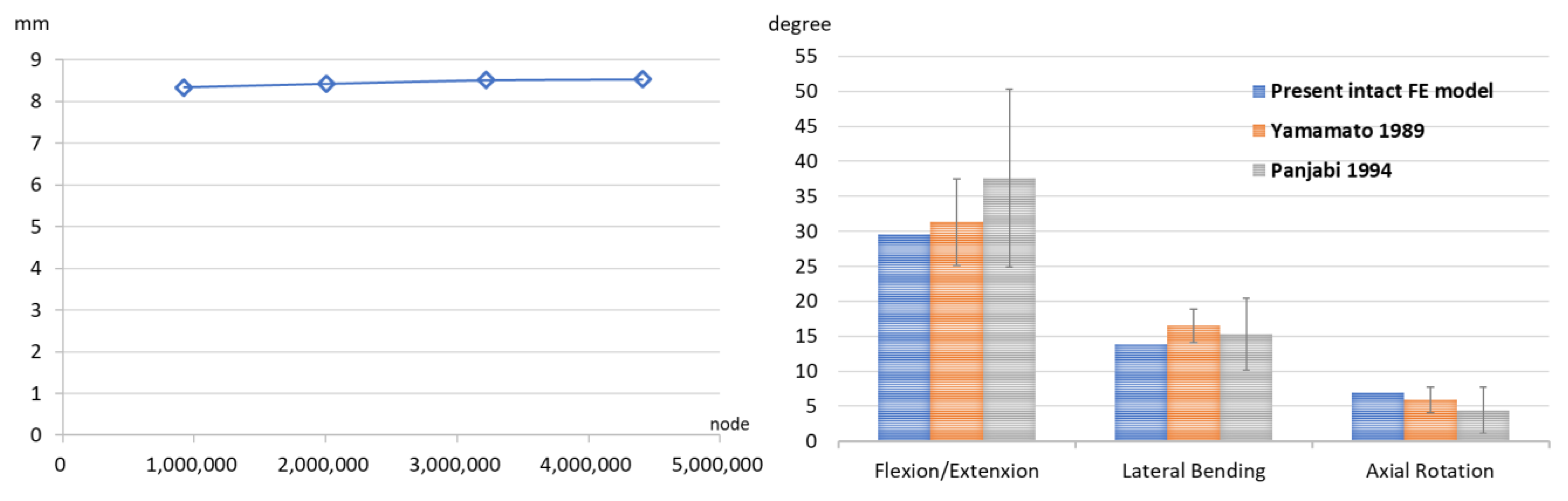
2.3. Convergence and Validation Tests
2.4. Boundary Condition
2.5. Index
3. Results
3.1. Convergence and Validation
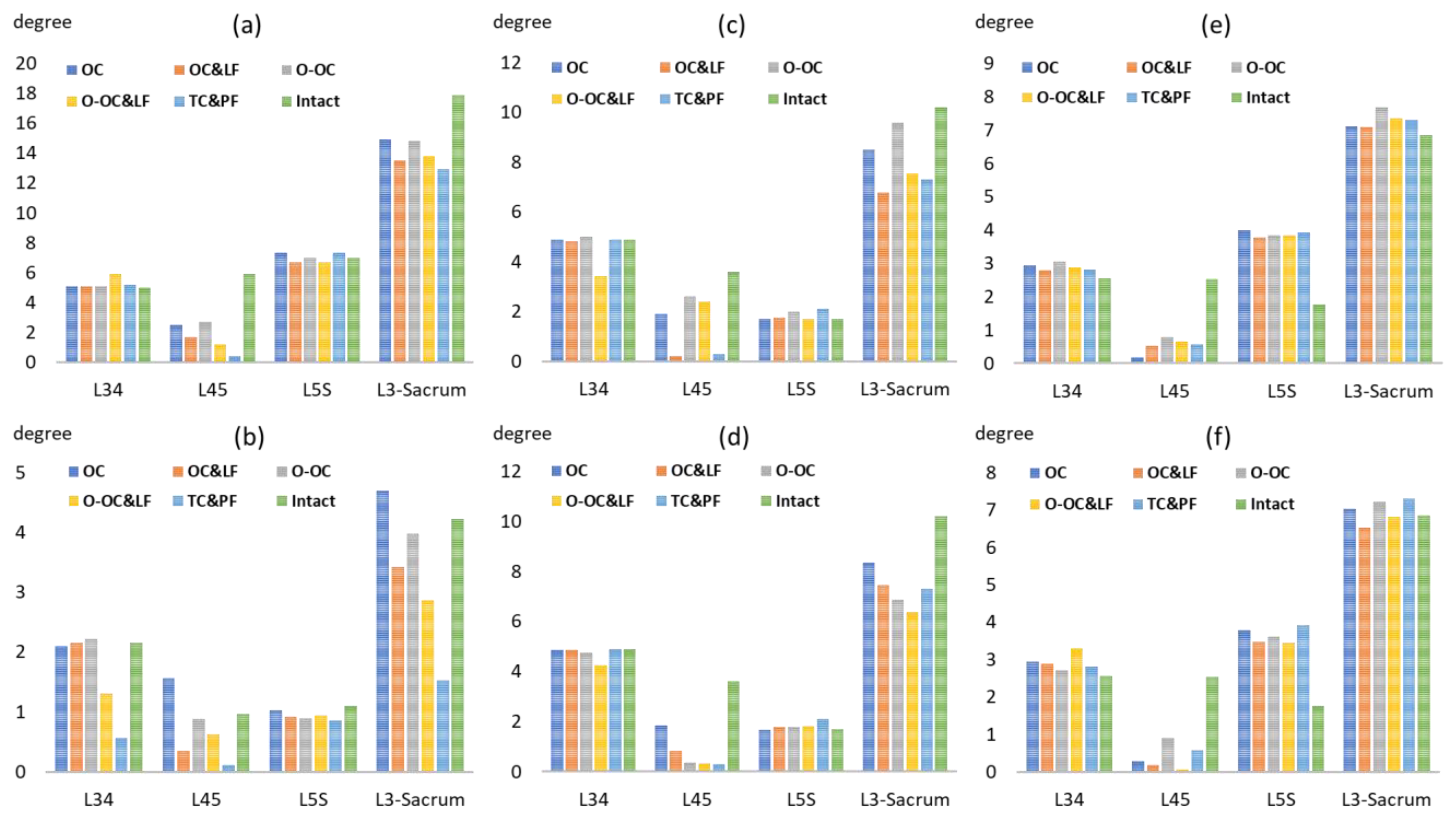
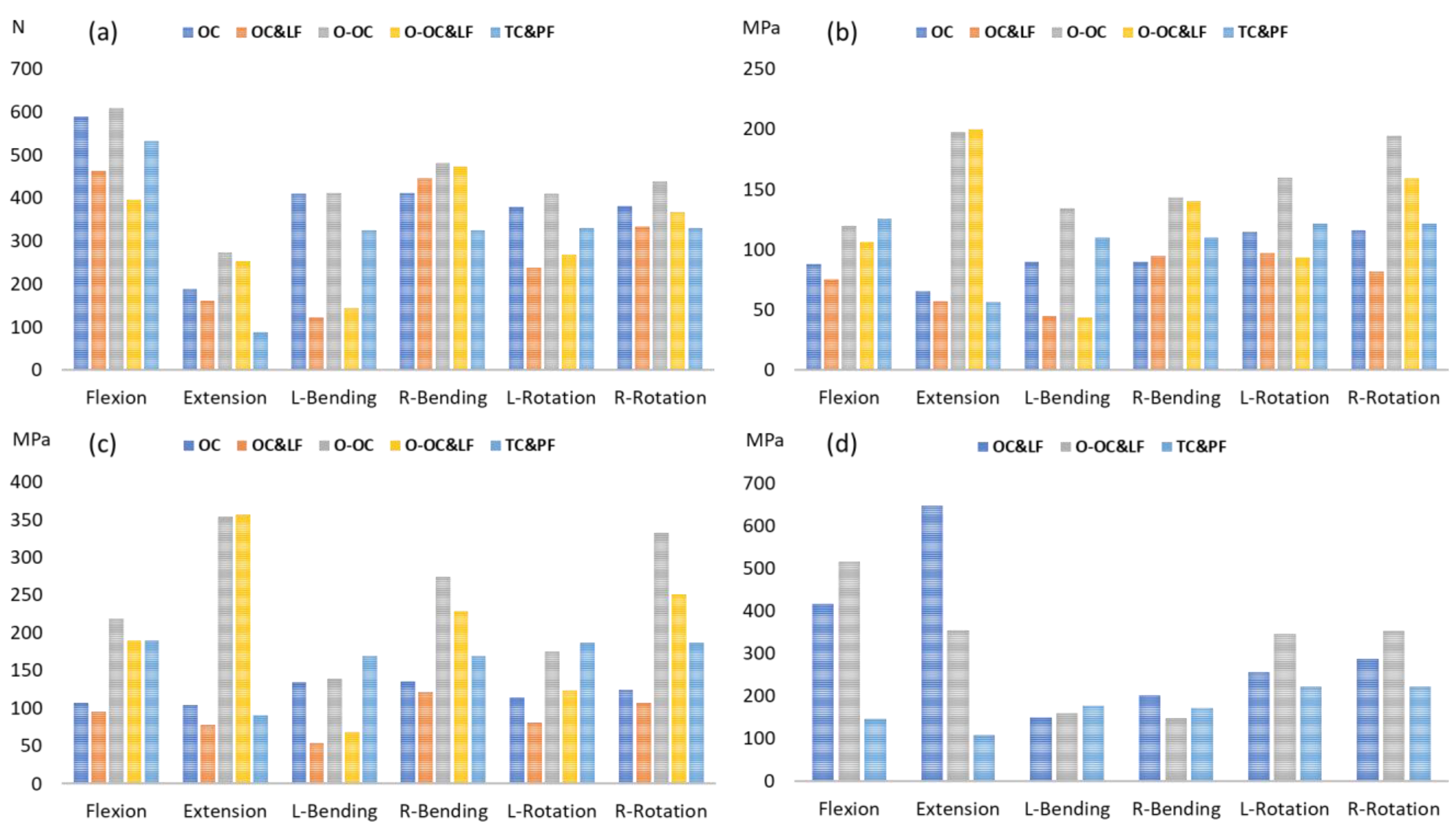
3.2. Range of Motion
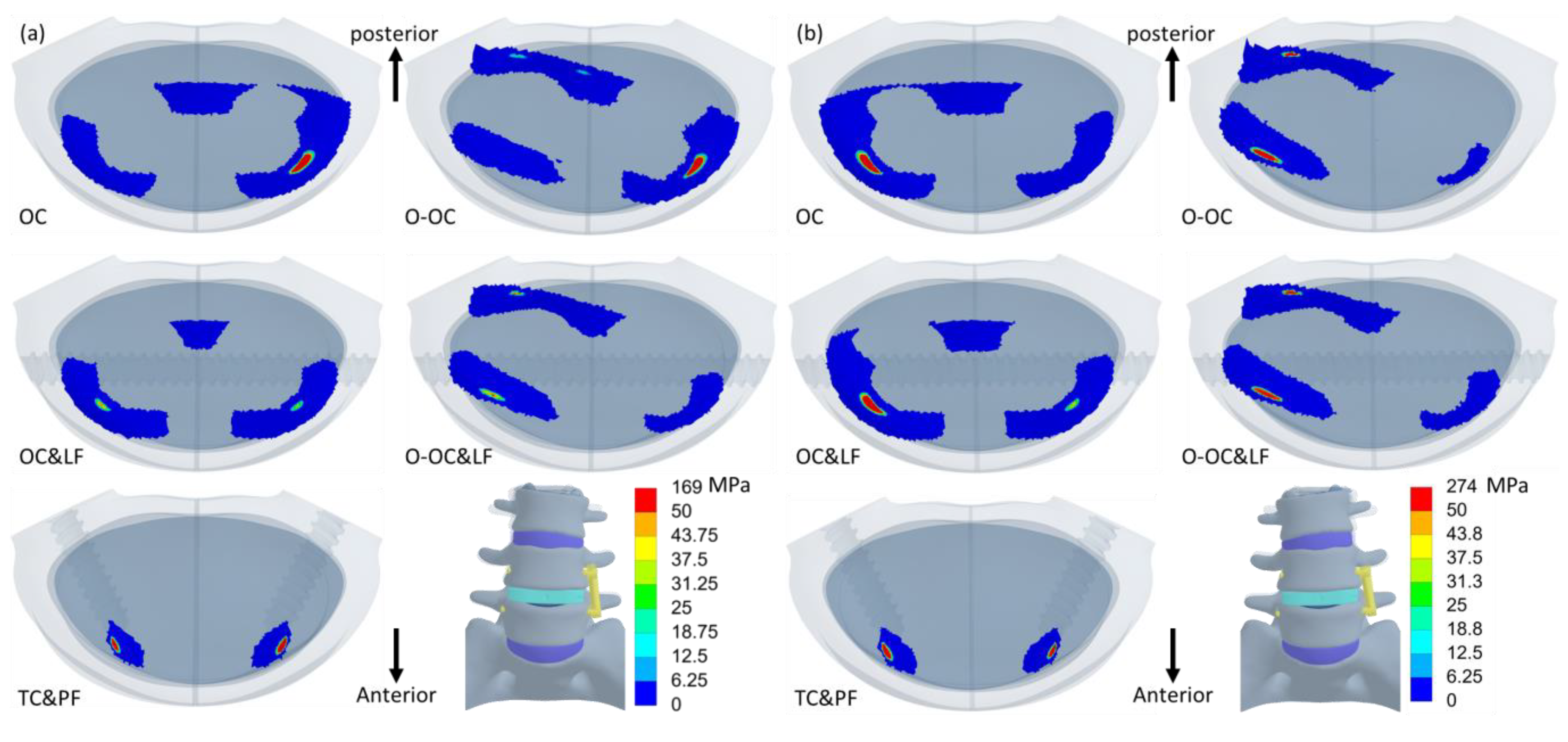
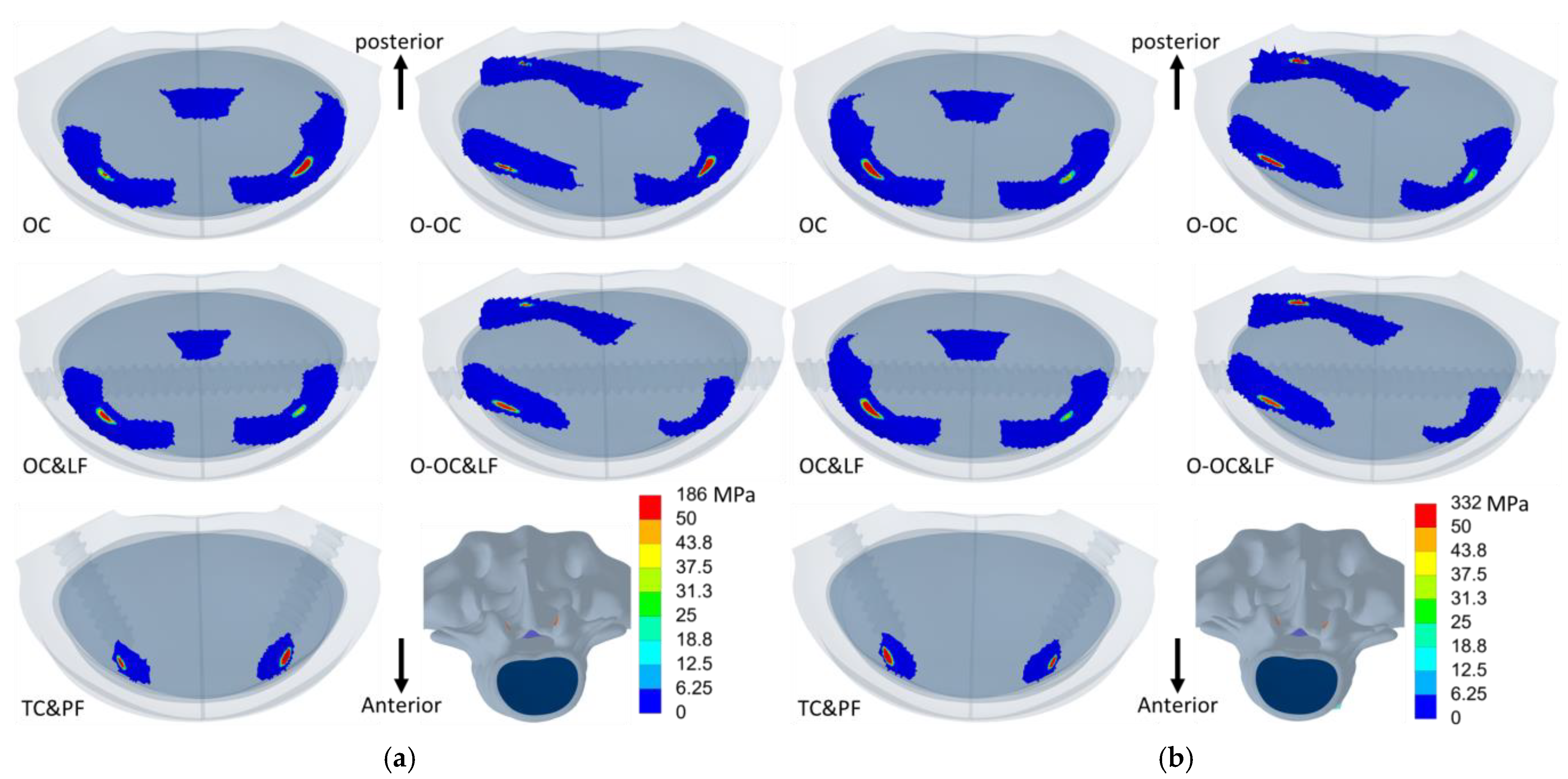
3.3. Loading and Stress on the Cage
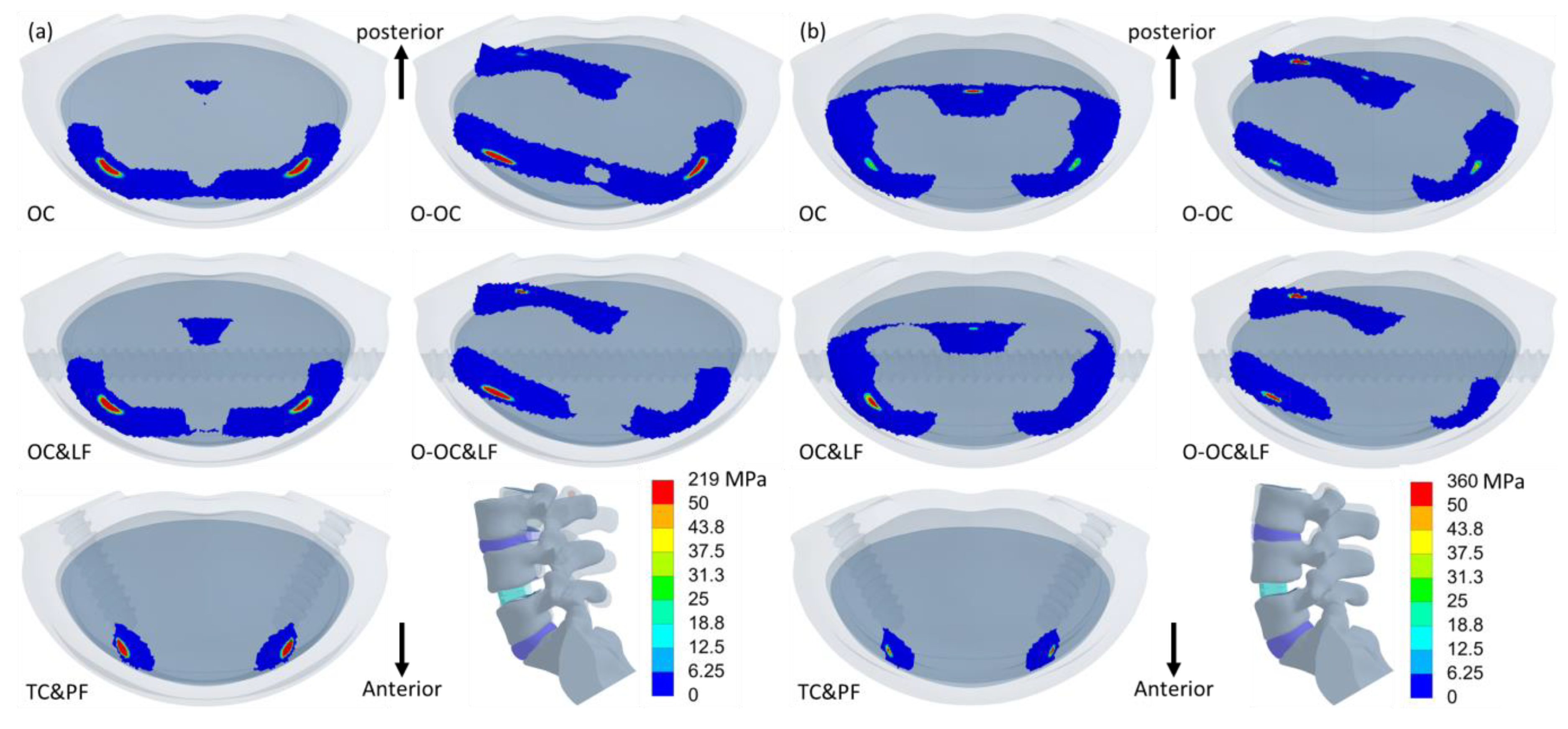
3.4. Contact Pressure on L5
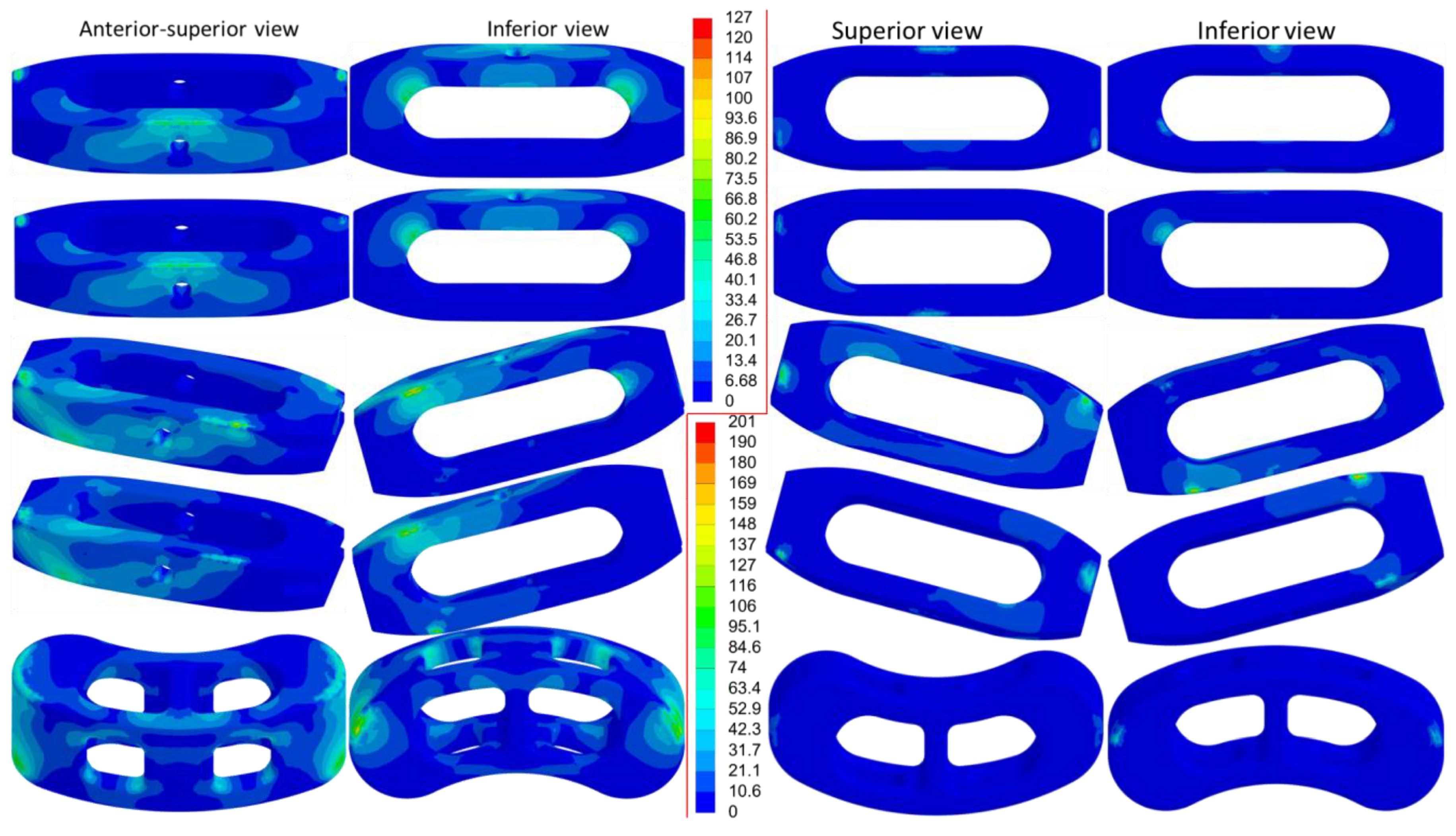
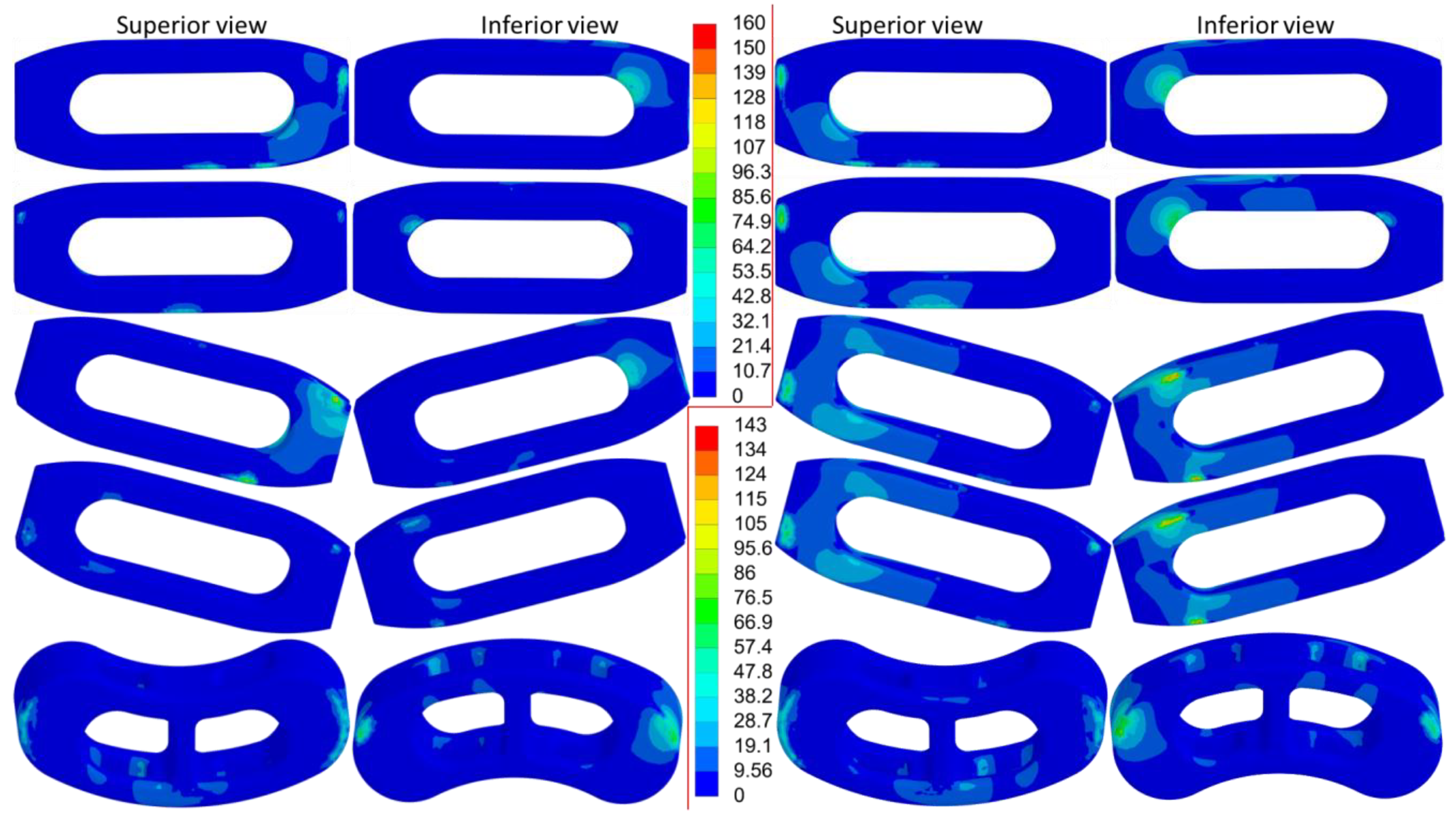
3.5. Equivalent Stress of the Metallic Implants
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hadjipavlou, A.G.; Tzermiadianos, M.N.; Bogduk, N.; Zindrick, M.R. The pathophysiology of disc degeneration. J. Bone Jt. Surg. Br. Vol. 2008, 90, 1261–1270. [Google Scholar] [CrossRef] [PubMed]
- Battié, M.C.; Videman, T. Lumbar Disc Degeneration: Epidemiology and Genetics. JBJS 2006, 88 (Suppl. S2), 3–9. [Google Scholar] [CrossRef]
- Zdeblick, T.A.; Phillips, F.M. Interbody Cage Devices. Spine 2003, 28, S2–S7. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.H.; Ha, K.Y.; Rhyu, K.W.; Park, H.Y.; Cho, C.H.; Kim, H.C.; Lee, H.J.; Kim, S.I. Lumbar Interbody Fusion: Techniques, Pearls and Pitfalls. Asian Spine J. 2020, 14, 730–741. [Google Scholar] [CrossRef]
- Silvestre, C.; Mac-Thiong, J.M.; Hilmi, R.; Roussouly, P. Complications and Morbidities of Mini-open Anterior Retroperitoneal Lumbar Interbody Fusion: Oblique Lumbar Interbody Fusion in 179 Patients. Asian Spine J. 2012, 6, 89–97. [Google Scholar] [CrossRef]
- Quillo-Olvera, J.; Lin, G.X.; Jo, H.J.; Kim, J.S. Complications on minimally invasive oblique lumbar interbody fusion at L2-L5 levels: A review of the literature and surgical strategies. Ann. Transl. Med. 2018, 6, 101. [Google Scholar] [CrossRef]
- Li, J.X.; Phan, K.; Mobbs, R. Oblique Lumbar Interbody Fusion: Technical Aspects, Operative Outcomes, and Complications. World Neurosurg. 2017, 98, 113–123. [Google Scholar] [CrossRef]
- Woods, K.R.; Billys, J.B.; Hynes, R.A. Technical description of oblique lateral interbody fusion at L1-L5 (OLIF25) and at L5-S1 (OLIF51) and evaluation of complication and fusion rates. Spine J. 2017, 17, 545–553. [Google Scholar] [CrossRef]
- Fujibayashi, S.; Kawakami, N.; Asazuma, T.; Ito, M.; Mizutani, J.; Nagashima, H.; Nakamura, M.; Sairyo, K.; Takemasa, R.; Iwasaki, M. Complications Associated With Lateral Interbody Fusion: Nationwide Survey of 2998 Cases During the First 2 Years of Its Use in Japan. Spine 2017, 42, 1478–1484. [Google Scholar] [CrossRef]
- Abe, K.; Orita, S.; Mannoji, C.; Motegi, H.; Aramomi, M.; Ishikawa, T.; Kotani, T.; Akazawa, T.; Morinaga, T.; Fujiyoshi, T.; et al. Perioperative Complications in 155 Patients Who Underwent Oblique Lateral Interbody Fusion Surgery: Perspectives and Indications From a Retrospective, Multicenter Survey. Spine 2017, 42, 55–62. [Google Scholar] [CrossRef]
- Zeng, Z.Y.; Xu, Z.W.; He, D.W.; Zhao, X.; Ma, W.H.; Ni, W.F.; Song, Y.X.; Zhang, J.Q.; Yu, W.; Fang, X.Q.; et al. Complications and Prevention Strategies of Oblique Lateral Interbody Fusion Technique. Orthop. Surg. 2018, 10, 98–106. [Google Scholar] [CrossRef] [PubMed]
- Ge, T.; Ao, J.; Li, G.; Lang, Z.; Sun, Y. Additional lateral plate fixation has no effect to prevent cage subsidence in oblique lumbar interbody fusion. J. Orthop. Surg. Res. 2021, 16, 584. [Google Scholar] [CrossRef] [PubMed]
- Fang, G.; Lin, Y.; Wu, J.; Cui, W.; Zhang, S.; Guo, L.; Sang, H.; Huang, W. Biomechanical Comparison of Stand-Alone and Bilateral Pedicle Screw Fixation for Oblique Lumbar Interbody Fusion Surgery—A Finite Element Analysis. World Neurosurg. 2020, 141, e204–e212. [Google Scholar] [CrossRef]
- Cai, X.Y.; Bian, H.M.; Chen, C.; Ma, X.L.; Yang, Q. Biomechanical study of oblique lumbar interbody fusion (OLIF) augmented with different types of instrumentation: A finite element analysis. J. Orthop. Surg. Res. 2022, 17, 269. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.W.; Chung, Y.H.; Chang, C.J.; Chen, Y.N.; Li, C.T.; Chang, C.H.; Peng, Y.T. Computational comparison of bone cement and poly aryl-ether-ether-ketone spacer in single-segment posterior lumbar interbody fusion: A pilot study. Australas. Phys. Eng. Sci. Med. 2019. online ahead of print. [Google Scholar] [CrossRef]
- Pintar, F.A.; Yoganandan, N.; Myers, T.; Elhagediab, A.; Sances, A., Jr. Biomechanical properties of human lumbar spine ligaments. J. Biomech. 1992, 25, 1351–1356. [Google Scholar] [CrossRef]
- Neumann, P.; Keller, T.S.; Ekström, L.; Hansson, T. Effect of strain rate and bone mineral on the structural properties of the human anterior longitudinal ligament. Spine 1994, 19, 205–211. [Google Scholar] [CrossRef]
- Polikeit, A.; Nolte, L.P.; Ferguson, S.J. The effect of cement augmentation on the load transfer in an osteoporotic functional spinal unit: Finite-element analysis. Spine 2003, 28, 991–996. [Google Scholar] [CrossRef]
- Xiao, Z.; Wang, L.; Gong, H.; Zhu, D.; Zhang, X. A non-linear finite element model of human L4-L5 lumbar spinal segment with three-dimensional solid element ligaments. Theor. Appl. Mech. Lett. 2011, 1, 064001. [Google Scholar] [CrossRef][Green Version]
- Jhong, G.H.; Chung, Y.H.; Li, C.T.; Chen, Y.N.; Chang, C.W.; Chang, C.H. Numerical Comparison of Restored Vertebral Body Height after Incomplete Burst Fracture of the Lumbar Spine. J. Pers. Med. 2022, 12, 253. [Google Scholar] [CrossRef]
- Schmidt, H.; Heuer, F.; Simon, U.; Kettler, A.; Rohlmann, A.; Claes, L.; Wilke, H.J. Application of a new calibration method for a three-dimensional finite element model of a human lumbar annulus fibrosus. Clin. Biomech. 2006, 21, 337–344. [Google Scholar] [CrossRef]
- Bonnheim, N.; Ansari, F.; Regis, M.; Bracco, P.; Pruitt, L. Effect of carbon fiber type on monotonic and fatigue properties of orthopedic grade PEEK. J. Mech. Behav. Biomed. Mater. 2019, 90, 484–492. [Google Scholar] [CrossRef] [PubMed]
- Niinomi, M. Mechanical properties of biomedical titanium alloys. Mater. Sci. Eng. A 1998, 243, 231–236. [Google Scholar] [CrossRef]
- Hasan, I.; Keilig, L.; Staat, M.; Wahl, G.; Bourauel, C. Determination of the frictional coefficient of the implant-antler interface: Experimental approach. Biomed Technol. 2012, 57, 359–363. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, I.; Panjabi, M.M.; Crisco, T.; Oxland, T. Three-dimensional movements of the whole lumbar spine and lumbosacral joint. Spine 1989, 14, 1256–1260. [Google Scholar] [CrossRef] [PubMed]
- Panjabi, M.M.; Oxland, T.R.; Yamamoto, I.; Crisco, J.J. Mechanical behavior of the human lumbar and lumbosacral spine as shown by three-dimensional load-displacement curves. J. Bone Jt. Surg. 1994, 76, 413–424. [Google Scholar] [CrossRef]
- Natarajan, R.N.; Andersson, G.B. The influence of lumbar disc height and cross-sectional area on the mechanical response of the disc to physiologic loading. Spine 1999, 24, 1873–1881. [Google Scholar] [CrossRef]
- Goto, K.; Tajima, N.; Chosa, E.; Totoribe, K.; Kubo, S.; Kuroki, H.; Arai, T. Effects of lumbar spinal fusion on the other lumbar intervertebral levels (three-dimensional finite element analysis). J. Orthop. Sci. 2003, 8, 577–584. [Google Scholar] [CrossRef]
- Schmidt, H.; Shirazi-Adl, A.; Galbusera, F.; Wilke, H.-J. Response analysis of the lumbar spine during regular daily activities—A finite element analysis. J. Biomech. 2010, 43, 1849–1856. [Google Scholar] [CrossRef]
- Xu, M.; Yang, J.; Lieberman, I.H.; Haddas, R. Lumbar spine finite element model for healthy subjects: Development and validation. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 1–15. [Google Scholar] [CrossRef]
- Jia, J.; Chen, C.; Wang, P.; Wang, L.; Liu, X. Comparison of Adjacent Segment Degeneration After Minimally Invasive or Open Transforaminal Lumbar Interbody Fusion: A Minimum 5-Year Follow-up. Clin. Spine Surg. 2023, 36, E45–E50. [Google Scholar] [CrossRef]
- Kuo, C.H.; Huang, W.C.; Wu, J.C.; Tu, T.H.; Fay, L.Y.; Wu, C.L.; Cheng, H. Radiological adjacent-segment degeneration in L4-5 spondylolisthesis: Comparison between dynamic stabilization and minimally invasive transforaminal lumbar interbody fusion. J. Neurosurg. Spine 2018, 29, 250–258. [Google Scholar] [CrossRef] [PubMed]
- Duan, P.G.; Mummaneni, P.V.; Wang, M.; Chan, A.K.; Li, B.; Mayer, R.; Berven, S.H.; Chou, D. Obesity may be associated with adjacent-segment degeneration after single-level transforaminal lumbar interbody fusion in spinopelvic-mismatched patients with a minimum 2-year follow-up. J. Neurosurg. Spine 2021, 34, 83–88. [Google Scholar] [CrossRef] [PubMed]
- Bryant, J.P.; Perez-Roman, R.J.; Burks, S.S.; Wang, M.Y. Antiresorptive and anabolic medications used in the perioperative period of patients with osteoporosis undergoing spine surgery: Their impact on the biology of fusion and systematic review of the literature. Neurosurg. Focus 2021, 50, E13. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.H.; Chung, C.J.; Wang, C.W.; Peng, Y.T.; Chang, C.H.; Chen, C.H.; Chen, Y.N.; Li, C.T. Computational comparison of three posterior lumbar interbody fusion techniques by using porous titanium interbody cages with 50% porosity. Comput. Biol. Med. 2016, 71, 35–45. [Google Scholar] [CrossRef]
- Chen, Y.N.; Chang, C.W. Computational comparison of three different cage porosities in posterior lumbar interbody fusion with porous cage. Comput. Biol. Med. 2021, 139, 105036. [Google Scholar] [CrossRef]
- Xie, T.; Wang, C.; Yang, Z.; Xiu, P.; Yang, X.; Wang, X.; Wang, D.; Song, Y.; Zeng, J. Minimally Invasive Oblique Lateral Lumbar Interbody Fusion Combined with Anterolateral Screw Fixation for Lumbar Degenerative Disc Disease. World Neurosurg. 2020, 135, e671–e678. [Google Scholar] [CrossRef]
- Liu, J.; Feng, H. Oblique Lateral Interbody Fusion (OLIF) with Supplemental Anterolateral Screw and Rod Instrumentation: A Preliminary Clinical Study. World Neurosurg. 2020, 134, e944–e950. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, C.; Cheng, C.; Jian, F.; Wu, H. Radiographic and Clinical Outcomes following Combined Oblique Lumbar Interbody Fusion and Lateral Instrumentation for the Treatment of Degenerative Spine Deformity: A Preliminary Retrospective Study. Biomed Res. Int. 2019, 2019, 5672162. [Google Scholar] [CrossRef]

| Ligament/Material | Stiffness (N/mm) | Spring Numbers at Each Tissue | Elastic Modulus (MPa) | Poisson’s Ratio | Reference |
|---|---|---|---|---|---|
| Ligament | |||||
| Anterior longitudinal | 25 | 3 | - | - | [17] |
| Posterior longitudinal | 20 | 1 | - | - | [16] |
| Ligamentum flavum | 10 | 2 | - | - | [16] |
| Interspinous | 5 | 2 | - | - | [16] |
| Supraspinous ligaments | 23 | 1 | - | - | [16] |
| Intertransverse | 25 | 1 | - | - | [16] |
| Joint capsule | 10 | 6 | - | - | [16] |
| Bone | |||||
| Cortex | - | - | 12,000 | 0.3 | [18] |
| Cancellous | - | - | 100 | 0.2 | [18] |
| Endplate | 1000 | 0.3 | [18] | ||
| Disc | |||||
| Nucleus | - | - | Mooney–Rivlin 2 ParameterC10, 0.12; C01, 0.09 | - | [19] |
| Ground substance | - | - | Mooney–Rivlin 2 ParameterC10, 0.56; C01, 0.14 | - | [19] |
| Annulus fibrosis | 8 | 25 | - | - | [20,21] |
| Implant | |||||
| Titanium | - | - | 110,000 | 0.3 | [23] |
| PEEK | - | - | 3900 | 0.3 | [22] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chung, Y.-H.; Hu, M.-H.; Su, H.-L.; Chen, Y.-N.; Chang, H.-C. Role of Additional Screws and Rod Fixation in Cage Loading During Oblique Lateral Interbody Fusion: A Finite Element Analysis. J. Clin. Med. 2025, 14, 1890. https://doi.org/10.3390/jcm14061890
Chung Y-H, Hu M-H, Su H-L, Chen Y-N, Chang H-C. Role of Additional Screws and Rod Fixation in Cage Loading During Oblique Lateral Interbody Fusion: A Finite Element Analysis. Journal of Clinical Medicine. 2025; 14(6):1890. https://doi.org/10.3390/jcm14061890
Chicago/Turabian StyleChung, Yu-Hsuan, Ming-Hsien Hu, Hong-Lin Su, Yen-Nien Chen, and Heng-Chih Chang. 2025. "Role of Additional Screws and Rod Fixation in Cage Loading During Oblique Lateral Interbody Fusion: A Finite Element Analysis" Journal of Clinical Medicine 14, no. 6: 1890. https://doi.org/10.3390/jcm14061890
APA StyleChung, Y.-H., Hu, M.-H., Su, H.-L., Chen, Y.-N., & Chang, H.-C. (2025). Role of Additional Screws and Rod Fixation in Cage Loading During Oblique Lateral Interbody Fusion: A Finite Element Analysis. Journal of Clinical Medicine, 14(6), 1890. https://doi.org/10.3390/jcm14061890









