Distribution and Demographic Correlates of Ocular Wavefront Aberrations in a Korean Population
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Design
2.2. Procedure
2.3. Outcome Measurements
2.4. Statistical Analysis
3. Results
3.1. Patient Demographics
3.2. Overall Magnitudes of RMS and Zernike Coefficients
3.3. Relative Contributions of Individual Zernike Terms
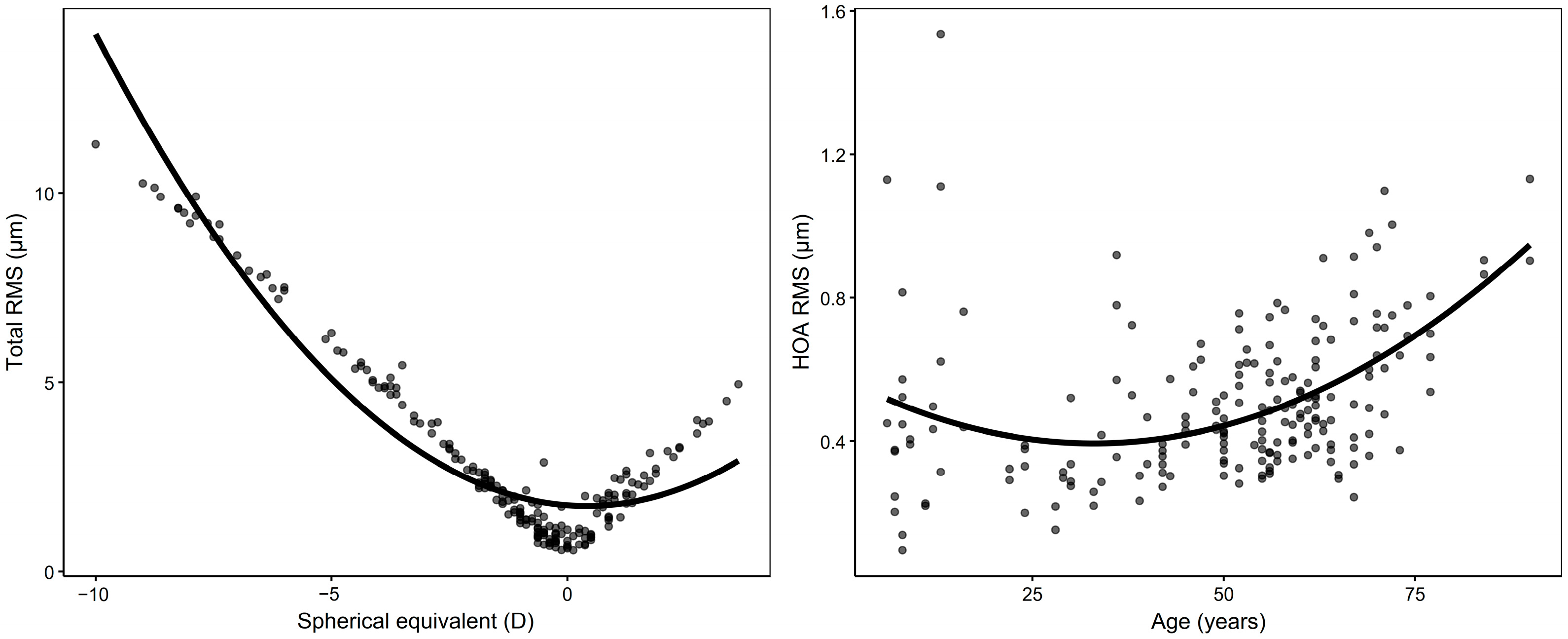
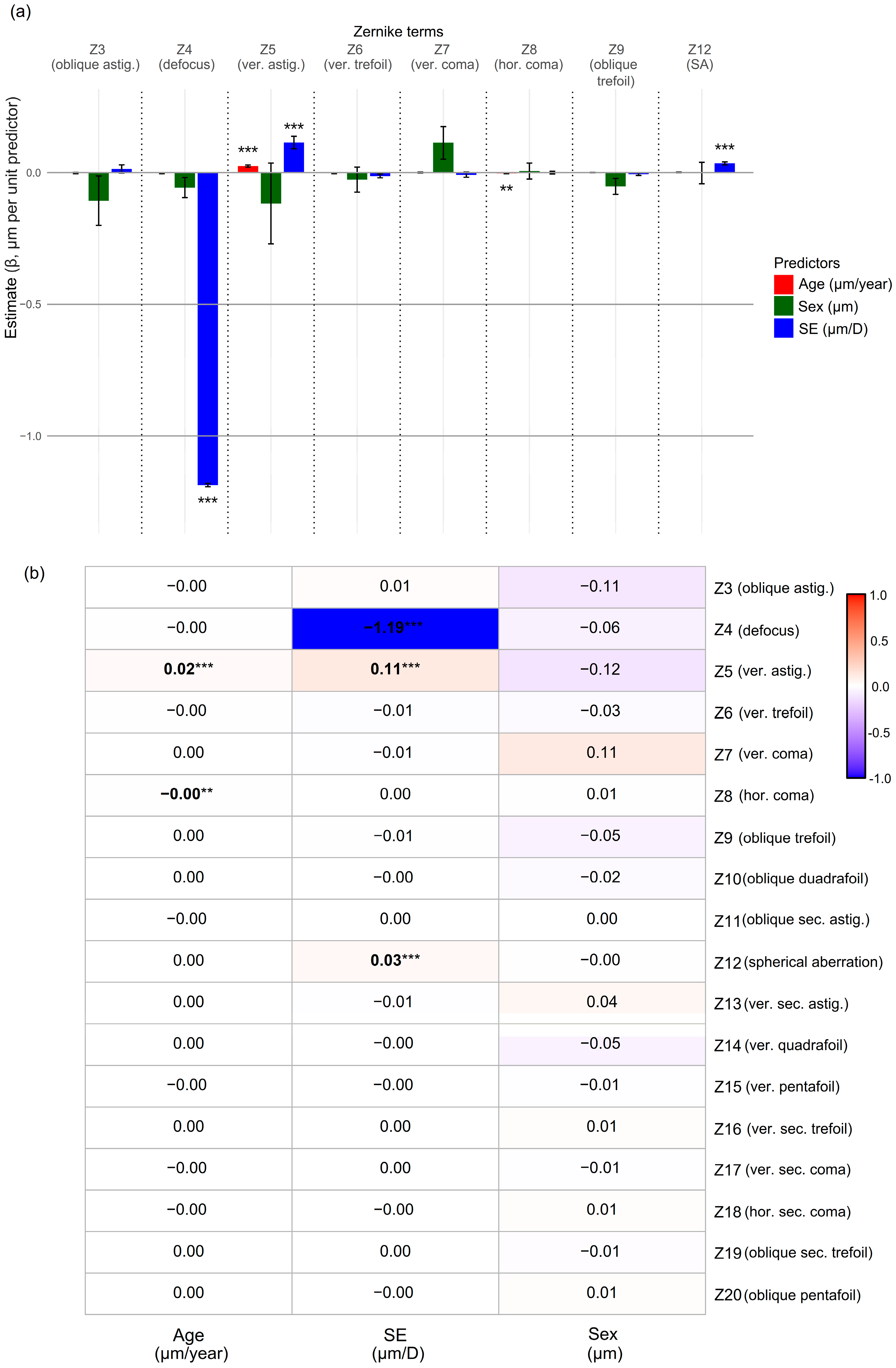
3.4. Associations with Age, SE, and Sex
3.5. Age- and SE-Stratified Reference Percentiles
3.6. Interocular Correlation of Zernike Coefficients
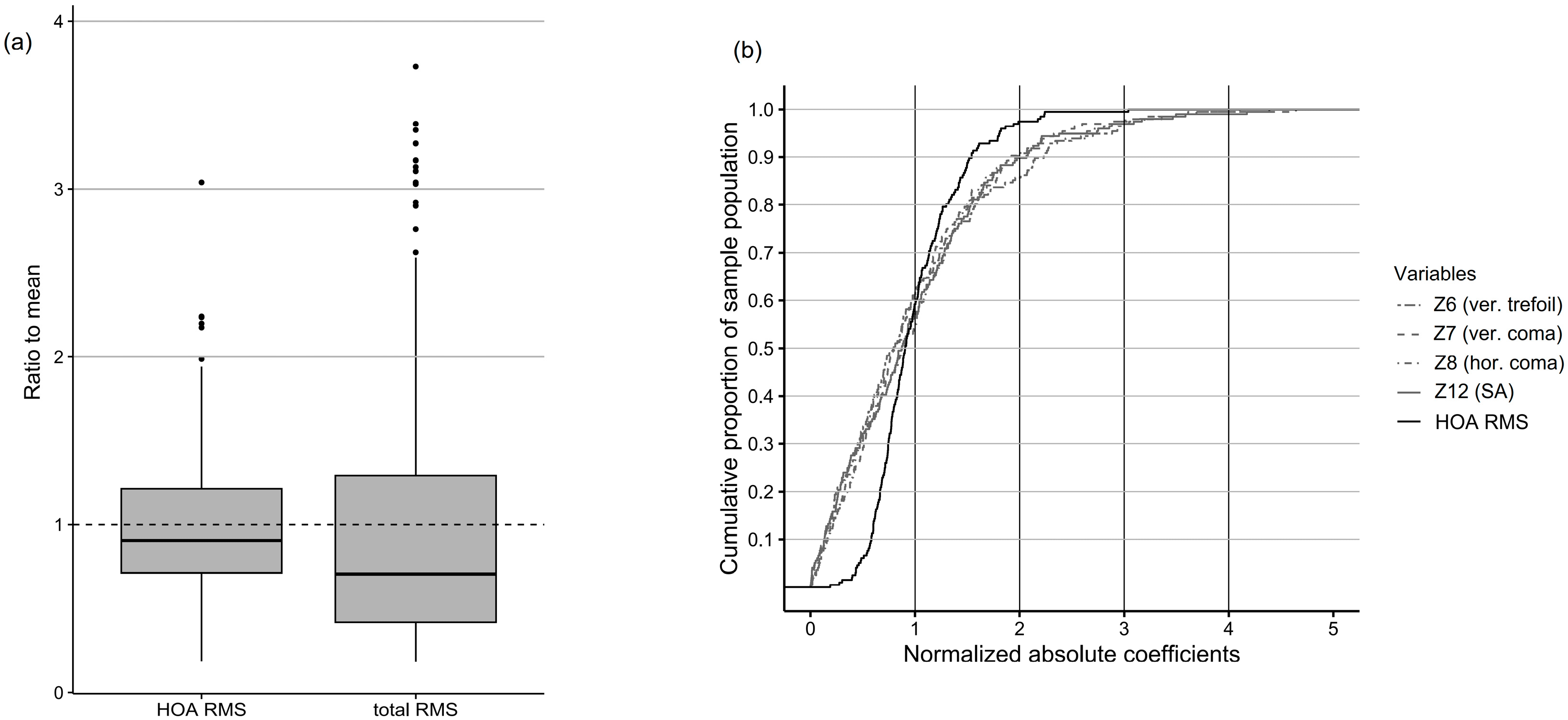
3.7. Normalization of RMS Values
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AIC | Akaike’s information criterion |
| abs mean | absolute mean |
| astig. | astigmatism |
| CoV | coefficient of variation |
| CIs | confidence intervals |
| HOAs | higher-order aberrations |
| hor. | horizontal |
| ICCs | intraclass correlation coefficients |
| IQR | interquartile range |
| LMMs | linear mixed-effects models |
| LOAs | lower-order aberrations |
| RMS | root mean square |
| SA | spherical aberration |
| SD | standard deviation |
| SE | spherical equivalent |
| Sw | within-subject standard deviation |
| sec. | secondary |
| sex (M) | male, female sex as reference |
| ver. | vertical |
| β | regression coefficient (from linear mixed-effects model) |
| ρ | Spearman’s rank correlation coefficient |
References
- Maeda, N. Clinical applications of wavefront aberrometry—A review. Clin. Exp. Ophthalmol. 2009, 37, 118–129. [Google Scholar] [CrossRef]
- Jayabalan, G.S.; Bille, J.F. The Development of Adaptive Optics and Its Application in Ophthalmology. In High Resolution Imaging in Microscopy and Ophthalmology: New Frontiers in Biomedical Optics; Bille, J.F., Ed.; Springer: Cham, Switzerland, 2019; pp. 339–358. [Google Scholar]
- von Sonnleithner, C.; Pilger, D.; Homburg, D.; Tobias, B.; Torun, N.; Bertelmann, E. Corneal higher-order aberrations after phacoemulsification: A comparison of 3 different incision sizes. Eur. J. Ophthalmol. 2017, 27, 402–406. [Google Scholar] [CrossRef]
- Li, Z.-J.; Liu, S.-H.; Yang, C.; Guo, J.; Duan, Y.-H. One-year clinical efficacy evaluation of selective corneal wavefront aberration-guided FS-LASIK correction in patients with high myopia. Int. J. Ophthalmol. 2023, 16, 1280–1286. [Google Scholar] [CrossRef]
- Ang, R.E.T.; Lee, P.L.; Torres, R.S.; Araneta, M.M.Q.; Cruz, E.M.; Torno, M.S.M. Higher-order aberrations and spherical aberration in various age groups after LASIK and cataract surgery. BMC Ophthalmol. 2025, 25, 271. [Google Scholar] [CrossRef] [PubMed]
- Marcos, S.; Barbero, S.; Jiménez-Alfaro, I. Optical quality and depth-of-field of eyes implanted with spherical and aspheric intraocular lenses. J. Refract. Surg. 2005, 21, 223–235. [Google Scholar] [CrossRef] [PubMed]
- Saxena, D.; Kanaujia, V.; Ranjan, A.; Jain, V.; Aishwarya, A.; Husain, A.; Agarwal, R. Impact of Cataract Surgery on Higher Order Aberrations and Comparative Analysis using Scheimpflug imaging and ray-tracing technology. Rom. J. Ophthalmol. 2025, 69, 60–67. [Google Scholar] [CrossRef]
- Marcos, S.; Martinez-Enriquez, E.; Vinas, M.; de Castro, A.; Dorronsoro, C.; Bang, S.P.; Yoon, G.; Artal, P. Simulating Outcomes of Cataract Surgery: Important Advances in Ophthalmology. Annu. Rev. Biomed. Eng. 2021, 23, 277–306. [Google Scholar] [CrossRef]
- Lyu, J.; Bang, S.P.; Yoon, G. Refractive extended depth-of-focus lens design based on periodic power profile for presbyopia correction. Ophthalmic Physiol. Opt. 2024, 44, 301–310. [Google Scholar] [CrossRef]
- Kohnen, T. Aberration-correcting intraocular lenses. J. Cataract. Refract. Surg. 2003, 29, 627–628. [Google Scholar] [CrossRef] [PubMed]
- Clark, C.A.; Parimi, V.; Elsner, A.E. Wavefront aberrations in aging measured with Hartmann-Shack at 3- and 5-mm pupil sizes. Optom. Vis. Sci. 2025, 102, 61–67. [Google Scholar] [CrossRef]
- Li, Y.-J.; Choi, J.A.; Kim, H.; Yu, S.-Y.; Joo, C.-K. Changes in ocular wavefront aberrations and retinal image quality with objective accommodation. J. Cataract. Refract. Surg. 2011, 37, 835–841. [Google Scholar] [CrossRef]
- Porter, J.; Guirao, A.; Cox, I.G.; Williams, D.R. Monochromatic aberrations of the human eye in a large population. J. Opt. Soc. Am. A 2001, 18, 1793. [Google Scholar] [CrossRef]
- Francisco Castejón-Mochón, J.; López-Gil, N.; Benito, A.; Artal, P. Ocular wave-front aberration statistics in a normal young population. Vis. Res. 2002, 42, 1611–1617. [Google Scholar] [CrossRef] [PubMed]
- Salmon, T.O.; Van De Pol, C. Normal-eye Zernike coefficients and root-mean-square wavefront errors. J. Cataract. Refract. Surg. 2006, 32, 2064–2074. [Google Scholar] [CrossRef]
- Rauscher, F.G.; Hiemisch, A.; Kiess, W.; Blendowske, R. Monochromatic ocular high-order aberrations in children and adolescents. Ophthalmic Physiol. Opt. 2023, 43, 842–859. [Google Scholar] [CrossRef] [PubMed]
- Fritzsch, M.; Dawczynski, J.; Jurkutat, S.; Vollandt, R.; Strobel, J. [Monochromatic aberration in accommodation. Dynamic wavefront analysis]. Ophthalmologe 2011, 108, 553–560. [Google Scholar] [CrossRef] [PubMed]
- Thibos, L.N.; Hong, X.; Bradley, A.; Cheng, X. Statistical variation of aberration structure and image quality in a normal population of healthy eyes. J. Opt. Soc. Am. A 2002, 19, 2329. [Google Scholar] [CrossRef]
- Namba, H.; Kawasaki, R.; Sugano, A.; Murakami, T.; Nishitsuka, K.; Kato, T.; Kayama, T.; Yamashita, H. Age-Related Changes in Ocular Aberrations and the Yamagata Study (Funagata). Cornea 2017, 36, S34–S40. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, G.; Jin, L.; Ruan, X.; Gu, X.; Wang, W.; Chen, X.; Wang, L.; Dai, Y.; Liu, Z.; et al. Profiles of intraocular higher-order aberrations in healthy phakic eyes: Prospective cross-sectional study. Ann. Transl. Med. 2020, 8, 850. [Google Scholar] [CrossRef]
- Lim, D.H.; Kim, W.; Han, G.; Bae, G.H.; Kim, M.H.; Kim, M.J.; Song, Y.-M.; Chung, E.-S.; Chung, T.-Y.; Sung, J.; et al. The Heritability of Corneal and Ocular Higher-Order Aberrations in Koreans: The Healthy Twin Study. Investig. Ophthalmol. Vis. Sci. 2015, 56, 3919–3928. [Google Scholar] [CrossRef]
- Kim, M.; Lee, Y.G.; Seo, K.R.; Kim, E.K.; Lee, H.K. Comparison of higher-order aberrations between eyes with natural supervision and highly myopic eyes in Koreans. Korean J. Ophthalmol. 2007, 21, 79–84. [Google Scholar] [CrossRef]
- Hee Sung, K.; Jin Hyoung, K.; Do Hyung, L.; So Ra, K.; Mijung, P. The Analysis of the Changing Patterns of High Order Aberrations by Age Groups. J. Korean Ophthalmol. Opt. Soc. 2017, 22, 243–252. [Google Scholar] [CrossRef]
- Kim, Y.S.; Ko, B.Y. Preoperative Ocular Aberrations Measured by Zywave® II Aberrometer in Individuals Screened for Refractive Surgery. J. Korean Ophthalmol. Soc. 2013, 54, 1680–1687. [Google Scholar] [CrossRef]
- Chun, D.H.; Choi, T.H.; Lee, H.B. Age and Spherical Equivalent Related Changes in Wavefront Aberrations. J. Korean Ophthalmol. Soc. 2004, 45, 266–272. Available online: https://www.koreamed.org/SearchBasic.php?RID=1822440 (accessed on 31 July 2025).
- Lee, S.B.; Choi, B.H. Analysis of Higher-Order Wavefront Aberrations in Standard PRK. J. Korean Ophthalmol. Soc. 2005, 46, 1454–1463. Available online: https://www.koreamed.org/SearchBasic.php?RID=2109911 (accessed on 31 July 2025).
- Smolek, M.K.; Klyce, S.D.; Sarver, E.J. Inattention to nonsuperimposable midline symmetry causes wavefront analysis error. Arch. Ophthalmol. 2002, 120, 439–447. [Google Scholar] [CrossRef] [PubMed]
- Surl, D.; Seo, Y.; Han, J. Trends in myopia prevalence among late adolescents in South Korea: A population-level study and future projections up to 2050. BMJ Open Ophthalmol. 2024, 9, e001748. [Google Scholar] [CrossRef] [PubMed]
- Baek, J.Y.; Lee, E.; Jung, H.W.; Jang, I.Y. Geriatrics Fact Sheet in Korea 2021. Ann. Geriatr. Med. Res. 2021, 25, 65–71. [Google Scholar] [CrossRef]
- Kwon, N.E.; Brown, N.; Jun, J.H.; Bang, S.P. Comparison of Ocular Wavefront in Seated and Supine Positions Using a Hand-Held Hartmann–Shack Aberrometer. J. Clin. Med. 2025, 14, 6688. [Google Scholar] [CrossRef]
- Thibos, L.N.; Applegate, R.A.; Schwiegerling, J.T.; Webb, R.; VSIA Standards Taskforce Members. Standards for reporting the optical aberrations of eyes. J. Refract. Surg. 2002, 18, S652–S660. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Koch, D.D. Ocular higher-order aberrations in individuals screened for refractive surgery. J. Cataract. Refract. Surg. 2003, 29, 1896–1903. [Google Scholar] [CrossRef]
- Jeong, S.; Lemke, B.N.; Dortzbach, R.K.; Park, Y.G.; Kang, H.K. The Asian upper eyelid: An anatomical study with comparison to the Caucasian eyelid. Arch. Ophthalmol. 1999, 117, 907–912. [Google Scholar] [CrossRef]
- Qin, B.; Tang, M.; Li, Y.; Zhang, X.; Chu, R.; Huang, D. Anterior segment dimensions in Asian and Caucasian eyes measured by optical coherence tomography. Ophthalmic Surg. Lasers Imaging 2012, 43, 135–142. [Google Scholar] [CrossRef]
- Hickson-Curran, S.; Brennan, N.A.; Igarashi, Y.; Young, G. Comparative evaluation of Asian and white ocular topography. Optom. Vis. Sci. 2014, 91, 1396–1405. [Google Scholar] [CrossRef]
- Osuagwu, U.L.; Verkicharla, P.; Suheimat, M.; Atchison, D.A. Peripheral Monochromatic Aberrations in Young Adult Caucasian and East Asian Eyes. Optom. Vis. Sci. 2018, 95, 234–238. [Google Scholar] [CrossRef] [PubMed]
- Vitale, S.; Ellwein, L.; Cotch, M.F.; Ferris, F.L.; Sperduto, R. Prevalence of refractive error in the United States, 1999–2004. Arch. Ophthalmol. 2008, 126, 1111–1119. [Google Scholar] [CrossRef] [PubMed]
- Takeuchi, M.; Meguro, A.; Yoshida, M.; Yamane, T.; Yatsu, K.; Okada, E.; Mizuki, N. Longitudinal analysis of 5-year refractive changes in a large Japanese population. Sci. Rep. 2022, 12, 2879. [Google Scholar] [CrossRef]
- Liu, Y.C.; Chou, P.; Wojciechowski, R.; Lin, P.Y.; Liu, C.J.; Chen, S.J.; Liu, J.H.; Hsu, W.M.; Cheng, C.Y. Power vector analysis of refractive, corneal, and internal astigmatism in an elderly Chinese population: The Shihpai Eye Study. Investig. Ophthalmol. Vis. Sci. 2011, 52, 9651–9657. [Google Scholar] [CrossRef] [PubMed]
- Mandel, Y.; Stone, R.A.; Zadok, D. Parameters associated with the different astigmatism axis orientations. Investig. Ophthalmol. Vis. Sci. 2010, 51, 723–730. [Google Scholar] [CrossRef]
- Refai, T.A. Evaluation of the orientation of the steepest meridian of regular astigmatism among highly myopic Egyptian patients seeking non-ablative surgical correction of the refractive error. Electron. Physician 2015, 7, 1296–1300. [Google Scholar] [CrossRef]
- Artal, P.; Berrio, E.; Guirao, A.; Piers, P. Contribution of the cornea and internal surfaces to the change of ocular aberrations with age. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2002, 19, 137–143. [Google Scholar] [CrossRef] [PubMed]
- Athaide, H.V.Z.; Campos, M.; Costa, C. Study of ocular aberrations with age. Arq. Bras. Oftalmol. 2009, 72, 617–621. [Google Scholar] [CrossRef] [PubMed]
- Berrio, E.; Tabernero, J.; Artal, P. Optical aberrations and alignment of the eye with age. J. Vis. 2010, 10, 34. [Google Scholar] [CrossRef]
- McLellan, J.S.; Marcos, S.; Burns, S.A. Age-related changes in monochromatic wave aberrations of the human eye. Investig. Ophthalmol. Vis. Sci. 2001, 42, 1390–1395. Available online: https://iovs.arvojournals.org/article.aspx?articleid=2162454 (accessed on 31 July 2025).
- Brunette, I.; Bueno, J.M.; Parent, M.; Hamam, H.; Simonet, P. Monochromatic Aberrations as a Function of Age, from Childhood to Advanced Age. Investig. Ophthalmol. Vis. Sci. 2003, 44, 5438. [Google Scholar] [CrossRef]
- Llorente, L.; Barbero, S.; Cano, D.; Dorronsoro, C.; Marcos, S. Myopic versus hyperopic eyes: Axial length, corneal shape and optical aberrations. J. Vis. 2004, 4, 288–298. [Google Scholar] [CrossRef]
- Kwan, W.C.; Yip, S.P.; Yap, M.K. Monochromatic aberrations of the human eye and myopia. Clin. Exp. Optom. 2009, 92, 304–312. [Google Scholar] [CrossRef]
- Khan, M.S.; Humayun, S.; Fawad, A.; Ishaq, M.; Arzoo, S.; Mashhadi, F. Comparison of higher order aberrations in patients with various refractive errors. Pak. J. Med. Sci. 2015, 31, 812–815. [Google Scholar] [CrossRef]
- Cheng, X.; Bradley, A.; Hong, X.; Thibos, L.N. Relationship between refractive error and monochromatic aberrations of the eye. Optom. Vis. Sci. 2003, 80, 43–49. [Google Scholar] [CrossRef]
- Mohaghegh, S.; Bamdad, S.; Kangari, H.; Rahmani, S. Associations between refractive error components and higher-order aberrations in simple myopia and compound myopic astigmatism. Front. Ophthalmol. 2025, 5, 1532931. [Google Scholar] [CrossRef]
- Kingston, A.C.; Cox, I.G. Population spherical aberration: Associations with ametropia, age, corneal curvature, and image quality. Clin. Ophthalmol. 2013, 7, 933–938. [Google Scholar] [CrossRef] [PubMed]
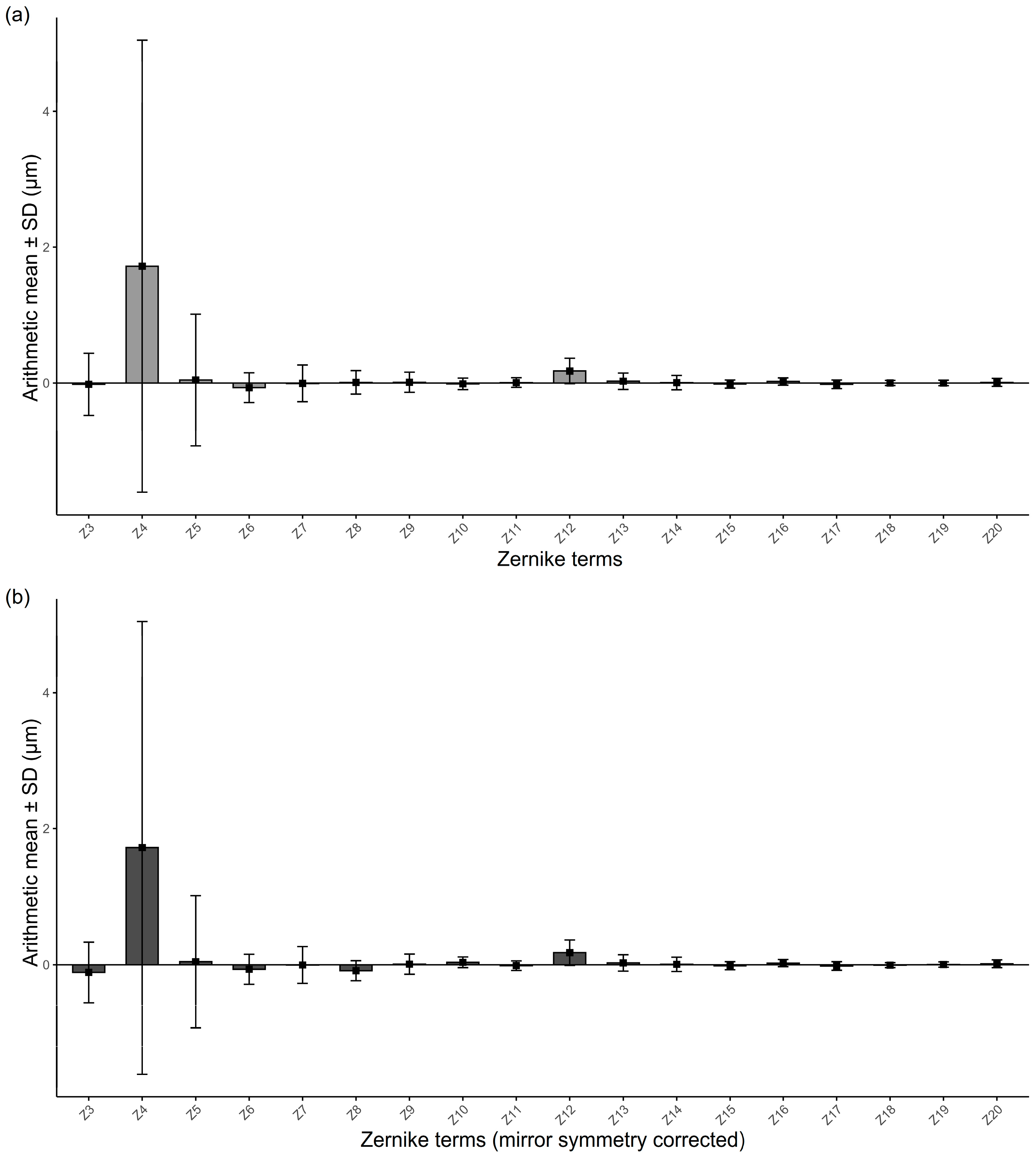
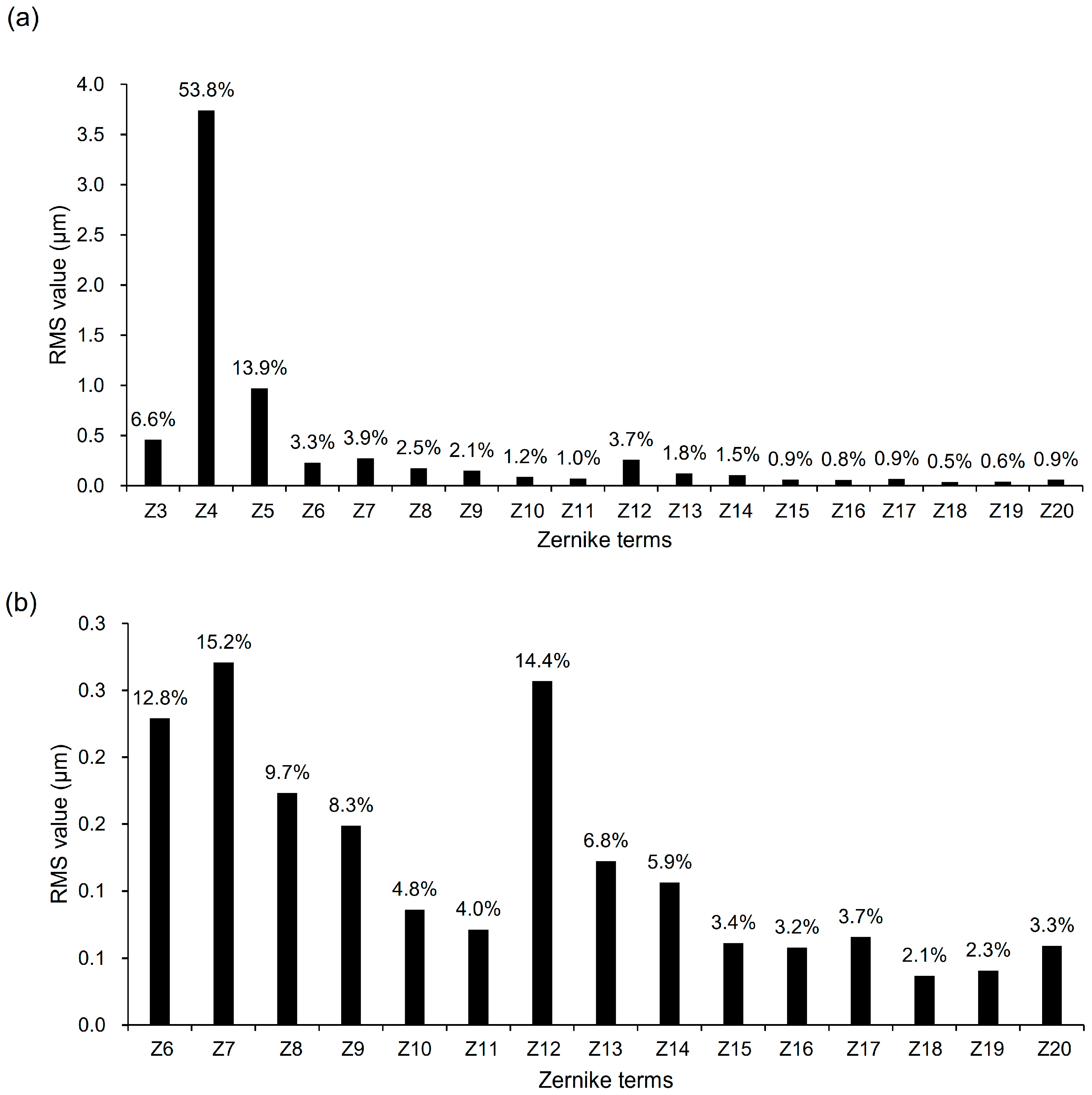
| abs Mean ± SD (μm) | |
|---|---|
| Z3 (oblique astig.) | 0.303 ± 0.343 |
| Z4 (defocus) | 2.676 ± 2.618 |
| Z5 (vertical astig.) | 0.749 ± 0.616 |
| Z6 (vertical trefoil) | 0.176 ± 0.147 |
| Z7 (vertical coma) | 0.208 ± 0.174 |
| Z8 (horizontal coma) | 0.137 ± 0.106 |
| Z9 (oblique trefoil) | 0.117 ± 0.092 |
| Z10 (oblique quadrafoil) | 0.063 ± 0.059 |
| Z11 (oblique sec. astig.) | 0.053 ± 0.048 |
| Z12 (spherical aberration) | 0.200 ± 0.161 |
| Z13 (vertical sec. astig.) | 0.094 ± 0.078 |
| Z14 (vertical quadrafoil) | 0.079 ± 0.071 |
| Z15 (vertical pentafoil) | 0.043 ± 0.044 |
| Z16 (vertical sec. trefoil) | 0.042 ± 0.040 |
| Z17 (vertical sec. coma) | 0.049 ± 0.044 |
| Z18 (horizontal sec. coma) | 0.026 ± 0.026 |
| Z19 (oblique sec. trefoil) | 0.027 ± 0.030 |
| Z20 (oblique pentafoil) | 0.038 ± 0.046 |
| Univariable Analysis | Multivariable Analysis | ||||||
|---|---|---|---|---|---|---|---|
| β | 95% CI | p-Value | β | 95% CI | p-Value | ICC | |
| Total RMS | 0.751 | ||||||
| Age (μm/year) | −0.048 | (−0.072, −0.025) | <0.001 * | 0.004 | (−0.012, 0.021) | 0.596 | |
| SE (μm/D) | −0.674 | (−0.760, −0.587) | <0.001 * | −0.678 | (−0.776, −0.579) | <0.001 * | |
| Sex (M) (μm) | 1.128 | (0.007, 2.248) | 0.049 * | 0.376 | (−0.277, 1.030) | 0.256 | |
| HOA RMS | 0.644 | ||||||
| Age (μm/year) | 0.003 | (0.001, 0.005) | 0.001 * | 0.003 | (0.001, 0.005) | 0.010 * | |
| SE (μm/D) | 0.017 | (0.004, 0.030) | 0.011 * | 0.009 | (−0.006, 0.023) | 0.246 | |
| Sex (M) (μm) | −0.002 | (−0.092, 0.089) | 0.971 | 0.061 | (−0.031, 0.153) | 0.191 | |
| Age | SE | |||||
|---|---|---|---|---|---|---|
| β (μm/year) | 95% CI | p-Value (Adjusted) | β (μm/D) | 95% CI | p-Value (Adjusted) | |
| Z3 (oblique astig.) | 0.000 | (−0.004, 0.004) | >0.99 | 0.011 | (−0.016, 0.037) | >0.99 |
| Z4 (defocus) | −0.089 | (−0.117, −0.061) | <0.001 * | −1.194 | (−1.210, −1.180) | <0.001 * |
| Z5 (vertical astig.) | 0.034 | (0.027, 0.041) | <0.001 * | 0.192 | (0.143, 0.240) | <0.001 * |
| Z6 (vertical trefoil) | −0.003 | (−0.005, −0.001) | 0.020 * | −0.021 | (−0.034, −0.008) | 0.044 * |
| Z7 (vertical coma) | −0.002 | (−0.004, 0.001) | >0.99 | −0.011 | (−0.028, 0.006) | >0.99 |
| Z8 (hor. coma) | −0.003 | (−0.004, −0.002) | <0.001 * | −0.010 | (−0.019, −0.001) | 0.463 |
| Z9 (oblique trefoil) | 0.000 | (−0.001, 0.001) | >0.99 | −0.004 | (−0.012, 0.005) | >0.99 |
| Z12 (SA) | 0.003 | (0.002, 0.005) | 0.006 * | 0.037 | (0.027, 0.047) | <0.001 * |
| ρ | p-Value (Adjusted) | |
|---|---|---|
| Z3 (oblique astigmatism) | 0.458 | <0.001 * |
| Z4 (defocus) | 0.896 | <0.001 * |
| Z5 (vertical astigmatism) | 0.839 | <0.001 * |
| Z6 (vertical trefoil) | 0.660 | <0.001 * |
| Z7 (vertical coma) | 0.708 | <0.001 * |
| Z8 (horizontal coma) | 0.639 | <0.001 * |
| Z9 (oblique trefoil) | 0.343 | 0.010 * |
| Z10 (oblique quadrafoil) | 0.147 | >0.99 |
| Z11 (oblique sec. astig.) | 0.214 | 0.617 |
| Z12 (spherical aberration) | 0.827 | <0.001 * |
| Z13 (vertical sec. astig.) | 0.489 | <0.001 * |
| Z14 (vertical quadrafoil) | 0.498 | <0.001 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seo, J.Y.; Kwon, N.E.; Jun, J.H.; Bang, S.P. Distribution and Demographic Correlates of Ocular Wavefront Aberrations in a Korean Population. J. Clin. Med. 2025, 14, 6981. https://doi.org/10.3390/jcm14196981
Seo JY, Kwon NE, Jun JH, Bang SP. Distribution and Demographic Correlates of Ocular Wavefront Aberrations in a Korean Population. Journal of Clinical Medicine. 2025; 14(19):6981. https://doi.org/10.3390/jcm14196981
Chicago/Turabian StyleSeo, Ji Young, Noh Eun Kwon, Jong Hwa Jun, and Seung Pil Bang. 2025. "Distribution and Demographic Correlates of Ocular Wavefront Aberrations in a Korean Population" Journal of Clinical Medicine 14, no. 19: 6981. https://doi.org/10.3390/jcm14196981
APA StyleSeo, J. Y., Kwon, N. E., Jun, J. H., & Bang, S. P. (2025). Distribution and Demographic Correlates of Ocular Wavefront Aberrations in a Korean Population. Journal of Clinical Medicine, 14(19), 6981. https://doi.org/10.3390/jcm14196981








