Can the Mismatch of Measured Pelvic Morphology vs. Lumbar Lordosis Predict Chronic Low Back Pain Patients?
Abstract
1. Introduction
2. Materials and Methods
2.1. Patient Data Collection
2.2. Lumbar Modeling
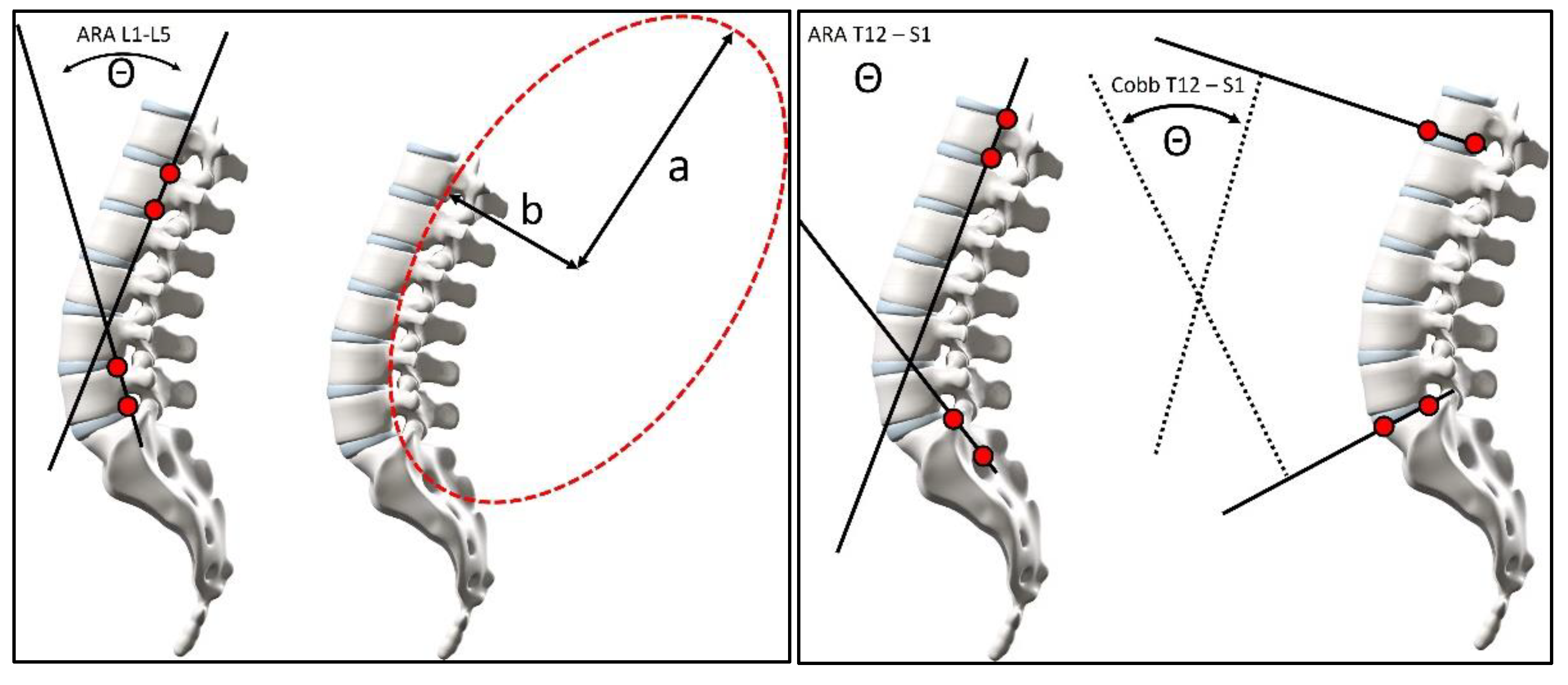
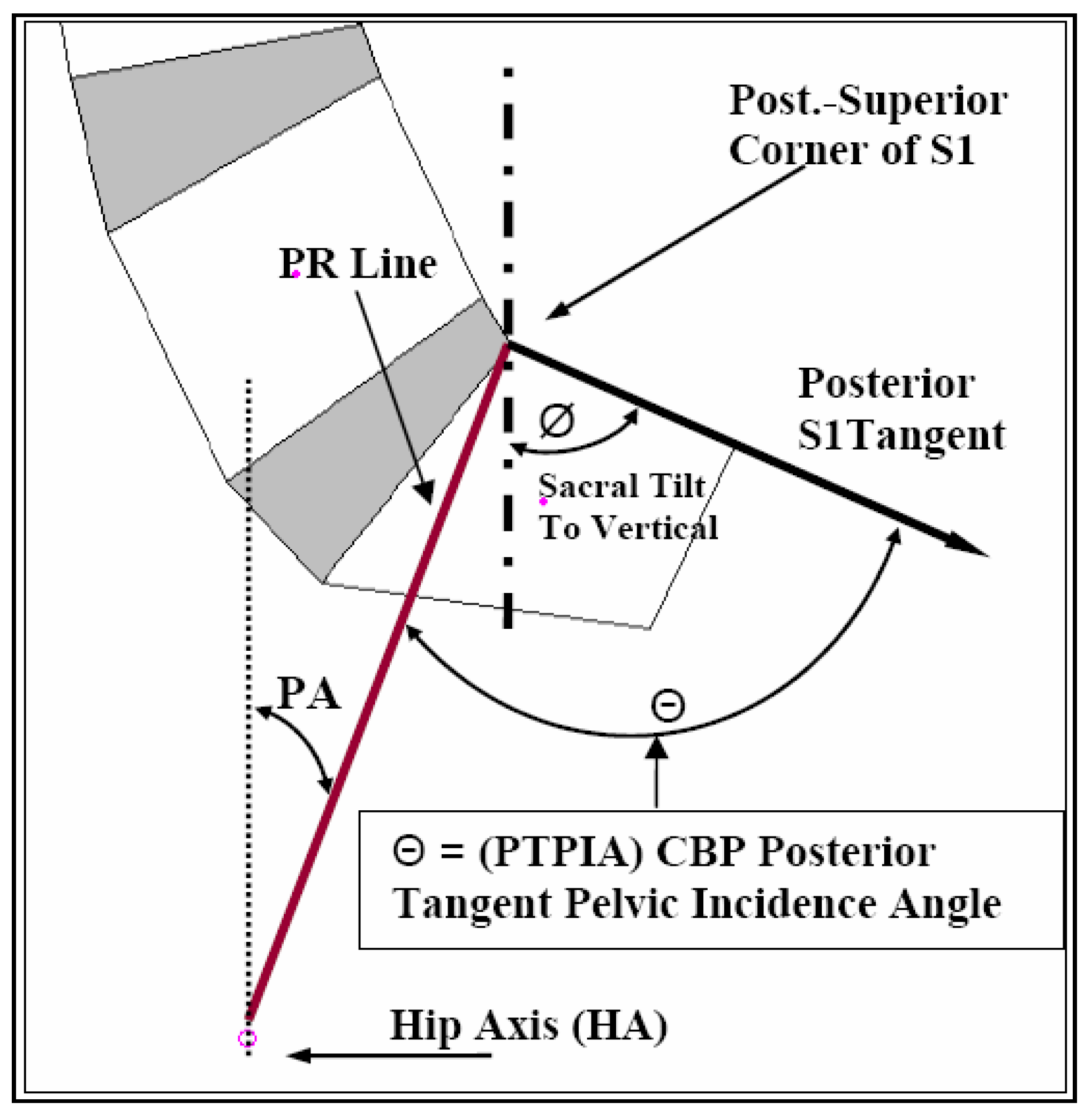
2.3. Radiographic Measurements
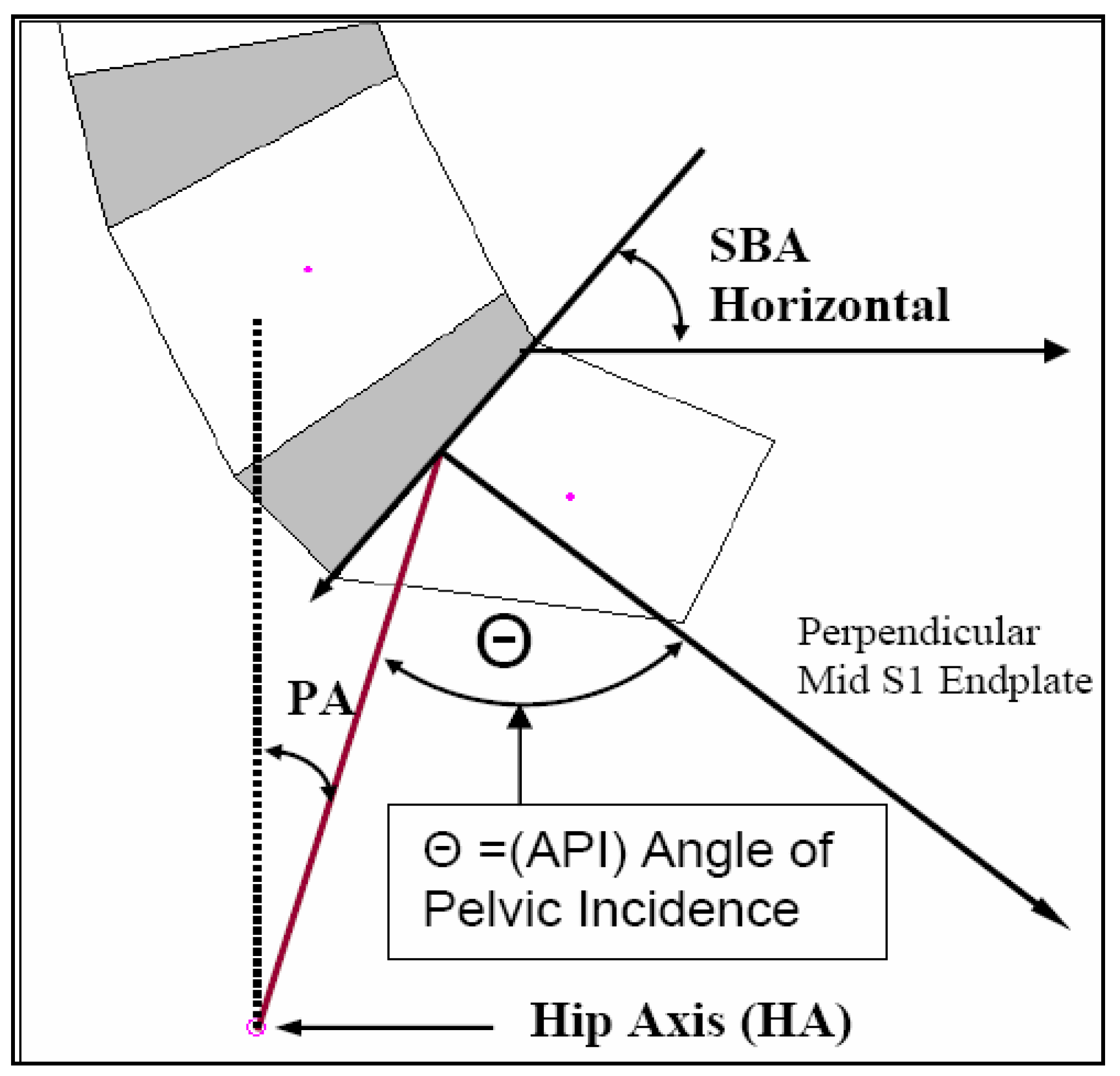
2.4. Pelvic Morphology
2.5. Statistical Analysis
3. Results
3.1. Means, Standard Deviation, and Minimum/Maximum Radiographic Parameters
3.2. Pelvic Morphology and Matrix of Correlations
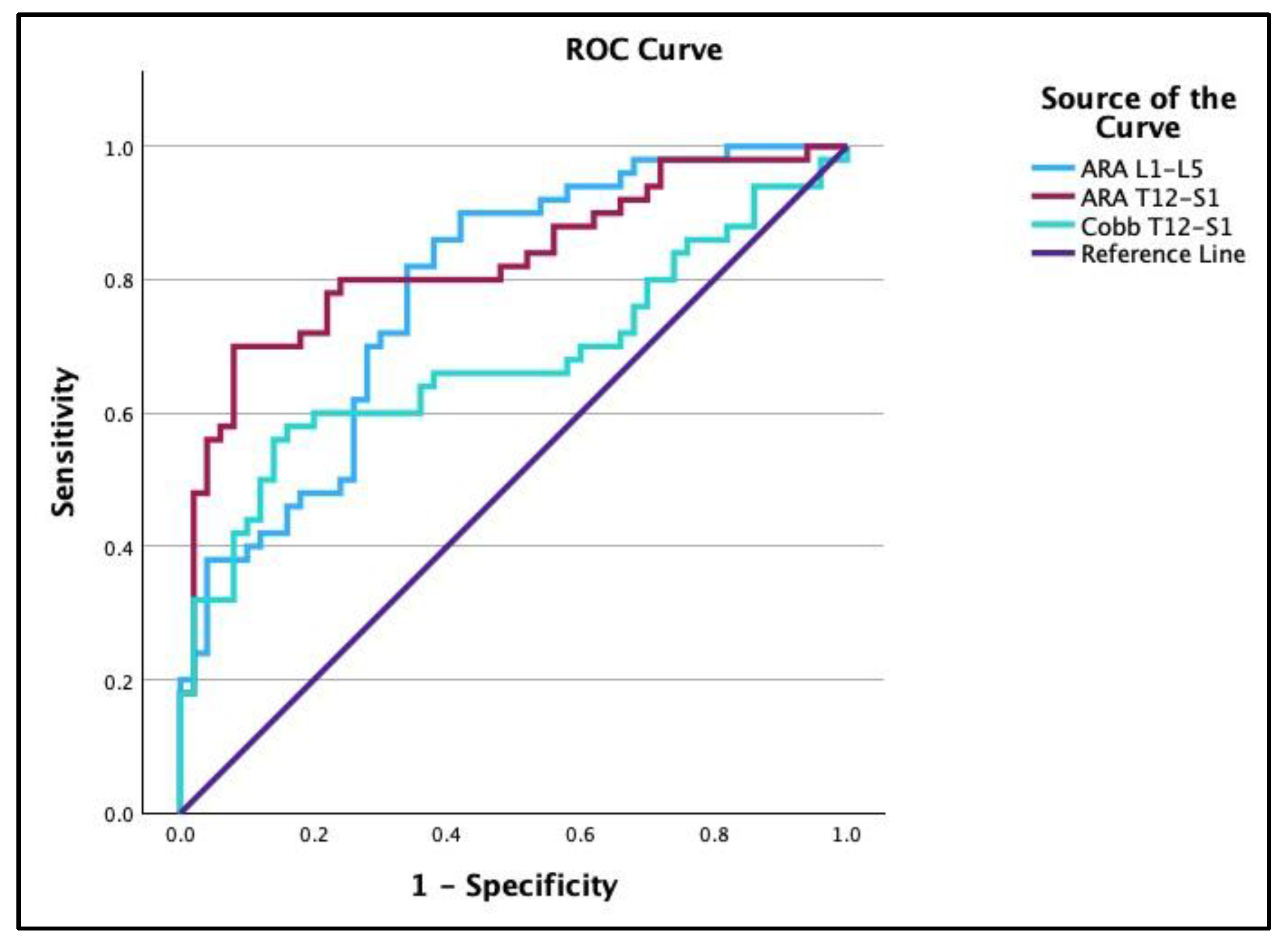
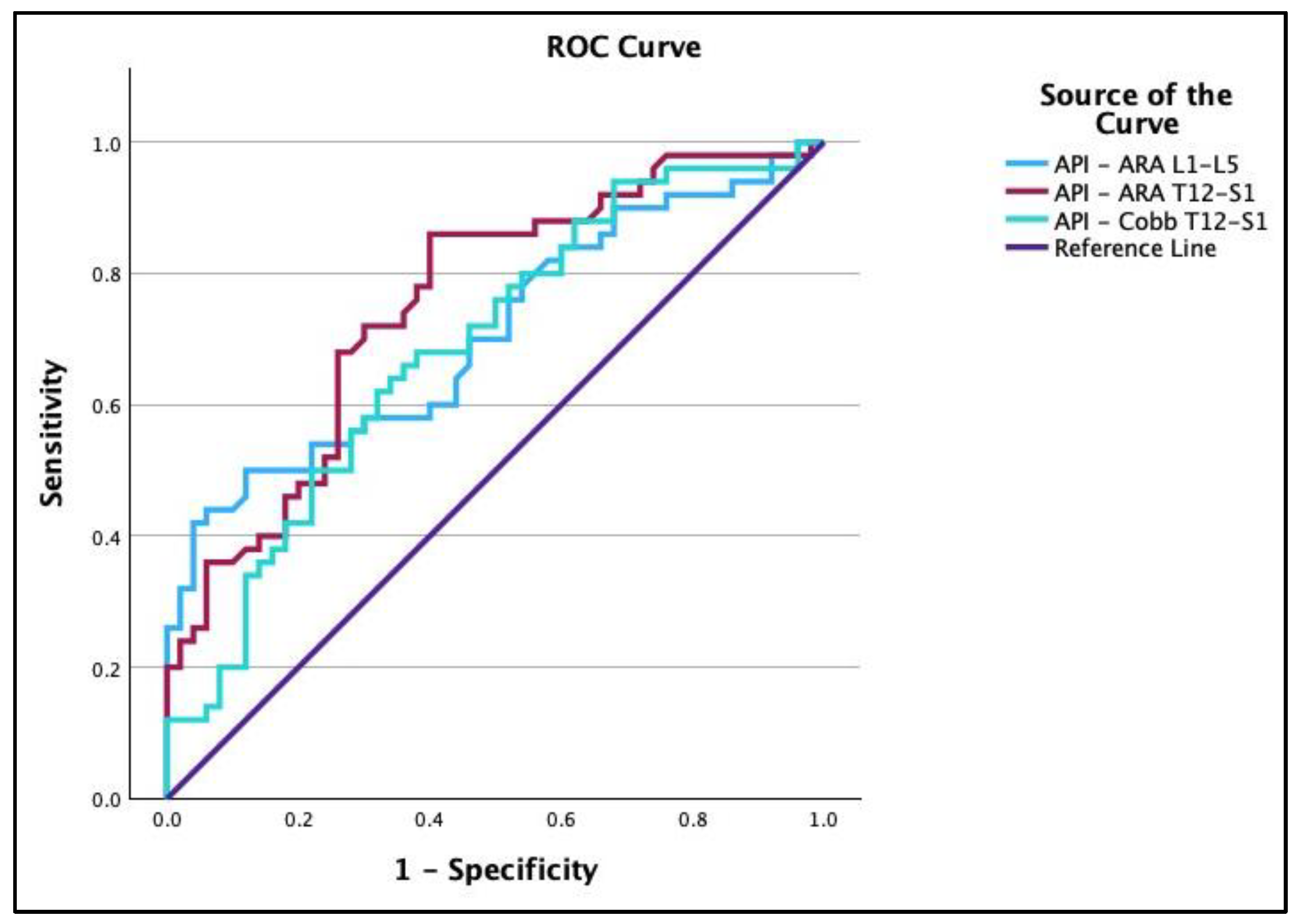
3.3. Receiver Operating Characteristic Curves
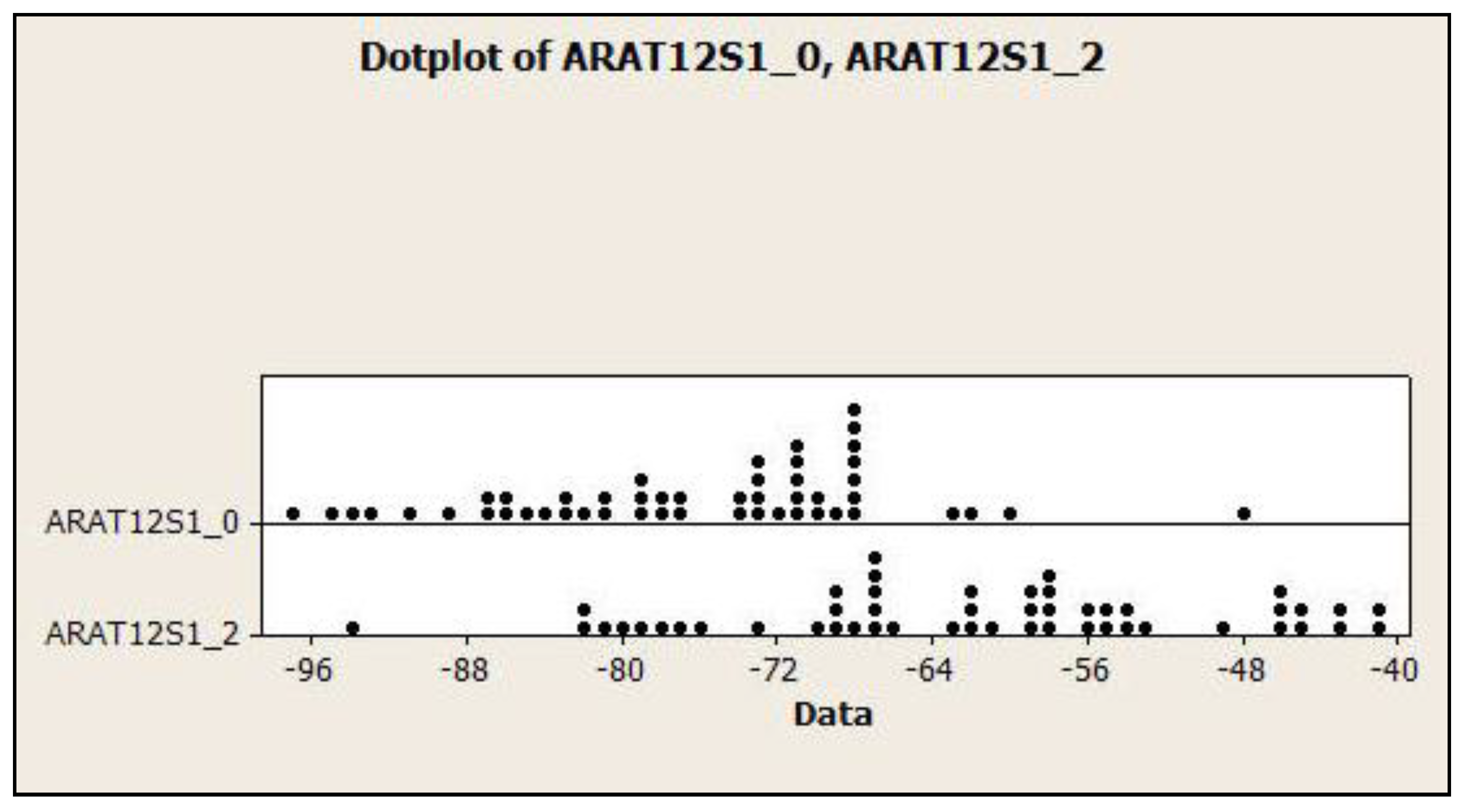
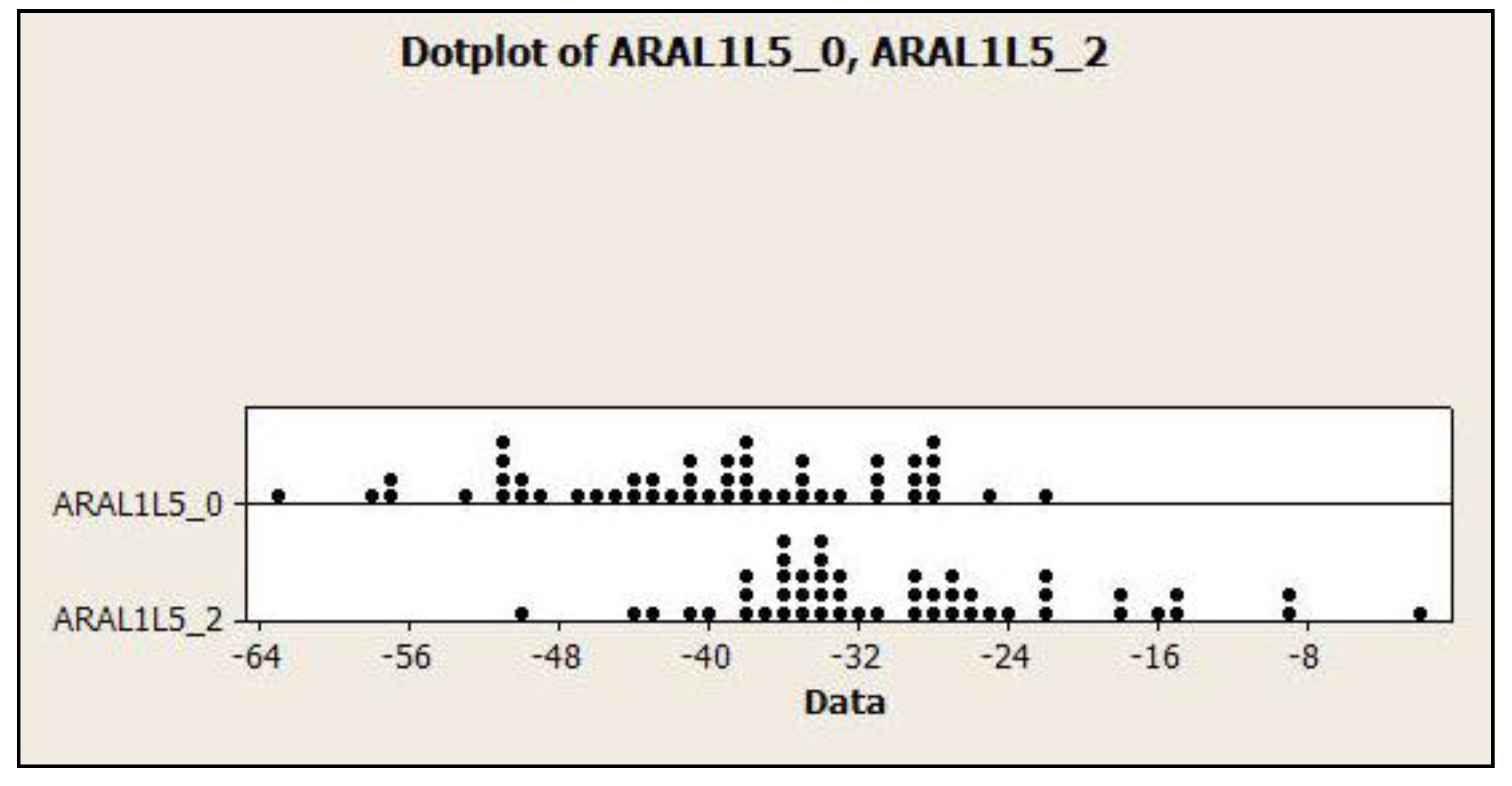
3.4. Dot Plots for the Relationship of Lumbar Lordosis in Normal vs. CLBP
4. Discussion
4.1. ROC Curve Analysis
4.2. Pelvic Morphology, Sacral Tilt, and Lordosis Mensuration
4.3. Study Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| API | Angle of pelvic incidence |
| ARA | Absolute rotation angle |
| CLBP | Chronic low back pain |
| HA | Hip axis |
| HOA | Hip osteoarthritis |
| LL | Lumbar lordosis |
| PTPIA | Posterior tangent pelvic incidence angle |
| ROC | Receiver operator characteristic curve |
| SBA | Sacral base angle |
References
- Gelb, D.E.; Lenke, L.G.; Bridwell, K.H.; Blanke, K.; McEnery, K.W. An analysis of sagittal spinal alignment in 100 asymptomatic middle and older aged volunteers. Spine 1995, 20, 1352–1358. [Google Scholar] [CrossRef]
- Kobayashi, T.; Atsuta, Y.; Matsuno, T.; Takeda, N. A longitudinal study of congruent sagittal spinal alignment in an adult cohort. Spine 2004, 29, 671–676. [Google Scholar] [CrossRef]
- Hammerberg, M.E.; Wood, K.B. Sagittal profile of the elderly. J. Spinal Disord. Technol. 2003, 16, 44–50. [Google Scholar] [CrossRef] [PubMed]
- Murrie, V.L.; Dixon, A.K.; Hollingworth, W.; Wilson, H.; Doyle, T.A.C. Lumbar Lordosis: Study of patients with and without low back pain. Clin. Anat. 2003, 16, 147. [Google Scholar] [CrossRef] [PubMed]
- Tuzun, C.; Yorulmaz Cindas, A.; Vatan, S. Low back pain and posture. Clin. Rheumatol. 1999, 18, 308–312. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.G.; Sun, Y.; Boonen, S.; Nicholson, P.H.; Brys, P.; Dequeker, J.; Felsenberg, D. Measurements of vertebral shape by radiographic morphometry: Sex differences and relationships with vertebral level and lumbar lordosis. Skelet. Radiol. 1998, 27, 380–384. [Google Scholar] [CrossRef]
- During, J.; Goudfrooij, H.; Keessen, W.; Beeker, T.W.; Crowe, A. Toward standards for posture: Postural characteristics of the lower back system in normal and pathologic conditions. Spine 1985, 10, 83–87. [Google Scholar] [CrossRef]
- Legaye, J.; Duval-Beaupere, G.; Hecquet, J.; Marty, C. Pelvic incidence: A fundamental pelvic parameter for three-dimensional regulation of spinal sagittal curves. Eur. Spine J. 1998, 7, 99–103. [Google Scholar] [CrossRef]
- Roussouly, P.; Gollogly, S.; Berthonnaud, E.; Dimnet, J. Classification of the normal variation in the sagittal alignment of the human lumbar spine and pelvis in the standing position. Spine 2005, 30, 346–353. [Google Scholar] [CrossRef]
- Vialle, R.; Levassor, N.; Rillardon, L.; Templier, A.; Skalli, W.; Guigui, P. Radiographic analysis of the sagittal alignment and balance of the spine in asymptomatic subjects. J. Bone Jt. Surg. 2005, 87, 260–267. [Google Scholar] [CrossRef]
- Boulay, C.; Tardieu, C.; Hecquet, J.; Benaim, C.; Mouilleseaux, B.; Marty, C.; Prat-Pradal, D.; Legaye, J.; Duval-Beaupère, G. Sagittal alignment of spine and pelvis regulated by pelvic incidence: Standard values and prediction of lordosis. Eur. Spine J. 2006, 15, 415–422. [Google Scholar] [CrossRef] [PubMed]
- Jackson, R.P.; Hales, C. Congruent spinopelvic alignment on standing lateral radiographs of adult volunteers. Spine 2000, 25, 2808–2815. [Google Scholar] [CrossRef] [PubMed]
- Jackson, R.P.; Kanemura, T.; Kawakami, N.; Hales, C. Lumbopelvic lordosis and pelvic balance on repeated standing lateral radiographs of adult volunteers and untreated patients with constant low back pain. Spine 2000, 25, 575–586. [Google Scholar] [CrossRef]
- Marty, C.; Boisaubert, B.; Descamps, H.; Montigny, J.P.; Hecquet, J.; Legaye, J.; Duval-Beaupere, G. The sagittal anatomy of the sacrum among young adults, infants, and spondylolisthesis patients. Eur. Spine J. 2002, 11, 119–125. [Google Scholar] [CrossRef]
- Antoniades, S.B.; Hammerberg, K.W.; DeWald, R.L. Sagittal plane configuration of the sacrum in spondylolisthesis. Spine 2000, 25, 1085–1091. [Google Scholar] [CrossRef]
- Jackson, R.P.; Peterson, M.D.; McManus, A.C.; Hales, C. Compensatory spinopelvic balance over the hip axis and better reliability in measuring lordosis to the pelvic radius on standing lateral radiographs of adult volunteers and patients. Spine 1998, 23, 1750–1767. [Google Scholar] [CrossRef]
- Troyanovich, S.J.; Cailliet, R.; Janik, T.J.; Harrison, D.D.; Harrison, D.E. Radiographic mensuration charac-teristics of the sagittal lumbar spine from a normal population with a method to synthesize prior studies of lordosis. J. Spinal Disord. 1997, 10, 380–386. [Google Scholar] [CrossRef] [PubMed]
- Jackson, R.P.; McManus, A.C. Radiographic analysis of sagittal plane alignment and balance in standing volunteers and patients with low back pain matched for age, sex, and size. Spine 1994, 19, 1611–1618. [Google Scholar] [CrossRef]
- Janik, T.J.; Harrison, D.D.; Cailliet, R.; Troyanovich, S.J.; Harrison, D.E. Can the Sagittal Lumbar Curvature be Closely Approximated by an Ellipse? J. Orthop. Res. 1998, 16, 766–770. [Google Scholar] [CrossRef]
- Harrison, D.D.; Cailliet, R.; Janik, T.J.; Troyanovich, S.J.; Harrison, D.E. Elliptical Modeling of the Sagittal lumbar lordosis and Segmental Rotation Angles as a Method to Discriminate Between Normal and Low Back Pain Subjects. J. Spinal Disord. 1998, 11, 430–439. [Google Scholar] [CrossRef]
- Korovessis, P.; Stamatakis, M.; Baikousis, A. Segmental roentgenographic analysis of vertebral inclination on sagittal plane in asymptomatic versus chronic low back pain patients. J. Spinal Disord. 1999, 12, 131–137. [Google Scholar] [CrossRef]
- Korovessis, P.; Dimas, A.; Iliopoulos, P.; Lambiris, E. Correlative analysis of lateral vertebral radiographic variables and medical out-comes study short-form health survey. A comparative study in asymptomatic volunteers versus patients with low back pain. J. Spinal Disord. Tech. 2002, 15, 384–390. [Google Scholar] [CrossRef] [PubMed]
- Splithoff, C.A. Lumbosacral junction. Roentgenographic comparison of patients with and without back-aches. JAMA 1953, 152, 1610–1612. [Google Scholar] [CrossRef]
- Tsuji, T.; Matsuyama, Y.; Sato, Y.; Hasegawa, Y.; Yimin, Y.; Iwata, H. Epidemiology of low back pain in the elderly: Correlation withlumbar lordosis. J. Orthop. Sci. 2001, 6, 307–311. [Google Scholar] [CrossRef] [PubMed]
- Tsuji, T.; Matsuyama, Y.; Goto, M.; Yimin, Y.; Sato, K.; Hasegawa, H.; Ishiguro, N. Knee-spine syndrome: Correlation between sacral inclination and patellofemoral joint pain. J. Orthop. Sci. 2002, 7, 519–523. [Google Scholar] [CrossRef] [PubMed]
- Hansson, T.; Bigos, S.; Beecher, P.; Wortley, M. The lumbar lordosis in acute and chronic low-back pain. Spine 1985, 10, 154–155. [Google Scholar] [CrossRef]
- Frymoyer, J.W.; Newberg, A.; Pope, M.H.; Wilder, D.G.; Clements, J.; MacPherson, B. Spine radiographs in patients with low-back pain. J. Bone Jt. Surg. 1984, 66, 1048–1055. [Google Scholar] [CrossRef]
- Chun, S.W.; Lim, C.Y.; Kim, K.; Hwang, J.; Chung, S.G. The relationships between low back pain and lumbar lordosis: A systematic review and meta-analysis. Spine J. 2017, 17, 1180–1191. [Google Scholar] [CrossRef]
- Sadler, S.G.; Spink, M.J.; Ho, A.; De Jonge, X.J.; Chuter, V.H. Restriction in lateral bending range of motion, lumbar lordosis, and hamstring flexibility predicts the development of low back pain: A systematic review of prospective cohort studies. BMC Musculoskelet. Disord. 2017, 18, 179. [Google Scholar] [CrossRef]
- Yoshimoto, H.; Sato, S.; Masuda, T.; Kanno, T.; Shundo, M.; Hyakumachi, T.; Yanagibashi, Y. Spinopelvic alignment in patients with osteoarthrosis of the hip. A radiographic comparison to patients with low back pain. Spine 2005, 30, 1650–1657. [Google Scholar] [CrossRef]
- Been, E.; Simonovich, A.; Kalichman, L. Spinal Posture and Pathology in Modern Humans. In Spinal Evolution: Morphology, Function, and Pathology of the Spine in Hominoid Evolution; Been, E., Gómez-Olivencia, A., Kramer, P.A., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 301–320. [Google Scholar] [CrossRef]
- Diebo, B.G.; Varghese, J.J.; Lafage, R.; Schwab, F.J.; Lafage, V. Sagittal alignment of the spine: What do you need to know? Clin. Neurol. Neurosurg. 2015, 139, 295–301. [Google Scholar] [CrossRef] [PubMed]
- Savarese, L.G.; Menezes-Reis, R.; Bonugli, G.P.; Herrero, C.F.P.D.S.; Defino, H.L.A.; Nogueira-Barbosa, M.H. Spinopelvic sagittal balance: What does the radiologist need to know? Radiol. Bras. 2020, 53, 175–184. [Google Scholar] [CrossRef] [PubMed]
- Protopsaltis, T.; Schwab, F.; Bronsard, N.; Smith, J.S.; Klineberg, E.; Mundis, G.; Ryan, D.J.; Hostin, R.; Hart, R.; Burton, D.; et al. TheT1 pelvic angle, a novel radiographic measure of global sagittal deformity, accounts for both spinal inclination and pelvic tilt and correlates with health-related quality of life. J. Bone Jt. Surg. Am. 2014, 96, 1631–1640. [Google Scholar] [CrossRef] [PubMed]
- Berthonnaud, E.; Labelle, H.; Roussouly, P.; Grimard, G.; Vaz, G.; Dimnet, J. A variability study of computerized sagittal spinopelvic radiologic measurements of trunk balance. J. Spinal Disord. Tech. 2005, 18, 66–71. [Google Scholar] [CrossRef] [PubMed]
- Hwang, J.H.; Modi, H.N.; Suh, S.W.; Hong, J.Y.; Park, Y.H.; Park, J.H.; Yang, J.H. Reliability of lumbar lordosis measurement in patients with spondylolisthesis: A case-control study comparing the Cobb, centroid, and posterior tangent methods. Spine 2010, 35, 1691–1700. [Google Scholar] [CrossRef]
- Harrison, D.E.; Keller, T.S.; Betz, J.W.; Colloca, C.J.; Haas, J.W.; Harrison, D.D.; Janik, T.J. Radiographic and biomechanical analysis of patients with low back pain: A prospective clinical trial. In Proceedings of the 32nd Annual Meeting of the International Society for the Study of the Lumbar Spine, New York, NY, USA, 10–14 May 2005; p. 162. [Google Scholar]
- Oakley, P.A.; Ehsani, N.N.; Moustafa, I.M.; Harrison, D.E. Restoring lumbar lordosis: A systematic review of controlled trials utilizing Chiropractic Bio Physics® (CBP®) non-surgical approach to increasing lumbar lordosis in the treatment of low back disorders. J. Phys. Ther. Sci. 2020, 32, 601–610. [Google Scholar] [CrossRef]
- Lee, C.H.; Heo, S.J.; Park, S.H.; Jeong, H.S.; Kim, S.Y. Functional Changes in Patients and Morphological Changes in the Lumbar Intervertebral Disc after Applying Lordotic Curve-Controlled Traction: A Double-Blind Randomized Controlled Study. Medicina 2019, 56, 4. [Google Scholar] [CrossRef]
- Li, Y.; Sun, J.; Wang, G. Lumbar lordosis morphology correlates to pelvic incidence and erector spinae muscularity. Sci. Rep. 2021, 11, 802. [Google Scholar] [CrossRef]
- Rothenfluh, D.A.; Mueller, D.A.; Rothenfluh, E.; Min, K. Pelvic incidence-lumbar lordosis mismatch predisposes to adjacent segment disease after lumbar spinal fusion. Eur. Spine J. 2015, 24, 1251–1258. [Google Scholar] [CrossRef]
- Inami, S.; Moridaira, H.; Takeuchi, D.; Shiba, Y.; Nohara, Y.; Taneichi, H. Optimum pelvic incidence minus lumbar lordosis value can be determined by individual pelvic incidence. Eur. Spine J. 2016, 25, 3638–3643. [Google Scholar] [CrossRef]
- Adams, M.A.; Mannion, A.F.; Dolan, P. Personal risk factors for first time low back pain. Spine 1999, 24, 2497–2505. [Google Scholar] [CrossRef] [PubMed]
- Casiano, V.E.; Sarwan, G.; Dydyk, A.M.; Varacallo, M. Back Pain. In StatPearls [Internet]; [Updated 2023 Dec 11]; StatPearls Publishing: Treasure Island, FL, USA, 2024. Available online: https://www.ncbi.nlm.nih.gov/books/NBK538173/ (accessed on 4 March 2024).
- Glassman, S.D.; Bridwell, K.; Dimar, J.R.; Horton, W.; Berven, S.; Schwab, F. The impact of positive sagittal balance in adult spinal deformity. Spine 2005, 30, 2024–2029. [Google Scholar] [CrossRef] [PubMed]
- Panjabi, M.; Yamamoto, I.; Oxland, T.; Crisco, J. How does posture affect coupling in the lumbar spine? Spine 1989, 14, 1002–1011. [Google Scholar] [CrossRef] [PubMed]
- Cholewicki, J.; Crisco JJ 3rd Oxland, T.R.; Yamamoto, I.; Panjabi, M.M. Effects of posture and structure on three-dimensional coupled rotations in the lumbar spine. A biomechanical analysis. Spine 1996, 21, 2421–2428. [Google Scholar] [CrossRef]
- Tamim, M.; Moustafa, I.M.; Alaparthi, G.K.; Oakley, P.A.; Harrison, D.E. Translational and Rotational Postural Aberrations Are Related to Pulmonary Functions and Skill-Related Physical Fitness Components in Collegiate Athletes. J. Clin. Med. 2023, 12, 4618. [Google Scholar] [CrossRef]
| Variable | Normal Group | CLBP Patients | ||||
|---|---|---|---|---|---|---|
| Mean ± SD | Max | Min | Mean ± SD | Max | Min | |
| Age yrs | 27.7 ± 8.5 | 52 | 18 | 29.5 ± 8 | 45 | 15 |
| Height cm | 171.5 $ | $ | $ | 174 $ | $ | $ |
| Weight kg | 70.8 $ | $ | $ | 74 $ | $ | $ |
| Sex | 29 Males, 21 Females | 29 Males, 21 Females | ||||
| ARA L1-L5 | −40.2 ± 9.4° | −22.1° | −62.9° | −29.6 ± 9.6° | −1.6° | −50.3° |
| ARA T12-S1 | −76.3 ± 9.9° | −47.8° | −97.3° | −61.9 ± 12.5° | −40.6° | −93.8° |
| Cobb T12-S1 | −65.4 ± 9.4° | −44.2° | −83.4 ° | −57.0 ± 14.7° | −27° | −85.3° |
| SBA | 39.4 ± 7.2° | 53.4° | 23.9° | 38.2 ± 11.6° | 61.5° | 14.0° |
| PT S1 | 50.3 ± 7.8° | 62.1° | 29.7° | 43.1 ± 8.8° | 74.2° | 19.6° |
| b/a | 0.389 ± 0.147 | 0.874 | 0.150 | 0.264 ± 0.181 | 0.747 | 0.000 |
| API | 56.8 ± 11° | 82.2° | 40.6° | 58.0 ± 15.6° | 95.2° | 29.4° |
| PTPIA | 73.9 ± 8.9° | 92.9° | 57.1° | 68.4 ± 10.7° | 92.4° | 45.6° |
| API − ARA T12-S1 | −19.5 ± 14.4° | 13.8° | −47.6° | −3.3 ± 18° | 49.3° | −40.1° |
| API − ARA L1-L5 | 16.6 ± 11.4° | 40° | −7.8° | 28.4 ± 16.2° | 59.2° | 1.5° |
| API − Cobb T12-S1 | −8.6 ± 12.9° | 18.9° | −33.7° | 1.0 ± 14.3° | 36.9° | −26.6° |
| Group | Variable | PTS1 | ARA T12S1 | Cobb T12S1 | ARA L1L5 | SBA | API | PTPIA |
|---|---|---|---|---|---|---|---|---|
| Normal | ||||||||
| SBA | 0.808 ** p < 0.001 | −0.644 ** p < 0.001 | −0.764 ** p < 0.001 | −0.604 ** p < 0.001 | ||||
| API | 0.231 p > 0.05 | −0.047 p > 0.05 | −0.200 p > 0.05 | −0.378 ** p = 0.007 | 0.451 ** p < 0.001 | |||
| PTPIA | 0.486 ** p < 0.001 | −0.233 p > 0.05 | −0.136 p > 0.05 | −0.325 * p = 0.021 | 0.390 ** p = 0.005 | 0.858 ** p < 0.001 | ||
| b/a | 0.267 p > 0.05 | −0.369 ** p = 0.008 | −0.558 ** p < 0.001 | −0.551 ** p < 0.001 | 0.399 ** p = 0.004 | 0.269 p > 0.05 | 0.112 p > 0.05 | |
| Chronic pain | ||||||||
| SBA | 0.649 ** p < 0.001 | −0.585 ** p < 0.001 | −0.897 ** p < 0.001 | −0.401 ** p = 0.004 | ||||
| API | 0.319 * p = 0.024 | −0.206 p > 0.05 | −0.558 ** p < 0.001 | −0.242 p > 0.05 | 0.728 ** p < 0.001 | |||
| PTPIA | 0.543 ** p < 0.001 | −0.348 * p = 0.013 | −0.255 p > 0.05 | −0.268 p > 0.05 | 0.362 * p = 0.01 | 0.729 ** p < 0.001 | ||
| b/a | 0.588 ** p < 0.001 | −0.703 ** p < 0.001 | −0.612 ** p < 0.001 | −0.550 ** p < 0.001 | 0.464 ** p < 0.001 | 0.375 ** p = 0.007 | 0.469 ** p < 0.001 |
| Groups | Variable | AUC | Cutoff | Sensitivity | Specificity |
|---|---|---|---|---|---|
| Normal vs. Chronic | ARA L1-L5 | 0.78 | −36.18° | 0.82 | 0.66 |
| ARA T12-S1 | 0.83 | −67.43° | 0.70 | 0.92 | |
| Cobb T12-S1 | 0.68 | −56.05° | 0.56 | 0.86 | |
| API − ARA T12-S1 | 0.75 | −17.95° | 0.86 | 0.6 | |
| API − ARA L1-L5 | 0.71 | 35.2° | 0.42 | 0.96 | |
| API − Cobb T12-S1 | 0.69 | −4.79° | 0.62 | 0.68 |
| Study | P. M. Method | Sample Size and Age in Years | P.M. Normals, Mean ± S.D (°) | P.M. LBP Groups, Mean ± S.D (°) | SBA or S1 Tangent, Mean ± S.D. (°) |
|---|---|---|---|---|---|
| During et al. [7] | Pelvi-sacral Angle | +N = 52 C, 44 DD++ and LBP, A = 16–46 | 41.27 ± 9.98 | ++DD = 37.4 ± 12.36 ++LBP = 37.3 ± 11.76 | SBA C = 40.4 ± 8.8, DD = 37.9 ± 8.2, LBP = 41.3 ± 8.6 Lordosis reduced in DD and LBP subjects |
| Current Study | 1. API 2. PR-S1 3. PTPIA | N= 50 C, N = 50 CLBP Mean A = 27–30 | 1. 56.8 ± 11° 2. 27.0 ± 9.1° 3. 73.9 ± 8.9° | 1. 58.0 ± 15.6° 2. 26.5 ± 13.5° 3. 68.4 ± 10.7° | Both SBA and S1 Tangent. Refer to Table 1 for Results. |
| Yoshimoto et al. [30] | API | HOA N = 150 A = 61 ± 11, LBP Patients N = 150 A = 58.9 ± 11.7 | NA | HOA = 58.5 ± 14, LBP = 51.9 ± 13.4 | SBA HOA = 41.4 ± 10.3, LBP = 31.2 ± 10.5 Lumbar lordosis was reduced in LBP |
| Jackson et al. [13] | PR-S1 | N = 20 C A = 27–75, N = 20 LBP A = 26–73 | −31.5 ± 8.7 Max = −16 Min = −47 | −33.6 ± 11.9 Max = −15 Min = −56 | NR T12-S1 Lumbar lordosis was decreased in LBP |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harrison, D.E.; Haas, J.W.; Moustafa, I.M.; Betz, J.W.; Oakley, P.A. Can the Mismatch of Measured Pelvic Morphology vs. Lumbar Lordosis Predict Chronic Low Back Pain Patients? J. Clin. Med. 2024, 13, 2178. https://doi.org/10.3390/jcm13082178
Harrison DE, Haas JW, Moustafa IM, Betz JW, Oakley PA. Can the Mismatch of Measured Pelvic Morphology vs. Lumbar Lordosis Predict Chronic Low Back Pain Patients? Journal of Clinical Medicine. 2024; 13(8):2178. https://doi.org/10.3390/jcm13082178
Chicago/Turabian StyleHarrison, Deed E., Jason W. Haas, Ibrahim M. Moustafa, Joseph W. Betz, and Paul A. Oakley. 2024. "Can the Mismatch of Measured Pelvic Morphology vs. Lumbar Lordosis Predict Chronic Low Back Pain Patients?" Journal of Clinical Medicine 13, no. 8: 2178. https://doi.org/10.3390/jcm13082178
APA StyleHarrison, D. E., Haas, J. W., Moustafa, I. M., Betz, J. W., & Oakley, P. A. (2024). Can the Mismatch of Measured Pelvic Morphology vs. Lumbar Lordosis Predict Chronic Low Back Pain Patients? Journal of Clinical Medicine, 13(8), 2178. https://doi.org/10.3390/jcm13082178












