1. Introduction
The presence of ions crucially influences membranes in terms of structural and mechanical properties, dynamics, thermodynamic stability and biological function [
1,
2,
3,
4,
5,
6,
7]. Understanding the molecular mechanisms underlying membrane structure and mechanics is important not only because of the biological relevance of membranes in aqueous electrolyte solutions, but also because the structural and mechanical characteristics of membranes will, in the future, be of increasing interest in the development of synthetic materials or engineered tissues [
8,
9].
The strength of ion-membrane binding is governed by the equilibrium between solvation and the membrane-interaction of the ions. Intuitively, electrostatic interactions are a key determinant of this equilibrium, which is why, at first glance, considerable differences in ion-membrane binding may be expected depending on the ion valency and the membrane charge. Divalent ions show stronger binding than monovalent ones, e.g., the (intrinsic) binding constants of Na
, Cl
and Ca
to zwitterionic 1,2-dipalmitoyl-
sn-glycero-3-phosphatidylcholine (DPPC) liposomes were measured at 25 °C as 0.25 M
, 0.28 M
and 37 M
, respectively [
10]. For comparison, the intrinsic binding constant at 25 °C of Na
to anionic phosphatidylserine-containing vesicles was suggested to be 0.6 M
[
11]. This illustrates the seemingly important role of electrostatic interactions. Considering the release of tightly-bound solvation-shell water molecules that accompanies the desolvation of a membrane-associated ion, entropy gain may also be seen as a main driving force for the binding of ions to membranes [
5]. The two mechanisms (the role of electrostatic interactions and entropy gain of released water) are, however, intimately connected, because the Coulomb interaction energy (between two charged species in water, expressing the solvent degrees of freedom via the dielectric constant of the solvent) can, due to the temperature dependence of the solvent relative dielectric permittivity, be interpreted as a free energy [
12], with entropic and enthalpic components per unit charge of
V and
V, respectively. Moreover, one may expect that the ionic strength of the electrolyte solution or the presence of other salts can affect ion binding constants, because other salts can, for instance, decrease the hydration of an ion in the electrolyte and, thus, enhance its association with the membrane.
Physical insight into the thermodynamics of ion-membrane association can be obtained experimentally via radiotracing of radioactive ion isotopes [
13], measurement of membrane electrophoretic mobilities [
10,
11,
14], isothermal titration calorimetry [
5,
14] or via computer experiments, e.g., through molecular dynamics (MD) simulation [
14,
15]. Due to the heterogeneous nature of the membrane (biological membranes are composed of a variety of lipids and proteins) and its environment (electrolyte solution), as well as the physical complexity of the forces at play (long-range electrostatic, short-range van der Waals interactions), neither a theoretical understanding, nor a predictive theoretical description of this equilibrium are straightforward. It was pointed out before [
16] that current models of specific ion effects are not sufficient to explain the interaction of chaotropic anions and kosmotropic cations with lipid membranes, i.e., the fact that anions and cations show opposite Hofmeister-series behavior, which hints at different binding mechanisms for the two types of ions. For zwitterionic lecithin (phosphatidylcholine) lipids, ion-lipid association can, to a certain extent, be explained in terms of the empirical law of matching water affinities [
17], based on which Garcia-Celma et al. [
16] interpreted cation binding to phosphate groups (both of kosmotropic nature) and anion binding to choline groups (both of chaotropic nature). However, this interpretation fails for other lipids, e.g., anionic surfactants [
16]. Leontidis and Aroti [
18] suggested that the different interaction behavior of cations and anions with the lipid membrane is drawn back to cations interacting directly with lipid headgroups, thus giving rise to density inhomogeneities through a clustering of lipids, whereas anions invade the created space of low lipid density. They also stressed the potential MD simulation has in unraveling ion-membrane interactions.
Numerous MD studies on ion-membrane interactions were performed in the past, e.g., focusing on the kinetics, stoichiometry and structural aspects of ion-lipid binding [
19,
20,
21,
22,
23] and the specific ion effects thereof [
24,
25,
26,
27]. Partly, the results have been found to depend strongly on the employed force field [
22], and it was emphasized that careful force-field optimization might be required to achieve simulation results in agreement with experimental findings [
14]. However, such a force-field recalibration is highly intricate as its aims, namely an accurate representation of both ion-ion, the ion-membrane functional group and ion-water interactions, might be irreconcilable with the approximations made by current “simple” force-field descriptions. In other words, it might be required to circumvent combination rules for Lennard–Jones parameters or/and account (explicitly) for polarization effects. Nevertheless, MD simulation is a valuable tool to investigate ion-membrane systems. Besides providing information about the thermodynamics of ion-membrane binding, it also offers atom-level insight concerning the structure, mechanics, order and dynamics of membranes.
Phospholipid membranes can exist in various alternative phases. The biologically most relevant phase is the liquid-crystalline phase, which is fluid-like, presenting the lipid chains in rather disordered configurations. The flexible nature of the membrane renders it susceptible to several types of deformation that may occur at room temperature and atmospheric pressure. The four most common types of membrane deformation include [
28] changes of membrane curvature, area, thickness and deformation due to shear forces. For a phospholipid bilayer, the most important deformation at room temperature is a change of curvature, i.e., bending. The associated bending rigidity is around 10–20
, where
is Boltzmann’s constant and
T the absolute temperature. The energetic cost of area changes is higher, Hooke’s law force constant for an area change being around 55–70
nm
. Stretching or compressing the membrane along its normal has a similar Hooke’s law force constant of around 60
nm
. Finally, shearing is not of relevance for fluid-like membranes, such as a membrane in the liquid-crystal phase, but may occur when membranes are attached to solid structures.
When lipid bilayers are immersed in aqueous electrolyte solutions in comparison to pure water, MD simulations evidence a reduction of membrane fluidity (i.e., of lateral lipid diffusion), a reduction of the area per lipid and an increase in membrane bilayer thickness [
14,
19,
23,
29]. Similar findings were obtained experimentally [
4], although the influence of salt concentration on some structural membrane properties appears to be more complex in the case of certain salts. For example, in the case of NaCl, the bilayer separation (thickness of the inter-membrane water layer) increases monotonously with salt concentration, whereas it decreases with increasing CaCl
concentration [
4]. Zimmermann et al. [
7] analyzed the effect of different salts on membrane fluidity in terms of a relationship between membrane fluidity and membrane charge. It was observed that, although chaotropic anions and kosmotropic cations can influence fluidity in a similar fashion, they have a different impact on membrane charge. A simple explanation for the effect of ions on membrane fluidity might be that the decrease of fluidity is caused by dehydration of lipid molecules due to ions near the membrane-water interface [
29].
In general, lipid order [
4] and area compressibility [
1] are found to increase upon the addition of salt. Concomitant with the increase of order, the elasticity of the bilayer decreases [
4]. A number of experimental studies on the bending stiffness of lipid membranes were performed [
30,
31,
32], illustrating, e.g., the influence of the electrostatic characteristics of the membrane-water interface [
30,
32] or membrane-active compounds [
31] on membrane mechanical properties. Membrane-water interfacial electrostatic properties are commonly described by the zeta potential, and it was found [
30] that the relation between zeta potential and bending stiffness is qualitatively captured by the theoretical model of Helfrich and Winterhalter [
33,
34]. Thus, one can decipher how ion binding affects membrane mechanics via altering surface charge. Ion binding does not only influence the properties of the membrane-water interface, but also intramembrane electrostatic properties, such as the membrane dipole potential. However, supposedly, there is no immediate connection between the membrane dipole potential and membrane mechanical properties [
30].
In MD simulations, surface charge is expected to be reflected in both physical (membrane stiffness) and artificial phenomena. As MD simulations of membrane-solvent systems are commonly performed under periodic boundary conditions, i.e., the separation of periodic bilayer copies (along the bilayer normal) is finite rather than infinite, membrane interfacial electrostatic properties translate into artificial repulsive forces between bilayer copies. The magnitude of the resulting disjoining pressure [
35] is proportional to the membrane area compressibility and the inverse of the solvent layer thickness. Thus, it may be difficult to separate physical and artificial effects of the membrane surface charge induced by ion-membrane association. An intuitive reasoning suggests that surface charge correlates with inter-bilayer repulsion, hence increasing inter-bilayer separation (i.e., the thickness of the solvent layer) and (due to solvent incompressibility) decreasing area per lipid.
In the present study, MD simulations are performed to investigate the above reasoning about salt effects on membranes. In particular, an existing ion-lipid force field is recalibrated to achieve similar binding affinities for Na
and Cl
ions to a 1-palmitoyl-2-oleoyl-
sn-glycero-3-phosphocholine (POPC) bilayer in an aqueous approximately 0.5 M NaCl solution. It is studied how membrane properties, as well as electrostatic interfacial properties are altered. The goal is to investigate whether a correct description of ion-membrane binding behavior reproduces experimental trends concerning salt effects on membrane structure, mechanics, order and dynamics. The paper is organized as follows.
Section 2 gives a brief outline of the employed biophysical theory about membrane-ion interactions, membrane-solvent interfacial electrostatics and inter-bilayer electrostatic forces.
Section 4 provides computational details about the MD simulations. Corresponding results are reported and discussed in
Section 3. Finally,
Section 5 summarizes the main conclusions.
3. Results and Discussion
Based on the simulations described in
Section 4.1, the original and modified force-field descriptions for ion-lipid interactions were compared in terms of their influence on structural properties (membrane area per lipid, area compressibility, bilayer thickness, water layer thickness, lipid order parameters), the thermodynamics of ion-membrane binding (apparent binding constants, coordination numbers), lipid diffusion coefficients, electrostatic potential variation along the bilayer normal and membrane rigidity.
In simulations with the modified force-field version, the area per lipid increases in comparison to the original force field by about 16 (S
(m1,wc)) or 14% (S
(m2,wc);
Table 1). It slightly exceeds the area per lipid of the membrane patch in pure water (0.607 nm
), namely by about 0.02 and 0.01 nm
in simulations S
(m1,wc) and S
(m2,wc), respectively (
Table 1). The results obtained with the modified force-field version entailing enhanced ion binding are thus in closer agreement to experimental data [
4]. The area per lipid in simulations with the Parrinello–Rahman barostat is overall similar to that observed in simulations with the weak-coupling barostat (differences of 0–0.009 nm
).
As a consequence of lateral membrane expansion (along with solvent incompressibility), the thickness of the solvent layer
decreases in simulations S
(m1,wc) and S
(m2,wc) compared to the simulation with the original force field (
Table 1). In addition, the bilayer thickness
decreases and basically adopts values observed for a membrane patch in pure water. For example, in simulations S
(m1,wc) and S
(m2,wc),
evaluates to 3.86 and 3.95 nm, respectively, i.e., it is very similar to the thickness found in simulation
(wc), 3.98 nm, and smaller than that found in simulation S
(o,wc), 4.31 nm. Experimentally, the presence of aqueous NaCl leads to an increase in
above NaCl concentrations of 0.6 M [
4]. This increase in bilayer thickness is in qualitative agreement with simulation S
(o,wc), but not with the simulations involving the new force-field versions. In comparison to simulation S
(o,wc), the binding of approximately equal amounts of cations and anions (S
(m1,wc), S
(m2,wc)) induces a contraction of the membrane along the bilayer normal and a lateral expansion. Intuitively, one can try to explain this in terms of repulsion between charged bilayer copies as present in simulation S
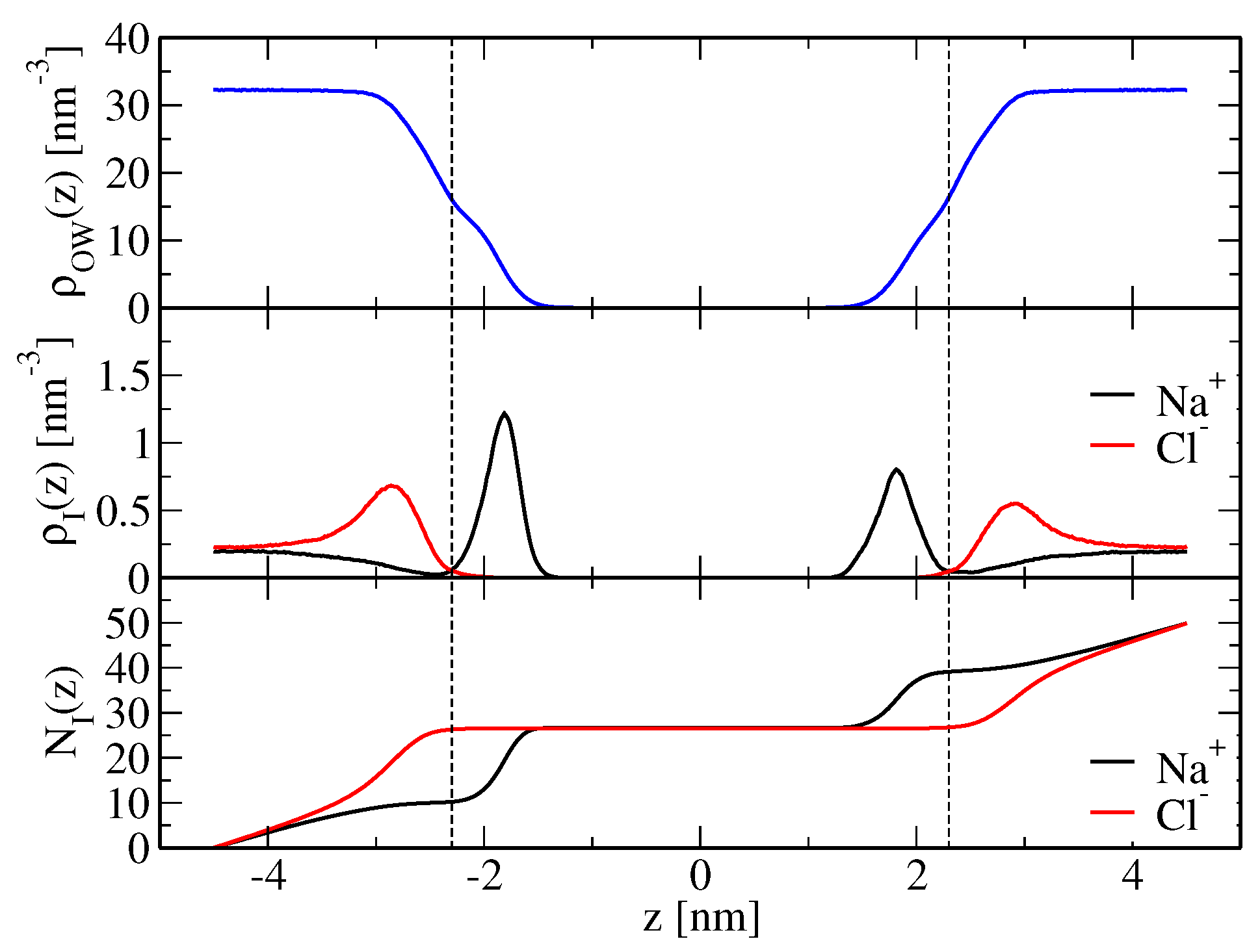
(o,wc). Here, predominantly sodium ions bind below the membrane shear plane, whereas chloride ions are mainly located above the shear plane (
Figure 1). Therefore, the membrane presents a net positive charge. An intuitive reasoning would suggest that the resulting electrostatic repulsion between periodic bilayer copies increases solvent layer thickness. Furthermore, due to solvent incompressibility, the
-plane of the simulation box has to contract, which would be reflected in a decreased area per lipid (
Table 1). However, an alternative mechanism is not based on electrostatic grounds, but ion-specific effects arising from direct ion-lipid interactions, i.e., the way in which ions bind to the lipid molecules may directly cause lateral compression or extension of the membrane. This is discussed in more detail below.
An increase of sodium-lipid and a decrease of chloride-lipid nonpolar repulsion, as achieved here by a scaling of corresponding Lennard–Jones
parameters (
Section 4.2), brings both cation and anion binding in better agreement with the experimental findings. Apparent ion-membrane binding constants from electrophoresis and isothermal titration measurements [
14] are
M
for Na
ions and
M
for Cl
ions. They may be compared to the corresponding values from the simulations performed here, which are reported in
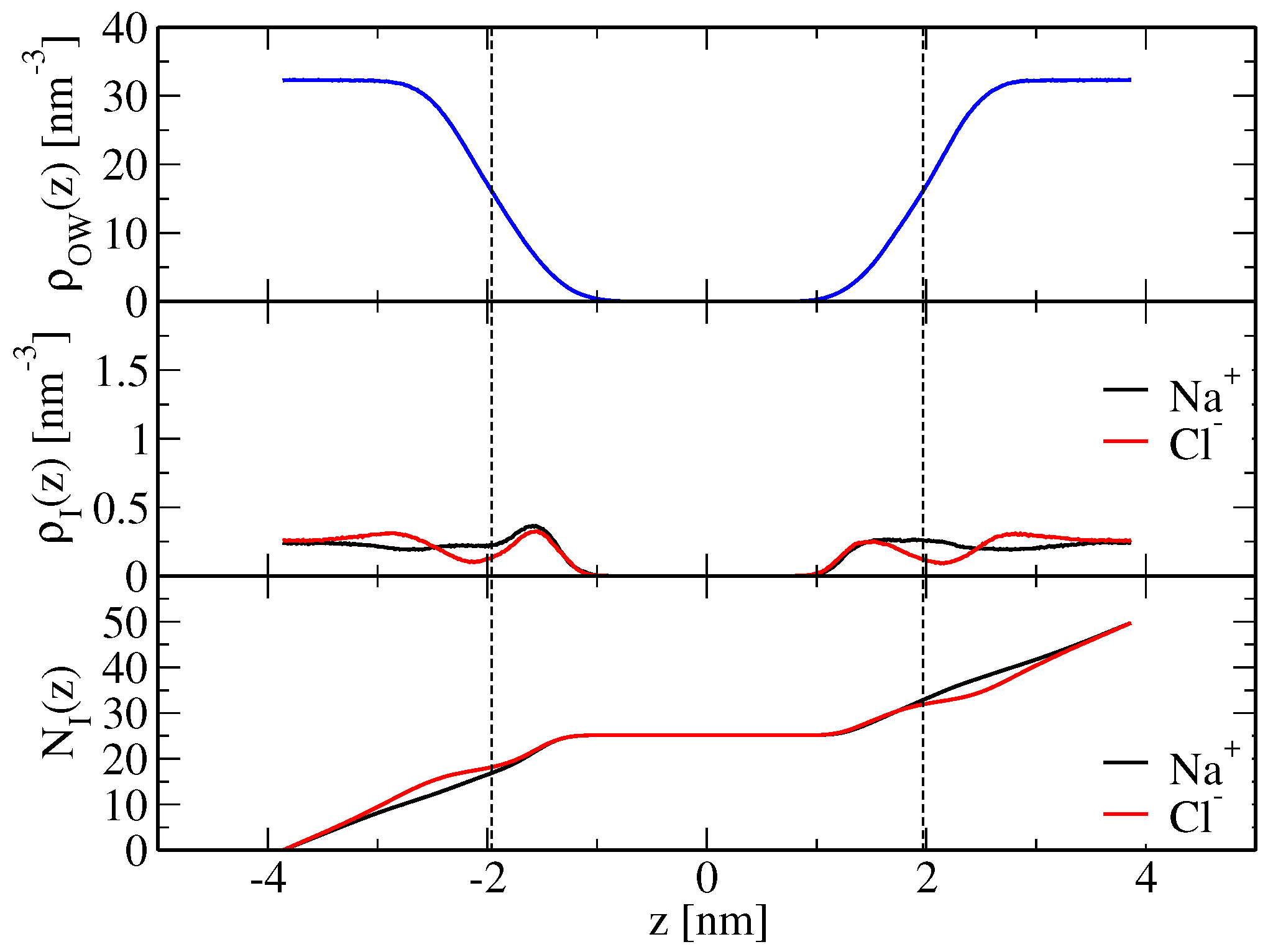
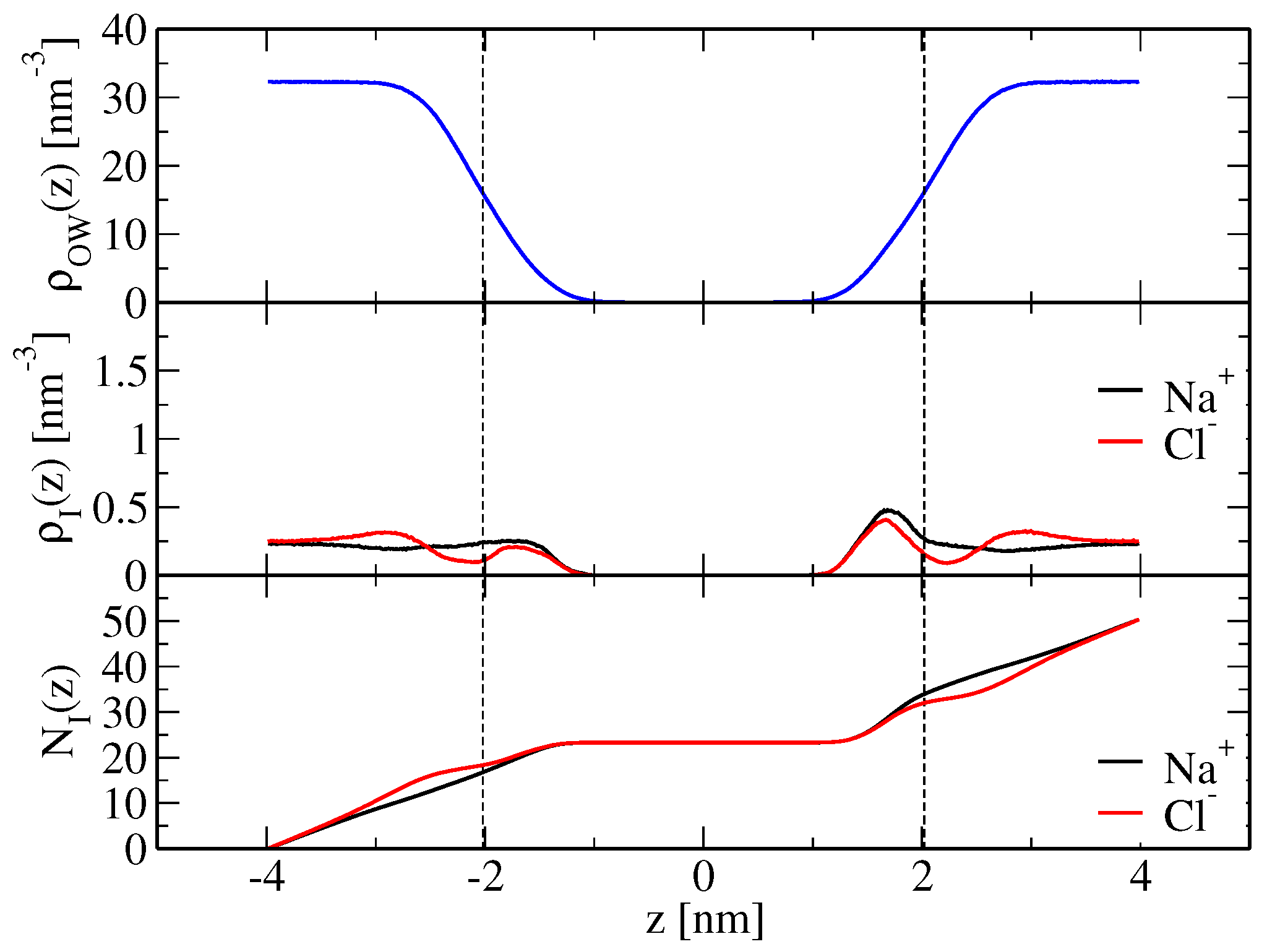
Table 2 and were calculated according to Equation (
21) based on the simulated ion density profiles along the bilayer normal, shown in
Figure 2 and
Figure 3 for the modified force-field versions m1 and m2, respectively. Sodium ion binding is overestimated by around a factor two in the original force field, i.e.,
M
, using the arithmetic mean of the binding constants pertaining to the two leaflets (0.71 and 1.02 M
;
Table 2), with the indicated error denoting the standard deviation. However, it is essentially in line with experimental data when the modified force fields m1 or m2 are used. The binding constants are
and
M
, respectively, again resulting from averaging over the two leaflets and using the standard deviation as an error estimate (
Table 2). Chloride ion binding is significantly underestimated by the original force field (
M
). By virtue of decreased chloride-ion lipid-tail nonpolar repulsion, the modified force-field versions allow those ions to cross the membrane shear plane (
Figure 2 and
Figure 3), thus leading to an increase in their apparent binding constants (
and
M
in simulations S
(m1,wc) and S
(m2,wc), respectively;
Table 2). Although chloride ion binding is still weaker than sodium binding, the structural features of the membrane basically correspond to those of a neutral membrane patch (see above and
Table 1).
Analysis of coordination numbers of the ions reveals that the new force-field descriptions enhance the first-shell coordination of chloride ions with lipid tail atoms by about three orders of magnitude, while leaving first-shell coordination of sodium ions with lipid tail atoms essentially unaffected (
Table 3). The first-shell coordination number of sodium ions with carbonyl- and phosphate-oxygen atoms is reduced by approximately two orders of magnitude in the new force-field description (
Table 3). In particular, the binding to the carbonyl oxygen atoms is reduced in that it occurs almost exclusively in a solvent-separated fashion, as evidenced by almost negligible first-coordination shell peaks (heights of 0.21 and 0.43 for simulations S
(m1,wc) and S
(m2,wc), respectively) in comparison to the second-coordination shell peaks (heights of 3.07 and 3.90 for simulations S
(m1,wc) and S
(m2,wc), respectively). Corresponding peak heights for simulation S
(o,wc) are 143.1 and 1.56, respectively, i.e., here, an enhanced direct binding in comparison to solvent-separated binding of sodium ions to the carbonyl oxygen atoms is observed. The force-field dependence of the relative balance of direct- and solvent-separated binding mechanisms of cations to lipid molecules has been noted before [
43,
44] and is of importance for the parameterization of ions in coarse-grained force-field descriptions (inclusion vs. omission of the first hydration shell in the beads representing ions). Although ion-water Lennard–Jones interaction parameters were not altered, the first-shell ion-water coordination numbers are slightly lower (chloride) or higher (sodium) when the new force-field description is employed (
Table 3). Concerning second-shell coordination numbers, similar qualitative trends as for the first shell are observed, except for sodium-ion binding to the carbonyl oxygen atoms, where the new force-field description leads to an enhancement of the second-shell coordination number by about a factor two (
Table 3).
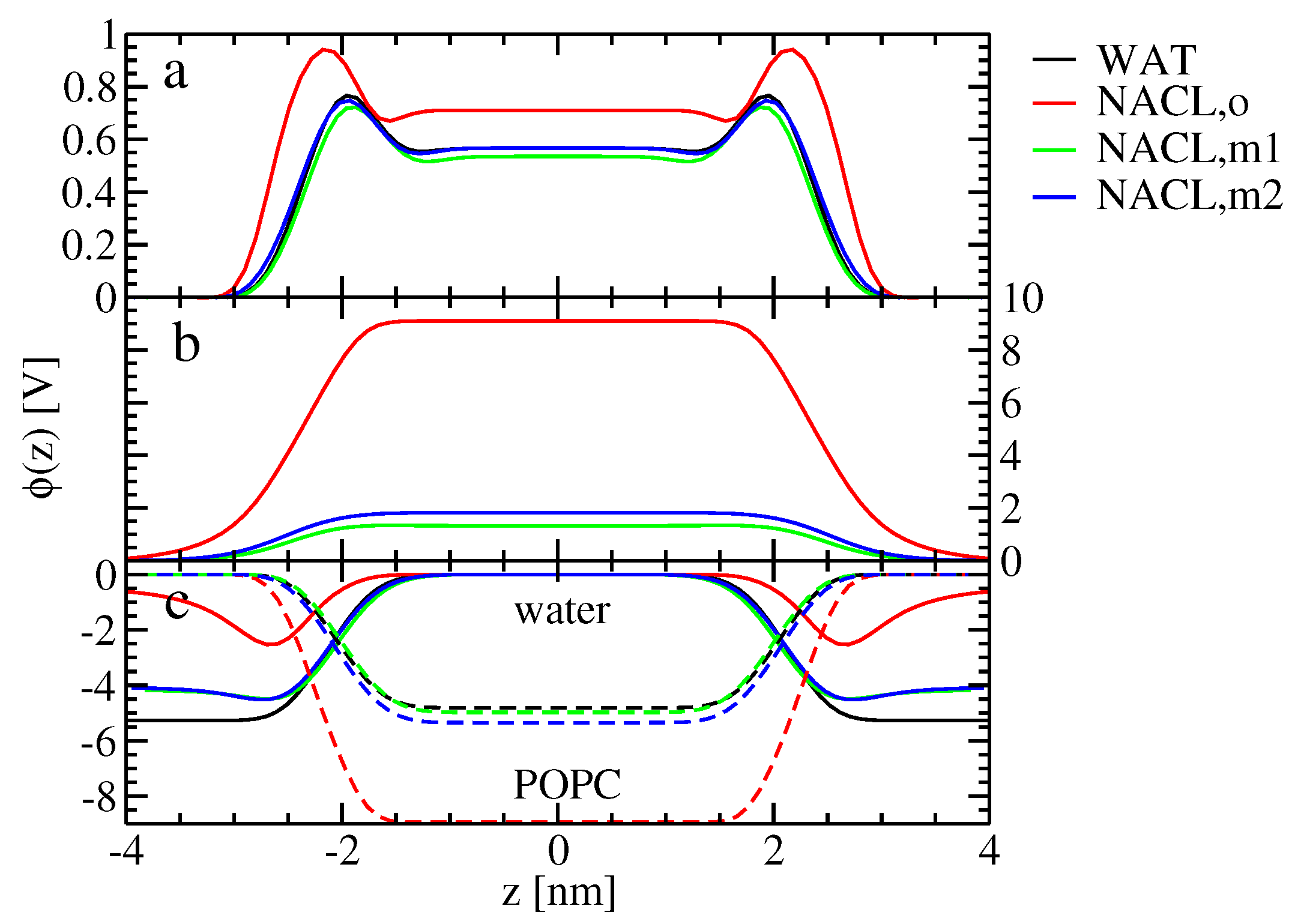
The alteration of ion-membrane binding is reflected in the electrostatic potential along the bilayer normal. In the absence of ions, the lipid headgroups (with the negatively-charged phosphate groups being closer to the membrane interior than the positively-charged choline groups) lead to a contribution of the electrostatic potential inside the membrane, which is negative with respect to the value in the bulk water (
Figure 4c). Water not only dielectrically screens this electrostatic potential contribution, but overcompensates it, such that the electrostatic potential contribution due to water, as well as the total electrostatic potential are positive inside the membrane (
Figure 4a,c). It was suggested before that this effect arises from the structure of water at the surface of hydrophobic media [
45]; however, this explanation might be misleading because of the limitations of Equation (
16) and the fact that preferential water orientation at hydrophobic surfaces is not per se decisive, but must be interpreted relative to a system with isotropically-oriented water molecules [
46]. For the old force field, the asymmetric binding of the cations and the anions leads to a contribution of the ions to the electrostatic potential, which is positive inside the membrane (
Figure 4b). Both water and lipids dielectrically screen (partially compensate) the effect of the ions on the electrostatic potential, which means that the contribution of both water and lipids to the electrostatic potential inside the membrane (with respect to the water) is decreased compared to the ion-free case. For the new force-field versions showing similar binding for both ion species, the effect of the ions on the electrostatic potential inside the membrane is much smaller. Hence, the change of the total electrostatic potential compared to the ion-free case, as well as the corresponding contributions from water and lipids are much smaller to negligible for the new force-field versions.
Membrane-associated net charge, as (considering apparent ion binding constants;
Table 2) strongly present in simulation S
(o,wc) and nearly vanishing in simulations S
(m1,wc) and S
(m2,wc), can cause a separation of membrane bilayer copies. This was already discussed above in terms of structural properties, e.g., an increase in the thickness of the water layer
. However, changes in membrane area or water layer thickness can occur as well via an entirely different mechanism, e.g., because ions interacting with the membrane can push apart or pull closer neighboring lipid molecules. The question about what is the physical mechanism underlying the area-per-lipid increase in the present study can be answered through analyzing the disjoining pressure
, which arises from differential ion concentrations in the center of the water layer (Equation (
7)). Here, it is found that
is indeed almost increased three-fold with the original force field in comparison to the modified force-field versions, the latter presenting more balanced association of cations and anions with the membrane (
Table 4). The disjoining pressure was also calculated as a function of area compressibility, water layer thickness and area-per-lipid change upon ion binding (
; Equation (
6)). The resulting pressures
obtained from the different simulations suggest that the forces influencing the distance between successive bilayer copies are indeed repulsive when the original force field is employed (positive disjoining pressure;
Table 4), but attractive when the modified force-field versions are used (negative disjoining pressure;
Table 4). These conclusions are independent of whether the water bilayer thickness and area-per-lipid change upon ion binding are taken from simulations with the weak-coupling or the Parrinello–Rahman barostat (
Table 4).
Note that
and
differ by about three orders of magnitude (
Table 4). This indicates that the change in area per lipid induced by the new force-field description is actually not due to the alteration of membrane-associated net charge, but must rather be understood as a consequence of ion-specific effects on the arrangement of lipid molecules. Sodium ions can be envisioned as decreasing the area per lipid, because they may be coordinated by oxygen atoms pertaining to multiple lipid molecules at the same time, which decreases the distance between lipid molecules. Because of their more smeared out charge, chloride ions have a somewhat higher affinity to nonpolar membrane regions than sodium ions. The association of chloride ions with more hydrophobic membrane regions leads to a larger exposure of the fatty-acid chains to water, which causes the area per lipid to increase.
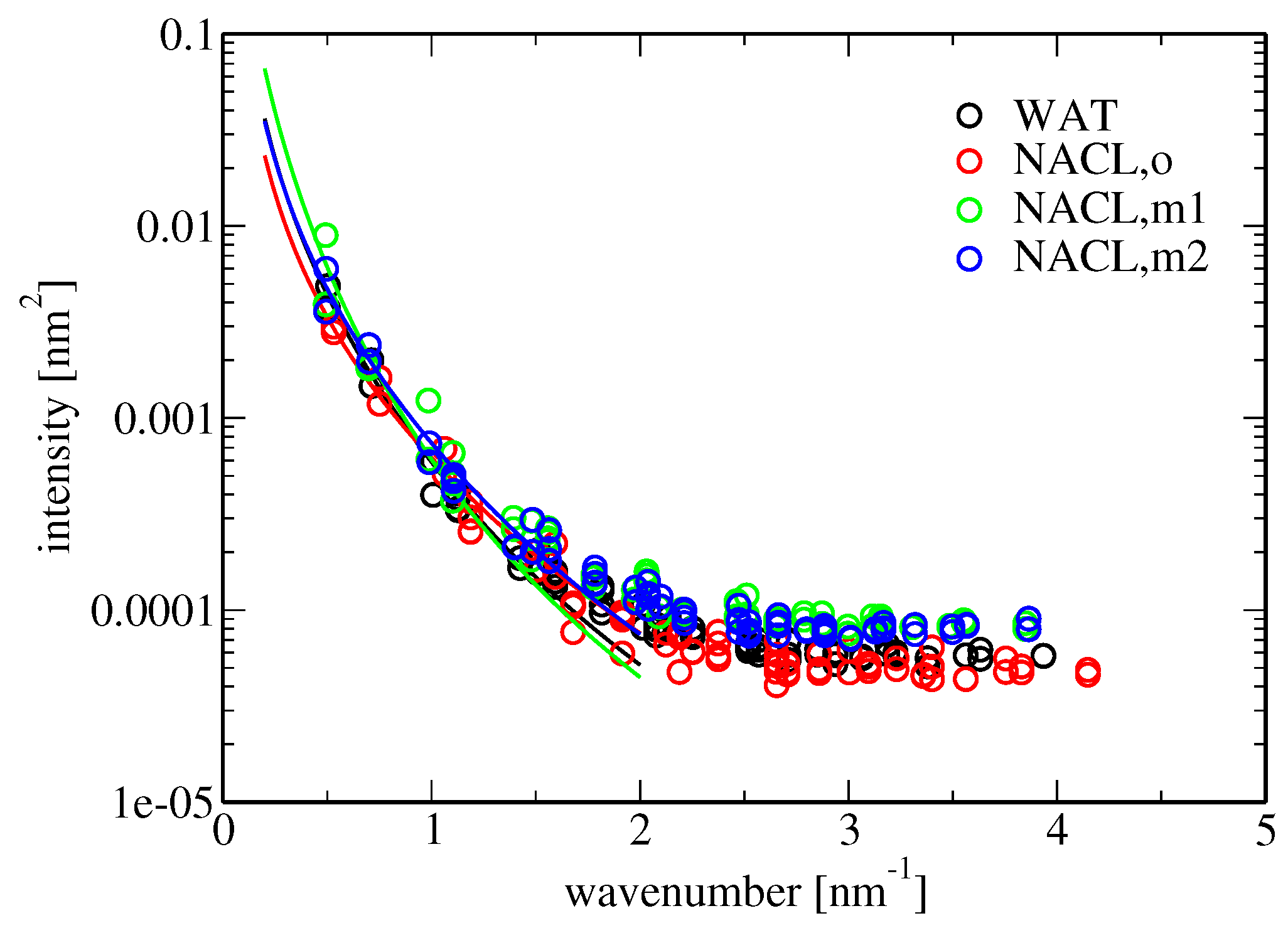
Membrane bending rigidity was calculated according to Equation (
18). The results are reported in
Table 5. The bending stiffness observed in the simulation involving pure water as the solvent (
J) is similar to those found in comparable simulation studies, e.g.,
J for the DPPC bilayer studied in [
47]. According to experimental investigations, the bending fluctuations of a POPC bilayer increase in the presence of aqueous NaCl (above concentrations of about 0.5 M) [
4], and concomitantly, the bending stiffness
is expected to decrease. Here, the presence of salt in the solvent leads to contradictory results for the change in bending rigidity in comparison to pure water when old or new force-field descriptions are used, namely values of
, 3.3 or 1.7
J in simulations L
(o,wc), L
(m1,wc) and L
(m2,wc), respectively (
Table 5). Because the error of
for the salt-free simulation is rather large, it is difficult to assess the effect of membrane-ion binding on
, as well as whether the effect agrees with the experiment. Comparing
in the presence of salt for the different force fields, the large difference between the similar force-field versions m1 and m2 is striking. This might be due to ill convergence of the simulations or a poor fit to the data points for the spectral intensity of undulation because of an insufficient number of data points in the considered low-wavenumber regime, i.e., a too large grid cell edge length (Equation (
18) and
Figure 5). Note that the grid employed for the analysis of membrane undulations was rather coarse (
Section 4.3.1).
The coefficient
B (Equation (
8)) characterizing leaflet interdigitation is considerably smaller than the value
commonly associated with the absence of interdigitation (
Table 5), indicating that the two leaflets move in an uncoupled fashion. The underestimation of
B in comparison to the theoretically-expected value of 1/48 may be due to an underestimation of
or/and an overestimation of
or/and of
in the present simulations. For the membrane in pure water, the latter quantities may be compared with readily-available experimental data. Experimentally,
,
and
are found to be
J [
48], 139 kJ·mol
nm
[
49] and 3.83 nm [
49], respectively, for a DPPC bilayer at ambient conditions. These values result in
(Equation (
8)), which is close to
. In comparison to the above experimental data, the simulated membrane shows a bending stiffness that is underestimated by 44% and an area compressibility that is overestimated by 45%, while the bilayer thickness is in fairly good agreement with the experimental value (
Table 1 and
Table 5). The membrane force field appears to render the membrane too soft (increased susceptibility to bending deformation and lateral compression), which results in the very small
B-coefficient observed here. Considering the relatively large error in
(
Table 5), the calculated values of
B are also affected by a rather large statistical uncertainty.
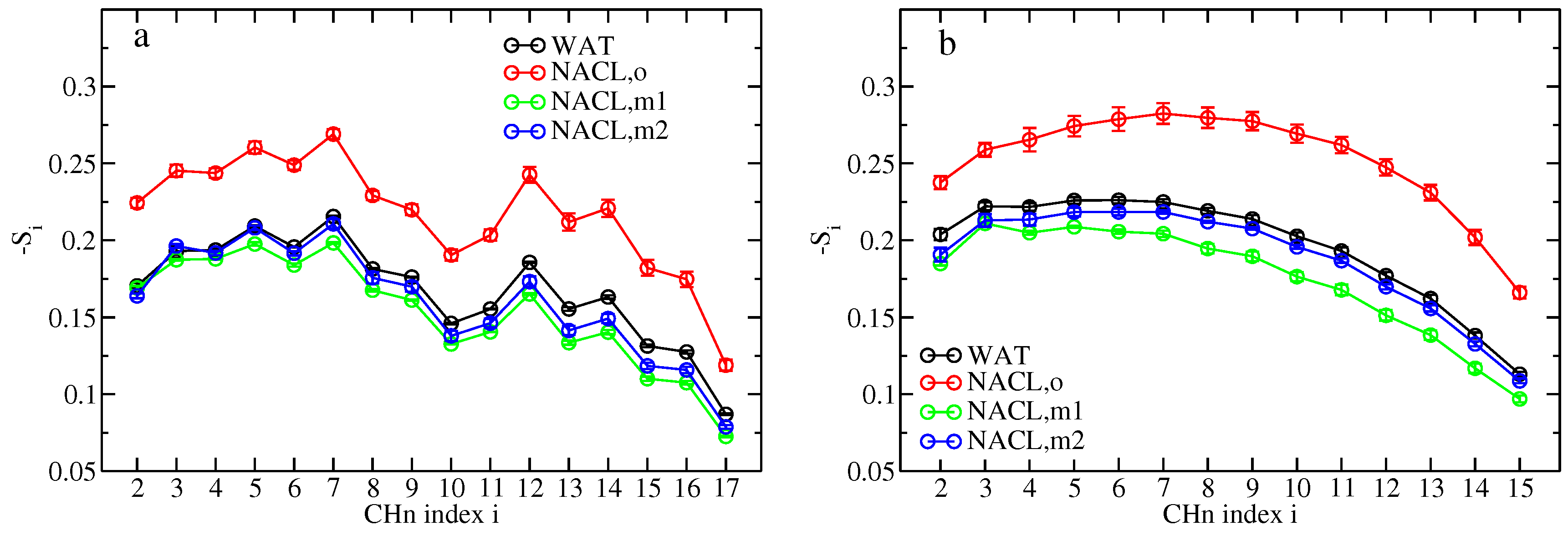
Comparing the effect of ions on lipid ordering and diffusion between the old and new force-field descriptions, the membrane properties appear to be closer to the pure-water situation when the latter is used. Deuterium order parameters of lipid tail CH
groups experience a minute decrease through sodium and chloride binding in simulations S
(m1,wc) and S
(m2,wc) in comparison to simulation S
(wc), whereas they are elevated on average by 30.5% for the oleoyl chains and by 30.3% for the palmitoyl chains in simulation S
(o,wc), i.e., lipid tail order is much enhanced through the unbalanced binding of sodium and chloride ions as occurring with the old force-field description (
Figure 6). Similarly, the lipid center of mass diffusion coefficients (across all three examined time scales) are closer to the pure-water situation with the new force-field description in comparison to the old one (
Table 6). With the latter, the long, medium and short time scale diffusion coefficients are reduced by 46.2, 31.7 and 13.0%, respectively, in comparison to the the diffusion coefficients found for the membrane in pure water. Thus, the excess of sodium-ion binding in simulation S
(o,wc) appears to lead to a drastic slowing down of the long time scale lipid motion (
Table 6).
Neutron scattering experiments deliver diffusion coefficients on a short timescale of 1–10 ps [
50,
51]; however, the influence of salts is unknown to date.
Experimental data based on fluorescence correlation spectroscopy (FCS) show that on millisecond timescales, lipid diffusion decreases with increasing NaCl concentration [
19]. Such timescales are not routinely accessed by MD simulations. Simulations by Böckmann et al. [
19] showed a decrease in lipid diffusion upon the addition of NaCl on nanosecond timescales. When inferring diffusion constants both from the simulations, as well as the experiments, analyses were performed based on a normal diffusion model. However, in fact, lipids undergo anomalous diffusion [
52]. Therefore, diffusion constants inferred assuming normal diffusion are effective diffusion constants, which depend on the timescale considered.
Table 6 shows that the effective diffusion constants decrease with increasing timescale. The smallest timescales considered in the table (2–10 ps) are similar to the timescales accessed by neutron scattering experiments (1–10 ps). Interestingly, the simulated diffusion coefficients on the 2–10-ps timescale are more similar to experimental values obtained at elevated temperatures ([
50] reports a translational diffusion coefficient of
cm
s
for a system at 30
C and 400 ×
cm
s
for a system at 63
C; [
51] reports in-plane diffusion coefficients on the order of 15 ×
–600 ×
cm
s
for a system at 60
C). As diffusion constants inferred from experiments and simulations typically depend on the timescale considered, also the effect of salt on the diffusion constants may depend on the timescales. Though the FCS experiments show a decrease in lipid diffusion on millisecond timescales [
19], to our knowledge, no experimental data on the influence of ions on the effective diffusion constants on (sub)nanosecond timescales are available. On such timescales, the old force field also employed in [
19] shows a decrease in lipid diffusion, whereas the force fields with the more realistic ion-membrane binding behavior introduced here do not show a substantial salt effect on lipid diffusion.