Ling’s Adsorption Theory as a Mechanism of Membrane Potential Generation Observed in Both Living and Nonliving Systems
Abstract
:1. Introduction
2. Preparation of Membranes and Solutions
2.1. Fabrication of Impermeable Membrane

2.2. Liquid Membrane
2.3. Electrolytic Solutions
3. Potential Measurement
3.1. Exp. I
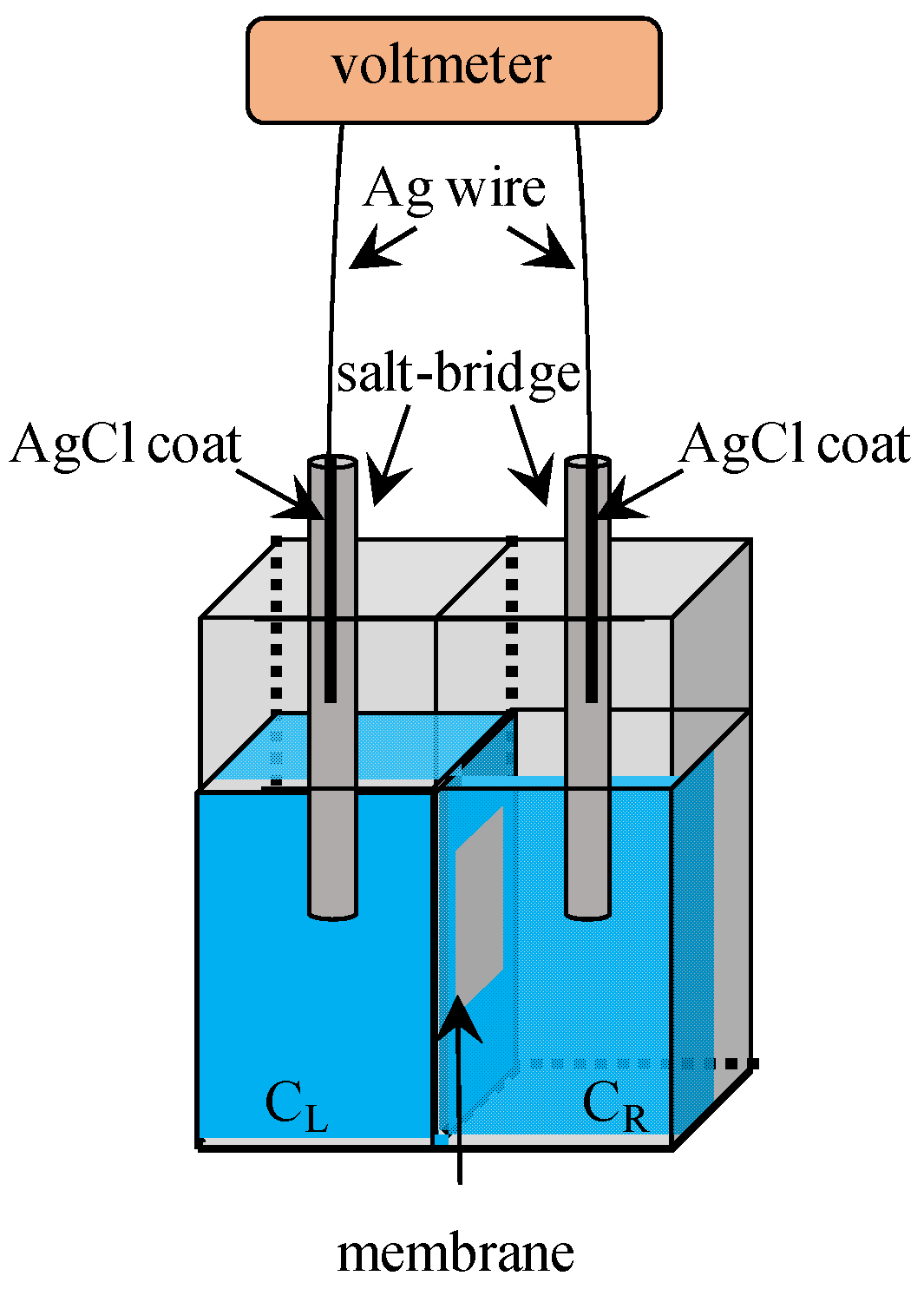
3.2. Exp. II

4. Results and Discussion
4.1. Potential Measurement
4.1.1. Exp. I
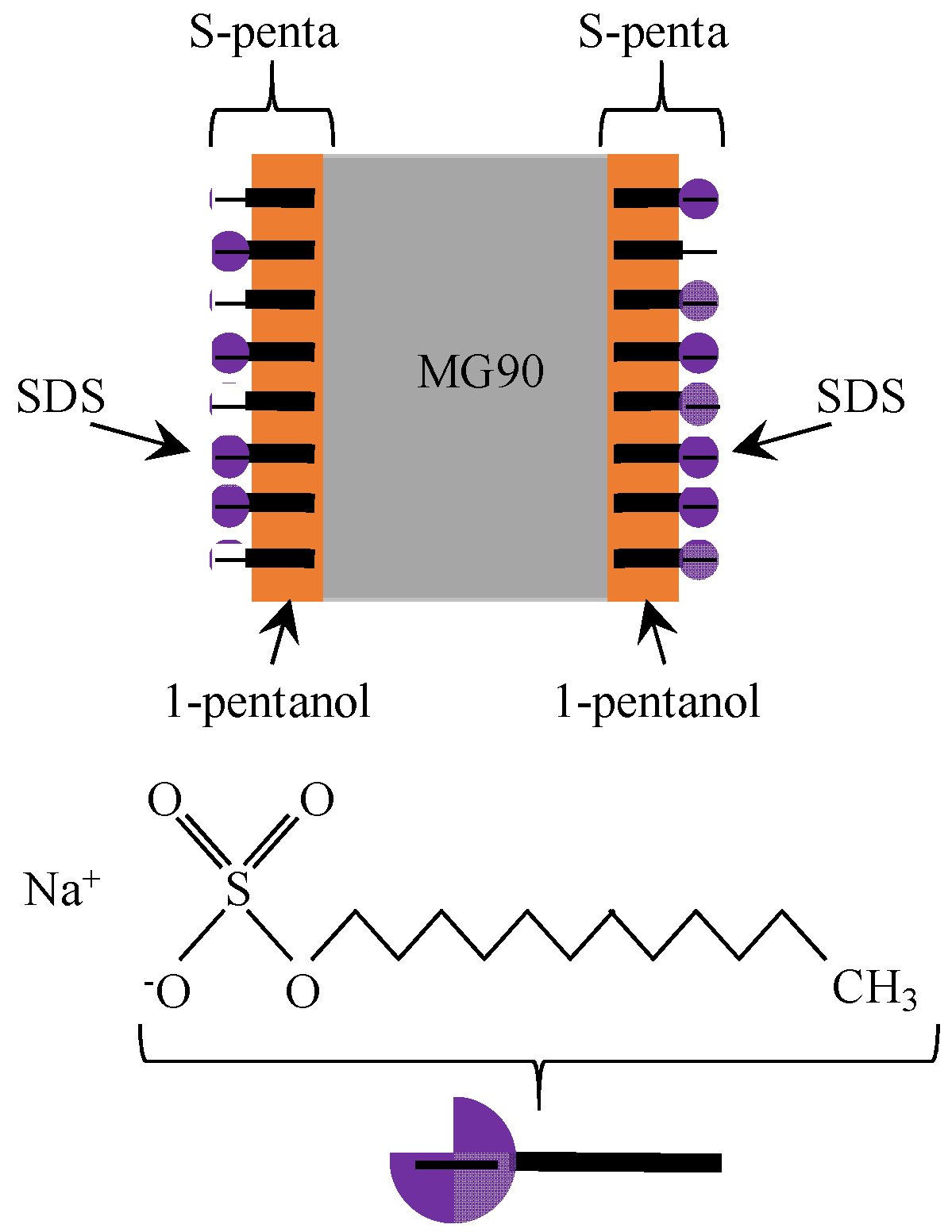
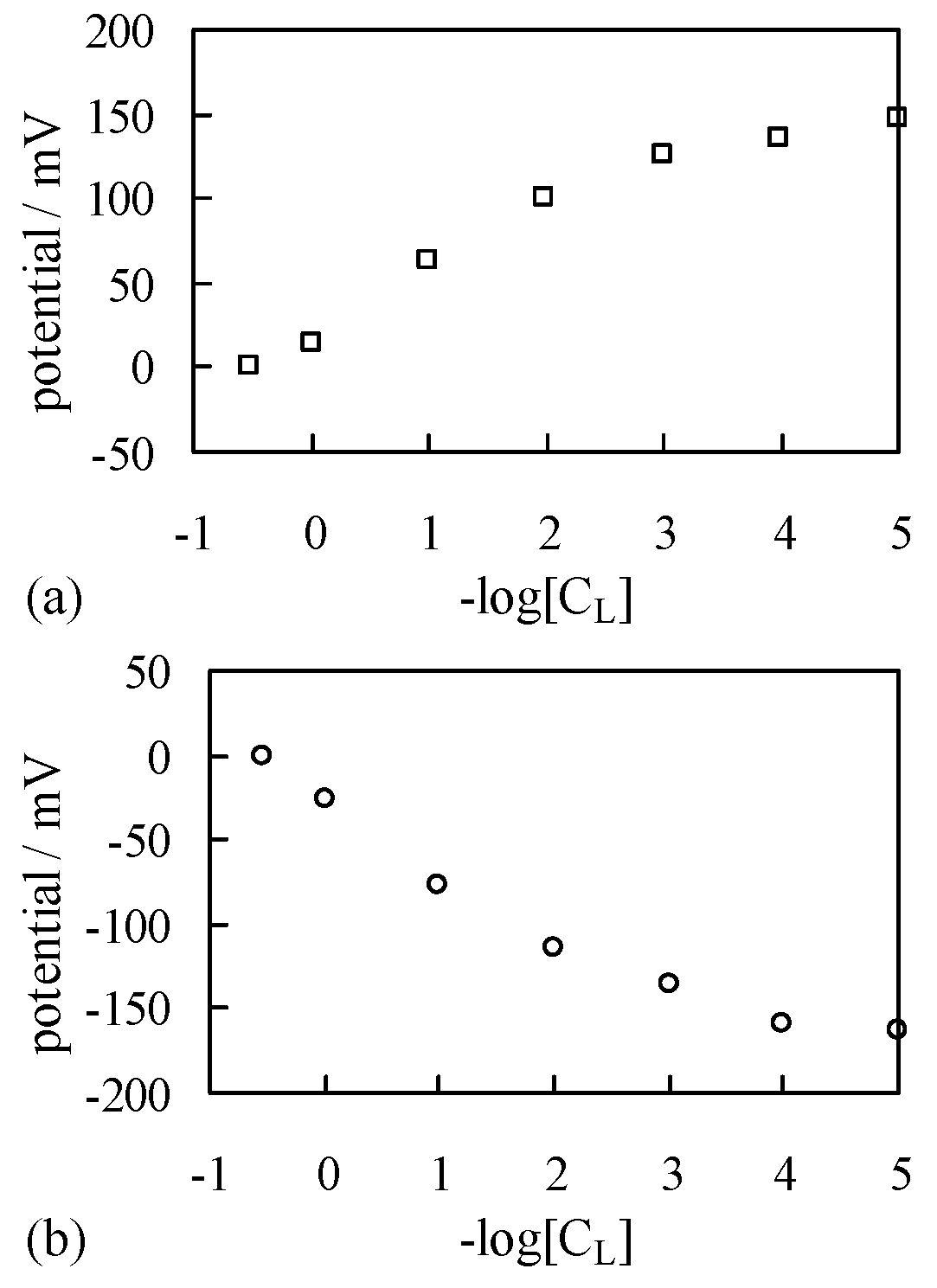
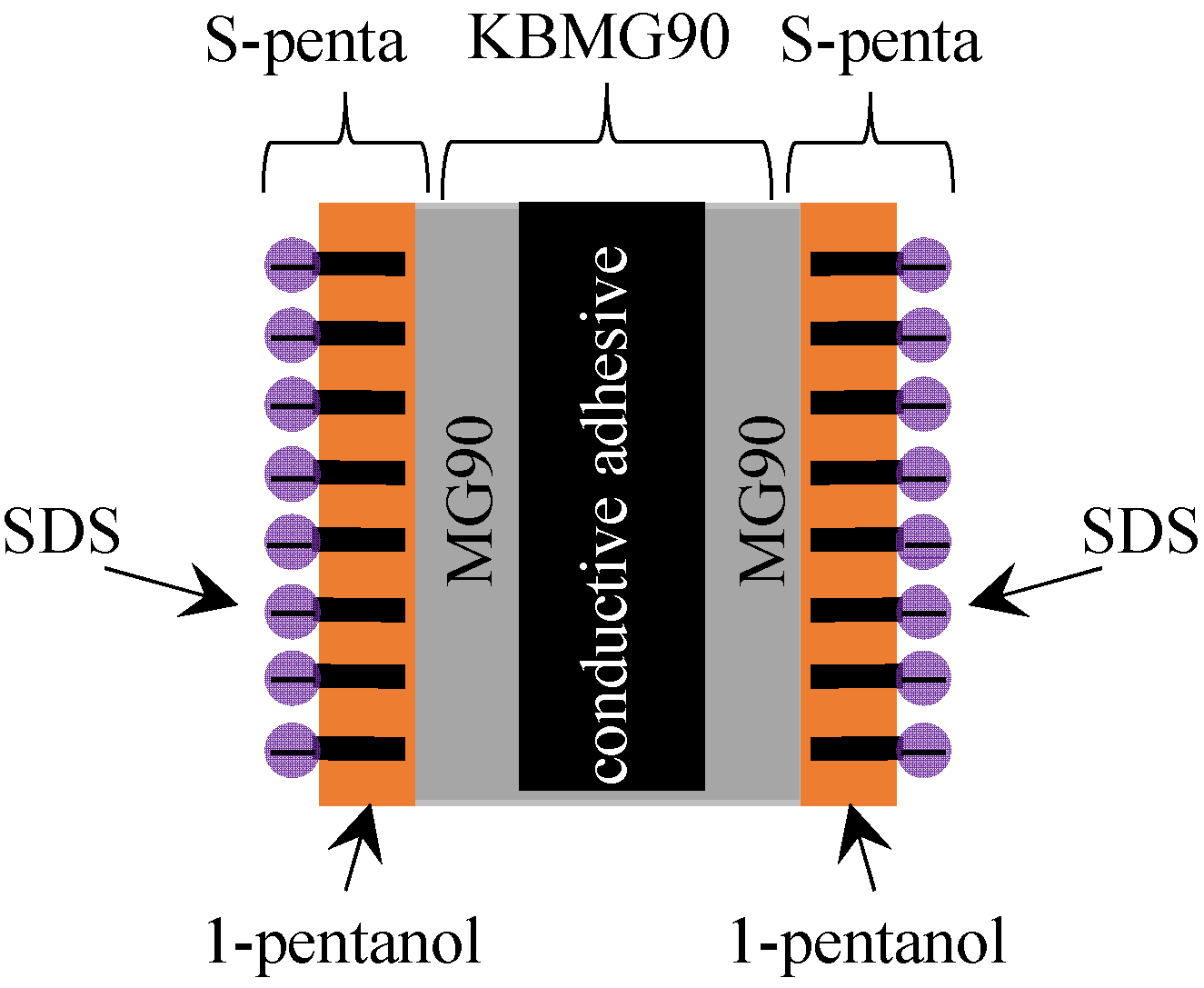
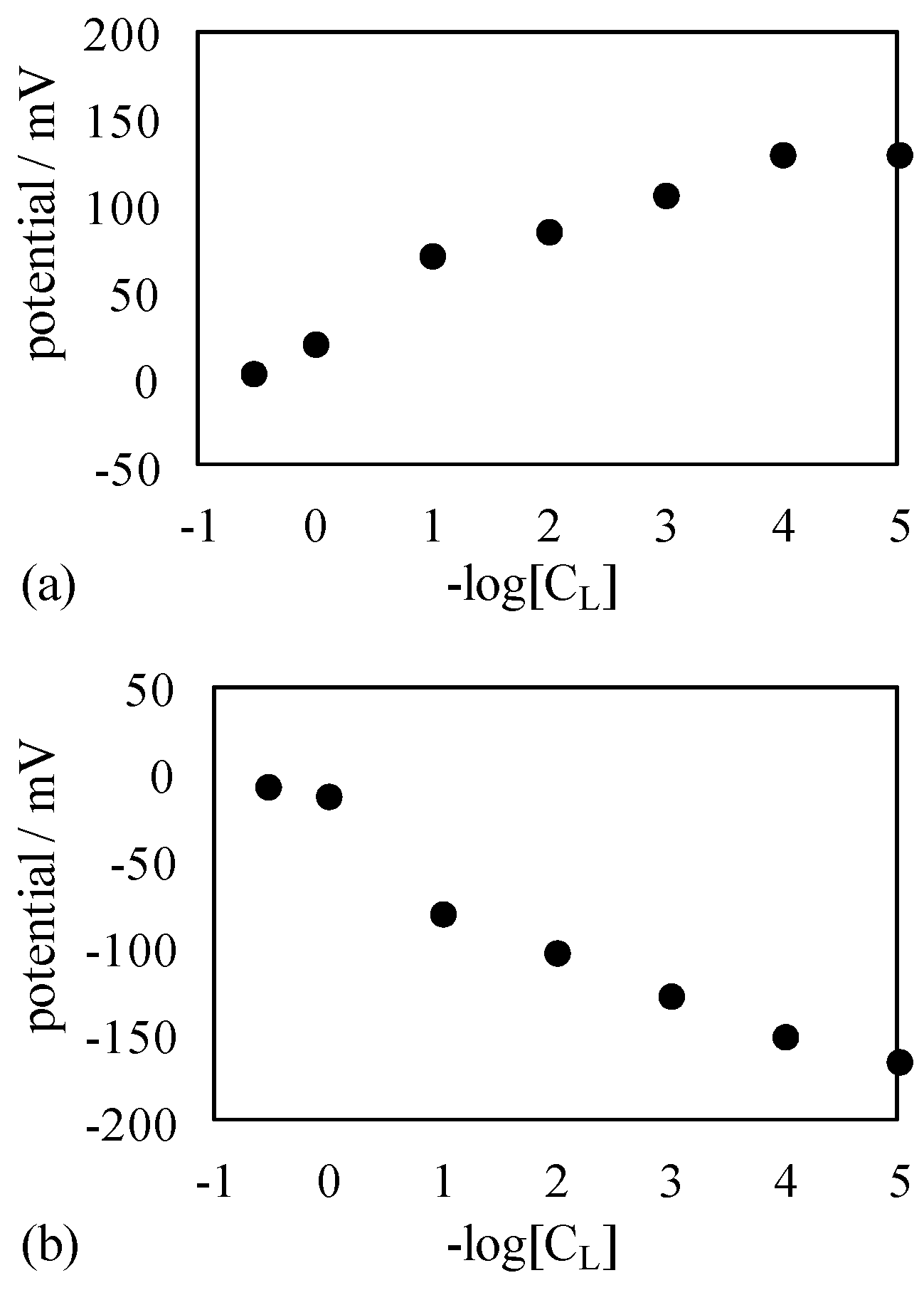
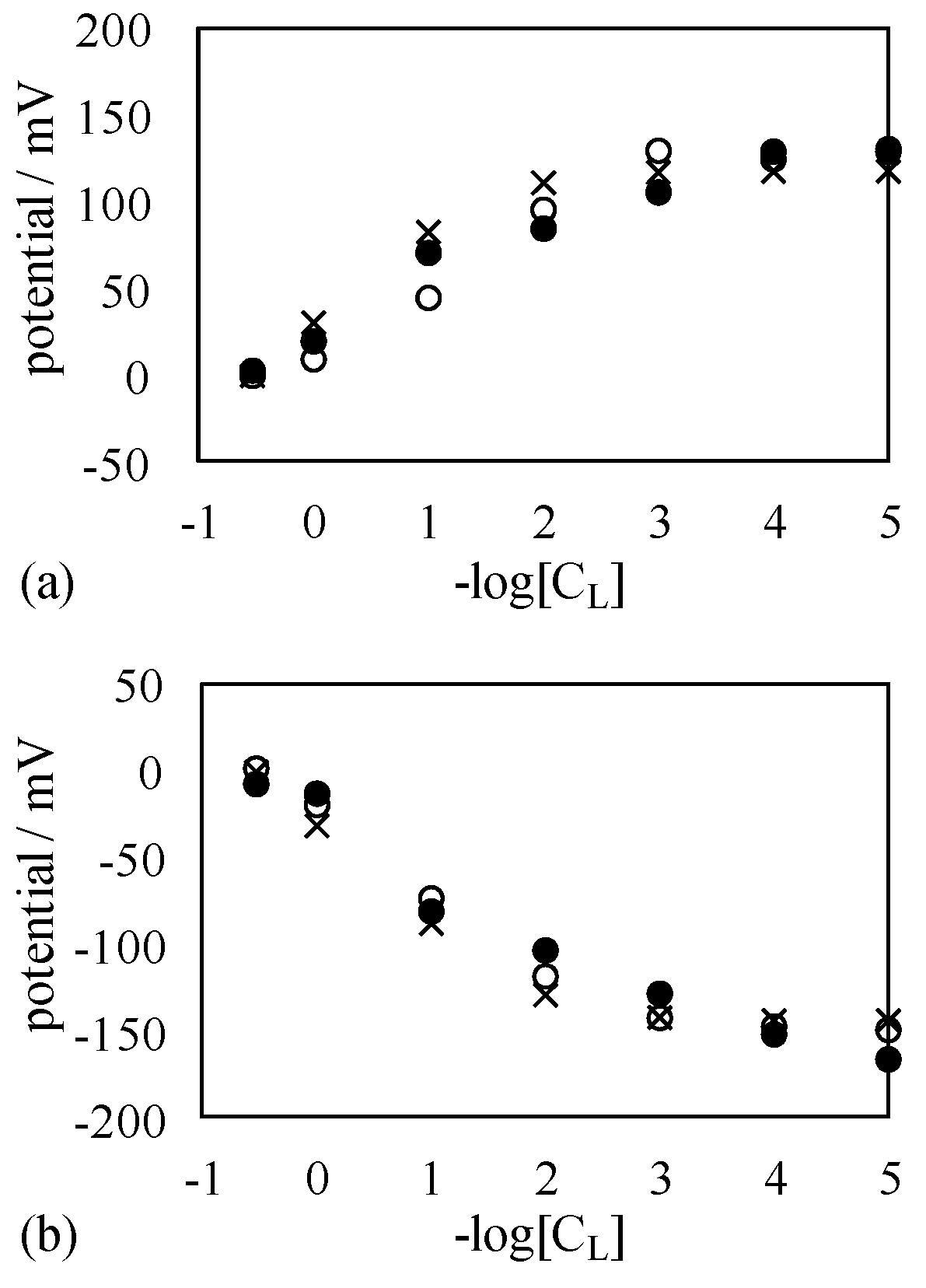
4.1.2. Exp. II
4.2. Mechanism of Potential Generation across the Impermeable Membrane
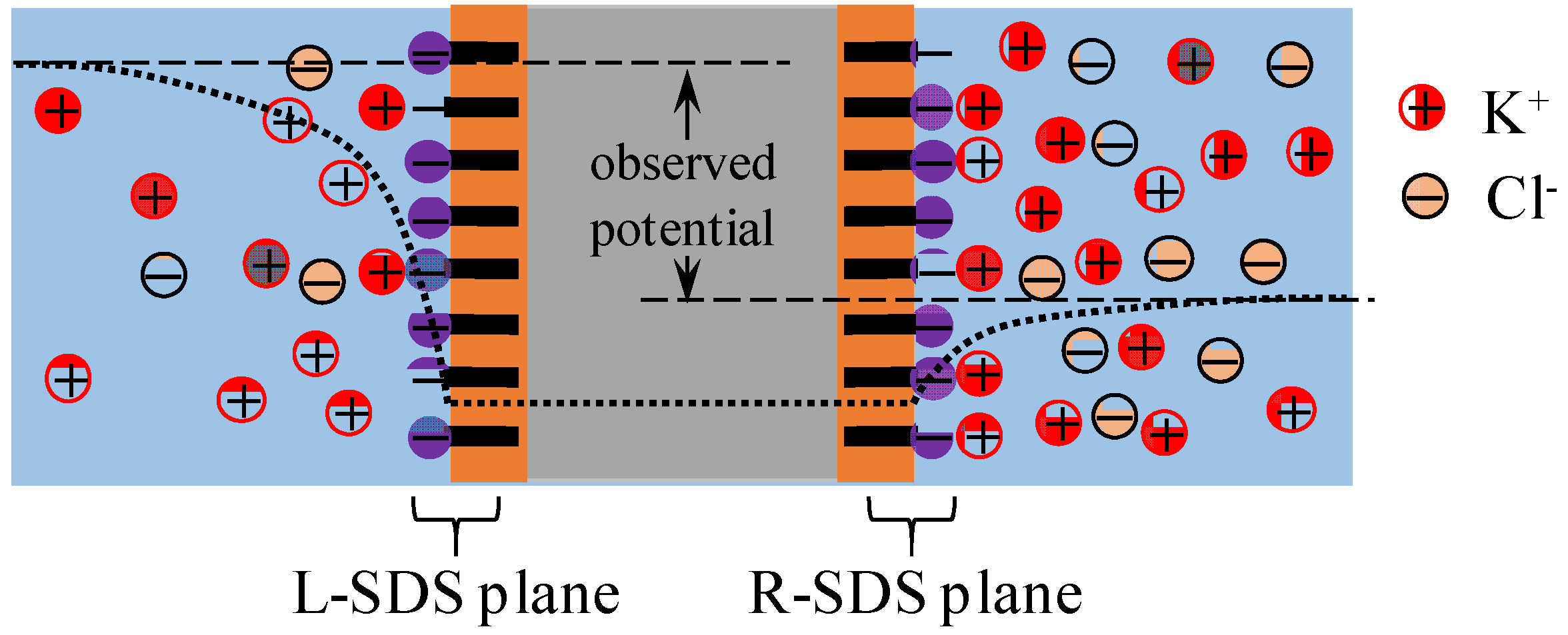
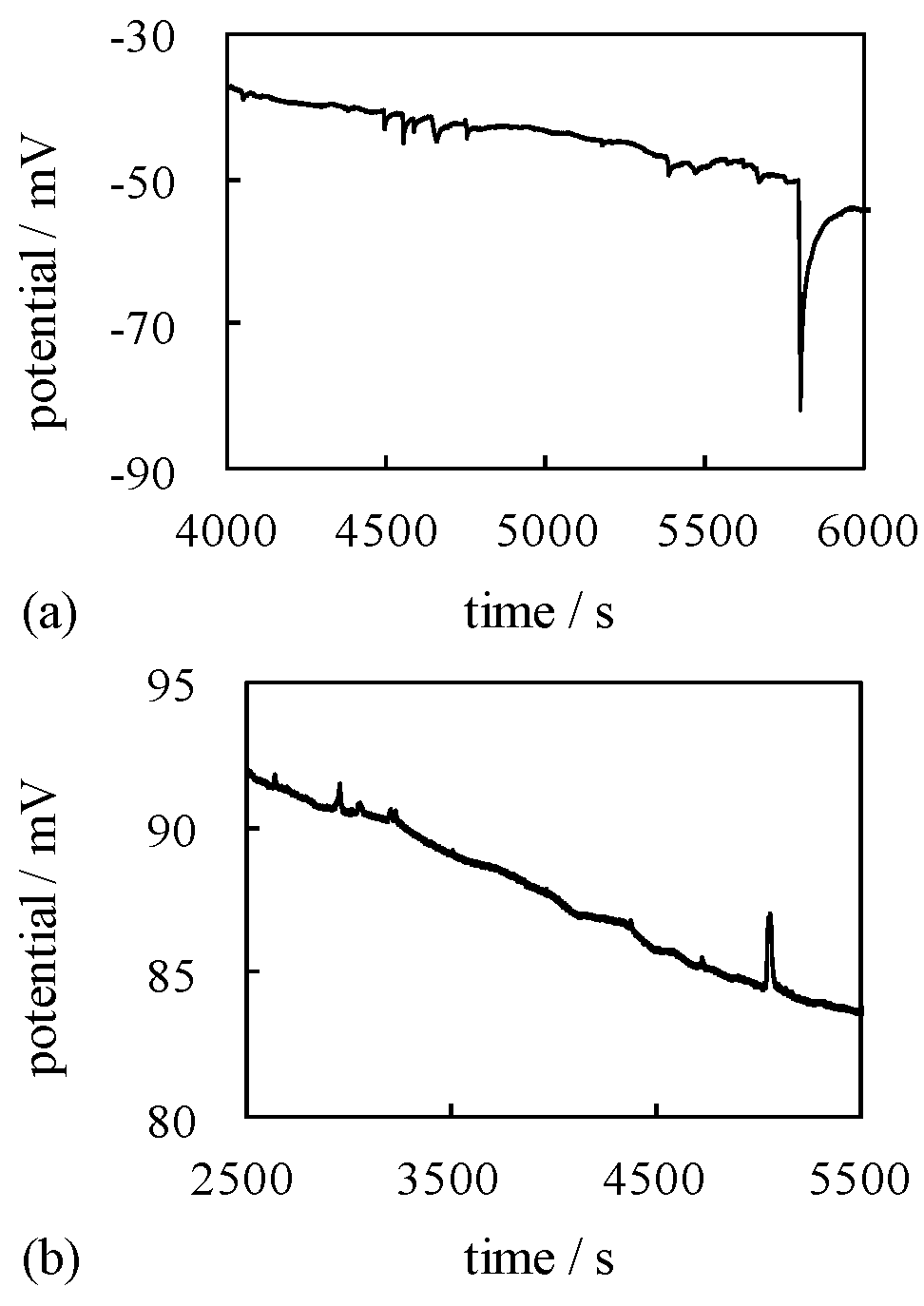
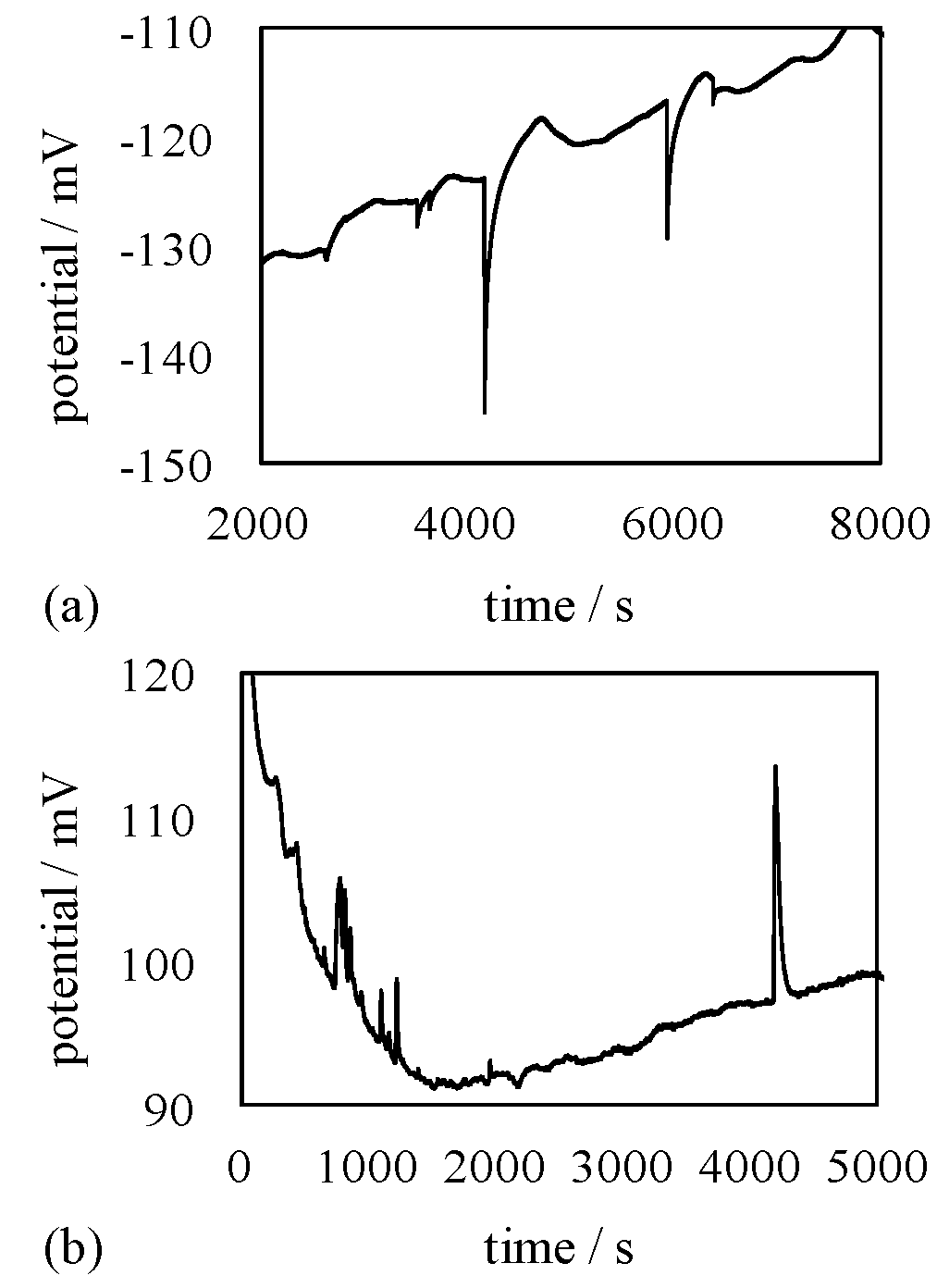
4.3. Mechanism of Potential Oscillation
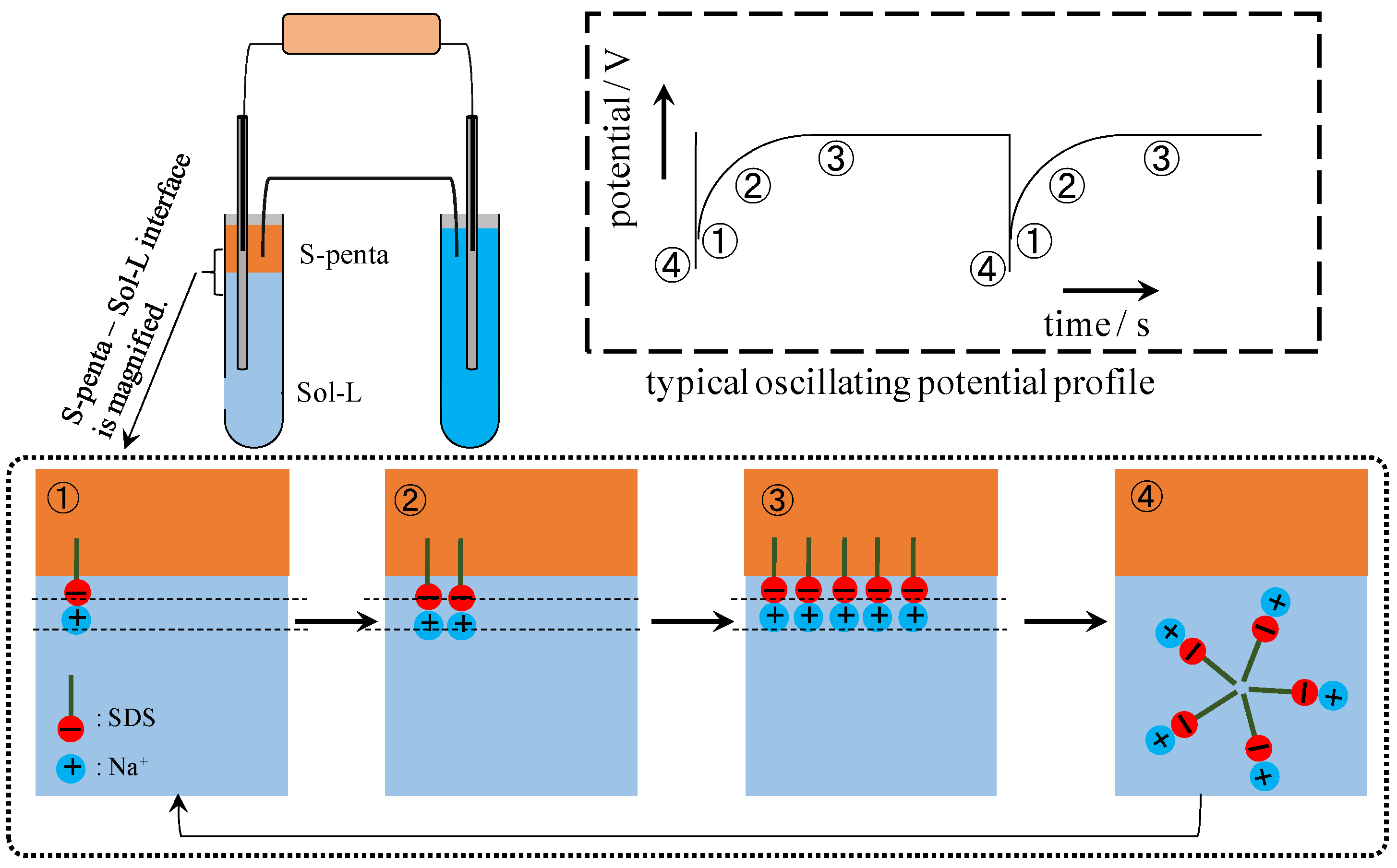
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ling, G.N. A Revolution in the Physiology of the Living Cell; Krieger Publishing Co.: Malabar, FL, USA, 1992. [Google Scholar]
- Sachs, F.; Qin, F. Gated, ion-selective channels observed with patch pipettes in the absence of membranes: Novel properties of a Gigaseal. Biophys. J. 1993, 65, 1101–1107. [Google Scholar] [CrossRef]
- Bogner, P.; Nagy, E.; Miseta, A. On the role of Na, K-ATPase: A challenge for the membrane—Pump and association-induction hypotheses. Physiol. Chem. Phys. Med. NMR 1998, 30, 81–87. [Google Scholar] [PubMed]
- Ling, G.N. Explaining on request a correlation between membrane Na, K-ATPase and K+ content in erythrocytes and other findings in the preceding paper. Physiol. Chem. Phys. Med. NMR 1998, 30, 89–97. [Google Scholar] [PubMed]
- Erisir, A.; Lau, D.; Rudy, B.; Leonard, C.S. Function of specific K+ channels in sustained high-frequency firing of fast-spiking neocortical interneurons. J. Neurophysiol. 1999, 85, 2476–2489. [Google Scholar]
- Clay, J.R.; Shrier, A. Action potentials occur spontaneously in squid giant axons with moderately alkaline intracellular pH. Biol. Bull. 2001, 201, 186–192. [Google Scholar] [CrossRef] [PubMed]
- Ling, G.N. Life at the Cell and Below-Cell Level: The Hidden History of a Fundamental Revolution in Biology; Pacific Press: New York, NY, USA, 2001. [Google Scholar]
- Sahin, A.; Cengelogu, Y.; Ersoz, M. The membrane potentials of periderm and cuticular membranes. Turk. J. Chem. 2002, 26, 777–782. [Google Scholar]
- Schumacher, M.; Adelman, J.P. An open and shut case. Nature 2002, 417, 501–502. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Lee, A.; Chen, J.; Cadene, M.; Chalt, B.T.; MacKinnon, R. The open pore conformation potassium channels. Nature 2002, 417, 523–526. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Lee, A.; Chen, J.; Cadene, M.; Chalt, B.T.; MacKinnon, R. Crystal structure and mechanism of a calcium-gated potassium channel. Nature 2002, 417, 515–522. [Google Scholar] [CrossRef] [PubMed]
- Clapham, D.E. TRP channels as cellular sensors. Nature 2003, 426, 517–524. [Google Scholar] [CrossRef] [PubMed]
- Bernard, C.; Johnston, D. Distance-dependent modifiable threshold for action potential back-propagation in hippocampal dendrites. J. Neurophysiol. 2003, 90, 1807–1816. [Google Scholar] [CrossRef] [PubMed]
- Bean, B.P. The action potential in mammalian central neurons. Nature 2007, 8, 451–465. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.W.; Bean, B.P. Kv2 Channel regulation of action potential repolarization and firing patterns in superior cervical ganglion neurons and hippocampal CA1 pyramidal neurons. J. Neurosci. 2014, 34, 4991–5002. [Google Scholar] [CrossRef] [PubMed]
- Goaillard, J.-M.; Dufour, M.A. The pros and cons of degeneracy. eLife 2014, 3, e02615. [Google Scholar] [CrossRef] [PubMed]
- Cronin, J. Mathematical Aspects of Hodgkin-Huxley Neural Theory; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Ermentrout, G.B.; Terman, D.H. Mathematical Foundations of Neuroscience; Springer: New York, USA, 2010. [Google Scholar]
- Colacicco, G. Electrical potential at an oil/water interface. Nature 1965, 207, 936–938. [Google Scholar] [CrossRef]
- Colacicco, G. Reversal of potential across a liquid non-aqueous membrane with regard to membrane excitability. Nature 1965, 207, 1045–1047. [Google Scholar] [CrossRef] [PubMed]
- Tamagawa, H.; Morita, S. Membrane potential generated by ion adsorption. Membranes 2014, 4, 257–274. [Google Scholar] [CrossRef] [PubMed]
- Tamagawa, H. Membrane potential generation without ion transport. Ionics 2014. published online. [Google Scholar]
- Cheng, K.L. Capacitor theory for nonfaradaic potentiometry. Microchem. J. 1990, 42, 5–24. [Google Scholar] [CrossRef]
- Huang, C.-M.; Jean, Y.C.; Cheng, K.L. Isotopic evidence disproving Ion exchange reaction between H+ and Na+ in pH glass electrode. J. Electrochem. Soc. 1995, 142, L175–L176. [Google Scholar] [CrossRef]
- Cheng, K.L. Explanation of misleading Nernst slope by Boltzmann equation. Microchem. J. 1998, 59, 457–461. [Google Scholar] [CrossRef]
- Temsamani, K.R.; Cheng, K.L. Studies of chloride adsorption on the Ag/AgCl electrode. Sens. Actuators B 2001, 76, 551–555. [Google Scholar] [CrossRef]
- Cheng, K.L. Recent development of non-faradaic potentiometry. Microchem. J. 2002, 72, 269–276. [Google Scholar] [CrossRef]
- Teorell, T. Electrokinetic membrane processes in relation to properties of excitable tissues I. experiments on oscillatory transport phenomena in artificial membranes. J. Gen. Physiol. 1959, 42, 831–845. [Google Scholar] [CrossRef]
- Kishimoto, U. Hodgkin-Huxley riron no mondaiten (problems around Hodgkin-Huxley theory). Seibutubutsuri (Biophysics) 1968, 8, 8–15. (In Japanese) [Google Scholar]
- Shinagawa, Y. Makudeni no butsuriteki kiso (physical basis of membrane potential). Maku (Membrane) 1976, 1, 176–183. (In Japanese) [Google Scholar]
- Ishima, Y.; Przybylski, A.T.; Fox, S.W. Electrical membrane phenomena in spherules from proteinoid and lecithin. Biosystems 1981, 13, 243–251. [Google Scholar] [CrossRef]
- Przybylski, A.T.; Stratten, W.P.; Syren, R.M.; Fox, S.W. Membrane, action, and oscillatory potentials in simulated protocells. Naturwissenschaften 1982, 69, 561–563. [Google Scholar] [CrossRef] [PubMed]
- Yoshikawa, K.; Matsubara, Y. Spontaneous oscillation of electrical potential across organic liquid membranes. Biophys. Chem. 1983, 17, 183–185. [Google Scholar] [CrossRef]
- Przybylski, A.T.; Fox, S.W. Excitable artificial cells of proteinoid. Appl. Biochem. Biotechnol. 1984, 10, 301–307. [Google Scholar] [CrossRef] [PubMed]
- Przybylski, A.T. Excitable cell made of thermal proteinoids. Biosystems 1985, 17, 281–288. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Sakabe, K.; Matsubara, Y.; Ota, T. Oscillation of electrical potential in a porous membrane doped with grycerol α-monoolate induced by an Na+/K+ concentration gradient. Biophys. Chem. 1984, 20, 107–109. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Sakabe, K.; Matsubara, Y.; Ota, T. Self-excitation in a porous membrane doped with sorbitan monooleate (Span-80) induced by an Na+/K+ concentration gradient. Biophys. Chem. 1985, 21, 33–39. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Omochi, T.; Matsubara, Y.; Kourai, H. A possibility to recognize chirality by an excitable artificial liquid membrane. Biophys. Chem. 1986, 24, 111–119. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Omochi, T.; Matsubara, Y. Chemoreception of sugars by an excitable liquid membrane. Biophys. Chem. 1986, 23, 211–214. [Google Scholar] [CrossRef]
- Vaughan, G.; Przybylski, A.T.; Fox, S.W. Thermal proteinoids as excitability-inducing materials. Biosystems 1987, 20, 219–223. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Shoji, M.; Nakata, S.; Maeda, S. An Excitable liquid membrane possibly mimicking the sensing mechanism of taste. Langmuir 1988, 4, 759–762. [Google Scholar] [CrossRef]
- Nakajo, N.; Yoshikawa, K.; Shoji, M.; Ueda, I. Spontaneous oscillation of artificial membrane: Equivalence in effects of temperature and volatile anesthetic. Biochem. Biophys. Res. Commun. 1990, 167, 450–455. [Google Scholar] [CrossRef]
- Yagisawa, K.; Naito, M.; Gondaira, K.; Kambara, T. A model for self-sustained potential oscillation of lipid bilayer membranes induced by the gel-liquid crystal phase transitions. Biophys. J. 1993, 64, 1461–1475. [Google Scholar] [CrossRef]
- Li, H.; Wang, M. Design of oscillations across the artificial liquid membrane between water and oil phases. Chem. Phys. Lett. 2000, 330, 503–508. [Google Scholar] [CrossRef]
- Srividhya, J.; Gopinathan, M.S. Modeling experimental oscillations in liquid membranes with delay equations. J. Phys. Chem. B 2003, 107, 1438–1443. [Google Scholar] [CrossRef]
- Kumar, A.; Pradeep, T. Stabilization of monolayers by metal nanoparticles manifested in oscillations of interfacial potentials. Mater. Sci. Eng. C 2004, 24, 535–539. [Google Scholar] [CrossRef]
- Gao, J.; Wang, L.; Yang, W.; Yang, F. Electrical potential oscillation in an anionic surfactant system with barbitone in octanol as an oil phase. J. Iran. Chem. Soc. 2005, 2, 71–77. [Google Scholar] [CrossRef]
- Ogawa, T.; Shimazaki, H.; Aoyagi, S.; Sakai, K. Electrical oscillation at a water/octanol interface in a hydrophobic container. J. Colloid Interface Sci. 2007, 305, 195–197. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.Z.; Dai, H.X.; Chen, H.; Ren, J.; Yang, W. Study on the oscillating phenomena of electrical potential across a liquid membrane. Chin. Chem. Lett. 2007, 18, 309–312. [Google Scholar] [CrossRef]
- Kovalchuk, N.M. Spontaneous non-linear oscillations of interfacial tension at oil/water interface. Open Chem. 2015, 13, 1–16. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamagawa, H.; Funatani, M.; Ikeda, K. Ling’s Adsorption Theory as a Mechanism of Membrane Potential Generation Observed in Both Living and Nonliving Systems. Membranes 2016, 6, 11. https://doi.org/10.3390/membranes6010011
Tamagawa H, Funatani M, Ikeda K. Ling’s Adsorption Theory as a Mechanism of Membrane Potential Generation Observed in Both Living and Nonliving Systems. Membranes. 2016; 6(1):11. https://doi.org/10.3390/membranes6010011
Chicago/Turabian StyleTamagawa, Hirohisa, Makoto Funatani, and Kota Ikeda. 2016. "Ling’s Adsorption Theory as a Mechanism of Membrane Potential Generation Observed in Both Living and Nonliving Systems" Membranes 6, no. 1: 11. https://doi.org/10.3390/membranes6010011
APA StyleTamagawa, H., Funatani, M., & Ikeda, K. (2016). Ling’s Adsorption Theory as a Mechanism of Membrane Potential Generation Observed in Both Living and Nonliving Systems. Membranes, 6(1), 11. https://doi.org/10.3390/membranes6010011




