Performance Analysis of Silica Fluidized Bed Membrane Reactor for Hydrogen Production as a Green Process Using CFD Modelling
Abstract
1. Introduction
2. Methodology
2.1. Reactor Design and Assumptions
- Neglect 3D effects and focus on a 2D cross-section.
- Consider axisymmetric geometry.
- Incompressible flow (due to low Mach numbers).
- Uniform catalyst size distribution.
- Spherical shape for catalysts.
- Assumed to have a bubbling fluidization regime for the FBMR and FBR cases.
- Use empirical Schiller–Naumann drag model for the FBMR and FBR cases.
- Neglect radiative heat transfer.
- Simplified mass transfer model for silica membrane permeation (activated molecular sieve mechanism based on single gases permeation).
- Uniform catalyst distribution.
- No-slip condition at walls.
- Simplified inlet and outlet conditions.
- Use Darcy’s law or Forchheimer equation for porous media flow (in PBMR case).
- Constant overall bed porosity (in PBMR case).
2.2. CFD Modelling Approach
2.2.1. Governing Equations
- Continuity equation.
- Momentum equation.
- Specious transport equation.
- Reaction rate correlations.
- Silica membrane permeation.
2.2.2. Boundary Conditions
2.2.3. Post Processing Definitions
2.3. Solving Method and Mesh Independency
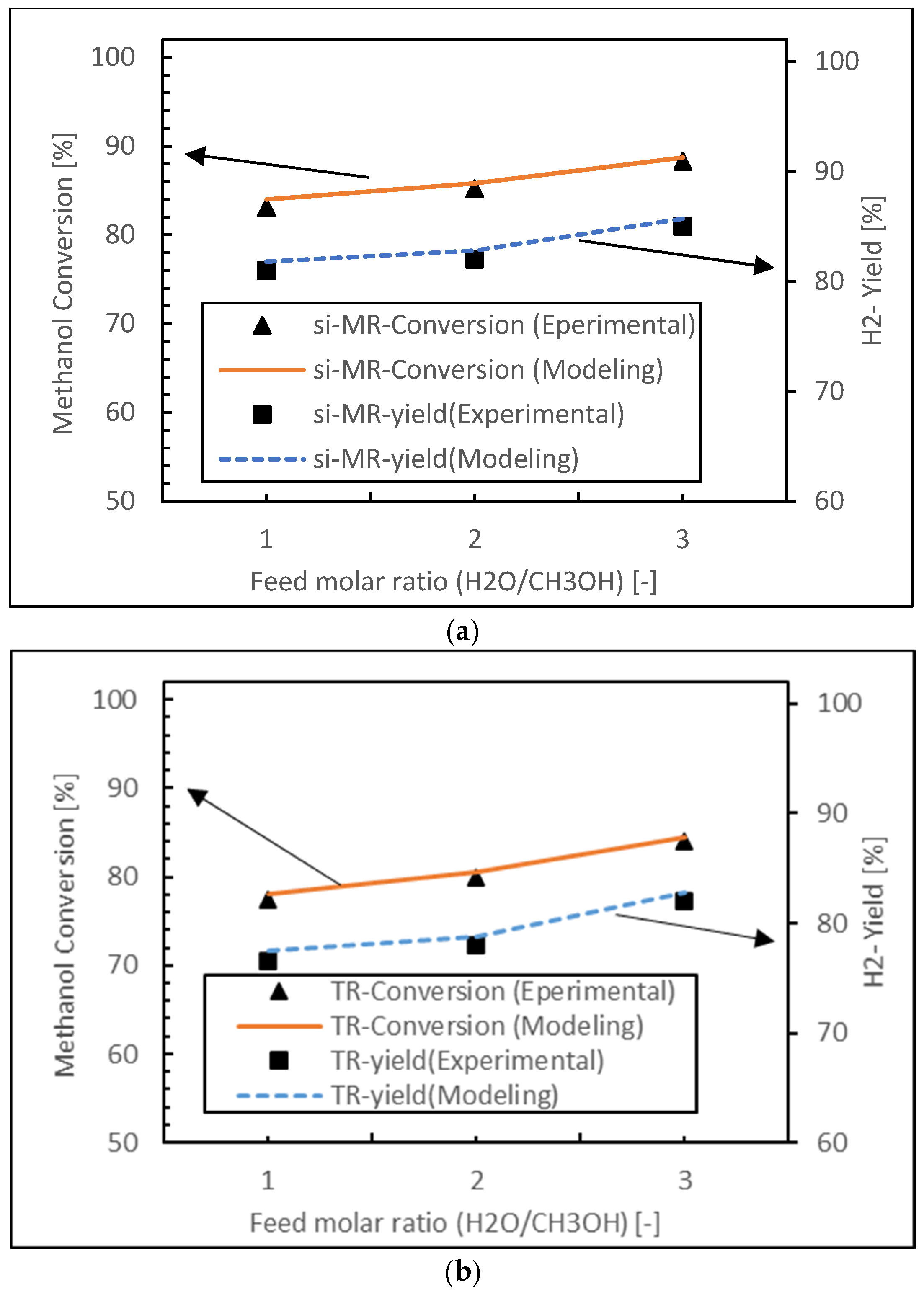
2.4. Model Validation
3. Results and Discussion
3.1. Effect Analysis of Operating Parameters
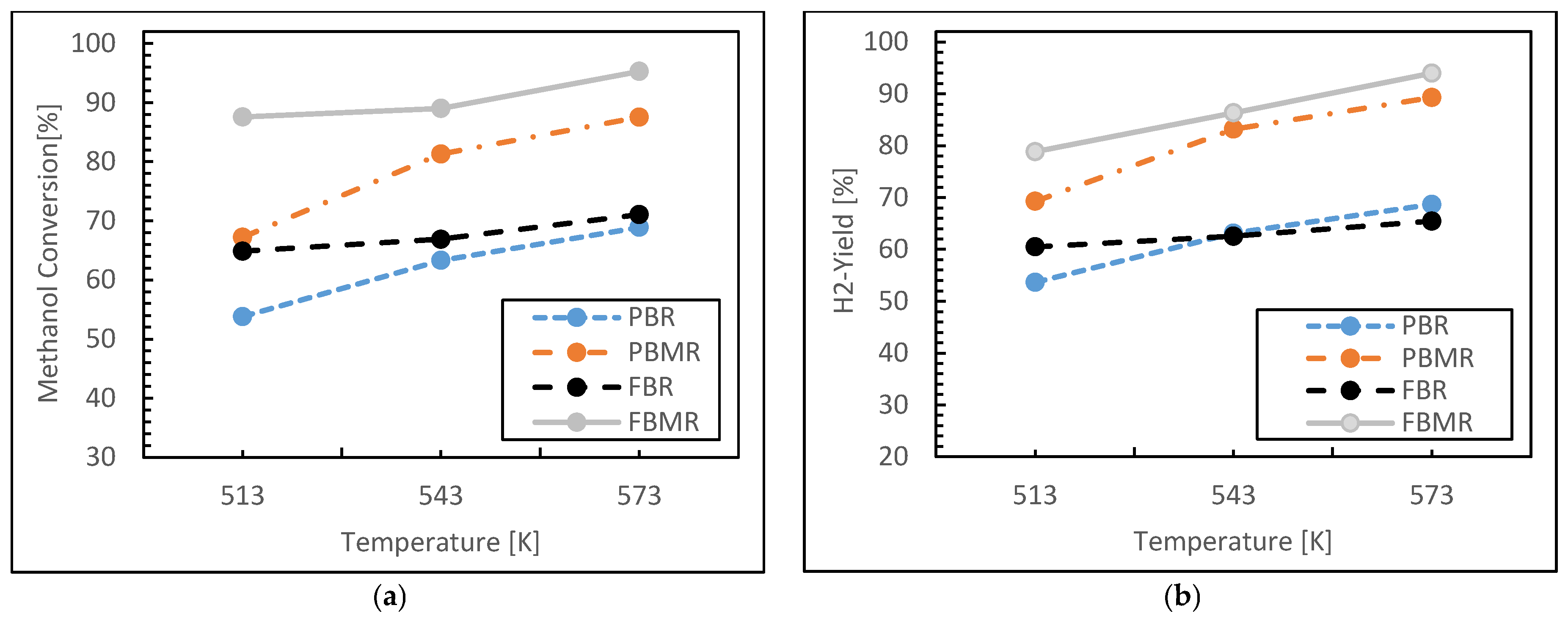
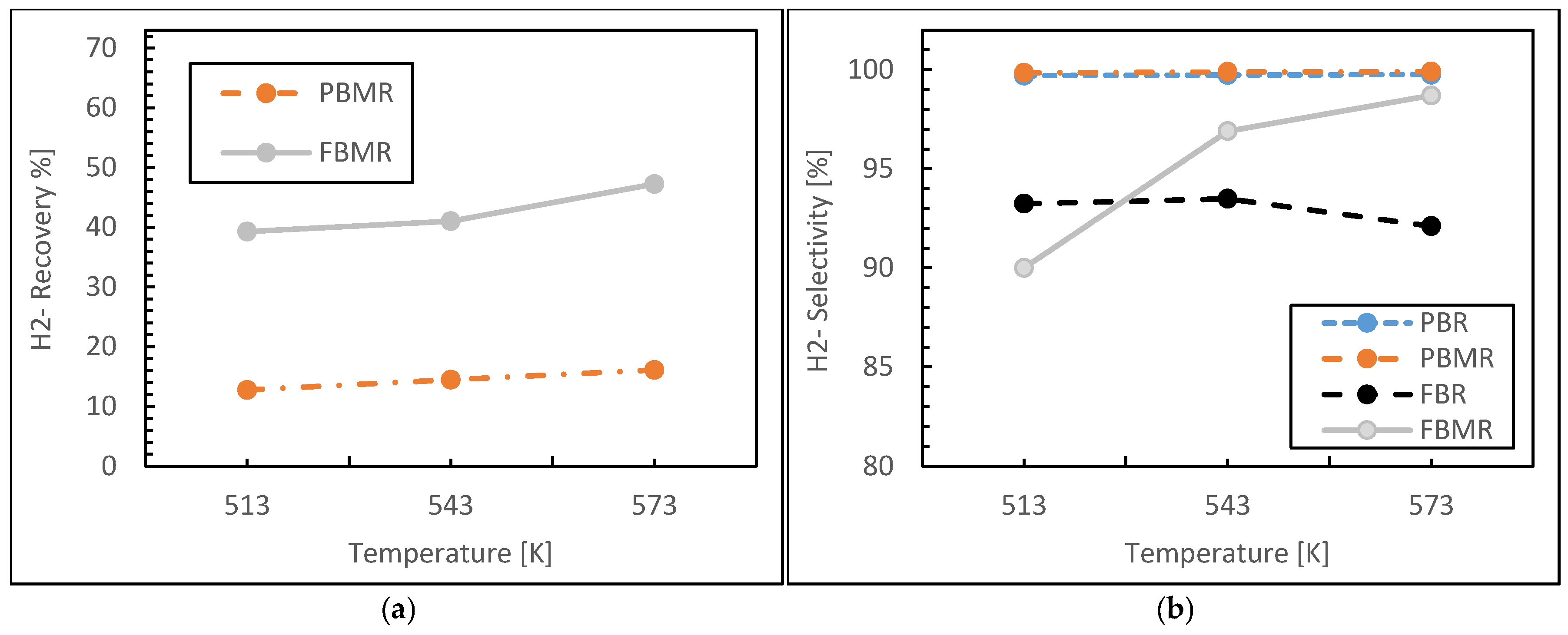
3.1.1. Reaction Temperature Effect
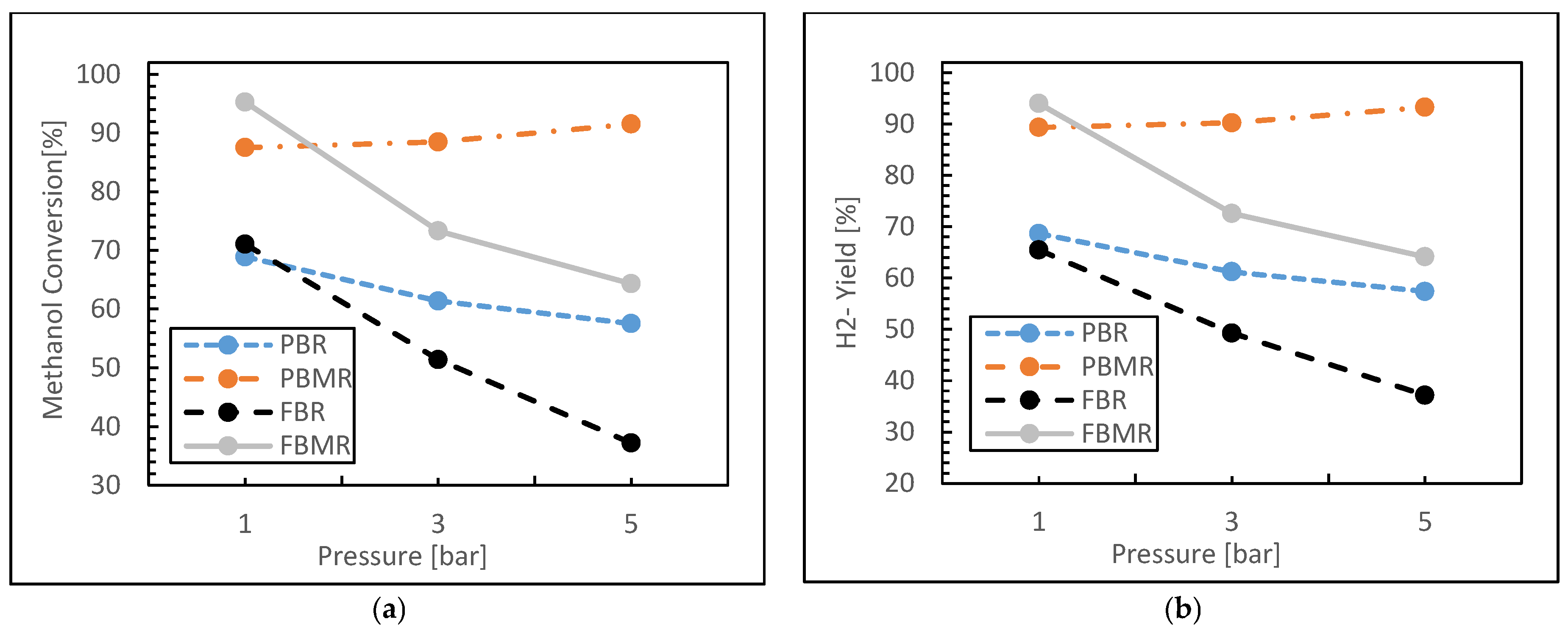
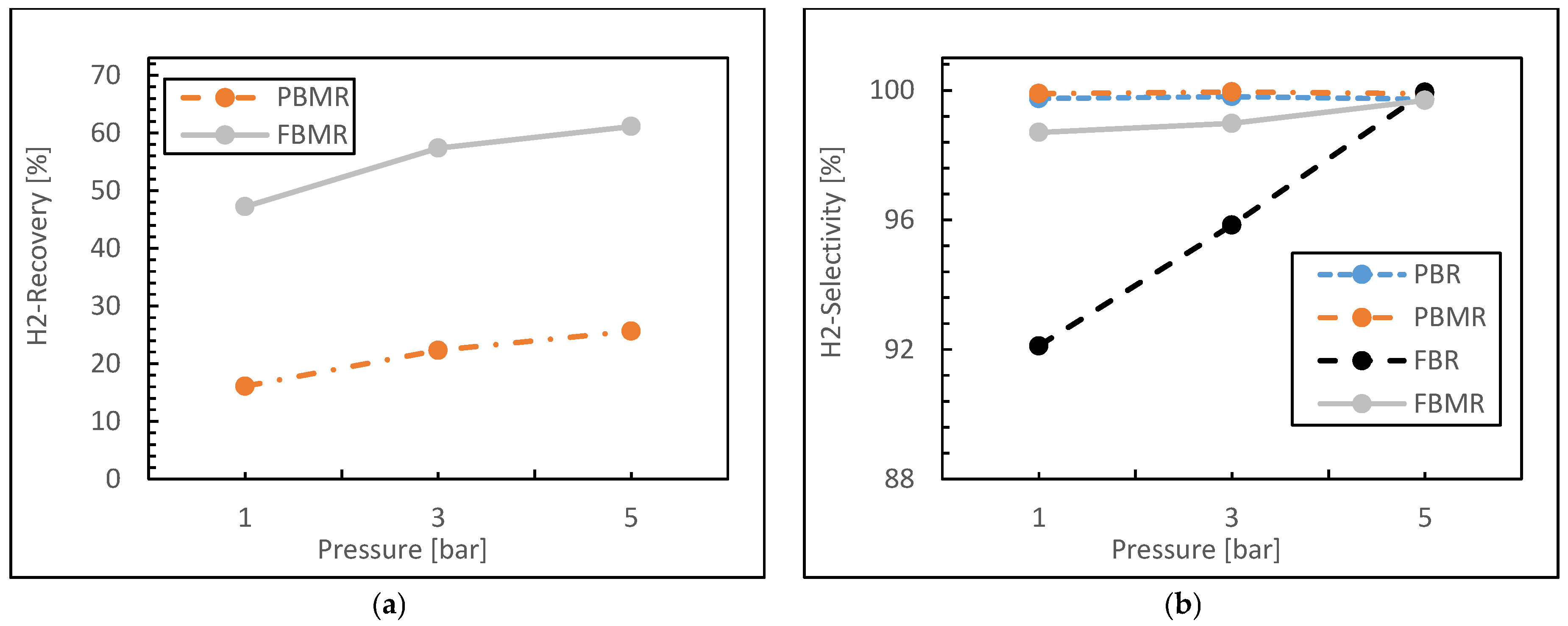
3.1.2. Reaction Pressure Effect
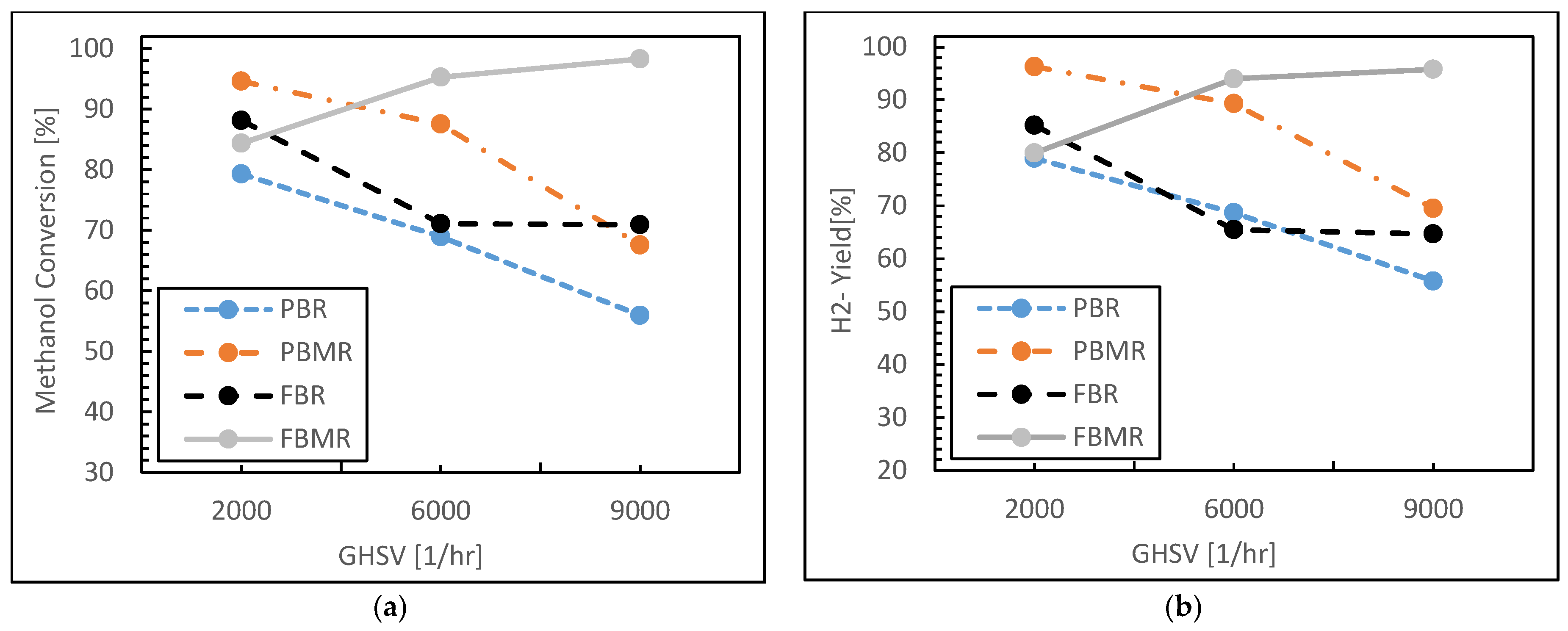
3.1.3. Residence Time Effect
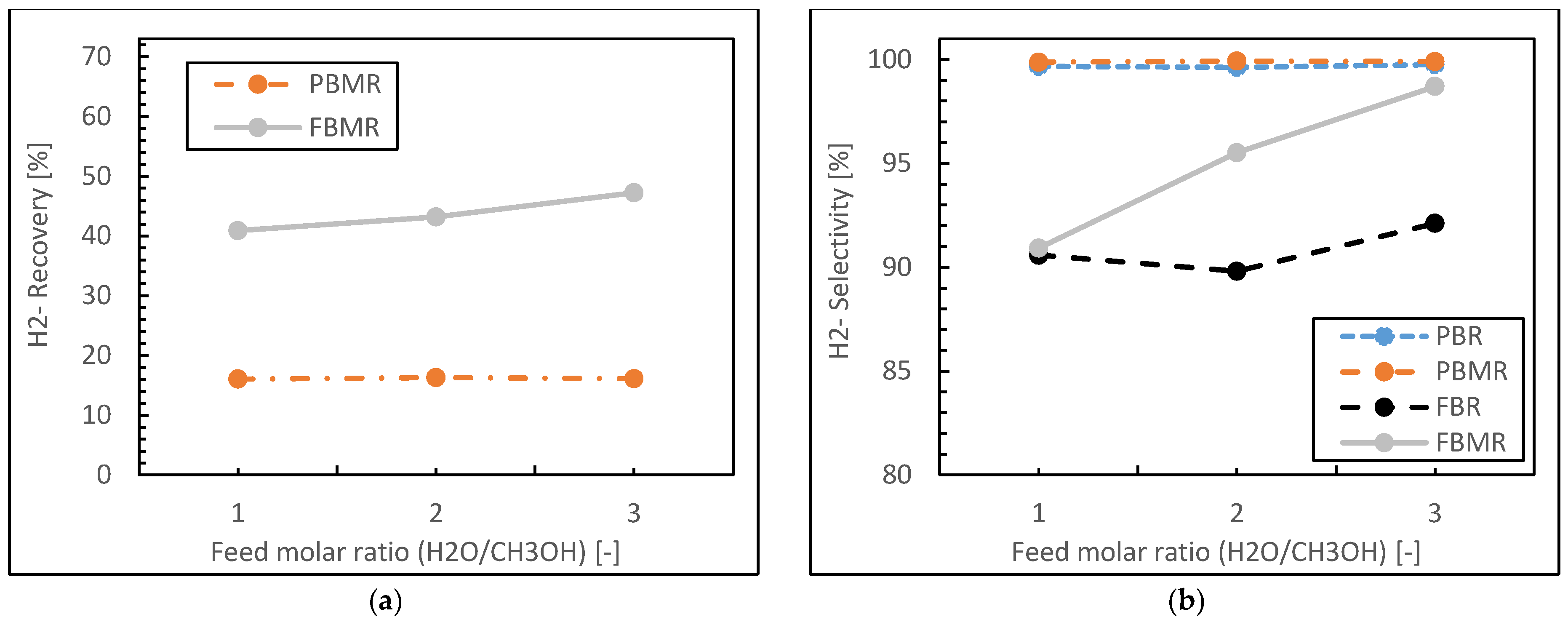
3.1.4. Feed Molar Ratio Effect
- Both packed bed configurations (PBMR and PBR) achieve near-perfect hydrogen selectivity across all feed ratios, regardless of membrane integration.
- The FBMR combines relatively high hydrogen recovery with increasing selectivity at higher feed ratios, making it effective for hydrogen production.
- Fluidized bed configurations (FBMR and FBR) show improved performance with increasing feed ratios, suggesting better utilization of excess water in the reaction.
- The PBMR maintains consistently high selectivity but shows lower hydrogen recovery compared to the FBMR, indicating a trade-off between these performance metrics.
- The FBR demonstrates lower selectivity compared to other reactor types, especially at lower feed ratios.
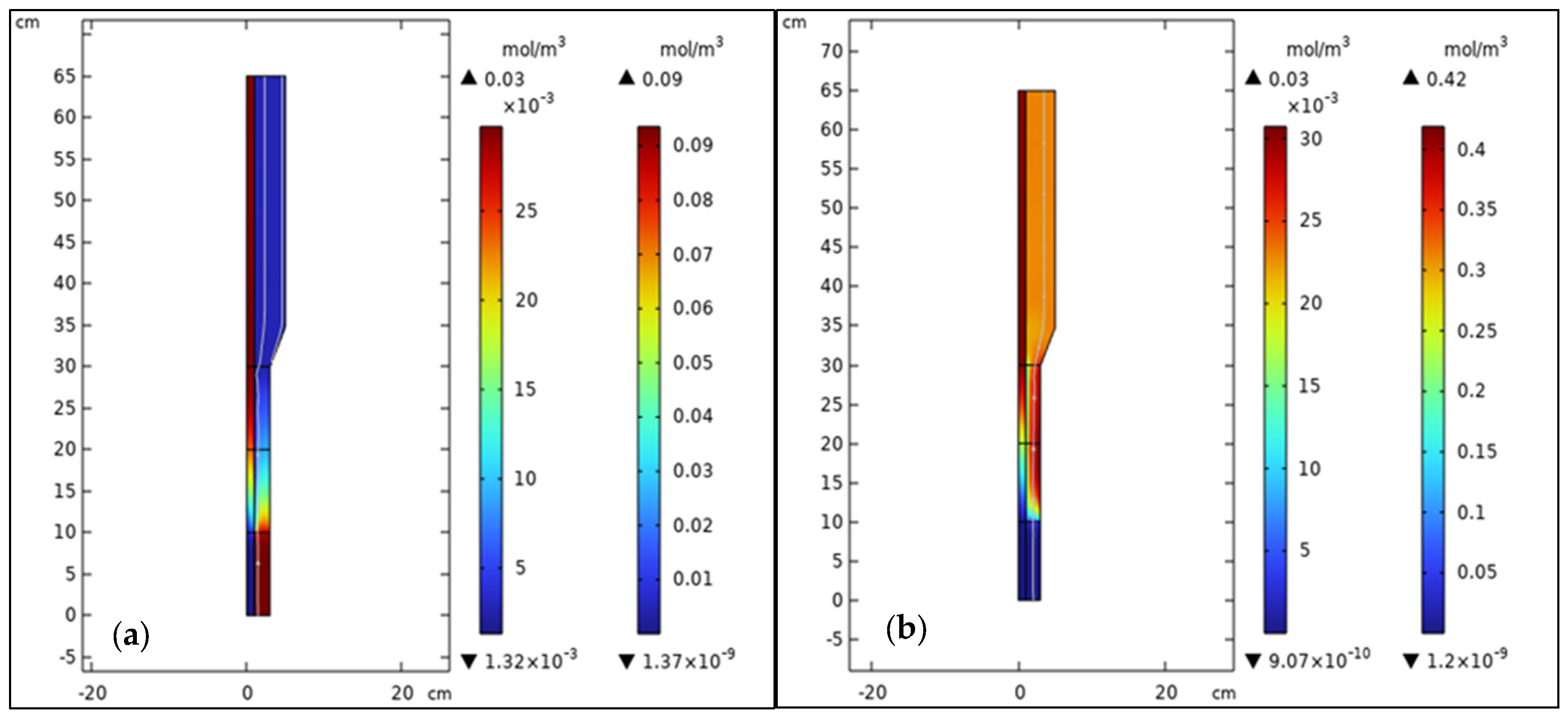
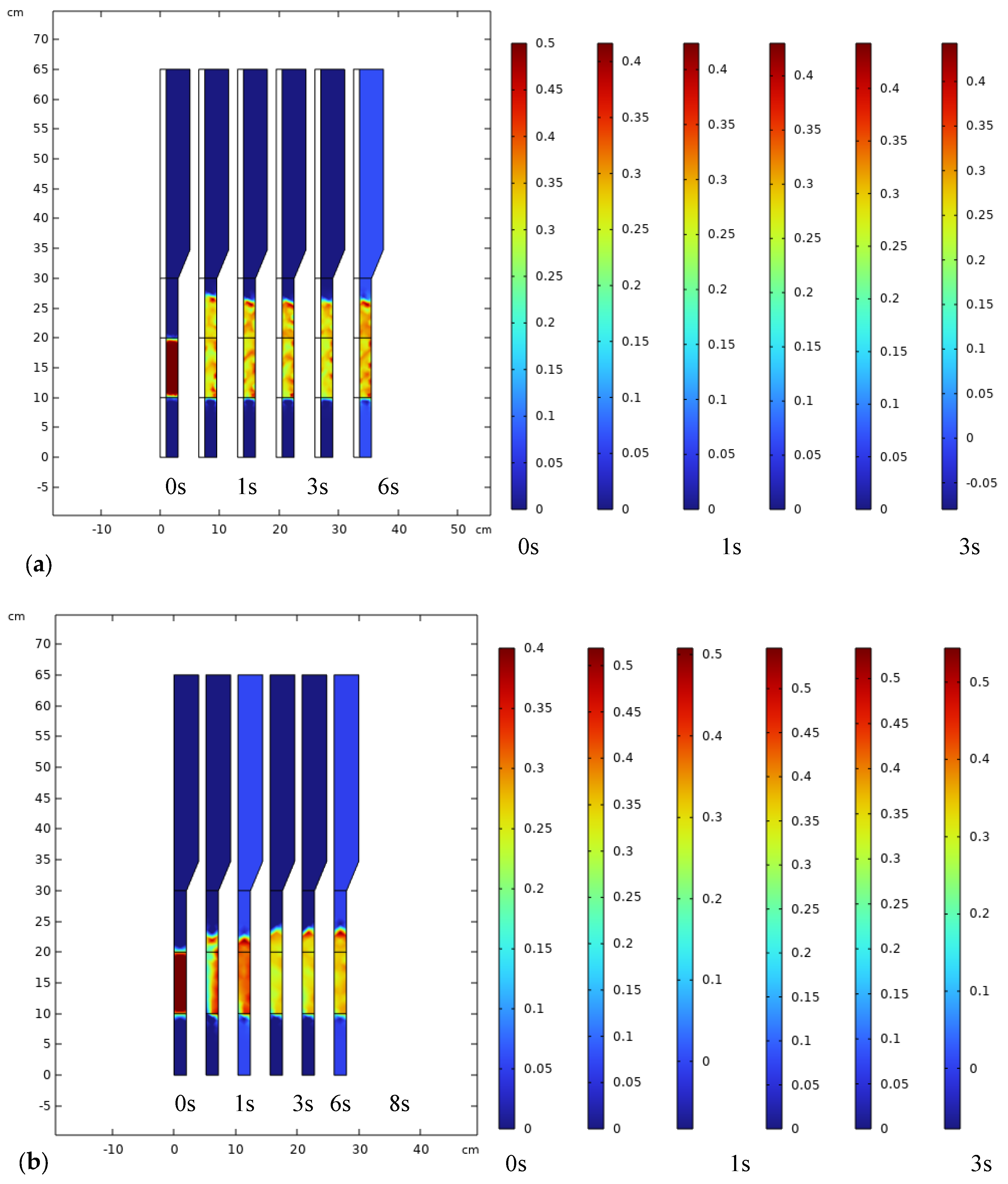
3.2. Components, Velocity, and Pressure Distributions
3.3. Analysis of Bubble Regime in FBMR
4. Conclusions and Future Trends
- Reactor Type: FBMR exhibited superior hydrogen yield and uniform thermal distribution due to enhanced mixing and gas–solid interactions.
- Temperature: 250–270 °C was identified as the optimal operating window, maximizing catalyst activity while minimizing side reactions or sintering risks.
- Pressure: Slightly elevated pressures (1.5–3 bar) improved membrane permeation without compromising reaction kinetics.
- Steam-to-Methanol Ratio (S/M): A molar ratio of 1.2–1.4 was ideal to reduce energy input while avoiding coke formation.
- Membrane Features: Thin hydrogen-selective membranes with high surface area (e.g., Pd-based or silica) improved hydrogen extraction and shifted the reaction equilibrium.
- Membrane Performance Targets: Selectivity (H2/others) > 1000; permeability > 10−6 mol·m−2·s−1·Pa−1.
- Hydrodynamics: In the bubbling regime, bubble rise velocities of 0.15–0.25 m/s significantly enhanced gas–solid mass transfer.
- Catalyst Size and Distribution: Uniform catalyst distribution and particle diameters of 100–200 μm prevented channeling and improved reaction efficiency.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronym | |
| FBMR | Fluidized bed membrane reactor |
| FBR | Fluidized bed reactor |
| GHSV | Gas hourly space velocity |
| MR | Membrane reactor |
| MD | Methanol decomposition |
| MSR | Methanol steam reforming |
| PBMR | Packed bed membrane reactor |
| PBR | Packed bed reactor |
| SR | Steam reforming |
| WGS | Water gas shift |
| Nomenclature | |
| A | Cross area of retentate side, m2 |
| Total surface concentration of site i, mol m−2 | |
| CH3OHin | Methanol molar flow rate fed to the reactor, mol s−1 |
| CH3OHout | Methanol molar flow rate going out from the reactor, mol s−1 |
| D | Membrane diameter, m |
| dp | Catalyst diameter, m |
| Ea | Apparent activation energy for membrane, J mol−1 |
| Ea,i | Transport activation energy for species i in the silica membrane, J mol−1 |
| Ei | Activation energy for rate constant of reaction i, kJ mol−1 |
| FCH3OH | Molar methanol inlet flow rate, mol s−1 |
| ΔHi | Heat of adsorption for surface species iii or heat of reaction for formation of surface Species i, kJ mol−1 |
| Ji | Flux of component i, mol m2 s−1 |
| kj | Rate constant for reaction j (units are specific to the form of the rate expression) |
| Pre-exponential term in Arrhenius expression; this is the intercept of the Arrhenius Equation as T→∞ | |
| Equilibrium constant of reaction j | |
| Equilibrium constant or adsorption coefficient for surface species i | |
| m | Feed molar ratio coefficient |
| Ni | Molar flow rate, mol m2 s−1 |
| P | Total pressure, bar |
| pi | Partial pressure of component i, bar |
| Permeance coefficient for silica membranes of species i, mol s−1 cm−2 atm−0.5 | |
| Pe | Permeability coefficient, mol s−1 cm−1 atm−0.5 |
| Hydrogen partial pressure in retentate side, bar | |
| Hydrogen partial pressure in permeate side, bar | |
| ri | Rate of reaction i, mol s−1 m−2, or rate of formation of species i, mol s−1gcatalyst−1 |
| R | Gas constant, kPa m3 mol−1 K−1 |
| ΔSi | Entropy of adsorption for species i, J mol−1 K−1 |
| SA | Surface area of fresh catalyst, m2 g−1 |
| T | Temperature, K |
| V | Volume of catalyst or reactor, m3 |
| U | Gas velocity, m s−1 |
| W | Mass of catalyst, g |
| z | Axial coordinate |
| Greek letter | |
| ρg | Density of gas, kg m−3 |
| Ρb | Density of the catalyst bed, kg m−3 |
| μ | Gas viscosity, kg m−1 s−1 |
| δ | Membrane thickness, m |
| ε | Porosity of the catalyst |
| νij | Stoichiometric coefficient |
References
- Silva, D.P.M.d.; Capaz, R.S. A Review of the Life Cycle Assessment of the Carbon–Water–Energy Nexus of Hydrogen Production Pathways. Hydrogen 2025, 6, 34. [Google Scholar] [CrossRef]
- Shen, L.; Zhang, C.; Shan, F.; Chen, L.; Liu, S.; Zheng, Z.; Zhu, L.; Wang, J.; Wu, X.; Zhai, Y. Review and Prospects of Key Technologies for Integrated Systems in Hydrogen Production from Offshore Superconducting Wind Power. Energies 2024, 18, 19. [Google Scholar] [CrossRef]
- Younas, M.; Shafique, S.; Hafeez, A.; Javed, F.; Rehman, F. An Overview of Hydrogen Production: Current Status, Potential, and Challenges. Fuel 2022, 316, 123317. [Google Scholar] [CrossRef]
- Jazani, O.; Bennett, J.; Liguori, S. Carbon-low, Renewable Hydrogen Production from Methanol Steam Reforming in Membrane Reactors—A Review. Chem. Eng. Process. Process Intensif. 2023, 189, 109382. [Google Scholar] [CrossRef]
- Ranjekar, A.M.; Yadav, G.D. Steam Reforming of Methanol for Hydrogen Production: A Critical Analysis of Catalysis, Processes, and Scope. Ind. Eng. Chem. Res. 2021, 60, 89–113. [Google Scholar] [CrossRef]
- Markov, A.A.; Merkulov, O.V.; Suntsov, A.Y. Development of Membrane Reactor Coupling Hydrogen and Syngas Production. Membranes 2023, 13, 626. [Google Scholar] [CrossRef]
- Helmi, A.; Gallucci, F. Latest Developments in Membrane (Bio)Reactors. Processes 2020, 8, 1239. [Google Scholar] [CrossRef]
- Israni, S.H.; Harold, M.P. Methanol Steam Reforming in Single-Fiber Packed Bed Pd–Ag Membrane Reactor: Experiments and Modeling. J. Membr. Sci. 2011, 369, 375–387. [Google Scholar] [CrossRef]
- Mironova, E.; Donstov, A.; Ievlev, V.; Yaroslavtsev, A. Methanol Steam Reforming in Traditional and Membrane Reactors over Pt–Rh/TiO2–In2O3 Catalyst Using Surface-Treated Pd–Cu Foil Membranes. Eng. Proc. 2022, 19, 11. [Google Scholar] [CrossRef]
- Mironova, E.Y.; Lytkina, A.A.; Ermilova, M.M.; Orekhova, N.V.; Zhilyaeva, N.A.; Roshan, N.R.; Ievlev, V.M.; Yaroslavtsev, A.B. Methanol Steam Reforming in a Reactor with a Palladium–Copper Membrane in the Presence of a Nickel–Copper Catalyst. Pet. Chem. 2020, 60, 1232–1238. [Google Scholar] [CrossRef]
- Ongis, M.; Di Marcoberardino, G.; Baiguini, M.; Gallucci, F.; Binotti, M. Optimization of Small-Scale Hydrogen Production with Membrane Reactors. Membranes 2023, 13, 331. [Google Scholar] [CrossRef]
- Alique, D.; Martinez-Diaz, D.; Sanz, R.; Calles, J.A. Review of Supported Pd-Based Membranes Preparation by Electroless Plating for Ultra-Pure Hydrogen Production. Membranes 2018, 8, 5. [Google Scholar] [CrossRef] [PubMed]
- Ghasemzadeh, K.; Aghaeinejad-Meybodi, A.; Vaezi, M.J.; Gholizadeh, A.; Abdi, M.A.; Babaluo, A.A.; Haghighi, M.; Basile, A. Hydrogen Production via Silica Membrane Reactor during the Methanol Steam Reforming Process: Experimental Study. RSC Adv. 2015, 5, 95823–95832. [Google Scholar] [CrossRef]
- Ghasemzadeh, K.; Harasi, J.N.; Amiri, T.Y.; Basile, A.; Iulianelli, A. Methanol Steam Reforming for Hydrogen Generation: A Comparative Modeling Study between Silica and Pd-Based Membrane Reactors by CFD Method. Fuel Process. Technol. 2020, 199, 106273. [Google Scholar] [CrossRef]
- Myagmarjav, O.; Tanaka, N.; Nomura, M.; Kubo, S. Comparison of Experimental and Simulation Results on Catalytic HI Decomposition in a Silica-Based Ceramic Membrane Reactor. Int. J. Hydrogen Energy 2019, 44, 30832–30839. [Google Scholar] [CrossRef]
- Binazadeh, M.; Mamivand, S.; Sohrabi, R.; Taghvaei, J.; Iulianelli, A. Membrane Reactors for Hydrogen Generation: From Single Stage to Integrated Systems. Int. J. Hydrogen Energy 2023, 48, 39225–39253. [Google Scholar] [CrossRef]
- Liang, R.; Song, X.; Lin, X.; Guan, K.; Peng, C.; Wu, J. Preparation of Porous Fused Silica Support with High UV Transmittance for Photocatalytic Membrane Reactors. Ceram. Int. 2022, 48, 2898–2901. [Google Scholar] [CrossRef]
- Meng, L.; Tsuru, T. Hydrogen Production from Energy Carriers by Silica-Based Catalytic Membrane Reactors. Catal. Today 2016, 268, 3–11. [Google Scholar] [CrossRef]
- Lian, Z.; Wang, Y.; Zhang, X.; Yusuf, A.; Famiyeh, L.; Murindabaraha, D.; Jin, H.; Liu, Y.; He, J.; Wang, Y.; et al. Hydrogen Production by Fluidised Bed Reactors: A Quantitative Perspective Using the Supervised Machine Learning Approach. Multidiscip. Sci. J. 2021, 4, 266–287. [Google Scholar] [CrossRef]
- Ghasemzadeh, K.; Torabi, T.; Yousefi Amiri, T.; Fortunelli, A.; Iulianelli, A. Parametric and Sensitivity Analysis of Pd-Ag Membrane Reactor Performance in Biogas Reforming to Generate Decarbonized Hydrogen by Computational Fluid Dynamic–Response Surface Methodology. Fuel 2024, 365, 131205. [Google Scholar] [CrossRef]
- Kassi, A.H.; Al-Hattab, T.A. A CFD Model of Natural Gas Steam Reforming in a Catalytic Membrane Reactor: Effect of Various Operating Parameters on the Performance of CMR. Int. J. Hydrogen Energy 2024, 56, 780–796. [Google Scholar] [CrossRef]
- Madadi Avargani, V.; Momeni, M.; Nowrouzi, M.; Rostami, A.; Zendehboudi, S. Design of a Novel Tubular Membrane Reactor with a Middle Annular Injector for Enhancement of Dry Reforming towards High Hydrogen Purity: CFD Analysis. Int. J. Hydrogen Energy 2024, 61, 1230–1250. [Google Scholar] [CrossRef]
- Caravella, A.; Melone, L.; Sun, Y.; Brunetti, A.; Drioli, E.; Barbieri, G. Concentration polarization distribution along Pd-based membrane reactors: A modelling approach applied to Water-Gas Shift. Int. J. Hydrogen Energy 2016, 41, 2660–2670. [Google Scholar] [CrossRef]
- Choi, H.; Kim, S.H.; Bae, J.; Katikaneni, S.P.R.; Jamal, A.; Harale, A.; Paglieri, S.N.; Lee, J.H. CFD Analysis and Scale-Up of a Baffled Membrane Reactor for Hydrogen Production by Steam Methane Reforming. Comput. Chem. Eng. 2022, 165, 107912. [Google Scholar] [CrossRef]
- Bian, Z.; Xia, H.; Zhong, W.; Jiang, B.; Yu, Y.; Wang, Z.; Yu, K. CFD Simulation on Hydrogen-Membrane Reactor Integrating Cyclohexane Dehydrogenation and CO2 Methanation Reactions: A Conceptual Study. Energy Convers. Manag. 2021, 235, 113989. [Google Scholar] [CrossRef]



| Gas Species, i | Q0, i (mol·m−2·s−1·Pa−1) | Ea,i (kJ·mol−1) |
|---|---|---|
| H2 | 2.22 × 10−6 | 8.78 |
| CO2 | 3.69 × 10−8 | −1.72 |
| CO | 2.17 × 10−7 | 5.33 |
| N2 | 8.62 × 10−8 | 3.55 |
| H2O | 7.11 × 10−8 | 3.49 |
| OH3CH | 1.68 × 10−8 | 2.52 |
| Position | Parameters | Value |
|---|---|---|
| Inlet (Z = 0) | FCH3OH (Methanol molar flow rate) | Varied (mol/s) |
| Inlet (Z = 0) | FH2O (Steam molar flow rate) | m. FCH3OH (m = 1, 2, 3) |
| Inlet (Z = 0) | FH2 (Hydrogen molar flow rate) | 1 × 10−12 FCH3OH |
| Inlet (Z = 0) | FCO (Carbon monoxide molar flow rate) | 1 × 10−12 FCH3OH |
| Inlet (Z = 0) | FCO2 (Carbon dioxide molar flow rate) | 1 × 10−12 FCH3OH |
| Inlet (Z = 0) | FN2 (Nitrogen molar flow rate) | 2.5 × 10−5 mol/s |
| Inlet (Z = 0) | Pinlet | Varied (bar) |
| Inlet (Z = 0) | Vinlet | Varied (m/s) |
| Position | Parameters | Value (mol/s) |
|---|---|---|
| Inlet (Z = 0) | NN2 (Nitrogen molar flow rate) | 1 × 10−4 |
| Inlet (Z = 0) | NCH3OH | 1 × 10−12 NN2 |
| Inlet (Z = 0) | NH2O (Steam molar flow rate) | 1 × 10−12 NN2 |
| Inlet (Z = 0) | NH2 (Hydrogen molar flow rate) | 1 × 10−12 NN2 |
| Inlet (Z = 0) | NCO (Carbon monoxide molar flow rate) | 1 × 10−12 NN2 |
| Inlet (Z = 0) | NCO2 (Carbon dioxide molar flow rate) | 1 × 10−12 NN2 |
| Inlet (Z = 0) | Pinlet | 1 bar |
| Inlet (Z = 0) | Vinlet | 0.01 m/s |
| Operating Parameters | Reaction Temperature | Reaction Pressure | Feed Molar Ratio | Feed Flow Rate/Catalyst Volume |
|---|---|---|---|---|
| T (K) | 513–573 | 573 | 573 | 573 |
| P (bar) | 1 | 1–5 | 1 | 1 |
| H2O/MeOH (−) | 3 | 3 | 1–3 | 3 |
| GHSV (h−1) | 6000 | 6000 | 6000 | 2000–9000 |
| Gas Velocity (m/s) | Bubble Rise Velocity (m/s) | Average Bubble Diameter (cm) | Gas–Solid Mass Transfer Coefficient (m/s) |
|---|---|---|---|
| 0.01 | 0.112 | 0.21 | 1.56 × 10−3 |
| 0.02 | 0.158 | 0.44 | 2.91 × 10−3 |
| 0.04 | 0.185 | 0.62 | 3.53 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barmaki, M.; Jalilnejad, E.; Ghasemzadeh, K.; Iulianelli, A. Performance Analysis of Silica Fluidized Bed Membrane Reactor for Hydrogen Production as a Green Process Using CFD Modelling. Membranes 2025, 15, 248. https://doi.org/10.3390/membranes15080248
Barmaki M, Jalilnejad E, Ghasemzadeh K, Iulianelli A. Performance Analysis of Silica Fluidized Bed Membrane Reactor for Hydrogen Production as a Green Process Using CFD Modelling. Membranes. 2025; 15(8):248. https://doi.org/10.3390/membranes15080248
Chicago/Turabian StyleBarmaki, Maryam, Elham Jalilnejad, Kamran Ghasemzadeh, and Adolfo Iulianelli. 2025. "Performance Analysis of Silica Fluidized Bed Membrane Reactor for Hydrogen Production as a Green Process Using CFD Modelling" Membranes 15, no. 8: 248. https://doi.org/10.3390/membranes15080248
APA StyleBarmaki, M., Jalilnejad, E., Ghasemzadeh, K., & Iulianelli, A. (2025). Performance Analysis of Silica Fluidized Bed Membrane Reactor for Hydrogen Production as a Green Process Using CFD Modelling. Membranes, 15(8), 248. https://doi.org/10.3390/membranes15080248







