Comparing Constant and Transient Membrane Transport Parameters for Use in Wave Desalination Models
Abstract
1. Introduction
- Correlations for apparent transport parameters developed under steady-state conditions can be used under dynamic conditions to predict system performance.
- Constant transport parameters determined under steady-state conditions can be used under dynamic conditions to predict system performance.
2. Materials and Methods
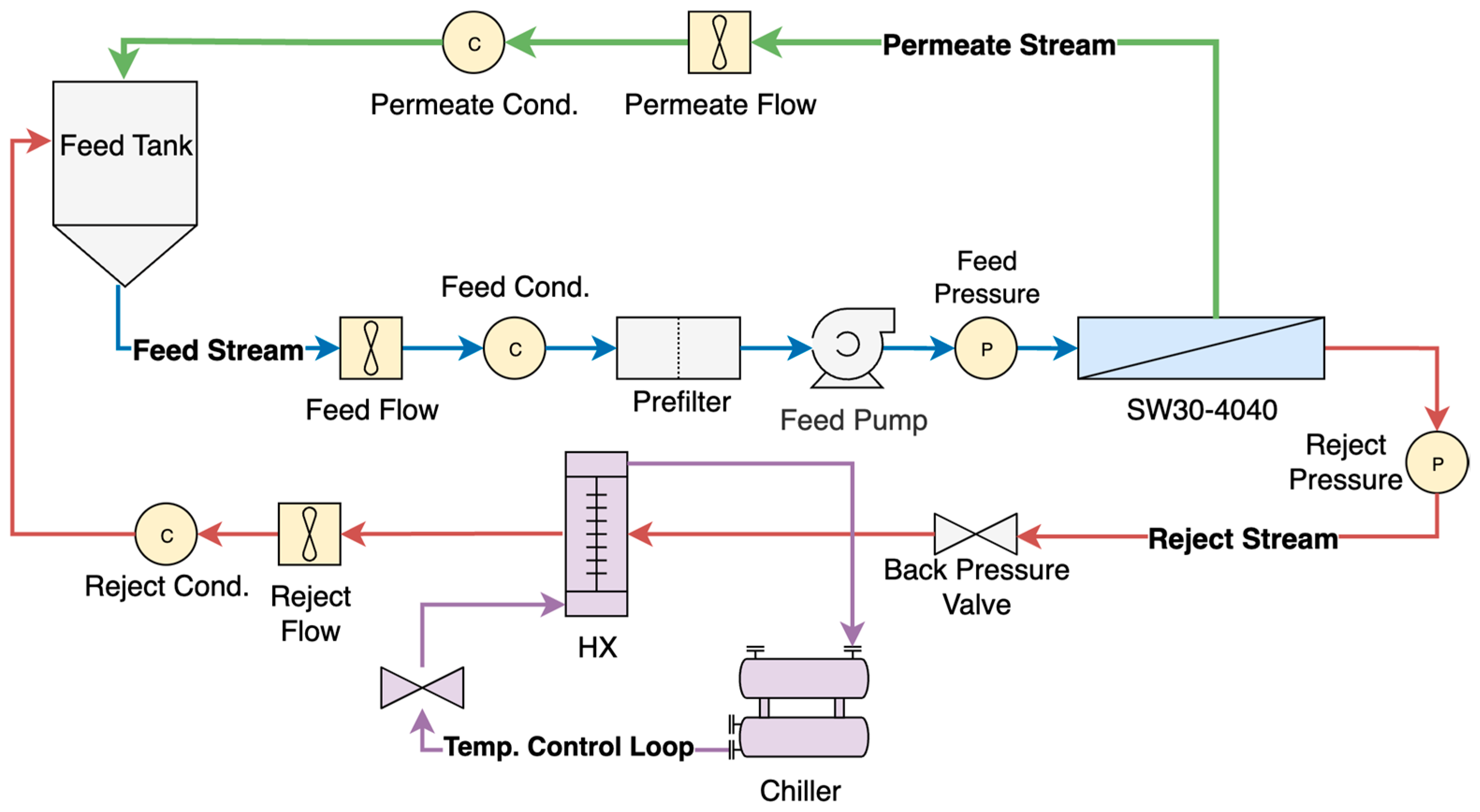
2.1. Experimental System
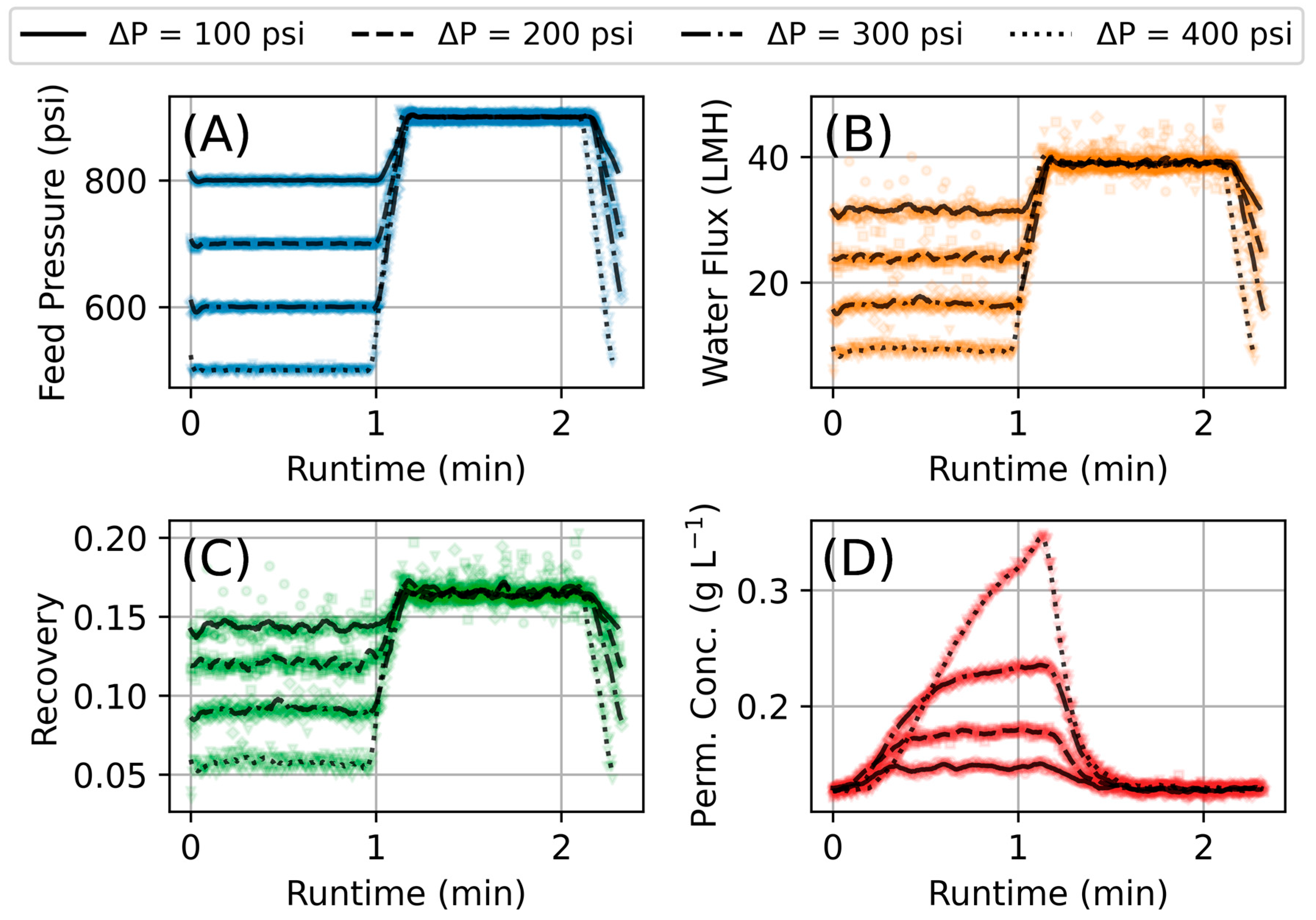
2.2. Experimental Conditions
2.3. Data Processing
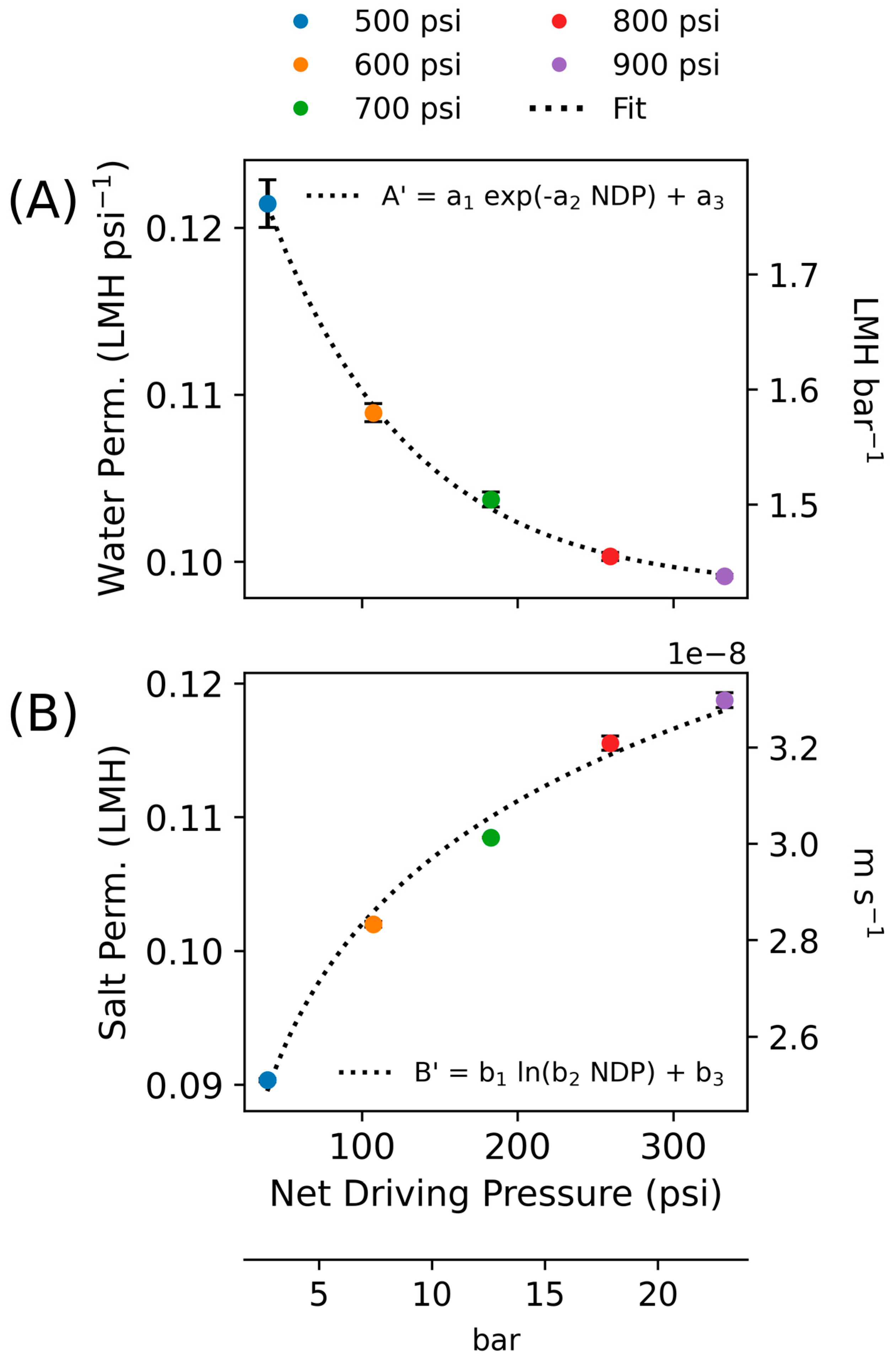
- An apparent water permeability () and salt permeability () parameter is calculated for each of the steady-state experiments. These values are then regressed as a function of the NDP, enabling calculation of apparent transient coefficients under ramping conditions.
- A constant value for each parameter is calculated from the entire steady-state experimental dataset.
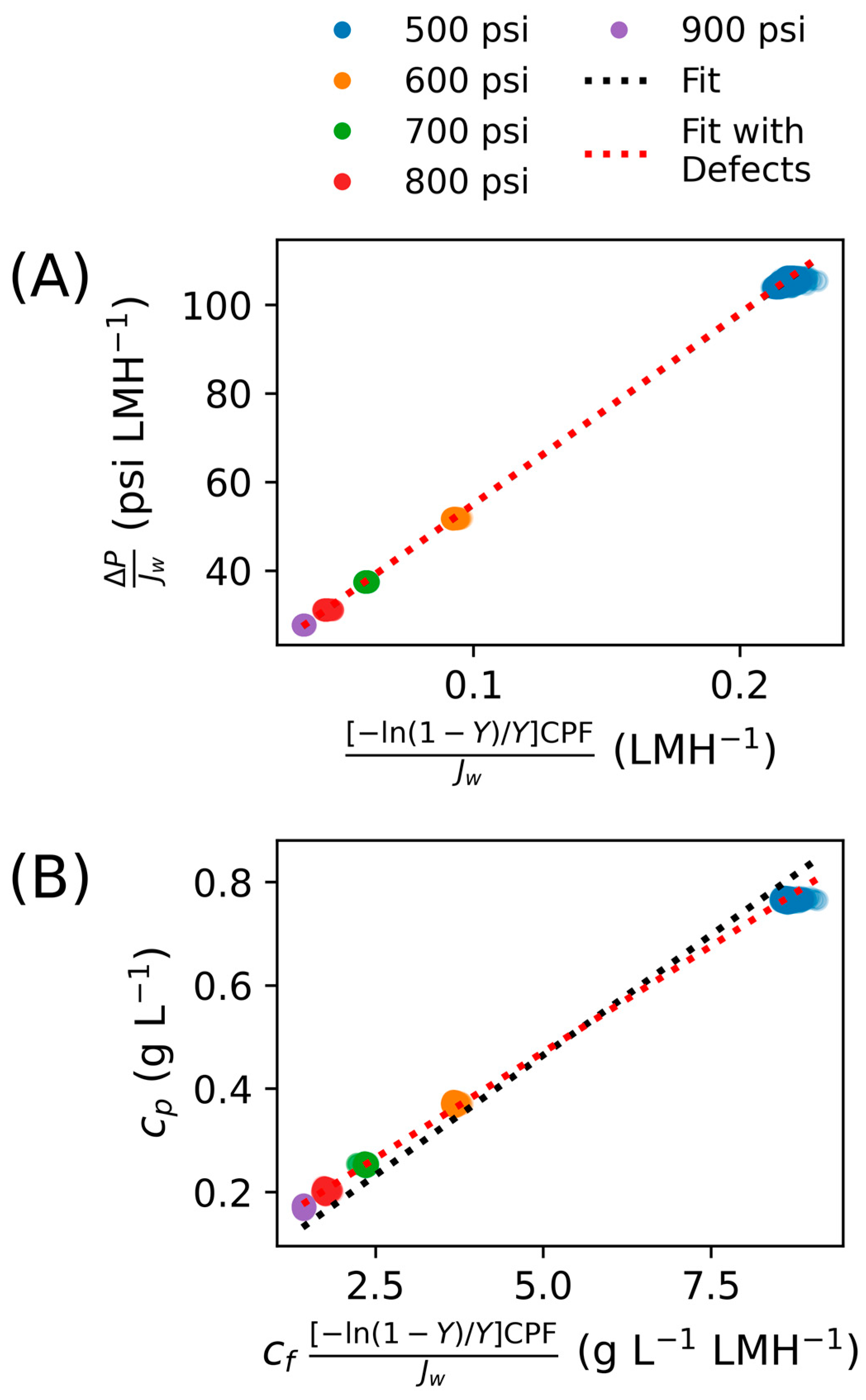
2.3.1. Apparent Parameter Calculation
2.3.2. Constant Parameter Calculation
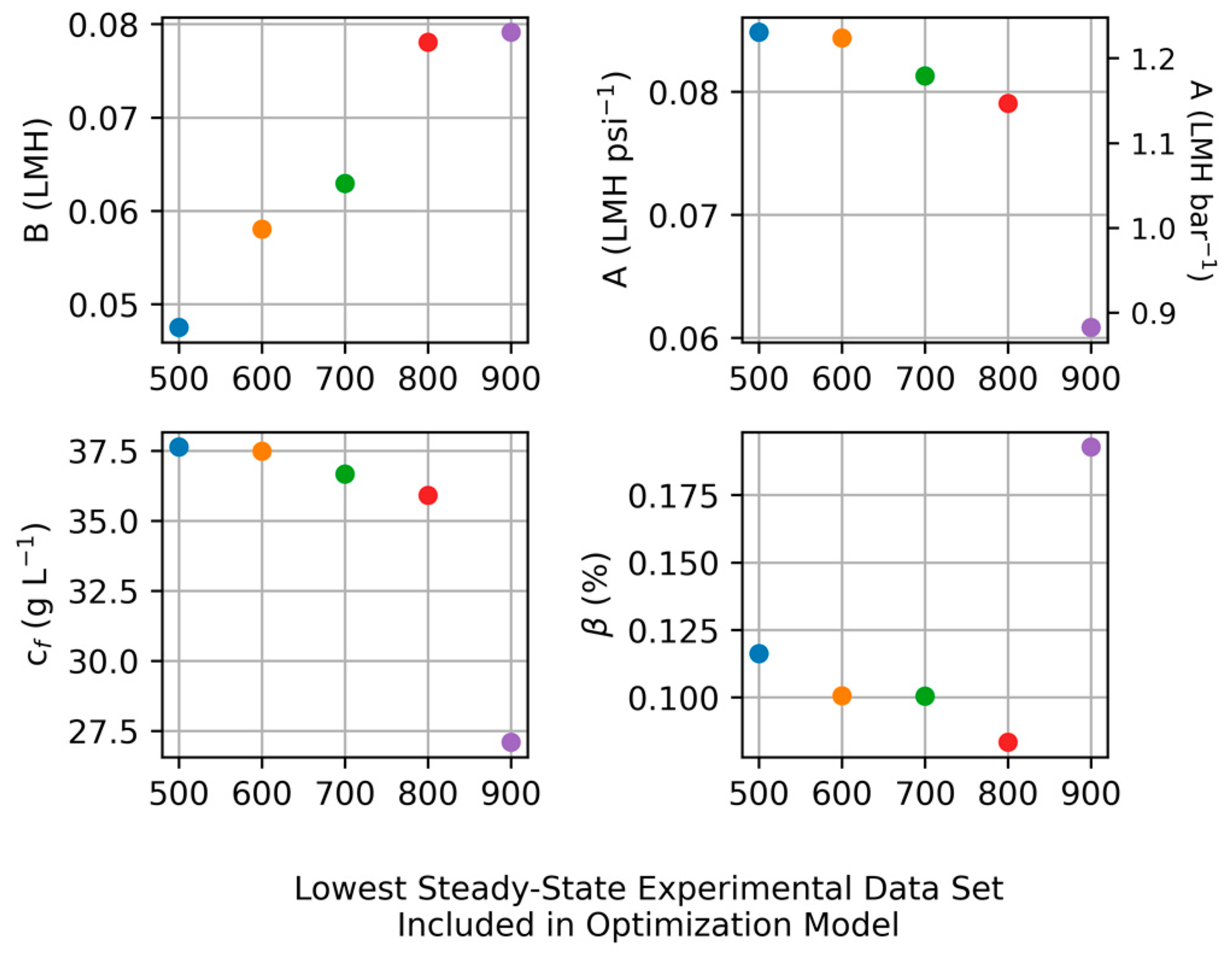
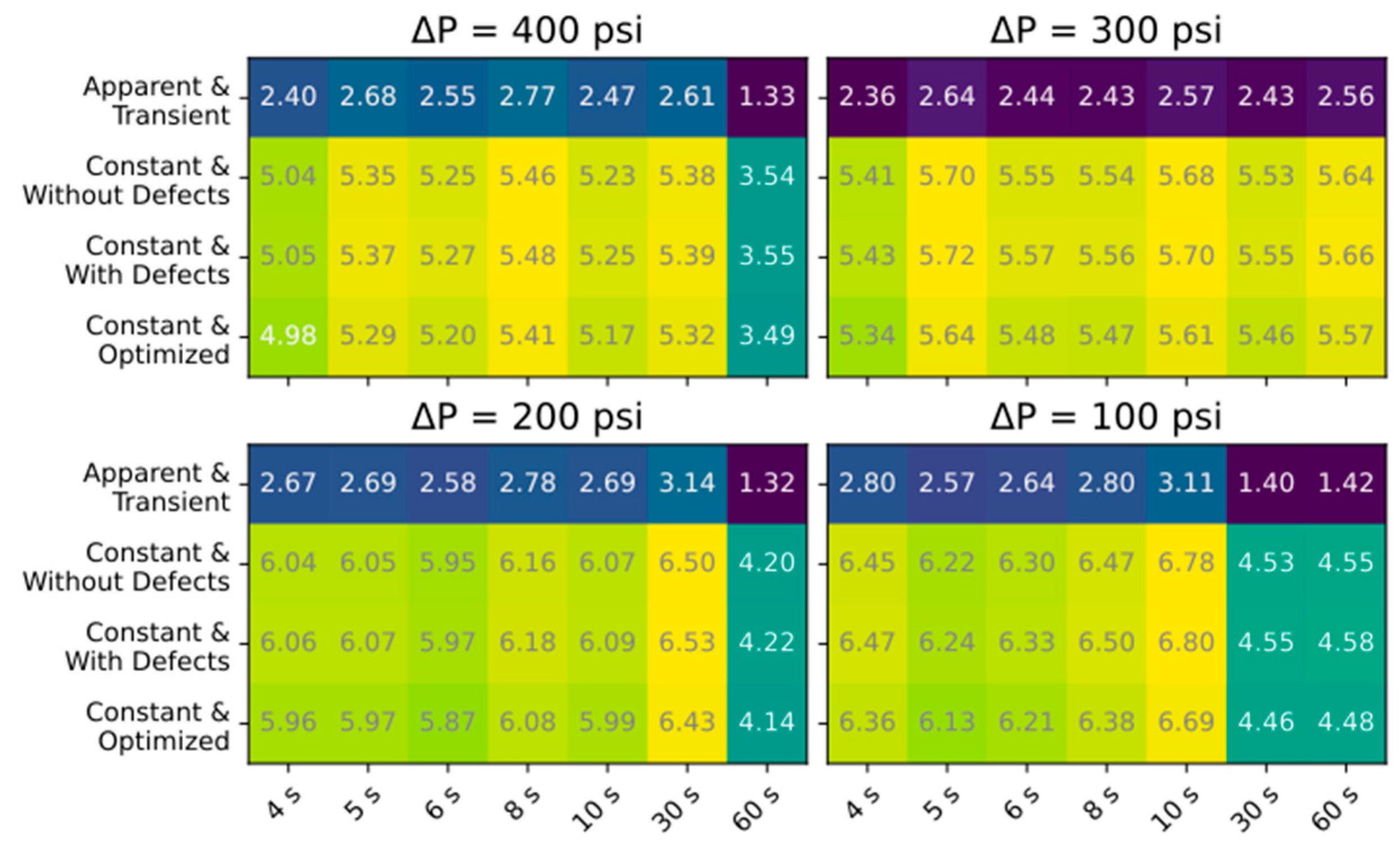
2.4. Parameter Comparison
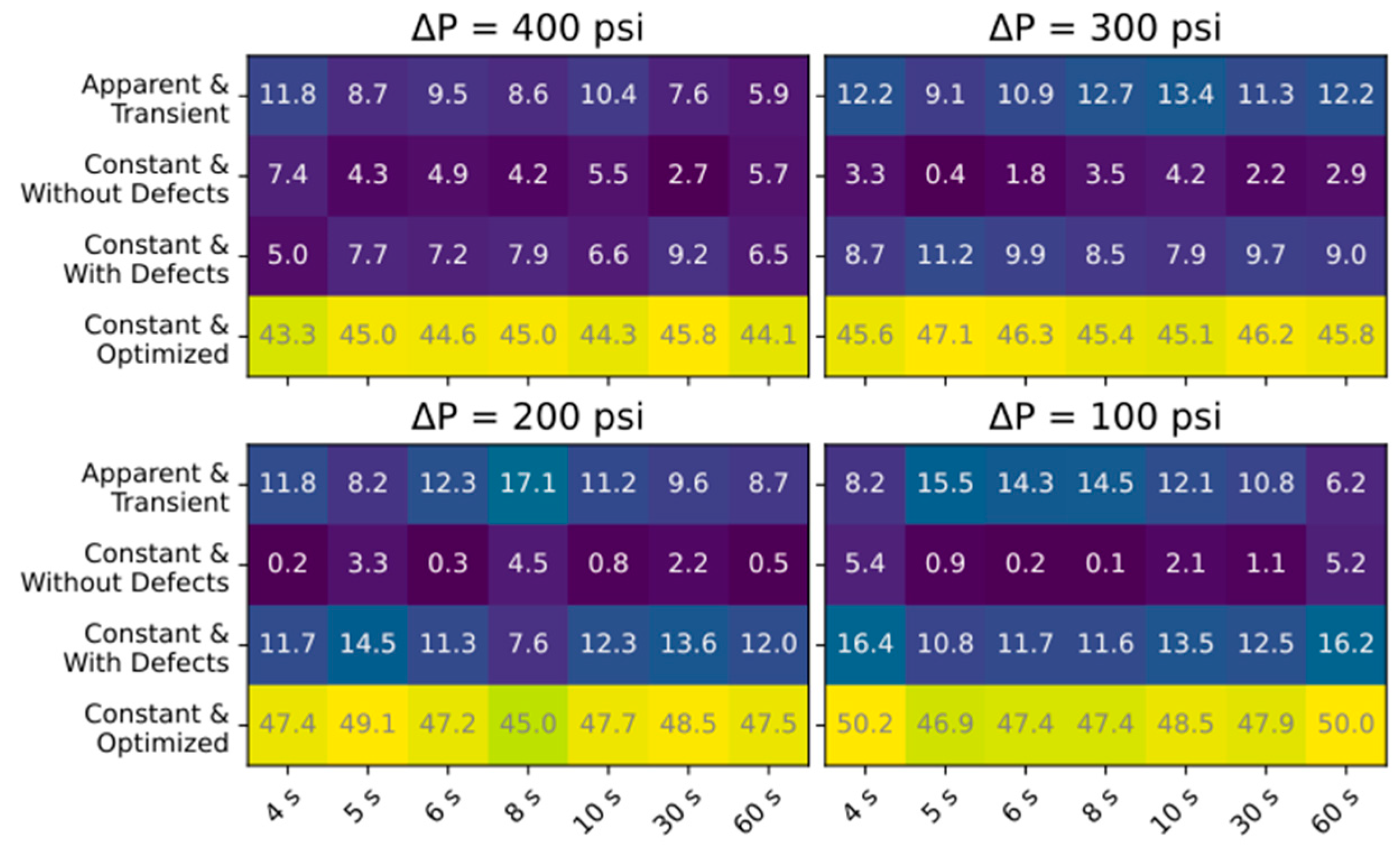
3. Results and Discussion
3.1. Steady-State Experiments
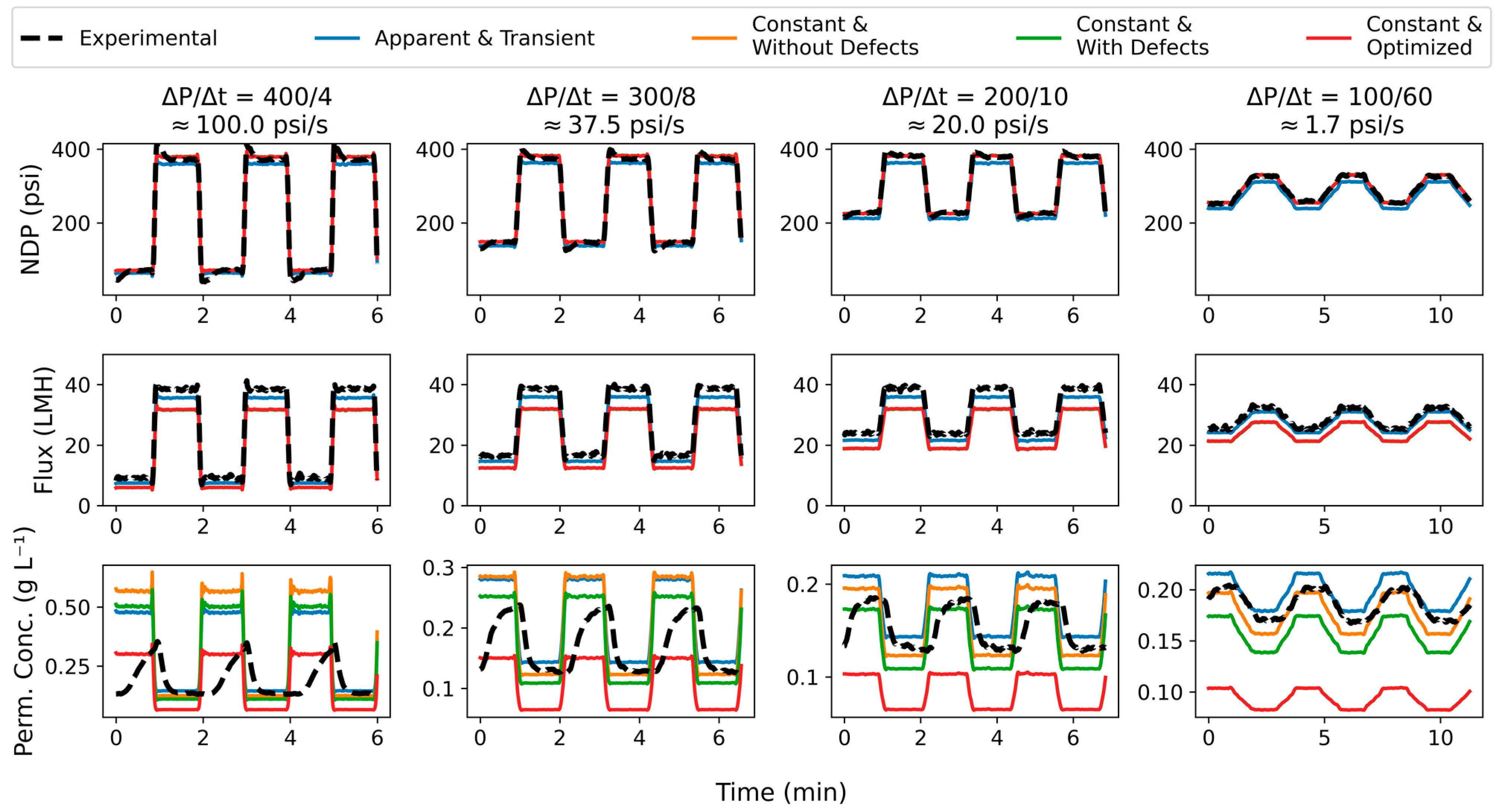
3.2. Ramping Experiments
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Declaration
Abbreviations
| CP | Concentration Polarization |
| CPF | Concentration Polarization Factor |
| LMH | Liters per meter squared per hour |
| MAE | Mean Absolute Error |
| NDP | Net Driving Pressure |
| RO | Reverse Osmosis |
| TMP | Transmembrane Pressure |
| WEC | Wave-Energy Converter |
References
- Ghazi, Z.M.; Rizvi, S.W.F.; Shahid, W.M.; Abdulhameed, A.M.; Saleem, H.; Zaidi, S.J. An overview of water desalination systems integrated with renewable energy sources. Desalination 2022, 542, 116063. [Google Scholar] [CrossRef]
- Alawad, S.M.; Mansour, R.B.; Al-Sulaiman, F.A.; Rehman, S. Renewable energy systems for water desalination applications: A comprehensive review. Energy Convers. Manag. 2023, 286, 117035. [Google Scholar] [CrossRef]
- LiVecchi, A.; Copping, A.; Jenne, D.; Gorton, A.; Preus, R.; Gill, G.; Robichaud, R.; Green, R.; Geerlofs, S.; Gore, S.; et al. Powering the Blue Economy: Exploring Opportunities for Marine Renewable Energy in Maritime Markets; US Department of Energy, Office of Energy Efficiency and Renwable Energy: Washington, DC, USA, 2019. [Google Scholar]
- Reikard, G.; Robertson, B.; Bidlot, J.-R. Combining wave energy with wind and solar: Short-term forecasting. Renew. Energy 2015, 81, 442–456. [Google Scholar] [CrossRef]
- Davies, P.A. Wave-powered desalination: Resource assessment and review of technology. Desalination 2005, 186, 97–109. [Google Scholar] [CrossRef]
- Al-Obaidi, M.A.; Mujtaba, I.M. Steady state and dynamic modeling of spiral wound wastewater reverse osmosis process. Comput. Chem. Eng. 2016, 90, 278–299. [Google Scholar] [CrossRef]
- Zubair, M.M.; Saleem, H.; Zaidi, S.J. Recent progress in reverse osmosis modeling: An overview. Desalination 2023, 564, 116705. [Google Scholar] [CrossRef]
- Cheddie, D.; Maharajh, A.; Ramkhalawan, A.; Persad, P. Transient modeling of wave powered reverse osmosis. Desalination 2010, 260, 153–160. [Google Scholar] [CrossRef]
- Alexiadis, A.; Bao, J.; Fletcher, D.F.; Wiley, D.E.; Clements, D.J. Dynamic response of a high-pressure reverse osmosis membrane simulation to time dependent disturbances. Desalination 2006, 191, 397–403. [Google Scholar] [CrossRef]
- Sitterley, K.A.; Cath, T.J.; Jenne, D.S.; Yu, Y.-H.; Cath, T.Y. Performance of reverse osmosis membrane with large feed pressure fluctuations from a wave-driven desalination system. Desalination 2022, 527, 115546. [Google Scholar] [CrossRef]
- Das, T.K.; Frost, C.; Folley, M.; Brewster, P. Application of an energy recovery device with RO membrane for wave powered desalination. Desalination 2024, 592, 118064. [Google Scholar] [CrossRef]
- Al-Bastaki, N.M.; Abbas, A. Periodic Operation of a Reverse Osmosis Water Desalination Unit. Sep. Sci. Technol. 1998, 33, 2531–2540. [Google Scholar] [CrossRef]
- Al-Bastaki, N.M.; Abbas, A. Improving the permeate flux by unsteady operation of a RO desalination unit. Desalination 1999, 123, 173–176. [Google Scholar] [CrossRef]
- Li, M. Reverse osmosis desalination under periodically oscillating conditions: Insight from spatiotemporal simulations. Desalination 2025, 612, 118942. [Google Scholar] [CrossRef]
- Yu, Y.-H.; Jenne, D. Numerical Modeling and Dynamic Analysis of a Wave-Powered Reverse-Osmosis System. J. Mar. Sci. Eng. 2018, 6, 132. [Google Scholar] [CrossRef]
- Mi, J.; Wu, X.; Capper, J.; Li, X.; Shalaby, A.; Chung, U.; Datla, R.; Hajj, M.; Zuo, L. Ocean Wave Powered Reverse Osmosis Desalination: Design, Modeling and Test Validation. IFAC-PapersOnLine 2022, 55, 782–787. [Google Scholar] [CrossRef]
- Cath, T.Y.; Elimelech, M.; McCutcheon, J.R.; McGinnis, R.L.; Achilli, A.; Anastasio, D.; Brady, A.R.; Childress, A.E.; Farr, I.V.; Hancock, N.T.; et al. Standard Methodology for Evaluating Membrane Performance in Osmotically Driven Membrane Processes. Desalination 2013, 312, 31–38. [Google Scholar] [CrossRef]
- Werber, J.R.; Deshmukh, A.; Elimelech, M. The Critical Need for Increased Selectivity, Not Increased Water Permeability, for Desalination Membranes. Environ. Sci. Technol. Lett. 2016, 3, 112–120. [Google Scholar] [CrossRef]
- Davenport, D.M.; Wang, L.; Shalusky, E.; Elimelech, M. Design principles and challenges of bench-scale high-pressure reverse osmosis up to 150 bar. Desalination 2021, 517, 115237. [Google Scholar] [CrossRef]
- Heiranian, M.; Fan, H.; Wang, L.; Lu, X.; Elimelech, M. Mechanisms and models for water transport in reverse osmosis membranes: History, critical assessment, and recent developments. Chem. Soc. Rev. 2023, 52, 8455–8480. [Google Scholar] [CrossRef]
- Wang, L.; Cao, T.; Dykstra, J.E.; Porada, S.; Biesheuvel, P.M.; Elimelech, M. Salt and Water Transport in Reverse Osmosis Membranes: Beyond the Solution-Diffusion Model. Environ. Sci. Technol. 2021, 55, 16665–16675. [Google Scholar] [CrossRef]
- Das, T.K.; Folley, M.; Lamont-Kane, P.; Frost, C. Performance of a SWRO membrane under variable flow conditions arising from wave powered desalination. Desalination 2024, 571, 117069. [Google Scholar] [CrossRef]
- Koutsou, C.P.; Yiantsios, S.G.; Karabelas, A.J. A numerical and experimental study of mass transfer in spacer-filled channels: Effects of spacer geometrical characteristics and Schmidt number. J. Membr. Sci. 2009, 326, 234–251. [Google Scholar] [CrossRef]
- Mi, J.; Wu, X.; Capper, J.; Li, X.; Shalaby, A.; Wang, R.; Lin, S.; Hajj, M.; Zuo, L. Experimental investigation of a reverse osmosis desalination system directly powered by wave energy. Appl. Energy 2023, 343, 121194. [Google Scholar] [CrossRef]
- Brodersen, K.M.; Bywater, E.A.; Lanter, A.M.; Schennum, H.H.; Furia, K.N.; Sheth, M.K.; Kiefer, N.S.; Cafferty, B.K.; Rao, A.K.; Garcia, J.M.; et al. Direct-drive ocean wave-powered batch reverse osmosis. Desalination 2022, 523, 115393. [Google Scholar] [CrossRef]
- Suchithra, R.; Das, T.K.; Rajagopalan, K.; Chaudhuri, A.; Ulm, N.; Prabu, M.; Samad, A.; Cross, P. Numerical modelling and design of a small-scale wave-powered desalination system. Ocean Eng. 2022, 256, 111419. [Google Scholar] [CrossRef]
- DuPont. FilmTec™ Reverse Osmosis Membranes Technical Manual; DuPont: Wilmington, DE, USA, 2024; Version 17. [Google Scholar]
- Mi, J.; Wu, X.; Capper, J.; Li, X.; Shalaby, A.; Chung, U.; Datla, R.; Hajj, M.; Zuo, L. Modelling, Characterization and Testing of an Ocean Wave Powered Desalination System. In Proceedings of the ASME 2022 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, St. Louis, MO, USA, 14–17 August 2022. [Google Scholar]
- Armstrong, M.D.; Vickers, R.; Coronell, O. Trends and errors in reverse osmosis membrane performance calculations stemming from test pressure and simplifying assumptions about concentration polarization and solute rejection. J. Memb. Sci. 2022, 660, 120856. [Google Scholar] [CrossRef]
- Yu, Y.-H.; Jenne, D.S. Analysis of a Wave-Powered, Reverse-Osmosis System and Its Economic Availability in the United States. In Proceedings of the American Society of Mechanical Engineers’ International Conference on Ocean, Offshore and Arctic Engineering, Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 2002, 36, 1627–1639. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Loeb, S. Effect of porous support fabric on osmosis through a Loeb-Sourirajan type asymmetric membrane. J. Membr. Sci. 1997, 129, 243–249. [Google Scholar] [CrossRef]
- Wu, J.; He, J.; Quezada-Renteria, J.A.; Xiao, M.; Le, J.; Au, K.; Guo, K.; Ye, N.; Toma, T.; Elimelech, M.; et al. Role of Transmembrane Pressure and Water Flux in Reverse Osmosis Composite Membrane Compaction and Performance. Environ. Sci. Technol. 2025, 59, 8856–8866. [Google Scholar] [CrossRef]
- FilmTec SW30-4040 Membrane Product Information Sheet. Available online: http://lenntech.com/Data-sheets/Dow-Filmtec-SW30-4040.pdf (accessed on 5 August 2025).
- Ruiz-García, A.; Nuez, I.; Khayet, M. Performance assessment and modeling of an SWRO pilot plant with an energy recovery device under variable operating conditions. Desalination 2023, 555, 116523. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Peiper, J.C.; Busey, R.H. Thermodynamic Properties of Aqueous Sodium Chloride Solutions. J. Phys. Chem. Ref. Data 1984, 13, 1–102. [Google Scholar] [CrossRef]
- Sparrow, B.S. Empirical equations for the thermodynamic properties of aqueous sodium chloride. Desalination 2003, 159, 161–170. [Google Scholar] [CrossRef]
- Dimitriou, E.; Boutikos, P.; Mohamed, E.S.; Koziel, S.; Papadakis, G. Theoretical performance prediction of a reverse osmosis desalination membrane element under variable operating conditions. Desalination 2017, 419, 70–78. [Google Scholar] [CrossRef]
- Schock, G.; Miquel, A. Mass transfer and pressure loss in spiral wound modules. Desalination 1987, 64, 339–352. [Google Scholar] [CrossRef]
- Taniguchi, M.; Kimura, S. Estimation of transport parameters of RO membranes for seawater desalination. AIChE J. 2000, 46, 1967–1973. [Google Scholar] [CrossRef]
- Baker, R.W. Membrane Technology and Applications; John Wiley & Sons: West Sussex, UK, 2012. [Google Scholar]
- Li, M.; Li, J. Incorporating convection into the solution-diffusion framework enhances modeling accuracy in reverse osmosis. Chem. Eng. Res. Des. 2025, 214, 441–445. [Google Scholar] [CrossRef]
- Li, M. Predictive modeling of a commercial spiral wound seawater reverse osmosis module. Chem. Eng. Res. Des. 2019, 148, 440–450. [Google Scholar] [CrossRef]
- Lim, Y.J.; Nadzri, N.; Lai, G.S.; Wang, R. Demystifying the compaction effects of TFC polyamide membranes in the desalination of hypersaline brine via high-pressure RO. J. Membr. Sci. 2024, 707, 122950. [Google Scholar] [CrossRef]
- Wu, J.; He, J.; Quezada-Renteria, J.A.; Le, J.; Au, K.; Guo, K.; Xiao, M.; Wang, X.; Dlamini, D.; Fan, H.; et al. Polyamide reverse osmosis membrane compaction and relaxation: Mechanisms and implications for desalination performance. J. Membr. Sci. 2024, 706, 122893. [Google Scholar] [CrossRef]
- Eriksson, P. Water and salt transport through two types of polyamide composite membranes. J. Membr. Sci. 1988, 36, 297–313. [Google Scholar] [CrossRef]
- Duan, J.; Litwiller, E.; Pinnau, I. Solution-diffusion with defects model for pressure-assisted forward osmosis. J. Membr. Sci. 2014, 470, 323–333. [Google Scholar] [CrossRef]
- Blankert, B.; Huisman, K.T.; Martinez, F.D.; Vrouwenvelder, J.S.; Picioreanu, C. Are commercial polyamide seawater and brackish water membranes effectively charged? J. Membr. Sci. Lett. 2022, 2, 100032. [Google Scholar] [CrossRef]
- Binger, Z.M.; O’Toole, G.; Achilli, A. Evidence of solution-diffusion-with-defects in an engineering-scale pressure retarded osmosis system. J. Membr. Sci. 2021, 625, 119135. [Google Scholar] [CrossRef]
- Rusydi, A.F. Correlation between conductivity and total dissolved solid in various type of water: A review. IOP Conf. Ser. Earth Environ. Sci. 2018, 118, 012019. [Google Scholar] [CrossRef]
- Biesheuvel, P.M.; Dykstra, J.E.; Porada, S.; Elimelech, M. New parametrization method for salt permeability of reverse osmosis desalination membranes. J. Membr. Sci. Lett. 2022, 2, 100010. [Google Scholar] [CrossRef]
- Liang, Y.; Dudchenko, A.V.; Mauter, M.S. Novel method for accurately estimating membrane transport properties and mass transfer coefficients in reverse osmosis. J. Membr. Sci. 2023, 679, 121686. [Google Scholar] [CrossRef]
- Gu, B.; Adjiman, C.S.; Xu, X.Y. Correlations for Concentration Polarization and Pressure Drop in Spacer-Filled RO Membrane Modules Based on CFD Simulations. Membranes 2021, 11, 338. [Google Scholar] [CrossRef]
- Ruiz-García, A.; Nuez, I. Simulation-based assessment of safe operating windows and optimization in full-scale seawater reverse osmosis systems. Desalination 2022, 533, 115768. [Google Scholar] [CrossRef]
- Xu, B.; Gao, W.; Liao, B.; Bai, H.; Qiao, Y.; Turek, W. A Review of Temperature Effects on Membrane Filtration. Membranes 2023, 14, 5. [Google Scholar] [CrossRef] [PubMed]
- Altmann, T.; Buijs, P.J.; Farinha, A.S.F.; Borges, V.R.P.; Farhat, N.M.; Vrouwenvelder, J.S.; Das, R. Seawater Reverse Osmosis Performance Decline Caused by Short-Term Elevated Feed Water Temperature. Membranes 2022, 12, 792. [Google Scholar] [CrossRef] [PubMed]
- Tow, E.W.; Wei, Q.J.; Abraham, A.R.; Chua, K.L.; Plumley, M.J.; Lienhard, J.H. Piloting batch reverse osmosis with a flexible bladder for water recovery from scaling-prone brine. npj Clean Water 2025, 8, 30. [Google Scholar] [CrossRef]
- Amusat, O.O.; Atia, A.A.; Dudchenko, A.V.; Bartholomew, T.V. Modeling Framework for Cost Optimization of Process-Scale Desalination Systems with Mineral Scaling and Precipitation. ACS ES T Eng. 2024, 4, 1028–1047. [Google Scholar] [CrossRef] [PubMed]
- Toray. Toray RO Handling Manual; Toray: Tokyo, Japan, 2024. [Google Scholar]
- Hydranautics. Membrane Start-Up, Shutdown, and Preservative Flushing Guidelines; Hydranautics: Oceanside, CA, USA, 2019. [Google Scholar]
- Sitterley, K.A.; Binger, Z.B.; Jenne, D. Experimental Wave Desalination Data with Variable Feed and Pressure Input. [Data Set]. Marine and Hydrokinetic Data Repository. National Renewable Energy Laboratory. Available online: https://mhkdr.openei.org/submissions/649 (accessed on 30 July 2025).
| Property | Value | Units | Reference |
|---|---|---|---|
| Membrane Active Area | 7.4 | m2 | [35] |
| Spacer Thickness 1 | 28 | mil | [35] |
| Spacer Porosity | 0.89 | - | [36] |
| 1.07 × 10−6 | m2 s−1 | [37,38] | |
| 1.32 × 10−9 | m2 s−1 | [37,38] | |
| 1025 | kg m−3 | [37,38] | |
| 998 | kg m−3 | [37,38] |
| Pressure psi | Net Driving Pressure psi | Water Permeability LMH psi−1 (LMH bar−1) | Salt Permeability LMH | Feed Flow Rate L min−1 | Flux LMH | Water Recovery % | Salt Rejection % | Effective Permeate Conc. mg L−1 |
|---|---|---|---|---|---|---|---|---|
| 500 | 39.2 ± 0.3 | 0.121 (1.75) | 0.090 | 16.2 ± 0.1 | 4.7 ± 0.5 | 3.0 ± 0.4 | 98.1 | 770 |
| 600 | 107.3 ± 0.1 | 0.109 (1.58) | 0.102 | 18.4 ± 0.1 | 11.7 ± 0.5 | 6.6 ± 0.3 | 99.1 | 375 |
| 700 | 182.7 ± 0.1 | 0.104 (1.51) | 0.108 | 20.4 ± 0.1 | 18.9 ± 0.5 | 9.6 ± 0.2 | 99.4 | 260 |
| 800 | 259.3 ± 0.1 | 0.100 (1.45) | 0.116 | 22.3 ± 0.1 | 25.9 ± 0.5 | 12.0 ± 0.5 | 99.5 | 210 |
| 900 | 332.7 ± 0.1 | 0.099 (1.44) | 0.119 | 24.1 ± 0.1 | 32.9 ± 0.5 | 14.2 ± 0.3 | 99.6 | 180 |
| Fit Parameter | Value |
|---|---|
| 0.03528 | |
| 0.01085 | |
| 0.09831 | |
| 0.01331 | |
| 0.15060 | |
| 0.06588 |
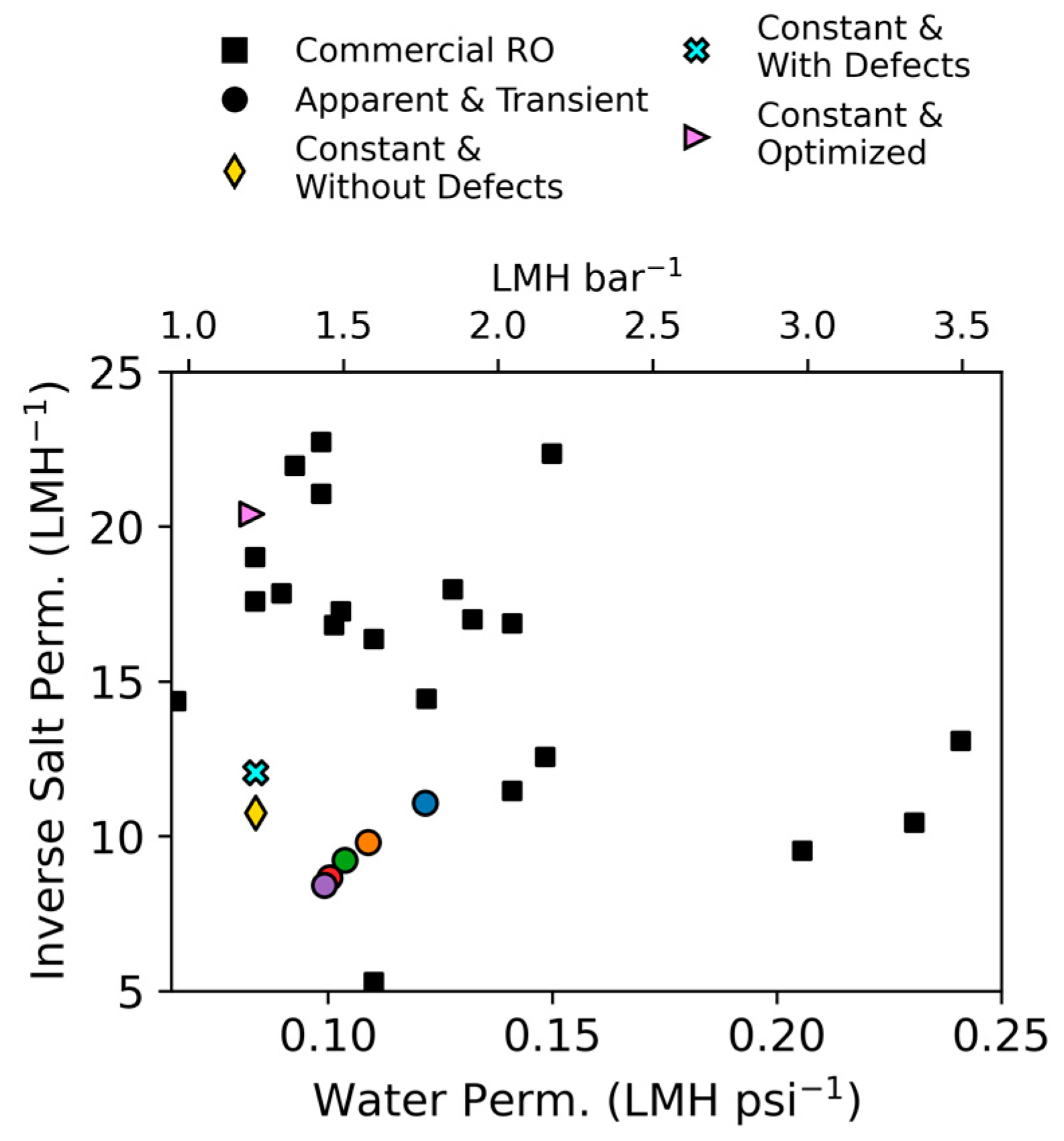
| Processing Approach | Water Permeability | Salt Permeability |
|---|---|---|
| Apparent and Transient | ||
| Constant and Without Defects | 0.083 LMH psi−1 (1.20 LMH bar−1) | 0.093 LMH |
| Constant and With Defects | 0.083 LMH psi−1 (1.20 LMH bar−1) | 0.082 LMH |
| Constant and Optimized | 0.084 LMH psi−1 (1.22 LMH bar−1) | 0.049 LMH |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sitterley, K.A.; Binger, Z.; Jenne, D.S. Comparing Constant and Transient Membrane Transport Parameters for Use in Wave Desalination Models. Membranes 2025, 15, 243. https://doi.org/10.3390/membranes15080243
Sitterley KA, Binger Z, Jenne DS. Comparing Constant and Transient Membrane Transport Parameters for Use in Wave Desalination Models. Membranes. 2025; 15(8):243. https://doi.org/10.3390/membranes15080243
Chicago/Turabian StyleSitterley, Kurban A., Zachary Binger, and Dale Scott Jenne. 2025. "Comparing Constant and Transient Membrane Transport Parameters for Use in Wave Desalination Models" Membranes 15, no. 8: 243. https://doi.org/10.3390/membranes15080243
APA StyleSitterley, K. A., Binger, Z., & Jenne, D. S. (2025). Comparing Constant and Transient Membrane Transport Parameters for Use in Wave Desalination Models. Membranes, 15(8), 243. https://doi.org/10.3390/membranes15080243







