Assessment and Discussion of the Steady-State Determination in Zeolite Composite Membranes for Multi-Component Diffusion
Abstract
1. Introduction
2. Mathematical Model and Numerical Procedures
2.1. Idea of the Method
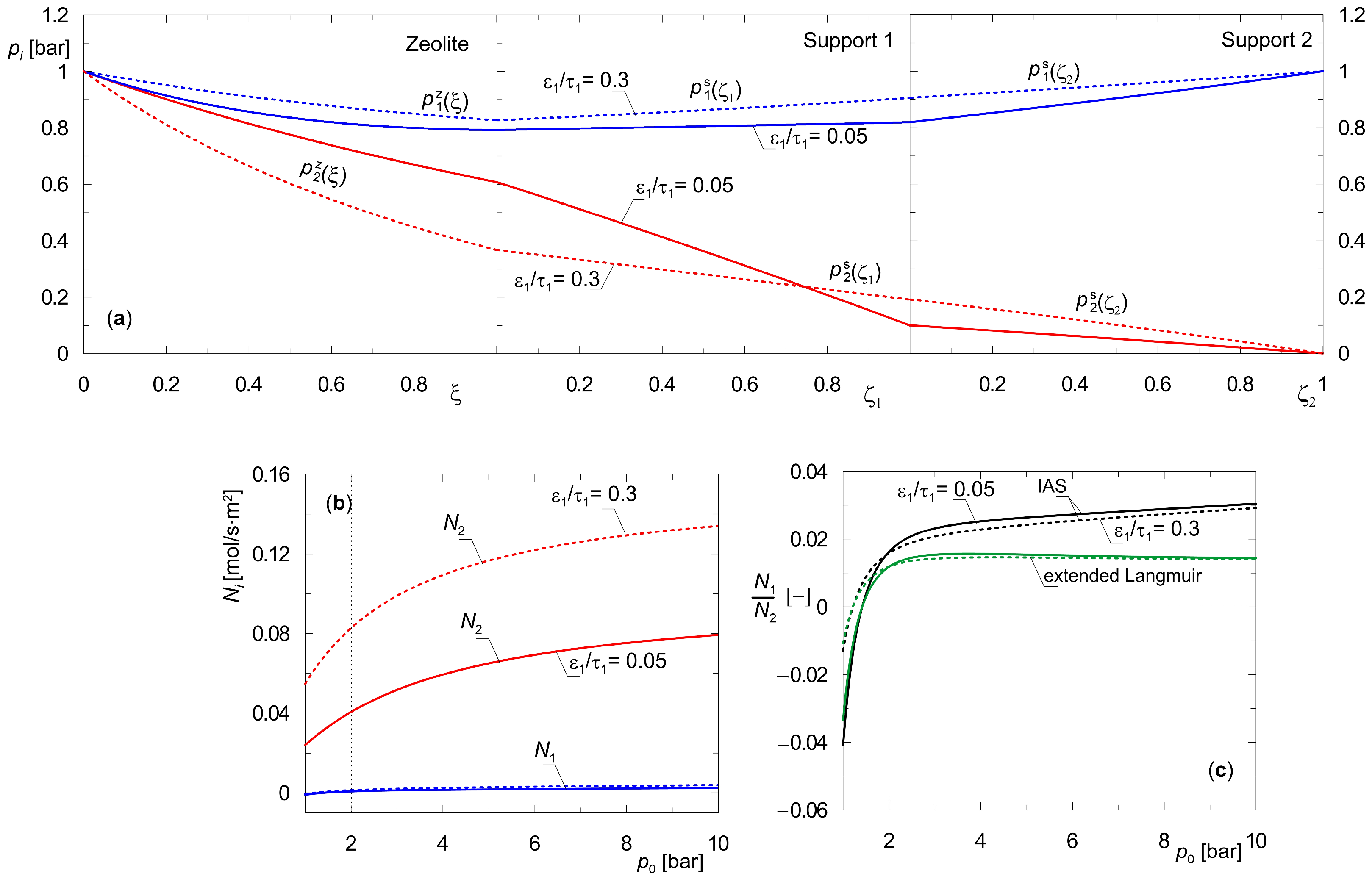
- (a)
- During dynamic simulations of diffusion in zeolite membranes, changes in all state variables should be tracked, and the magnitude that varies in the slowest manner should be selected to evaluate the arrival at the steady state; moreover, such information should be included in the published scientific report;
- (b)
- The use of partial pressures in the mathematical model simplifies such an assessment, as it indicates that partial pressures tend to approach the steady state in the slowest way, and thus also the measured total pressure.
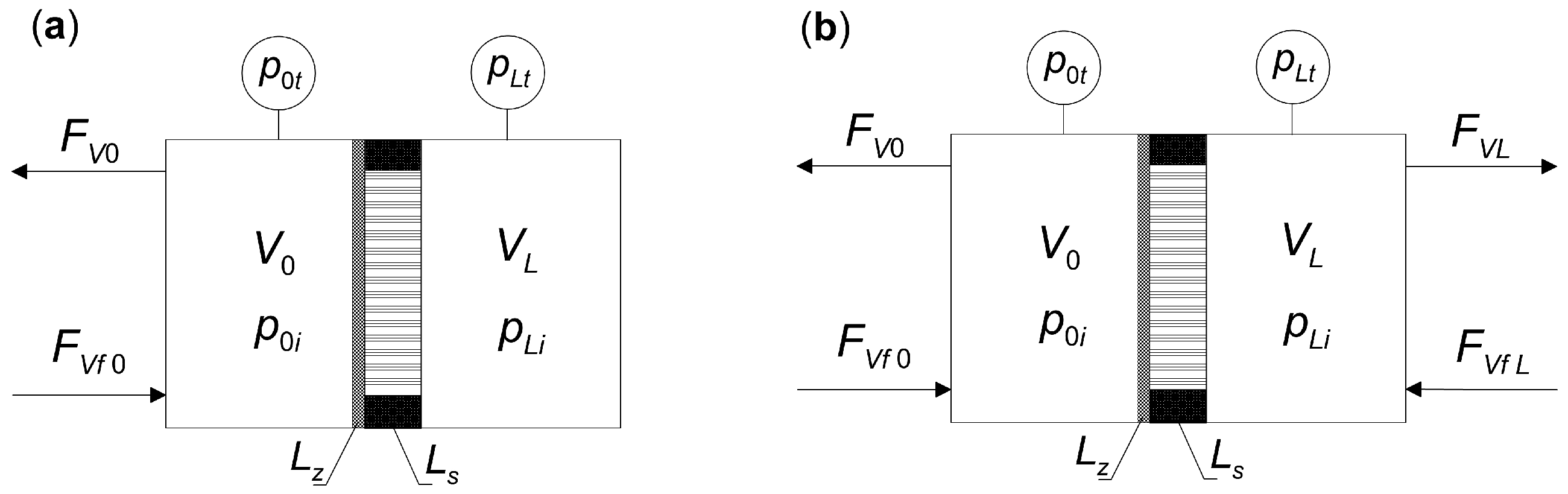
2.2. Determining the Steady States of Multi-Component Diffusion in a Composite Membrane
- (a)
- Support located on the permeate side, as in Figure 1;
- (b)
- Support located on the retentate side.
| Algorithm 1 Algorithm for the determination of steady states of composite membranes, for Equations (7) and (8) and boundary conditions (19) and (20) |
| Step 1: Adopt boundary conditions (19) Step 2: Assume preliminary values of molar flux densities N (Formula (10)) Step 3: Integrate the system of Equation (7) in the interval ξ ∈ [0, 1] Step 4: Assume ps(0) = pz(1) Step 5: Integrate the system of Equation (8) Step 6: Check the satisfaction of the boundary condition (20) Step 7: If the boundary condition (20) is not satisfied with the assumed accuracy, then improve the values of N according to the external Newton algorithm and return to Step 3 |
| Algorithm 2 Algorithm for the determination of steady states of composite membranes, for Equations (7) and (8) and boundary conditions (21) and (22) |
| Step 1: Adopt boundary conditions (21) Step 2: Assume preliminary values of molar flux densities N (Formula (10)) Step 3: Integrate the system of Equation (8) in the interval ζ ∈ [0, 1] Step 4: Assume pz(0) = ps(1) Step 5: Integrate the system of Equation (7) Step 6: Check the satisfaction of the boundary condition (22) Step 7: If the boundary condition (22) is not satisfied with the assumed accuracy, then improve the values of N according to the external Newton algorithm and return to Step 3 |
3. Results and Discussion
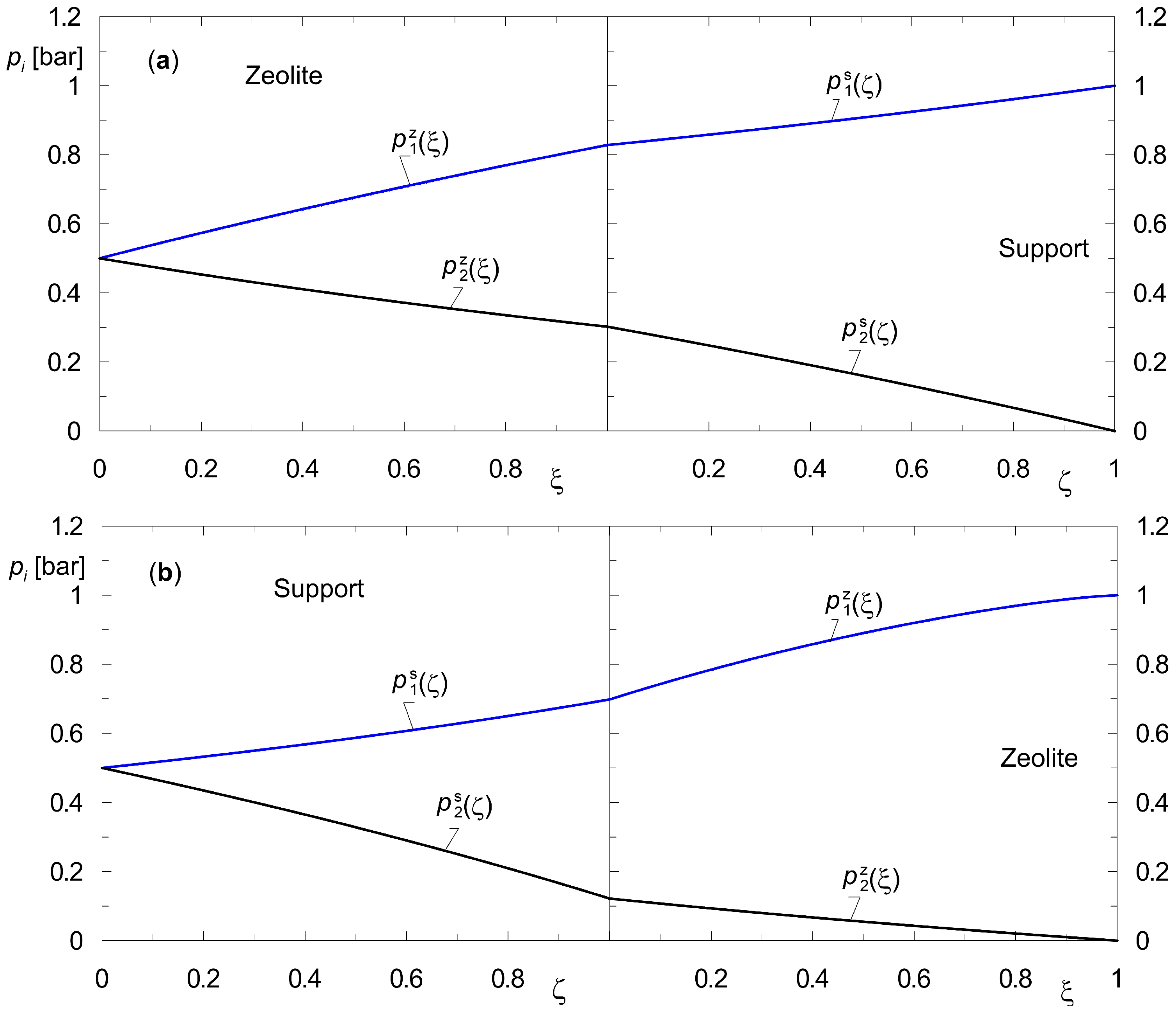
3.1. Steady States of the Two-Layer Composite Membrane (Zeolite–Support)
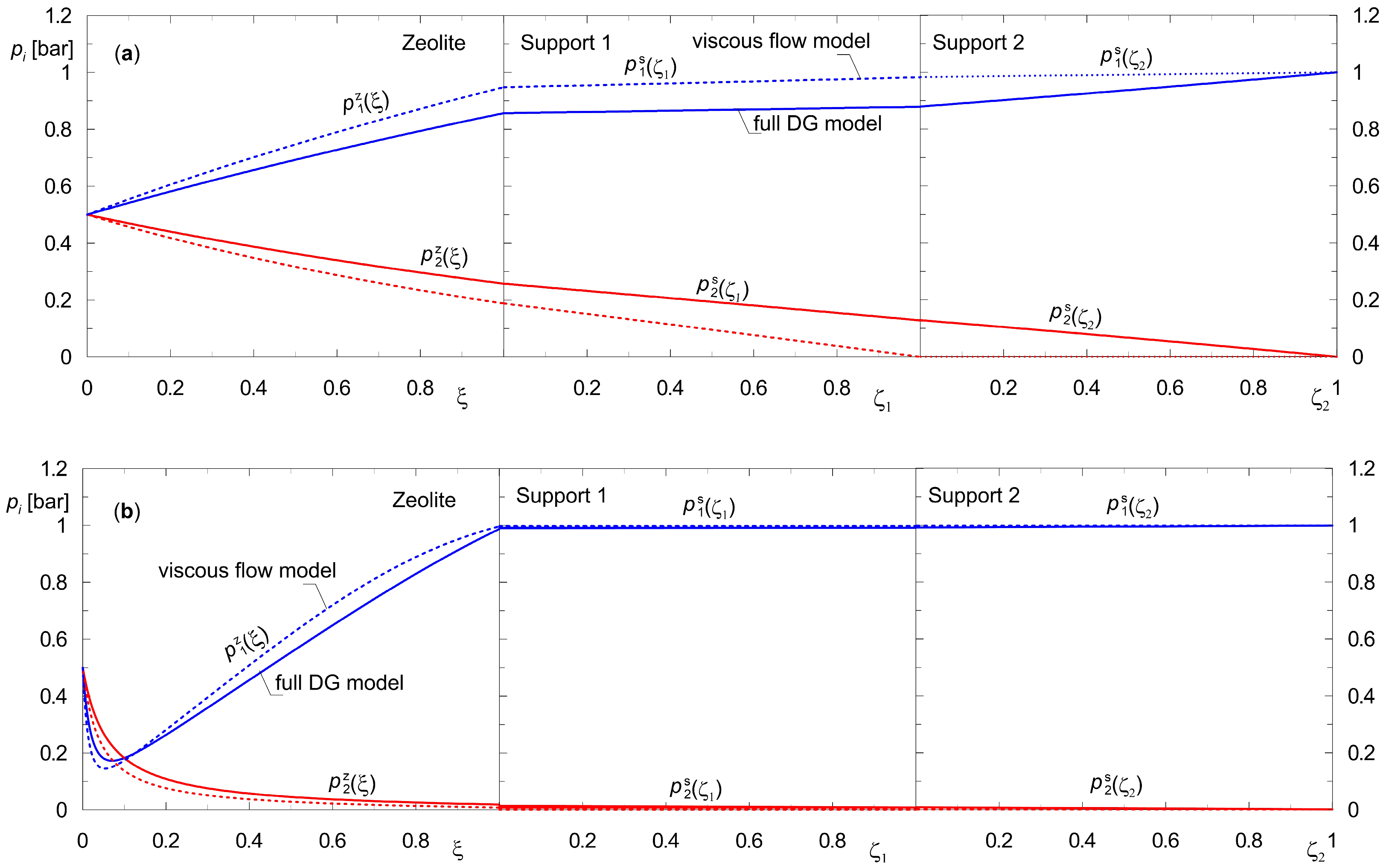
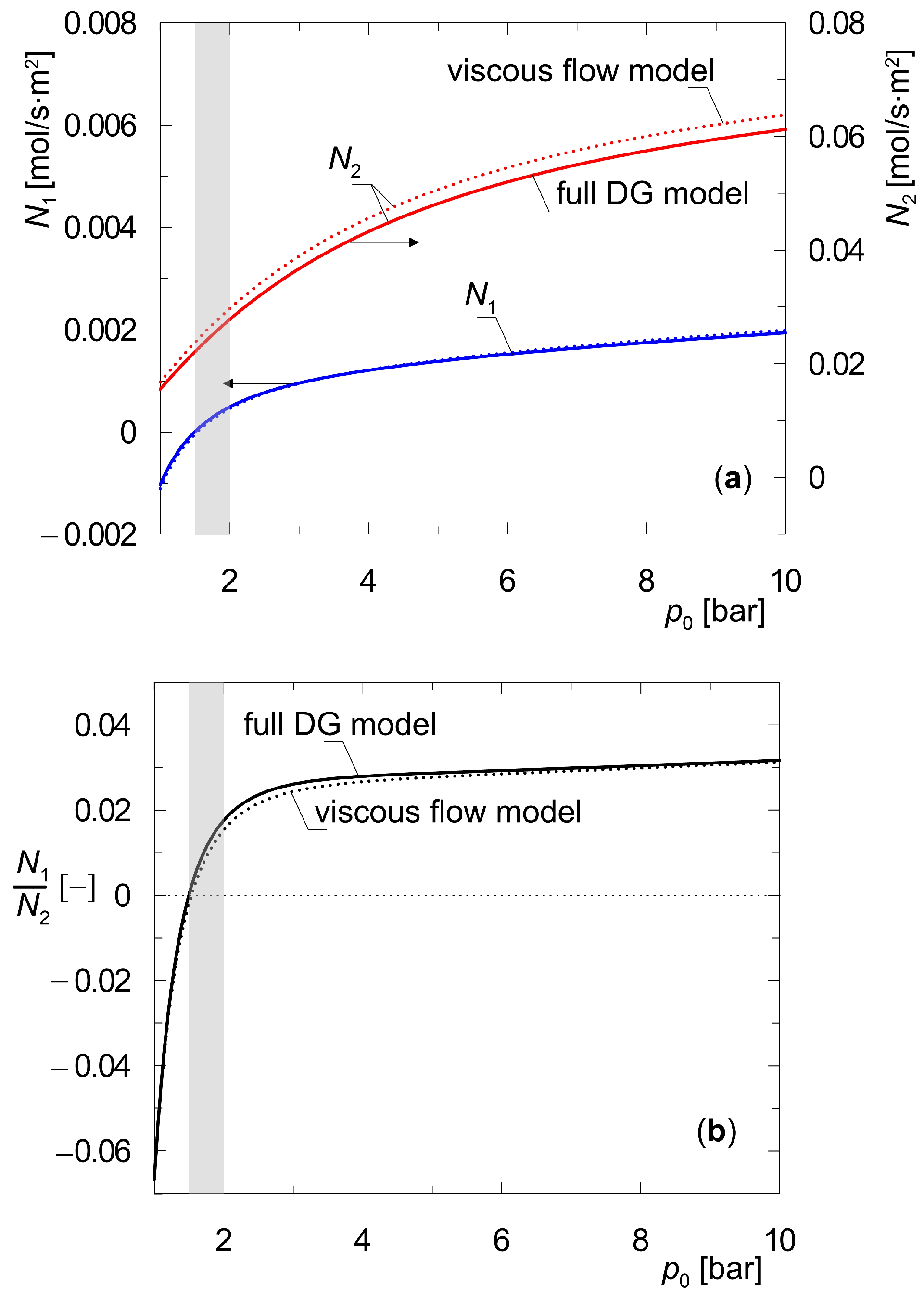
3.2. Steady State of a Three-Layer Composite Membrane (Zeolite–Support 1–Support 2)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature and Abbreviations
| Ai | The i-th component. |
| {A1, A2} | Mixture with composition A1, A2. |
| Be | Effective permeability coefficient, m2. |
| bi | Langmuir parameter, Pa−1, bar−1. |
| dp | Pore diameter in the support, m. |
| Effective binary Maxwell–Stefan diffusion coefficient, m2·s−1. | |
| Maxwell–Stefan diffusion coefficient in zeolite, m2·s−1. | |
| Binary Maxwell–Stefan diffusion coefficients in zeolite, m2·s−1. | |
| Effective Knudsen diffusion coefficient of the i-th component, m2·s−1. | |
| DGM | Dusty gas model. |
| FV | Volumetric flow rate, m3·s−1. |
| IAS | Ideal adsorption solution. |
| J | Jacobi matrix dq/dp. |
| K | Number of species. |
| K0 | Structural parameter of the porous medium, m. |
| Ls, Lz | Thickness of the support and zeolite film, respectively, m. |
| L | Total thickness of the composite membrane, m. |
| Mi | Molar mass of species i, kg·mol−1. |
| MS | Maxwell–Stefan model. |
| Ni | Molar flux density of the i-th component, mol·s−1·m−2. |
| N | Vector of molar flux densities, mol·s−1·m−2. |
| pt | Total pressure, bar, Pa, in figures. |
| Δpt | Transmembrane gradient of total pressure, bar. |
| pi | Partial pressure of i-th component, bar or Pa. |
| p | Vector of partial pressures, bar or Pa. |
| qi | Molar concentration in the adsorbed phase, mol·kg−1. |
| Saturation concentration, mol·kg−1. | |
| q | Vector of concentrations in the adsorbed phase, mol·kg−1. |
| R | Universal gas constant, J·mol−1·K−1. |
| t | Time, s. |
| T | Temperature, K. |
| V | Volume of chamber of the W-K diffusion cell, m3. |
| W-K | Wicke–Kallenbach. |
| x | Spatial coordinate in support, m. |
| yi | Molar fraction of i-th component in gas phase. |
| z | Spatial coordinate in zeolite, m. |
| Greek letters | |
| Γij | Thermodynamic factors. |
| Γ | Matrix of thermodynamic factors. |
| εs, εz | Support and zeolite porosity, respectively. |
| θi | Fractional occupancy of i-th component. |
| θt | Total surface coverage. |
| θ | Vector of fractional surface occupancies. |
| μi | Chemical potential, J·mol−1. |
| ξ | Dimensionless spatial coordinate in zeolite film. |
| ζ | Dimensionless spatial coordinate in support. |
| η | Viscosity of the gaseous mixture, Pa·s. |
| ρz | Solid density of zeolite, kg·m−3. |
| τ | Tortuosity factor. |
| Superscripts | |
| O | Refers to the standard state. |
| g | Refers to gas phase. |
| z | Refers to zeolite surface or diffusion in zeolite. |
| s | Refers to diffusion in support. |
| si | i-th support in three-layer composite membrane. |
| Subscripts | |
| 0 | Refers to feed side of composite membrane. |
| f | Feed stream. |
| i,j | i-th/j-th species in mixture. |
| L | Refers to permeate side of composite membrane. |
References
- Michalkiewicz, B.; Koren, Z.C. Zeolite membranes for hydrogen production from natural gas: State of the art. J. Porous Mater. 2015, 22, 635–646. [Google Scholar] [CrossRef]
- Algieri, C.; Drioli, E. Zeolite membranes: Synthesis and applications. Sep. Purif. Technol. 2021, 278, 119295. [Google Scholar] [CrossRef]
- Masuda, T.; Fukumoto, N.; Kitamura, M.; Mukai, S.R.; Hashimoto, K.; Tanaka, T.; Funabiki, T. Modification of pore size of MFI-type zeolite by catalytic cracking of silane and application to preparation of H2-separating zeolite membrane. Microporous Mesoporous Mater. 2001, 48, 239–245. [Google Scholar] [CrossRef]
- Wang, H.; Li, Y.S. Synthesis and modification of ZSM-5/silicalite bilayer membrane with improved hydrogen separation performance. J. Membr. Sci. 2012, 396, 128–137. [Google Scholar] [CrossRef]
- Adnan, A.I.; Ong, M.Y.; Nomanbhay, S.; Chew, K.W.; Show, P.L. Technologies for Biogas Upgrading to Biomethane: A Review. Bioengineering 2019, 6, 92. [Google Scholar] [CrossRef] [PubMed]
- Gkotsis, P.; Kougias, P.; Mitrakas, M.; Zouboulis, A. Biogas upgrading technologies- Recent advances in membrane-based processes. Int. J. Hydrogen Energy 2023, 48, 3965–3993. [Google Scholar] [CrossRef]
- Baker, R.W.; Lokhandwala, K. Natural gas processing with membranes: An overview. Ind. Eng. Chem. Res. 2008, 47, 2109–2121. [Google Scholar] [CrossRef]
- Azizi, B.; Vessally, E.; Ahmadi, S.; Ebadi, A.G.; Azamat, J. Separation of CH4/N2 gas mixture using MFI zeolite nanosheet: Insights from molecular dynamics simulation. Colloids Surf. A 2022, 641, 128527. [Google Scholar] [CrossRef]
- Hou, R.; Fong, C.; Freeman, B.D.; Hill, M.R.; Xie, Z. Current status and advances in membrane technology for carbon capture. Sep. Purif. Technol. 2022, 300, 121863. [Google Scholar] [CrossRef]
- Mfoumou, C.M.; Tonda-Mikiela, P.; Ngoye, F.; Belin, T.; Mignard, S. Dynamic adsorption and desorption of CO2 from binary mixtures of CH4 and C3H8 on X type zeolites. Am. J. Environ. Prot. 2022, 10, 83–90. [Google Scholar] [CrossRef]
- Gallucci, F.; Fernandez, E.; Corengia, P.; van Sint Annaland, M. Recent advances on membranes and membrane reactors for hydrogen production. Chem. Eng. Sci. 2013, 92, 40–66. [Google Scholar] [CrossRef]
- Bitter, J.H.; Tashvigh, A.A. Recent advances in polybenzimidazole membranes for hydrogen purification. Ind. Eng. Chem. Res. 2022, 61, 6125–6134. [Google Scholar] [CrossRef]
- Gkotsis, P.; Peleka, E.; Zouboulis, A. Membrane-based technologies for post-combustion CO2 capture from flue gases: Recent progress in commonly employed membrane materials. Membranes 2023, 13, 898. [Google Scholar] [CrossRef]
- Han, X.; Xu, W.; Meng, F.; Liu, Z.; Liao, C. Recent advances in zeolite membranes for gas separation and pervaporation in petrochemicals. J. Mater. Chem. A 2025, 13, 10358–10387. [Google Scholar] [CrossRef]
- Fu, L.; Chen, T.; Wu, H.; Zhang, Y.; Zhang, Y. A novel polymer dual-phase membrane for hydrogen separation under atmospheric-pressure. Int. J. Hydrogen Energy 2025, 124, 164–174. [Google Scholar] [CrossRef]
- Wang, D.; Wu, H.; Xu, Y.; Chen, T.; Zhang, Y.; Hu, Z.; Wang, Z.; Tan, X.; Liu, S. Self-catalytic nickel hollow fiber membrane reactor for hydrogen production via toluene steam reforming. J. Membr. Sci. 2023, 686, 121992. [Google Scholar] [CrossRef]
- Ovalle-Encinia, O.; Pfeiffer, H.; Ortiz-Landeros, J. CO2 separation improvement produced on a ceramic–carbonate dense membrane superficially modified with Au–Pd. Ind. Eng. Chem. Res. 2018, 57, 9261–9268. [Google Scholar] [CrossRef]
- Shi, X.; Chen, T.; Fu, L.; Zhang, Y.; Zhang, Y.; Liu, S. Fluorite-perovskite-carbonate composite hollow fiber membrane for CO2 permeation. Chem. Eng. J. 2025, 504, 158809. [Google Scholar] [CrossRef]
- van de Graaf, J.M.; Kapteijn, F.; Moulijn, J.A. Modeling permeation of binary mixtures through zeolite membranes. AIChE J. 1999, 45, 497–511. [Google Scholar] [CrossRef]
- Krishna, R.; van den Broeke, L.J.P. The Maxwell-Stefan description of mass transport across zeolite membranes. Chem. Eng. J. 1995, 57, 155–162. [Google Scholar] [CrossRef]
- Krishna, R.; Paschek, D. Separation of hydrocarbon mixtures using zeolite membranes: A modelling approach combining molecular simulations with the Maxwell–Stefan theory. Sep. Purif. Technol. 2000, 21, 111–136. [Google Scholar] [CrossRef]
- Krishna, R.; Baur, R. Analytic solution of the Maxwell-Stefan equations for multicomponent permeation across a zeolite membrane. Chem. Eng. J. 2004, 97, 37–45. [Google Scholar] [CrossRef]
- Krishna, R.; Baur, R. Modelling issues in zeolite based separation processes. Sep. Purif. Technol. 2003, 33, 213–254. [Google Scholar] [CrossRef]
- Krishna, R.; van Baten, J.M. Maxwell-Stefan modeling of slowing-down effects in mixed gas permeation across porous membranes. J. Membr. Sci. 2011, 383, 289–300. [Google Scholar] [CrossRef]
- Krishna, R. Using the Maxwell-Stefan formulation for highlighting the influence of interspecies (1-2) friction on binary mixture permeation across microporous and polymeric membranes. J. Membr. Sci. 2017, 540, 261–276. [Google Scholar] [CrossRef]
- Krishna, R.; van Baten, J.M. Using the spreading pressure to inter-relate the characteristics of unary, binary and ternary mixture permeation across microporous membranes. J. Membr. Sci. 2022, 643, 120049. [Google Scholar] [CrossRef]
- Kapteijn, F.; Bakker, W.J.W.; van de Graaf, J.; Zheng, G.; Poppe, J.; Moulijn, J.A. Permeation and separation behaviour of a silicalite-1 membrane. Catal. Today 1995, 25, 213–218. [Google Scholar] [CrossRef]
- Kapteijn, F.; Bakker, W.J.W.; Zheng, G.; Poppe, J.; Moulijn, J.A. Permeation and separation of light hydrocarbons through a silicalite-1 membrane. Application of the generalized Maxwell-Stefan equations. Chem. Eng. J. 1995, 57, 145–153. [Google Scholar] [CrossRef]
- Kapteijn, F.; Moulijn, J.A.; Krishna, R. The generalized Maxwell–Stefan model for diffusion in zeolites: Sorbate molecules with different saturation loadings. Chem. Eng. Sci. 2000, 55, 2923–2930. [Google Scholar] [CrossRef]
- Farooq, S.; Karimi, L.A. Modeling support resistance in zeolite membranes. J. Membr. Sci. 2001, 186, 109–121. [Google Scholar] [CrossRef]
- de Bruijn, F.T.; Sun, L.; Olujić, Z.; Jansens, P.J.; Kapteijn, F. Influence of the support layer on the flux limitation in pervaporation. J. Membr. Sci. 2003, 223, 141–156. [Google Scholar] [CrossRef]
- Hanebuth, M.; Dittmeyer, R.; Mabande, G.T.P.; Schwieger, W. On the combination of different transport mechanisms for the simulation of steady-state mass transfer through composite systems using H2/SF6 permeation through stainless steel supported silicalite-1 membranes as a model system. Catal. Today 2005, 104, 352–359. [Google Scholar] [CrossRef]
- Wirawan, S.K.; Creaser, D.; Lindmark, J.; Hedlund, J.; Bendiyasa, I.M.; Sediawan, W.B. H2/CO2 permeation through a silicalite-1 composite membrane. J. Membr. Sci. 2011, 375, 313–322. [Google Scholar] [CrossRef]
- Kangas, J.; Sandström, L.; Malinen, I.; Hedlund, J.; Tanskanen, J. Maxwell–Stefan modeling of the separation of H2 and CO2 at high pressure in an MFI membrane. J. Membr. Sci. 2013, 435, 186–206. [Google Scholar] [CrossRef]
- Skoulidas, A.I.; Sholl, D.S. Multiscale model of sweep gas and porous support effects on zeolite membranes. AIChE J. 2005, 51, 867–877. [Google Scholar] [CrossRef]
- Hamdi, S.; Schiesser, W.E.; Griffiths, G.W. Method of lines. Scholarpedia 2011, 2, 2859. [Google Scholar] [CrossRef]
- Martinek, J.G.; Gardner, T.Q.; Noble, R.D.; Falconer, J.L. Modeling transient permeation mixtures through zeolite membranes. Ind. Eng. Chem. Res. 2006, 45, 6032–6043. [Google Scholar] [CrossRef]
- Hu, X.; Do, D.D. Multicomponent adsorption kinetics of hydrocarbons onto activated carbon: Effect of adsorption equilibrium equations. Chem. Eng. Sci. 1992, 47, 1715–1725. [Google Scholar] [CrossRef]
- Kapteijn, F.; Wang, X. Zeolite membranes—The importance of support analysis. Chem. Ing. Tech. 2022, 94, 23–30. [Google Scholar] [CrossRef]
- Mason, E.A.; Malinauskas, A.P. Gas Transport in Porous Media: The Dusty Gas Model; Elsevier: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Boroń, D.; Bizon, K.; Tabiś, B. Efficiency and capacity of nanoporous solids subjected to periodic disturbances of concentration. Sep. Purif. Technol. 2024, 340, 126721. [Google Scholar] [CrossRef]
- Do, D.D. Adsorption Analysis. Equilibria and Kinetics, 1st ed.; Imperial College Press: London, UK, 1998. [Google Scholar]
- Boroń, D.; Bizon, K.; Tabiś, B. Short-time and long-time dynamics of the zeolite films in the light of alternative diffusion models. Int. J. Heat Mass Transf. 2024, 235, 126163. [Google Scholar] [CrossRef]
- Vignes, A. Diffusion in binary solutions. Variation of diffusion coefficient with composition. Ind. Eng. Chem. Fundam. 1966, 5, 189–199. [Google Scholar] [CrossRef]
- Krishna, R. Multicomponent surface diffusion of adsorbed species: A description based on the generalized Maxwell-Stefan equation. Chem. Eng. Sci. 1990, 45, 1779–1791. [Google Scholar] [CrossRef]
- Reed, D.A.; Ehrlich, G. Surface diffusion, atomic jump rates and thermodynamics. Surf. Sci. 1981, 102, 588–609. [Google Scholar] [CrossRef]
- Krishna, R. Diffusion in porous crystalline materials. Chem. Soc. Rev. 2012, 41, 3099–3118. [Google Scholar] [CrossRef]
- Krishna, R. Investigating the validity of the Knudsen diffusivity prescription for mesoporous and macroporous materials. Ind. Eng. Chem. Res. 2016, 55, 4749–4759. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’Connel, J.P. The Properties of Gases and Liquids; Mc Graw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Thomas, S.; Schafer, R.; Caro, J.; Seidel-Morgenstern, A. Investigation of mass transfer through inorganic membranes with several layers. Catal. Today 2001, 67, 205–216. [Google Scholar] [CrossRef]
- Jareman, F.; Hedlund, J.; Creaser, D.; Sterte, J. Modelling of single gas permeation in real MFI membranes. J. Membr. Sci. 2004, 236, 81–89. [Google Scholar] [CrossRef]




| Parameter | {A1, A2} = {H2, CO2} | {A1, A2} = {H2, n-C4H10} |
|---|---|---|
| [mol·kg−1] | 5.4 | 0.7323 |
| [mol·kg−1] | 2.025 | 2.1953 |
| ρz [kg·m−3] | 2503 | 2560 |
| [m2·s−1] | 7.4153 × 10−8 | 1.0 × 10−9 |
| [m2·s−1] | 3.81 × 10−9 | 5.0 × 10−11 |
| b1 [Pa−1] | 4.703 × 10−8 | 1.1089 × 10−5 |
| b2 [Pa−1] | 1.8377 × 10−5 | 1.1 × 10−3 |
| References | Kangas et al. (2013) [34] | Kapteijn et al. (1995) [27] Krishna and Paschek (2000) [21] |
| Parameter | Support 1 | Support 2 |
|---|---|---|
| Lsi [m] | 3.0 × 10−5 | 3.0 × 10−3 |
| dpi [m] | 1.0 × 10−7 | 3.0 × 10−6 |
| (ε/τ)i | 0.027 | 0.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bizon, K.; Boroń, D.; Tabiś, B. Assessment and Discussion of the Steady-State Determination in Zeolite Composite Membranes for Multi-Component Diffusion. Membranes 2025, 15, 301. https://doi.org/10.3390/membranes15100301
Bizon K, Boroń D, Tabiś B. Assessment and Discussion of the Steady-State Determination in Zeolite Composite Membranes for Multi-Component Diffusion. Membranes. 2025; 15(10):301. https://doi.org/10.3390/membranes15100301
Chicago/Turabian StyleBizon, Katarzyna, Dominika Boroń, and Bolesław Tabiś. 2025. "Assessment and Discussion of the Steady-State Determination in Zeolite Composite Membranes for Multi-Component Diffusion" Membranes 15, no. 10: 301. https://doi.org/10.3390/membranes15100301
APA StyleBizon, K., Boroń, D., & Tabiś, B. (2025). Assessment and Discussion of the Steady-State Determination in Zeolite Composite Membranes for Multi-Component Diffusion. Membranes, 15(10), 301. https://doi.org/10.3390/membranes15100301







