Two-Dimensional Theoretical Analysis and Experimental Study of Mass Transfer in a Hollow-Fiber Dialysis Module Coupled with Ultrafiltration Operations
Abstract
1. Introduction
2. Mathematical Formulations
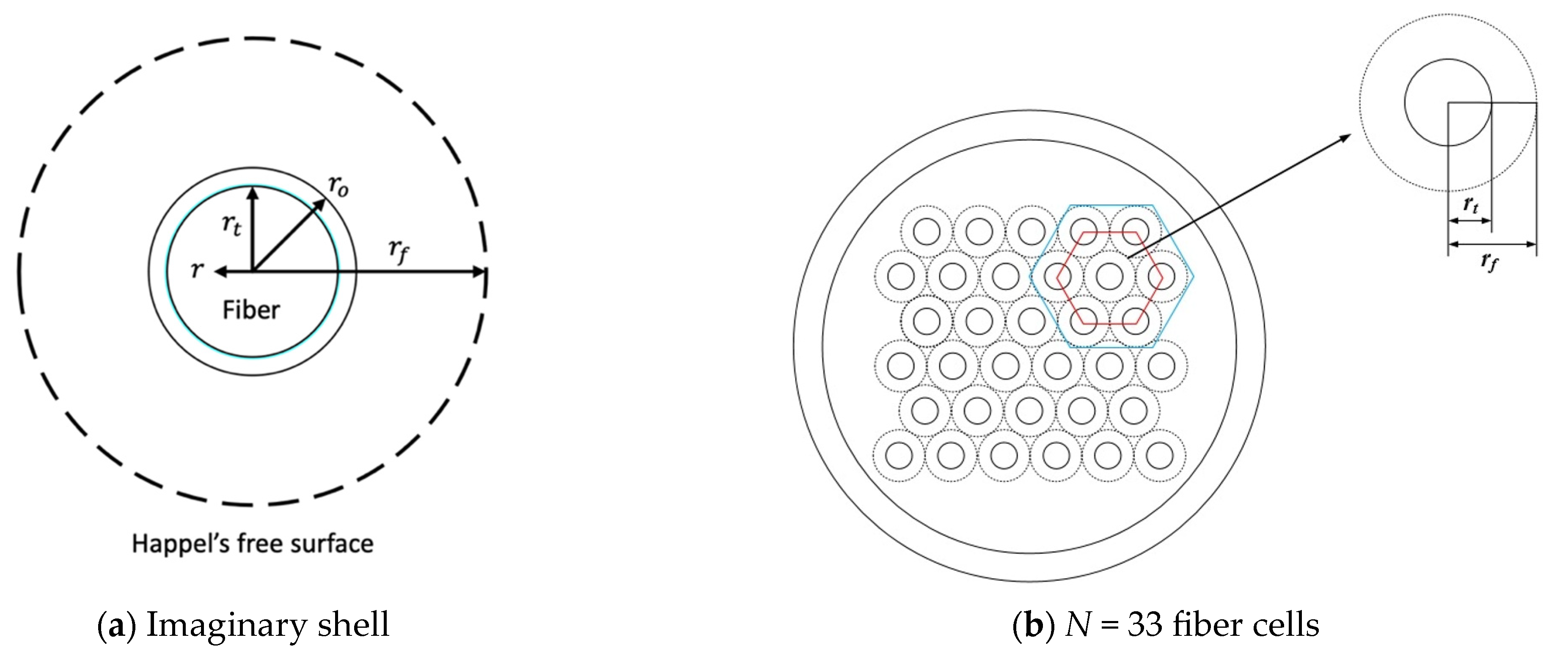
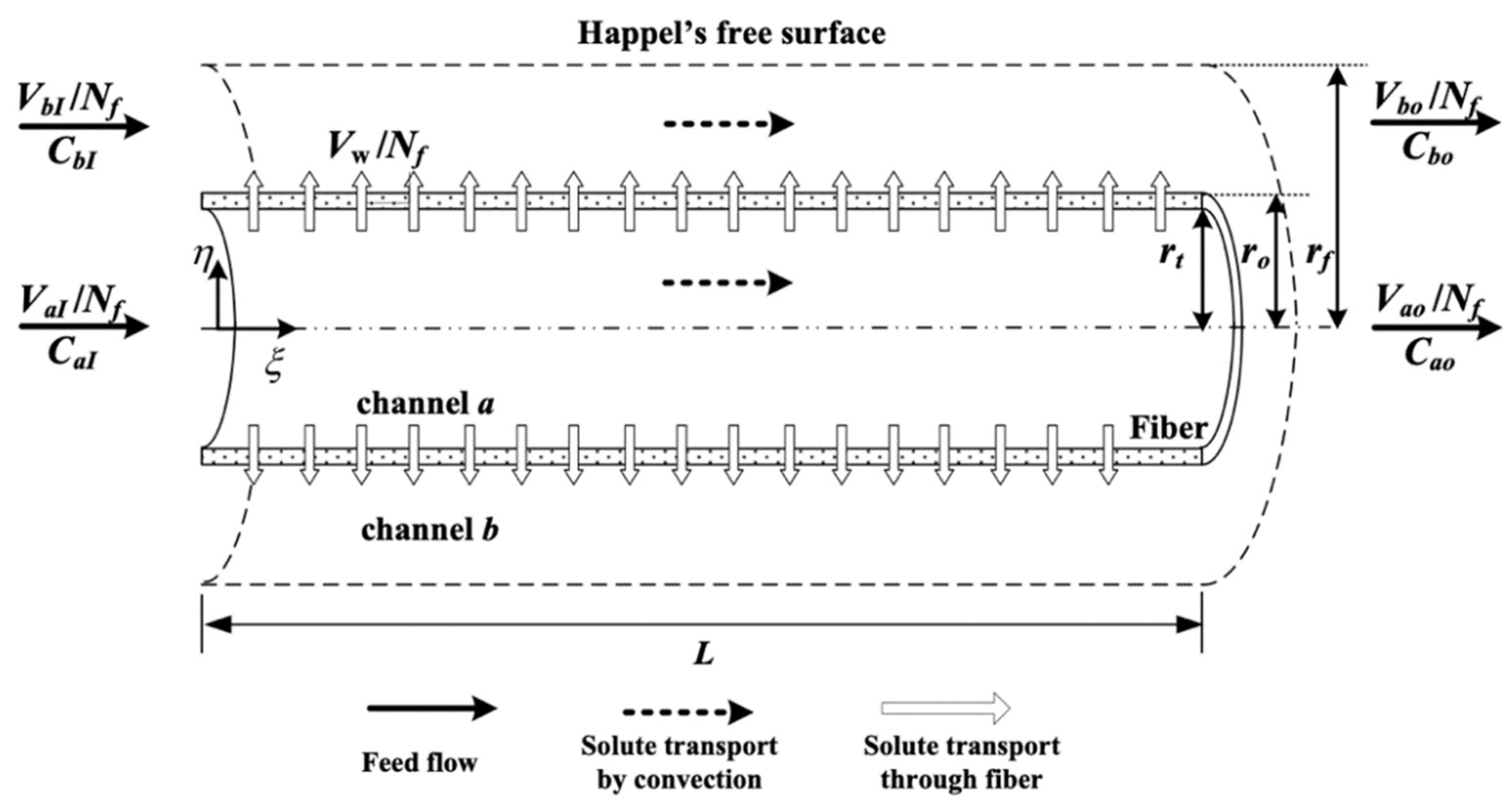
2.1. Dialysis-and-Ultrafiltration in a Hollow-Fiber Membrane Dialyzer Module
2.1.1. Velocity Profiles
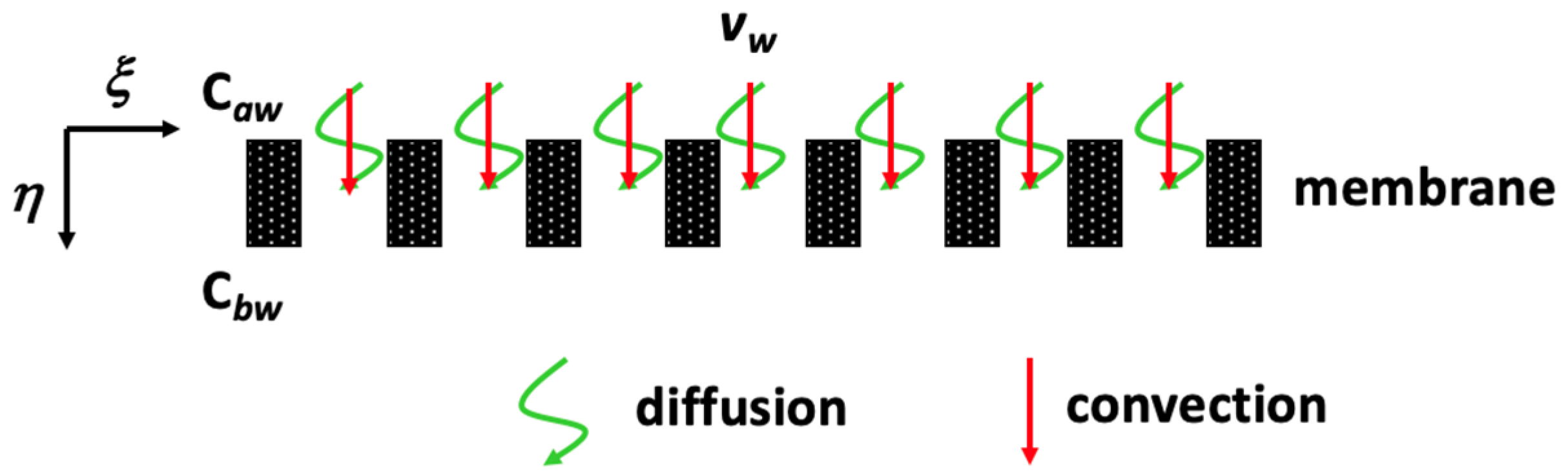
2.1.2. Mass Balance Equations
2.2. Pure Membrane Dialysis in a Hollow-Fiber Membrane Dialyzer Module
3. Dialysis Rate, Dialysis Efficiency, and Dialysis Rate Improvement
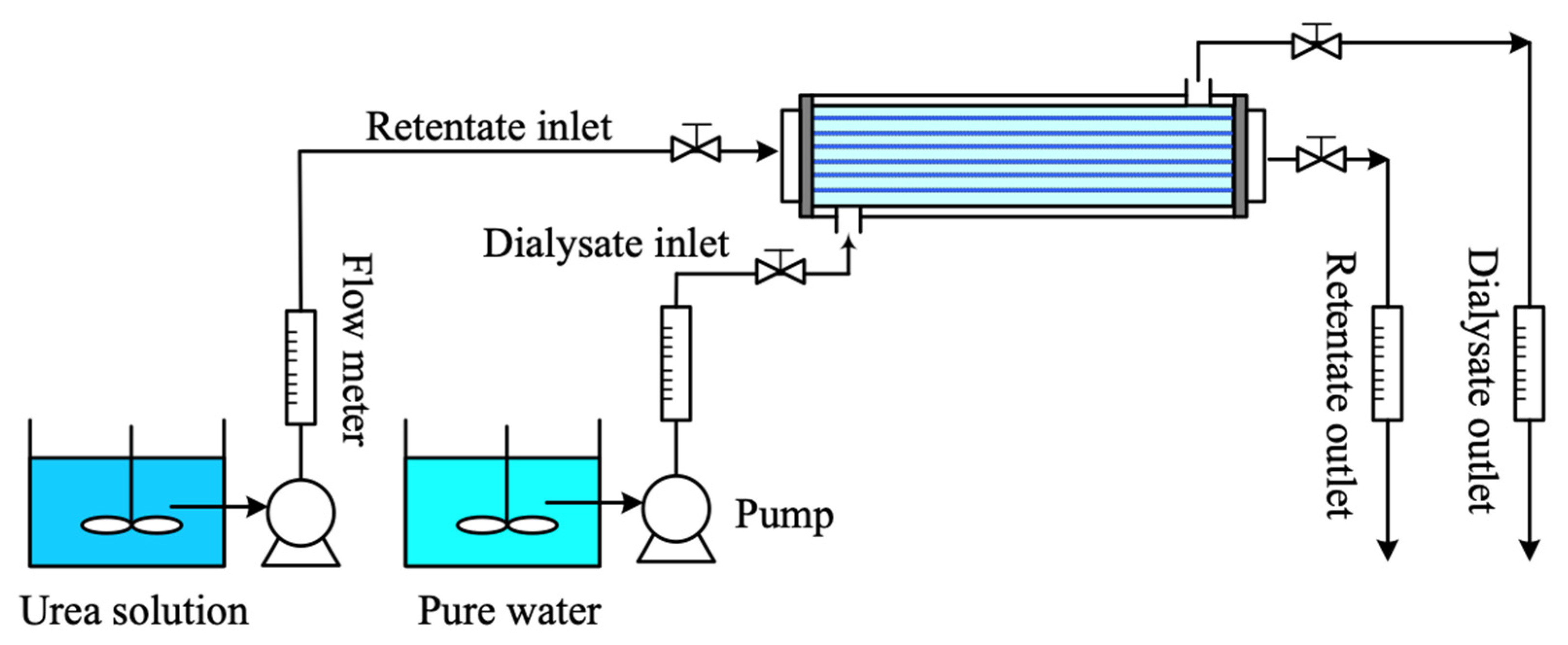
4. Experimental Runs
5. Results and Discussions
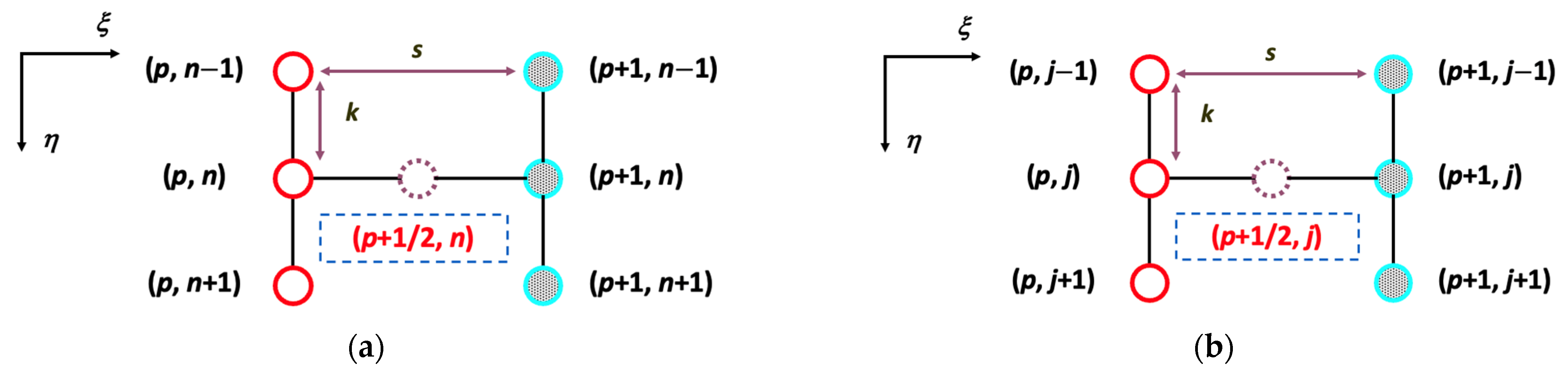
5.1. The Numerical Solutions of the Crank–Nicolson Method Validated by Convergence Tolerance
5.2. Average Concentration Distributions
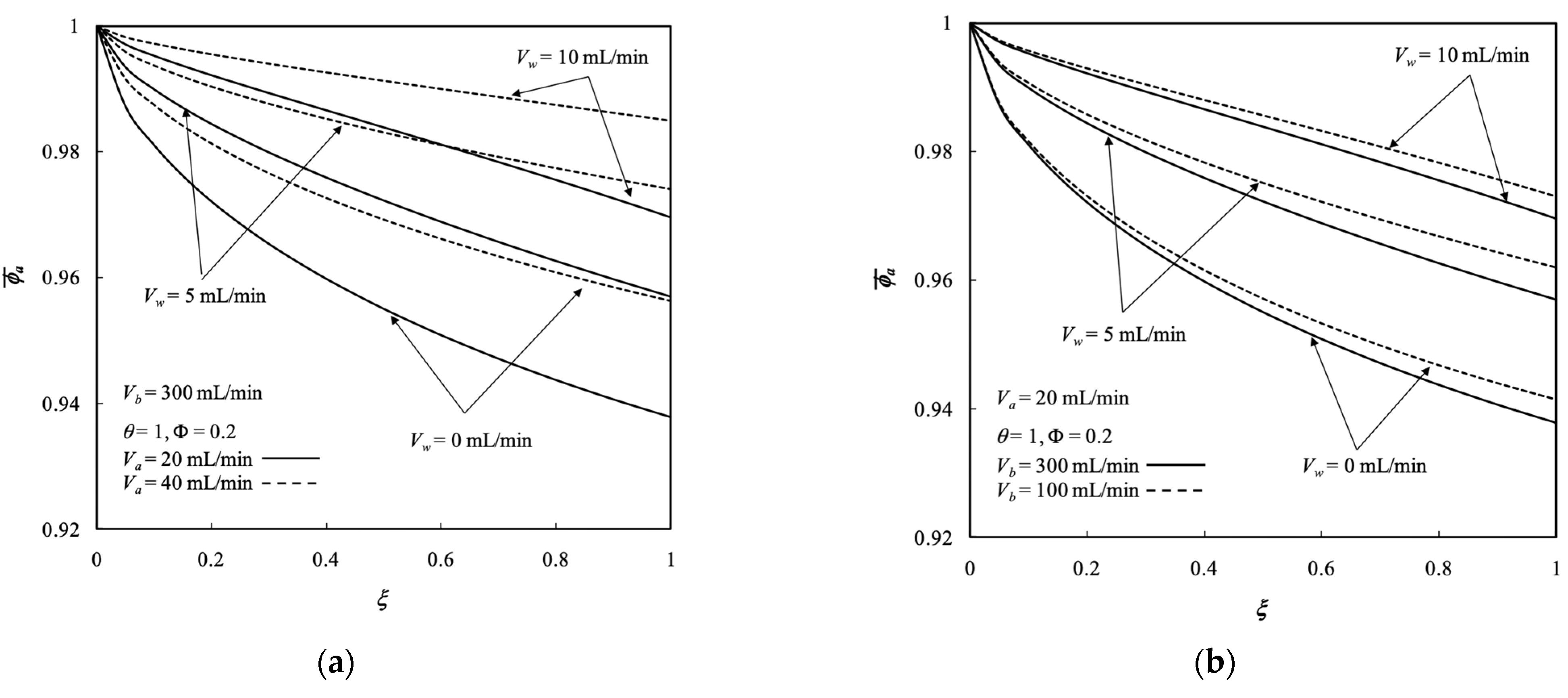
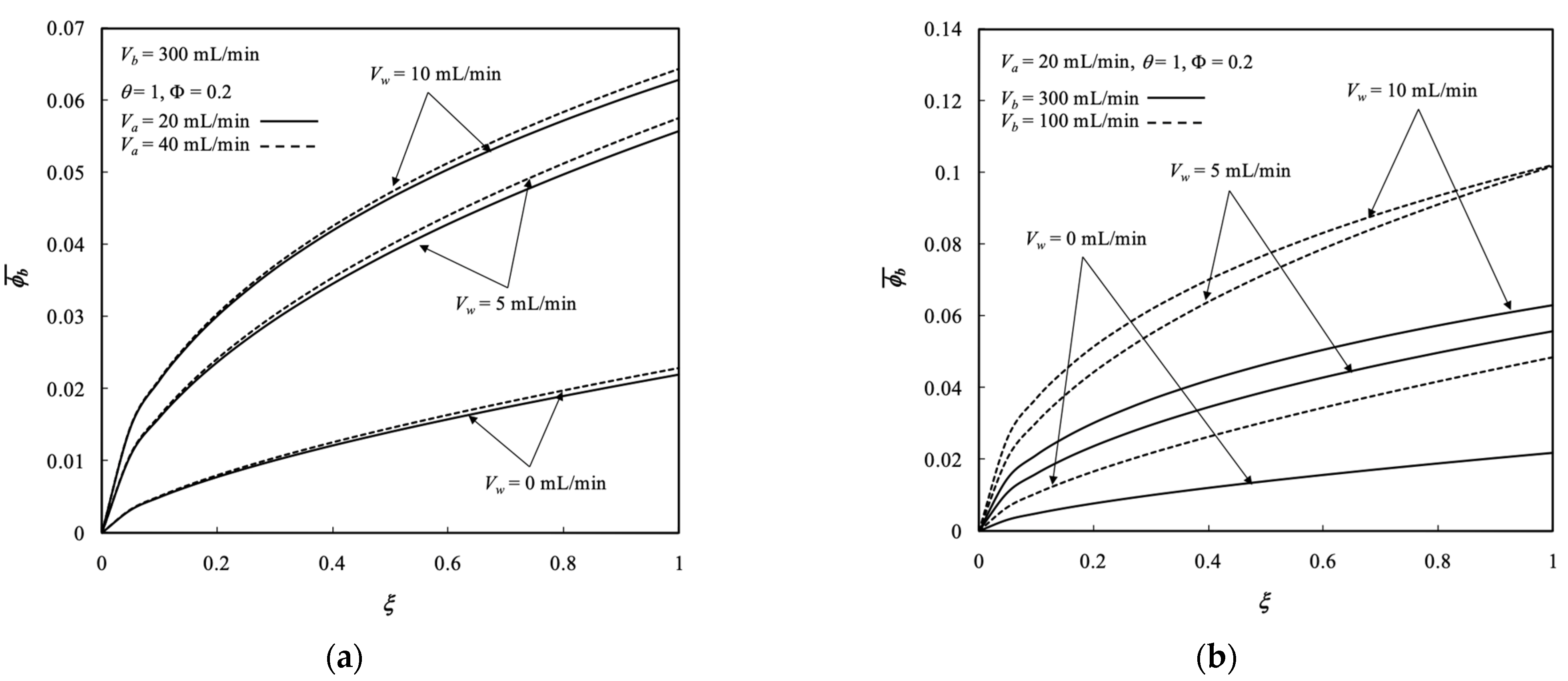
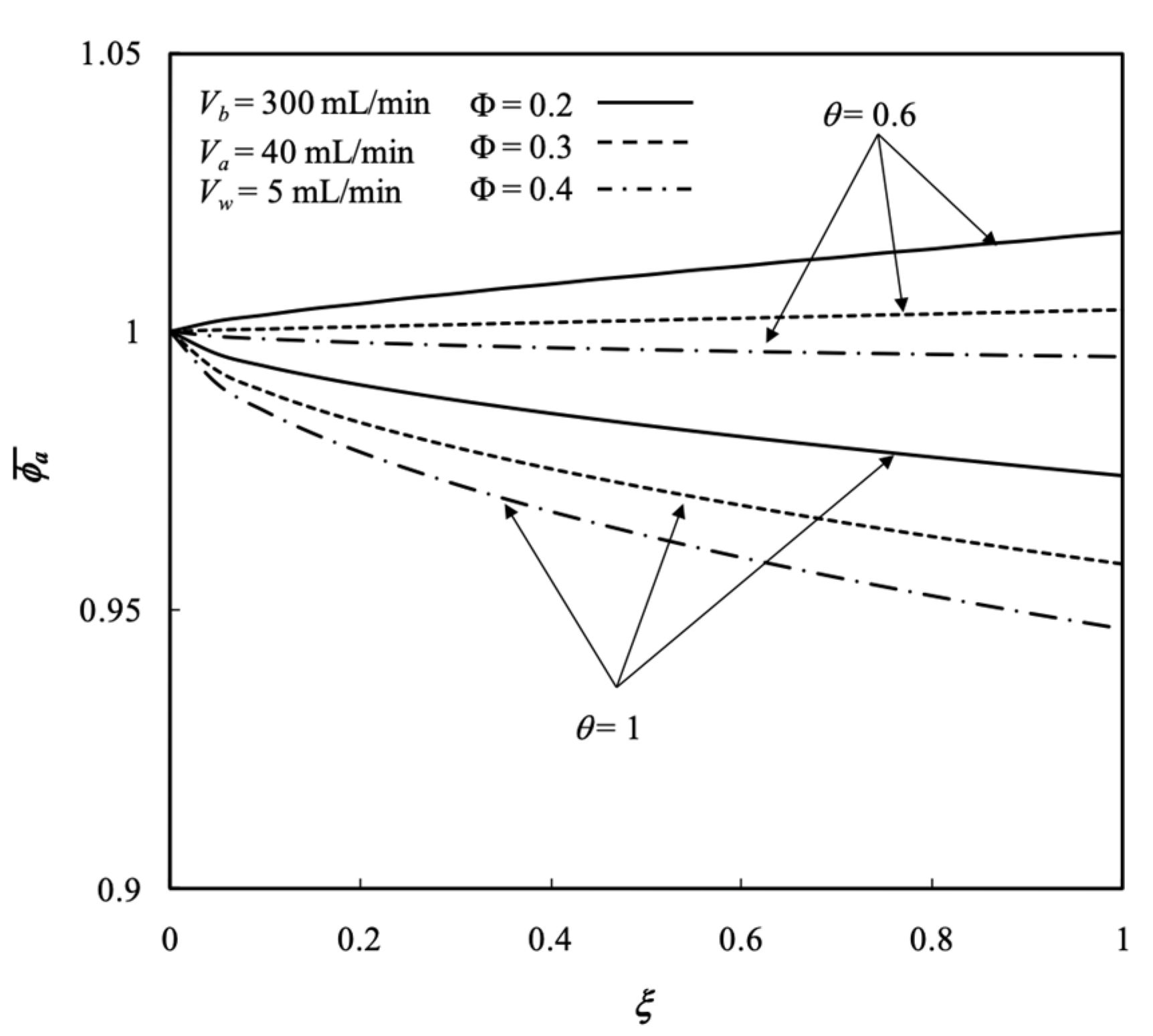
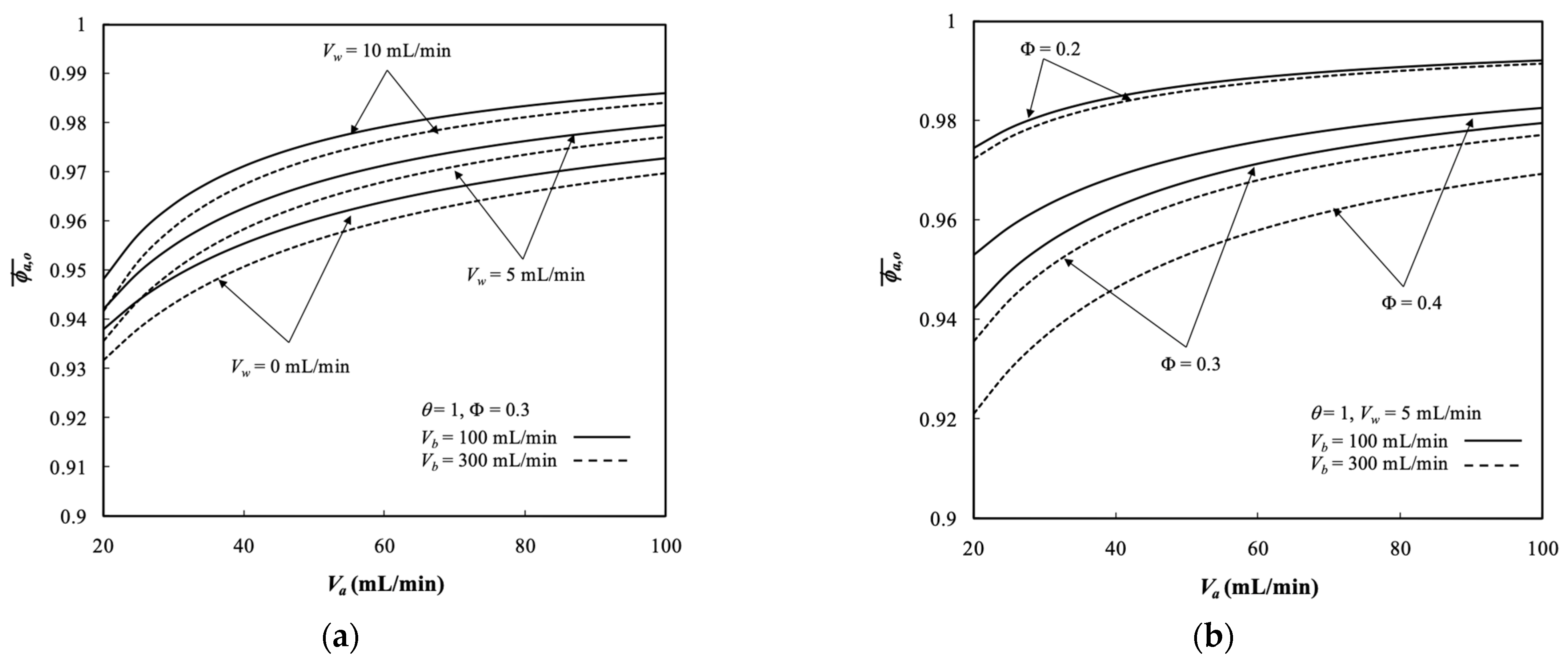
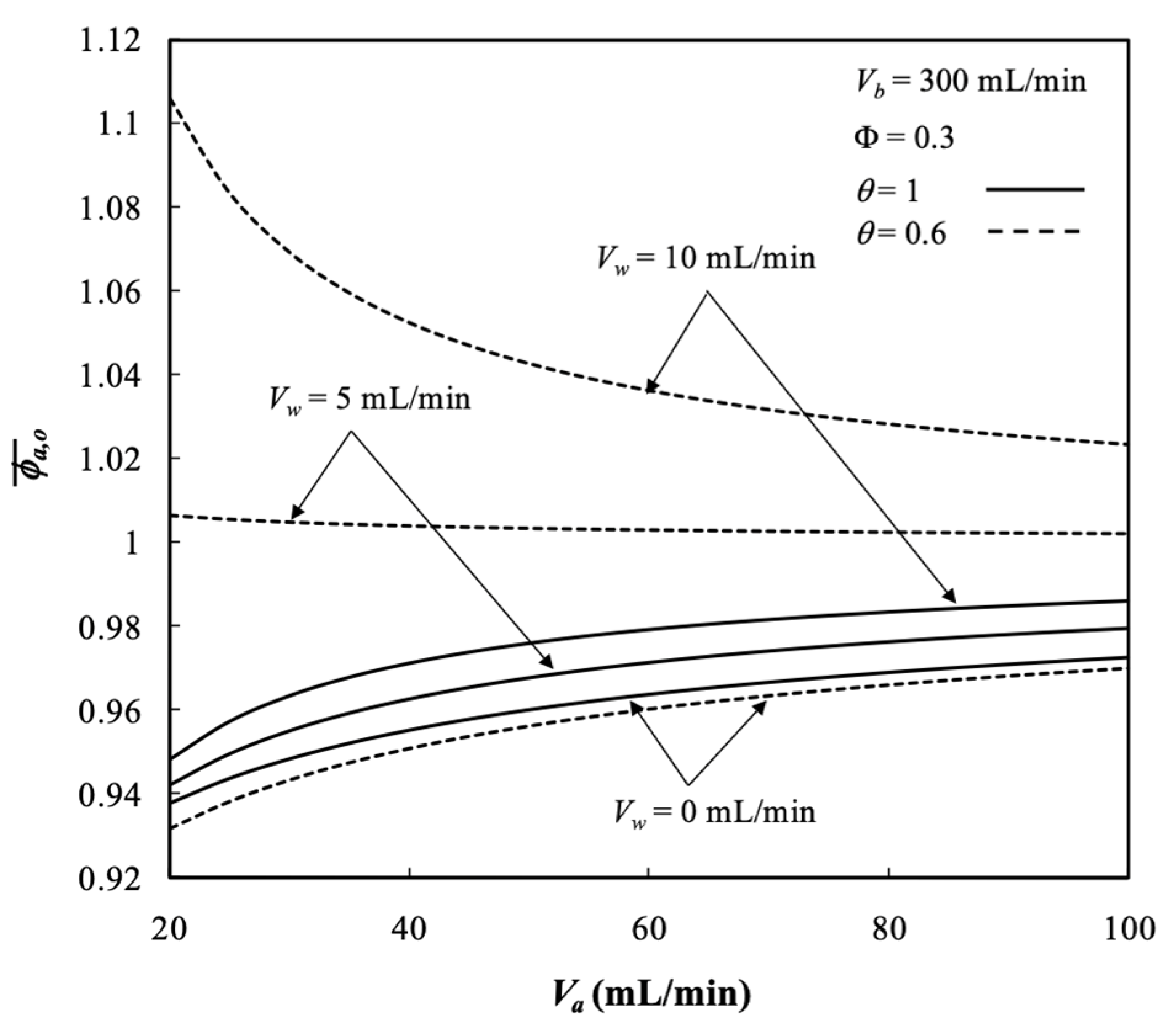
5.3. Average Outlet Concentrations
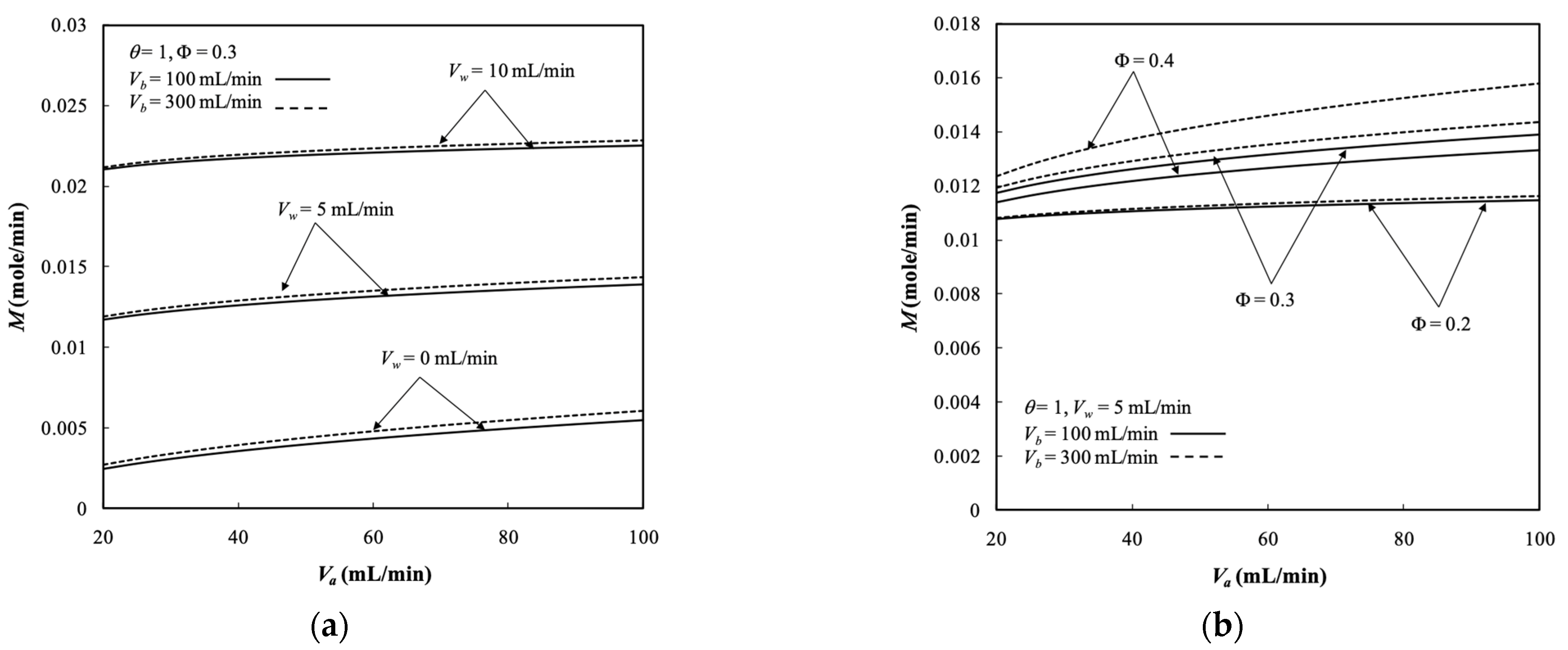
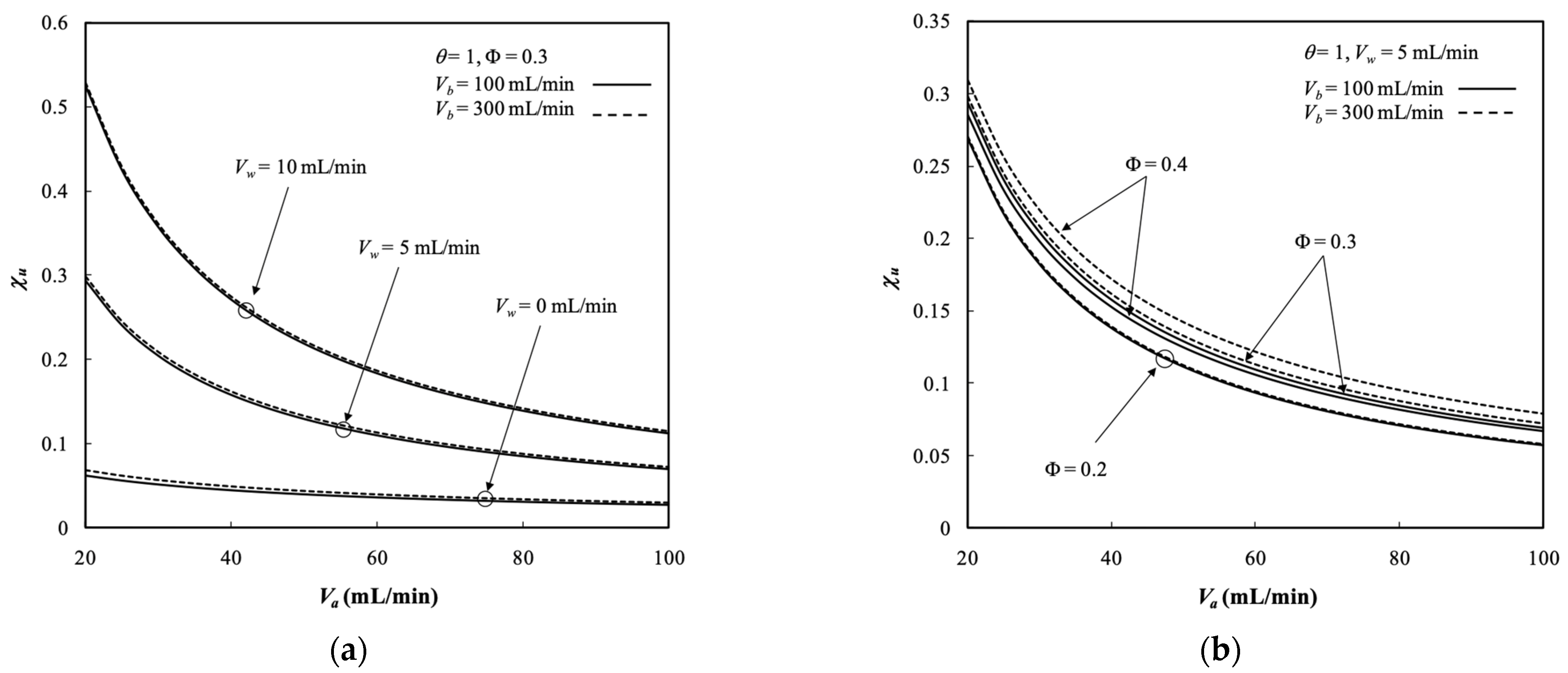
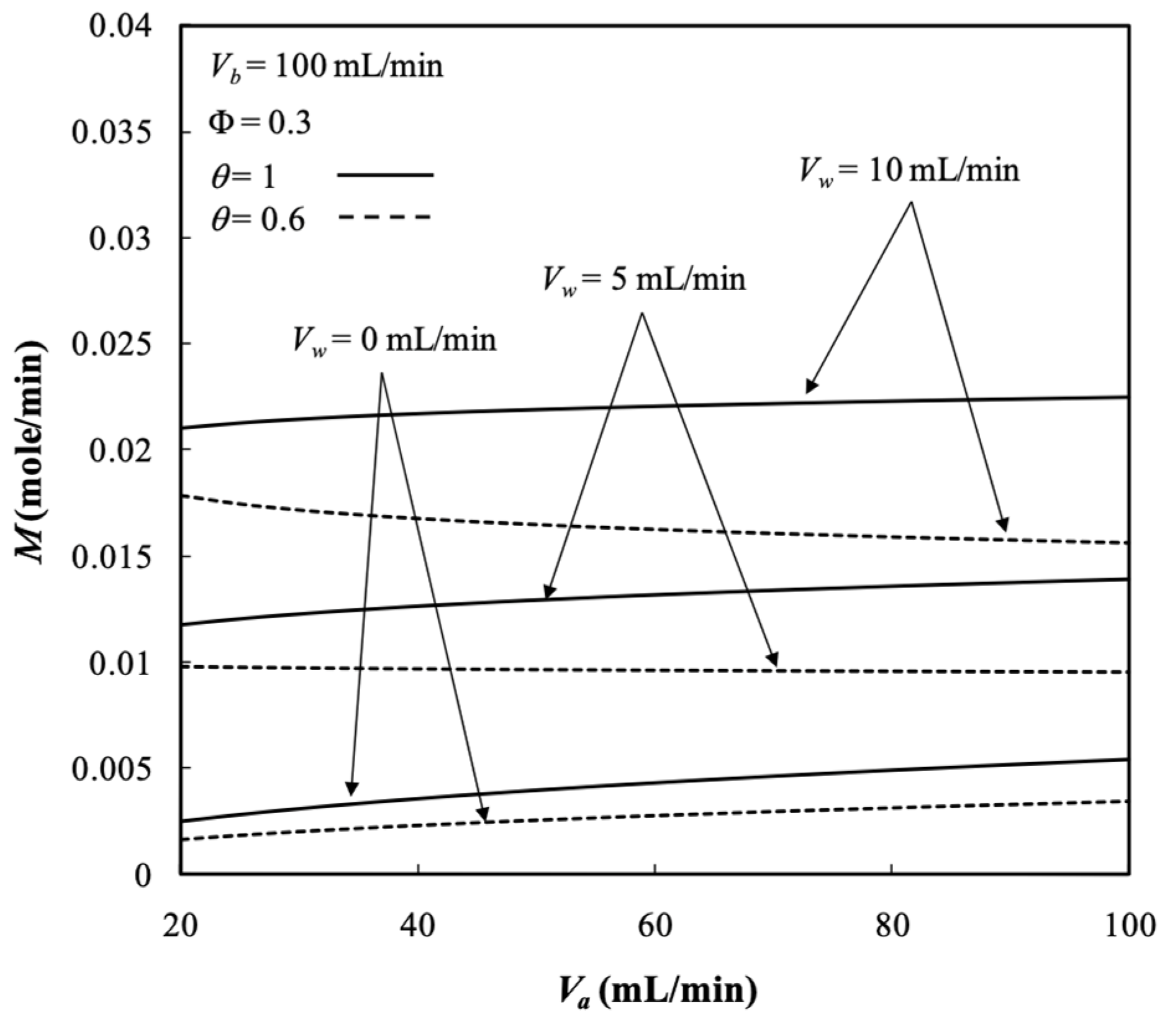
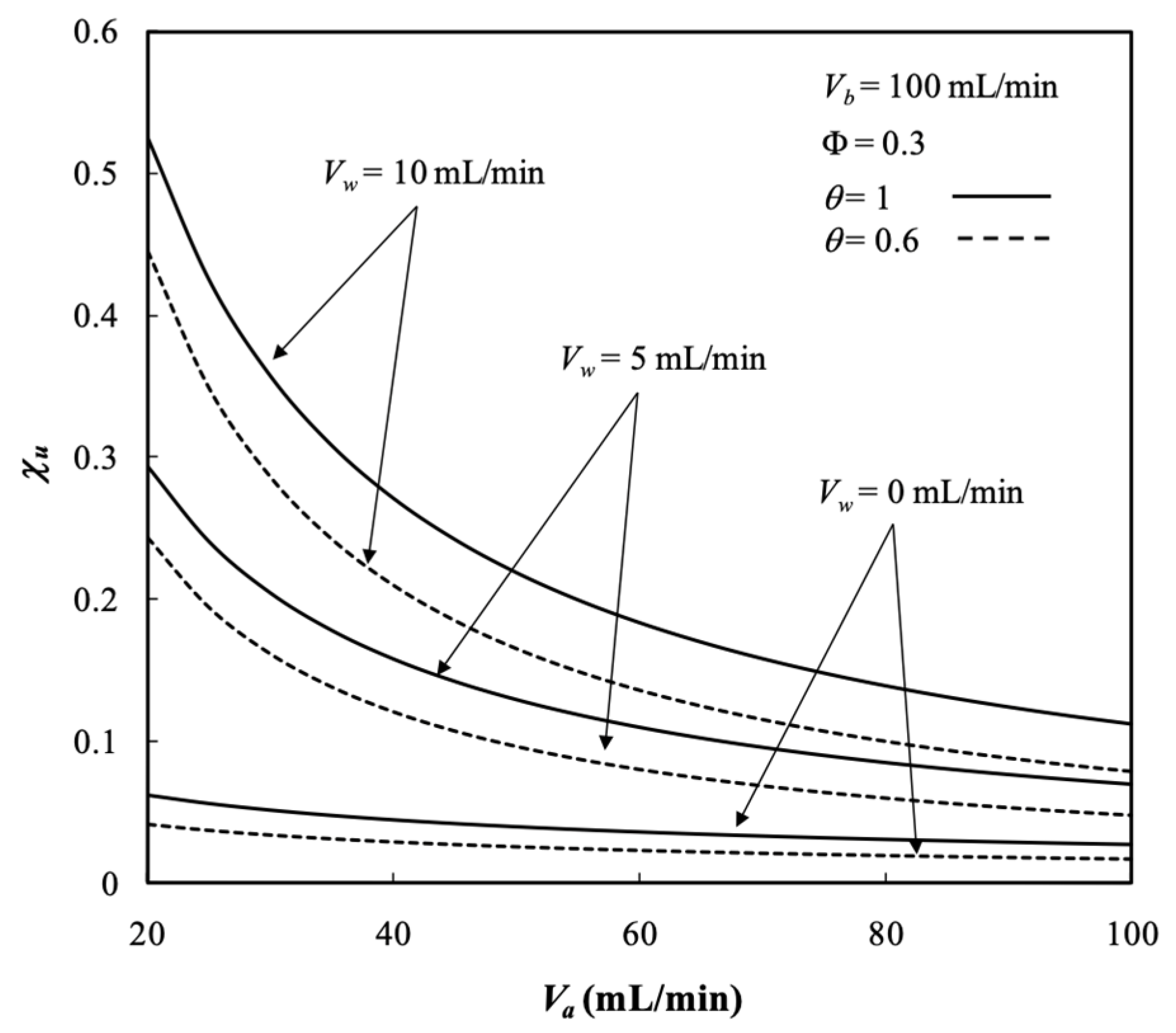
5.4. Dialysis Rate, Dialysis Efficiency, and Dialysis Rate Improvement
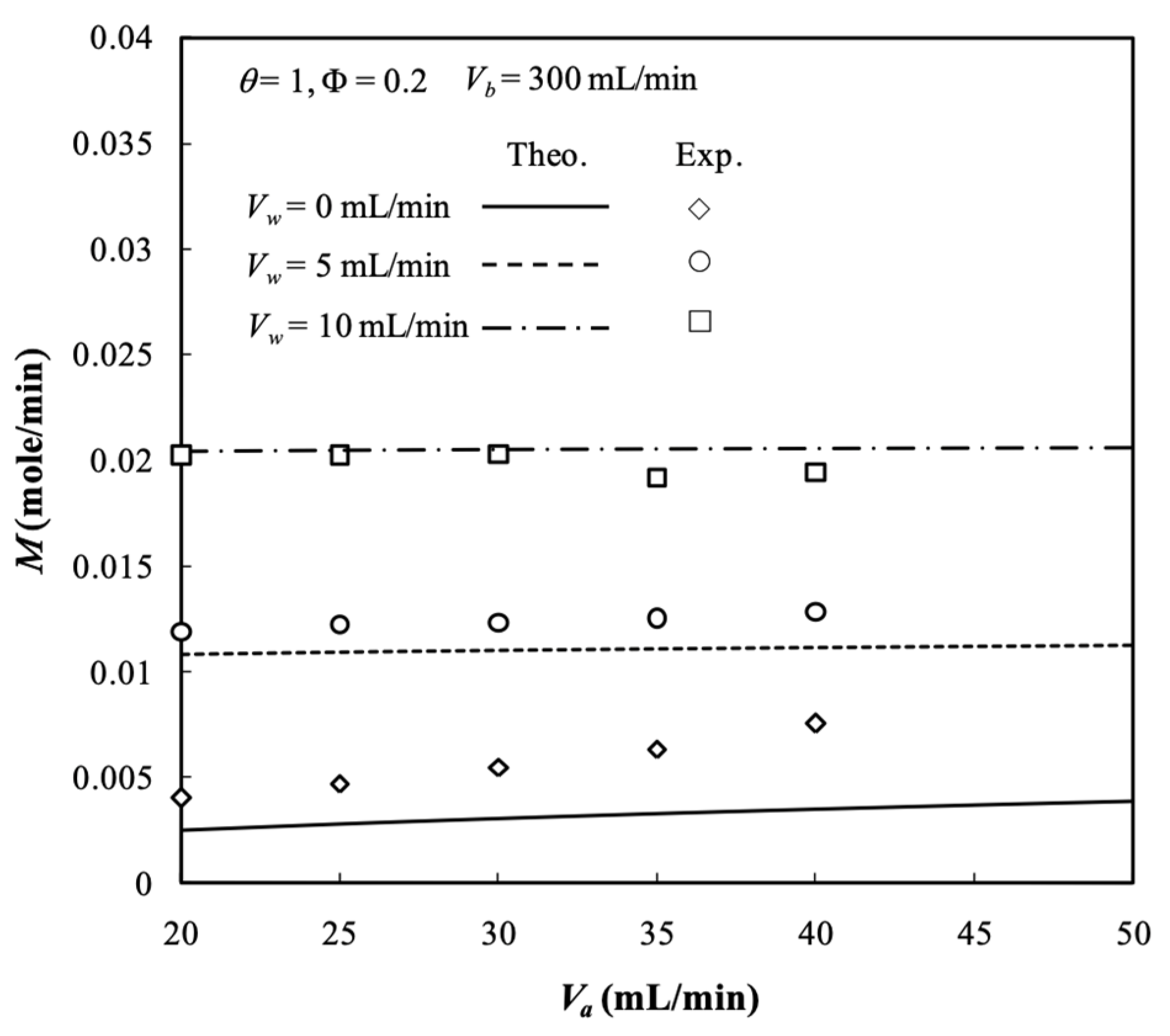
5.5. Experimental Results
5.6. Effects of the Membrane Sieving Coefficient on Hollow-Fiber Dialyzer Performance
6. Conclusions
- The average outlet concentration of retentate phase increased with the retentate phase flow rate and ultrafiltration rate because the residence time decreased with dialysate phase flow rate, membrane sieving coefficient, and packing density.
- The results show that the dialysis rate increased with both retentate and dialysate phase flow rates, membrane sieving coefficient, ultrafiltration rate, and packing density with respect to the system without ultrafiltration operation.
- The results indicate that the packing density had a significant influence on the mass transfer rate in the membrane dialysis operations, and thus, the dialysis efficiency increased with the packing density.
- The dialysis efficiency increased with the dialysate phase flow rate, ultrafiltration rate, membrane sieving coefficient, and packing density but decreased with the retentate phase flow rate.
- The dialysis rate improvements increased with the ultrafiltration rate and membrane sieving coefficient but decreased with retentate phase flow rate.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Solute concentration in the stream (mol m−3) | |
| Solute diffusivity in both retentate and dialysate phases (m2 s−1) | |
| Solute diffusivity in membrane (m2 s−1) | |
| Dialysis rate improvement | |
| Node numbers in -direction of dialysate phase | |
| Length of membrane dialyzer (m) | |
| Dialysis rate (mol s−1) | |
| Node numbers in -direction of retentate phase | |
| Number of fiber cells | |
| Node numbers in -direction | |
| -direction step sizes of the Crank–Nicolson method | |
| Pressure in retentate phase, (N m−2) | |
| Pressure in dialysate phase, (N m−2) | |
| Transversal coordinate (m) | |
| Imaginary free surface radius (m) | |
| Outside radius of inner tube (m) | |
| Inside radius of the shell tube (m) | |
| Inside radius of inner tube (m) | |
| Reynolds number | |
| Velocity distribution of the retentate phase (m s−1) | |
| Velocity distribution of the dialysate phase (m s−1) | |
| Averaged velocity of the retentate phase (m s−1) | |
| Averaged velocity of the dialysate phase (m s−1) | |
| Volumetric flow rate of the retentate phase (m3 s−1) | |
| Volumetric flow rate of the dialysate phase (m3 s−1) | |
| Ultrafiltration rate (m3 s−1) | |
| Velocity distribution of the dialysate phase (m s−1) | |
| Ultrafiltration flux distribution (m s−1) | |
| Average ultrafiltration flux on the inner surface of the membrane (m s−1) | |
| Average ultrafiltration flux on the outer surface of the membrane (m s−1) | |
| Axial coordinate along the flow direction (m) | |
| Greek letters | |
| Ratio of inside radius of inner tube to imaginary free surface radius, | |
| Ratio of outside radius of inner tube to imaginary free surface radius, | |
| Membrane thickness (m) | |
| Membrane porosity | |
| Dimensionless transversal coordinate | |
| Membrane sieving coefficient | |
| Wall Reynolds number of the retentate phase, | |
| Wall Reynolds number of the dialysate phase, | |
| Wall Reynolds number of the dialysate phase () | |
| Dimensionless longitudinal coordinate | |
| Density () | |
| Kinetic viscosity () | |
| Dimensionless solute concentration | |
| Dimensionless average solute concentration | |
| Packing density | |
| Dialysis efficiency | |
| Stream function | |
| Subscripts | |
| In the retentate phase | |
| In the dialysate phase | |
| At the inlet | |
| At the outlet | |
| Dialyzer module with ultrafiltration operation | |
| On the membrane surface |
Appendix A
References
- Lake, M.A.; Melsheimer, N.J. Mass transfer characterization of Donnan dialysis. AIChE J. 1978, 24, 130–137. [Google Scholar] [CrossRef]
- Moonen, H.; Niefind, H. Alcohol reduction in beer by means of dialysis. Desalination 1982, 41, 327–335. [Google Scholar] [CrossRef]
- Palatý, Z.; Žáková, A.; Petřík, P.A. Continuous dialysis of carboxylic acids. Permeability of Neosepta-AMH membrane. Desalination 2007, 216, 345–355. [Google Scholar]
- Ho, W.S.W.; Sirkar, K.K. Handbook of Membranes; Van Nostrand Reinhold: New York, NY, USA, 1992. [Google Scholar]
- Humes, H.; Fissell, W.; Tiranathanagul, K. The future of hemodialysis membranes. Kidney Int. 2006, 69, 1115–1119. [Google Scholar] [CrossRef] [PubMed]
- Klein, E.; Holland, F.; Lebeouf, A.; Donnaud, A.; Smith, J. Transport and mechanical properties of hemodialysis hollow fibers. J. Membr. Sci. 1976, 1, 371–396. [Google Scholar] [CrossRef]
- Walker, G.; Davis, T. Mass transfer in laminar flow between parallel permeable plates. Amer. Inst. Chem. Eng. J. 1974, 20, 881–889. [Google Scholar] [CrossRef]
- Happel, J. Viscous flow relative to arrays of cylinders. AIChE J. 1959, 5, 174–177. [Google Scholar] [CrossRef]
- Zheng, J.-M.; Xu, Y.-Y.; Xu, Z.-K. Shell Side Mass Transfer Characteristics in a Parallel Flow Hollow Fiber Membrane Module. Sep. Sci. Technol. 2003, 38, 1247–1267. [Google Scholar] [CrossRef]
- Liao, Z.; Poh, C.K.; Huang, Z.; Hardy, P.A.; Clark, W.R.; Gao, D. A Numerical and Experimental Study of Mass Transfer in the Artificial Kidney. J. Biomech. Eng. 2003, 125, 472–480. [Google Scholar] [CrossRef]
- Jagannathan, R.; Shettigar, U.R. Analysis of a tubular hemodialyser-effect of ultrafiltration and dialysate concentration. Med. Biol. Eng. Comput. 1977, 15, 500–512. [Google Scholar] [CrossRef]
- Abbas, M.; Tyagi, V. Analysis of a hollow-fibre artificial kidney performing simultaneous dialysis and ultrafiltration. Chem. Eng. Sci. 1987, 42, 133–142. [Google Scholar] [CrossRef]
- Abbas, M.; Tyagi, V. On the mass transfer in a circular conduit dialyzer when ultrafiltration is coupled with dialysis. Int. J. Heat Mass Transf. 1988, 31, 591–602. [Google Scholar] [CrossRef]
- Tu, J.-W.; Ho, C.-D. Two-Dimensional Mass-Transfer Model of a Flat-Plate Dialyzer with Ultrafiltration Operation. Chem. Eng. Technol. 2010, 33, 1358–1368. [Google Scholar] [CrossRef]
- Henderson, L.W. Current Status of Hemofiltration. Artif. Organs 1978, 2, 120–124. [Google Scholar] [CrossRef] [PubMed]
- Leber, H.-W.; Wizemann, V.; Goubeaud, G.; Rawer, P.; Schütterle, G. Hemodiafiltration: A New Alternative to Hemofiltration and Conventional Hemodialysis. Artif. Organs 1978, 2, 150–153. [Google Scholar] [CrossRef]
- Meng, F.; Seredych, M.; Chen, C.; Gura, V.; Mikhalovsky, S.; Sandeman, S.; Ingavle, G.; Ozulumba, T.; Miao, L.; Anasori, B.; et al. MXene Sorbents for Removal of Urea from Dialysate: A Step toward the Wearable Artificial Kidney. ACS Nano 2018, 12, 10518–10528. [Google Scholar] [CrossRef]
- Chen, Q.; He, Y.; Zhao, Y.; Chen, L. Intervening oxidative stress integrated with an excellent biocompatibility of hemodialysis membrane fabricated by nucleobase-recognized co-immobilization strategy of tannic acid, looped PEtOx brush and heparin. J. Membr. Sci. 2021, 625, 119174. [Google Scholar] [CrossRef]
- Qi, Z.; Cussler, E. Microporous hollow fibers for gas absorption: II. Mass transfer across the membrane. J. Membr. Sci. 1985, 23, 333–345. [Google Scholar] [CrossRef]
- Costello, M.J.; Fane, A.G.; Hogan, P.A.; Schofield, R.W. The effect of shell side hydrodynamics on the performance of axial flow hollow fiber modules. J. Membr. Sci. 1993, 80, 1–11. [Google Scholar] [CrossRef]
- Lipnizki, F.; Field, R.W. Mass transfer performance for hollow fiber modules with shell-side axial feed flow: Using an engineering approach to develop a framework. J. Membr. Sci. 2001, 193, 195–208. [Google Scholar] [CrossRef]
- Roger, J.D.; Long, R. Modeling hollow fiber membrane contactors using film theory, Voronoi tessellations, and facilitation factors for systems with interface reactions. J. Membr. Sci. 1997, 134, 1–17. [Google Scholar] [CrossRef]
- Noda, I.; Gryte, C.C. Mass transfer in regular arrays of hollow fibers in countercurrent dialysis. AIChE J. 1979, 25, 113–122. [Google Scholar] [CrossRef]
- Yoshikawa, S. Effects of Velocity Distribution of Dialysate on Mass Transfer in the Shell Side of a Hollow-Fiber Dialyzer. J. Chem. Eng. Jpn. 2003, 36, 1076–1084. [Google Scholar] [CrossRef]
- Ding, W.P.; He, L.Q.; Zhao, G.; Shu, Z.Q.; Cheng, S.X.; Gao, D.Y. A novel theoretical model for mass transfer of hollow fiber hemodialyzers. Chin. Sci. Bull. 2003, 48, 2386–2390. [Google Scholar] [CrossRef]
- Amini, Y.; Ghaednian-Jahromi, A.; Karimi-Sabet, J.; Dastbaz, A.; Hassanvand, A. CFD Simulation of He/CH4 Separation by Hyflon AD60X Membrane. Chem. Biochem. Eng. Q. 2021, 35, 355–367. [Google Scholar] [CrossRef]
- Prado, M.; Roa, L.M.; Palma, A.; Milán, J.A. Improving Hollow Fiber Dialyzer Efficiency with a Recirculating Dialysate System I: Theory and Applicability. Ann. Biomed. Eng. 2005, 33, 642–655. [Google Scholar] [CrossRef]
- Levy, J.; Brown, E.; Lawrence, A. Oxford Handbook of Dialysis; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Berman, A.S. Laminar Flow in Channels with Porous Walls. J. Appl. Phys. 1953, 24, 1232–1235. [Google Scholar] [CrossRef]
- Yuan, S.W.; Finkelstein, A.B.; Brooklyn, N.Y. Laminar pipe flow with injection and suction through a porous wall. Trans. ASME 1956, 78, 719–724. [Google Scholar] [CrossRef]
- Lin, J.; Huang, J.; Wang, J.; Yu, J.; You, X.; Lin, X.; Van der Bruggen, B.; Zhao, S. High-performance porous anion exchange membranes for efficient acid recovery from acidic wastewater by diffusion dialysis. J. Membr. Sci. 2021, 624, 119116. [Google Scholar] [CrossRef]
- Alborzi, Z.S.; Amini, Y.; Amirabedi, P.; Raveshiyan, S.; Hassanvand, A. Computational Fluid Dynamics Simulation of a Membrane Contactor for CO2 Separation: Two Types of Membrane Evaluation. Chem. Eng. Technol. 2023. [CrossRef]
- Wang, J.; Liu, Z.; Qiu, M.; He, C. Heparin-mimicking semi-interpenetrating composite membrane with multiple excellent performances for promising hemodialysis. J. Membr. Sci. 2021, 618, 118740. [Google Scholar] [CrossRef]
- Liu, Y.; Li, G.; Han, Q.; Lin, H.; Li, Q.; Hua, J.; Liu, F. Anticoagulant dialyzer with enhanced Ca2+ chelation and hydrophilicity for heparin free hemodialysis. J. Membr. Sci. 2020, 604, 118082. [Google Scholar] [CrossRef]
- Du, X.; Wang, Z.; Zhang, H.; Yuan, Y.; Wang, H.; Zhang, Z. Prepared poly(aryl piperidinium) anion exchange membranes for acid recovery to improve dialysis coefficients and selectivity. J. Membr. Sci. 2021, 619, 118805. [Google Scholar] [CrossRef]
- Moschona, A.; Kostoglou, M.; Karabelas, A.J. Mass Transfer Characteristics of Haemofiltration Modules—Experiments and Modeling. Membranes 2022, 12, 62. [Google Scholar] [CrossRef]
| Dimensionless Concentration | P = 100 | P = 200 | ||
|---|---|---|---|---|
| N = J = 200 | N = J = 300 | N = J = 200 | N = J = 300 | |
| 0.89 | 0.89 | 0.89 | 0.89 | |
| 0.97 | 0.97 | 0.97 | 0.97 | |
| 0.36 | 0.36 | 0.36 | 0.36 | |
| 0.06 | 0.06 | 0.06 | 0.06 | |
| Zero Order | First Order | Zero Order | First Order | |
|---|---|---|---|---|
| 0.42 | 0.58 | 0.58 | 0.59 | 0.59 |
| 0.70 | 1.11 | 1.11 | 1.14 | 1.14 |
| 1.0 | 1.61 | 1.61 | 1.65 | 1.65 |
| 0.2 | 25.65 | 38.47 | 51.29 | 28.30 | 56.60 | 84.91 |
| 0.3 | 16.93 | 25.39 | 33.85 | 21.39 | 42.78 | 64.18 |
| 0.4 | 12.82 | 19.23 | 25.65 | 17.74 | 35.48 | 53.23 |
| 296.35 | 674.65 | 259.04 | 554.41 | |
| 223.56 | 535.70 | 186.71 | 405.89 | |
| 183.07 | 457.15 | 147.01 | 327.63 | |
| 20 | 0.899 | 0.938 | 4.32 | 0.937 | 0.972 | 3.79 | 0.987 | 0.980 | 0.66 |
| 25 | 0.906 | 0.953 | 5.18 | 0.944 | 0.982 | 4.01 | 0.991 | 0.984 | 0.24 |
| 30 | 0.909 | 0.949 | 4.42 | 0.954 | 0.980 | 2.68 | 0.992 | 0.987 | 0.50 |
| 35 | 0.910 | 0.953 | 4.76 | 0.958 | 0.982 | 2.53 | 1.016 | 0.989 | 2.65 |
| 40 | 0.903 | 0.956 | 5.89 | 0.973 | 0.984 | 1.01 | 1.022 | 0.990 | 3.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, C.-D.; Tu, J.-W.; Chen, Y.-H.; Chew, T.L. Two-Dimensional Theoretical Analysis and Experimental Study of Mass Transfer in a Hollow-Fiber Dialysis Module Coupled with Ultrafiltration Operations. Membranes 2023, 13, 702. https://doi.org/10.3390/membranes13080702
Ho C-D, Tu J-W, Chen Y-H, Chew TL. Two-Dimensional Theoretical Analysis and Experimental Study of Mass Transfer in a Hollow-Fiber Dialysis Module Coupled with Ultrafiltration Operations. Membranes. 2023; 13(8):702. https://doi.org/10.3390/membranes13080702
Chicago/Turabian StyleHo, Chii-Dong, Jr-Wei Tu, Yih-Hang Chen, and Thiam Leng Chew. 2023. "Two-Dimensional Theoretical Analysis and Experimental Study of Mass Transfer in a Hollow-Fiber Dialysis Module Coupled with Ultrafiltration Operations" Membranes 13, no. 8: 702. https://doi.org/10.3390/membranes13080702
APA StyleHo, C.-D., Tu, J.-W., Chen, Y.-H., & Chew, T. L. (2023). Two-Dimensional Theoretical Analysis and Experimental Study of Mass Transfer in a Hollow-Fiber Dialysis Module Coupled with Ultrafiltration Operations. Membranes, 13(8), 702. https://doi.org/10.3390/membranes13080702










