Comparative Study of Different Ion-Exchange Membrane Types in Diffusion Dialysis for the Separation of Sulfuric Acid and Nickel Sulfate
Abstract
1. Introduction
2. Materials and Methods
2.1. Ion-Exschange Membranes
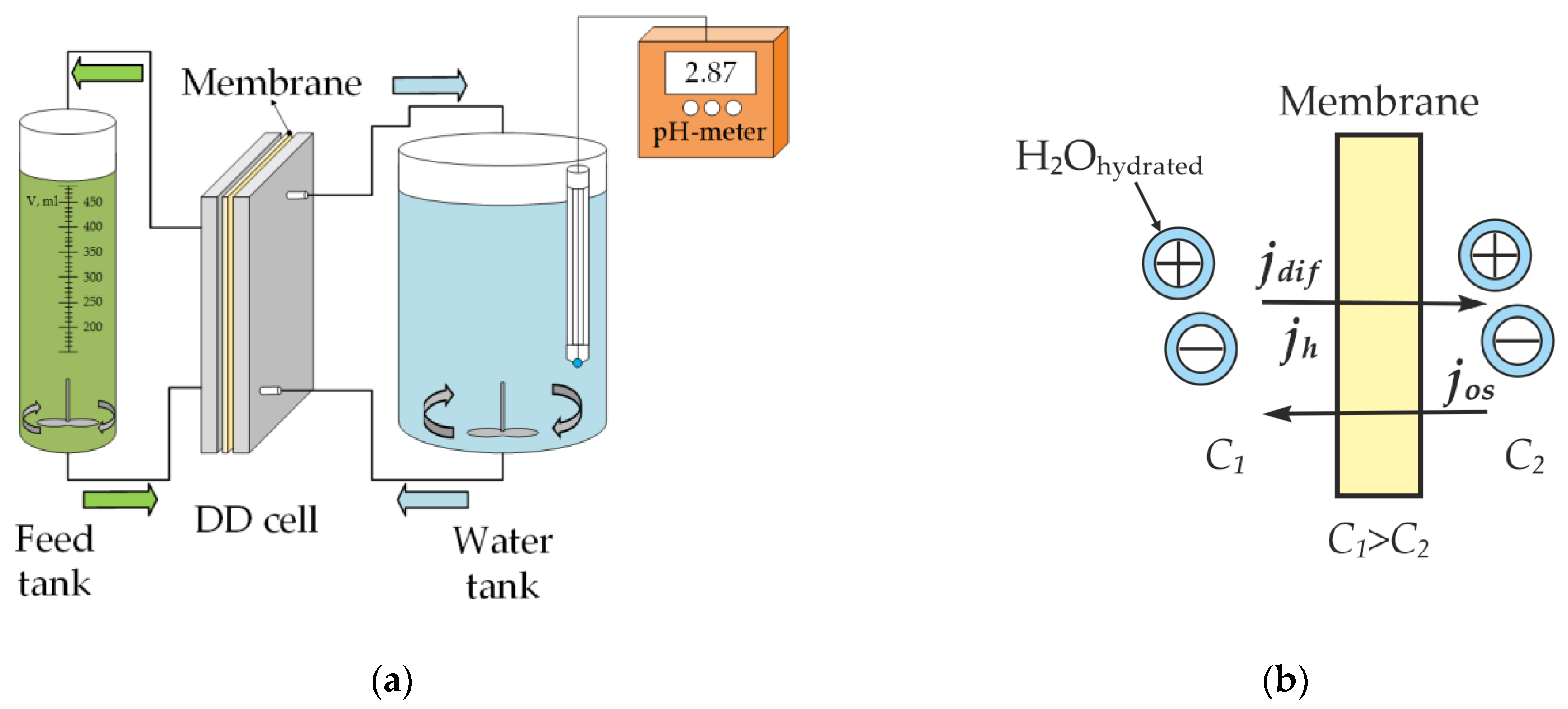
2.2. Method of Dialysis
3. Results
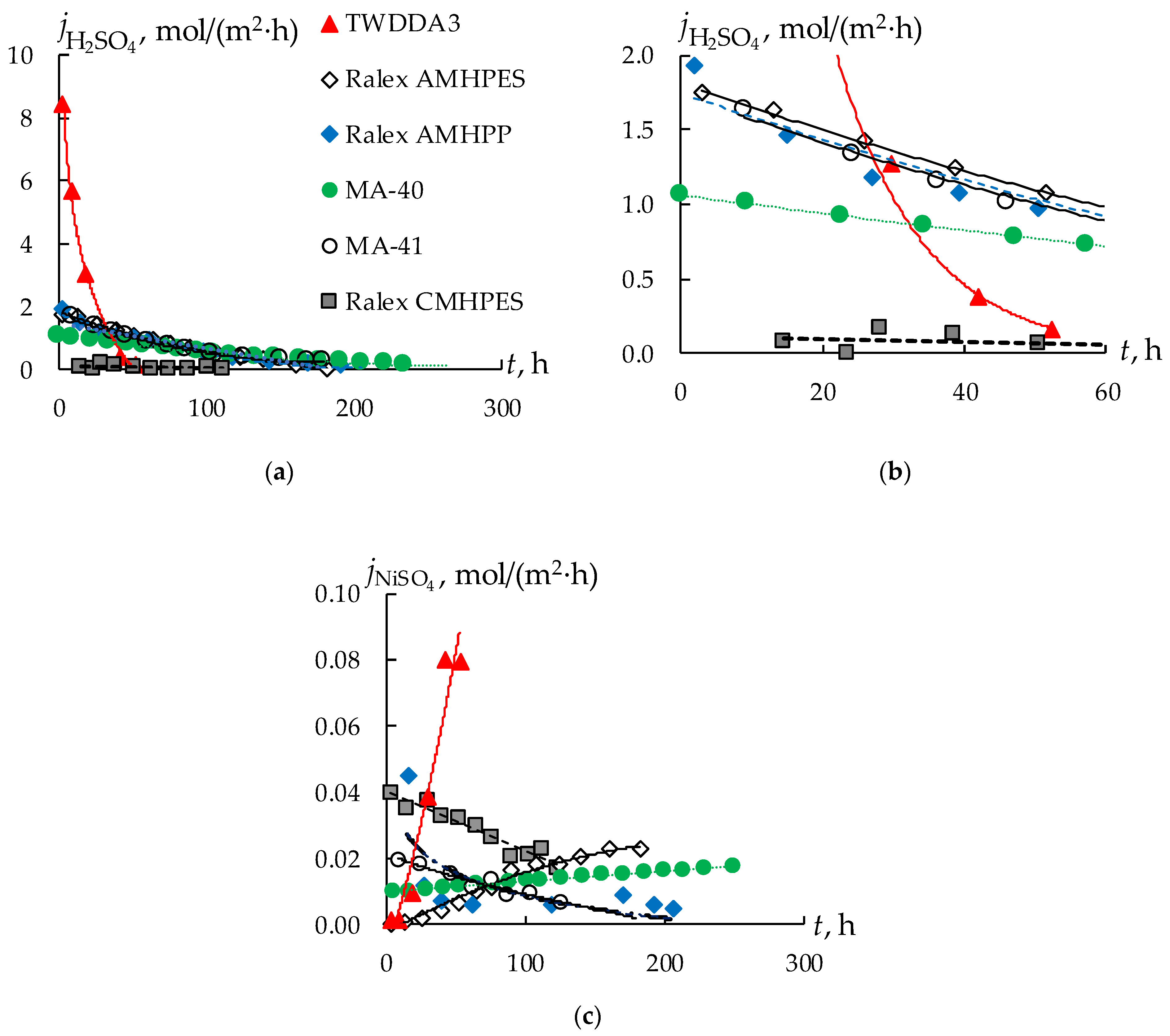
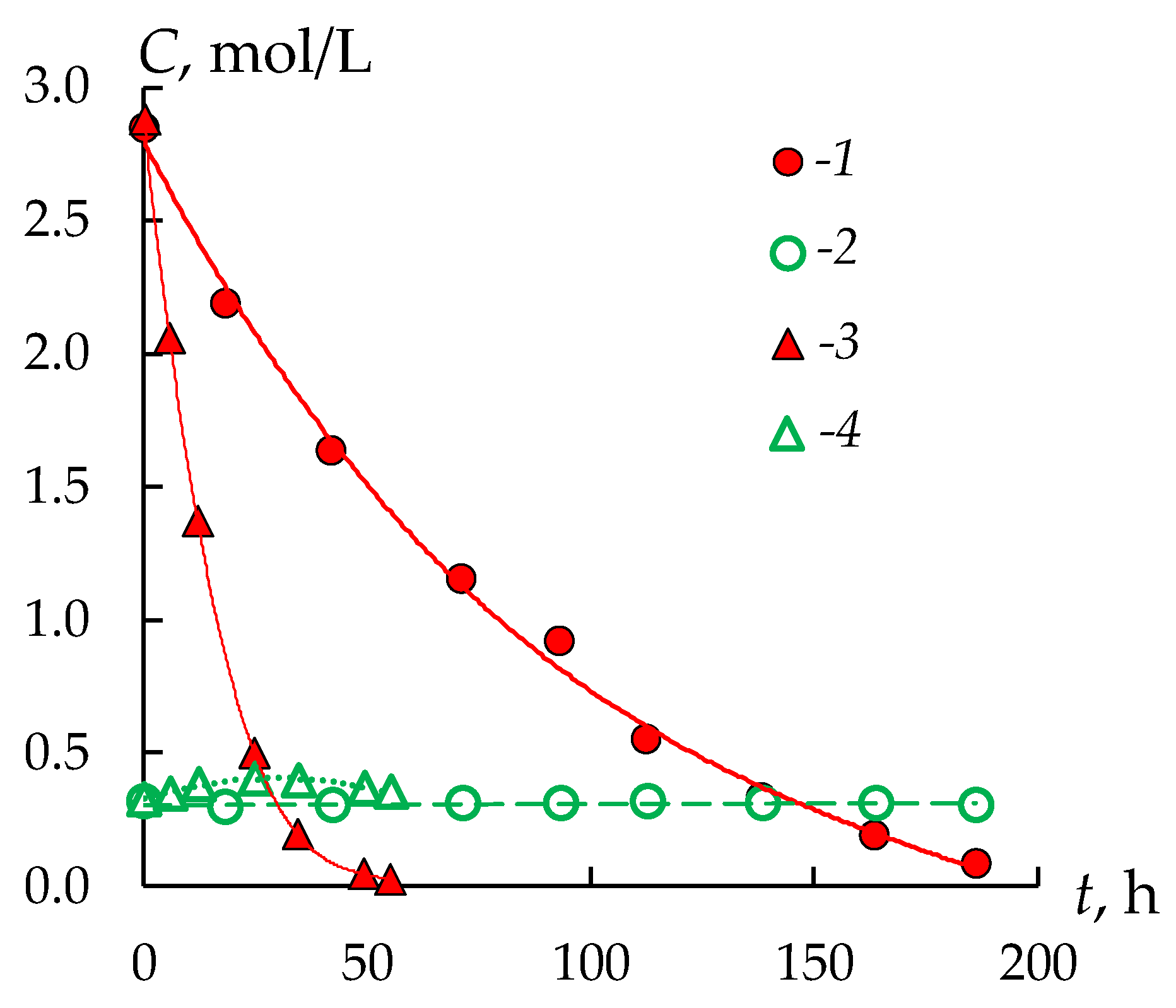
3.1. Sulfuric Acid and Nickel Sulfate Transfer through Membranes
3.2. Water Transport during Diffusion Dialysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols and Abbreviations
| Abbreviations: | ||
| AEM | anion-exchange membrane | |
| CEM | cation-exchange membrane | |
| DD | diffusion dialysis | |
| ED | electrodialysis | |
| IEM | ion-exchange membrane | |
| Greek Letters | ||
| Parameter | Description | Dimension |
| Δ | change in a variable | |
| Χ | recovery of sulfuric acid or loss of nickel sulfate | % |
| Π | osmotic pressure | Pa |
| Φ | molal osmotic coefficient | |
| Ν | Van’t Hoff coefficient | |
| density | ||
| English letters | ||
| Parameter | Description | Dimension |
| C | molar concentration | |
| C | molality of electrolyte | |
| , and | the solvation number of the H+, and Ni2+ ions, respectively | |
| total water flux | ||
| osmotic water flux | ||
| drag flux | ||
| ji | fluxes of i electrolyte | |
| average flux of i electrolyte in time t | ||
| kiso | the membrane gel phase conductivity | S/m |
| l | membrane thickness | m |
| M | molecular weight | |
| m | mass | kg |
| n | amount of a substance | mol |
| water permeability of the IEM | ||
| water permeability coefficient | ||
| Q | ion-exchange capacity | |
| R | universal gas constant | |
| S | membrane area | m2 |
| T | temperature | K |
| t | time | h |
| V | volume | m3 |
| partial molar volume | ||
Appendix A
References
- UN. Secretary-General; World Commission on Environment and Development. Report of the World Commission on Environment and Development: Our Common Future. Available online: https://digitallibrary.un.org/record/139811 (accessed on 17 January 2023).
- Abidli, A.; Huang, Y.; Ben Rejeb, Z.; Zaoui, A.; Park, C.B. Sustainable and efficient technologies for removal and recovery of toxic and valuable metals from wastewater: Recent progress, challenges, and future perspectives. Chemosphere 2022, 292, 133102. [Google Scholar] [CrossRef] [PubMed]
- Du, J.; Waite, T.D.; Biesheuvel, P.M.; Tang, W. Recent advances and prospects in electrochemical coupling technologies for metal recovery from water. J. Hazard. Mater. 2023, 442, 130023. [Google Scholar] [CrossRef] [PubMed]
- Deliyanni, E.A.; Kyzas, G.Z.; Matis, K.A. Various flotation techniques for metal ions removal. J. Mol. Liq. 2017, 225, 260–264. [Google Scholar] [CrossRef]
- Coman, V.; Robotin, B.; Ilea, P. Resources, Conservation and Recycling Nickel recovery/removal from industrial wastes: A review. Resour. Conserv. Recycl. 2013, 73, 229–238. [Google Scholar] [CrossRef]
- Panagopoulos, A. Brine management (saline water & wastewater effluents): Sustainable utilization and resource recovery strategy through Minimal and Zero Liquid Discharge (MLD & ZLD) desalination systems. Chem. Eng. Process. Process Intensif. 2022, 176, 108944. [Google Scholar] [CrossRef]
- Bello, A.S.; Zouari, N.; Da’ana, D.A.; Hahladakis, J.N.; Al-Ghouti, M.A. An overview of brine management: Emerging desalination technologies, life cycle assessment, and metal recovery methodologies. J. Environ. Manag. 2021, 288, 112358. [Google Scholar] [CrossRef]
- Tsai, J.H.; Macedonio, F.; Drioli, E.; Giorno, L.; Chou, C.Y.; Hu, F.C.; Li, C.L.; Chuang, C.J.; Tung, K.L. Membrane-based zero liquid discharge: Myth or reality? J. Taiwan Inst. Chem. Eng. 2017, 80, 192–202. [Google Scholar] [CrossRef]
- Koros, W.J.; Ma, Y.H.; Shimidzu, T. Terminology for membranes and membrane processes (IUPAC Recommendations 1996). Pure Appl. Chem. 1996, 68, 1479–1489. [Google Scholar] [CrossRef]
- Luo, J.; Wu, C.; Xu, T.; Wu, Y. Diffusion dialysis-concept, principle and applications. J. Memb. Sci. 2011, 366, 1–16. [Google Scholar] [CrossRef]
- Vasil’eva, V.I.; Vorob’Eva, E.A. Dynamics of the separation of amino acid and mineral salt in the stationary dialysis of solutions with an MK-40 profiled sulfo group cation exchange membrane. Russ. J. Phys. Chem. A 2012, 86, 1726–1731. [Google Scholar] [CrossRef]
- Vasil’eva, V.; Goleva, E.; Pismenskaya, N.; Kozmai, A.; Nikonenko, V. Effect of surface profiling of a cation-exchange membrane on the phenylalanine and NaCl separation performances in diffusion dialysis. Sep. Purif. Technol. 2019, 210, 48–59. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, W.; Wang, Y. Diffusion dialysis for acid recovery from acidic waste solutions: Anion exchange membranes and technology integration. Membranes 2020, 10, 169. [Google Scholar] [CrossRef] [PubMed]
- Sonoc, A.C.; Jeswiet, J.; Murayama, N.; Shibata, J. A study of the application of Donnan dialysis to the recycling of lithium ion batteries. Hydrometallurgy 2018, 175, 133–143. [Google Scholar] [CrossRef]
- Bendova, H.; Weidlich, T. Application of diffusion dialysis in hydrometallurgical separation of nickel from spent Raney Ni catalyst. Sep. Sci. Technol. 2018, 53, 1218–1222. [Google Scholar] [CrossRef]
- Ng, P.K.; Snyder, D. Mass Transport Characterization of Donnan Dialysis: The Nickel Sulfate System. Proc. Electrochem. Soc. 1981, 81–82, 71–87. [Google Scholar] [CrossRef]
- Yan, J.; Wang, H.; Fu, R.; Fu, R.; Li, R.; Chen, B.; Jiang, C.; Ge, L.; Liu, Z.; Wang, Y.; et al. Ion exchange membranes for acid recovery: Diffusion Dialysis (DD) or Selective Electrodialysis (SED)? Desalination 2022, 531, 115690. [Google Scholar] [CrossRef]
- Merkel, A.; Čopák, L.; Dvořák, L.; Golubenko, D.; Šeda, L. Recovery of spent sulphuric acid by diffusion dialysis using a spiral wound module. Int. J. Mol. Sci. 2021, 22, 11819. [Google Scholar] [CrossRef]
- Ruiz-Aguirre, A.; Lopez, J.; Gueccia, R.; Randazzo, S.; Cipollina, A.; Cortina, J.L.; Micale, G. Diffusion dialysis for the treatment of H2SO4-CuSO4 solutions from electroplating plants: Ions membrane transport characterization and modelling. Sep. Purif. Technol. 2021, 266, 118215. [Google Scholar] [CrossRef]
- Gueccia, R.; Randazzo, S.; Martino, D.C.; Cipollina, A.; Micale, G. Experimental investigation and modeling of diffusion dialysis for HCl recovery from waste pickling solution. J. Environ. Manag. 2019, 235, 202–212. [Google Scholar] [CrossRef]
- Gueccia, R.; Aguirre, A.R.; Randazzo, S.; Cipollina, A.; Micale, G. Diffusion dialysis for separation of hydrochloric acid, iron and zinc ions from highly concentrated pickling solutions. Membranes 2020, 10, 129. [Google Scholar] [CrossRef]
- Xu, T.; Weihua, Y. Tuning the diffusion dialysis performance by surface cross-linking of PPO anion exchange membranes—Simultaneous recovery of sulfuric acid and nickel from electrolysis spent liquor of relatively low acid concentration. J. Hazard. Mater. 2004, 109, 157–164. [Google Scholar] [CrossRef]
- Chen, H.; Rose, M.; Fleming, M.; Souizi, S.; Shashvatt, U.; Blaney, L. Recent advances in Donnan dialysis processes for water/wastewater treatment and resource recovery: A critical review. Chem. Eng. J. 2022, 455, 140522. [Google Scholar] [CrossRef]
- Hammache, Z.; Bensaadi, S.; Berbar, Y.; Audebrand, N.; Szymczyk, A.; Amara, M. Recovery of rare earth elements from electronic waste by diffusion dialysis. Sep. Purif. Technol. 2021, 254, 117641. [Google Scholar] [CrossRef]
- Cheng, C.; Li, P.; He, Y.; Hu, X.; Emmanuel, K. Branched Polyvinyl Alcohol Hybrid Membrane for Acid Recovery via Diffusion Dialysis. Chem. Eng. Technol. 2019, 42, 1180–1187. [Google Scholar] [CrossRef]
- Vatanpour, V.; Teber, O.O.; Mehrabi, M.; Koyuncu, I. Polyvinyl alcohol-based separation membranes: A comprehensive review on fabrication techniques, applications and future prospective. Mater. Today Chem. 2023, 28, 101381. [Google Scholar] [CrossRef]
- Noubli, A.; Akretche, D.E.; Crespo, J.G.; Velizarov, S. Complementary membrane-based processes for recovery and preconcentration of phosphate from industrial wastewater. Sep. Purif. Technol. 2020, 234, 116123. [Google Scholar] [CrossRef]
- Technical Datasheet. Spiral Membrane Module. Available online: https://www.spiraltecgmbh.com/en/downloads-en.html (accessed on 17 January 2023).
- Demina, O.A.; Demin, A.V.; Gnusin, N.P.; Zabolotskii, V.I. Effect of an aprotic solvent on the properties and structure of ion-exchange membranes. Polym. Sci. Ser. A 2010, 52, 1270–1282. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Demin, A.V.; Demina, O.A. Solvation of lithium chloride in aqueous and mixed solutions of an aprotic solvent. Russ. J. Phys. Chem. A 2013, 87, 194–198. [Google Scholar] [CrossRef]
- Product Data Sheet. Ralex® Membrane. Available online: https://www.mega.cz/membranes/ (accessed on 17 January 2023).
- Zabolotskiy, V.I.; But, A.Y.; Vasil’eva, V.I.; Akberova, E.M.; Melnikov, S.S. Ion transport and electrochemical stability of strongly basic anion-exchange membranes under high current electrodialysis conditions. J. Memb. Sci. 2017, 526, 60–72. [Google Scholar] [CrossRef]
- Berezina, N.P.; Kononenko, N.A.; Demina, O.A.; Gnusin, N.P. Model approach for describing the properties of ion-exchange membranes. Polym. Sci. Ser. A 2004, 46, 672–680. [Google Scholar]
- Melnikov, S.; Kolot, D.; Nosova, E.; Zabolotskiy, V. Peculiarities of transport-structural parameters of ion-exchange membranes in solutions containing anions of carboxylic acids. J. Memb. Sci. 2018, 557, 1–12. [Google Scholar] [CrossRef]
- Davydov, D.; Nosova, E.; Loza, S.; Achoh, A.; Korzhov, A.; Sharafan, M.; Melnikov, S. Use of the microheterogeneous model to assess the applicability of ion-exchange membranes in the process of generating electricity from a concentration gradient. Membranes 2021, 11, 406. [Google Scholar] [CrossRef] [PubMed]
- Demina, O.A.; Berezina, N.P.; Sata, T.; Demin, A.V. Transport-structural parameters of domestic and foreign anion-exchange membranes. Russ. J. Electrochem. 2002, 38, 896–902. [Google Scholar] [CrossRef]
- Loza, S.; Loza, N.; Kutenko, N.; Smyshlyaev, N. Profiled Ion-Exchange Membranes for Reverse and Conventional Electrodialysis. Membr. Technol. 2022, 12, 985. [Google Scholar] [CrossRef] [PubMed]
- Yaroslavtsev, A.B.; Nikonenko, V.V. Ion-exchange membrane materials: Properties, modification, and practical application. Nanotechnol. Russ. 2009, 4, 137–159. [Google Scholar] [CrossRef]
- Volodina, E.; Pismenskaya, N.; Nikonenko, V.; Larchet, C.; Pourcelly, G. Ion transfer across ion-exchange membranes with homogeneous and heterogeneous surfaces. J. Colloid Interface Sci. 2005, 285, 247–258. [Google Scholar] [CrossRef]
- Akberova, E.M.; Vasil’eva, V.I. Effect of the resin content in cation-exchange membranes on development of electroconvection. Electrochem. Commun. 2020, 111, 106659. [Google Scholar] [CrossRef]
- Melnikov, S.; Shkirskaya, S. Transport properties of bilayer and multilayer surface-modified ion-exchange membranes. J. Memb. Sci. 2019, 590, 117272. [Google Scholar] [CrossRef]
- Vasil’eva, V.I.; Kranina, N.A.; Malykhin, M.D.; Akberova, E.M.; Zhiltsova, A.V. The surface inhomogeneity of ion-exchange membranes by SEM and AFM data. J. Surf. Investig. 2013, 7, 144–153. [Google Scholar] [CrossRef]
- Kononenko, N.; Nikonenko, V.; Grande, D.; Larchet, C.; Dammak, L.; Fomenko, M.; Volfkovich, Y. Porous structure of ion exchange membranes investigated by various techniques. Adv. Colloid Interface Sci. 2017, 246, 196–216. [Google Scholar] [CrossRef]
- Berezina, N.P.; Kononenko, N.A.; Dyomina, O.A.; Gnusin, N.P. Characterization of ion-exchange membrane materials: Properties vs. structure. Adv. Colloid Interface Sci. 2008, 139, 3–28. [Google Scholar] [CrossRef] [PubMed]
- Zabolotsky, V.I.; Nikonenko, V.V. Effect of structural membrane inhomogeneity on transport properties. J. Memb. Sci. 1993, 79, 181–198. [Google Scholar] [CrossRef]
- Diffusion Dialysis Membrane for Acid Recovery. Product Introduction. Available online: http://en.sdtianwei.com/product/145.html (accessed on 17 January 2023).
- Demina, O.A.; Kononenko, N.A.; Falina, I.V.; Demin, A.V. Theoretical estimation of differential coefficients of ion-exchange membrane diffusion permeability. Colloid J. 2017, 79, 317–327. [Google Scholar] [CrossRef]
- Robinson, R.A.; Stokes, R.H. Electrolyte solutions. In The Measurement and Interpretation of Conductance, Chemical Potential and Diffusion in Solutions of Simple Electrolytes, 2nd ed.; Butterworths Scientific Publications: London, UK, 1959. [Google Scholar]
- Pitzer, K.S.; Roy, R.N.; Silvester, L.F. Thermodynamics of Electrolytes. 7. Sulfuric Acid. J. Am. Chem. Soc. 1977, 99, 4930–4936. [Google Scholar] [CrossRef]
- Pitzer, K.S. Thermodynamics of electrolytes. I. Theoretical basis and general equations. J. Phys. Chem. 1972, 77, 268–277. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Mayorga, G. Thermodynamics of electrolytes. II. Activity and osmotic coefficients for strong electrolytes with one or both ions univalent. J. Phys. Chem. 1973, 77, 2300–2308. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Mayorga, G. Thermodynamics of electrolytes. III. Activity and osmotic coefficients for 2-2 electrolytes. J. Solut. Chem. 1974, 3, 539–546. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Kim, J.J. Thermodynamics of Electrolytes. IV. Activity and Osmotic Coefficients for Mixed Electrolytes. J. Am. Chem. Soc. 1974, 96, 5701–5707. [Google Scholar] [CrossRef]
- Van Gauwbergen, D.; Baeyens, J.; Creemers, C. Modeling osmotic pressures for aqueous solutions for 2-1 and 2-2 electrolytes. Desalination 1997, 109, 57–65. [Google Scholar] [CrossRef]
- Sergievskii, V.V.; Rudakov, A.M. Dependence of the osmotic coefficients and average ionic activity coefficients on hydrophobic hydration in solutions. Russ. J. Phys. Chem. A 2016, 90, 1567–1573. [Google Scholar] [CrossRef]
- Rudakov, A.M.; Sergievskii, V.V.; Nagovitsyna, O.A. Dependences of the osmotic coefficients of aqueous calcium chloride solutions on concentration at different temperatures. Russ. J. Phys. Chem. A 2017, 91, 2361–2365. [Google Scholar] [CrossRef]
- Adapa, S.; Malani, A. Cation hydration by confined water and framework-atoms have crucial role on thermodynamics of clay swelling. Sci. Rep. 2022, 12, 17810. [Google Scholar] [CrossRef] [PubMed]
- Kiriukhin, M.Y.; Collins, K.D. Dynamic hydration numbers for biologically important ions. Biophys. Chem. 2002, 99, 155–168. [Google Scholar] [CrossRef]
- Ohtaki, H.; Radnai, T. Structure and Dynamics of Hydrated Ions. Chem. Rev. 1993, 93, 1157–1204. [Google Scholar] [CrossRef]
- Vchirawongkwin, V.; Rode, B.M.; Persson, I. Structure and dynamics of sulfate ion in aqueous solution-an ab initio QMCF MD simulation and large angle X-ray scattering study. J. Phys. Chem. B 2007, 111, 4150–4155. [Google Scholar] [CrossRef]
- Mulder, M. Basic Principles of Membrane Technology, 2nd ed.; Springer Dordrecht: Dordrecht, The Netherlands, 1996; ISBN 978-0-7923-4248-9. [Google Scholar]
- Schlögl, R. Elektrodiffusion in freier Lösung und geladenen Membranen. Z. Phys. Chem. 1954, 1, 305–339. [Google Scholar] [CrossRef]


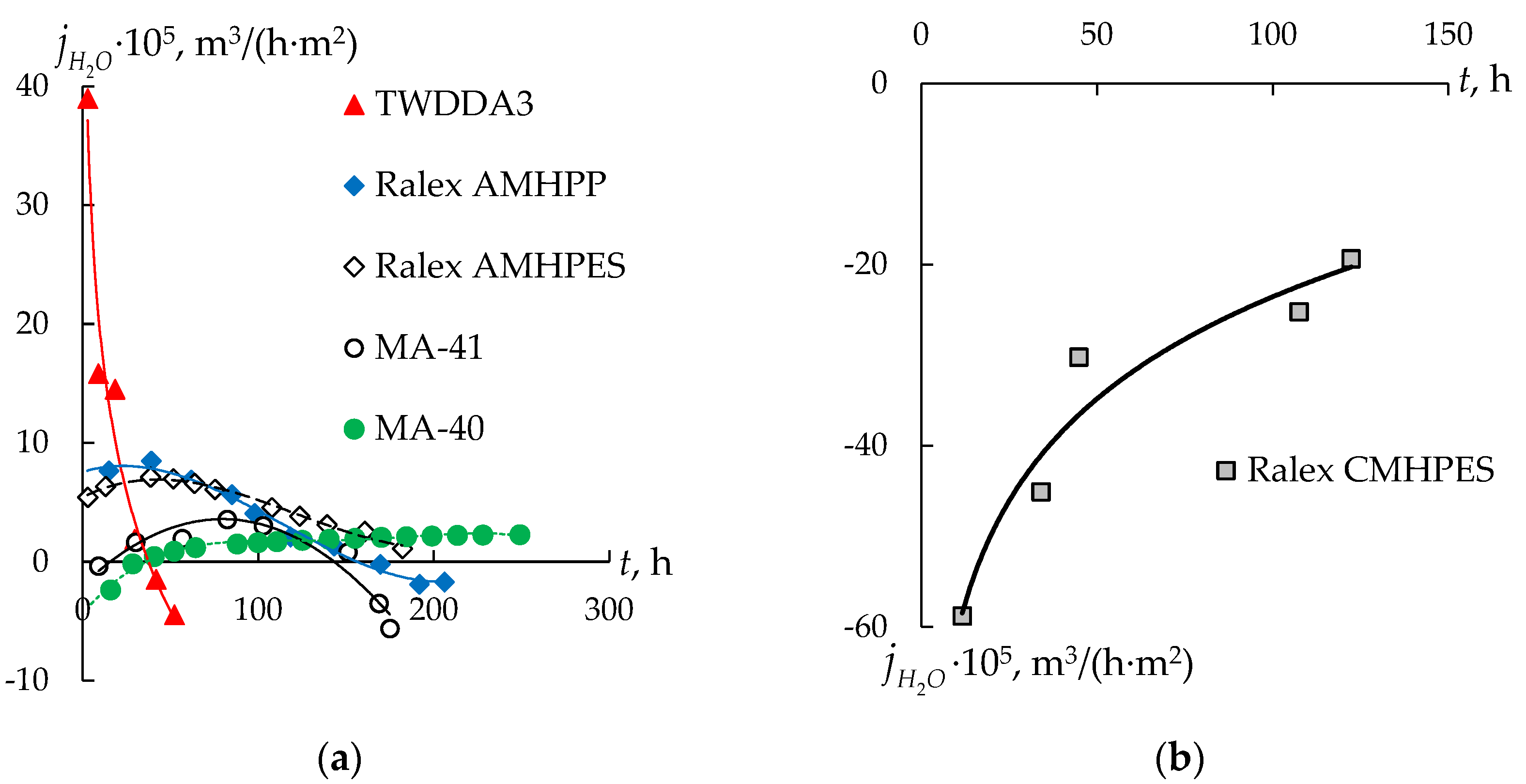
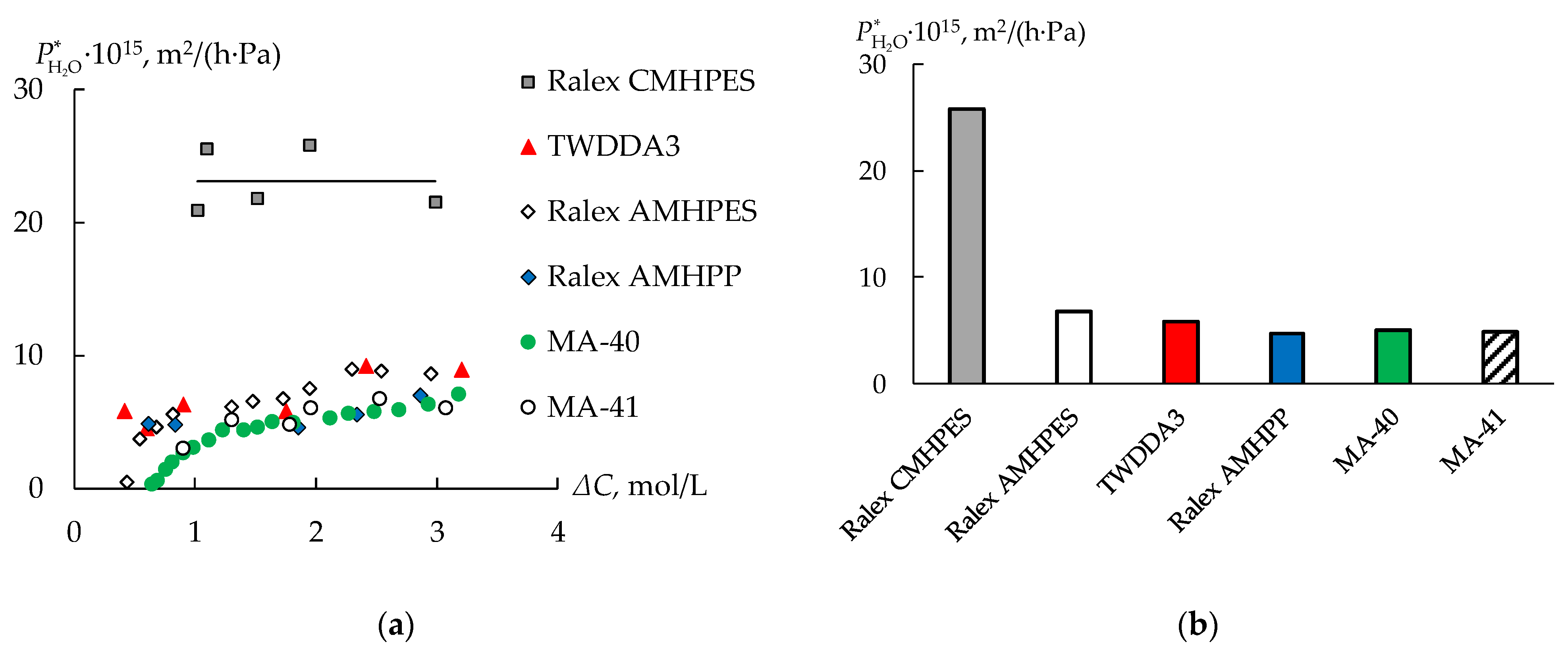
| Sample No. | Membrane | Ionogenic Groups | Reinforcing Mesh | Q, mmol/gwet | W, % | kiso, S/m | Counter-Ion Transport Number | l, μm |
|---|---|---|---|---|---|---|---|---|
| 1 | Ralex AMHPES | quaternary ammonium bases | polyester | 1.05 | 66.3 | 0.42–0.46 [34,35] | >0.95 [31] | 550 |
| 2 | Ralex AMHPP | quaternary ammonium bases | polypropylene | 0.97 | 71.3 | - | >0.95 [31] | 550 |
| 3 | Ralex CMHPES | sulfonic groups | polyester | 1.16 | 79.9 | 0.35–0.40 [34,35] | >0.95 [31] | 530 |
| 4 | MA-40 | secondary and tertiary amines | nylon | 2.15 | 53.0 | 0.08 [33,36] | 0.94 [36] | 520 |
| 5 | MA-41 | quaternary ammonium bases | nylon | 0.54 | 49.1 | 0.19–0.28 [35,37] | 0.96 [36] | 420 |
| 6 | TWDDA3 | quaternary ammonium bases | polyphenylene oxide | 0.49 | 98.3 | - | - | 145 |
| Solution Component | Concentration, g/L |
|---|---|
| H2SO4 | 252.3 |
| Ni2+ | 20.9 |
| Zn2+ | 2.3 |
| Fe2+ | 1.08 |
| Cu2+ | 0.90 |
| Total Sn | 0.080 |
| Total Sb | 0.050 |
| Total Cd | 0.045 |
| Total Pb | 0.015 |
| Total As | 0.003 |
| 80 | 85 | 90 | 95 | |
|---|---|---|---|---|
| TWDDA3 | ||||
| H2SO4 | 4.63 | 4.64 | 4.48 | 3.95 |
| NiSO4 | 0.001 | 0.003 | 0.004 | 0.010 |
| MA-41 | ||||
| H2SO4 | 1.02 | 0.96 | 0.88 | 0.77 |
| NiSO4 | 0.016 | 0.016 | 0.015 | 0.010 |
| MA-40 | ||||
| H2SO4 | 0.66 | 0.62 | 0.56 | 0.49 |
| NiSO4 | 0.0003 | 0.001 | 0.002 | 0.003 |
| Ralex AMHPES | ||||
| H2SO4 | 1.12 | 1.06 | 0.98 | 0.87 |
| NiSO4 | 0.001 | 0.003 | 0.004 | 0.007 |
| Ralex AMHPP | ||||
| H2SO4 | 1.08 | 1.03 | 0.94 | 0.82 |
| NiSO4 | 0.012 | 0.011 | 0.010 | 0.010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loza, S.; Loza, N.; Kovalchuk, N.; Romanyuk, N.; Loza, J. Comparative Study of Different Ion-Exchange Membrane Types in Diffusion Dialysis for the Separation of Sulfuric Acid and Nickel Sulfate. Membranes 2023, 13, 396. https://doi.org/10.3390/membranes13040396
Loza S, Loza N, Kovalchuk N, Romanyuk N, Loza J. Comparative Study of Different Ion-Exchange Membrane Types in Diffusion Dialysis for the Separation of Sulfuric Acid and Nickel Sulfate. Membranes. 2023; 13(4):396. https://doi.org/10.3390/membranes13040396
Chicago/Turabian StyleLoza, Sergey, Natalia Loza, Nikita Kovalchuk, Nazar Romanyuk, and Julia Loza. 2023. "Comparative Study of Different Ion-Exchange Membrane Types in Diffusion Dialysis for the Separation of Sulfuric Acid and Nickel Sulfate" Membranes 13, no. 4: 396. https://doi.org/10.3390/membranes13040396
APA StyleLoza, S., Loza, N., Kovalchuk, N., Romanyuk, N., & Loza, J. (2023). Comparative Study of Different Ion-Exchange Membrane Types in Diffusion Dialysis for the Separation of Sulfuric Acid and Nickel Sulfate. Membranes, 13(4), 396. https://doi.org/10.3390/membranes13040396







