Pore-Scale Modeling of Microporous Layer for Proton Exchange Membrane Fuel Cell: Effective Transport Properties
Abstract
:Highlights
- Stochastic numerical method is carried out to reconstruct the realistic microstructure of microporous layer (MPL) in a PEMFC.
- Computation of effective transport properties by Pore Scale Model and lattice Boltzmann Method is carried out.
- The relationships between effective transport properties and compression strain are summarized.
- Correlations between effective transport properties and compression strain are obtained and used to predict PEMFC performance.
Abstract
1. Introduction
2. Numerical Analysis Procedure
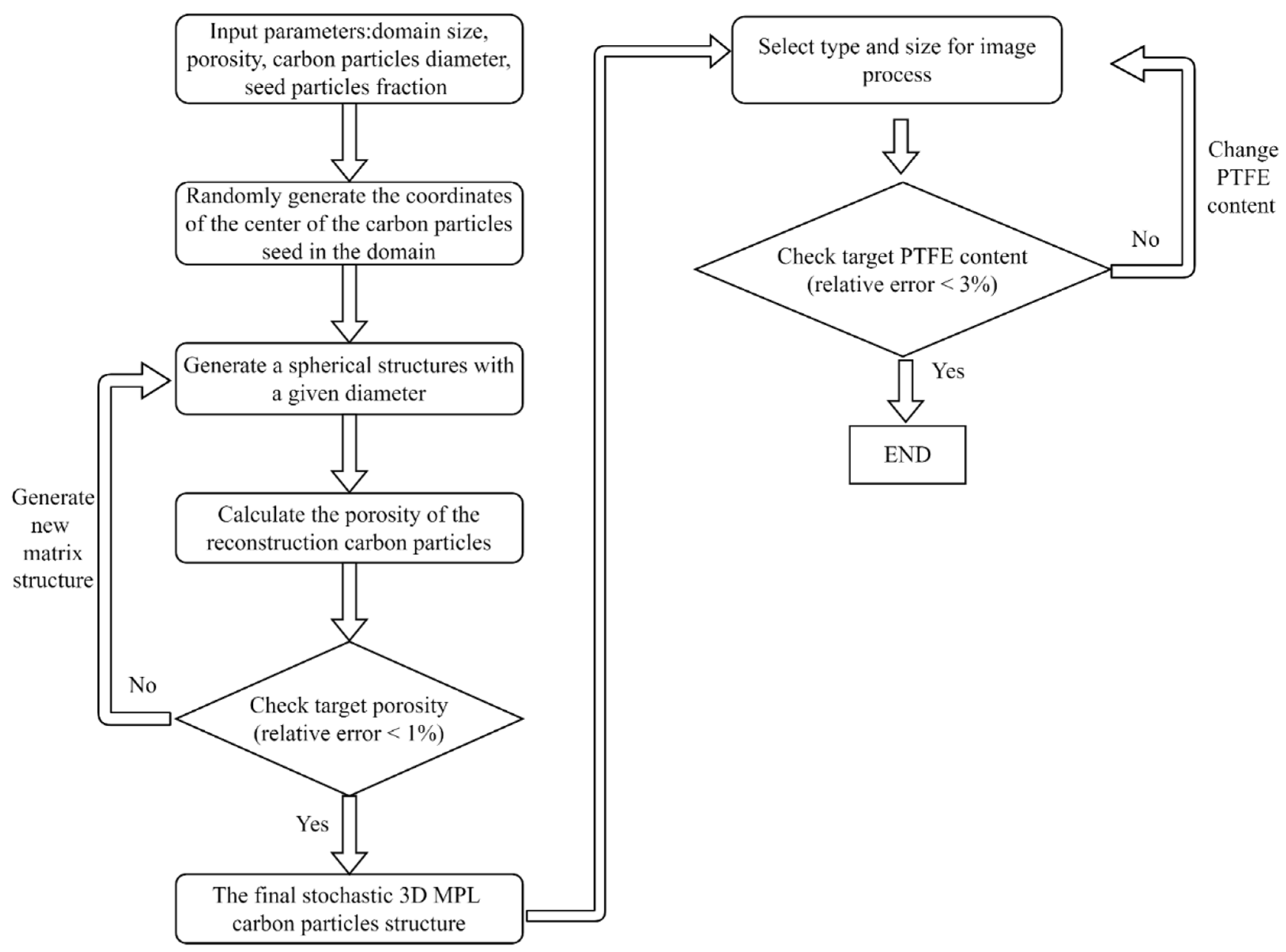
2.1. 3D Reconstruction of the MPL
2.2. Governing Equations of PSM
2.3. Governing Equations of LBM
3. Results and Discussions
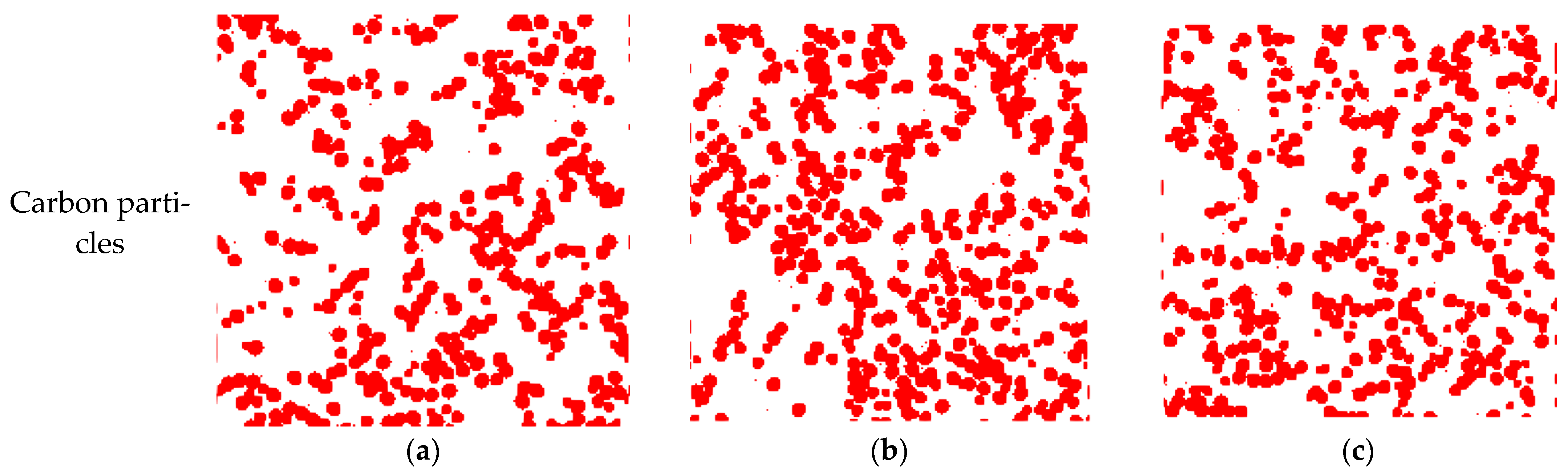
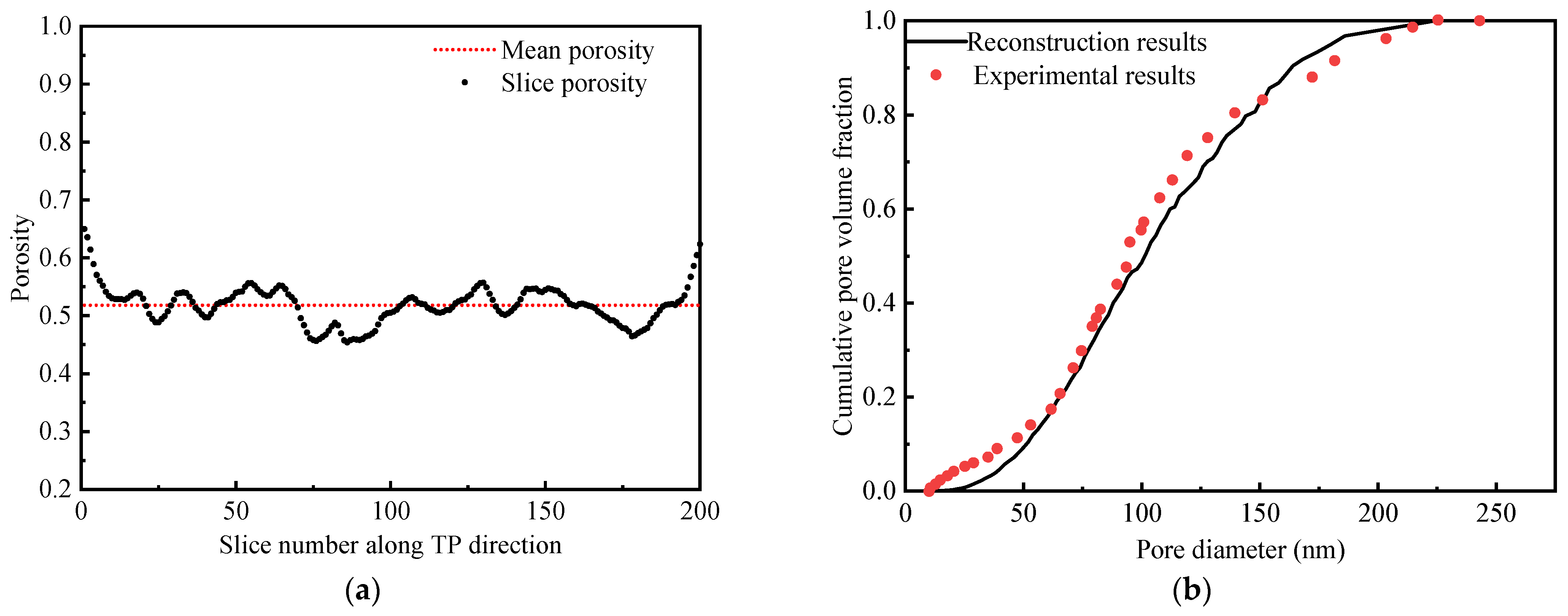
3.1. Reconstructed MPL Microstructure
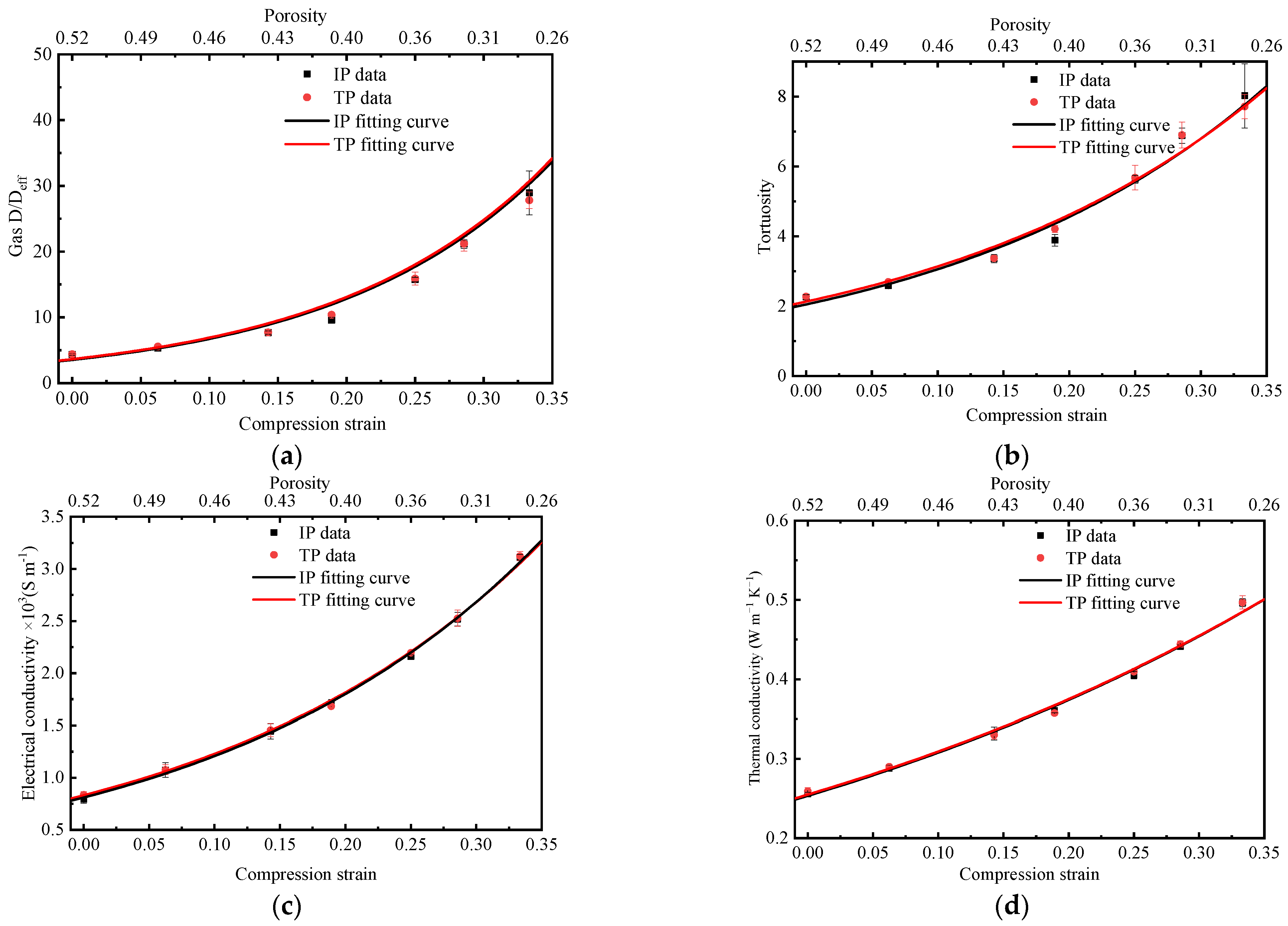
3.2. Effective Gas Diffusivity, Thermal and Electrical Conductivity
3.3. Effective Liquid Water Permeability and Saturation
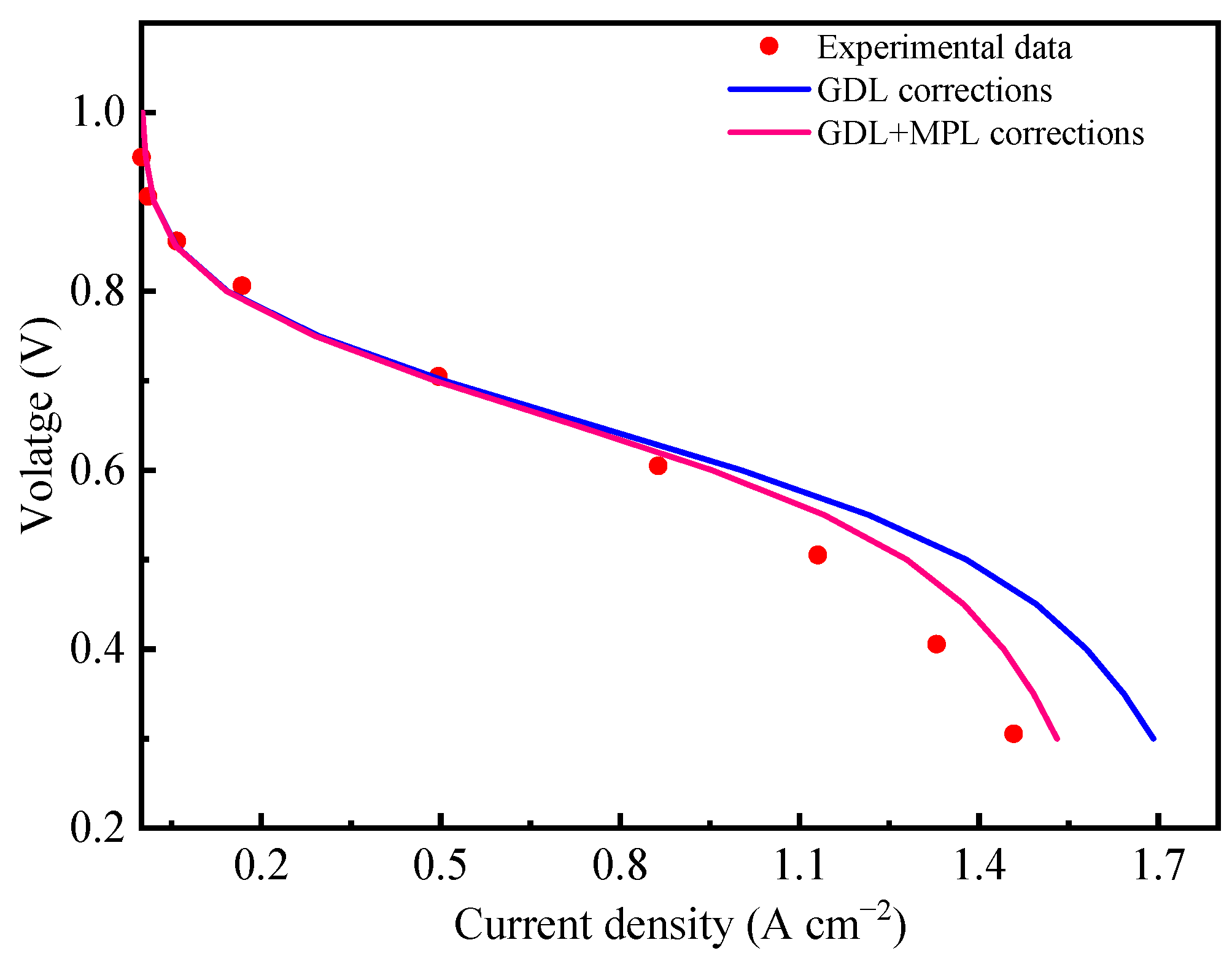
3.4. Application of Effective Transport Parameters in an MPL
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiao, K.; Xuan, J.; Du, Q.; Bao, Z.; Xie, B.; Wang, B.; Zhao, Y.; Fan, L.; Wang, H.; Hou, Z.; et al. Designing the next generation of proton-exchange membrane fuel cells. Nature 2021, 595, 361–369. [Google Scholar] [CrossRef] [PubMed]
- Sarker, M.; Rahman, A.; Mojica, F.; Mehrazi, S.; Kort-Kamp, W.J.; Chuang, P.-Y.A. Experimental and computational study of the microporous layer and hydrophobic treatment in the gas diffusion layer of a proton exchange membrane fuel cell. J. Power Sources 2021, 509, 230350. [Google Scholar] [CrossRef]
- Mojica, F.; Rahman, A.; Sarker, M.; Hussey, D.S.; Jacobson, D.L.; LaManna, J.M.; Chuang, P.-Y.A. Study of converging-diverging channel induced convective mass transport in a proton exchange membrane fuel cell. Energy Convers. Manag. 2021, 237, 114095. [Google Scholar] [CrossRef]
- Zhang, H.; Xiao, L.; Chuang, P.-Y.A.; Djilali, N.; Sui, P.-C. Coupled stress–strain and transport in proton exchange membrane fuel cell with metallic bipolar plates. Appl. Energy 2019, 251, 113316. [Google Scholar] [CrossRef]
- Chuang, P.-Y.A.; Rahman, A.; Mojica, F.; Hussey, D.S.; Jacobson, D.L.; LaManna, J.M. The interactive effect of heat and mass transport on water condensation in the gas diffusion layer of a proton exchange membrane fuel cell. J. Power Sources 2020, 480, 229121. [Google Scholar] [CrossRef]
- Mehrazi, S.; Sarker, M.; Mojica, F.; Rolfe, P.; Chuang, P.-Y.A. A rheological approach to studying process-induced structural evolution of the microporous layer in a proton exchange membrane fuel cell. Electrochimica Acta 2021, 389, 138690. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, B.; Jin, J.; Yang, S.; Li, G. A review of the microporous layer in proton exchange membrane fuel cells: Materials and structural designs based on water transport mechanism. Renew. Sustain. Energy Rev. 2022, 156, 111998. [Google Scholar] [CrossRef]
- Bock, R.; Shum, A.D.; Xiao, X.; Karoliussen, H.; Seland, F.; Zenyuk, I.V.; Burheim, O.S. Thermal Conductivity and Compaction of GDL-MPL Interfacial Composite Material. J. Electrochem. Soc. 2018, 165, F514–F525. [Google Scholar] [CrossRef]
- Zhou, J.; Shukla, S.; Putz, A.; Secanell, M. Analysis of the role of the microporous layer in improving polymer electrolyte fuel cell performance. Electrochimica Acta 2018, 268, 366–382. [Google Scholar] [CrossRef]
- Zhang, H.; Rahman, A.; Mojica, F.; Sui, P.; Chuang, P.A. A comprehensive two-phase proton exchange membrane fuel cell model coupled with anisotropic properties and mechanical deformation of the gas diffusion layer. Electrochimica Acta 2021, 382, 138273. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Karageorgiou, C.; Eller, J.; Schmidt, T.J.; Büchi, F.N. Determination of the porosity and its heterogeneity of fuel cell mi-croporous layers by X-ray tomographic microscopy. J. Power Sources 2022, 539, 231612. [Google Scholar] [CrossRef]
- Li, B.; Xie, M.; Ji, H.; Chu, T.; Yang, D.; Ming, P.; Zhang, C. Optimization of cathode microporous layer materials for proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2021, 46, 14674–14686. [Google Scholar] [CrossRef]
- Simon, C.; Kartouzian, D.; Müller, D.; Wilhelm, F.; Gasteiger, H.A. Impact of Microporous Layer Pore Properties on Liquid Water Transport in PEM Fuel Cells: Carbon Black Type and Perforation. J. Electrochem. Soc. 2017, 164, F1697–F1711. [Google Scholar] [CrossRef]
- Tabe, Y.; Aoyama, Y.; Kadowaki, K.; Suzuki, K.; Chikahisa, T. Impact of micro-porous layer on liquid water distribution at the catalyst layer interface and cell performance in a polymer electrolyte membrane fuel cell. J. Power Sources 2015, 287, 422–430. [Google Scholar] [CrossRef]
- Prass, S.; Hasanpour, S.; Sow, P.K.; Phillion, A.B.; Mérida, W. Microscale X-ray tomographic investigation of the interfacial morphology between the catalyst and micro porous layers in proton exchange membrane fuel cells. J. Power Sources 2016, 319, 82–89. [Google Scholar] [CrossRef]
- Nagai, Y.; Eller, J.; Hatanaka, T.; Yamaguchi, S.; Kato, S.; Kato, A.; Marone, F.; Xu, H.; Büchi, F.N. Improving water management in fuel cells through mi-croporous layer modifications: Fast operando tomographic imaging of liquid water. J. Power Sources 2019, 435, 226809. [Google Scholar] [CrossRef]
- Lee, J.; Liu, H.; George, M.; Banerjee, R.; Ge, N.; Chevalier, S.; Kotaka, T.; Tabuchi, Y.; Bazylak, A. Microporous layer to carbon fibre substrate interface impact on polymer electrolyte membrane fuel cell performance. J. Power Sources 2019, 422, 113–121. [Google Scholar] [CrossRef]
- Spernjak, D.; Mukundan, R.; Borup, R.L.; Connolly, L.G.; Zackin, B.I.; De Andrade, V.; Wojcik, M.; Parkinson, D.Y.; Jacobson, D.L.; Hussey, D.S.; et al. Enhanced Water Management of Polymer Electrolyte Fuel Cells with Additive-Containing Microporous Layers. ACS Appl. Energy Mater. 2018, 1, 6006–6017. [Google Scholar] [CrossRef]
- Xu, Y.; Fan, R.; Chang, G.; Xu, S.; Cai, T. Investigating temperature-driven water transport in cathode gas diffusion media of PEMFC with a non-isothermal, two-phase model. Energy Convers. Manag. 2021, 248, 114791. [Google Scholar] [CrossRef]
- Ira, Y.; Bakhshan, Y.; Khorshidimalahmadi, J. Effect of wettability heterogeneity and compression on liquid water transport in gas diffusion layer coated with microporous layer of PEMFC. Int. J. Hydrogen Energy 2021, 46, 17397–17413. [Google Scholar] [CrossRef]
- Hou, Y.; Li, X.; Du, Q.; Jiao, K.; Zamel, N. Pore-Scale Investigation of the Effect of Micro-Porous Layer on Water Transport in Proton Exchange Membrane Fuel Cell. J. Electrochem. Soc. 2020, 167, 144504. [Google Scholar] [CrossRef]
- El Hannach, M.; Singh, R.; Djilali, N.; Kjeang, E. Micro-porous layer stochastic reconstruction and transport parameter determi-nation. J. Power Sources 2015, 282, 58–64. [Google Scholar] [CrossRef]
- Andisheh-Tadbir, M.; Kjeang, E.; Bahrami, M. Thermal conductivity of microporous layers: Analytical modeling and experimental validation. J. Power Sources 2015, 296, 344–351. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Y.; Ostadi, H.; Jiang, K.; Chen, R. Modelling water intrusion and oxygen diffusion in a reconstructed microporous layer of PEM fuel cells. Int. J. Hydrogen Energy 2014, 39, 17222–17230. [Google Scholar] [CrossRef]
- Sadeghifar, H.; Djilali, N.; Bahrami, M. Effect of Polytetrafluoroethylene (PTFE) and micro porous layer (MPL) on thermal con-ductivity of fuel cell gas diffusion layers: Modeling and experiments. J. Power Sources 2014, 248, 632–641. [Google Scholar] [CrossRef]
- Becker, J.; Wieser, C.; Fell, S.; Steiner, K. A multi-scale approach to material modeling of fuel cell diffusion media. Int. J. Heat Mass Transf. 2011, 54, 1360–1368. [Google Scholar] [CrossRef]
- Zamel, N.; Becker, J.; Wiegmann, A. Estimating the thermal conductivity and diffusion coefficient of the microporous layer of polymer electrolyte membrane fuel cells. J. Power Sources 2012, 207, 70–80. [Google Scholar] [CrossRef]
- Deng, H.; Hou, Y.; Jiao, K. Lattice Boltzmann simulation of liquid water transport inside and at interface of gas diffusion and micro-porous layers of PEM fuel cells. Int. J. Heat Mass Transf. 2019, 140, 1074–1090. [Google Scholar] [CrossRef]
- Aoyama, Y.; Suzuki, K.; Tabe, Y.; Chikahisa, T.; Tanuma, T. Water Transport and PEFC Performance with Different Interface Structure between Micro-Porous Layer and Catalyst Layer. J. Electrochem. Soc. 2016, 163, F359–F366. [Google Scholar] [CrossRef]
- Nozaki, R.; Tabe, Y.; Chikahisa, T.; Tanuma, T. Analysis of Oxygen Transport Resistance Components and Water Transport Phe-nomena with Hydrophilic and Hydrophobic MPL in PEFC. ECS Trans. 2017, 80, 335. [Google Scholar] [CrossRef]
- Nanjundappa, A.; Alavijeh, A.S.; El Hannach, M.; Harvey, D.; Kjeang, E. A customized framework for 3-D morphological charac-terization of microporous layers. Electrochimica Acta 2013, 110, 349–357. [Google Scholar] [CrossRef]
- Zhu, L.; Yang, W.; Xiao, L.; Zhang, H.; Gao, X.; Sui, P.-C. Stochastically Modeled Gas Diffusion Layers: Effects of Binder and Polytet-rafluoroethylene on Effective Gas Diffusivity. J. Electrochem. Soc. 2021, 168, 014514. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, L.; Harandi, H.B.; Duan, K.; Zeis, R.; Sui, P.-C.; Chuang, P.A. Microstructure reconstruction of the gas diffusion layer and analyses of the anisotropic transport properties. Energy Convers. Manag. 2021, 241, 114293. [Google Scholar] [CrossRef]
- Lange, K.J.; Sui, P.-C.; Djilali, N. Pore scale modeling of a proton exchange membrane fuel cell catalyst layer: Effects of water vapor and temperature. J. Power Sources 2011, 196, 3195–3203. [Google Scholar] [CrossRef]
- Sui, P.C.; Djilali, N.; Wang, Q. A Pore Scale Model for the Transport Phenomena in the Catalyst Layer of a PEM Fuel Cell. In Proceedings of the ASME 2008 First International Conference on Micro/Nanoscale Heat Transfer, Tainan, Taiwan, 6–9 June 2008. [Google Scholar] [CrossRef]
- Lange, K.J.; Sui, P.-C.; Djilali, N. Pore Scale Simulation of Transport and Electrochemical Reactions in Reconstructed PEMFC Catalyst Layers. J. Electrochem. Soc. 2010, 157, B1434–B1442. [Google Scholar] [CrossRef]
- Niu, X.-D.; Munekata, T.; Hyodo, S.-A.; Suga, K. An investigation of water-gas transport processes in the gas-diffusion-layer of a PEM fuel cell by a multiphase multiple-relaxation-time lattice Boltzmann model. J. Power Sources 2007, 172, 542–552. [Google Scholar] [CrossRef]
- Gallagher, K.G.; Darling, R.M.; Patterson, T.W.; Perry, M.L. Capillary Pressure Saturation Relations for PEM Fuel Cell Gas Diffusion Layers. J. Electrochem. Soc. 2008, 155, B1225–B1231. [Google Scholar] [CrossRef]
- Rahman, A.; Mojica, F.; Sarker, M.; Chuang, P.-Y.A. Development of 1-D multiphysics PEMFC model with dry limiting current experimental validation. Electrochimica Acta 2019, 320, 134601. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, H.; Xiao, L.; Bazylak, A.; Gao, X.; Sui, P.-C. Pore-scale modeling of gas diffusion layers: Effects of compression on transport properties. J. Power Sources 2021, 496, 229822. [Google Scholar] [CrossRef]
- Chi, P.; Chan, S.; Weng, F.; Su, A.; Sui, P.; Djilali, N. On the effects of non-uniform property distribution due to compression in the gas diffusion layer of a PEMFC. Int. J. Hydrogen Energy 2010, 35, 2936–2948. [Google Scholar] [CrossRef]
- Nishiyama, N.; Yokoyama, T. Permeability of porous media: Role of the critical pore size. J. Geophys. Res. Solid Earth 2017, 122, 6955–6971. [Google Scholar] [CrossRef]
- Bao, Z.; Li, Y.; Zhou, X.; Gao, F.; Du, Q.; Jiao, K. Transport properties of gas diffusion layer of proton exchange membrane fuel cells: Effects of compression. Int. J. Heat Mass Transf. 2021, 178, 121608. [Google Scholar] [CrossRef]
- Cai, J.; Yu, B. A Discussion of the Effect of Tortuosity on the Capillary Imbibition in Porous Media. Transp. Porous Media 2011, 89, 251–263. [Google Scholar] [CrossRef]
- Lin, R.; Chen, L.; Zheng, T.; Tang, S.; Yu, X.; Dong, M.; Hao, Z. Interfacial water management of gradient microporous layer for self-humidifying proton exchange membrane fuel cells. Int. J. Heat Mass Transf. 2021, 175, 121340. [Google Scholar] [CrossRef]




| Parameters | ||
|---|---|---|
| mol m−3 | 8 | 7.9 |
| /mol m−3 | 9.9 | 10 |
| V | 0.75 | 0.76 |
| 355.9 | 356 |
| In-Plane | Through-Plane | |||||||
|---|---|---|---|---|---|---|---|---|
| Equation (Porosity) | R2 | Equation (Strain) | R2 | Equation (Porosity) | R2 | Equation (Strain) | R2 | |
| 97.5% | 98.8% | 96.8% | 98.4% | |||||
| 96.5% | 98.6% | 95.4% | 98.2% | |||||
| k (W m−1 K−1) | 99.8% | 99.5% | 99.7% | 99.3% | ||||
| σ (S m−1) | 98.97% | 99.8% | 99.2% | 99.8% | ||||
| (um2) | 99.8% | 97.3% | 97.5% | 97.8% | ||||
| S (kPa) | 98.3% | 99.1% | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Shao, X.; Zhan, Z.; Sarker, M.; Sui, P.-C.; Chuang, P.-Y.A.; Pan, M. Pore-Scale Modeling of Microporous Layer for Proton Exchange Membrane Fuel Cell: Effective Transport Properties. Membranes 2023, 13, 219. https://doi.org/10.3390/membranes13020219
Zhang H, Shao X, Zhan Z, Sarker M, Sui P-C, Chuang P-YA, Pan M. Pore-Scale Modeling of Microporous Layer for Proton Exchange Membrane Fuel Cell: Effective Transport Properties. Membranes. 2023; 13(2):219. https://doi.org/10.3390/membranes13020219
Chicago/Turabian StyleZhang, Heng, Xuanyu Shao, Zhigang Zhan, Mrittunjoy Sarker, Pang-Chieh Sui, Po-Ya Abel Chuang, and Mu Pan. 2023. "Pore-Scale Modeling of Microporous Layer for Proton Exchange Membrane Fuel Cell: Effective Transport Properties" Membranes 13, no. 2: 219. https://doi.org/10.3390/membranes13020219
APA StyleZhang, H., Shao, X., Zhan, Z., Sarker, M., Sui, P.-C., Chuang, P.-Y. A., & Pan, M. (2023). Pore-Scale Modeling of Microporous Layer for Proton Exchange Membrane Fuel Cell: Effective Transport Properties. Membranes, 13(2), 219. https://doi.org/10.3390/membranes13020219







