Modeling Receptor Motility along Advecting Lipid Membranes
Abstract
1. Introduction
2. Continuum Models of Receptor Motility
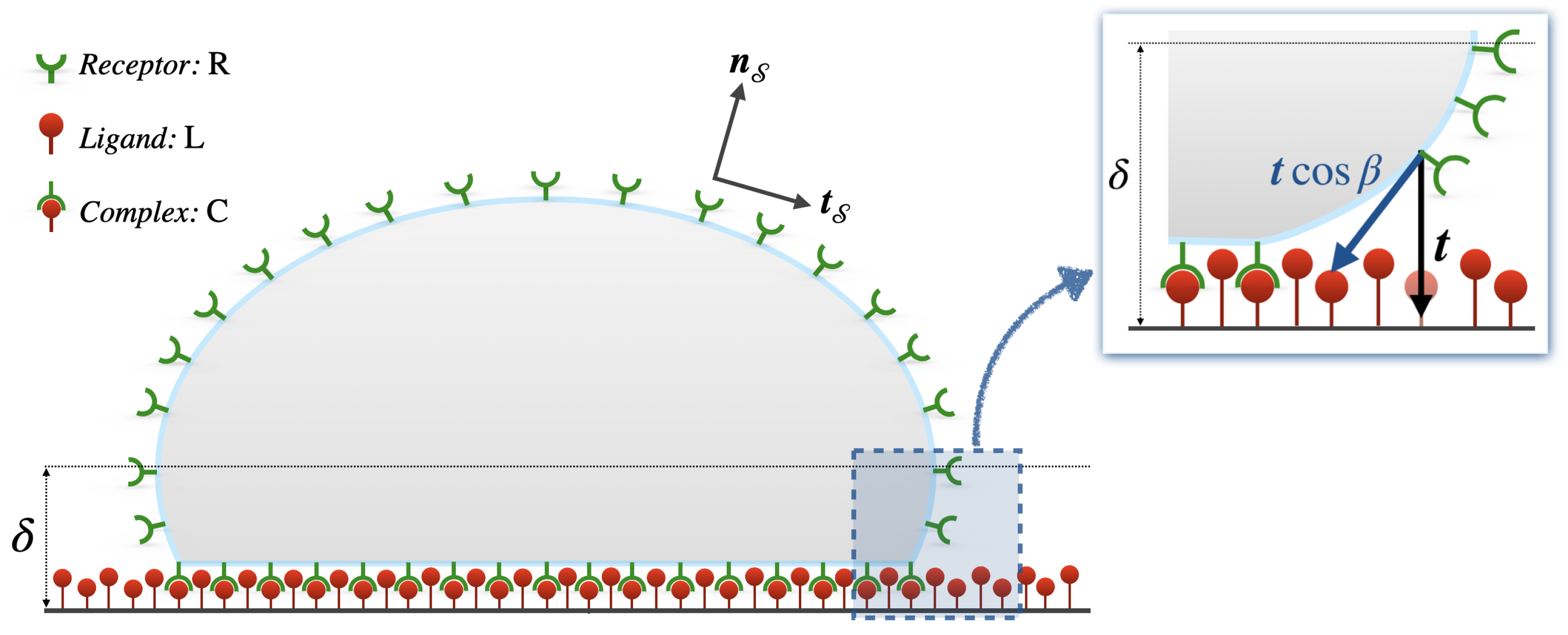
2.1. Receptor–Ligand-Mediated Cell Adhesion
2.2. Cell Contractility
2.3. Protein Relocation on Advecting Membranes
2.4. Receptor Mediated Endocytosis
2.5. Protein Motility Miscellanea
3. Statistical Models of Receptor Motility
4. Discussion
4.1. Modeling the Mass Flux of Receptors
4.2. Evaluation of the Protein Diffusion Coefficient
4.3. Modeling Receptor–Ligand Kinetics
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gurtin, M.E.; Fried, E.; Anand, L. The Mechanics and Thermodynamics of Continua; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Tadmor, E.B.; Miller, R.E.; Elliott, R.S. Continuum Mechanics and Thermodynamics: From Fundamental Concepts to Governing Equations; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- De, S.; Kuwahara, S.; Saito, A. The Endocytic Receptor Megalin and its Associated Proteins in Proximal Tubule Epithelial Cells. Membranes 2014, 4, 333–355. [Google Scholar] [CrossRef]
- Haering, S.C.; Tapken, D.; Pahl, S.; Hollmann, M. Auxiliary Subunits: Shepherding AMPA Receptors to the Plasma Membrane. Membranes 2014, 4, 469–490. [Google Scholar] [CrossRef] [PubMed]
- Bucci, C.; Alifano, P.; Cogli, L. The Role of Rab Proteins in Neuronal Cells and in the Trafficking of Neurotrophin Receptors. Membranes 2014, 4, 642–677. [Google Scholar] [CrossRef]
- Klinger, S.C.; Siupka, P.; Nielsen, M.S. Retromer-Mediated Trafficking of Transmembrane Receptors and Transporters. Membranes 2015, 5, 288–306. [Google Scholar] [CrossRef]
- Kawaguchi, R.; Zhong, M.; Kassai, M.; Ter-Stepanian, M.; Sun, H. Vitamin A Transport Mechanism of the Multitransmembrane Cell-Surface Receptor STRA6. Membranes 2015, 5, 425–453. [Google Scholar] [CrossRef]
- Azad, T.; Singaravelu, R.; Crupi, M.J.F.; Jamieson, T.; Dave, J.; Brown, E.E.F.; Rezaei, R.; Taha, Z.; Boulton, S.; Martin, N.T.; et al. Implications for SARS-CoV-2 Vaccine Design: Fusion of Spike Glycoprotein Transmembrane Domain to Receptor-Binding Domain Induces Trimerization. Membranes 2020, 10, 215. [Google Scholar] [CrossRef]
- Klaiss-Luna, M.C.; Manrique-Moreno, M. Infrared Spectroscopic Study of Multi-Component Lipid Systems: A Closer Approximation to Biological Membrane Fluidity. Membranes 2022, 12, 534. [Google Scholar] [CrossRef]
- Aragón-Muriel, A.; Lisciano, Y.; Morales-Morales, D.; Polo-Cerón, D.; Oñate-Garzón, J. A Study of the Interaction of a New Benzimidazole Schiff Base with Synthetic and Simulated Membrane Models of Bacterial and Mammalian Membranes. Membranes 2021, 11, 449. [Google Scholar] [CrossRef]
- Brémaud, E.; Favard, C.; Mariaux, D. Deciphering the Assembly of Enveloped Viruses Using Model Lipid Membranes. Membranes 2022, 12, 441. [Google Scholar] [CrossRef]
- Fletcher, A. The cell membrane and receptors. Anaesth. Intens. Care Med. 2017, 18, 316–320. [Google Scholar] [CrossRef]
- Martí, J.; Calero, C. Modeling and Simulation of Lipid Membranes. Membranes 2022, 12, 549. [Google Scholar] [CrossRef] [PubMed]
- Zec, N.; Mangiapia, G.; Hendry, A.C.; Barker, R.; Koutsioubas, A.; Frielinghaus, H.; Campana, M.; Ortega-Roldan, J.L.; Bush, S. Mutually Beneficial Combination of Molecular Dynamics Computer Simulations and Scattering Experiments. Membranes 2021, 11, 507. [Google Scholar] [CrossRef] [PubMed]
- Radhakrishnan, N.; Kaul, S.C.; Wadhwa, R.; Sundar, D.; Hernández-Machado, A. Phosphatidylserine Exposed Lipid Bilayer Models for Understanding Cancer Cell Selectivity of Natural Compounds: A Molecular Dynamics Simulation Study. Membranes 2022, 12, 64. [Google Scholar] [CrossRef] [PubMed]
- Trejo-Soto, C.; Lázaro, G.R.; Pagonabarraga, I.; Hernández-Machado, A. Microfluidics Approach to the Mechanical Properties of Red Blood Cell Membrane and Their Effect on Blood Rheology. Membranes 2022, 12, 217. [Google Scholar] [CrossRef]
- Sessa, L.; Concilio, S.; Walde, P.; Robinson, T.; Dittrich, P.S.; Porta, A.; Panunzi, B.; Caruso, U.; Piotto, S. Study of the Interaction of a Novel Semi-Synthetic Peptide with Model Lipid Membranes. Membranes 2020, 10, 294. [Google Scholar] [CrossRef]
- Bell, G.I. Models for the specific adhesion of cells to cells. Science 1978, 200, 618–627. [Google Scholar] [CrossRef]
- Bell, G.I.; Dembo, M.; Bongrand, P. Cell adhesion. Competition between nonspecific repulsion and specific bonding. Biophys. J. 1984, 45, 1051–1064. [Google Scholar] [CrossRef]
- Goldstein, B.; Wofsy, C.; Bell, G.I. Interactions of low density lipoprotein receptors with coated pits on human fibroblasts: Estimate of the forward rate constant and comparison with the diffusion limit. Proc. Natl. Acad. Sci. USA 1981, 78, 5695–5698. [Google Scholar] [CrossRef]
- Goldstein, B.; Griego, R.; Wofsy, C. Diffusion-limited forward rate constants in two dimensions. Application to the trapping of cell surface receptors by coated pits. Biophys. J. 1984, 46, 573–586. [Google Scholar] [CrossRef]
- Boulbitch, A.; Guttenberg, Z.; Sackmann, E. Kinetics of membrane adhesion mediated by ligand-receptor interaction studied with a biomimetic system. Biophys. J. 2001, 81, 2743–2751. [Google Scholar] [CrossRef]
- Freund, L.B.; Lin, Y. The role of binder mobility in spontaneous adhesive contact and implication for cell adhesion. J. Mech. Phys. Solids 2004, 52, 2455–2472. [Google Scholar] [CrossRef]
- Shenoy, V.B.; Freund, L.B. Growth and shape stability of a biological membrane adhesion complex in the diffusion-mediated regime. PNAS 2005, 102, 3213–3218. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Zhang, Y.W.; Cheng, Q.H.; Lu, C. Simulation of the spreading of a vesicle on a substrate surface mediated by receptor-ligand binding. J. Mech. Phys. Solids 2007, 55, 1166–1181. [Google Scholar] [CrossRef]
- Cheng, Q.H.; Liu, P.; Gao, H.J.; Zhang, Y.W. A computational modeling for micropipette-manipulated cell detachment from a substrate mediated by receptor-ligand binding. J. Mech. Phys. Solids 2009, 57, 205–220. [Google Scholar] [CrossRef]
- Golestaneh, A.F.; Nadler, B. Modeling of cell adhesion and deformation mediated by receptor-ligand interactions. Biomech. Model. Mechanobiol. 2016, 15, 371–387. [Google Scholar] [CrossRef] [PubMed]
- Sohail, T.; Tang, T.; Nadler, B. Adhesive contact of a fluid-filled membrane driven by electrostatic forces. Int. J. Solids Struct. 2013, 50, 2678–2690. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Mrksich, M.; McMeeking, R.M.; Evans, A.G. A bio-mechanical model for coupling cell contractility with focal adhesion formation. J. Mech. Phys. Solids 2008, 56, 1484–1510. [Google Scholar] [CrossRef]
- Pathak, A.; McMeeking, R.M.; Evans, A.G.; Deshpande, V.S. An Analysis of the Cooperative Mechano-Sensitive Feedback Between Intracellular Signaling, Focal Adhesion Development, and Stress Fiber Contractility. J. Appl. Mech. 2011, 78, 041001. [Google Scholar] [CrossRef]
- Ronan, W.; Deshpande, V.S.; McMeeking, R.M.; McGarry, J.P. Numerical investigation of the active role of the actin cytoskeleton in the compression resistance of cells. J. Mech. Behav. Biomed. 2012, 14, 143–157. [Google Scholar] [CrossRef]
- Ronan, W.; Deshpande, V.S.; McMeeking, R.M.; McGarry, J.P. Cellular contractility and substrate elasticity: A numerical investigation of the actin cytoskeleton and cell adhesion. Biomech. Model. Mechanobiol. 2014, 13, 417–435. [Google Scholar] [CrossRef]
- Vigliotti, A.; McMeeking, R.M.; Deshpande, V.S. Simulation of the cytoskeletal response of cells on grooved or patterned substrates. J. R. Soc. Interface 2015, 12. [Google Scholar] [CrossRef] [PubMed]
- McEvoy, E.; Deshpande, V.S.; McGarry, P. Free energy analysis of cell spreading. J Mech. Behav. Biomed. 2017, 74, 283–295. [Google Scholar] [CrossRef] [PubMed]
- McMeeking, R.M.; Deshpande, V.S. A Bio-chemo-mechanical Model for Cell Contractility, Adhesion, Signaling, and Stress-Fiber Remodeling. In Biomechanics: Trends in Modeling and Simulation; Holzapfel, G., Ogden, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 20. [Google Scholar]
- Deshpande, V.S.; McMeeking, R.M.; Evans, A.G. A bio-chemo-mechanical model for cell contractility. Pnas 2006, 103, 17064–17065. [Google Scholar] [CrossRef] [PubMed]
- Deshpande, V.S.; McMeeking, R.M.; Evans, A.G. A model for the contractility of the cytoskeleton including the effects of stress-fiber formation and dissociation. Proc. R. Soc. Math. Phys. Eng. Sci. 2007, 463, 787–815. [Google Scholar]
- Vernerey, F.J.; Farsad, M. A mathematical model of the coupled mechanisms of cell adhesion, contraction and spreading. J. Math. Biol. 2014, 68, 989–1022. [Google Scholar] [CrossRef][Green Version]
- Mikucki, M.; Zhou, Y.C. Curvature-driven molecular flow on membrane surface. Siam J. Appl. Math. 2017, 77, 1587–1605. [Google Scholar] [CrossRef][Green Version]
- Carotenuto, A.R.; Lunghi, L.; Piccolo, V.; Babaei, M.; Dayal, K.; Pugno, N.; Zingales, M.; Deseri, L.; Fraldi, M. Mechanobiology predicts raft formations triggered by ligand-receptor activity across the cell membrane. J. Mech. Phys. Solids 2020, 141, 103974. [Google Scholar] [CrossRef]
- Bubba, F.; Lorenzi, T.; Macfarlane, F.R. From a discrete model of chemotaxis with volume-filling to a generalized Patlak–Keller–Segel model. Proc. R. Soc. A 2020, 476, 20190871. [Google Scholar] [CrossRef]
- Damioli, V.; Salvadori, A.; Beretta, G.P.; Ravelli, C.; Mitola, S. Multi-physics interactions drive VEGFR2 relocation on endothelial cells. Sci. Rep. 2017, 7, 16700. [Google Scholar] [CrossRef]
- Serpelloni, M.; Arricca, M.; Damioli, V.; Ravelli, C.; Grillo, E.; Mitola, S.; Salvadori, A. A Model of Integrin and VEGF Receptors Recruitment on Endothelial Cells. In Developments and Novel Approaches in Biomechanics and Metamaterials; Abali, B.E., Giorgio, I., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 163–198. [Google Scholar]
- Serpelloni, M. Response of Endothelial Cells to Angiogenic Stimuli: Experiments, Modeling and Simulations. Ph.D. Thesis, University of Brescia, Brescia, Italy, 2020. [Google Scholar]
- Serpelloni, M.; Arricca, M.; Bonanno, C.; Salvadori, A. Modeling cells spreading, motility, and receptors dynamics: A general framework. Acta Mech. Sin. 2021, 37, 1013–1030. [Google Scholar] [CrossRef]
- Mitola, S.; Ravelli, C.; Moroni, E.; Salvi, V.; Leali, D.; Ballmer-Hofer, K.; Zammataro, L.; Presta, M. Gremlin is a novel agonist of the major proangiogenic receptor VEGFR2. Blood 2010, 116, 3677–3680. [Google Scholar] [CrossRef] [PubMed]
- Grillo, E.; Ravelli, C.; Corsini, M.; Ballmer-Hofer, K.; Oreste, P.; Zoppetti, G.; Tobia, C.; Ronca, R.; Presta, M.; Mitola, S. Monomeric gremlin is a novel vascular endothelial growth factor receptor-2 antagonist. Oncotarget 2016, 7, 35353–35368. [Google Scholar] [CrossRef] [PubMed]
- Ravelli, C.; Grillo, E.; Corsini, M.; Coltrini, D.; Presta, M.; Mitola, S. β3 Integrin Promotes Long-Lasting Activation and Polarization of Vascular Endothelial Growth Factor Receptor 2 by Immobilized Ligand. Arterioscl. Throm. Vas. 2015, 35, 2161–2171. [Google Scholar] [CrossRef] [PubMed]
- Salvadori, A.; Damioli, V.; Ravelli, C.; Mitola, S. Modeling and simulation of VEGF receptors recruitment in angiogenesis. Math. Probl. Eng. 2018, 2018, 4705472. [Google Scholar] [CrossRef]
- Salvadori, A.; McMeeking, R.M.; Grazioli, D.; Magri, M. A coupled model of transport-reaction-mechanics with trapping. Part I—small strain analysis. J. Mech. Phys. Solids 2018, 114, 1–30. [Google Scholar] [CrossRef]
- Salvadori, A.; Grazioli, D.; Geers, M.; Danilov, D.; Notten, P. A multiscale-compatible approach in modeling ionic transport in the electrolyte of (Lithium ion) batteries. J. Power Sour. 2015, 293, 892–911. [Google Scholar] [CrossRef]
- Salvadori, A.; Grazioli, D.; Magri, M.; Geers, M.; Danilov, D.; Notten, P. On the role of saturation in modeling ionic transport in the electrolyte of (Li-ion) batteries. J. Power Sour. 2015, 294, 696–710. [Google Scholar] [CrossRef]
- Cabras, L.; Danilov, D.; Subber, W.; Oancea, V.; Salvadori, A. A two-mechanism and multiscale compatible approach for solid state electrolytes of (Li-ion) batteries. J. Energy Storage 2022, 48, 103842. [Google Scholar] [CrossRef]
- Ravelli, C.; Mitola, S.; Corsini, M.; Presta, M. Involvement of αvβ3 integrin in gremlin-induced angiogenesis. Angiogenesis 2013, 35, 235–243. [Google Scholar] [CrossRef]
- Gao, H.; Shi, W.; Freund, L.B. Mechanics of receptor-mediated endocytosis. Proc. Natl. Acad. Sci. USA 2005, 102, 9469–9474. [Google Scholar] [CrossRef]
- Decuzzi, P.; Ferrari, M. The receptor-mediated endocytosis of nonspherical particles. Biophys. J. 2008, 94, 3790–3797. [Google Scholar] [CrossRef] [PubMed]
- Gao, H. Probing mechanical principles of cell–nanomaterial interactions. J. Mech. Phys. Solids 2014, 62, 312–339. [Google Scholar] [CrossRef]
- Wiegold, T.; Klinge, S.; Gilbert, R.P.; Holzapfel, G.A. Computational modeling of adhesive contact between a virus and a cell during receptor driven endocytosis. PAMM 2019, 19, e201900161. [Google Scholar] [CrossRef]
- Wiegold, T.; Klinge, S.; Gilbert, R.P.; Holzapfel, G.A. Numerical simulation of the viral entry into a cell driven by the receptor diffusion. bioRxiv 2019, 84, 224–243. [Google Scholar] [CrossRef]
- Lee, R.C.; Gowrishankar, T.R.; Basch, R.M.; Patel, K.K.; Golan, D.E. Cell shape-dependent rectification of surface receptor transport in a sinusoidal electric field. Biophys. J. 1993, 64, 44–57. [Google Scholar] [CrossRef]
- Mac Gabhann, F.; Popel, A.S. Model of competitive binding of vascular endothelial growth factor and placental growth factor to VEGF receptors on endothelial cells. Am. J. Physiol. Heart Circ. Physiol. 2004, 286, H153–H164. [Google Scholar] [CrossRef]
- Filion, R.J.; Popel, A.S. A Reaction-Diffusion Model of Basic Fibroblast Growth Factor Interactions with Cell Surface Receptors. Ann. Biomed. Eng. 2004, 32, 645–663. [Google Scholar] [CrossRef]
- Rattanakul, C.; Lenbury, Y.; Bell, J.; Chatsudthipong, V.; Triampo, W.; Crooke, P.S. Spatial Turing-type Pattern Formation in a Model of Signal Transduction Involving Membrane-based Receptors Coupled by G Proteins. Cancer Inform. 2006, 2, 329–343. [Google Scholar] [CrossRef]
- Earnshaw, B.A.; Bressloff, P.C. Biophysical Model of AMPA Receptor Trafficking and Its Regulation during Long-Term Potentiation/Long-Term Depression. J. Neurosci. 2006, 26, 12362–12373. [Google Scholar] [CrossRef]
- Earnshaw, B.A.; Bressloff, P.C. Modeling the role of lateral membrane diffusion in AMPA receptor trafficking along spiny dendrite. J. Comput. Neurosci. 2008, 25, 366–389. [Google Scholar] [CrossRef]
- Daniels, D.R. Receptor-ligand diffusion-limited reaction rates on curved membranes. Chem. Phys. Lett. 2022, 795, 139516. [Google Scholar] [CrossRef]
- Kusumi, A.; Sako, Y.; Yamamoto, M. Confined Lateral Diffusion of Membrane Receptors as Studied by Single Particle Tracking (Nanovid Microscopy). Effects of Calcium-induced Differentiation in Cultured Epithelial Cells. Biophys. J. 1993, 65, 2021–2040. [Google Scholar] [CrossRef]
- Ritchie, K.; Shan, X.Y.; Kondo, J.; Iwasawa, K.; Fujiwara, T.; Kusumi, A. Detection of Non-Brownian Diffusion in the Cell Membrane in Single Molecule Tracking. Biophys. J. 2005, 88, 2266–2277. [Google Scholar] [CrossRef] [PubMed]
- Atilgan, E.; Sun, X.C. Shape transitions in lipid membranes and protein mediated vesicle fusion and fission. J. Chem. Phys. 2007, 16, 095102. [Google Scholar] [CrossRef] [PubMed]
- Briddon, S.J.; Gandía, J.; Amaral, O.B.; Ferré, S.; Lluís, C.; Franco, R.; Hill, S.J.; Ciruela, F. Plasma membrane diffusion of g protein-coupled receptor oligomers. Biochim. Biophys. Acta 2008, 1783, 2262–2268. [Google Scholar] [CrossRef]
- Paszek, M.J.; Boettiger, D.; Weaver, V.M.; Hammer, D.A. Integrin Clustering Is Driven by Mechanical Resistance from the Glycocalyx and the Substrate. PLoS Comput. Biol. 2009, 5, e1000604. [Google Scholar] [CrossRef]
- Duke, T.; Graham, I. Equilibrium mechanisms of receptor clustering. Prog. Biophys. Mol. Biol. 2009, 100, 18–24. [Google Scholar] [CrossRef]
- Allard, J.F.; Dushek, O.; Coombs, K.; van der Merwe, P.A. Mechanical Modulation of Receptor-Ligand Interactions at Cell-Cell Interface. Biophys. J. 2012, 102, 1265–1273. [Google Scholar] [CrossRef]
- Iron, D.; Rumsey, J. A model of surface receptor aggregation. J. Math. Biol. 2017, 75, 705–731. [Google Scholar] [CrossRef]
- Martini, L.; Brameyer, S.; Hoyer, E.; Jung, K.; Gerland, U. Dynamics of chromosomal target search by a membrane-integrated one-component receptor. PLoS Comput. Biol. 2021, 17, e1008680. [Google Scholar] [CrossRef]
- Dubin-Thaler, B.J.; Giannone, G.; Döbereiner, H.G.; Sheetz, M.P. Nanometer Analysis of Cell Spreading on MAtrix-Coated Surfaces Reveals Two Distinct Cell States and STEPs. Biophys. J. 2004, 86, 1794–1806. [Google Scholar] [CrossRef]
- Reinhart-King, C.A.; Dembo, M.; Hammer, D.A. The dynamics and mechanics of endothelial cell spreading. Biophys. J. 2005, 89, 676–689. [Google Scholar] [CrossRef] [PubMed]
- Saffman, P.G.; Delbrück, M. Brownian motion in biological membranes. PNAS 1975, 72, 3111–3113. [Google Scholar] [CrossRef] [PubMed]
- Reister, E.; Seifert, U. Lateral diffusion of a protein on a fluctuating membrane. EPL 2005, 71, 859–865. [Google Scholar] [CrossRef]
- Leitenberger, S.; Reister-Gottfried, E.; Seifert, U. Curvature Coupling Dependence of Membrane Protein Diffusion Coefficients. Langmuir 2008, 24, 1254–1261. [Google Scholar] [CrossRef][Green Version]
- Reister-Gottfried, E.; Leitenberger, S.M.; Seifert, U. Diffusing proteins on a fluctuating membrane: Analytical theory and simulations. Phys. Rev. E 2010, 81, 031903. [Google Scholar] [CrossRef]
- Gambin, Y.; Lopez-Esparza, R.; Reffay, M.; Sierecki, E.; Gov, N.S.; Genest, M.; Hodges, R.S.; Urbach, W. Lateral mobility of proteins in liquid membranes revisited. PNAS 2006, 103, 2098–2102. [Google Scholar] [CrossRef]
- Gambin, Y.; Reffay, M.; Sierecki, E.; Homblé, F.; Hodges, R.S.; Gov, N.S.; Taulier, N.; Urbach, W. Variation of the Lateral Mobility of Transmembrane Peptides with Hydrophobic Mismatch. J. Phys. Chem. B 2010, 144, 3559–3566. [Google Scholar] [CrossRef]
- Saffman, P.G. Brownian motion in thin sheets of viscous fluid. J. Fluid Mech. 1975, 73, 593–602. [Google Scholar] [CrossRef]
- Oppenheimer, N.; Diamant, H. Correlated Diffusion of Membrane Proteins and Their Effect on Membrane Viscosity. Biophys. J 2009, 96, 3041–3049. [Google Scholar] [CrossRef]
- Oppenheimer, N.; Diamant, H. In-Plane Dynamics of Membranes with Immobile Inclusions. Phys. Rev. Lett. 2011, 107, 258102. [Google Scholar] [CrossRef] [PubMed]
- Camley, B.A.; Brown, F.L.H. Contributions to membrane-embedded-protein diffusion beyond hydrodynamic theories. Phys. Rev. E 2012, 85, 061921. [Google Scholar] [CrossRef] [PubMed]
- Camley, B.A.; Brown, F.L.H. Diffusion of complex objects embedded in free and supported lipid bilayer membranes: Role of shape anisotropy and leaflet structure. Soft Matter. 2013, 9, 4767–4779. [Google Scholar] [CrossRef]
- Camley, B.A.; Lerner, M.G.; Pastor, R.W.; Brown, F.L.H. Strong influence of periodic boundary conditions on lateral diffusion in lipid bilayer membranes. J. Chem. Phys. 2015, 143, 12B604_1. [Google Scholar] [CrossRef]
- Venable, R.M.; Ingólfsson, H.I.; Lerner, M.G.; Perrin, B.S., Jr.; Camley, B.A.; Marrink, S.J.; Brown, F.L.H.; Pastor, R.W. Lipid and Peptide Diffusion in Bilayers: The Saffman-Delbrück Model and Periodic Boundary Conditions. J. Phys. Chem. B 2017, 121, 3443–3457. [Google Scholar] [CrossRef]
- Ramadurai, S.; Holt, A.; Krasnikov, V.; van den Bogaart, G.; Killian, J.A.; Poolman, B. Lateral Diffusion of Membrane Proteins. J. Am. Chem. Soc. 2009, 131, 12650–12656. [Google Scholar] [CrossRef]
- Ramadurai, S.; Holt, A.; Schäfer, L.V.; Krasnikov, V.V.; Rijkers, D.T.S.; Marrink, S.J.; Killian, J.A.; Poolman, B. Influence of Hydrophobic Mismatch and Amino Acid Composition on the Lateral Diffusion of Transmembrane Peptides. Biophys. J. 2010, 99, 1447–1454. [Google Scholar] [CrossRef]
- Lee, M.W.; Schmidt, N.W.; Wong, G.C.L. Mechanisms of Membrane Curvature Generation by Peptides and Proteins: A Unified Perspective on Antimicrobial Peptides. In Handbook of Lipid Membranes; Safinya, C.R., Rädler, J.O., Eds.; CRC Press: Boca Raton, FL, USA, 2021; Volume 1. [Google Scholar] [CrossRef]
- Lee, M.W.; Han, M.; Bossa, G.V.; Snell, C.; Song, Z.; Tang, H.; Yin, L.; Cheng, J.; May, S.; Luijten, E.; et al. Interactions between Membranes and “Metaphilic” Polypeptide Architectures with Diverse Side-Chain Populations. ACS Nano 2017, 11, 2858–2871. [Google Scholar] [CrossRef]
- Callan-Jones, A.; Durand, M.; Fournier, J.B. Hydrodynamics of bilayer membranes with diffusing transmembrane proteins. Soft Matter. 2016, 12, 1791–1800. [Google Scholar] [CrossRef]
- Worch, R.; Petrášek, Z.; Schwille, P.; Weidemann, T. Diffusion of Single-Pass Transmembrane Receptors: From the Plasma Membrane into Giant Liposomes. J. Membrane Biol. 2017, 250, 393–406. [Google Scholar] [CrossRef]
- Houser, J.R.; Busch, D.J.; Bell, D.; Li, B.; Ren, P.; Stachowlak, J.C. The Impact of Physiological Crowding on the Diffusivity of Membrane Bound Proteins. Soft Matter. 2016, 12, 2127–2134. [Google Scholar] [CrossRef] [PubMed]
- Naji, A.; Levine, A.J.; Pincus, P.A. Corrections to the Saffman-Delbrück Mobility for Membrane Bound Proteins. Biophys. J. 2007, 93, L49–L51. [Google Scholar] [CrossRef] [PubMed]
- De Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Dover: Downers Grove, IL, USA, 1984. [Google Scholar]
- Evans, E. Detailed mechanic of membrane-membrane adhesion and separation. I. Continuum of molecular cross-bridges. Biophys. J. 1985, 48, 175–183. [Google Scholar] [CrossRef]
- Dembo, M.; Torney, D.; Saxman, K.; Hammer, D.A. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. R. Soc. Lond. Ser. Biol. Sci. 1988, 234, 55–83. [Google Scholar]
- Ubbink, M. The courtship of proteins: Understanding the encounter complex. FEBS Lett. 2009, 583, 1060–1066. [Google Scholar] [CrossRef] [PubMed]
- Selzer, T.; Schreiber, G. New insights into the mechanism of protein-protein association. Proteins Struct. Funct. Genet. 2001, 45, 190–198. [Google Scholar] [CrossRef]
- Vigliotti, A.; Ronan, W.; Baaijens, F.P.T.; Deshpande, V.S. A thermodynamically motivated model for stress-fiber reorganization. Biomech. Model Mechan 2016, 15, 761–789. [Google Scholar] [CrossRef]
- Kruse, K.; Joanny, J.F.; Jülicher, F.; Prost, J.; Sekimoto, K. Generic theory of active polar gels: A paradigm for cytoskeletal dynamics. Eur. Phys. J. E 2005, 16, 5–16. [Google Scholar] [CrossRef]
- Joanny, J.F.; Kruse, K.; Prost, J.; Ramaswamy, S. The actin cortex as an active wetting layer. Eur. Phys. J. E 2013, 36, 1–6. [Google Scholar] [CrossRef]
- Prost, J.; Jülicher, F.; Joanny, J.F. Active gel physics. Nat. Phys. 2015, 11, 111–117. [Google Scholar] [CrossRef]
- Rahimi, M.; Arroyo, M. Shape dynamics, lipid hydrodynamics, and the complex viscoelasticity of bilayer membranes. Phys. Rev. E 2012, 86, 011932. [Google Scholar] [CrossRef] [PubMed]
- Latorre, E.; Kale, S.; Casares, L.; Gómez-González, M.; Uroz, M.; Valon, L.; Nair, R.V.; Garreta, E.; Montserrat, N.; del Campo, A.; et al. Active superelasticity in three-dimensional epithelia of controlled shape. Nature 2018, 563, 203–208. [Google Scholar] [CrossRef] [PubMed]
- Evans, E. New membrane concept applied to the analysis of fluid shear and micro-pipette deformed red blood cells. Biophys. J 1973, 13, 941–954. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arricca, M.; Salvadori, A.; Bonanno, C.; Serpelloni, M. Modeling Receptor Motility along Advecting Lipid Membranes. Membranes 2022, 12, 652. https://doi.org/10.3390/membranes12070652
Arricca M, Salvadori A, Bonanno C, Serpelloni M. Modeling Receptor Motility along Advecting Lipid Membranes. Membranes. 2022; 12(7):652. https://doi.org/10.3390/membranes12070652
Chicago/Turabian StyleArricca, Matteo, Alberto Salvadori, Claudia Bonanno, and Mattia Serpelloni. 2022. "Modeling Receptor Motility along Advecting Lipid Membranes" Membranes 12, no. 7: 652. https://doi.org/10.3390/membranes12070652
APA StyleArricca, M., Salvadori, A., Bonanno, C., & Serpelloni, M. (2022). Modeling Receptor Motility along Advecting Lipid Membranes. Membranes, 12(7), 652. https://doi.org/10.3390/membranes12070652






