Theoretical and Experimental Considerations for Investigating Multicomponent Diffusion in Hydrated, Dense Polymer Membranes
Abstract
1. Introduction
2. Modeling of Multicomponent Diffusion
2.1. Solution-Diffusion Model
2.2. Multicomponent Diffusion
2.3. Simulating Multicomponent Diffusion Coefficients
3. Experimental Approaches to Investigating Multicomponent Diffusion
4. Future Outlook and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Pi | Permeability |
| Di | Fick’s law diffusivity |
| Ki | Solubility |
| n | Number of components |
| ns | Number of solutes |
| ci | Concentration of component i inside the membrane |
| ci,f | Concentration of component i in feed solution |
| ci,p | Concentration of component i in permeate solution |
| vi | Average velocity of component i |
| v | Reference velocity |
| ji | Diffusive flux relative to reference velocity |
| i | Mass fraction of component i |
| Mi | Molecular weight of component i |
| Total mass density | |
| Chemical gradient of component i | |
| Lij | Onsager coefficient |
| Onsager diffusion coefficient | |
| Đik | Maxwell Stefan diffusion coefficient |
| Dij | Multicomponent Fick diffusion coefficient |
| Absorbance at wavenumber λ | |
| Molar absorptivity of the solute at wavenumber λ | |
| I | Transmitted light intensity |
| Io | Incident light intensity |
| Effective molar absorptivity | |
| l | Light’s path length |
References
- Eswari, J.S.; Naik, S. A Critical Analysis on Various Technologies and Functionalized Materials for Manufacturing Dialysis Membranes. Mater. Sci. Energy Technol. 2020, 3, 116–126. [Google Scholar] [CrossRef]
- Kim, Y.S.; Hickner, M.A.; Dong, L.; Pivovar, B.S.; McGrath, J.E. Sulfonated Poly(Arylene Ether Sulfone) Copolymer Proton Exchange Membranes: Composition and Morphology Effects on the Methanol Permeability. J. Membr. Sci. 2004, 243, 317–326. [Google Scholar] [CrossRef]
- Li, L.; Wang, Y. Quaternized Polyethersulfone Cardo Anion Exchange Membranes for Direct Methanol Alkaline Fuel Cells. J. Membr. Sci. 2005, 262, 1–4. [Google Scholar] [CrossRef]
- Lee, A.; Elam, J.W.; Darling, S.B. Membrane Materials for Water Purification: Design, Development, and Application. Environ. Sci. Water Res. Technol. 2015, 2, 17–42. [Google Scholar] [CrossRef]
- Madhura, L.; Kanchi, S.; Sabela, M.I.; Singh, S.; Bisetty, K.; Inamuddin. Membrane Technology for Water Purification. Environ. Chem. Lett. 2018, 16, 343–365. [Google Scholar] [CrossRef]
- Ghosal, K.; Freeman, B.D. Gas Separation Using Polymer Membranes: An Overview. Polym. Advan. Technol. 1994, 5, 673–697. [Google Scholar] [CrossRef]
- Robeson, L.M. Polymer Membranes for Gas Separation. Curr. Opin. Solid State Mater. Sci. 1999, 4, 549–552. [Google Scholar] [CrossRef]
- Kang, G.; Cao, Y. Development of Antifouling Reverse Osmosis Membranes for Water Treatment: A Review. Water Res. 2012, 46, 584–600. [Google Scholar] [CrossRef] [PubMed]
- Wenten, I.G.; Khoiruddin. Reverse Osmosis Applications: Prospect and Challenges. Desalination 2016, 391, 112–125. [Google Scholar] [CrossRef]
- Cabassud, C.; Wirth, D. Membrane Distillation for Water Desalination: How to Chose an Appropriate Membrane? Desalination 2003, 157, 307–314. [Google Scholar] [CrossRef]
- Werber, J.R.; Osuji, C.O.; Elimelech, M. Materials for Next-Generation Desalination and Water Purification Membranes. Nat. Rev. Mater. 2016, 1, 16018. [Google Scholar] [CrossRef]
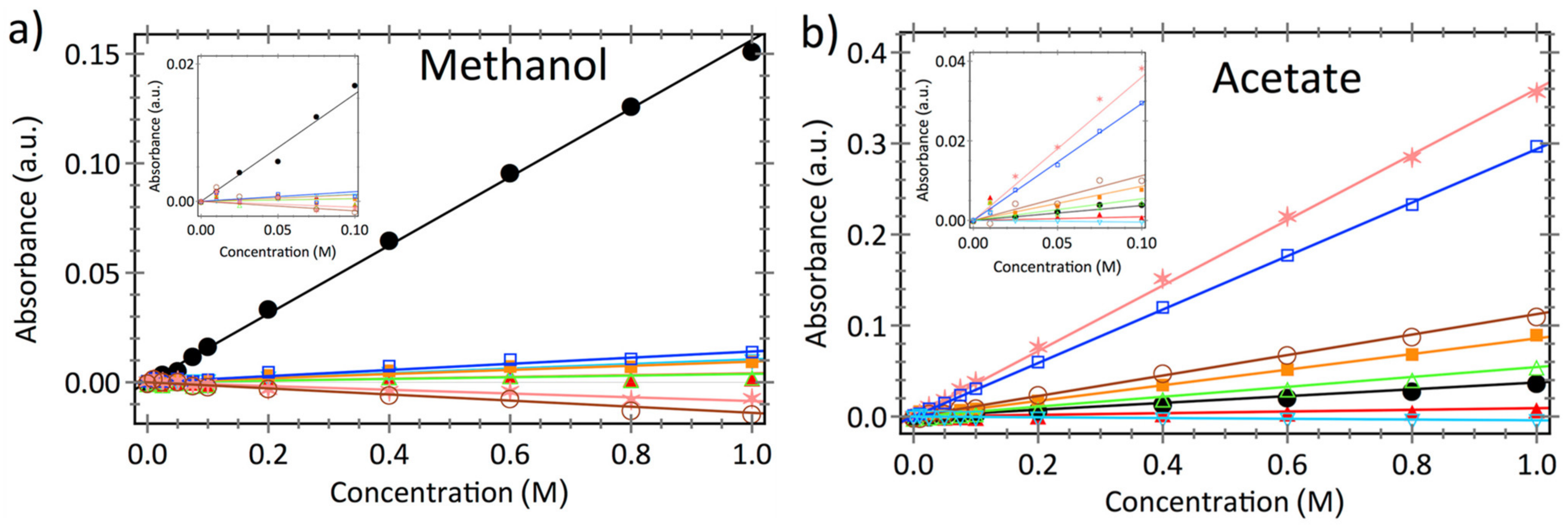
- Dobyns, B.M.; Kim, J.M.; Beckingham, B.S. Multicomponent Transport of Methanol and Sodium Acetate in Poly(Ethylene Glycol) Diacrylate Membranes of Varied Fractional Free Volume. Eur. Polym. J. 2020, 134, 109809. [Google Scholar] [CrossRef]
- Van de Vossenberg, J.L.C.M.; Driessen, A.J.M.; da Costa, M.S.; Konings, W.N. Homeostasis of the Membrane Proton Permeability in Bacillus Subtilis Grown at Different Temperatures. Biochim. Biophys. Acta BBA Biomembr. 1999, 1419, 97–104. [Google Scholar] [CrossRef]
- Wohnsland, F.; Faller, B. High-Throughput Permeability PH Profile and High-Throughput Alkane/Water Log P with Artificial Membranes. J. Med. Chem. 2001, 44, 923–930. [Google Scholar] [CrossRef]
- Daniel David, E. In Situ Hydraulic Conductivity Tests for Compacted Clay. J. Geotech. Eng. 1989, 115, 1205–1226. [Google Scholar] [CrossRef]
- Hamilton, J.; Daniel, D.; Olson, R. Measurement of Hydraulic Conductivity of Partially Saturated Soils. In Permeability and Groundwater Contaminant Transport; Zimmie, T., Riggs, C., Eds.; ASTM International: West Conshohocken, PA, USA, 1981. [Google Scholar] [CrossRef]
- Steudle, E.; Tyerman, S.D. Determination of Permeability Coefficients, Reflection Coefficients, and Hydraulic Conductivity OfChara Corallina Using the Pressure Probe: Effects of Solute Concentrations. J. Membr. Biol. 1983, 75, 85–96. [Google Scholar] [CrossRef]
- Kuchuk, F.J.; Onur, M. Estimating Permeability Distribution from 3D Interval Pressure Transient Tests. J. Pet. Sci. Eng. 2003, 39, 5–27. [Google Scholar] [CrossRef]
- Dumas, F.; Aussel, C.; Pernet, P.; Martin, C.; Giboudeau, J. Gas Chromatography Applied to the Lactulose—Mannitol Intestinal Permeability Test. J. Chromatogr. B Biomed. Sci. App. 1994, 654, 276–281. [Google Scholar] [CrossRef]
- Farhadi, A.; Keshavarzian, A.; Holmes, E.W.; Fields, J.; Zhang, L.; Banan, A. Gas Chromatographic Method for Detection of Urinary Sucralose: Application to the Assessment of Intestinal Permeability. J. Chromatogr. B 2003, 784, 145–154. [Google Scholar] [CrossRef]
- Wang, Z.; Hop, C.E.C.A.; Leung, K.H.; Pang, J. Determination of in Vitro Permeability of Drug Candidates through a Caco-2 Cell Monolayer by Liquid Chromatography/Tandem Mass Spectrometry. J. Mass Spectrom. 2000, 35, 71–76. [Google Scholar] [CrossRef]
- McAuley, W.J.; Mader, K.T.; Tetteh, J.; Lane, M.E.; Hadgraft, J. Simultaneous Monitoring of Drug and Solvent Diffusion across a Model Membrane Using ATR-FTIR Spectroscopy. Eur. J. Pharm. Sci. 2009, 38, 378–383. [Google Scholar] [CrossRef]
- Beckingham, B.S.; Lynd, N.A.; Miller, D.J. Monitoring Multicomponent Transport Using in Situ ATR FTIR Spectroscopy. J. Membr. Sci. 2018, 550, 348–356. [Google Scholar] [CrossRef]
- Kim, J.M.; Dobyns, B.M.; Zhao, R.; Beckingham, B.S. Multicomponent Transport of Methanol and Acetate in a Series of Crosslinked PEGDA-AMPS Cation Exchange Membranes. J. Membr. Sci. 2020, 614, 118486. [Google Scholar] [CrossRef]
- Dobyns, B.M.; Kim, J.M.; Li, J.; Jiang, Z.; Beckingham, B.S. Multicomponent Transport of Alcohols in Nafion 117 Measured by in Situ ATR FTIR Spectroscopy. Polymer 2020, 209, 123046. [Google Scholar] [CrossRef]
- Hegde, V.H.; Doherty, M.F.; Squires, T.M. A Two-Phase Model That Unifies and Extends the Classical Models of Membrane Transport. Science 2022, 377, 186–191. [Google Scholar] [CrossRef]
- Lonsdale, H.K.; Merten, U.; Riley, R.L. Transport Properties of Cellulose Acetate Osmotic Membranes. J. Appl. Polym. Sci. 1965, 9, 1341–1362. [Google Scholar] [CrossRef]
- Paul, D.R. The Solution-Diffusion Model for Swollen Membranes. Sep. Purif Rev. 1976, 5, 33–50. [Google Scholar] [CrossRef]
- Wijmans, J.G.; Baker, R.W. The Solution-Diffusion Model: A Review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Deen, W.M. Analysis of Transport Phenomena, 2nd ed.; Oxford University Press: New York, NY, USA, 2012. [Google Scholar]
- Soniat, M.; Dischinger, S.M.; Weng, L.; Beltran, H.M.; Weber, A.Z.; Miller, D.J.; Houle, F.A. Toward Predictive Permeabilities: Experimental Measurements and Multiscale Simulation of Methanol Transport in Nafion. J. Polym. Sci. 2021, 59, 594–613. [Google Scholar] [CrossRef]
- Groot, S.R.D. Thermodynamics of Irreversible Processes; North-Holland Publishing Company: Amsterdam, The Netherlands, 1963. [Google Scholar]
- Hooyman, G.J.; Holtan, H.; Mazur, P.; de Groot, S.R. Thermodynamics of Irreversible Processes in Rotating Systems. Physica 1953, 19, 1095–1108. [Google Scholar] [CrossRef]
- Hooyman, G.J. Thermodynamics of Diffusion in Multicomponent Systems. Physica 1956, 22, 751–759. [Google Scholar] [CrossRef]
- Hooyman, G.J.; Groot, S.R.D. Phenomenological Equations and Onsager Relations The Case of Dependent Fluxes or Forces. Physica 1954, 21, 73–76. [Google Scholar] [CrossRef]
- Krishna, R.; van Baten, J.M. The Darken Relation for Multicomponent Diffusion in Liquid Mixtures of Linear Alkanes: An Investigation Using Molecular Dynamics (MD) Simulations. Ind Eng. Chem. Res. 2005, 44, 6939–6947. [Google Scholar] [CrossRef]
- Krishna, R.; Wesselingh, J.A. The Maxwell-Stefan Approach to Mass Transfer. Chem. Eng. Sci. 1997, 52, 861–911. [Google Scholar] [CrossRef]
- Liu, X.; Vlugt, T.J.H.; Bardow, A. Predictive Darken Equation for Maxwell-Stefan Diffusivities in Multicomponent Mixtures. Ind Eng. Chem. Res. 2011, 50, 10350–10358. [Google Scholar] [CrossRef]
- Mutoru, J.W.; Firoozabadi, A. Form of Multicomponent Fickian Diffusion Coefficients Matrix. J. Chem. 2011, 43, 1192–1203. [Google Scholar] [CrossRef]
- Liu, X.; Schnell, S.K.; Simon, J.-M.; Krüger, P.; Bedeaux, D.; Kjelstrup, S.; Bardow, A.; Vlugt, T.J.H. Diffusion Coefficients from Molecular Dynamics Simulations in Binary and Ternary Mixtures. Int J. Thermophys. 2013, 34, 1169–1196. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: New York, NY, USA, 2017. [Google Scholar]
- Bansal, A. The Interferometric Study of Liquid Transport across M. Ph.D. Thesis, University of Surrey, Guildford, UK, 1998. [Google Scholar]
- Cussler, E.L. Measurement of ternary Diffusion. Multicomponent Diffusion, 1st ed.; Churchill, S.W., Ed.; Elsevier Science Publishing Company: Amsterdam, The Netherlands, 1976; Volume 3. [Google Scholar]
- Robinson, C. Interferometric Studies in Diffusion: I Determination of Concentration Distributions. Proc. Roy. Soc. A 1950, 204, 339. [Google Scholar] [CrossRef]
- Crank, J.; Robinson, C. Interferometric Studies in Diffusion: II Influence of Concentration and Orientation on Diffusion in Cellulose Acetate. Proc. Roy. Soc. A 1951, 204, 549. [Google Scholar] [CrossRef]
- Spiegler, K.S.; Weiner, S.A.; Ewoldsen, E.I.; Hubata, R. Electrodialysis; Report No. 66-1; Sea Water Conversion Laboratory, University of California: Berkeley, CA, USA, 1965. [Google Scholar]
- Lerche, D. Temporal and Local Concentration Changes in Diffusion Layers at Cellulose Membranes Due to Concentration Differences between the Solutions on Both Sides of the Membrane. J. Membr. Biol. 1976, 27, 193–205. [Google Scholar] [CrossRef]
- Johnson, A.R. Concentration Polarization in Reverse Osmosis under Natural Convection. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1971. [Google Scholar]
- Bollenbeck, P.H. A Modified Rayleigh Interferometer for Membrane Transport Studies. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 1973. [Google Scholar]
- Welinder, A.S. Experimental Studies on Concentration in Reverse Osmosis. Ph.D. Thesis, The Technical University of Denmark, Lyngby, Denmark, 1974. [Google Scholar]
- Zhang, X.; Ning, Z.; Wang, D.K.; Diniz da Costa, J.C. A Novel Ethanol Dehydration Process by Forward Osmosis. Chem. Eng. J. 2013, 232, 397–404. [Google Scholar] [CrossRef]
- Møller, S.E. Quantification of Physiological Amino Acids by Gradient Ion-Exchange High-Performance Liquid Chromatography. J. Chromatogr. B Biomed. Sci. Appl. 1993, 613, 223–230. [Google Scholar] [CrossRef]
- Cataldi, T.R.I.; Rubino, A.; Ciriello, R. Sensitive Quantification of Iodide by Ion-Exchange Chromatography with Electrochemical Detection at a Modified Platinum Electrode. Anal. Bioanal. Chem. 2005, 382, 134–141. [Google Scholar] [CrossRef] [PubMed]
- Danielsson, L.-G.; Magnusson, B.; Westerlund, S. An Improved Metal Extraction Procedure for the Determination of Trace Metals in Sea Water by Atomic Absorption Spectrometry with Electrothermal Atomization. Anal. Chim. Acta 1978, 98, 47–57. [Google Scholar] [CrossRef]
- Malmali, M.; Stickel, J.J.; Wickramasinghe, S.R. Sugar Concentration and Detoxification of Clarified Biomass Hydrolysate by Nanofiltration. Sep. Purif. Technol. 2014, 132, 655–665. [Google Scholar] [CrossRef]
- McCormick, P.; Pellegrino, J.; Mantovani, F.; Sarti, G. Water, Salt, and Ethanol Diffusion through Membranes for Water Recovery by Forward (Direct) Osmosis Processes. J. Membr. Sci. 2008, 325, 467–478. [Google Scholar] [CrossRef]
- Langergraber, G.; Fleischmann, N.; Hofstädter, F. A Multivariate Calibration Procedure for UV/VIS Spectrometric Quantification of Organic Matter and Nitrate in Wastewater. Water Sci. Technol. 2003, 47, 63–71. [Google Scholar] [CrossRef]
- Varcoe, J.R.; Slade, R.C.T.; Yee, E.L.H.; Poynton, S.D.; Driscoll, D.J. Investigations into the Ex Situ Methanol, Ethanol and Ethylene Glycol Permeabilities of Alkaline Polymer Electrolyte Membranes. J. Power Sources 2007, 173, 194–199. [Google Scholar] [CrossRef][Green Version]
- Carter, B.M.; Dobyns, B.M.; Beckingham, B.S.; Miller, D.J. Multicomponent Transport of Alcohols in an Anion Exchange Membrane Measured by In-Situ ATR FTIR Spectroscopy. Polymer 2017, 123, 144–152. [Google Scholar] [CrossRef]
- Sammon, C.; Yarwood, J.; Everall, N. A FTIR–ATR Study of Liquid Diffusion Processes in PET Films: Comparison of Water with Simple Alcohols. Polymer 2000, 41, 2521–2534. [Google Scholar] [CrossRef]
- Wu, P.; Siesler, H.W. Water Diffusion into Epoxy Resin: A 2D Correlation ATR-FTIR Investigation. Chem. Phys. Lett. 2003, 374, 74–78. [Google Scholar] [CrossRef]
- Döppers, L.-M.; Breen, C.; Sammon, C. Diffusion of Water and Acetone into Poly(Vinyl Alcohol)–Clay Nanocomposites Using ATR-FTIR. Vib. Spectrosc. 2004, 35, 27–32. [Google Scholar] [CrossRef]
- Elabd, Y.A.; Baschetti, M.G.; Barbari, T.A. Time-resolved Fourier Transform Infrared/Attenuated Total Reflection Spectroscopy for the Measurement of Molecular Diffusion in Polymers. J. Polym. Sci. Part B Polym. Phys. 2004, 42, 365. [Google Scholar] [CrossRef]
- Hallinan, D.T.; Elabd, Y.A. Diffusion and Sorption of Methanol and Water in Nafion Using Time-Resolved Fourier Transform Infrared−Attenuated Total Reflectance Spectroscopy. J. Phys. Chem. B 2007, 111, 13221–13230. [Google Scholar] [CrossRef]
- Neto, A.O.; Nandenha, J.; Assumpção, M.H.M.T.; Linardi, M.; Spinacé, E.V.; de Souza, R.F.B. In Situ Spectroscopy Studies of Ethanol Oxidation Reaction Using a Single Fuel Cell/ATR-FTIR Setup. Int J. Hydrogen Energy 2013, 38, 10585–10591. [Google Scholar] [CrossRef]
- Kim, J.M.; Beckingham, B.S. Comonomer Effects on Co-Permeation of Methanol and Acetate in Cation Exchange Membranes. Eur. Polym. J. 2021, 147, 110307. [Google Scholar] [CrossRef]
- Kim, J.M.; Mazumder, A.; Li, J.; Jiang, Z.; Beckingham, B.S. Impact of PEGMA on Transport and Co-Transport of Methanol and Acetate in PEGDA-AMPS Cation Exchange Membranes. J. Membr. Sci. 2022, 642, 119950. [Google Scholar] [CrossRef]

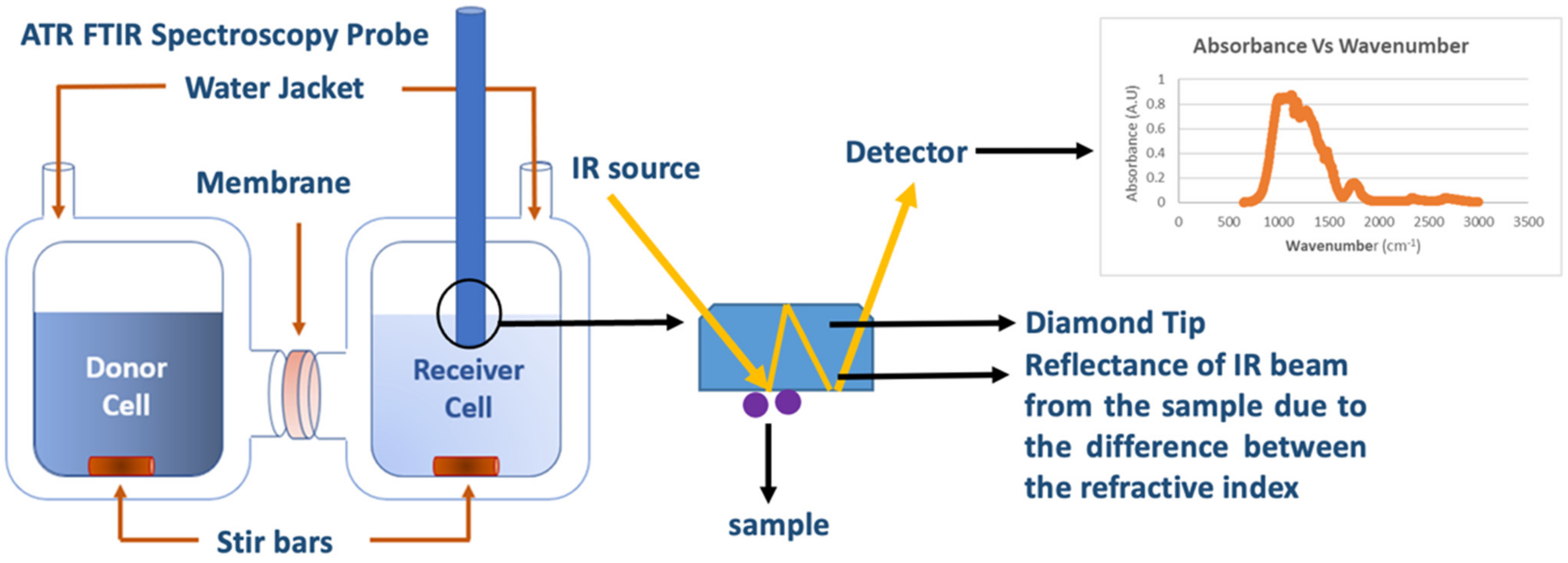

| Model | Driving Force | Transport Coefficient | Notes |
|---|---|---|---|
| Solution-diffusion model with Fick’s law (Equation (3)) | Composition gradient | Pi | Based on Fick’s law for diffusion (Equation (2)), which neglects off-diagonal (i ≠ j) fluxes in Equation (8). Pi is the product of the diffusivity, Di, and the solubility, Ki. |
| Multicomponent Fick’s law (Equation (8)) | Composition gradient | Dij | Dij can be related to Lij or Đij using a thermodynamic model. |
| Nonequilibrium thermodynamics (Equation (5)) | Chemical potential gradient | Lij or | Lij are measurable in equilibrium molecular dynamics simulations (Equation (9)). |
| Maxwell–Stefan (Equation (7)) | Chemical potential gradient | Đij | Đij are independent of reference velocity, can be computed from Lij. |
| Experimental Approach | Variables to Measure | Significance |
|---|---|---|
| Interferometry | Measures refractive index variation in liquid layers adjacent to membrane | Measured refractive index used to calculate diffusivity coefficients (Di). Experiments and calculations are quite complex. |
| Diffusion-Cell experiments with aliquotic sampling | Measures solute(s) concentration(s) in receiver cell utilizing ex situ spectroscopic methods | Measured solute(s) concentration(s) used in Yasuda model to determine permeability (Pi). For multicomponent systems sampling results in non- constant volume in cell and is aliquot analysis time-consuming. |
| Diffusion-Cell experiments coupled with in situ ATR FTIR | Measures solute (s) concentration(s) variation in receiver cell using in situ ATR FTIR spectroscopy. | Real time concentration data obtained from the diffusion cell for use in Yasuda’s model to extract multi-solute permeabilities (Pi). |
| Sorption-desorption experiment | Measures concentration of solute desorbed from membrane after equilibrium sorption. | Desorbed solute(s) concentration(s) used with measured membrane volume to calculate membrane solubility (Ki) to the solute(s). |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazumder, A.; Dobyns, B.M.; Howard, M.P.; Beckingham, B.S. Theoretical and Experimental Considerations for Investigating Multicomponent Diffusion in Hydrated, Dense Polymer Membranes. Membranes 2022, 12, 942. https://doi.org/10.3390/membranes12100942
Mazumder A, Dobyns BM, Howard MP, Beckingham BS. Theoretical and Experimental Considerations for Investigating Multicomponent Diffusion in Hydrated, Dense Polymer Membranes. Membranes. 2022; 12(10):942. https://doi.org/10.3390/membranes12100942
Chicago/Turabian StyleMazumder, Antara, Breanna M. Dobyns, Michael P. Howard, and Bryan S. Beckingham. 2022. "Theoretical and Experimental Considerations for Investigating Multicomponent Diffusion in Hydrated, Dense Polymer Membranes" Membranes 12, no. 10: 942. https://doi.org/10.3390/membranes12100942
APA StyleMazumder, A., Dobyns, B. M., Howard, M. P., & Beckingham, B. S. (2022). Theoretical and Experimental Considerations for Investigating Multicomponent Diffusion in Hydrated, Dense Polymer Membranes. Membranes, 12(10), 942. https://doi.org/10.3390/membranes12100942










