Mutually Beneficial Combination of Molecular Dynamics Computer Simulations and Scattering Experiments
Abstract
:1. Introduction
2. Background
2.1. Scattering Length Density
2.2. Reflectometry
2.3. Small-Angle Scattering
2.4. Molecular Dynamics Simulations
3. Materials and Methods
3.1. Materials
3.2. Reflectometry
3.3. Small-Angle Scattering
3.4. Molecular Dynamics Simulations
4. Results
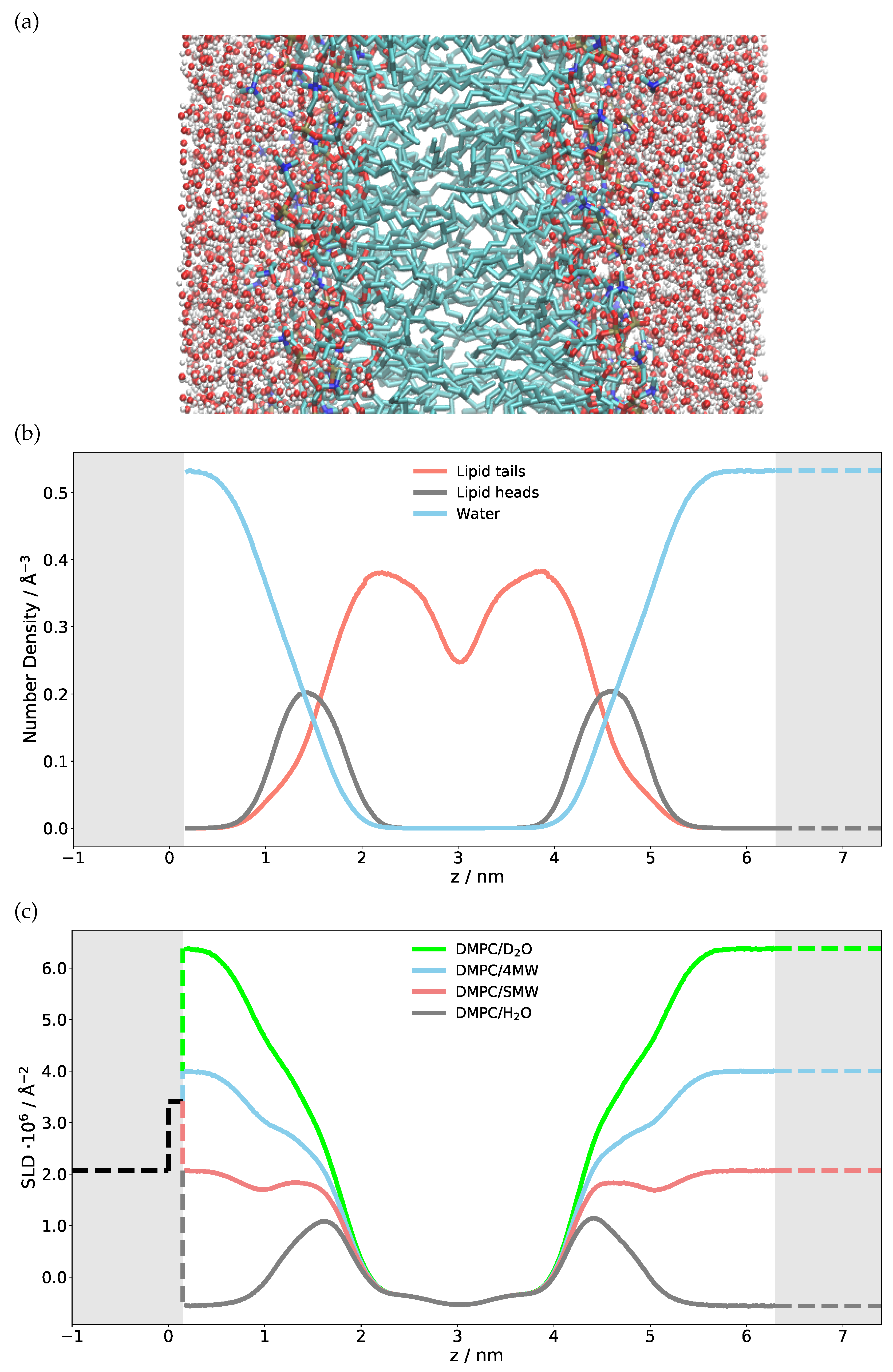
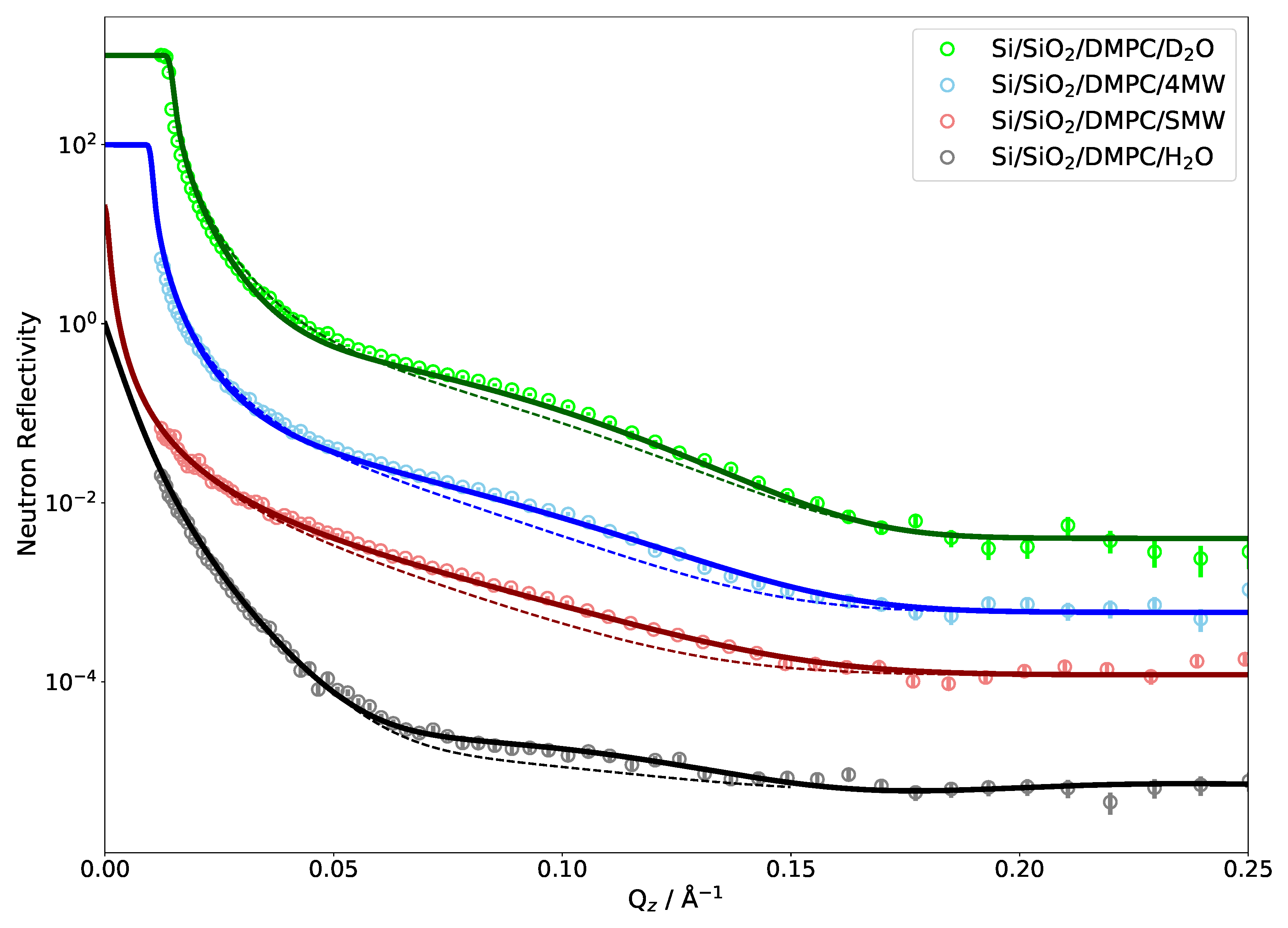
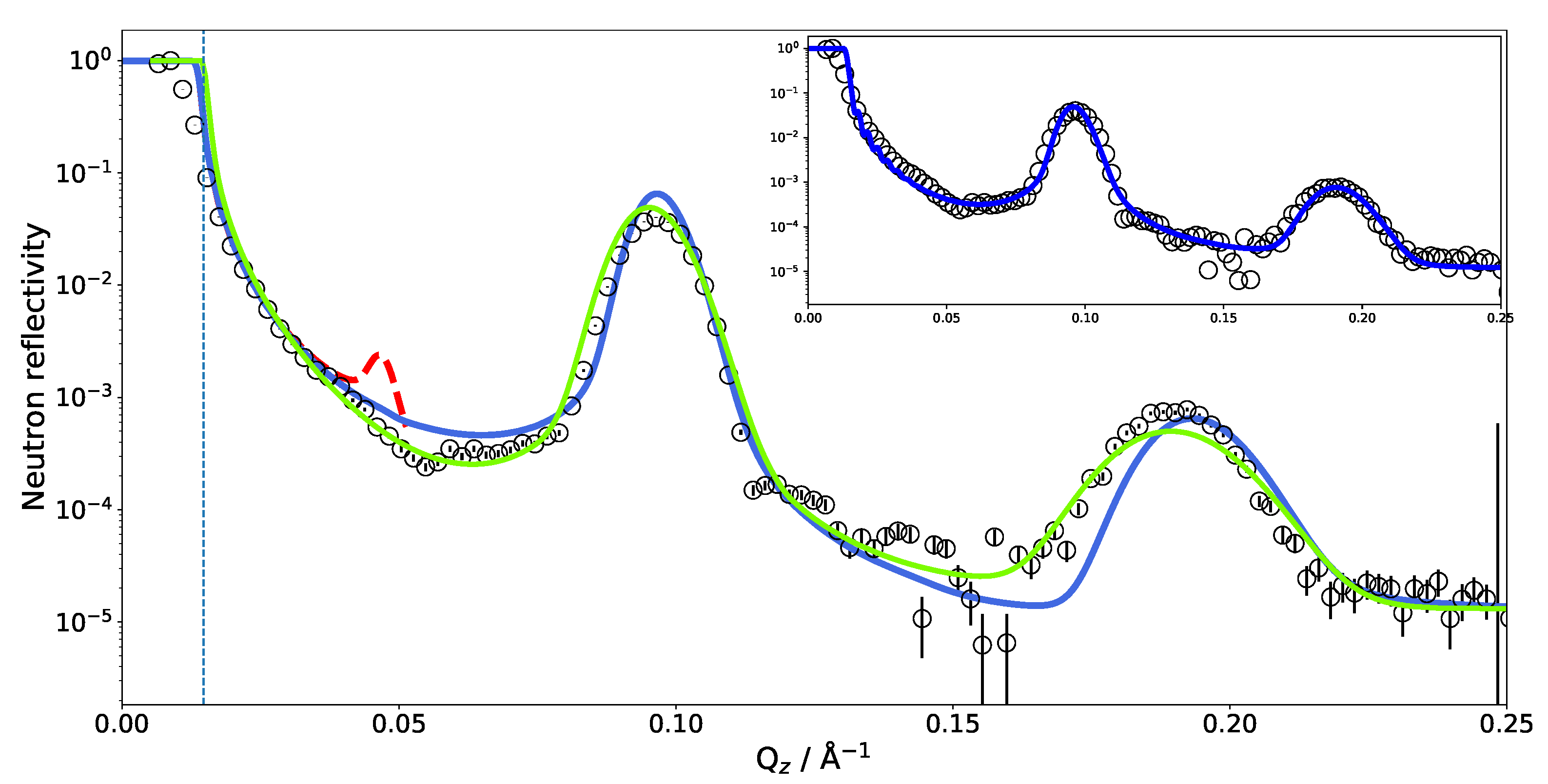
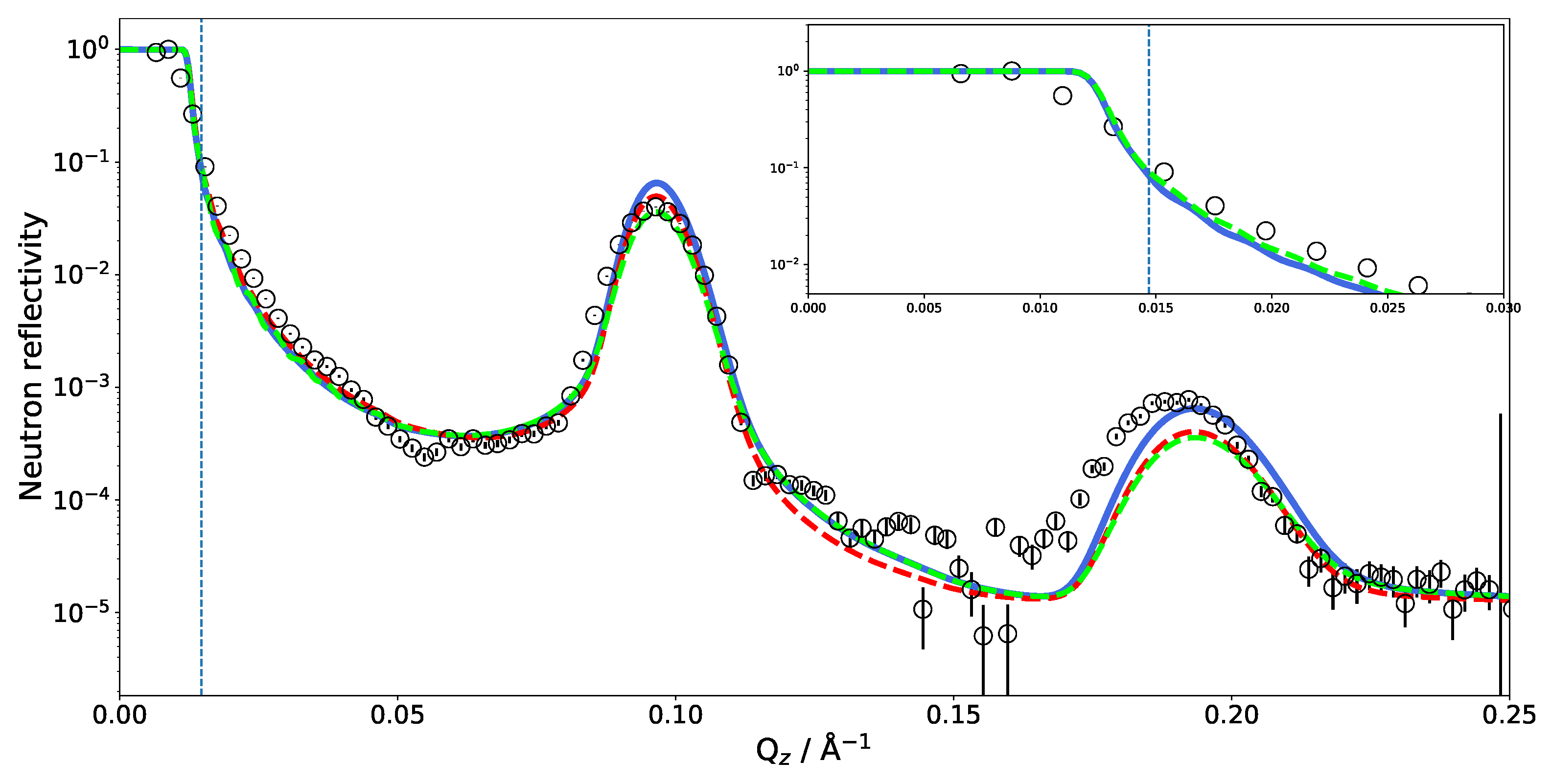
4.1. Single Bilayer Neutron Reflectivity of a DMPC Bilayer
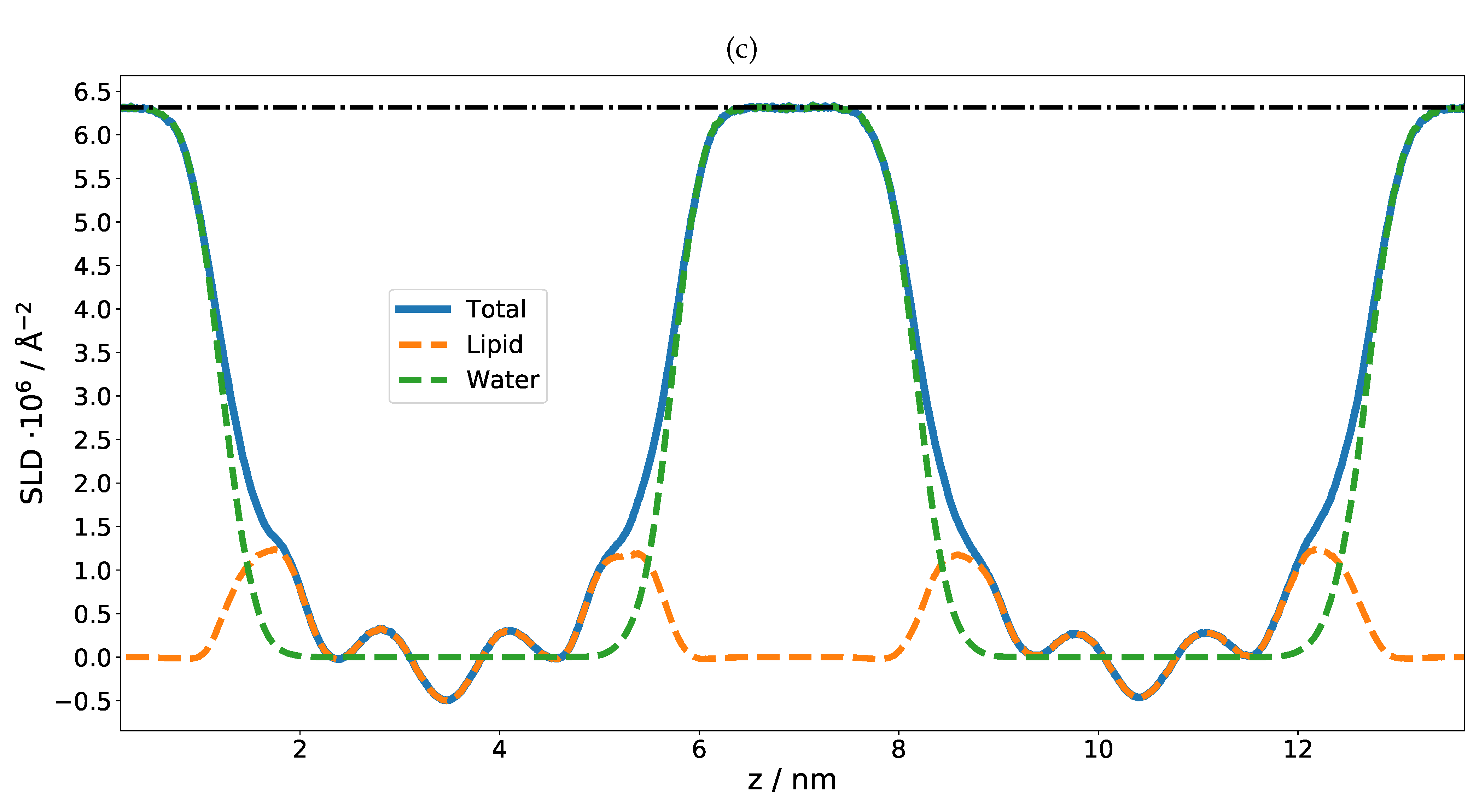
4.2. Neutron Reflectivity of a SoyPC Multilayer
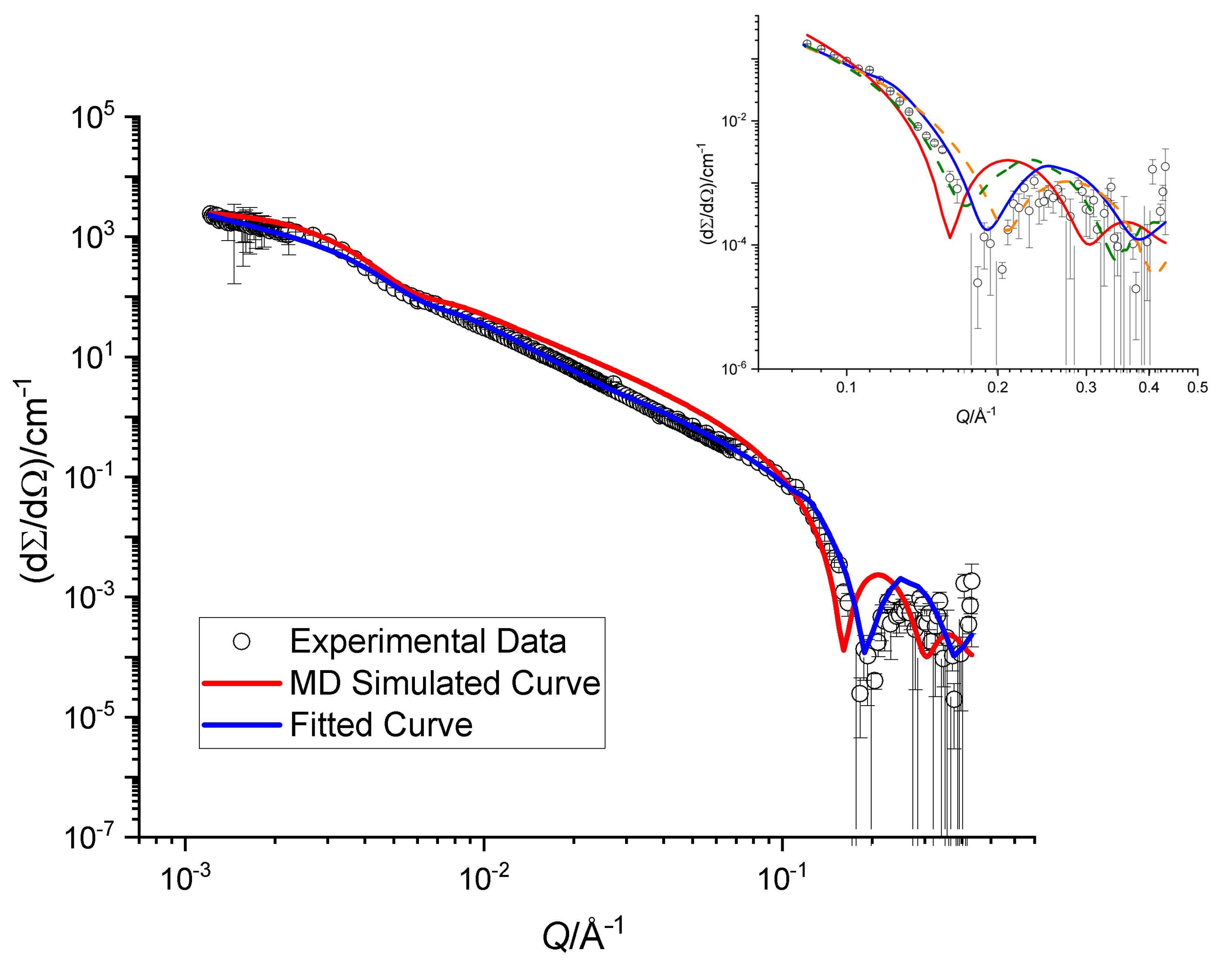
4.3. Small-Angle Neutron Scattering of SoyPC Bilayers
5. Discussion
5.1. Reflectometry
- Every instrument will have sources of background which contaminate the intensity with a more or less random noise. These can be independent of the experiment (e.g., the perfectly random detection of cosmic particles) or instrument setting related (e.g., scattering of the probing particles on air or windows in the beam—also random and scattering on slits—a usually more or less strongly peaked effect).
- When the sample is illuminated under a very shallow angle, it might happen that only a fraction of the beam actually illuminates the sample. This geometric effect will be a function of the incident angle and the real intensity distribution in the beam (usually treated as Gaussian). In some configurations, this function could be strongly wavelength dependent, due to the ballistic effect: on their way to the sample, long wavelength neutrons, being slower, fall more than the short wavelength ones under the action of gravitation. They will thus impinge on the sample at a different spot and slightly different incident angle (an effect which also has to be taken into account to properly evaluate Q).
- Both aforementioned effects contribute to a normalization issue: since R is a relative measurement, one must ascertain that the full incident intensity is accurately measured. This can cause practical problems since the primary beam intensity is always orders of magnitude more intense than the reflected one. Gross errors in this step can be detected if enough data points have been taken in the regime of total reflection, but more subtle effects such as the above-mentioned over-illumination are much more difficult to detect if they affect the region where reflectivity intrinsically varies. It should be stressed that it is quite easy to overlook significant systematic errors since the R value is usually plotted on a logarithmic scale with 5–6 orders of magnitude.
- The measured intensity can be described by the convolution of the ideal signal with the instrumental resolution function. This convolution smears the measured curve and limits the possibility to resolve adjacent features (oscillations, peaks) in Q space. In real space, this translates to an upper limit for the measurable layer thickness and sensitivity to long-range correlations. Typically, the instrumental resolution of neutron reflectometers ranges about 1–10% and consists of contributions of the often dominant wavelength uncertainty and the beam divergence.
- A very careful treatment of error propagation during data reduction of the counted intensities is needed in order to preserve the possibility to evaluate the statistical agreement between a simulation and experimental data. Obviously, the error bar validity issue is paramount when dealing with fitting methods, and this is even more so when the fitted data vary over several orders of magnitude, as is the case for both reflectivity and SANS [78].
- The sample membrane in a reflectometry measurement has to be supported by a substrate, either solid or liquid. This substrate can have an influence on the membrane properties, such as its rigidity. Studies looking at embedding larger proteins into the membrane might even experience collisions between the proteins and the substrate [46]. Further, the surface of the substrate can be ill-defined. While a reasonably thin silicon oxide layer usually does not influence the scattering data too much, the surface roughness of the substrate has an immediate effect on the data and can render the data useless if the roughness is not controlled to be below ∼5 Å. Besides influencing the quality of the data, it is clear that large surface irregularities will also affect the membrane morphology. The other half-infinite side also adds possibilities for imperfections that might not be mapped into the simulation: the solvent (especially when deuterated) might be contaminated with another isotope—either from the experimental setup of channels leading to the sample chamber or by hydrogen or hydrogen-containing groups escaping from the sample layer. This might have happened in the DLPC multilayer presented here where an amount of bilayers could have detached from the multilayer and float in some form through the solvent, lowering its SLD.
- A more subtle point concerns the water contrast variation. In order to make use of the different contrasts that can be achieved by isotopic substitution, one has to assume that the exchange between hydrogen and deuterium changes only the scattering lengths and not the actual structure. This is generally a justifiable approximation. The density [79,80] and many of the molecular interactions do change between HO and DO [80,81], but mostly very slightly. These—usually small—changes that happen in the real sample will of course not be reproduced by only one simulation where the isotopic exchange is performed a posteriori by assigning different scattering lengths to the atoms.
- The sample layer itself can also deviate from the modeled version in several aspects: concerning the SLD, it is basically impossible for an experimenter to ascertain the deuteration degree of the purchased phospholipids. Further, the deposition of phospholipids on the substrate might not have produced the structure that was intended (e.g., a single bilayer)—either on the complete sample or as inhomogeneities within the membrane plane. Neutron reflectometry measurements probe a surface on the order of 10–100 cm: it is rather unrealistic that a phospholipid layer would coat such a large area homogeneously. Last, inhomogeneities can of course also occur in the direction of the membrane normal, such as a disorder of the water layer thickness between neighboring membranes in a multilayer.
- The sample will not only scatter neutrons/X-rays into the specular spot, but will also itself contribute an isotropic background which will add up to the extrinsic background sources discussed above. In the case of neutron scattering, this sample-related background level is dominated by the incoherent scattering from hydrogen atoms in the sample and will therefore vary between different contrasts of a given system. In the case of X-rays, the diffuse background is generated by the inelastic Compton scattering. It is measured and subtracted from the signal together with the off-specular scattering (see below). A remaining Q-independent background has to be accounted for in the modeling.
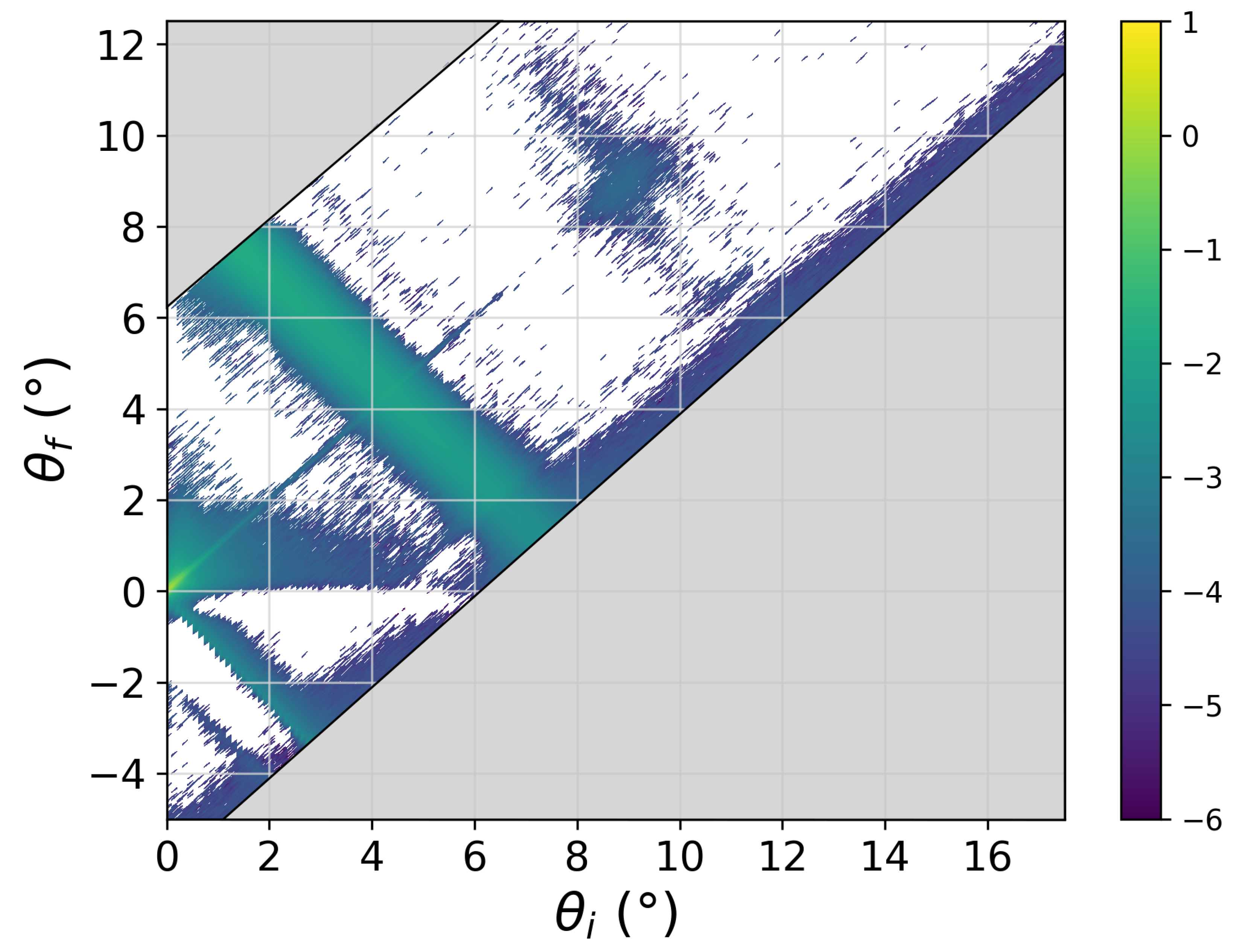
- Most importantly, in reflectometry, the sample will also generate off-specular scattering. This scattering intensity is caused by fluctuations of the SLD profile parallel to the membrane due, for instance, to membrane fluctuations. In the current context, this additional intensity overlaps the purely specular signal and needs to be subtracted from the experimental values before R can be evaluated. The length scale of the fluctuations responsible for off-specular scattering is up to the micrometer regime [20], which renders, as hinted above, an evaluation from the computer simulations impossible. The usual approach is therefore to measure the scattered intensity on both sides of the specular condition near to it in order to then interpolate the background intensity. On modern instruments using bidimensional detectors, one does not need to perform any additional experiment since a whole range of reflected angles is being covered around the specular direction. Figure 7 shows the intensity distribution as a function of incident angle () and reflection angle (). The specular line is seen along the main diagonal (), and it shows the total reflection region at the smallest angles. Along this line, the intensity maxima correspond to the Bragg peaks. The most prominent feature of this intensity map is, however, the broad off-specular band which follows the condition , which in Q space translates to . As hinted above, this intensity band is thus characteristic of the in-plane correlations of the structures responsible for the Bragg peak. The broad width of the Bragg peak in the reciprocal space shows that the bilayers are only coherent over very small length scales. Subtraction of the underlying off-specular signal is clearly a challenging task, especially in regions where the overall reflectivity is low, leading to poor statistics. One needs to be aware of the risk of introducing systematic deviations from the true specular reflectivity during this data reduction step.
5.2. Small-Angle Scattering
5.3. Molecular Dynamics Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cooper, G. The Cell: A Molecular Approach; Sinauer Associates, Inc.: Sunderland, MA, USA, 2016. [Google Scholar]
- Alberts, B.; Johnson, A.; Lewis, J.; Morgan, D.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell; Garland Science, Taylor and Francis Group: New York, NY, USA, 2015. [Google Scholar]
- Stone, M.B.; Shelby, S.A.; Veatch, S.L. Super-Resolution Microscopy: Shedding Light on the Cellular Plasma Membrane. Chem. Rev. 2017, 117, 7457–7477. [Google Scholar] [CrossRef]
- Connell, S.D.; Smith, D.A. The atomic force microscope as a tool for studying phase separation in lipid membranes (Review). Mol. Membr. Biol. 2006, 23, 17–28. [Google Scholar] [CrossRef] [PubMed]
- Macháň, R.; Hof, M. Recent Developments in Fluorescence Correlation Spectroscopy for Diffusion Measurements in Planar Lipid Membranes. Int. J. Mol. Sci. 2010, 11, 427–457. [Google Scholar] [CrossRef] [Green Version]
- Binder, H. The Molecular Architecture of Lipid Membranes—New Insights from Hydration-Tuning Infrared Linear Dichroism Spectroscopy. Appl. Spectrosc. Rev. 2003, 38, 15–69. [Google Scholar] [CrossRef]
- Salditt, T.; Münster, C.; Mennicke, U.; Ollinger, C.; Fragneto, G. Thermal Fluctuations of Oriented Lipid Membranes by Nonspecular Neutron Reflectometry. Langmuir 2003, 19, 7703–7711. [Google Scholar] [CrossRef]
- Marquardt, D.; Heberle, F.A.; Pan, J.; Cheng, X.; Pabst, G.; Harroun, T.A.; Kučerka, N.; Katsaras, J. The structures of polyunsaturated lipid bilayers by joint refinement of neutron and X-ray scattering data. Chem. Phys. Lipids 2020, 229, 104892. [Google Scholar] [CrossRef] [PubMed]
- Mills, T.T.; Toombes, G.E.; Tristram-Nagle, S.; Smilgies, D.M.; Feigenson, G.W.; Nagle, J.F. Order Parameters and Areas in Fluid-Phase Oriented Lipid Membranes Using Wide Angle X-Ray Scattering. Biophys. J. 2008, 95, 669–681. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kučerka, N.; Nagle, J.F.; Sachs, J.N.; Feller, S.E.; Pencer, J.; Jackson, A.; Katsaras, J. Lipid Bilayer Structure Determined by the Simultaneous Analysis of Neutron and X-Ray Scattering Data. Biophys. J. 2008, 95, 2356–2367. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marrink, S.J.; de Vries, A.H.; Tieleman, D.P. Lipids on the move: Simulations of membrane pores, domains, stalks and curves. Biochim. Biophys. Acta BBA Biomembr. 2009, 1788, 149–168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kirsch, S.A.; Böckmann, R.A. Membrane pore formation in atomistic and coarse-grained simulations. Biochim. Biophys. Acta BBA Biomembr. 2016, 1858, 2266–2277. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Martí, J.; Calero, C. Pair interactions among ternary DPPC/POPC/cholesterol mixtures in liquid-ordered and liquid-disordered phases. Soft Matter 2016, 12, 4557–4561. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, J.; Calero, C.; Martí, J. Diffusion and spectroscopy of water and lipids in fully hydrated dimyristoylphosphatidylcholine bilayer membranes. J. Chem. Phys. 2014, 140, 104901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harroun, T.A.; Wignall, G.D.; Katsaras, J. Neutron Scattering for Biology. In Neutron Scattering in Biology: Techniques and Applications; Springer: Berlin/Heidelberg, Germany, 2006; pp. 1–18. [Google Scholar]
- Krueger, S.; Meuse, C.W.; Majkrzak, C.F.; Dura, J.A.; Berk, N.F.; Tarek, M.; Plant, A.L. Investigation of Hybrid Bilayer Membranes with Neutron Reflectometry: Probing the Interactions of Melittin. Langmuir 2001, 17, 511–521. [Google Scholar] [CrossRef]
- Fragneto, G. Neutrons and model membranes. Eur. Phys. J. Spec. Top. 2012, 213, 327–342. [Google Scholar] [CrossRef]
- Campbell, R.A. Recent advances in resolving kinetic and dynamic processes at the air/water interface using specular neutron reflectometry. Curr. Opin. Colloid Interface Sci. 2018, 37, 49–60. [Google Scholar] [CrossRef] [Green Version]
- Luchini, A.; Gerelli, Y.; Fragneto, G.; Nylander, T.; Pálsson, G.K.; Appavou, M.S.; Paduano, L. Neutron Reflectometry reveals the interaction between functionalized SPIONs and the surface of lipid bilayers. Colloids Surf. B Biointerfaces 2017, 151, 76–87. [Google Scholar] [CrossRef]
- Pynn, R.; Baker, S.M.; Smith, G.; Fitzsimmons, M. Off-specular scattering in neutron reflectometry. J. Neutron Res. 1999, 7, 139–158. [Google Scholar] [CrossRef] [Green Version]
- Sivia, D.S. Elementary Scattering Theory: For X-ray and Neutron Users; Oxford University Press: Oxford, UK; New York, NY, USA, 2011. [Google Scholar]
- Zec, N.; Mangiapia, G.; Zheludkevich, M.L.; Busch, S.; Moulin, J.F. Revealing the interfacial nanostructure of a deep eutectic solvent at a solid electrode. Phys. Chem. Chem. Phys. 2020, 22, 12104–12112. [Google Scholar] [CrossRef]
- Benz, R.W.; Castro-Roman, F.; Tobias, D.J.; White, S.H. Experimental validation of molecular dynamics simulations of lipid bilayers: A new approach. Biophys. J. 2005, 88, 805–817. [Google Scholar] [CrossRef] [Green Version]
- Dodda, L.S.; de Vaca, I.C.; Tirado-Rives, J.; Jorgensen, W.L. LigParGen web server: An automatic OPLS-AA parameter generator for organic ligands. Nucleic Acids Res. 2017, 45, W331–W336. [Google Scholar] [CrossRef] [Green Version]
- Malde, A.K.; Zuo, L.; Breeze, M.; Stroet, M.; Poger, D.; Nair, P.C.; Oostenbrink, C.; Mark, A.E. An Automated Force Field Topology Builder (ATB) and Repository: Version 1.0. J. Chem. Theory Comput. 2011, 7, 4026–4037. [Google Scholar] [CrossRef] [PubMed]
- Zoete, V.; Cuendet, M.A.; Grosdidier, A.; Michielin, O. SwissParam: A fast force field generation tool for small organic molecules. J. Comput. Chem. 2011, 32, 2359–2368. [Google Scholar] [CrossRef]
- Siligardi, G.; Hussain, R.; Patching, S.G.; Phillips-Jones, M.K. Ligand- and drug-binding studies of membrane proteins revealed through circular dichroism spectroscopy. Biochim. Biophys. Acta BBA Biomembr. 2014, 1838, 34–42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Upert, G.; Luther, A.; Obrecht, D.; Ermert, P. Emerging peptide antibiotics with therapeutic potential. Med. Drug Discov. 2021, 9, 100078. [Google Scholar] [CrossRef]
- van Hoogevest, P.; Wendel, A. The use of natural and synthetic phospholipids as pharmaceutical excipients. Eur. J. Lipid Sci. Technol. 2014, 116, 1088–1107. [Google Scholar] [CrossRef] [Green Version]
- Jaksch, S.; Lipfert, F.; Koutsioubas, A.; Mattauch, S.; Holderer, O.; Ivanova, O.; Frielinghaus, H.; Hertrich, S.; Fischer, S.F.; Nickel, B. Influence of ibuprofen on phospholipid membranes. Phys. Rev. E 2015, 91, 022716. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mangiapia, G.; Gvaramia, M.; Kuhrts, L.; Teixeira, J.; Koutsioubas, A.; Soltwedel, O.; Frielinghaus, H. Effect of benzocaine and propranolol on phospholipid-based bilayers. Phys. Chem. Chem. Phys. 2017, 19, 32057–32071. [Google Scholar] [CrossRef] [Green Version]
- Xue, Y.; He, L.; Middelberg, A.P.J.; Mark, A.E.; Poger, D. Determining the Structure of Interfacial Peptide Films: Comparing Neutron Reflectometry and Molecular Dynamics Simulations. Langmuir 2014, 30, 10080–10089. [Google Scholar] [CrossRef]
- Vanegas, J.M.; Heinrich, F.; Rogers, D.M.; Carson, B.D.; La Bauve, S.; Vernon, B.C.; Akgun, B.; Satija, S.; Zheng, A.; Kielian, M.; et al. Insertion of Dengue E into lipid bilayers studied by neutron reflectivity and molecular dynamics simulations. Biochim. Biophys. Acta BBA Biomembr. 2018, 1860, 1216–1230. [Google Scholar] [CrossRef]
- Reguera, J.; Ponomarev, E.; Geue, T.; Stellacci, F.; Bresme, F.; Moglianetti, M. Contact angle and adsorption energies of nanoparticles at the air–liquid interface determined by neutron reflectivity and molecular dynamics. Nanoscale 2015, 7, 5665–5673. [Google Scholar] [CrossRef] [Green Version]
- Hughes, A.V.; Ciesielski, F.; Kalli, A.C.; Clifton, L.A.; Charlton, T.R.; Sansom, M.S.P.; Webster, J.R.P. On the interpretation of reflectivity data from lipid bilayers in terms of molecular-dynamics models. Acta Crystallogr. Sect. Struct. Biol. 2016, 72, 1227–1240. [Google Scholar] [CrossRef] [Green Version]
- Koutsioubas, A. Combined Coarse-Grained Molecular Dynamics and Neutron Reflectivity Characterization of Supported Lipid Membranes. J. Phys. Chem. B 2016, 120, 11474–11483. [Google Scholar] [CrossRef]
- McCluskey, A.R.; Grant, J.; Smith, A.J.; Rawle, J.L.; Barlow, D.J.; Lawrence, M.J.; Parker, S.C.; Edler, K.J. Assessing molecular simulation for the analysis of lipid monolayer reflectometry. J. Phys. Commun. 2019, 3, 075001. [Google Scholar] [CrossRef]
- Kučerka, N.; Katsaras, J.; Nagle, J.F. Comparing Membrane Simulations to Scattering Experiments: Introducing the SIMtoEXP Software. J. Membr. Biol. 2010, 235, 43–50. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Darré, L.; Iglesias-Fernandez, J.; Kohlmeyer, A.; Wacklin, H.; Domene, C. Molecular Dynamics Simulations and Neutron Reflectivity as an Effective Approach To Characterize Biological Membranes and Related Macromolecular Assemblies. J. Chem. Theory Comput. 2015, 11, 4875–4884. [Google Scholar] [CrossRef]
- Grillo, I. Small-Angle Neutron Scattering and Applications in Soft Condensed Matter. In Soft Matter Characterization; Springer: Dordrecht, The Netherlands, 2008; pp. 723–782. [Google Scholar]
- Fischer, H.E.; Barnes, A.C.; Salmon, P.S. Neutron and X-ray diffraction studies of liquids and glasses. Rep. Prog. Phys. 2005, 69, 233–299. [Google Scholar] [CrossRef]
- Tristram-Nagle, S.; Liu, Y.; Legleiter, J.; Nagle, J.F. Structure of Gel Phase DMPC Determined by X-ray Diffraction. Biophys. J. 2002, 83, 3324–3335. [Google Scholar] [CrossRef] [Green Version]
- Salditt, T.; Li, C.; Spaar, A.; Mennicke, U. X-ray reflectivity of solid-supported, multilamellar membranes. Eur. Phys. J. E 2002, 7, 105–116. [Google Scholar] [CrossRef]
- Sears, V.F. Neutron scattering lengths and cross sections. Neutron News 1992, 3, 26–37. [Google Scholar] [CrossRef]
- Heinrich, F.; Kienzle, P.A.; Hoogerheide, D.P.; Lösche, M. Information gain from isotopic contrast variation in neutron reflectometry on protein–membrane complex structures. J. Appl. Crystallogr. 2020, 53, 800–810. [Google Scholar] [CrossRef]
- Böhm, P.; Koutsioubas, A.; Moulin, J.F.; Rädler, J.O.; Sackmann, E.; Nickel, B. Probing the Interface Structure of Adhering Cells by Contrast Variation Neutron Reflectometry. Langmuir 2018, 35, 513–521. [Google Scholar] [CrossRef]
- Junghans, A.; Watkins, E.B.; Barker, R.D.; Singh, S.; Waltman, M.J.; Smith, H.L.; Pocivavsek, L.; Majewski, J. Analysis of biosurfaces by neutron reflectometry: From simple to complex interfaces. Biointerphases 2015, 10, 019014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mushtaq, A.U.; Ådén, J.; Clifton, L.A.; Wacklin-Knecht, H.; Campana, M.; Dingeldein, A.P.G.; Persson, C.; Sparrman, T.; Gröbner, G. Neutron reflectometry and NMR spectroscopy of full-length Bcl-2 protein reveal its membrane localization and conformation. Commun. Biol. 2021, 4, 507. [Google Scholar] [CrossRef]
- Nielsen, J. Elements of Modern X-ray Physics; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Parratt, L.G. Surface Studies of Solids by Total Reflection of X-Rays. Phys. Rev. 1954, 95, 359–369. [Google Scholar] [CrossRef]
- Abelès, F. La théorie générale des couches minces. J. Phys. Radium 1950, 11, 307–309. [Google Scholar] [CrossRef]
- Born, M. Principles of Optics: Electromagnetic Theory of Propagation, Interference, and Diffraction of Light; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Névot, L.; Croce, P. Caractérisation des surfaces par réflexion rasante de rayons X. Application à l’étude du polissage de quelques verres silicates. Rev. Phys. Appl. 1980, 15, 761–779. [Google Scholar] [CrossRef]
- Penfold, J.; Thomas, R.K. Neutron reflectivity and small angle neutron scattering: An introduction and perspective on recent progress. Curr. Opin. Colloid Interface Sci. 2014, 19, 198–206. [Google Scholar] [CrossRef]
- Brumberger, H. (Ed.) Modern Aspects of Small-Angle Scattering; Springer: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Svergun, D.I. Structure Analysis by Small-Angle X-ray and Neutron Scattering; Plenum Press: New York, NY, USA, 1987. [Google Scholar]
- Poger, D.; Caron, B.; Mark, A.E. Validating lipid force fields against experimental data: Progress, challenges and perspectives. Biochim. Biophys. Acta BBA Biomembr. 2016, 1858, 1556–1565. [Google Scholar] [CrossRef]
- Knight, C.J.; Hub, J.S. MemGen: A general web server for the setup of lipid membrane simulation systems: Fig. 1. Bioinformatics 2015, 31, 2897–2899. [Google Scholar] [CrossRef] [PubMed]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Moradi, S.; Nowroozi, A.; Shahlaei, M. Shedding light on the structural properties of lipid bilayers using molecular dynamics simulation: A review study. RSC Adv. 2019, 9, 4644–4658. [Google Scholar] [CrossRef] [Green Version]
- Khattari, Z.; Köhler, S.; Xu, Y.; Aeffner, S.; Salditt, T. Stalk formation as a function of lipid composition studied by X-ray reflectivity. Biochim. Biophys. Acta BBA Biomembr. 2015, 1848, 41–50. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Penfold, J.; Richardson, R.M.; Zarbakhsh, A.; Webster, J.R.P.; Bucknall, D.G.; Rennie, A.R.; Jones, R.A.L.; Cosgrove, T.; Thomas, R.K.; Higgins, J.S.; et al. Recent advances in the study of chemical surfaces and interfaces by specular neutron reflection. J. Chem. Soc. Faraday Trans. 1997, 93, 3899–3917. [Google Scholar] [CrossRef]
- Roldan, J.L.O.; Campana, M.; Barker, R.; Yoldi, I.; Hendry, A. Elucidating the Membrane Interaction Mechanism of Chloride Intracellular Channel Proteins; STFC ISIS Neutron and Muon Source: 2018. Available online: https://doi.org/10.5286/ISIS.E.RB1820565 (accessed on 1 June 2021).
- Mattauch, S.; Koutsioubas, A.; Pütter, S. MARIA: Magnetic reflectometer with high incident angle. J. Large Scale Res. Facil. 2015, 1, 8. [Google Scholar] [CrossRef]
- Mattauch, S.; Koutsioubas, A.; Rücker, U.; Korolkov, D.; Fracassi, V.; Daemen, J.; Schmitz, R.; Bussmann, K.; Suxdorf, F.; Wagener, M.; et al. The high-intensity reflectometer of the Jülich Centre for Neutron Science: MARIA. J. Appl. Crystallogr. 2018, 51, 646–654. [Google Scholar] [CrossRef] [PubMed]
- Frielinghaus, H.; Feoktystov, A.; Berts, I.; Mangiapia, G. KWS-1: Small-angle scattering diffractometer. J. Large Scale Res. Facil. JLSRF 2015, 1, 28. [Google Scholar] [CrossRef] [Green Version]
- Wignall, G.D.; Bates, F.S. Absolute calibration of small-angle neutron scattering data. J. Appl. Crystallogr. 1987, 20, 28–40. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [Green Version]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Berger, O.; Edholm, O.; Jähnig, F. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 1997, 72, 2002–2013. [Google Scholar] [CrossRef] [Green Version]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Brehm, M.; Thomas, M.; Gehrke, S.; Kirchner, B. TRAVIS—A free analyzer for trajectories from molecular simulation. J. Chem. Phys. 2020, 152, 164105. [Google Scholar] [CrossRef] [Green Version]
- Brehm, M.; Kirchner, B. TRAVIS—A Free Analyzer and Visualizer for Monte Carlo and Molecular Dynamics Trajectories. J. Chem. Inf. Model. 2011, 51, 2007–2023. [Google Scholar] [CrossRef] [Green Version]
- Krueger, S.; Koenig, B.W.; Orts, W.J.; Berk, N.F.; Majkrzak, C.F.; Gawrisch, K. Neutron Reflectivity Studies of Single Lipid Bilayers Supported on Planar Substrates. In Neutrons in Biology; Springer: Boston, MA, USA, 1996; pp. 205–213. [Google Scholar]
- Nouhi, S.; Koutsioubas, A.; Kapaklis, V.; Rennie, A.R. Distortion of surfactant lamellar phases induced by surface roughness. Eur. Phys. J. Spec. Top. 2020, 229, 2807–2823. [Google Scholar] [CrossRef]
- Degiorgio, V. Physics of Amphiphiles—Micelles, Vesicles, and Microemulsions: Varenna on Lake Como, Villa Monastero, 19–29 July 1983; Elsevier Science Publishers: New York, NY, USA, 1983. [Google Scholar]
- Kotlarchyk, M.; Chen, S.H. Analysis of small angle neutron scattering spectra from polydisperse interacting colloids. J. Chem. Phys. 1983, 79, 2461–2469. [Google Scholar] [CrossRef]
- Pardo, L.C.; Rovira-Esteva, M.; Busch, S.; Moulin, J.F.; Tamarit, J.L. Fitting in a complex χ2 landscape using an optimized hypersurface sampling. Phys. Rev. E 2011, 84, 046711. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soper, A.K. The Radial Distribution Functions of Water as Derived from Radiation Total Scattering Experiments: Is There Anything We Can Say for Sure? ISRN Phys. Chem. 2013, 2013, 1–67. [Google Scholar] [CrossRef] [Green Version]
- Jancsó, G. Isotope Effects. In Handbook of Nuclear Chemistry; Springer: Boston, MA, USA, 2011; pp. 699–725. [Google Scholar]
- Jelińska-Kazimierczuk, M.; Szydłowski, J. Isotope effect on the solubility of amino acids in water. J. Solut. Chem. 1996, 25, 1175–1184. [Google Scholar] [CrossRef]
- Silva, R.; Ferreira, H.; Cavaco-Paulo, A. Sonoproduction of Liposomes and Protein Particles as Templates for Delivery Purposes. Biomacromolecules 2011, 12, 3353–3368. [Google Scholar] [CrossRef] [Green Version]
- Karge, L.; Gilles, R.; Busch, S. Calibrating SANS data for instrument geometry and pixel sensitivity effects: Access to an extendedQrange. J. Appl. Crystallogr. 2017, 50, 1382–1394. [Google Scholar] [CrossRef] [Green Version]
- Klauda, J.B.; Monje, V.; Kim, T.; Im, W. Improving the CHARMM Force Field for Polyunsaturated Fatty Acid Chains. J. Phys. Chem. B 2012, 116, 9424–9431. [Google Scholar] [CrossRef] [PubMed]
- Fernández, R.G.; Abascal, J.L.F.; Vega, C. The melting point of ice Ih for common water models calculated from direct coexistence of the solid-liquid interface. J. Chem. Phys. 2006, 124, 144506. [Google Scholar] [CrossRef] [PubMed]
- Pospelov, G.; Van Herck, W.; Burle, J.; Carmona Loaiza, J.M.; Durniak, C.; Fisher, J.M.; Ganeva, M.; Yurov, D.; Wuttke, J. BornAgain: Software for simulating and fitting grazing-incidence small-angle scattering. J. Appl. Crystallogr. 2020, 53, 262–276. [Google Scholar] [CrossRef] [Green Version]
- Udby, L.; Willendrup, P.; Knudsen, E.; Niedermayer, C.; Filges, U.; Christensen, N.; Farhi, E.; Wells, B.; Lefmann, K. Analysing neutron scattering data using McStas virtual experiments. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2011, 634, S138–S143. [Google Scholar] [CrossRef]
- Chen, P.C.; Shevchuk, R.; Strnad, F.M.; Lorenz, C.; Karge, L.; Gilles, R.; Stadler, A.M.; Hennig, J.; Hub, J.S. Combined Small-Angle X-ray and Neutron Scattering Restraints in Molecular Dynamics Simulations. J. Chem. Theory Comput. 2019, 15, 4687–4698. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zec, N.; Mangiapia, G.; Hendry, A.C.; Barker, R.; Koutsioubas, A.; Frielinghaus, H.; Campana, M.; Ortega-Roldan, J.L.; Busch, S.; Moulin, J.-F. Mutually Beneficial Combination of Molecular Dynamics Computer Simulations and Scattering Experiments. Membranes 2021, 11, 507. https://doi.org/10.3390/membranes11070507
Zec N, Mangiapia G, Hendry AC, Barker R, Koutsioubas A, Frielinghaus H, Campana M, Ortega-Roldan JL, Busch S, Moulin J-F. Mutually Beneficial Combination of Molecular Dynamics Computer Simulations and Scattering Experiments. Membranes. 2021; 11(7):507. https://doi.org/10.3390/membranes11070507
Chicago/Turabian StyleZec, Nebojša, Gaetano Mangiapia, Alex C. Hendry, Robert Barker, Alexandros Koutsioubas, Henrich Frielinghaus, Mario Campana, José Luis Ortega-Roldan, Sebastian Busch, and Jean-François Moulin. 2021. "Mutually Beneficial Combination of Molecular Dynamics Computer Simulations and Scattering Experiments" Membranes 11, no. 7: 507. https://doi.org/10.3390/membranes11070507
APA StyleZec, N., Mangiapia, G., Hendry, A. C., Barker, R., Koutsioubas, A., Frielinghaus, H., Campana, M., Ortega-Roldan, J. L., Busch, S., & Moulin, J.-F. (2021). Mutually Beneficial Combination of Molecular Dynamics Computer Simulations and Scattering Experiments. Membranes, 11(7), 507. https://doi.org/10.3390/membranes11070507







