Oily Water Separation Process Using Hydrocyclone of Porous Membrane Wall: A Numerical Investigation
Abstract
1. Introduction
- (a)
- Free oil, dispersed in the form of drops with large diameters, above 100 μm, which, since it is already completely stratified in water, can be removed with relative ease, exclusively by physical processes.
- (b)
- Soluble oil, which is composed of hydrocarbons less insoluble in water, such as benzene, toluene, ethylbenzene, and xylene (BTEX) and phenols.
- (c)
- Emulsified oil, which exists in the dispersed form in small water drops, with a diameter varying from 20 to 100 μm.
2. Methodology
2.1. The Physical Problem and Geometry
2.2. The Mathematical Model
- Incompressible and Newtonian fluid with constant physical–chemical properties;
- Steady-state, turbulent and isothermal flow;
- Mass transfer, interfacial momentum, and mass source are disregarded;
- Non-drag interfacial forces such as lift forces, wall lubrication, virtual mass, turbulent dispersion, and solid pressure are neglected;
- The water stream is a multicomponent mixture of water and oil (solute);
- The walls are static and non-deformable;
- The porous wall (ceramic membrane) has constant permeability and porosity;
- The concentration polarization layer thickness is considered uniform and homogeneous;
- Chemical reaction or adsorption phenomena of the solute on the contact surface in the porous medium are neglected.
- (a)
- Mass Conservation Equation:where the Greek sub-index α represents the phase involved in the two-phase water/oil mixture; f, , and e are the volume fraction, density, and velocity vector, respectively.
- (b)
- Momentum Conservation Equation:where is the pressure of phase and describes the drag force per unit volume on phase α due to the interaction with phase β, being defined by:where is the dimensionless drag coefficient given by:where CD = 0.44 represents the drag coefficient and dp represents the particle diameter. The term is the momentum transfer induced by the interfacial mass transfer, and is the effective viscosity, defined by:where μ is the dynamic viscosity and is the turbulent viscosity. The turbulent viscosity is a function of turbulent flow intensity and is unknown. It is necessary to use models to predict their values.The following mass transport equation was used:where is the solute concentration and is the mass diffusion coefficient, defined as:where μ is the dynamic viscosity and corresponds to the Schmidt number.
- (c)
- Turbulence modelThe turbulence model chosen for the continuous phase was the well-known SST (Shear Stress Transport) turbulence model. In this model, close to the fluid/membrane interface, the model is applied, and according to the need, where this model does not show good results, the model is applied. The choice of the model was because the cases studied have more pronounced pressure and concentration gradients near the fluid/membrane interface.
- (d)
- Separation efficiencyTo evaluate the efficiency of water/oil separation, the total efficiency was used, which can be calculated as the ratio between the mass flow rate of oil droplets of a given size found in the overflow, , and the mass flow rate of the oil in the feed, , given by the equation:To verify only the amount of oil collected in the overflow by the exclusive effect of the hydrocyclone centrifugal field, the reduced separation efficiency was considered as follows:where is a parameter that relates the mass flow rate of water collected in the overflow and the mass flow rate of water fed in the hydrocyclone , called the liquid ratio:
2.3. Boundary Conditions
2.4. Process Parameters and Evaluated Cases
3. Results and Discussion
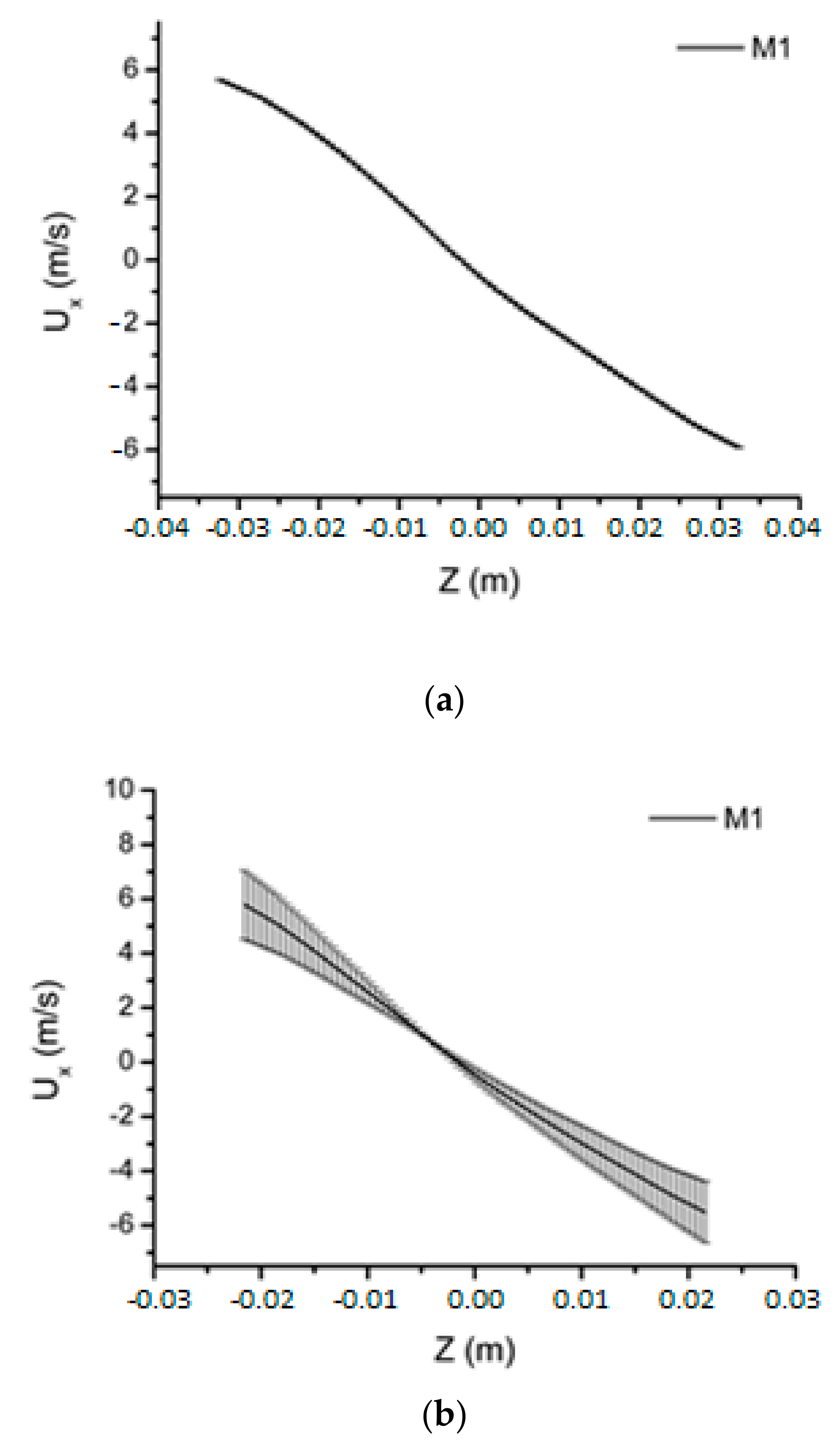
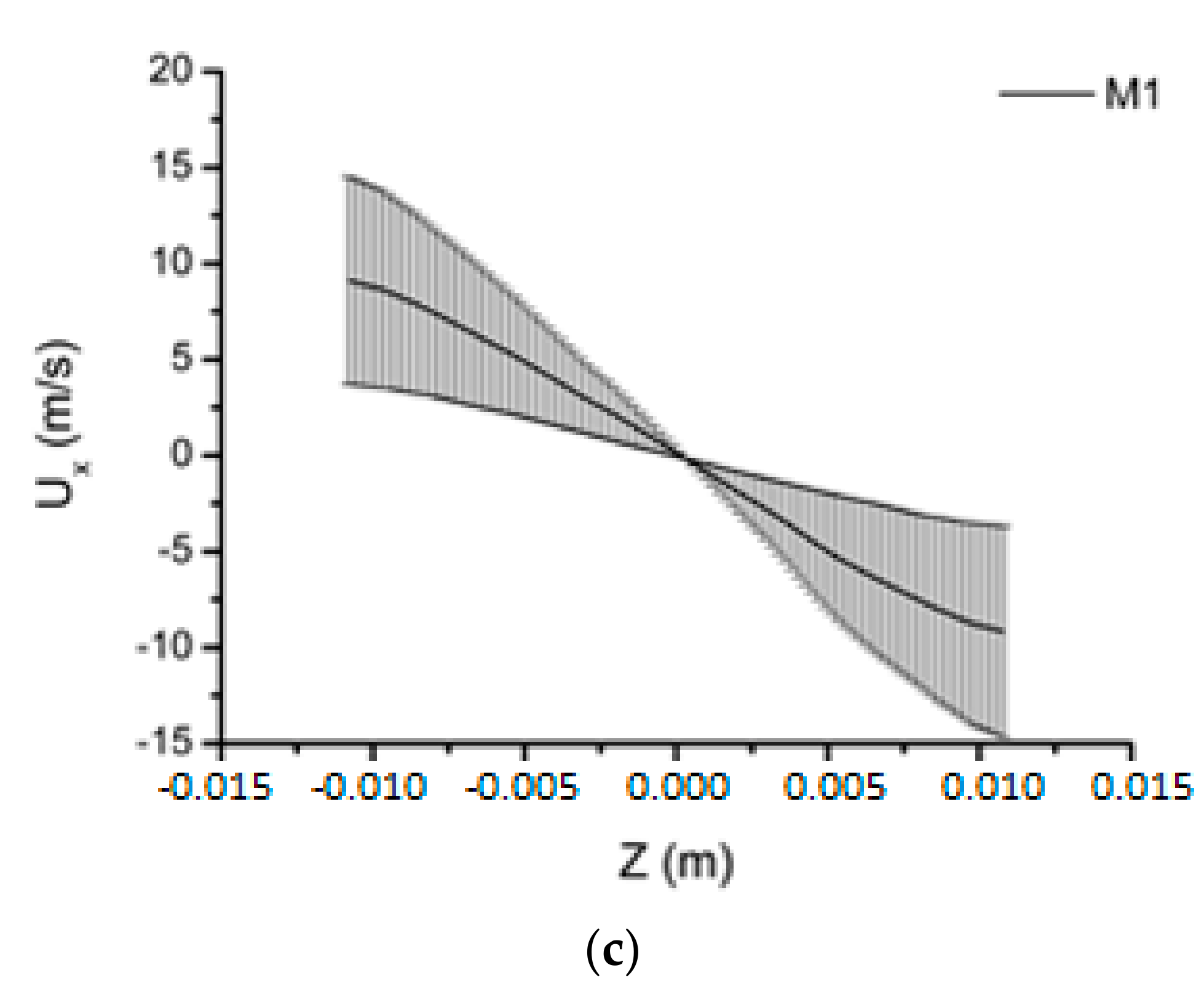
3.1. Mesh Refinement Study
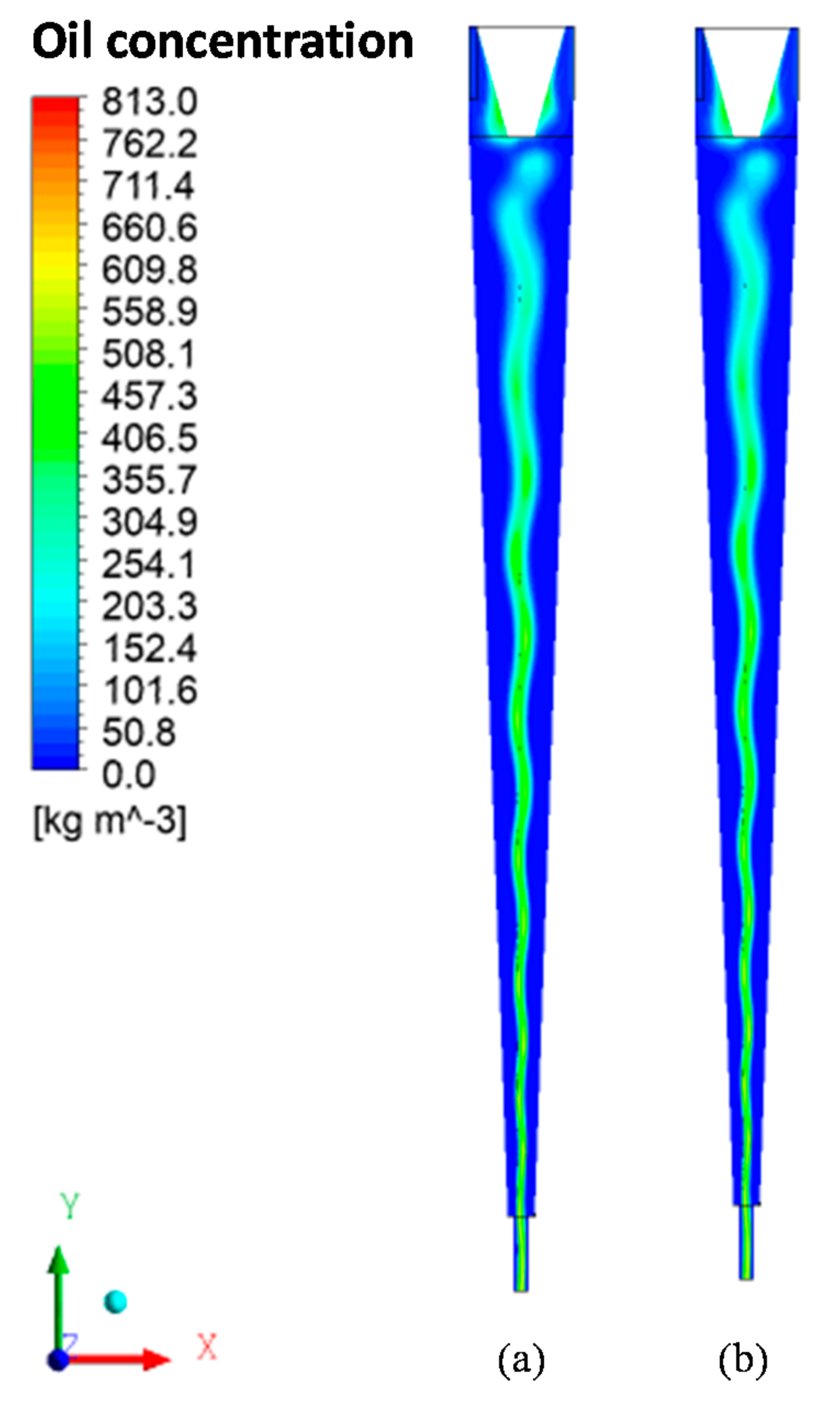
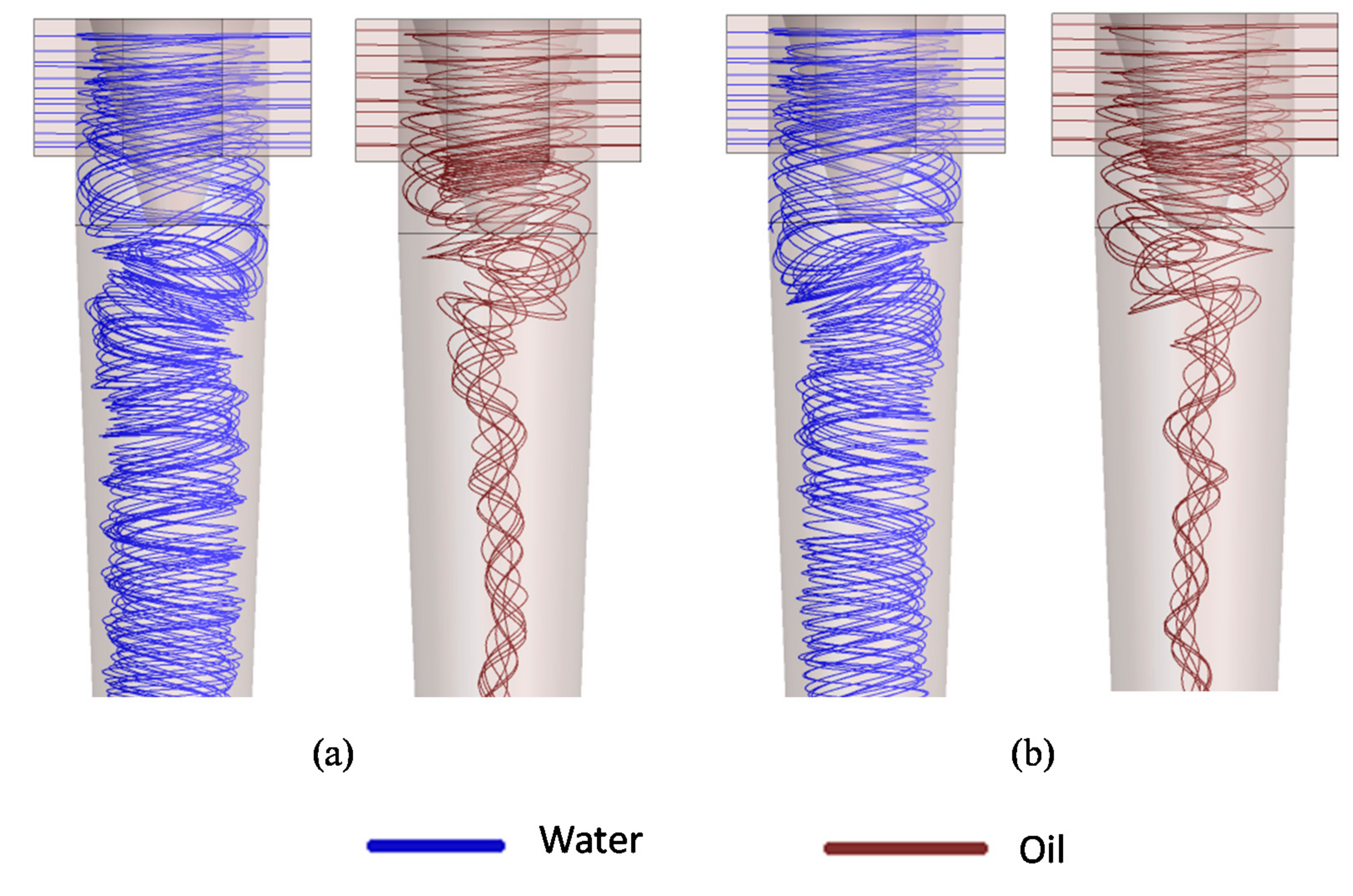
3.2. Hydrodynamic and Performance Analyses
4. Conclusions
- (a)
- The proposed mathematical modeling successfully correctly described the multiphase flow behavior within a hydrocyclone with a porous membrane wall.
- (b)
- The hydrocycloning process assisted by the filtration process was capable of altering the performance of the separation equipment.
- (c)
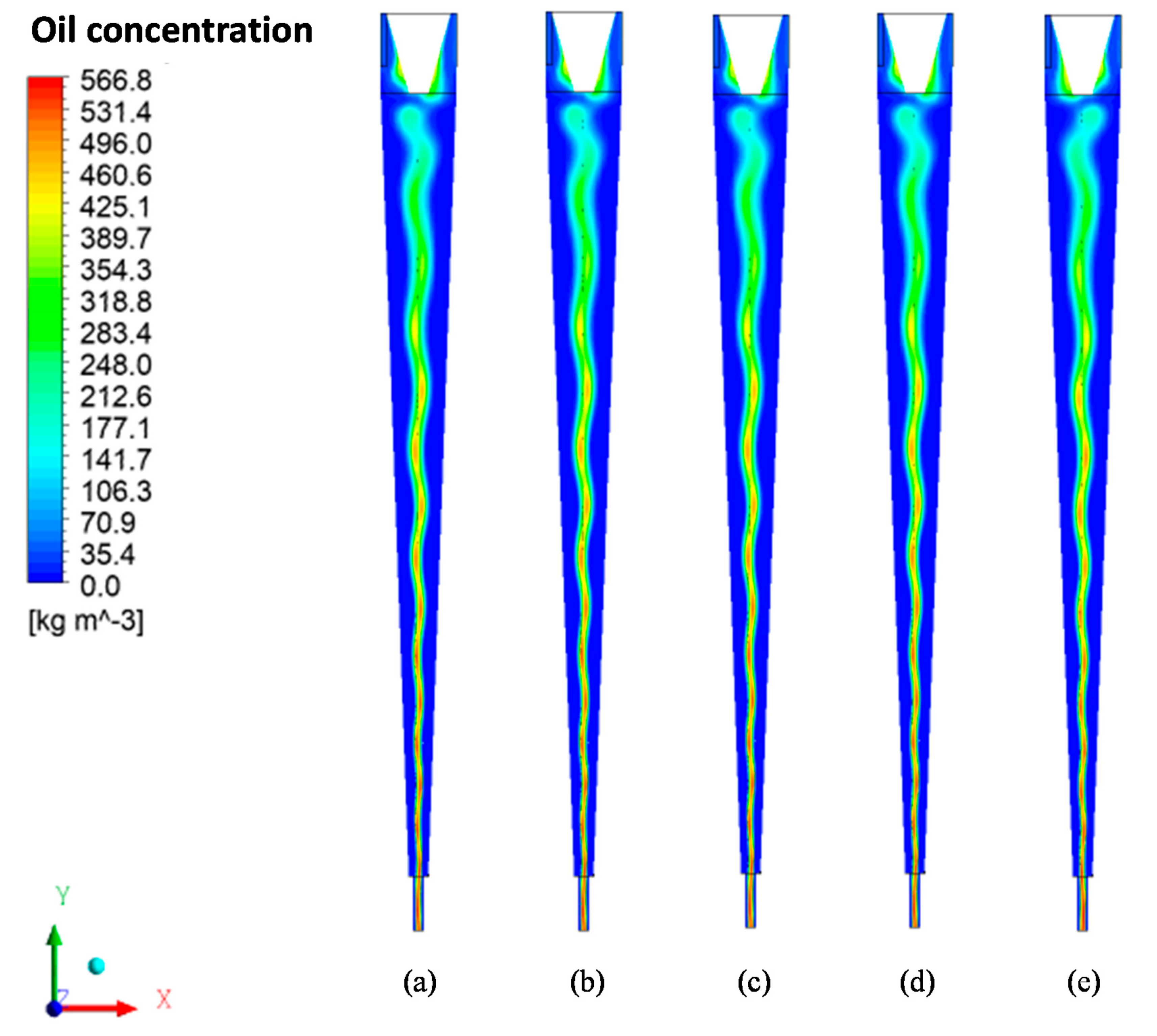
- The hydrocyclone tends to concentrate the oil in the central region throughout the flow. However, for high oil concentrations, the core expanded and the oil particles approached the porous membrane wall of the device.
- (d)
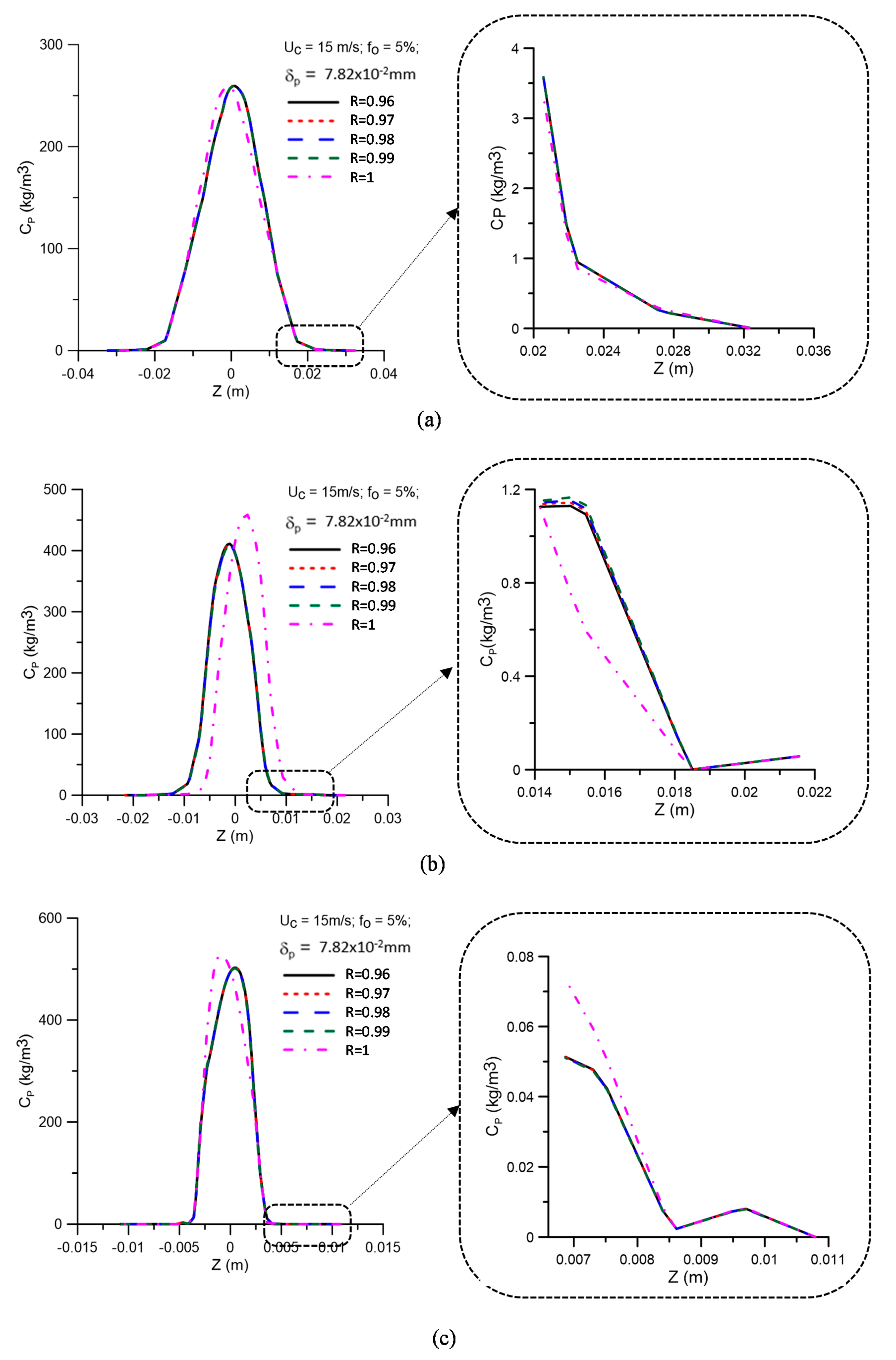
- The oil concentration profile is not significantly affected when considering the effect of the concentration polarization layer thickness in the central region of the equipment on the membrane surface, in the range of 0 ≤ ≤ 7.82 × 10−2 mm.
- (e)
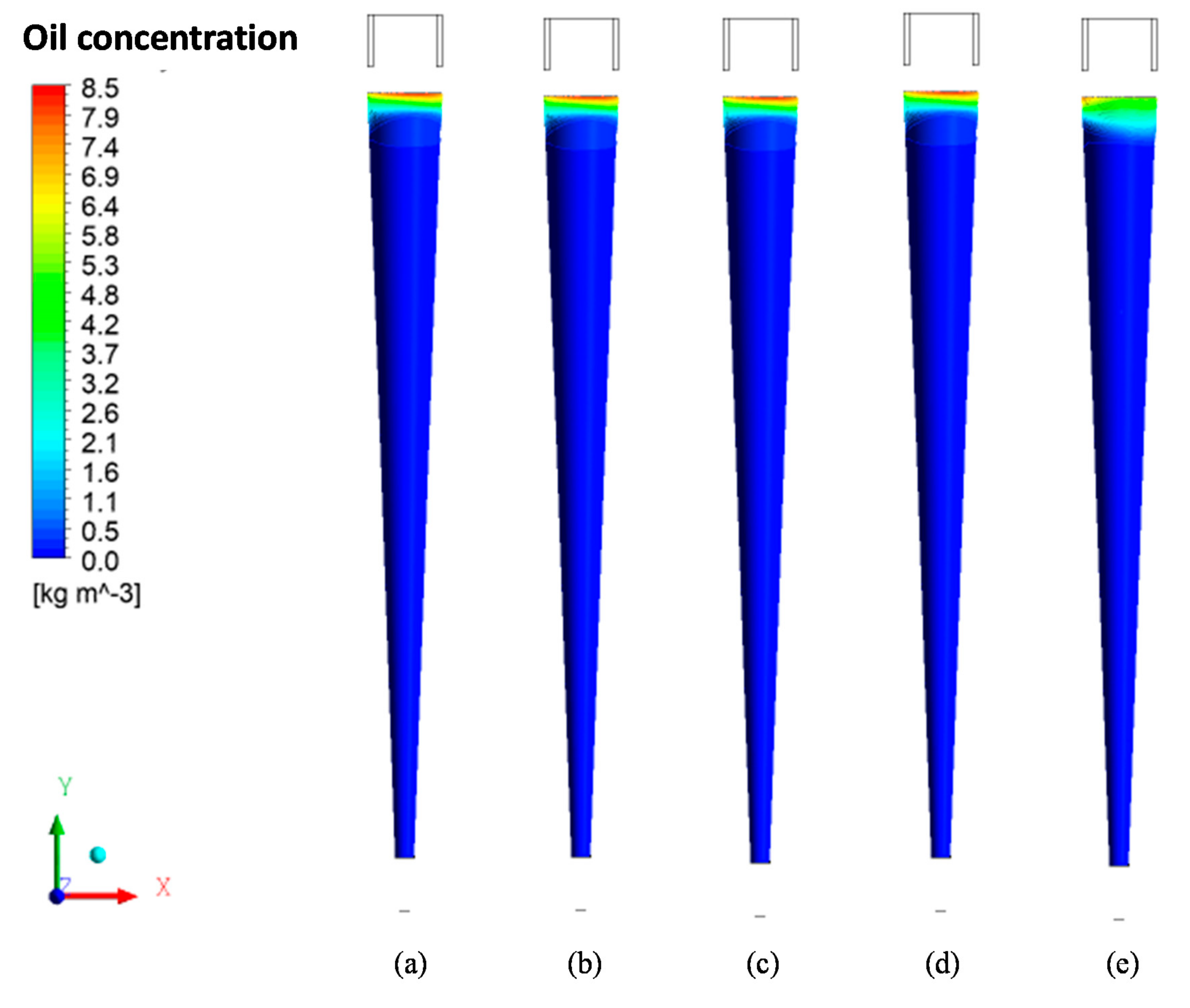
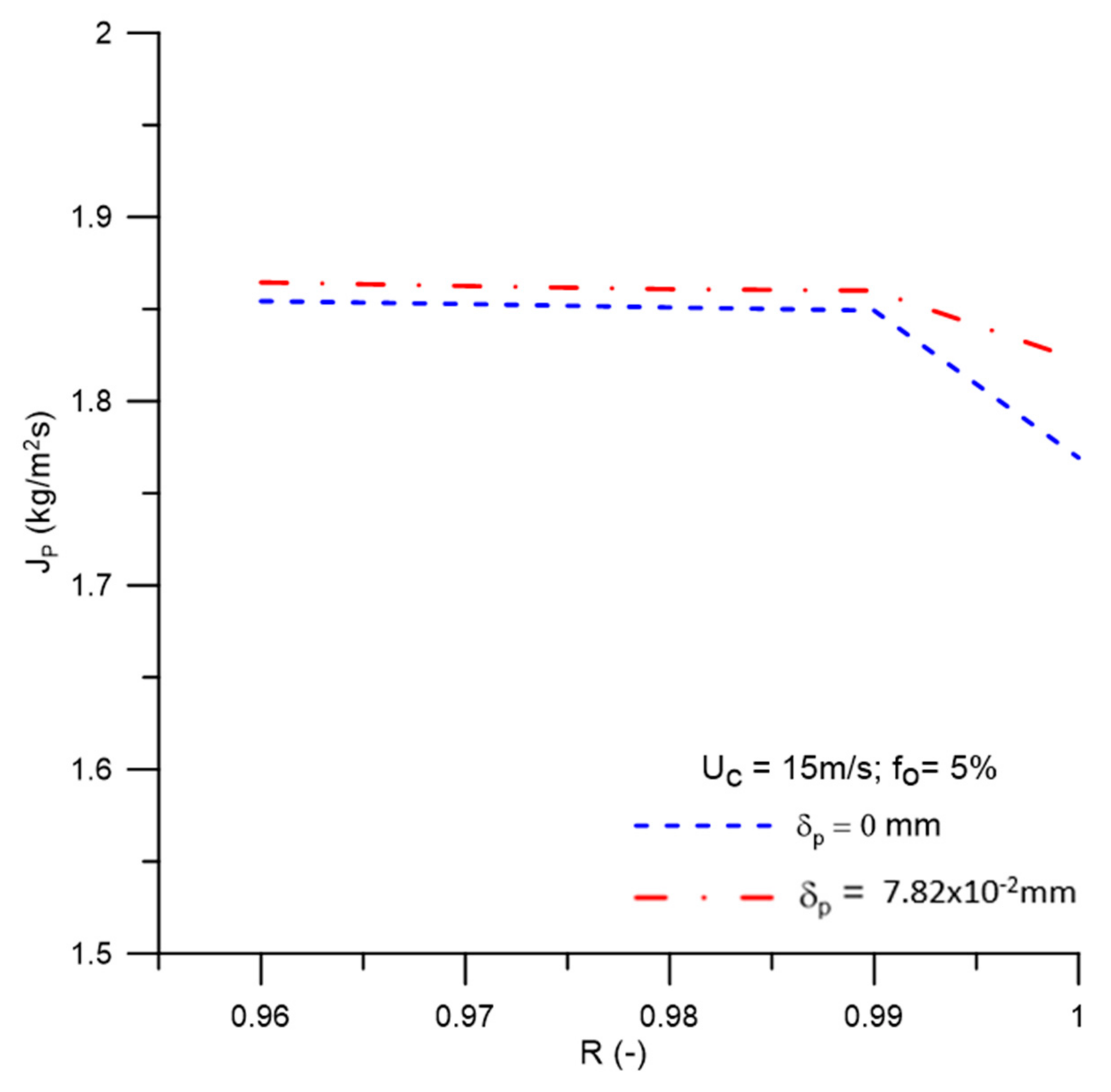
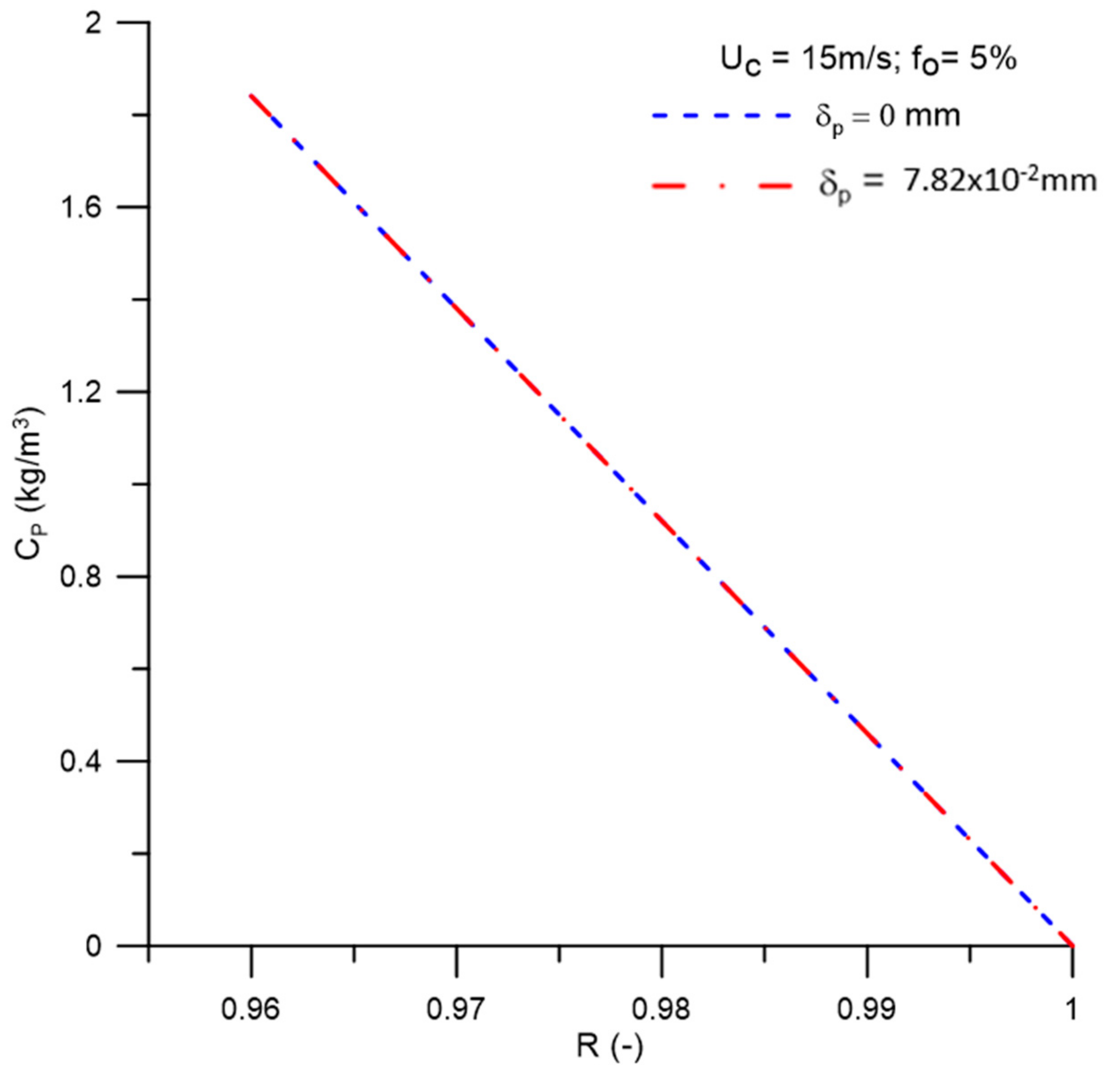
- The solute rejection coefficient by the membrane does not significantly affect the hydrodynamic behavior of the fluids inside the filtering cyclonic separator in the range 0.96 ≤ R ≤ 1.00. However, for higher membrane rejection coefficients (R = 1.00), there is a decrease in the mass flow rate of the permeate (1.822 kg/m2s), with minimal oil concentration in this mixture (0.0 kg/m3).
- (f)
- When the selective capacity of the membrane is increased, the transmembrane pressure remains practically constant (≈787.2 kPa), with a slight increase (≈806.0 kPa) when considering the concentration polarization layer thickness ( = 7.82 × 10−2 mm).
- (g)
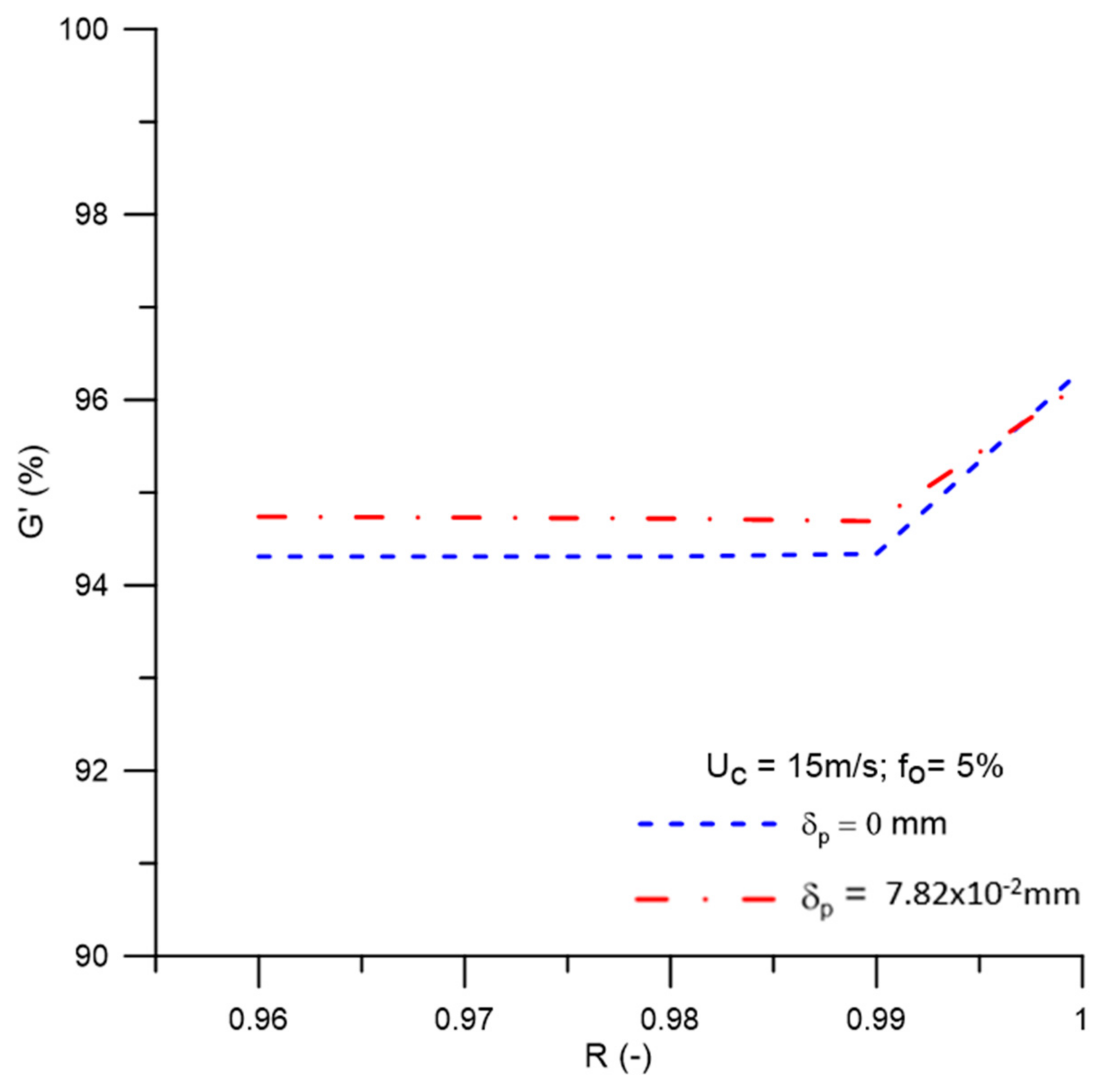
- The efficiency of the hydrocyclone remained approximately constant in the range of 0.96 ≤ R ≤ 0.99 (≈94.3%), rising from this point until reaching a value of 96.33% for R = 1.00. This parameter was higher when the concentration polarization layer thickness was varied from = 0 mm to = 7.82 × 10−2 mm, except for R = 1.00, where an inverse behavior was verified (≈96.18%).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Amini, S.; Mowla, D.; Golkar, M.; Esmaelzadeh, F. Mathematical modelling of a hydrocyclone for the down-hole oil-water separation (DOWS). Chem. Eng. Res. Des. 2012, 90, 2186–2195. [Google Scholar] [CrossRef]
- Silva, A.L.F.; Souza Filho, J.E.; Ramalho, J.B.V.S.; Melo, M.V.; Leite, M.M.; Brasil, N.I.; Pereira Junior, O.A.; Oliveira, R.C.G.; Alves, R.P.; Costa, R.F.D.; et al. Primary Oil Processing, Petrobras University; School of Science and Technology E&P: Rio de Janeiro, Brazil, 2007. (In Portuguese) [Google Scholar]
- BRASIL. National Environment Council (CONAMA). Resolution No. 393 of August 8, 2007. In Provides for the Disposal of Process or Production Water on Offshore Oil and Natural Gas Platforms, and Makes Other Provisions; Official Gazette [of] the Federative Republic of Brazil: Brasília, Brazil, 2007; Volume 79, pp. 72–73. (In Portuguese) [Google Scholar]
- Farias, F.P.M.; Souza, J.S.; Lima, W.C.P.B.; Mâcedo, A.C.; Farias Neto, S.R.; Lima, A.G.B. Influence of Geometric Parameters of the Hydrocyclone and Sand Concentration on the Water/Sand/Heavy-Oil Separation Process: Modeling and Simulation. Int. J. Multiphys. 2011, 5, 187–202. [Google Scholar] [CrossRef]
- Souza, J.S.; Farias, F.P.M.; Swarnakar, R.; Farias Neto, S.R.; Lima, A.G.B. Non-Isothermal Separation Process of Two-Phase Mixture Water/Ultra-Viscous Heavy Oil by Hydrocyclone. Adv. Chem. Eng. Sci. 2011, 1, 271–279. [Google Scholar] [CrossRef][Green Version]
- Barbosa, E.S. Geometrical and Hydrodynamic Aspects of a Hydrocyclone in the Separation Process of Multiphase Systems: Application to the Oil Industry. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2011. (In Portuguese). [Google Scholar]
- Luna, F.D.T. Numerical Study of the Separation Process of a Two-Phase System in a Cyclonic Separator. Master’s Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2014. (In Portuguese). [Google Scholar]
- Cavalcante, D.C.M. Study of the Fluid Dynamics of the Solid Particle/Water Separation Process via Filtering Hydrocyclone: Modeling and Simulation. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2017. (In Portuguese). [Google Scholar]
- Liu, L.; Zhao, L.; Yang, X.; Wang, Y.; Xu, B.; Liang, B. Innovative Design and Study of an Oil-water Coupling Separation Magnetic Hydrocyclone. Sep. Purif. Technol. 2019, 213, 389–400. [Google Scholar] [CrossRef]
- Al-Kayiem, H.H.; Osei, H.; Hashim, F.M.; Hamza, J.E. Flow structures and their impact on single and dual inlets hydrocyclone performance for oil-water separation. J. Pet. Explor. Prod. Technol. 2019, 9, 2943–2952. [Google Scholar] [CrossRef]
- Ishak, K.E.H.K.; Ayoub, M.A. Performance of liquid–liquid hydrocyclone (LLHC) for treating produced water from surfactant flooding produced water. World J. Eng. 2019, 17, 215–222. [Google Scholar] [CrossRef]
- Al-Kayiem, H.H.; Hamza, J.E.; Lemmu, T.A. Performance enhancement of axial concurrent liquid–liquid hydrocyclone separator through optimization of the swirler vane angle. J. Pet. Explor. Prod. Technol. 2020, 10, 1957–2967. [Google Scholar] [CrossRef]
- Li, S.; Li, R.; Nicolleau, F.C.G.A.; Wang, S.; Yan, Y.; Xu, Y.; Chen, X. Study on oil–water two-phase flow characteristics of the hydrocyclone under periodic excitation. Chem. Eng. Res. Des. 2020, 159, 215–224. [Google Scholar] [CrossRef]
- Hamza, J.E.; Al-Kayiem, H.H.; Lemma, T.A. Experimental investigation of the separation performance of oil/water mixture by compact conical axial hydrocyclone. Therm. Sci. Eng. Prog. 2020, 17, 100358. [Google Scholar] [CrossRef]
- Liu, S.; Yan, Y.; Gao, Y. Optimization of geometry parameters with separation efficiency and flow split ratio for downhole oil-water hydrocyclone. Therm. Sci. Eng. Prog. 2018, 8, 370–374. [Google Scholar]
- Svarovsky, L. Hidrocyclones; Holt, Rinehard & Winston: Esatbourne, UK, 1984; Volume 1, p. 198. [Google Scholar]
- Zaini, M.A.A.; Holdich, R.G.; Cumming, I.W. Crossflow microfiltration of oil in water emulsion via tubular filters: Evaluation by mathematical models on droplet deformation and filtration. J. Technol. 2010, 53, 19–28. [Google Scholar]
- Abadi, S.R.H.; Sebzari, M.R.; Hemati, M.; Rekabdar, F.; Mohammadi, T.O. Ceramic membrane performance in microfiltration of oily wastewater. Desalination 2011, 265, 222–228. [Google Scholar] [CrossRef]
- Souza, J.S. Theoretical Study of the Microfiltration Process in Ceramic Membranes. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2014. (In Portuguese). [Google Scholar]
- Cunha, A.L. Treatment of Effluents from the Oil Industry via Ceramic Membranes—Modeling and Simulation. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2014. (In Portuguese). [Google Scholar]
- Nunes, S.A. Modeling and Simulation of Produced Water Treatment Using a Ciclonc Filter Separator. Ph.D. Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2019. (In Portuguese). [Google Scholar]
- Magalhães, H.L.F.; Moreira, G.; Gomez, R.S.; Porto, T.R.N.; Correia, B.R.B.; Silva, A.M.V.; Farias Neto, S.R.; Lima, A.G.B. Non-Isothermal Treatment of Oily Waters Using Ceramic Membrane: A Numerical Investigation. Energies 2020, 13, 92. [Google Scholar] [CrossRef]
- Salama, A. Modeling of flux decline behavior during the filtration of oily-water systems using porous membranes: Effect of pinning of nonpermeating oil droplets. Sep. Purif. Technol. 2018, 207, 240–254. [Google Scholar] [CrossRef]
- Behroozi, A.H. A modified resistance model for simulating baffle arrangement impacts on cross-flow microfiltration performance for oily wastewater. Chem. Eng. Process. Process Intensif. 2020, 153, 1–14. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, C.; Yang, J.; Huang, X.-J.; Xu, Z.-K. Wettability Switchable Membranes for Separating Both Oil-in-water and water-in-oil emulsions. J. Membr. Sci. 2020, 1, 118976. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Ding, Y.; Zhou, S.; Liu, F. In situ generated micro-bubbles enhanced membrane antifouling for separation of oil-in-water emulsion. J. Membr. Sci. 2020, 621, 119005. [Google Scholar] [CrossRef]
- Anis, S.F.; Lalia, B.S.; Lesimple, A.; Hashaikeh, R.; Hilal, N. Superhydrophilic and underwater superoleophobic nano zeolite membranes for efficient oil-in-water nanoemulsion separation. J. Water Process Eng. 2020, 1, 101802. [Google Scholar] [CrossRef]
- Yang, Y.; Ali, N.; Bilal, M.; Khan, A.; Ali, F.; Mao, P.; Ni, L.; Gao, X.; Hung, K.; Rasool, K.; et al. Robust membranes with tunable functionalities for sustainable oil/water separation. J. Mol. Liq. 2020, 321, 114701. [Google Scholar] [CrossRef]
- Xu, H.; Liu, H.; Huang, Y.; Xiao, C. Three-dimensional structure design of tubular polyvinyl chloride hybrid nanofiber membranes for water-in-oil emulsion separation. J. Membr. Sci. 2020, 1, 118905. [Google Scholar]
- Liu, Y.; Yang, B.; Zhao, H.; He, Y. Oil-water separation performance of aligned single walled carbon nanotubes membrane: A reactive molecular dynamics simulation study. J. Mol. Liq. 2020, 321, 114174. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, X.; Yan, L.; Bai, Y.; Li, S.; Sorokin, P. Biomimetic nanoparticle-engineered superwettable membranes for efficient oil/water separation. J. Membr. Sci. 2021, 618, 118525. [Google Scholar] [CrossRef]
- Yang, X.; Yan, L.; Ran, F.; Huang, Y.; Pan, D.; Bai, Y.; Shao, L. Mussel-/diatom-inspired silicified membrane for high-efficiency water remediation. J. Membr. Sci. 2020, 597, 117753. [Google Scholar] [CrossRef]
- Vieira, L.G.M.; Damasceno, J.J.R.; Barrozo, M.A.S. Improvement of hydrocyclone separation performance by incorporating a conical filtering wall. Chem. Eng. Process. Process Intensif. 2010, 49, 460–467. [Google Scholar] [CrossRef]
- Silva, N.K.G.; Silva, D.O.; Vieira, L.G.M.; Barrozo, M.A.S. Effects of underflow diameter and vortex finder length on the performance of a newly designed filtering hydrocyclone. Powder Technol. 2015, 286, 305–310. [Google Scholar] [CrossRef]
- Salvador, F.F.; Barrozo, M.A.S.; Vieira, L.G.M. Filtering cylindrical-conical hydrocyclone. Particuology 2019, 47, 54–62. [Google Scholar] [CrossRef]
- Façanha, J.M.F.; Silva, D.O.; Barrozo, M.A.S.; Vieira, L.G.M. Analysis of the use of a filtering medium in different parts of a centrifugal separator. Mater. Sci. Forum 2012, 727–728, 20–25. [Google Scholar]
- Nunes, S.A.; Magalhães, H.L.F.; Farias Neto, S.R.; Lima, A.G.B.; Nascimento, L.P.C.; Farias, F.P.M.; Lima, E.S. Impact of Permeable Membrane on the Hydrocyclone Separation Performance for Oily Water Treatment. Membranes 2020, 10, 350. [Google Scholar] [CrossRef]
- Huang, L.; Deng, S.; Guam, J.; Chen, M.; Hua, W. Development of a novel high-efficiency dynamic hydrocyclone for oil-water separation. Chem. Eng. Res. Des. 2018, 130, 266–273. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A method for uniform Reporting of Grid Refinement studies. ASME J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Damak, K.; Ayadi, A.; Zeghmati, B.; Schmitz, P. Concentration polarisation in tubular membranes—A numerical approach. Desalination 2004, 171, 139–153. [Google Scholar] [CrossRef]
- Svarovsky, L.; Svarovsky, J. A new method of testing hydrocyclone grade efficiencies. In Hydrocyclones: Analysis and Applications, Fluid Mechanics and Its Applications Series, V. 12; Svarovsky, L., Thew, M.T., Eds.; Springer Science+Business Media Dordrecht: Letchworth, UK, 1992; pp. 135–145. [Google Scholar]
- Karatekin, I.C.O. Numerical Experiments on Application of Richarson Extrapolation with Nonuniform Grids. Asme J. Fluid Eng. 1997, 119, 584–590. [Google Scholar]
- Paudel, S.; Saenger, N. Grid refinement study for three dimensional CFD model involving incompressible free surface flow and rotating object. Comput. Fluids 2017, 143, 134–140. [Google Scholar] [CrossRef]
- Zimmermann, M.S. Lead/Air Separation Process Using Cyclonic Separator: Modeling and Simulation. Master’s Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2018. (In Portuguese). [Google Scholar]
- Magalhães, H.L.F. Study of Thermofluidodynamics of Wastewater Treatment Using Ceramic Membrane: Modeling and Simulation. Master’s Thesis, Federal University of Campina Grande, Campina Grande, Brazil, 2017. (In Portuguese). [Google Scholar]
- Paris, J.; Guichardon, P.; Charbit, F. Transport phenomena in ultrafiltration: A new two-dimensional model compared with classical models. J. Membr. Sci. 2020, 207, 43–58. [Google Scholar] [CrossRef]
- Pradanos, P.; Arribas, J.I.; Hernandez, A. Mass transfer coefficient and retention of PEGs in low pressure cross-flow ultrafiltration through asymmetric membranes. J. Membr. Sci. 1995, 99, 1–20. [Google Scholar] [CrossRef]
- Habert, A.C.; Borges, C.P.; Nobrega, R. Membrane Separation Processes; E-papers Serviços Editoriais Ltd.: Rio de janeiro, Brazil, 2006; 180p. (In Portuguese) [Google Scholar]


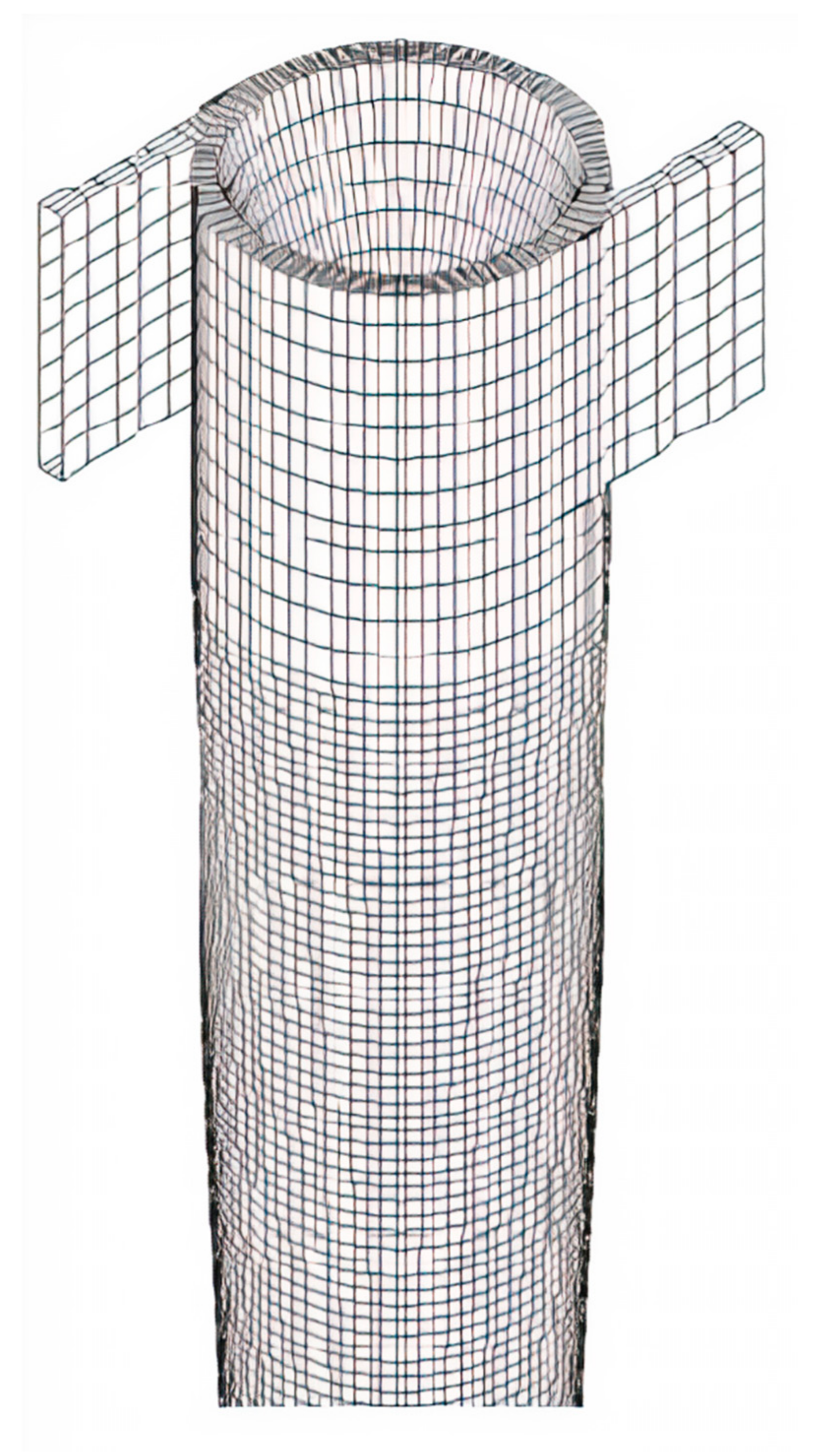





| Tangential inlets (mm) | Height (A1) | 50 |
| Length (C1) | 50 | |
| Width (L1) | 5 | |
| Upper conical part (mm) | Height (A2) | 75 |
| Width (L2) | 5 | |
| Top Diameter (D1) | 65 | |
| Bottom Diameter (D2) | 18 | |
| Cylindrical section (mm) | Height (A2) | 75 |
| Diameter (D5) | 70 | |
| Conical section (mm) | Height (A3) | 725 |
| Annular outlet (mm) | Diameter (D3) | 18 |
| Tubular outlet (mm) | Diameter (D4) | 10 |
| Height (A4) | 50 |
| Membrane | Permeability | [21] |
| Polarization layer thickness | [21] | |
| Water | Density | |
| Viscosity | ||
| Molar mass | ||
| Oil | Density | |
| Viscosity | ||
| Molar mass | ||
| Average oil drop diameter |
| Case | Input Velocity (m/s) | Oil Volume Fraction (%) | Membrane Rejection Coefficient R (-) | Polarization Layer Thickness (mm) |
|---|---|---|---|---|
| 1 | 5 | 5.0 | 1 | 0 |
| 2 | 15 | 5 | 1 | 0 |
| 3 | 15 | 5 | 1 | 7.82 × 10−2 |
| 4 | 5 | 5 | 0.99 | 7.82 × 10−2 |
| 5 | 15 | 5 | 0.98 | 7.82 × 10−2 |
| 6 | 15 | 5 | 0.97 | 7.82 × 10−2 |
| 7 | 5 | 5 | 0.96 | 7.82 × 10−2 |
| Mesh | Number of Elements | Simulation Time |
|---|---|---|
| M1 | 337,360 | 3 d 8 h 4′2″ |
| M2 | 71,352 | 21 h 38′40″ |
| M3 | 10,571 | 17′4″ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nunes, S.A.; Magalhães, H.L.F.; Gomez, R.S.; Vilela, A.F.; Figueiredo, M.J.; Santos, R.S.; Rolim, F.D.; Souza, R.A.A.; Farias Neto, S.R.d.; Lima, A.G.B. Oily Water Separation Process Using Hydrocyclone of Porous Membrane Wall: A Numerical Investigation. Membranes 2021, 11, 79. https://doi.org/10.3390/membranes11020079
Nunes SA, Magalhães HLF, Gomez RS, Vilela AF, Figueiredo MJ, Santos RS, Rolim FD, Souza RAA, Farias Neto SRd, Lima AGB. Oily Water Separation Process Using Hydrocyclone of Porous Membrane Wall: A Numerical Investigation. Membranes. 2021; 11(2):79. https://doi.org/10.3390/membranes11020079
Chicago/Turabian StyleNunes, Sirlene A., Hortência L. F. Magalhães, Ricardo S. Gomez, Anderson F. Vilela, Maria J. Figueiredo, Rosilda S. Santos, Fagno D. Rolim, Rodrigo A. A. Souza, Severino R. de Farias Neto, and Antonio G. B. Lima. 2021. "Oily Water Separation Process Using Hydrocyclone of Porous Membrane Wall: A Numerical Investigation" Membranes 11, no. 2: 79. https://doi.org/10.3390/membranes11020079
APA StyleNunes, S. A., Magalhães, H. L. F., Gomez, R. S., Vilela, A. F., Figueiredo, M. J., Santos, R. S., Rolim, F. D., Souza, R. A. A., Farias Neto, S. R. d., & Lima, A. G. B. (2021). Oily Water Separation Process Using Hydrocyclone of Porous Membrane Wall: A Numerical Investigation. Membranes, 11(2), 79. https://doi.org/10.3390/membranes11020079






