Model-Based Quality, Exergy, and Economic Analysis of Fluidized Bed Membrane Reactors
Abstract
:1. Introduction
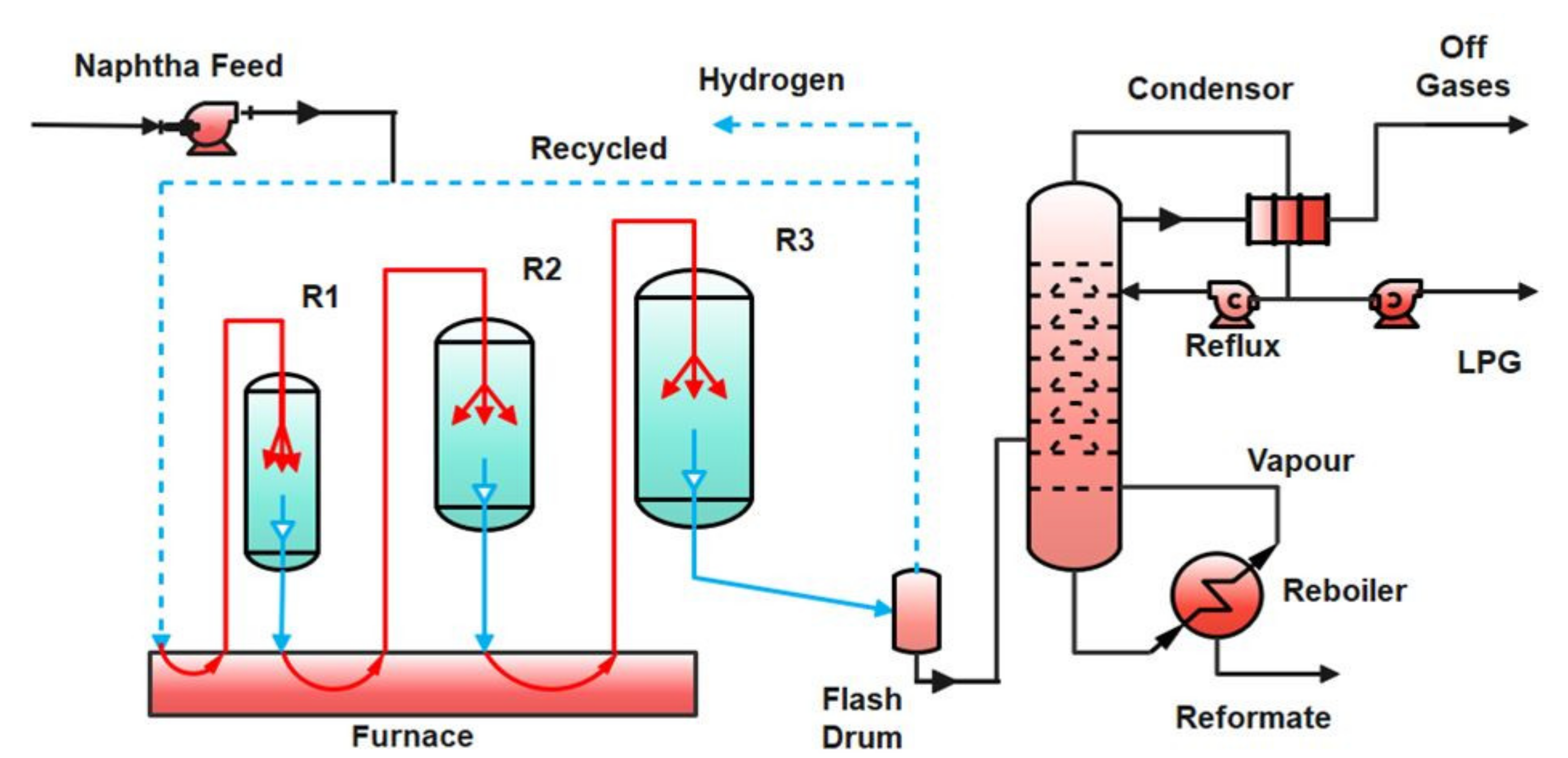
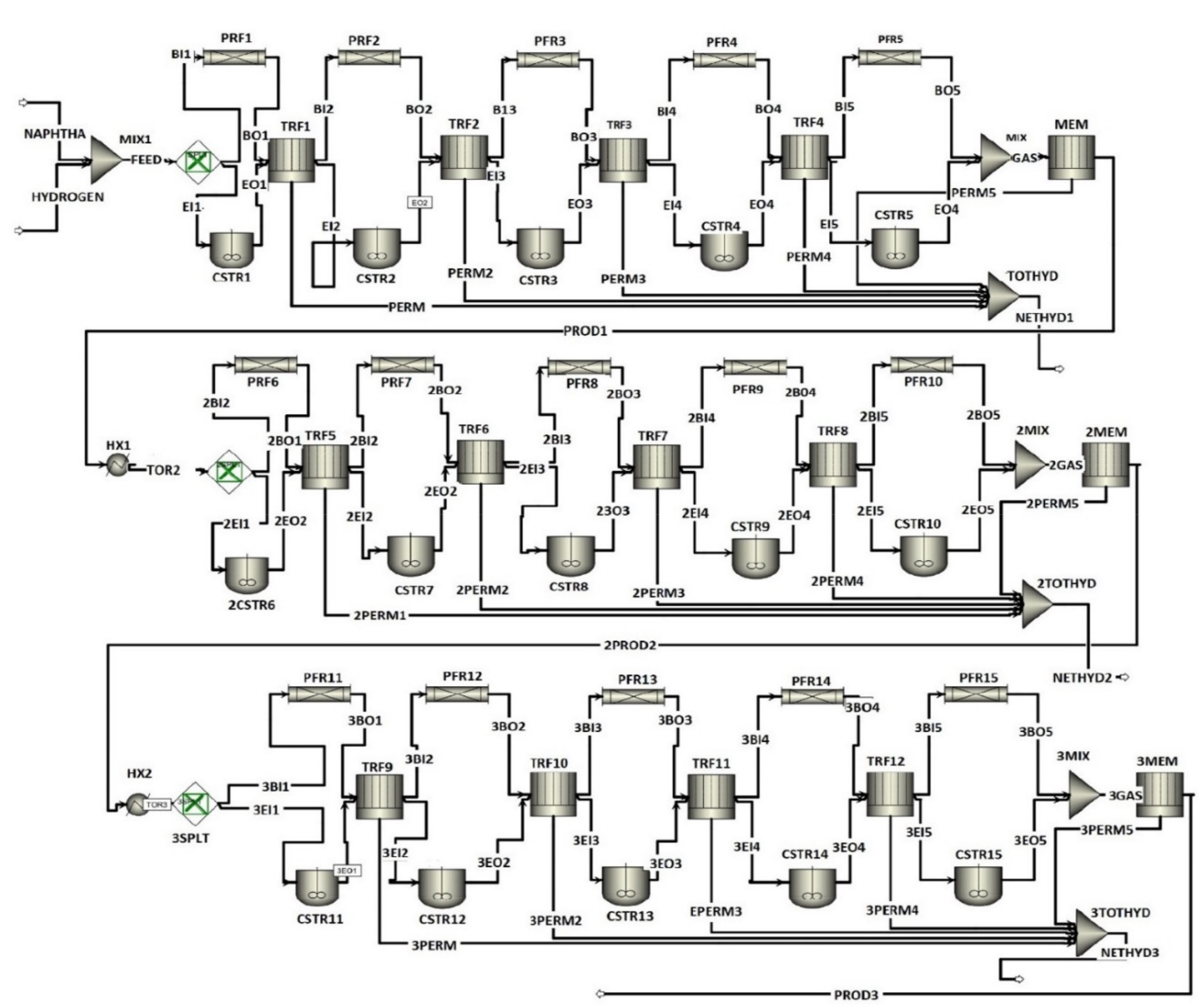
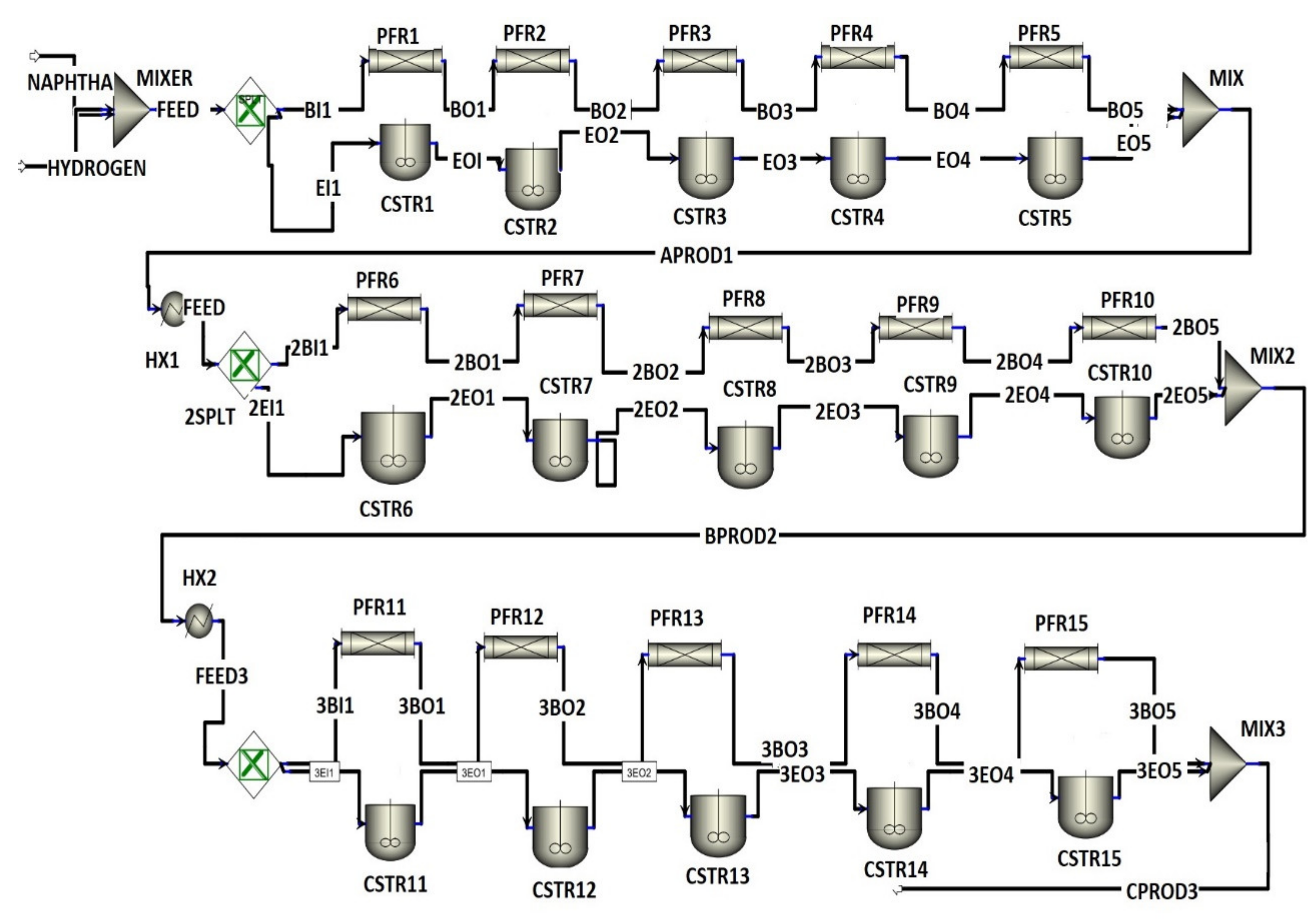
2. Process Description
3. Modelling and Analysis Methods
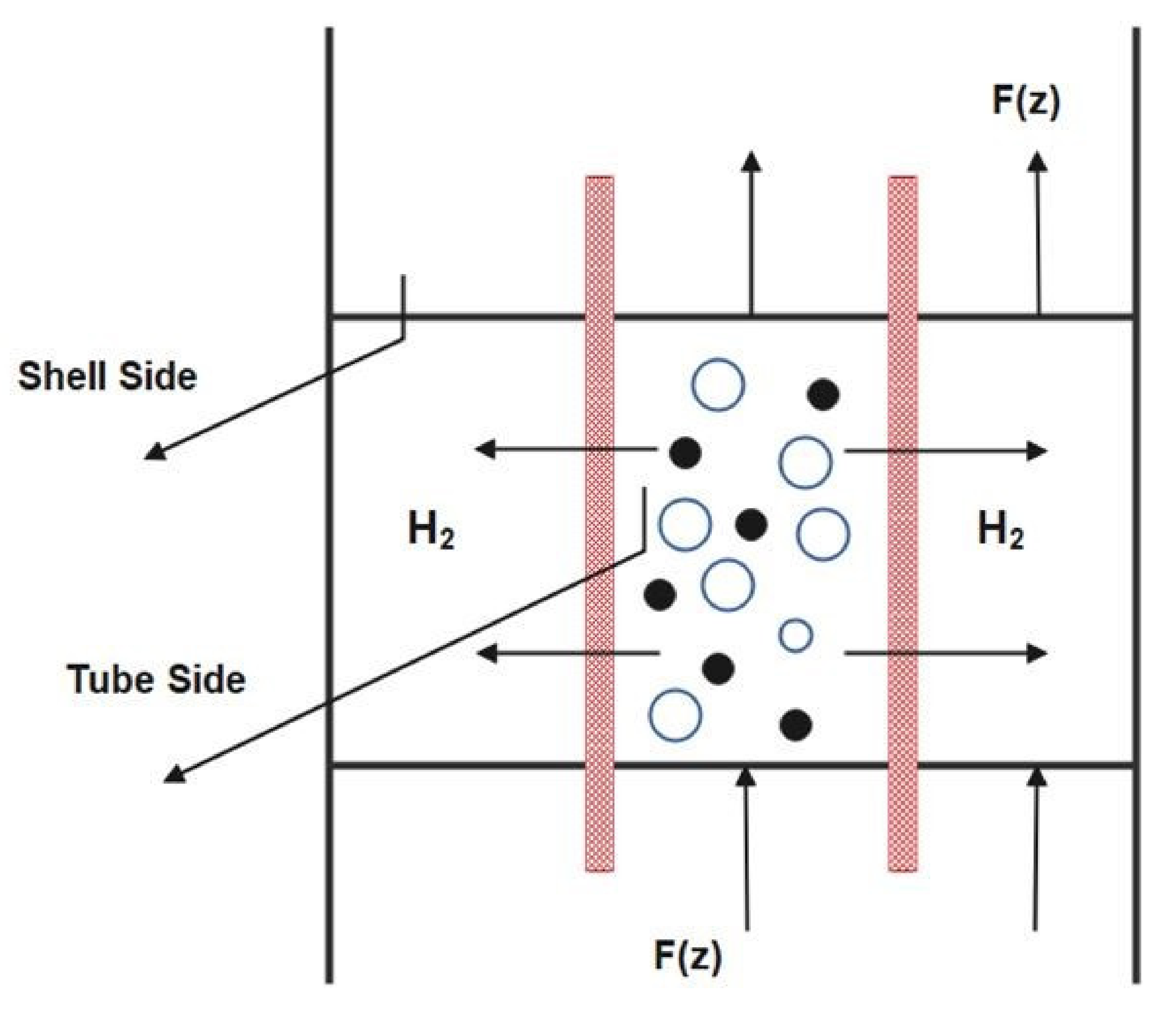
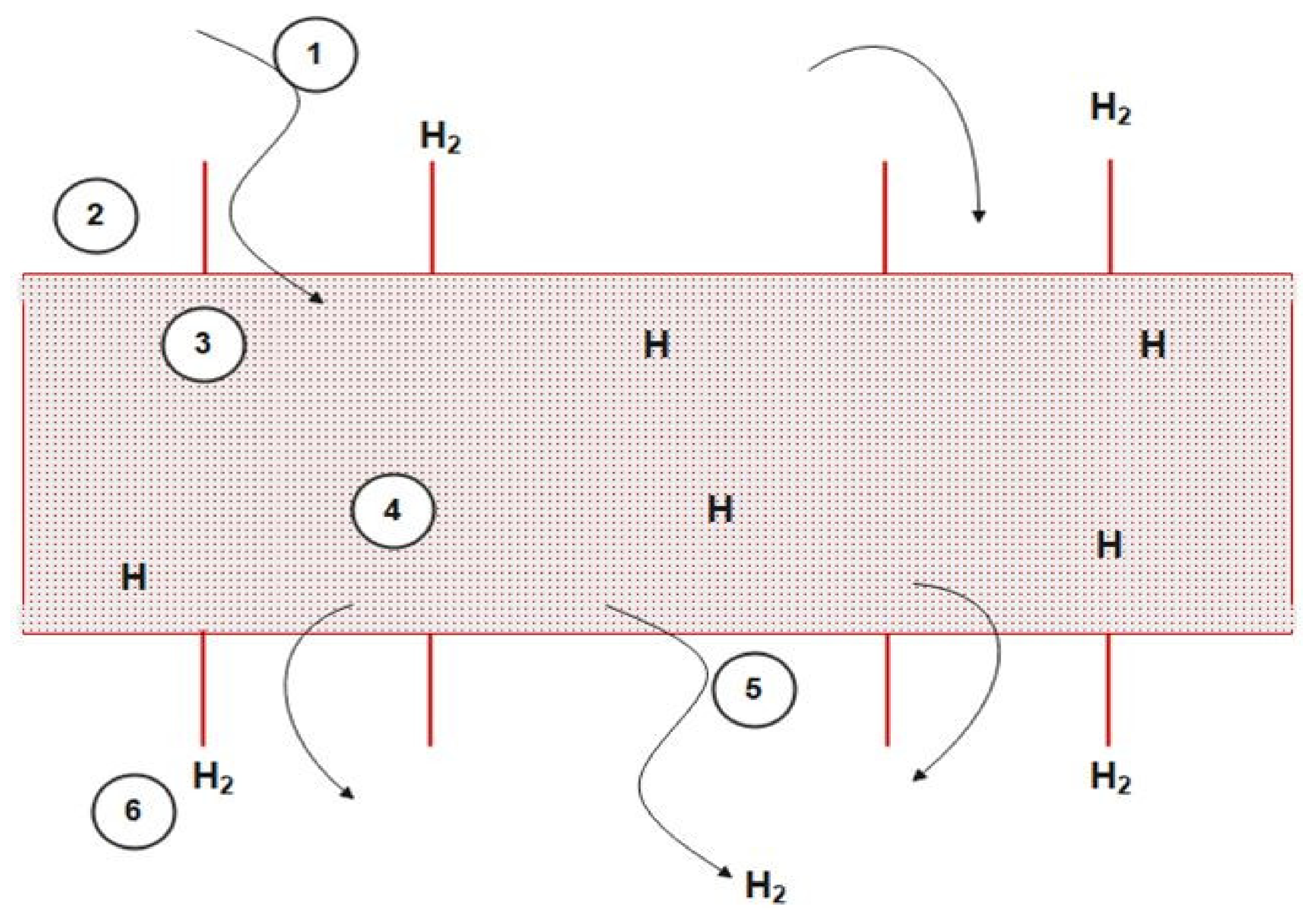
3.1. Membrane Reactor and its Modelling Method
3.2. Preliminary Assumptions:
- The dense catalyst bed has two identifiable phases: A bubble phase and an emulsion phase.
- Steady-state and pseudo-steady-state operation is assumed.
- Much of the reactions occur within the emulsion phase.
- Permeation of hydrogen is assumed to occur from the emulsion phase only.
- Hydrogen diffuses through the membrane radially.
- Assumption of spherical bubbles hold.
- The movement of gas in bubbles is assumed to follow the plug flow. Additionally, due to a very low quantity of catalyst, the reaction rates are very low compared to the emulsion gas phase velocity.
- Contents of the bed are well mixed and both emulsion and bubble phases are at a uniform temperature.
- Adiabatic conditions.
- Sieverts’ law is applicable for hydrogen permeation through the membrane [35] (Equation (1)).
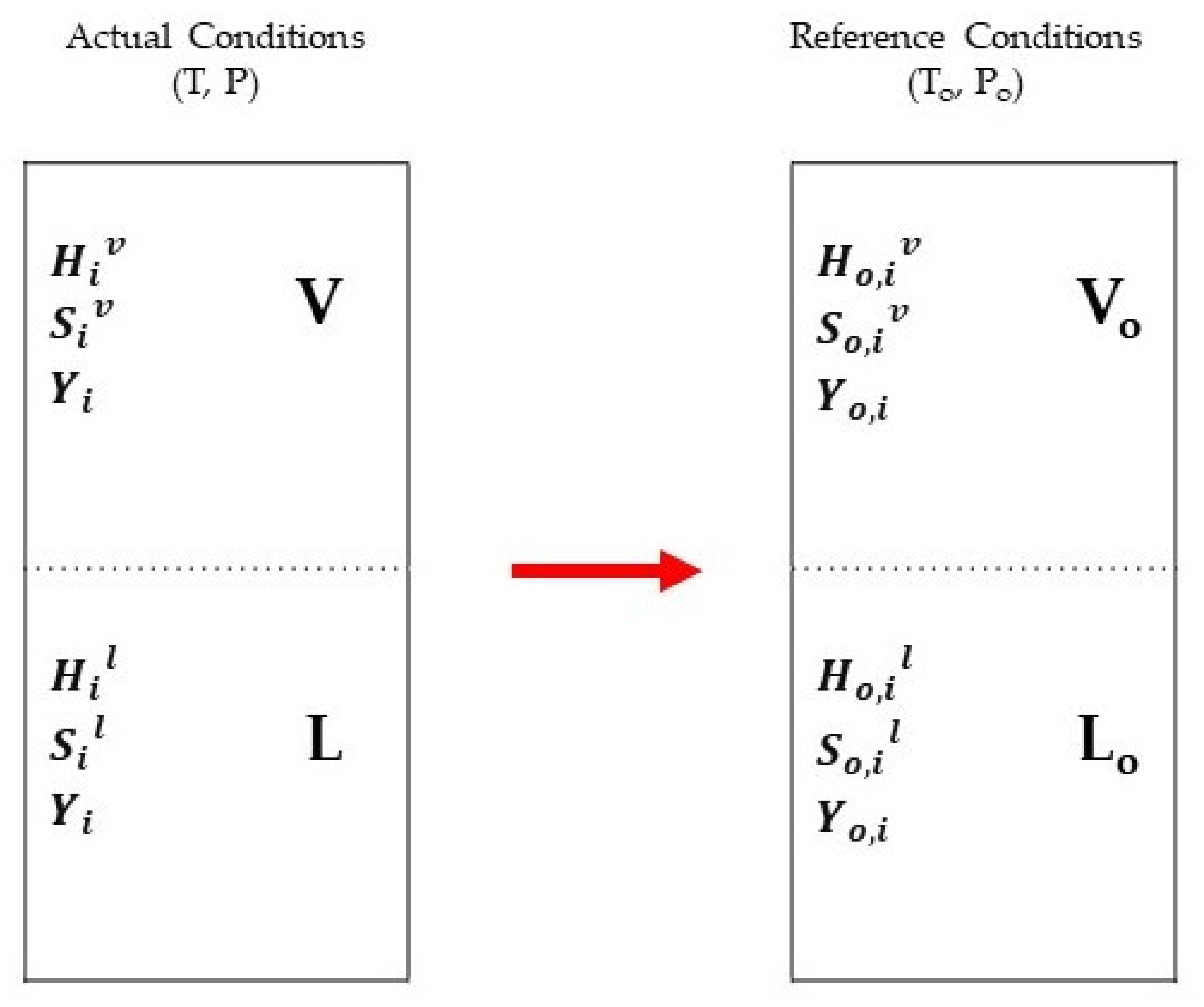
3.3. Exergy Analysis
3.4. Economic Analysis
4. Results and Discussion
4.1. FBMR vs. FBR Model Design
4.2. Parametric Analysis
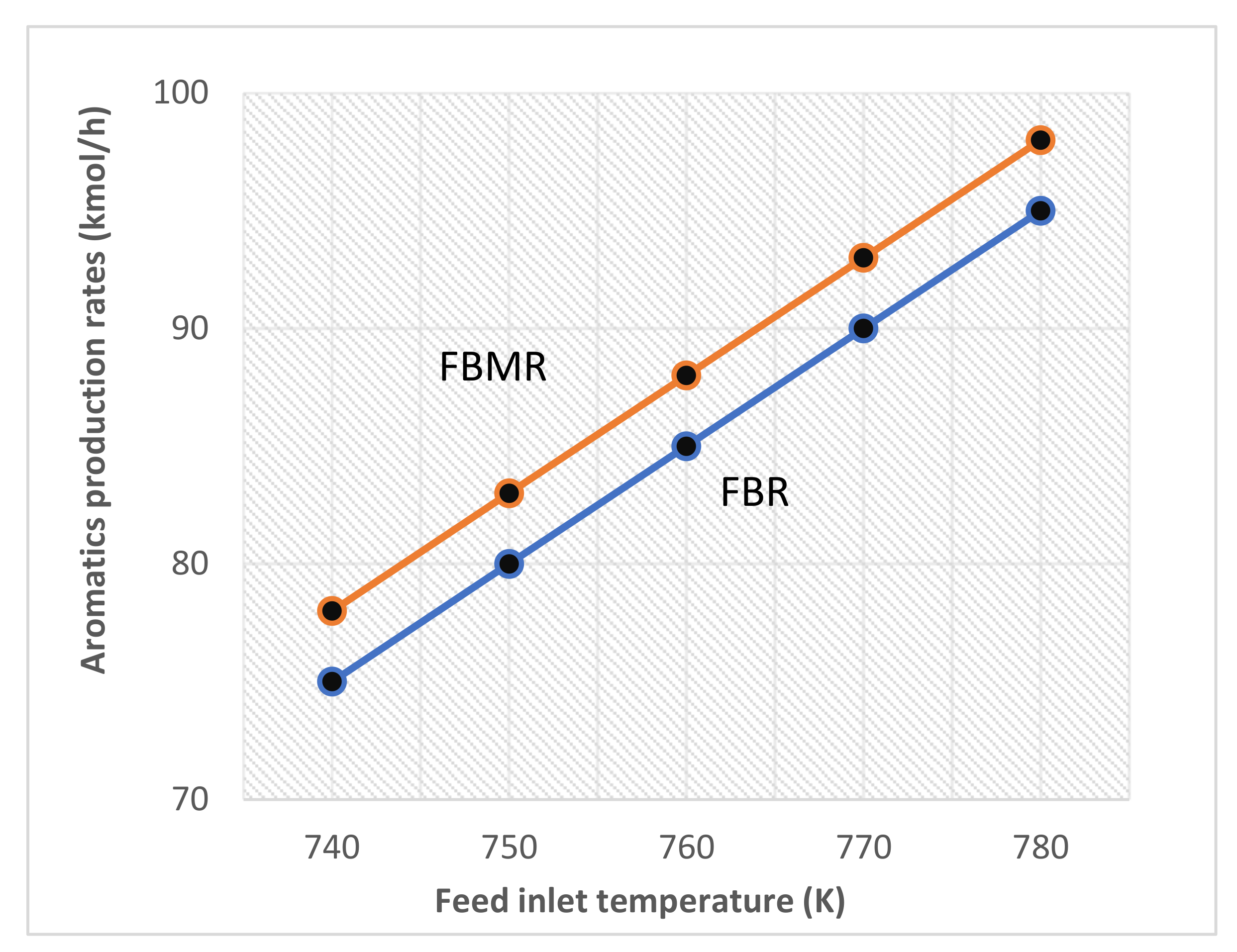
4.2.1. Influence of Reactor Temperature
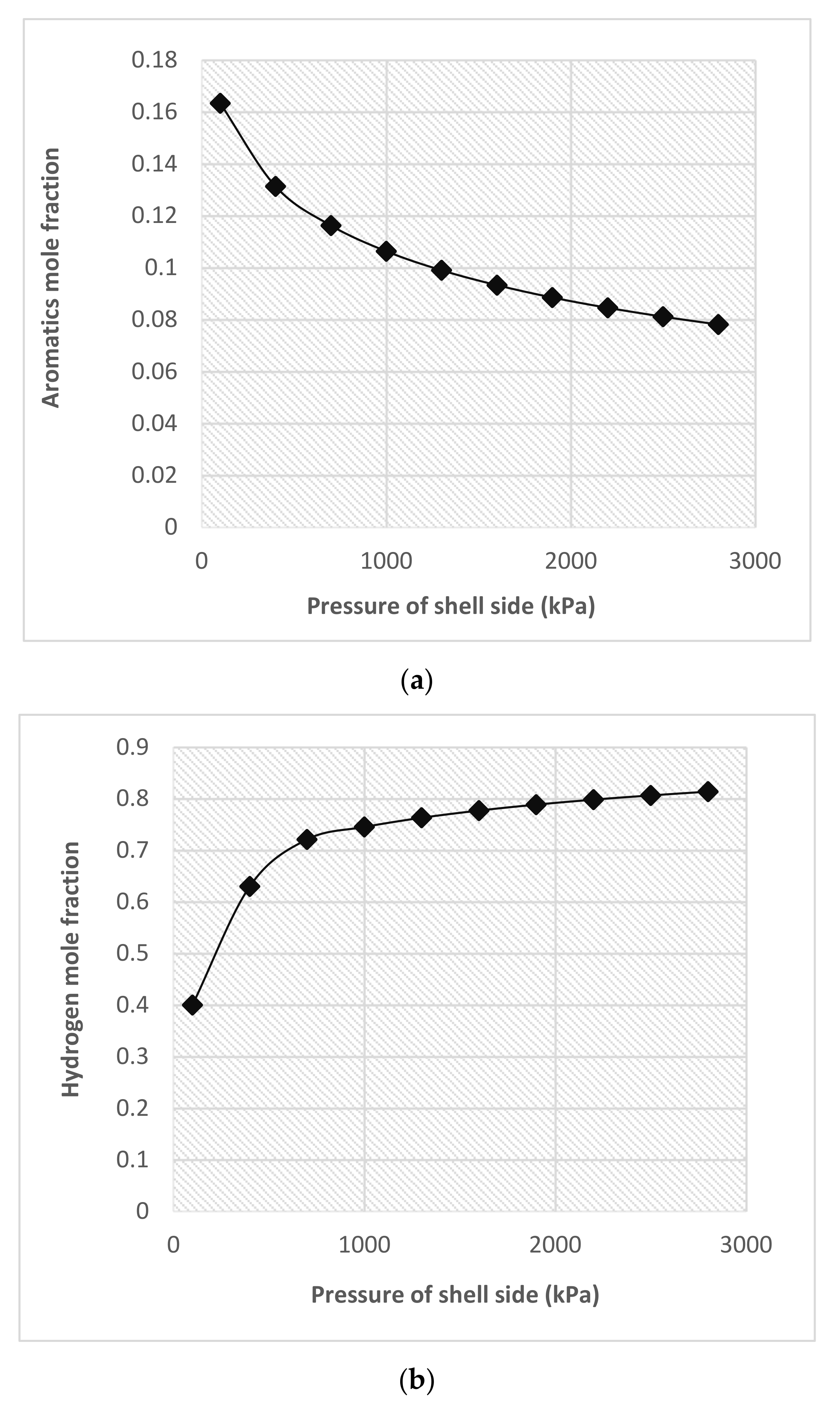
4.2.2. Influence of Shell-Side Pressure
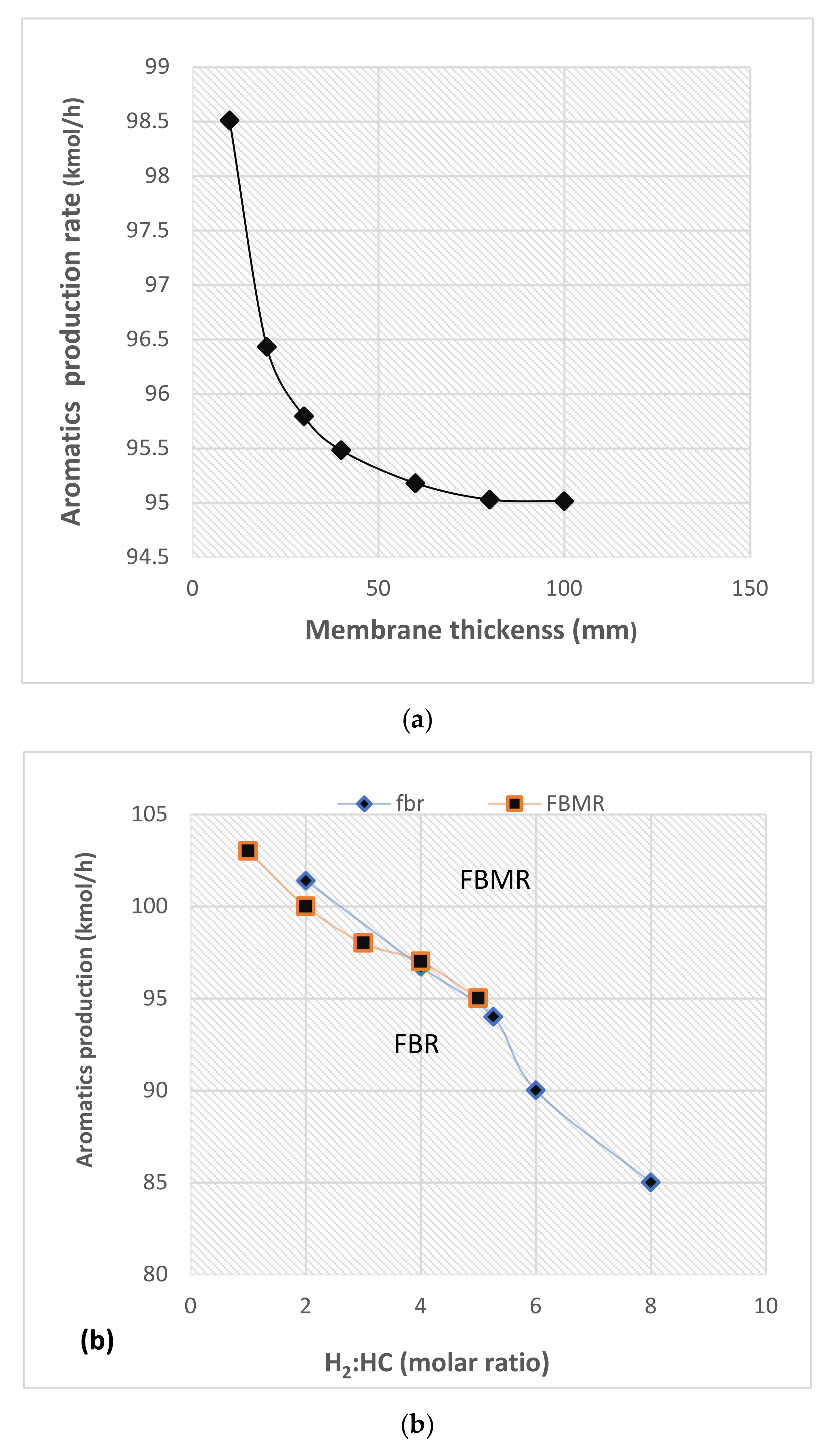
4.2.3. Influence of Membrane Thickness
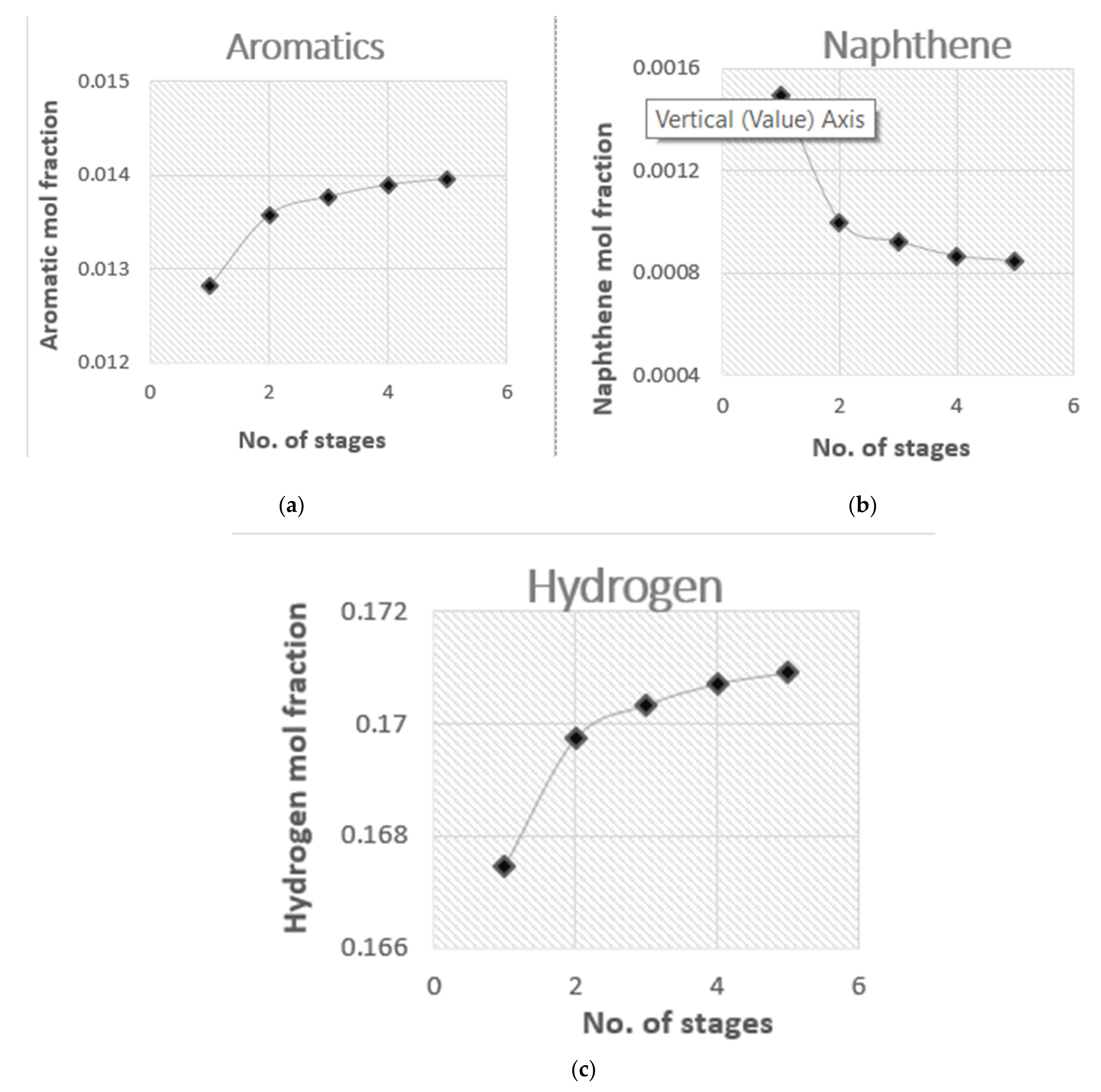
4.3. Aromatics and Hydrogen Yields
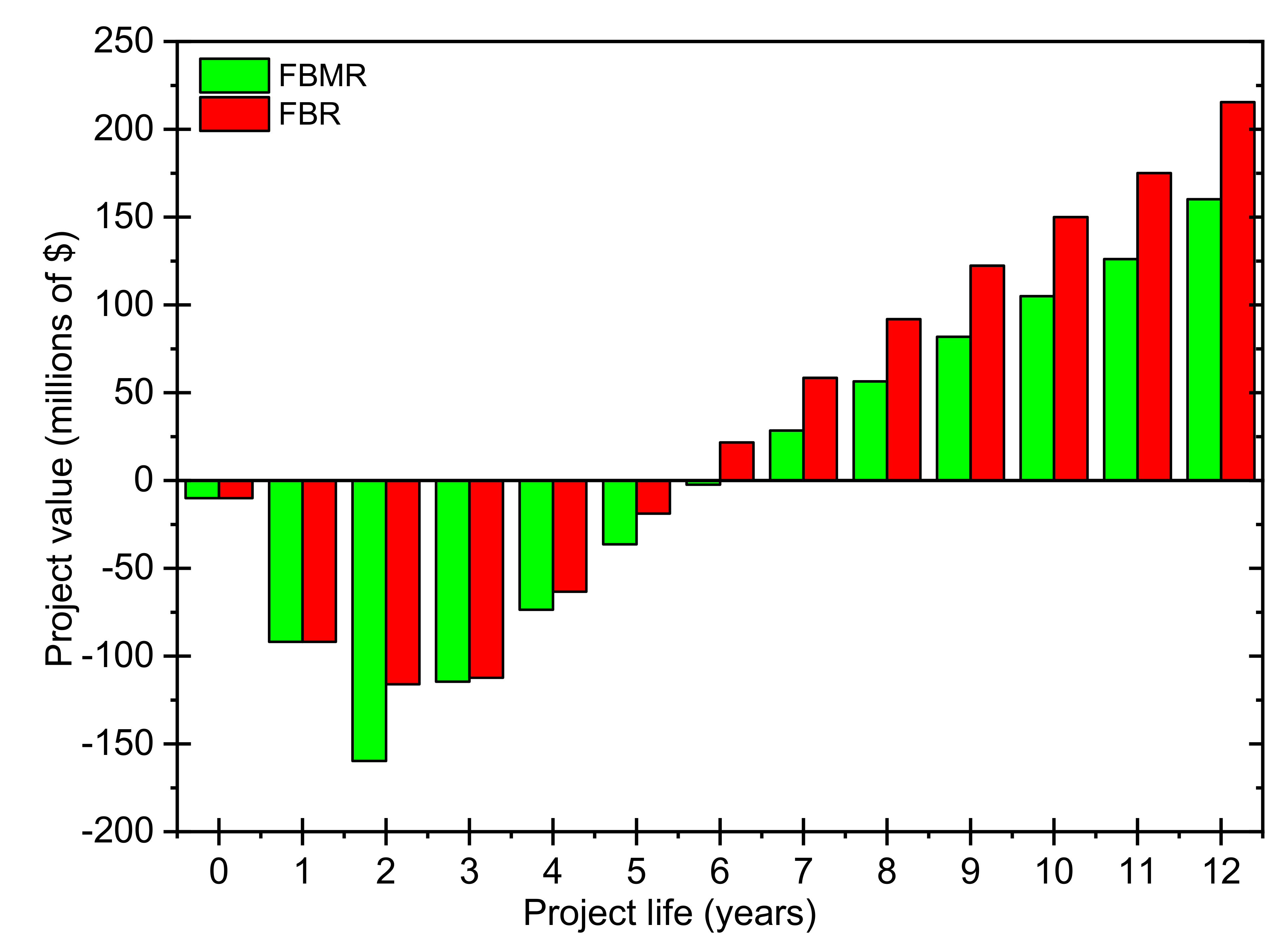
4.4. Thermoeconomic Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Ac | cross section of reactor, m2 |
| CSTR | continuous stirred tank reactor |
| db | bubble diameter, m |
| Ei | activation energy for the ith reaction, kJ/kmol |
| Ep | activation energy of permeability, kJ/mol |
| FBP | final boiling pint (°C) |
| FSH2 | flow rate of H2 in shell side gas, kmol/h |
| Ft | total molar flow rate, kmol/h |
| IBP | initial boiling point, °C |
| RON | research octane number |
| kci | coefficient for mass transfer of specie i, m/h |
| Kei | equilibrium coefficient |
| kfi | forward rate constant |
| L | length of reactor, m |
| MR | membrane reactor |
| pi | partial pressure of specie i, kPa |
| Pt | total pressure, kPa |
| pRH2 | reaction side hydrogen partial pressure, Pa |
| pS H2 | shell side hydrogen partial pressure, Pa |
| P | permeability of hydrogen through Pd–Ag layer, mol/m2 s Pa0.5 |
| P0 | pre-exponential factor of hydrogen permeability, mol/m2 s Pa0.5 |
| PBR | packed bed reactor |
| PFR | plug flow reactor |
| R | gas constant, kJ/kmol K |
| ri | rate of reaction for the i reaction, kmol/kg cat h |
| T | temperature of gas phase, K |
| TBP | true boiling point, °C |
| t | time, h |
| ub | velocity of rise of bubbles, m s−1 |
| Cmp | membrane permeation capacity (membrane surface area/thickness) |
| Ep | activation energy for permeation, J mol−1 |
| k | pre-exponential factor, mol km−1 h−1 Pa−0.5 |
| Greek letters | |
| αH | hydrogen permeation rate constant, mol/m s Pa0.5 |
| d | thickness of palladium layer, mm |
| ρb | catalyst bed density, kg/m3 |
| ρg | density of gas phase, kg/m3 |
| vij | stoichiometric coefficient of specie i in reaction j |
| ∆H | heat of reaction, kJ/kmol |
| ɛb | void fraction of catalyst bed |
| ɛmf | void fraction of catalytic bed at minimum fluidization |
| φ | catalyst particle shape factor |
| δ | fraction of gas in bubble phase |
| ƞ | permeation effectiveness factor |
References
- Rahimpour, M.R.; Jafari, M.; Iranshahi, D. Progress in Catalytic Naphtha Reforming Process: A Review. Appl. Energy 2013, 109, 79–93. [Google Scholar] [CrossRef]
- Patil, C.S.; van Sint Annaland, M.; Kuipers, J.A. Design of a Novel Autothermal Membrane-Assisted Fluidized-Bed Reactor for the Production of Ultrapure Hydrogen from Methane. Ind. Eng. Chem. Res. 2005, 44, 9502–9512. [Google Scholar] [CrossRef]
- McKetta, J., Jr. Encyclopedia of Chemical Processing and Design: Volume 48-Residual Refining and Processing to Safety: Operating Discipline; Routledge: Oxfordshire, UK, 2017. [Google Scholar]
- Shu, J.; Grandjean, B.P.; Kaliaguine, S. Methane Steam Reforming in Asymmetric Pd-and Pd-Ag/Porous SS Membrane Reactors. Appl. Catal. A Gen. 1994, 119, 305–325. [Google Scholar] [CrossRef]
- Helmi, A.; Fernandez, E.; Melendez, J.; Pacheco Tanaka, D.A.; Gallucci, F.; van Sint Annaland, M. Fluidized Bed Membrane Reactors for Ultra Pure H2 Production—A Step Forward towards Commercialization. Molecules 2016, 21, 376. [Google Scholar] [CrossRef] [Green Version]
- Rahimpour, M.R. Enhancement of Hydrogen Production in a Novel Fluidized-Bed Membrane Reactor for Naphtha Reforming. Intern. J. Hydrog. Energy 2009, 34, 2235–2251. [Google Scholar] [CrossRef]
- Rahimpour, M.R.; Iranshahi, D.; Pourazadi, E.; Bahmanpour, A.M. A Comparative Study on a Novel Combination of Spherical and Membrane Tubular Reactors of the Catalytic Naphtha Reforming Process. Intern. J. Hydrog. Energy 2011, 36, 505–517. [Google Scholar] [CrossRef]
- Keuler, J.N.; Lorenzen, L. Comparing and Modeling the Dehydrogenation of Ethanol in a Plug-Flow Reactor and a Pd- Ag Membrane Reactor. Ind. Eng. Chem. Res. 2002, 41, 1960–1966. [Google Scholar] [CrossRef]
- Howard, B.H.; Killmeyer, R.P.; Rothenberger, K.S.; Cugini, A.V.; Morreale, B.D.; Enick, R.M.; Bustamante, F. Hydrogen Permeance of Palladium–Copper Alloy Membranes over a Wide Range of Temperatures and Pressures. J. Membr. Sci. 2004, 241, 207–218. [Google Scholar] [CrossRef]
- Barbieri, G.; Di Maio, F.P. Simulation of the Methane Steam Re-Forming Process in a Catalytic Pd-Membrane Reactor. Ind. Eng. Chem. Res. 1997, 36, 2121–2127. [Google Scholar] [CrossRef]
- Rahimpour, M.R.; Vakili, R.; Pourazadi, E.; Iranshahi, D.; Paymooni, K. A Novel Integrated, Thermally Coupled Fluidized Bed Configuration for Catalytic Naphtha Reforming to Enhance Aromatic and Hydrogen Productions in Refineries. Intern. J. Hydrog. Energy 2011, 36, 2979–2991. [Google Scholar] [CrossRef]
- Pasha, M.K.; Ahmad, I.; Mustafa, J.; Kano, M. Modeling of a Nickel-Based Fluidized Bed Membrane Reactor for Steam Methane Reforming Process. J. Chem. Soc. Pakistan 2019, 41, 219–229. [Google Scholar]
- Tosti, S.; Basile, A.; Bettinali, L.; Borgognoni, F.; Gallucci, F.; Rizzello, C. Design and Process Study of Pd Membrane Reactors. Intern. J. Hydrog. Energy 2008, 33, 5098–5105. [Google Scholar] [CrossRef]
- Roy, S.; Cox, B.G.; Adris, A.M.; Pruden, B.B. Economics and Simulation of Fluidized Bed Membrane Reforming. Intern. J. Hydrog. Energy 1998, 23, 745–752. [Google Scholar] [CrossRef]
- Mostafazadeh, A.K.; Rahimpour, M.R. A Membrane Catalytic Bed Concept for Naphtha Reforming in the Presence of Catalyst Deactivation. Chem. Eng. Process. 2009, 48, 683–694. [Google Scholar] [CrossRef]
- Itoh, N. Inorganic Membranes for Reaction and Separation. AIChE J. 1987, 33, 1576. [Google Scholar] [CrossRef]
- Mazzieri, V.A.; Pieck, C.L.; Vera, C.R.; Yori, J.C.; Grau, J.M. Effect of Ge Content on the Metal and Acid Properties of Pt-Re-Ge/Al2O3-Cl Catalysts for Naphtha Reforming. Appl. Catal., A: General 2009, 353, 93–100. [Google Scholar] [CrossRef]
- Van Gool, W. Exergy Analysis of Industrial Processes. Energy 1992, 17, 791–803. [Google Scholar] [CrossRef]
- Gilbert, A.; Mesmer, B.; Watson, M.D. Uses of Exergy in Systems Engineering. In Proceedings of the 2016 Conference on Systems Engineering Research, Huntsville, AL, USA, 22–24 March 2016; pp. 22–24. [Google Scholar]
- Nimkar, S.C.; Mewada, R.K. An Overview of Exergy Analysis for Chemical Process Industries. Int. J. Exergy 2014, 15, 468–507. [Google Scholar] [CrossRef]
- Montelongo-Luna, J.M.; Svrcek, W.Y.; Young, B.R. An Exergy Calculator Tool for Process Simulation. Asia Pac. J. Chem. Eng. 2007, 2, 431–437. [Google Scholar] [CrossRef]
- Hinderink, A.P.; Kerkhof, F.; Lie, A.B.K.; Arons, J.D.S.; Van Der Kooi, H.J. Exergy Analysis with a Flowsheeting Simulator—I. Theory; Calculating Exergies of Material Streams. Chem. Eng. Sci. 1996, 51, 4693–4700. [Google Scholar] [CrossRef]
- Hinderink, A.P.; Kerkhof, F.; Lie, A.B.K.; Arons, J.D.S.; Van Der Kooi, H.J. Exergy Analysis with a Flowsheeting Simulator—II. Application; Synthesis Gas Production from Natural Gas. Chem. Eng. Sci. 1996, 51, 4701–4715. [Google Scholar] [CrossRef]
- Sarvar-Amini, A.; Sotudeh-Gharebagh, R.; Bashiri, H.; Mostoufi, N.; Haghtalab, A. Sequential Simulation of a Fluidized Bed Membrane Reactor for the Steam Methane Reforming Using ASPEN PLUS. Energy Fuels 2007, 21, 3593–3598. [Google Scholar] [CrossRef]
- Samoila, P.; Boutzeloit, M.; Benitez, V.; D’Ippolito, S.A.; Especel, C.; Epron, F.; Vera, C.R.; Marecot, P.; Pieck, C.L. Influence of the Pretreatment Method on the Properties of Trimetallic Pt–Ir–Ge/Al2O3 Prepared by Catalytic Reduction. Appl. Catal. A: General 2007, 332, 37–45. [Google Scholar] [CrossRef]
- Murzin, D.Y. Selectivity of Complex Heterogeneous Catalytic Reactions over Energetically Nonuniform Surfaces. React. Kinet. Catal. Lett. 1996, 59, 117–123. [Google Scholar] [CrossRef]
- Smith, R.B. Kinetic Analysis of Naphtha Reforming with Platinum Catalyst. Chem. Eng. Prog 1959, 55, 76–80. [Google Scholar]
- Marin, G.B.; Froment, G.F.; Lerou, J.J.; De Backer, W. Simulation of a Catalytic Naphtha Reforming Unit. Eur. Fed. Chem. Eng. 1983, 1–7. [Google Scholar]
- Ramage, M.P.; Graziani, K.R.; Krambeck, F.J. 6 Development of Mobil’s Kinetic Reforming Model. Chem. Eng. Sci. 1980, 35, 41–48. [Google Scholar] [CrossRef]
- Ancheyta-Juarez, J.; Villafuerte-Macías, E. Kinetic Modeling of Naphtha Catalytic Reforming Reactions. Energy Fuels 2000, 14, 1032–1037. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, W.; Su, H.; Chu, J. A Dynamic Model for Naphtha Catalytic Reformers. In Proceedings of the 2004 IEEE International Conference on Control Applications, Taipei, Taiwan, 2–4 September 2004; Volume 1, pp. 159–164. [Google Scholar]
- Vathi, G.P.; Chaudhuri, K.K. Modelling and Simulation of Commercial Catalytic Naphtha Reformers. Can. J. Chem. Eng. 1997, 75, 930–937. [Google Scholar] [CrossRef]
- Hou, W.; Su, H.; Hu, Y.; Chu, J. Modeling, Simulation and Optimization of a Whole Industrial Catalytic Naphtha Reforming Process on Aspen Plus Platform. Chin. J. Chem. Eng. 2006, 14, 584–591. [Google Scholar] [CrossRef]
- Yun, S.; Ted Oyama, S. Correlations in Palladium Membranes for Hydrogen Separation: A Review. J. Membr. Sci. 2011, 375, 28–45. [Google Scholar] [CrossRef]
- Vadrucci, M.; Borgognoni, F.; Moriani, A.; Santucci, A.; Tosti, S. Hydrogen Permeation through Pd–Ag Membranes: Surface Effects and Sieverts’ Law. Int. J. Hydrogen Energy 2013, 38, 4144–4152. [Google Scholar] [CrossRef]
- Mori, S.; Wen, C.Y. Estimation of Bubble Diameter in Gaseous Fluidized Beds. AIChE J. 1975, 21, 109–115. [Google Scholar] [CrossRef]
- Querol, E.; Gonzalez-Regueral, B.; Ramos, A.; Perez-Benedito, J.L. Novel Application for Exergy and Thermoeconomic Analysis of Processes Simulated with Aspen Plus®. Energy 2011, 36, 964–974. [Google Scholar] [CrossRef]
- Guthrie, K.M. Capital Cost Estimation. Chem. Engng. 1969, 24, 114–142. [Google Scholar]
- Smith, R. Chemical Process: Design and Integration; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Shabani, M.R.; Yekta, R.B. Chemical Processes Equipment Cost Estimating Using Parametric Models. Cost Eng. Ann. Arbor Then Morgant. 2006, 48, 26. [Google Scholar]
- Lang, H.J. Cost Relationships in Preliminary Cost Estimation. Chem. Eng 1947, 54, 117–121. [Google Scholar]
- Tamhankar, S.; Gulamhusein, A.; Boyd, T.; DaCosta, D.; Golben, M. DOE Hydrogen, Fuel Cells and Infrastructure Technologies Program Integrated Hydrogen Production, Purification and Compression System; Linde LLC: Guildford, UK, 2011. [Google Scholar]
- Wieland, S.; Melin, T.; Lamm, A. Membrane Reactors for Hydrogen Production. Chem. Eng. Sci. 2002, 57, 1571–1576. [Google Scholar] [CrossRef]
- Tong, J.; Matsumura, Y. Pure Hydrogen Production by Methane Steam Reforming with Hydrogen-Permeable Membrane Reactor. Catal. Today 2006, 111, 147–152. [Google Scholar] [CrossRef]
- Mustafa, J.; Ahmad, I.; Ahsan, M.; Kano, M. Computational Fluid Dynamics Based Model Development and Exergy Analysis of Naphtha Reforming Reactors. Int. J. Exergy 2017, 24, 344–363. [Google Scholar] [CrossRef]
- Akram, A.U.; Ahmad, I.; Chughtai, A.; Kano, M. Exergy Analysis and Optimisation of Naphtha Reforming Process with Uncertainty. Int. J. Exergy 2018, 26, 247–262. [Google Scholar] [CrossRef]
| a | A | B | |||
| C6 | 68.73 | 18.75 | 19.50 | 59.90 | |
| C7 | 208.47 | 20.70 | 19.50 | 60.23 | |
| C8 | |||||
| for An = MX * | 64.50 | 17.89 | 19.50 | 60.37 | |
| for An = OX * | 65.10 | 19.15 | 19.50 | 60.32 | |
| for An = PX * | 64.74 | 18.66 | 19.50 | 60.13 | |
| for An = EB * | 68.70 | 18.71 | 19.50 | 60.40 | |
| C9+ | 66.05 | 20.38 | 19.50 | 61.05 | |
| Studied Parameter | Model Equation |
|---|---|
| Superficial velocity at minimum fluidization | |
| Archimedes’ number | |
| Bubble diameter | |
| Coefficient of mass transfer (Bubble to emulsion phase) | |
| The velocity of bubble rise | |
| The volume fraction of the bubble phase to the overall bed | |
| Specific surface area for bubble | |
| Density for emulsion phase |
| Capital Cost for Fluid Processing | |
|---|---|
| Item | Factor |
| Direct costs | |
| Equipment delivered cost | 1 |
| Equipment erection, fEQPR | 0.4 |
| Piping (installed), fPIPING | 0.7 |
| Instrumentation and controls (installed), fINSTR | 0.2 |
| Electrical (installed), fELEC | 0.1 |
| Utilities, fUTILITY | 0.5 |
| Off-sites, fOffS | 0.2 |
| Buildings (including services), fBUILD | 0.2 |
| Site preparation, fSiteP | 0.1 |
| The total capital cost of installed equipment | 3.4 |
| Indirect costs | |
| Design, engineering, and construction, fDECONC | 1 |
| Contingency (about 10% of fixed capital costs), fCONT | 0.4 |
| Total fixed capital cost | 4.8 |
| Working capital | |
| Working capital (15% of the total capital cost), fWRKC | 0.7 |
| Total capital cost, f I | 5.8 |
| Components | FEED | FBR (CPROD3) | FBMR (PROD3) |
|---|---|---|---|
| Mole Fractions | kmol/h | kmol/h | |
| METHA-01 | 0.0089 | 17.14 | 202.537 |
| ETHAN-01 | 0.0098 | 18.76 | 66.443 |
| PROPA-01 | 0.0085 | 16.41 | 16.405 |
| N-BUT-01 | 0.0045 | 8.60 | 8.590 |
| ISOBU-01 | 0.0031 | 5.94 | 5.947 |
| N-PEN-01 | 0.0015 | 2.84 | 2.836 |
| 2-MET-01 | 0.0032 | 6.18 | 6.178 |
| N-HEX-01 | 0.0097 | 15.04 | 0.026 |
| 2-MET-02 | 0.0098 | 15.34 | 0.028 |
| N-HEP-01 | 0.0124 | 19.11 | 0.032 |
| 2-MET-03 | 0.0133 | 20.65 | 0.036 |
| N-OCT-01 | 0.0101 | 9.21 | 0.001 |
| 2:2:4-01 | 0.0143 | 13.53 | 0.002 |
| N-NON-01 | 0.0066 | 10.01 | 0.014 |
| 2:2:5-01 | 0.0103 | 15.90 | 0.026 |
| CYCLO-01 | 0.0033 | 0.91 | 0.072 |
| METHY-01 | 0.0036 | 0.88 | 0.077 |
| ETHYL-01 | 0.0049 | 0.31 | 0.012 |
| N-PRO-01 | 0.0008 | 0.19 | 0.017 |
| CYCLO-02 | 0.0000 | 0.08 | 0.081 |
| METHY-02 | 0.0013 | 2.43 | 2.383 |
| ETHYL-02 | 0.0028 | 5.25 | 5.091 |
| N-PRO-02 | 0.0036 | 6.79 | 6.569 |
| N-BUT-02 | 0.0005 | 0.97 | 0.938 |
| BENZE-01 | 0.0036 | 19.40 | 205.080 |
| TOLUE-01 | 0.0046 | 24.28 | 0.773 |
| M-XYL-01 | 0.0006 | 9.01 | 5.561 |
| O-XYL-01 | 0.0007 | 8.80 | 2.448 |
| P-XYL-01 | 0.0015 | 12.45 | 0.679 |
| ETHYL-03 | 0.0009 | 10.08 | 0.553 |
| N-PRO-03 | 0.0011 | 9.97 | 0.065 |
| HYDRO-01 | 0.8403 | 1866.82 | 595.781 |
| Components | Feed (kg/h) | FBR | FBMR | Increase Using the Membrane | |
|---|---|---|---|---|---|
| Out (kg/h) | Out (kg/h) | Daily Increase (kg/day) | Yearly Increase (kg/Y) | ||
| Hydrogen | 3250 | 14,913.65 | 17,080.07 | 2166.42 | 790,743 |
| Aromatics | 2374 | 4182.849 | 4267.602 | 84.753 | 30,934.84 |
| FBR | |||||||
|---|---|---|---|---|---|---|---|
| Stream Name | T (K) | P (KPa) | HR | SR | HS | SS | Physical Exergy |
| FEED | 780 | 3702.991 | −26.7816 | −0.08856 | 5.069967 | −0.05384 | 11,468.25 |
| PROD1 | 770.025 | 3702.991 | −7.69063 | −0.03791 | 15.70902 | −0.02079 | 12,726.43 |
| PROD2 | 775.9731 | 3604.925 | −4.9959 | −0.02995 | 17.30305 | −0.01549 | 13,092.23 |
| PROD3 | 777.4178 | 3506.858 | −4.3791 | −0.02766 | 17.4909 | −0.01418 | 13,129.03 |
| FBMR | |||||||
| Stream Name | T (K) | P (KPa) | HR | SR | HS | SS | Physical Exergy |
| FEED | 780 | 3702.991 | −26.7816 | −0.08856 | 5.069967 | −0.05384 | 11,468.25 |
| NETHYD1 | 776.9028 | 2800 | 0.000873 | −1.46 × 10−06 | 14.05493 | 0.000402 | 30.9085 |
| NETHYD2 | 776.9891 | 900 | 0.000873 | −1.46 × 10−06 | 14.0306 | 0.009842 | 2540.903 |
| NETHYD3 | 777.0001 | 900 | 0.000873 | −1.46 × 10−06 | 14.03092 | 0.009842 | 2122.787 |
| PROD1 | 776.4373 | 3702.991 | −5.83885 | −0.03361 | 17.30526 | −0.01722 | 13,053.95 |
| PROD2 | 776.9417 | 3604.925 | −7.23389 | −0.04482 | 19.21282 | −0.02147 | 9810.164 |
| PROD3 | 777.0003 | 3506.858 | −12.8969 | −0.07652 | 21.80172 | −0.03476 | 7016.567 |
| Gross Annual Sales of FBR | |||
|---|---|---|---|
| Material Name | Price ($/kg) | Flow Rate (kg/h) | Annual Cost |
| Naphtha | 0.30 | 28,178.00 | 70,349,195 |
| Natural gas | 0.00254 | 4790.505 | 79,733 |
| Gasoline | 0.90 | 6523.001 | 48,855,965 |
| Aromatics | 0.99 | 14,913.65 | 123,125,549 |
| Hydrogen | 1.80 | 4182.849 | 62,644,687 |
| Gross Annual Sales of FBMR | |||
|---|---|---|---|
| Material Name | Price ($/kg) | Flow Rate (kg/h) | Annual Cost |
| Naphtha | 0.30 | 28,178.00 | 70,349,195 |
| Natural Gas | 0.00254 | 7,466.072 | 155,330 |
| Gasoline | 0.90 | 1,596.609 | 11,953,721 |
| Aromatics | 0.99 | 17,080.07 | 140,718,362 |
| Hydrogen | 1.80 | 4,267.602 | 62,926,971 |
| Cost | FBMR | FBR |
|---|---|---|
| Equipment cost | $42,904,400 | $29,904,400 |
| Bare module cost | $65,575,400 | $45,575,400 |
| Total module | $77,378,972 | $53,778,972 |
| Total grass root cost | $77,550,922 | $53,950,922 |
| Lang factor | 4.74 | 4.74 |
| Lang factor cost | $203,366,856 | $141,746,856 |
| Raw materials costs | $70,349,195 | $70,349,195 |
| Working capital | $22,100,000 | $22,100,000 |
| Cost of utilities | $866,000 | $866,000 |
| Cost of operating labor | $802,920 | $802,890 |
| Cost of manufacturing | $117,079,279 | $116,810,749 |
| Revenue from Sales | $216,754,384 | $234,705,934 |
| Discounted Profitability Criteria | |
|---|---|
| Net Present Value (millions) | 160.19 |
| Discounted Cash Flow Rate of Return | 26.17% |
| Discounted Payback Period (years) | 3.2 |
| Non-Discounted Profitability Criteria | |
| Cumulative Cash Position (million) | 465.31 |
| Rate of Return on Investment | 31.02% |
| Payback Period (years) | 2.5 |
| Discounted Profitability Criteria | |
|---|---|
| Net Present Value (millions) | 215.48 |
| Discounted Cash Flow Rate of Return | 30.24% |
| Discounted Payback Period (years) | 2.6 |
| Non-Discounted Profitability Criteria | |
| Cumulative Cash Position (million) | 582.09 |
| Rate of Return on Investment | 38.81% |
| Payback Period (years) | 2.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nafees, T.; Bhatti, A.A.; Jadoon, U.K.; Ahmad, F.; Ahmad, I.; Kano, M.; Menezes, B.C.; Ahsan, M.; Syed, N.u.H. Model-Based Quality, Exergy, and Economic Analysis of Fluidized Bed Membrane Reactors. Membranes 2021, 11, 765. https://doi.org/10.3390/membranes11100765
Nafees T, Bhatti AA, Jadoon UK, Ahmad F, Ahmad I, Kano M, Menezes BC, Ahsan M, Syed NuH. Model-Based Quality, Exergy, and Economic Analysis of Fluidized Bed Membrane Reactors. Membranes. 2021; 11(10):765. https://doi.org/10.3390/membranes11100765
Chicago/Turabian StyleNafees, Tabassam, Adnan Ahmed Bhatti, Usman Khan Jadoon, Farooq Ahmad, Iftikhar Ahmad, Manabu Kano, Brenno Castrillon Menezes, Muhammad Ahsan, and Naveed ul Hasan Syed. 2021. "Model-Based Quality, Exergy, and Economic Analysis of Fluidized Bed Membrane Reactors" Membranes 11, no. 10: 765. https://doi.org/10.3390/membranes11100765
APA StyleNafees, T., Bhatti, A. A., Jadoon, U. K., Ahmad, F., Ahmad, I., Kano, M., Menezes, B. C., Ahsan, M., & Syed, N. u. H. (2021). Model-Based Quality, Exergy, and Economic Analysis of Fluidized Bed Membrane Reactors. Membranes, 11(10), 765. https://doi.org/10.3390/membranes11100765







