Analysis of Host Immunological Response of Adenovirus-Based COVID-19 Vaccines
Abstract
:1. Introduction
2. Model
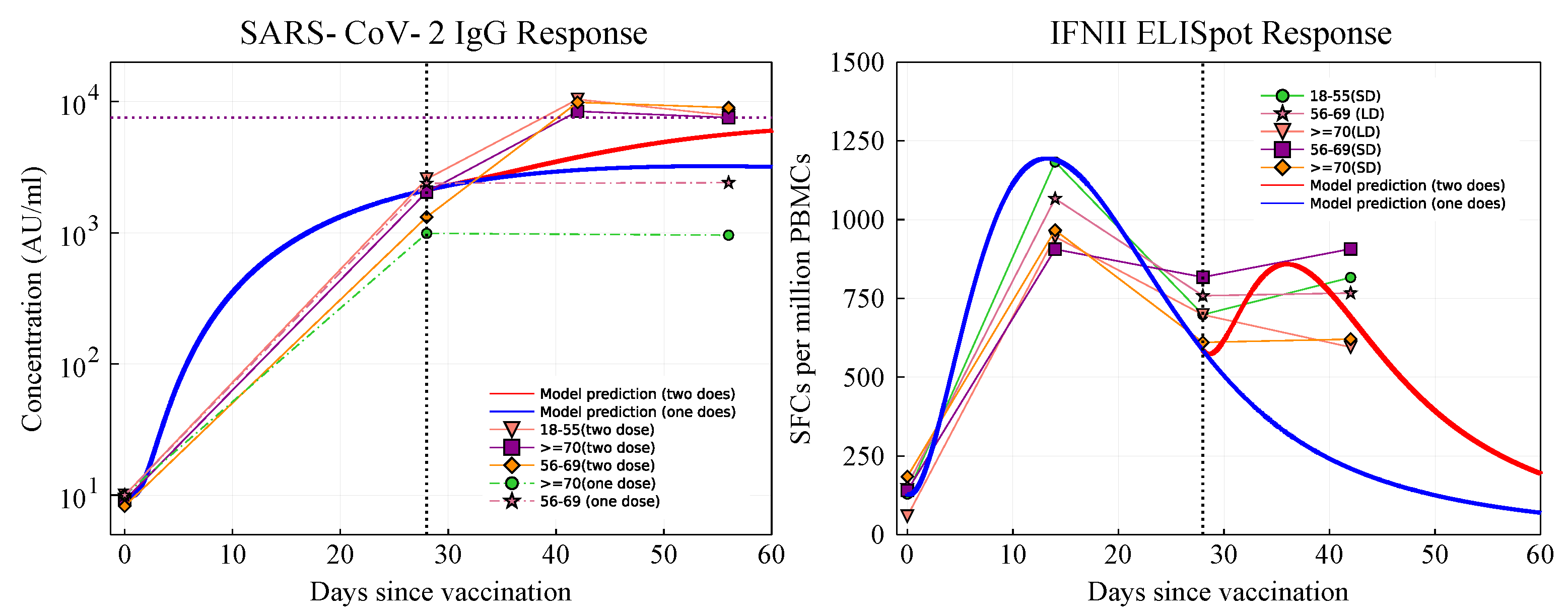
2.1. Parameter Fitting
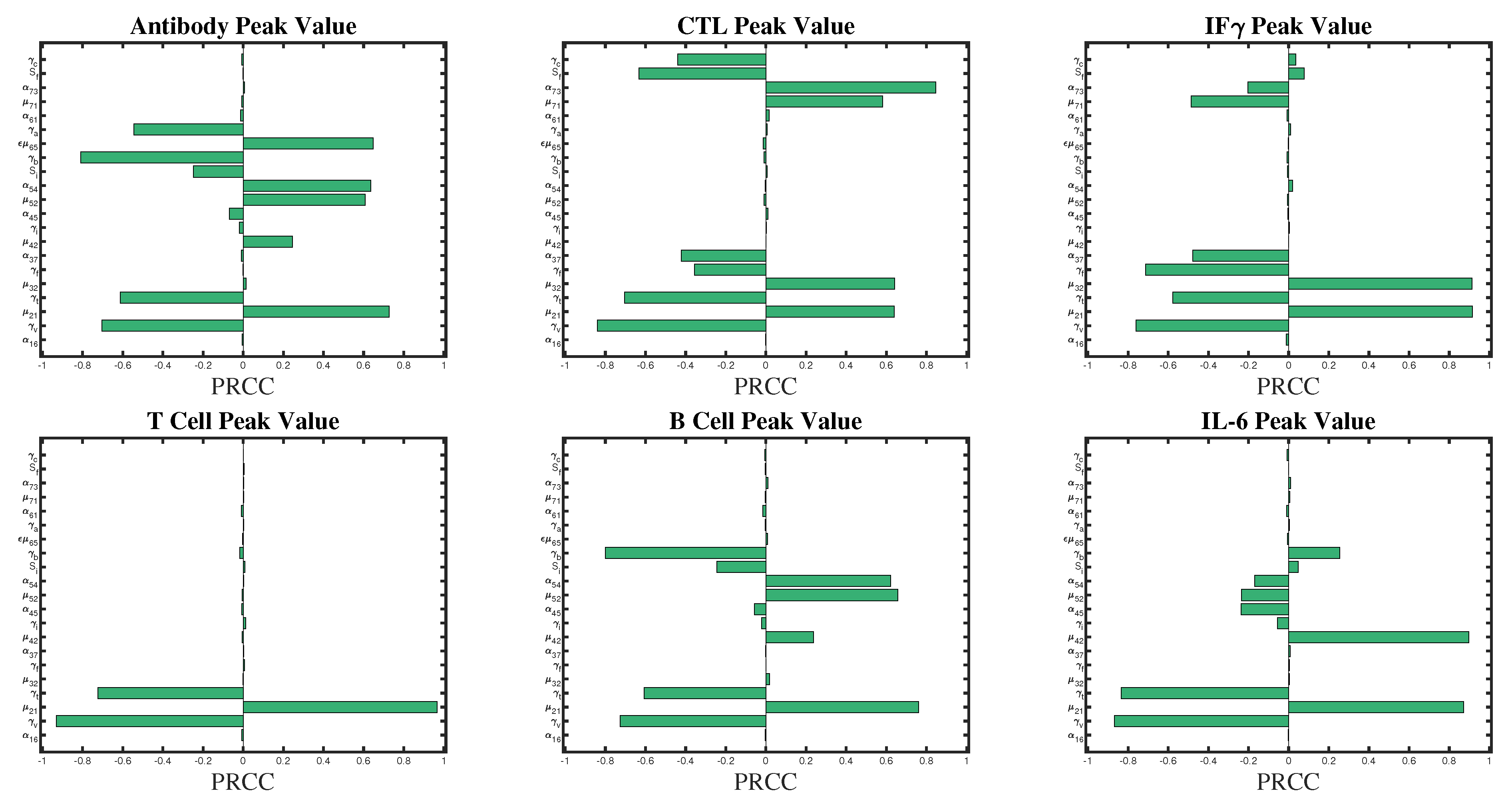
2.2. Sensitivity Analysis
3. Results
3.1. Sensitivity Analysis
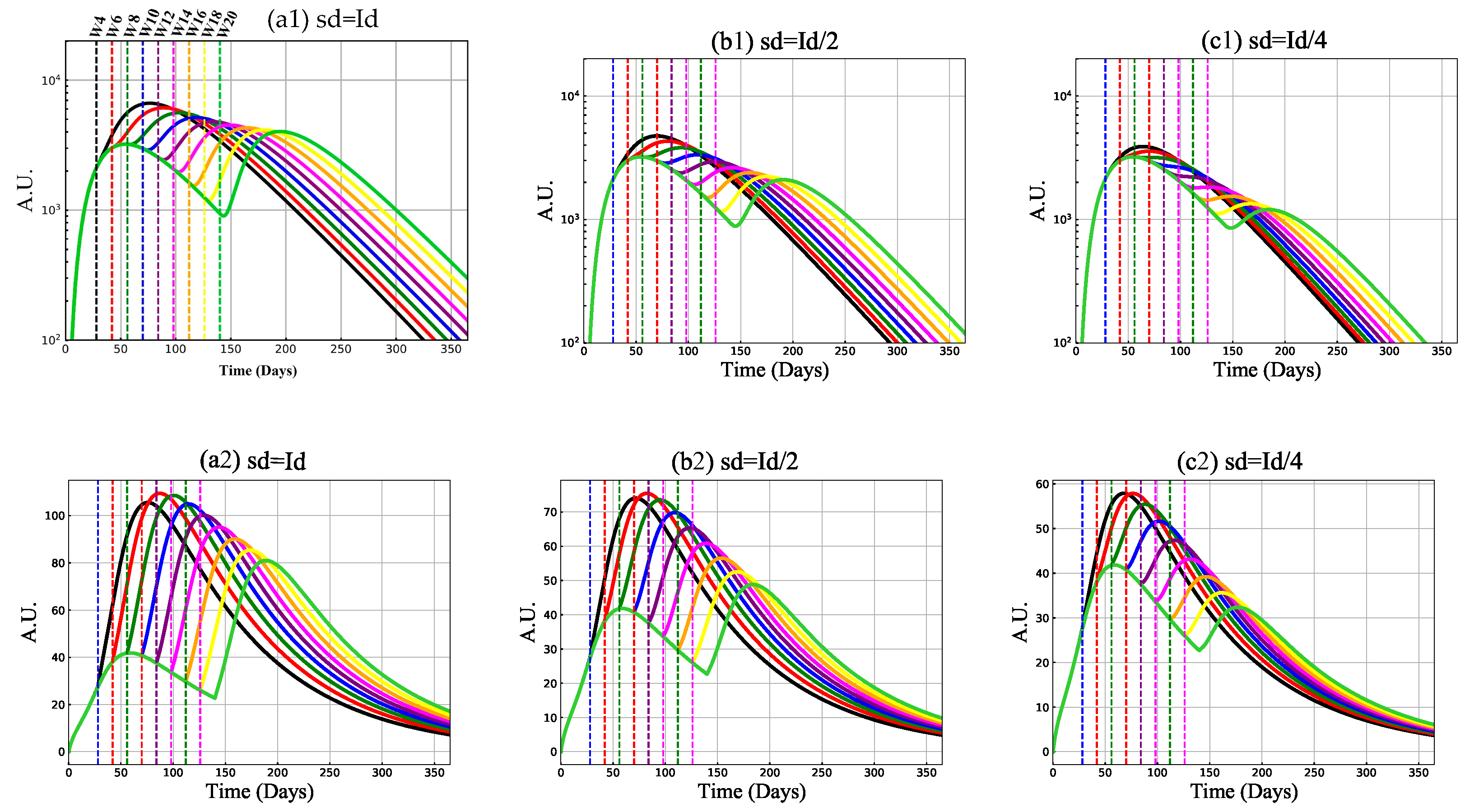
3.2. Mechanism of Vaccine-Induced Immunity with Booster Delay and Sparing
3.2.1. Antibody and Cytotoxic T-Cell Responses
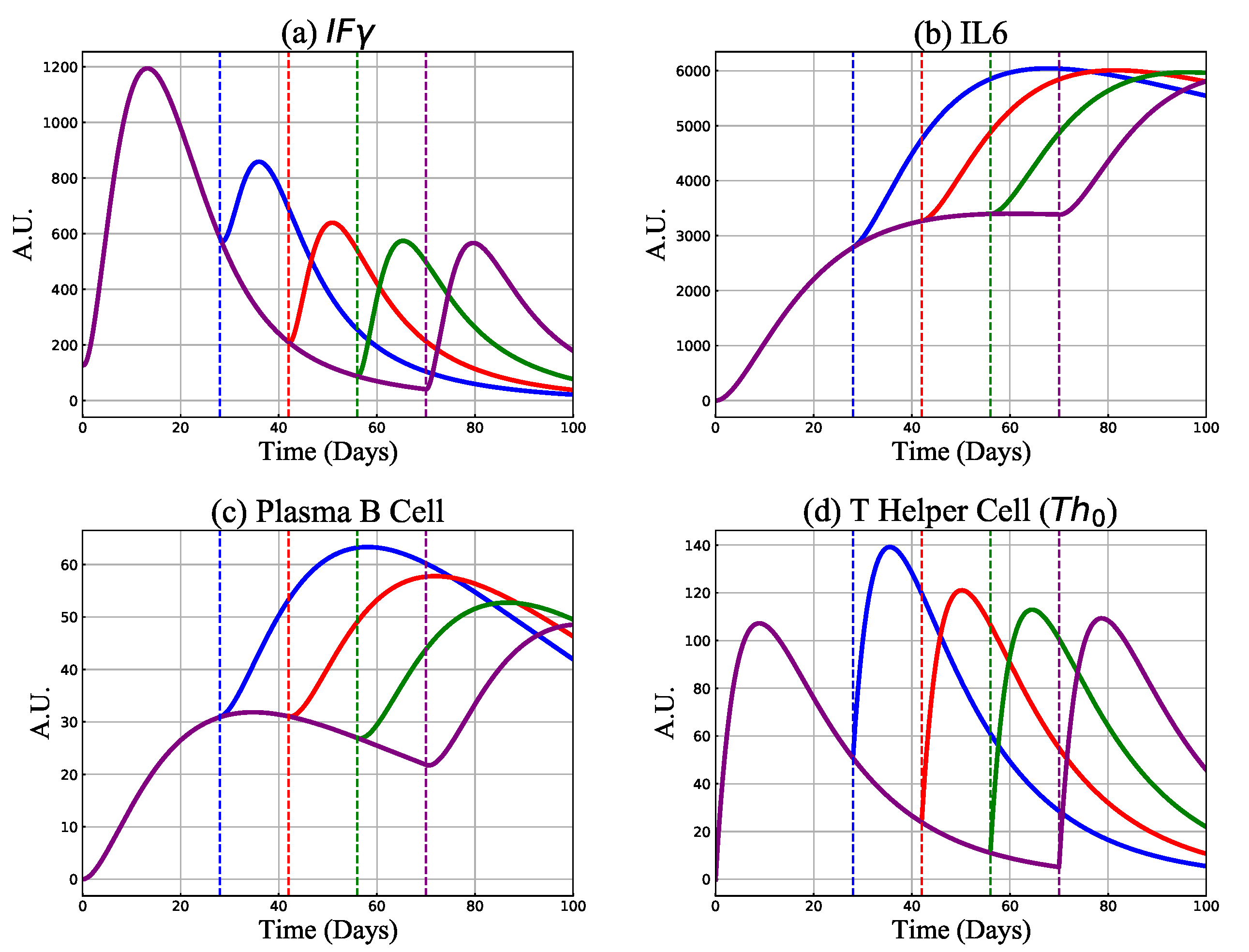
3.2.2. Cytokines, B and Th Cell Responses
3.2.3. Protective Capacity
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| APC | Antigen-Presenting Cell |
| MHC | Major Histocompatibility Complex |
| T Helper Cell Type 0 | |
| T Helper Cell Type 1 | |
| T Helper Cell Type 2 | |
| NK | Natural Killer Cell |
| CTL | Cytotoxic T Lymphocyte |
| IL | Interleukin |
| Interferon | |
| Transforming Growth Factor | |
| Neutralizing Antibody | |
| Immunoglobulin G |
References
- Ramasamy, M.N.; Minassian, A.M.; Ewer, K.J.; Flaxman, A.L.; Folegatti, P.M.; Owens, D.R.; Voysey, M.; Aley, P.K.; Angus, B.; Babbage, G.; et al. Safety and immunogenicity of ChAdOx1 nCoV-19 vaccine administered in a prime-boost regimen in young and old adults (COV002): A single-blind, randomised, controlled, phase 2/3 trial. Lancet 2020, 396, 1979–1993. [Google Scholar] [CrossRef]
- Quinn, K.M.; Zak, D.E.; Costa, A.; Yamamoto, A.; Kastenmuller, K.; Hill, B.J.; Lynn, G.M.; Darrah, P.A.; Lindsay, R.W.; Wang, L.; et al. Antigen expression determines adenoviral vaccine potency independent of IFN and STING signaling. J. Clin. Investig. 2015, 125, 1129–1146. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.; Wang, A.; Liu, M.; Wang, Q.; Chen, J.; Xia, S.; Ling, Y.; Zhang, Y.; Xun, J.; Lu, L.; et al. Neutralizing antibody responses to SARS-CoV-2 in a COVID-19 recovered patient cohort and their implications. medRxiv 2020. [Google Scholar] [CrossRef]
- Zhang, L. Multi-epitope vaccines: A promising strategy against tumors and viral infections. Cell. Mol. Immunol. 2018, 15, 182–184. [Google Scholar] [CrossRef] [Green Version]
- Kar, T.; Narsaria, U.; Basak, S.; Deb, D.; Castiglione, F.; Mueller, D.M.; Srivastava, A.P. A candidate multi-epitope vaccine against SARS-CoV-2. Sci. Rep. 2020, 10, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Estrada, E. COVID-19 and SARS-CoV-2. Modeling the present, looking at the future. Phys. Rep. 2020. [Google Scholar] [CrossRef] [PubMed]
- Janeway, C.A., Jr.; Travers, P.; Walport, M.; Shlomchik, M.J. The complement system and innate immunity. In Immunobiology: The Immune System in Health and Disease, 5th ed.; Garland Science: New York, NY, USA, 2001. [Google Scholar]
- Clem, A.S. Fundamentals of vaccine immunology. J. Glob. Infect. Dis. 2011, 3, 73. [Google Scholar] [CrossRef] [PubMed]
- Lees, J.R. Interferon gamma in autoimmunity: A complicated player on a complex stage. Cytokine 2015, 74, 18–26. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Costela-Ruiz, V.J.; Illescas-Montes, R.; Puerta-Puerta, J.M.; Ruiz, C.; Melguizo-Rodríguez, L. SARS-CoV-2 infection: The role of cytokines in COVID-19 disease. Cytokine Growth Factor Rev. 2020. [Google Scholar] [CrossRef] [PubMed]
- Morris, R.; Kershaw, N.J.; Babon, J.J. The molecular details of cytokine signaling via the JAK/STAT pathway. Protein Sci. 2018, 27, 1984–2009. [Google Scholar] [CrossRef] [Green Version]
- Kishimoto, T. Interleukin-6: Discovery of a pleiotropic cytokine. Arthritis Res. Ther. 2006, 8, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Velazquez-Salinas, L.; Verdugo-Rodriguez, A.; Rodriguez, L.L.; Borca, M.V. The role of interleukin 6 during viral infections. Front. Microbiol. 2019, 10, 1057. [Google Scholar] [CrossRef] [Green Version]
- Akira, S.; Kishimoto, T. IL-6 and NF-IL6 in acute-phase response and viral infection. Immunol. Rev. 1992, 127, 25–50. [Google Scholar] [CrossRef]
- Tanaka, T.; Narazaki, M.; Kishimoto, T. IL-6 in inflammation, immunity, and disease. Cold Spring Harb. Perspect. Biol. 2014, 6, a016295. [Google Scholar] [CrossRef]
- Miller, J.P.; Mitchell, G. Cell to cell interaction in the immune response: I. Hemolysin-forming cells in neonatally thymectomized mice reconstituted with thymus or thoracic duct lymphocytes. J. Exp. Med. 1968, 128, 801–820. [Google Scholar] [CrossRef]
- Kopf, M.; Baumann, H.; Freer, G.; Freudenberg, M.; Lamers, M.; Kishimoto, T.; Zinkernagel, R.; Bluethmann, H.; Köhler, G. Impaired immune and acute-phase responses in interleukin-6-deficient mice. Nature 1994, 368, 339–342. [Google Scholar] [CrossRef] [PubMed]
- Chen, N.; Zhou, M.; Dong, X.; Qu, J.; Gong, F.; Han, Y.; Qiu, Y.; Wang, J.; Liu, Y.; Wei, Y.; et al. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: A descriptive study. Lancet 2020, 395, 507–513. [Google Scholar] [CrossRef] [Green Version]
- Wenjun, W.; Xiaoqing, L.; Sipei, W.; Puyi, L.; Liyan, H.; Yimin, L.; Linling, C.; Sibei, C.; Lingbo, N.; Yongping, L.; et al. The definition and risks of Cytokine Release Syndrome-Like in 11 COVID-19-Infected Pneumonia critically ill patients: Disease Characteristics and Retrospective Analysis. MedRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Mehta, P.; McAuley, D.F.; Brown, M.; Sanchez, E.; Tattersall, R.S.; Manson, J.J. COVID-19: Consider cytokine storm syndromes and immunosuppression. Lancet 2020, 395, 1033–1034. [Google Scholar] [CrossRef]
- Chen, L.; Liu, H.; Liu, W.; Liu, J.; Liu, K.; Shang, J.; Deng, Y.; Wei, S. Analysis of clinical features of 29 patients with 2019 novel coronavirus pneumonia. Zhonghua Jie He He Hu Xi Za Zhi = Zhonghua Jiehe He HUXI Zazhi= Chin. J. Tuberc. Respir. Dis. 2020, 43, E005. [Google Scholar]
- Chu, H.; Chan, J.F.W.; Wang, Y.; Yuen, T.T.T.; Chai, Y.; Hou, Y.; Shuai, H.; Yang, D.; Hu, B.; Huang, X.; et al. Comparative replication and immune activation profiles of SARS-CoV-2 and SARS-CoV in human lungs: An ex vivo study with implications for the pathogenesis of COVID-19. Clin. Infect. Dis. 2020, 71, 1400–1409. [Google Scholar] [CrossRef] [Green Version]
- Diao, B.; Wang, C.; Tan, Y.; Chen, X.; Liu, Y.; Ning, L.; Chen, L.; Li, M.; Liu, Y.; Wang, G.; et al. Reduction and functional exhaustion of T cells in patients with coronavirus disease 2019 (COVID-19). Front. Immunol. 2020, 11, 827. [Google Scholar] [CrossRef]
- Dong, L.; Tian, J.; He, S.; Zhu, C.; Wang, J.; Liu, C.; Yang, J. Possible vertical transmission of SARS-CoV-2 from an infected mother to her newborn. Jama 2020, 323, 1846–1848. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, P.; Liu, Y.; Qiu, L.; Liu, X.; Liu, D.; Li, J. Tocilizumab treatment in COVID-19: A single center experience. J. Med. Virol. 2020, 92, 814–818. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Xia, P.; Zhou, Y.; Liu, Z.; Zhou, X.; Wang, J.; Li, T.; Yan, X.; Chen, L.; Zhang, S.; et al. Potential effect of blood purification therapy in reducing cytokine storm as a late complication of critically ill COVID-19. Clin. Immunol. 2020, 214, 108408. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, S.F.; Ho, Y.C. SARS-CoV-2: A storm is raging. J. Clin. Investig. 2020, 130, 2202–2205. [Google Scholar] [CrossRef] [PubMed]
- Ruan, Q.; Yang, K.; Wang, W.; Jiang, L.; Song, J. Clinical predictors of mortality due to COVID-19 based on an analysis of data of 150 patients from Wuhan, China. Intensive Care Med. 2020, 46, 846–848. [Google Scholar] [CrossRef] [Green Version]
- Sun, D.; Li, H.; Lu, X.X.; Xiao, H.; Ren, J.; Zhang, F.R.; Liu, Z.S. Clinical features of severe pediatric patients with coronavirus disease 2019 in Wuhan: A single center’s observational study. World J. Pediatr. 2020, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.; Yang, B.; Li, Q.; Wen, L.; Zhang, R. Clinical features of 69 cases with coronavirus disease 2019 in Wuhan, China. Clin. Infect. Dis. 2020, 71, 769–777. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Chen, X.; Cai, Y.; Zhou, X.; Xu, S.; Huang, H.; Zhang, L.; Zhou, X.; Du, C.; Zhang, Y.; et al. Risk factors associated with acute respiratory distress syndrome and death in patients with coronavirus disease 2019 pneumonia in Wuhan, China. JAMA Intern. Med. 2020, 180, 934–943. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Shen, C.; Li, J.; Yuan, J.; Yang, M.; Wang, F.; Li, G.; Li, Y.; Xing, L.; Peng, L.; et al. Exuberant elevation of IP-10, MCP-3 and IL-1ra during SARS-CoV-2 infection is associated with disease severity and fatal outcome. MedRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Eagar, T.N.; Miller, S.D. 16 - Helper T-Cell Subsets and Control of the Inflammatory Response. In Clinical Immunology, 5th ed.; Rich, R.R., Fleisher, T.A., Shearer, W.T., Schroeder, H.W., Frew, A.J., Weyand, C.M., Eds.; Elsevier: London, UK, 2019; pp. 235–245.e1. [Google Scholar]
- Nezlin, R. The Immunoglobulins: Structure and Function; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Schroeder, H.W., Jr.; Cavacini, L. Structure and function of immunoglobulins. J. Allergy Clin. Immunol. 2010, 125, S41–S52. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McKaya, M.; Beckmana, R.; Conoverb, W. Comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Blower, S.M.; Hartel, D.; Dowlatabadi, H.; Anderson, R.M.; May, R.M. Drugs, sex and HIV: A mathematical model for New York City. In Philosophical Transactions of the Royal Society of London; Series B: Biological Sciences; Royal Society: London, UK, 1991; Volume 331, pp. 171–187. [Google Scholar]
- Wu, J.; Dhingra, R.; Gambhir, M.; Remais, J.V. Sensitivity analysis of infectious disease models: Methods, advances and their application. J. R. Soc. Interface 2013, 10, 20121018. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gomero, B. Latin Hypercube Sampling and Partial Rank Correlation Coefficient Analysis Applied to an Optimal Control Problem. Ph.D. Thesis, University of Tennessee, Knoxville, TN, USA, 2012. [Google Scholar]
- Sanchez, S.; Palacio, N.; Dangi, T.; Ciucci, T.; Penaloza-MacMaster, P. Limiting the priming dose of a SARS CoV-2 vaccine improves virus-specific immunity. bioRxiv 2021. [Google Scholar] [CrossRef]
- Geoffroy, F.; Traulsen, A.; Uecker, H. Vaccination strategies when vaccines are scarce: On conflicts between reducing the burden and avoiding the evolution of escape mutants. medRxiv 2021. [Google Scholar] [CrossRef]

| Variable | Definition |
|---|---|
| V | Vaccine cell |
| T | T helper type 0 cell (Th) |
| F | Interferon gamma () |
| I | Interleukin 6 () |
| B | Plasma B-cell |
| A | Antibody |
| C | Cytotoxic T-cell |
| Parameter | Definition | Value | Unit | Comment |
|---|---|---|---|---|
| Vaccine neutralizing rate by antibody molecules | 1 | day(a.u.) | Handle et al., 2018 | |
| Vaccine clearance rate | 0.2 | day | Cao et al., 2016 | |
| Th cells activation rate by vaccine particles | 0.035 | day | Chosen | |
| Th cells natural death rate | 0.055 | day | Cao et al., 2016 | |
| IFN stimulation rate by Th | 2.55 | day | Fitted | |
| IFN natural degradation rate | 0.13 | day | Fitted | |
| IFN absorption rate by CTL for mitotic signals | 0.006 | day(a.u.) | Fitted | |
| IL6 release rate by Th | 1.3 | day | Fitted | |
| IL6 natural degradation rate | 0.0008 | day | Chosen | |
| IL6 absorption rate by B-cells for mitotic signals | 0.0001 | day(a.u.) | Fitted | |
| B-cell activation rate by Th | 0.02 | day | Fitted | |
| B-cell stimulation rate by IL | 0.05 | day(a.u.) | Fitted | |
| B-cell duplication threshold due to IL | 1000 | a.u. | Chosen | |
| B-cell natural death rate | 0.06 | day | Fitted | |
| Released Ab rate by B-cells | 7 | day | Fitted | |
| Ab natural degradation rate | 0.06 | day | Fitted | |
| Ab - V cells binding rate | 1 | day(a.u.) | Chosen | |
| CTL activation rate by vaccine | 0.002 | day | Fitted | |
| CTL stimulation rate by IFN | 0.09 | day(a.u.) | Fitted | |
| CTL duplication threshold due to IFN | 600 | a.u. | Chosen | |
| CTL natural death rate | 0.01 | day | Wang et al., 2016 |
| Variable | Parameter | Absolute PRCC Value |
|---|---|---|
| A (Antibody) | ||
| ≈ | ||
| ≈ | ||
| ≈ | ||
| ≈ | ||
| ≈ | ||
| ≈ | ||
| C (CTL) | ||
| ≈ | ||
| ≈ | ||
| F (IFN) | ≈ | |
| ≈ | ||
| ≈ | ||
| ≈ | ||
| ≈ | ||
| ≈1 | ||
| T (Th) | ≈1 | |
| ≈ | ||
| Plasma B | ≈ | |
| ≈ | ||
| ≈ | ||
| ≈ | ||
| I (IL6) | ≈ | |
| ≈ | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farhang-Sardroodi, S.; Korosec, C.S.; Gholami, S.; Craig, M.; Moyles, I.R.; Ghaemi, M.S.; Ooi, H.K.; Heffernan, J.M. Analysis of Host Immunological Response of Adenovirus-Based COVID-19 Vaccines. Vaccines 2021, 9, 861. https://doi.org/10.3390/vaccines9080861
Farhang-Sardroodi S, Korosec CS, Gholami S, Craig M, Moyles IR, Ghaemi MS, Ooi HK, Heffernan JM. Analysis of Host Immunological Response of Adenovirus-Based COVID-19 Vaccines. Vaccines. 2021; 9(8):861. https://doi.org/10.3390/vaccines9080861
Chicago/Turabian StyleFarhang-Sardroodi, Suzan, Chapin S. Korosec, Samaneh Gholami, Morgan Craig, Iain R. Moyles, Mohammad Sajjad Ghaemi, Hsu Kiang Ooi, and Jane M. Heffernan. 2021. "Analysis of Host Immunological Response of Adenovirus-Based COVID-19 Vaccines" Vaccines 9, no. 8: 861. https://doi.org/10.3390/vaccines9080861
APA StyleFarhang-Sardroodi, S., Korosec, C. S., Gholami, S., Craig, M., Moyles, I. R., Ghaemi, M. S., Ooi, H. K., & Heffernan, J. M. (2021). Analysis of Host Immunological Response of Adenovirus-Based COVID-19 Vaccines. Vaccines, 9(8), 861. https://doi.org/10.3390/vaccines9080861





