Abstract
There is a growing public health need for effective preventive interventions against dengue, and a safe, effective and affordable dengue vaccine against the four serotypes would be a significant achievement for disease prevention and control. Two tetravalent dengue vaccines, Dengvaxia (CYD-TDV—Sanofi Pasteur) and DENVax (TAK 003—Takeda Pharmaceutical Company), have now completed phase 3 clinical trials. Although Dengvaxia resulted in serious adverse events and had to be restricted to individuals with prior dengue infections, DENVax has shown, at first glance, some encouraging results. Using the available data for the TAK 003 trial, we estimate, via the Bayesian approach, vaccine efficacy (VE) of the post-vaccination surveillance periods of 12 and 18 months. Although better measurement over a long time was expected for the second part of the post-vaccination surveillance, variation in serotype-specific efficacy needs careful consideration. Besides observing that individual serostatus prior to vaccination is determinant of DENVax vaccine efficacy, such as for Dengvaxia, we also noted, after comparing the VE estimations for 12- and 18-month periods, that vaccine efficacy is decreasing over time. The comparison of efficacies over time is informative and very important, and brings up the discussion of the role of temporary cross-immunity in dengue vaccine trials and the impact of serostatus prior to vaccination in the context of dengue fever epidemiology.
1. Introduction
Dengue fever is a viral mosquito-borne infection of major international public health concern, with approximately 3 billion people at risk of acquiring the infection. Caused by four antigenically related but distinct serotypes (DENV-1 to DENV-4), it is estimated that 390 million dengue infections occur every year, of which 96 million manifest symptoms with any level of disease severity [1]. Antibodies generated by exposure to any one type cross-react with other types, providing short duration cross-protective immunity. Subsequent infections by any other of the 3 heterotypic serotypes increases the risk of developing severe dengue due to an immunological process called antibody-dependent enhancement (ADE) [2,3,4,5]. Treatment of uncomplicated dengue cases is only supportive, and severe dengue cases require hospitalization. There is a compelling public health need for an effective preventive intervention against dengue. A safe, effective and affordable dengue vaccine against the four serotypes would be a significant achievement for disease prevention and control.
Two tetravalent dengue vaccines have now completed phase 3 clinical trials, and a third vaccine is currently in a phase 3 trial [6,7,8,9,10,11]. The first product, Dengvaxia (CYD-TDV), is a chimeric yellow fever tetravalent dengue vaccine developed by Sanofi Pasteur which resulted in a higher rate of hospitalized severe dengue cases when given to seronegative children, compared with age-matched seronegative controls [6,7,8]. The risks behind giving this vaccine have been discussed [12,13]. An age structured mathematical model was developed, based on Sanofi’s recommendation, and its analysis has shown a significant increase in the number of hospitalizations in a population when this vaccine was administered without population screening [14], i.e., given to both seropositive and seronegative individuals as previously suggested in [15]. Reviews in 2016–2017 identified individual serostatus prior to vaccination as determinants of Dengvaxia efficacy and adverse events [16,17], anticipating Sanofi Pasteur’s retest of the entire phase 3 serum collection announced in November 2017 [18,19]. Dengvaxia is licensed in more than 20 countries, although mass vaccination programs, initiated in the Philippines [20] and in the South of Brazil, are now suspended.
Based upon recent licensing statements (in 2019) by the E.U. and the US Food and Drug Administration (FDA), Dengvaxia administration is restricted to individuals with prior dengue infections. An issue that must be addressed is the availability of a screening test that will accurately identify dengue seropositives. This is a technical challenge, since ELISA IgG tests vary in specificity and sensitivity [21].
The second product, DENVax (TAK 003), a tetravalent chimeric vaccine developed by Takeda Pharmaceutical Company, consists of a live attenuated dengue 2 virus (DENV-2) that provides the genetic backbone for DENV 1, 3 and 4. A DENVax phase 3 trial consisting of fever-based surveillance of vaccine efficacy (VE) followed by a period of hospitalization surveillance has been completed. Case surveillance over the first 12 months after vaccination of Latin American and Asian children yielded initial encouraging results [9]. Vaccine efficacy against virologically confirmed dengue disease and hospitalization was higher and more balanced than efficacies reported for Dengvaxia [8]. DENVax achieved a and efficacy level [9] compared with Dengvaxia’s and efficacies in seronegative and seropositive children, respectively [8].
Vaccine efficacy data have now been extended to 18 months of surveillance [10] indicating that similarly to Dengvaxia, individual serostatus prior to vaccination is determinant of vaccine efficacy. Vaccine efficacy estimations for 12 and 18 months show that DENVax efficacy is decreasing over time and therefore, long-term surveillance consisting of prudent and careful observation of vaccine phase 3 recipients is required [20].
In this manuscript, DENVax vaccine efficacy for virologically confirmed dengue cases was estimated via a Bayesian approach. Vaccine efficacy measurements over time, six months apart, are compared and the variations observed in serotype-specific efficacies brings up the discussion of the role of temporary cross-immunity on dengue vaccine trials and the impact of serostatus prior to vaccination in the context of dengue fever epidemiology.
2. Results
Using the publicly available DENVax phase 3 trial raw data [9,10], we estimated the vaccine efficacy for virologically confirmed dengue cases via a Bayesian approach, shown in Table 1 and Table 2 for each post-vaccination surveillance period. We obtained the probability for the vaccine efficacy k with infected individuals in the vaccine group and infected individuals in the control group. The statistical description of the vaccine trial data was in good agreement with the published surveillance results as described below. For detailed calculations, see Section 4. From our Bayesian analysis, vaccine efficacy estimations by serotype and serostatus are shown in Table 1 part A, using data for the first 12-month surveillance period [9]. As expected, vaccine efficacy against serotype 2, the serotype that provides the genetic “backbone” for Takeda’s DENVax, was very high independent of the individual serostatus prior to vaccination. For seropositives and seronegatives respectively, our estimations were and , in good agreement with and reported by [9]. Please note that in the seronegative vaccinated group, no dengue 2 cases were observed, but in the seropositive group there were. Vaccine efficacy against serotype 1 was observed to be slightly smaller in seronegative (estimated as reported in [9]) than in seropositive individuals (estimated , in good agreement with reported in [9]). There was a negative vaccine efficacy estimated for serotype 3 in seronegative individuals (estimated and reported in [9]) against an intermediate vaccine efficacy in seropositives (estimated and reported in [9]), shown in Table 1 Section part A, in light blue color. Results for serotype 4 were shown to be statistically insignificant for seropositives (estimated with CI [–) and completely “inconclusive” for seronegatives, as no cases were observed in any of the groups, vaccinated or control (see Figure 1a). Figure 2, shows the vaccine efficacy changing in time.

Table 1.
Compilation of vaccine efficacies estimation for Takeda’s DENVax vaccine phase 3 trial post-vaccination surveillance period part 1 (12 months). Section A shows the vaccine efficacies by serostatus and serotype, and Section B shows the overall vaccine efficacy by serotype. Highlighting problems observed for serotypes 3 (blue) and 4 (grey) are indicated. The raw data used for the Bayesian analysis are available in [9].

Table 2.
Compilation of vaccine efficacies estimation for Takeda’s DENVax vaccine phase 3 trial post-vaccination surveillance period part 2 (18 months). Section A shows the vaccine efficacies by serostatus and serotype, and Section B shows the overall vaccine efficacy by serotype. Highlighting problems observed for serotypes 3 (blue) and 4 (grey) are indicated. The raw data used for the Bayesian analysis are available in [10].

Figure 1.
Bayesian estimate of DENVax vaccine efficacies (VE) against virologically confirmed dengue for the first 12-month surveillance (part 1). In (a) DEN3 serotype-specific vaccine efficacy by serostatus. Red and blue curves show our estimates for the seronegative and seropositive individuals, respectively. In (b) serotype-specific VE estimations. The raw data used to estimate the distribution by dengue serotype for individuals aged 4–16 years old was obtained in [9] and are shown in Table 1. High vaccine efficacy for dengue serotype 2 and intermediate to low vaccine efficacy for the other serotypes are observed.
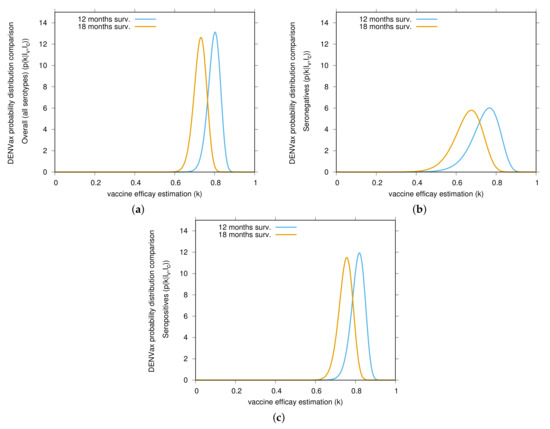
Figure 2.
Bayesian estimates comparison of DENVax vaccine efficacies (VE) against virologically confirmed dengue cases. Yellow and light blue curves show the estimates for the first 12 months (part 1) and the 18 months (part 2) surveillance, respectively. In (a) overall VE estimations for all serotypes, in (b) VE estimation for seronegative individuals and in (c) VE estimations for seropositive individuals. Data from Table 1 and Table 2, in good agreement with results reported in [9,10], are used to estimate the distribution by dengue serotype and serostatus for individuals aged 4–16 years old. Vaccine efficacy is decreasing over time.
Table 1 Section B presents, in yellow, the overall vaccine efficacy (not by serostatus, but by serotype only), with high efficacy for serotype 2 (estimated , in good agreement with reported in [9]) and intermediate efficacies for serotypes 1 (estimated , in good agreement with reported in [9]) and serotype 3 (estimated , in good agreement with reported in [9]). Results for serotype 4 were statistically insignificant due to small numbers (see Figure 1b).
Table 2 is also divided in “Section A”, presenting our estimations obtained by serotype and serostatus, and in “Section B”, showing the results stratified by serotype only.
A slight decrease in vaccine efficacies was observed for the second surveillance period, with the overall vaccine efficacy estimated to be of and the -CI [, ], instead of and the -CI [, ] estimated for the first surveillance period. Overall vaccine efficacy for specific dengue serotype 2 was estimated to be high, [, ], whereas vaccine efficacy for dengue serotype 1, [, ] and dengue serotype 3, [, ], were estimated to be much lower than the estimations obtained for the first 12 months of surveillance. Results for serotype 4 were still statistically insignificant, [, ], including negative vaccine efficacy. Figure 3b shows our Bayesian estimates of DENVax serotype-specific vaccine efficacy.

Figure 3.
Bayesian estimate of vaccine efficacies (VE) against virologically confirmed dengue. In (a) serotype-specific VE for Dengvaxia, Sanofi Pasteur. The raw data used for VE estimation by dengue serotype for individuals aged 9 years and older was obtained in [8]. In (b) serotype-specific VE for DENVax, Takeda. The raw data used to estimate the VE by dengue serotype for individuals aged 4–16 years old was obtained in [10] and are shown in Table 2.
Regarding the estimations obtained by serotype and serostatus, shown in Table 2 Section A, vaccine efficacy estimation was kept very high against DENV serotype 2, with and for seropositive and seronegative respectively. Vaccine efficacy against serotype 1 was observed to be slightly lower for seronegative, with [, ], than in seropositive individuals, with [, ]. Of concern, as shown in Table 2 section A, blue color, negative vaccine efficacy, [, ], was estimated for vaccinated seronegative individuals who were infected with serotype 3, as opposed to an intermediate efficacy, [, ] for seropositives. As with the other serotypes, DENV 3 efficacy declined over the following 6 months of surveillance data (see Figure 3b).
In Figure 2, we show the vaccine efficacy changing in time, decreasing from 12 to 18 months. The overall VE estimation is shown in Figure 2a. Changes in VE for seronegative individuals (see Figure 2b) and for seropositive individuals (see Figure 2c) as also shown. Although VE for seronegative individuals are lower, as also observed for Dengvaxia, the trend of VE lowering over time is also observed for seropositive individuals. Vaccine efficacy estimations for serotype 4 were kept statistically insignificant during the 18 months of surveillance. The small number of cases contained a suggestion of negative vaccine efficacy for vaccinated seropositive children. The possibility exists that efficacy against DENV 4 may follow the pattern of serotype 3 as case numbers increase.
Curiously, for both trials combined, the Asian-Pacific and the Latin American, Sanofi Pasteur’s Dengvaxia produced higher vaccine efficacies against serotypes 3 and 4 (over , see Figure 3a) than to serotypes 1 and 2 (around ) [22] while the pattern of Takeda DENVax efficacy has been the opposite, high overall vaccine efficacies for serotypes 1 and 2 and moderate to low vaccine efficacy for serotypes 3 and 4 (see Figure 3b)).
3. Discussion
DENVax vaccine efficacy against virologically confirmed dengue disease and hospitalization were shown to be higher than efficacies reported for the Sanofi Pasteur tetravalent dengue vaccine, Dengvaxia, with a more balanced efficacy in seronegatives and seropositives. Although Takeda’s DENVax vaccine efficacy was estimated to be of for participants who were seronegative and for participants who were seropositive at baseline (see Table 1, Section B), the Sanofi Pasteur’s Dengvaxia has shown a and vaccine efficacies in seronegative and seropositive individuals respectively [8]. Although more investigation is needed to identify the reason for DENVax presenting a more balanced VE by serotype than Dengvaxia, it is important to acknowledge that the trial design for the Takeda’ vaccine has enabled an immediate and detailed assessment of vaccine efficacy of subgroups.
Using the new DENVax phase 3 trial data, vaccine efficacy measurements over time, six months apart, are compared. Significant variations in vaccine efficacy are observed, with estimations decreasing over time in serotype-specific analysis. It is important to note that these results obtained within 12–18 months post-vaccination periods are still within the well-established period of cross-protective immunity against clinical disease that follows a first dengue infection [23,24]. This trend suggests that early DENVax protective efficacy may be attributed to cross-protection and therefore may continue to decline over time.
Of concern, negative vaccine efficacy was estimated for vaccinated seronegative individuals who were infected with serotype 3, as opposed to an intermediate efficacy for seropositives. The possibility exists that efficacy against DENV 4 may follow the pattern of serotype 3 as case numbers increase, therefore, efficacy and safety conclusions require long-term surveillance.
Variations in serotype-specific efficacies of DENVax are concerning when it is recalled that for Dengvaxia high rates of hospitalization of vaccinated young children, mis-interpreted as vaccine failure, were resolved long after the vaccine was widely licensed and administered in millions of children. For Dengvaxia, initial low vaccine efficacy was shown to include vaccine adverse events and a significant incidence of hospitalization for severe dengue in vaccinated seronegative children. With respect to DENVax we urge the vaccine community to adopt the stance of “watch and wait” because VE is not a static measure but appears to be time dependent due to, for example, temporary cross-protection. Final conclusions can only be drawn after some year of evaluation. It is too soon to understand the behavior of this vaccine in individuals of differing immunological serostatus or age.
Besides observing that individual serostatus prior to vaccination is determinant of DENVax vaccine efficacy, we also noted that the DENVax efficacy is decreasing over time. The comparison of efficacies over time is informative and very important since it brings up the discussion of the role of temporary cross-immunity on dengue vaccine trials and the impact of serostatus prior to vaccination in the context of dengue fever epidemiology.
With respect to DENVax, long-term surveillance consisting of prudent and careful observation of vaccine phase 3 recipients is required. Careful design of vaccine policies is urgently needed and recommendations concerning the use of dengue vaccines should consider a better measurement of vaccine efficacy over time and safety through enhanced phase 4 surveillance.
4. Materials and Methods
Vaccine trials can be modeled using a previously investigated simple epidemiological process, the linear infection model [25], which can be solved analytically in all aspects, and thus serve as a test model for many further aspects, like parameter estimation, model comparison, or analytics of approximation schemes. [26,27,28].
In this section, we describe the methodology used to estimate DENVax vaccine efficacy via a Bayesian approach, using the data from Takeda’s dengue vaccine trial in Latin America and Asia [9,10].
4.1. Linear Infection Model
The basic assumptions for modeling a vaccine trial are exactly the ones described by the linear infection model, which has the following reaction scheme
for infected I and susceptibles , with population size N, and infection rate as the only possible transition. The underlying model hypothesis is that infection can be acquired from outside the considered trial population of size N by meeting a constant number of infected individuals from a much larger background population. The master equation for the probability is
which can be solved using the characteristic function
with as the external infection level, and initial condition , as described in more detail in [26]. The solution of the master equation is given by
Due to the special initial conditions of having exactly infected at time this solution is at the same time the transition probability , needed to construct the likelihood function for parameter estimation of data vector . See [26] for further discussion on this point.
4.2. Modeling Vaccine Trials with the Linear Infection Model
For modeling a vaccine trial, we have the special case of one data point each for the processes of the “control group” and the “vaccine group”. For the control group we have the scheme
and with initially participants in the control group, we have after a time interval (here respectively 18 months for the DENVax vaccine trial [9,10]) the solution of the process given by the probability of having disease cases in the control group
with parameter incorporating the effects of external infection levels over the time period T. The parameter is also the probability not to become infected over the considered time interval. For parameter estimation purposes, the solution of the master equation is also the likelihood of the single model parameter of the control group process, hence , with the last notation as used in the Bayesian statistical framework [25,26,27].
For the vaccine group we have the same epidemiological process, but with (hopefully) reduced infectivity instead of , or with vaccine efficacy ,
and solution for participants in the vaccine group to find infected still (despite the vaccination effort)
now with parameter . The master equation solution is now again to be interpreted as a likelihood function or in terms of the already estimated we have as well . Hence we must estimate the parameter of external infection level from the data of the control group, and then estimate the vaccine efficacy k from the information of the vaccine group. Via the Bayesian approach we obtain explicitly a probability for the vaccine efficacy based on the empirical data from the vaccine trial, , where insecurity of the intermediate parameter of external infection level is taken into account by marginalizing over this parameter.
Previously, we have given from the linear infection model the statistical description of the vaccine trial data via the Bayesian approach in very good agreement with the results in [9,10].
5. Bayesian Analysis
From the above-mentioned likelihood functions we can immediately calculate posterior distributions for the parameters given the data, once the priors for the parameters are chosen. For details especially concerning the linear infection model see [25], and then also [26,27].
In detail, from the likelihood function of for the control group of the vaccine trial which has the form of a beta-distribution, we can obtain the posterior distribution by using for the prior a conjugate form of a beta-distribution with parameters a and b as
with a normalization constant, also called “evidence” in the context of model comparison [27] and further references cited there, . Then the prior can be given as
with parameters a and b to be chosen to be much smaller than the respective exponents in the likelihood function.
We chose giving a dish shaped distribution with lowest values around , hence in no way resembling any one-humped distribution as expected for the posterior. After some calculations, see [25] for any details, we obtain the posterior distribution, the probability density to find the background infection level conditioned on the control group outcome data, as
with and as data dependent parameters. Please note that another constant is used in likelihood maximization and cancels out in the Bayesian approach [28].
To calculate the finally sought quantity we also need to obtain from the likelihood for the vaccine group the Bayesian posterior with
with as defined above. Again, after some calculations using the conjugate prior
being as uninformed as possible by choosing again, we obtain the result
with and as defined above.
However, to calculate the finally sought , using the previously calculated posteriors and , we need to integrate over the parameter whose insecurity has not been taken into account by our considerations up to now. Hence we calculate as the marginal probability distribution of the joint probability distribution , namely
with the final result plotted in Figure 1, and its cumulative distribution function in order to read off the confidence intervals around the median as the best estimator in the Bayesian approach.
From the data which generates Figure 1a for example (the others follow accordingly), we obtain from the median of the marginalized posterior the Bayesian estimate of the vaccine efficacy for overall seropositives and the -confidence interval from the 0.025 and 0.975 quantiles, hence for the lower bound and for the upper bound . This is in good agreement with the values given in [9] (with xx% (95%-CI: xx–xx)), given the somewhat arbitrary Bayesian priors with their parameters a, b, and .
In total we have given from the linear infection model the statistical description of the vaccine trial data via the Bayesian approach in very good agreement with the results in [9,10] and in addition the graphical representation of the posteriors and Figure 1, Figure 2 and Figure 3, indicating where the bulks of the probabilities are concentrated.
Author Contributions
Conceptualization, M.A.; Formal analysis, M.A. and N.S.; Funding acquisition, M.A.; Investigation, M.A.; Methodology, M.A. and N.S.; Writing—original draft, M.A. and N.S.; Writing—review & editing, M.A. and N.S. All authors have read and agreed to the published version of the manuscript.
Funding
Maíra Aguiar has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 792494.
Acknowledgments
We thank Scott B. Halstead for fruitful discussions during the writing of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Bhatt, S.; Gething, P.W.; Brady, O.J.; Messina, J.P.; Farlow, A.W.; Moyes, C.L.; Drake, J.M.; Brownstein, J.S.; Hoen, A.G.; Sankoh, O.; et al. The global distribution and burden of dengue. Nature 2013, 496, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Halstead, S.B. Antibody-dependent Enhancement of Infection: A Mechanism for Indirect Virus Entry into Cells. In Cellular Receptors for Animal Viruses; Cold Spring Harbor Laboratory Press: New York, NY, USA, 1994; Chapter 25; pp. 493–516. ISBN 0-87969-429-7. [Google Scholar]
- Dejnirattisai, W.; Jumnainsong, A.; Onsirisakul, N.; Fitton, P.; Vasanawathana, S.; Limpitikul, W.; Puttikhunt, C.; Edwards, C.; Duangchinda, T.; Supasa, S.; et al. Cross-Reacting Antibodies Enhance Dengue Virus Infection in Humans. Science 2010, 328, 745–748. [Google Scholar] [CrossRef] [PubMed]
- Halstead, S.B. Dengue antibody-dependent enhancement: Knowns and unknowns. Microbiol. Spectrum. 2014, 2, AID-0022-2014. [Google Scholar]
- Katzelnick, L.C.; Gresh, L.; Halloran, M.E.; Mercado, J.C.; Kuan, G.; Gordon, A.; Balmaseda, A.; Harris, E. Antibody-dependent enhancement of severe dengue disease in humans. Science 2017, 358, 929–932. [Google Scholar] [CrossRef] [PubMed]
- Capeding, M.R.; Tran, N.H.; Hadinegoro, R.S.; MuhammadIsmail, H.I.H.J.; Chotpitayasunondh, T.; Chua, M.N.; Luong, C.Q.; Rusmil, K.; Wirawan, D.N.; Nallusamy, R.; et al. Clinical efficacy and safety of a novel tetravalent dengue vaccine in healthy children in Asia: A phase 3, randomised, observer-masked, placebo-controlled trial. Lancet 2014, 384, 1358–1365. [Google Scholar] [CrossRef]
- Villar, L.; Dayan, G.H.; Arredondo-García, J.L.; Rivera, D.M.; Cunha, R.; Deseda, C.; Reynales, H.; Costa, M.S.; Morales-Ramírez, J.O.; Carrasquilla, G.; et al. Efficacy of a tetravalent dengue vaccine in children in Latin America. N. Engl. J. Med. 2015, 372, 113–123. [Google Scholar] [CrossRef]
- Hadinegoro, S.R.; Arredondo-García, J.L.; Capeding, M.R.; Deseda, C.; Chotpitayasunondh, T.; Dietze, R.; Ismail, H.I.H.M.; Reynales, H.; Limkittikul, K.; Rivera-Medina, D.M.; et al. Efficacy and long term safety of a dengue vaccine in regions of endemic disease. N. Engl. J. Med. 2015, 373, 1195–1206. [Google Scholar] [CrossRef]
- Biswal, S.; Reynales, H.; Saez-Llorens, X.; Lopez, P.; Borja-Tabora, C.; Kosalaraksa, P.; Sirivichayakul, C.; Watanaveeradej, V.; Rivera, L.; Espinoza, F.; et al. Efficacy of a Tetravalent Dengue Vaccine in Healthy Children and Adolescents. N. Engl. J. Med. 2019, 381, 2009–2019. [Google Scholar] [CrossRef]
- Biswal, S.; Borja-Tabora, C.; Martinez Vargas, L.; Velásquez, H.; Alera, M.T.; Sierr, V.; Rodriguez-Arenales, E.J.; Yu, D.; Wickramasinghe, V.P.; Moreira, E.D., Jr.; et al. Efficacy of a tetravalent dengue vaccine in healthy children aged 4–16 years: A randomised, placebo-controlled, phase 3 trial. Lancet 2020, 395, 1423–1433. [Google Scholar] [CrossRef]
- Kallas, E.G.; Precioso, A.R.; Palacio, R.; Thomé, B.; Braga, P.E.; Vanni, T.; Campos, L.M.A.; Ferrari, L.; Mondini, G.; Salomão, M.D.; et al. Safety and immunogenicity of the tetravalent, live-attenuated dengue vaccine Butantan-DV in adults in Brazil: A two-step, double-blind, randomised placebo-controlled phase 2 trial. Lancet Infect. Dis. 2020, 20, 839–850. [Google Scholar] [CrossRef]
- Aguiar, M.; Stollenwerk, N.; Halstead, S.B. The risks behind Dengvaxia recommendation. Lancet Infect. Dis. 2016, 16, 882–883. [Google Scholar] [CrossRef]
- Halstead, S.B.; Russell, P.K. Protective and Immunological Behavior of Yellow Fever Dengue Chimeric Vaccine. Vaccine 2016, 34, 1643–1647. [Google Scholar] [CrossRef] [PubMed]
- Aguiar, M.; Stollenwerk, N.; Halstead, S.B. The impact of the newly licensed dengue vaccine in endemic countries. PLoS Negl. Trop. Dis. 2016, 10, e0005179. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization Strategic Advisory Group of Experts (SAGE) on Immunization. Background Paper on Dengue Vaccines Prepared by the SAGE Working Group on Dengue Vaccines and the WHO Secretariat. 2016. Available online: http://www.who.int/immunization/sage/meetings/2016/april/1_Background_Paper_Dengue_Vaccines_2016_03_17.pdf? (accessed on 2 April 2016).
- Aguiar, M.; Stollenwerk, N. Dengvaxia efficacy dependency on serostatus: A closer look at more recent data. Clin. Infect. Dis. 2018, 66, 641–642. [Google Scholar] [CrossRef] [PubMed]
- Aguiar, M.; Stollenwerk, N. Dengvaxia: Age as surrogate for serostatus. Lancet Infect. Dis. 2018, 18, 245. [Google Scholar] [CrossRef]
- Sanofi Updates Information on Dengue Vaccine. Available online: https://www.sanofi.com/en/media-room/press-releases/2017/2017-11-29-17-36-30 (accessed on 29 November 2017).
- World Health Organization. Revised SAGE Recommendation on Use of Dengue Vaccine. 2018. Available online: https://www.who.int/immunization/diseases/dengue/revised_SAGE_recommendations_dengue_vaccines_apr2018/en/ (accessed on 19 April 2018).
- Halstead, S.B.; Katzelnick, L.C.; Russell, P.K.; Markoff, L.; Aguiar, M.; Dans, L.R.; Dans, A.L. Ethics of a partially effective dengue vaccine: Lessons from the Philippines. Vaccine 2020, 38, 5572–5576. [Google Scholar] [CrossRef]
- Aguiar, M. Dengue vaccination: A more ethical approach is needed. Lancet 2018, 391, 1769–1770. [Google Scholar] [CrossRef]
- Aguiar, M.; Mateus, L.; Stollenwerk, N. The currently best estimate for worldwide dengue vaccine efficacy. AIP Conf. Proc. 2016, 1738, 390014. [Google Scholar]
- Sabin, A.B. Research on dengue during World War II. Am. J. Trop. Med. Hyg. 1952, 1, 30–50. [Google Scholar] [CrossRef]
- Anderson, K.B.; Gibbons, R.V.; Cummings, D.A.; Nisalak, A.; Green, S.; Libraty, D.H.; Jarman, R.G.; Srikiatkhachorn, A.; Mammen, M.P.; Darunee, B.; et al. A Shorter Time Interval Between First and Second Dengue Infections Is Associated With Protection From Clinical Illness in a School-based Cohort in Thailand. J. Infect. Dis. 2013, 209, 360–368. [Google Scholar] [CrossRef]
- Stollenwerk, N.; Jansen, V. Population Biology and Criticality: From Critical Birth—Death Processes to Self-Organized Criticality in Mutation Pathogen Systems; Imperial College Press; World Scientific: London, UK, 2011. [Google Scholar]
- Stollenwerk, N.; Aguiar, M.; Ballesteros, S.; Boto, J.; Kooi, B.; Mateus, L. Dynamic noise, chaos and parameter estimation in population biology. R. Soc. Interface Focus 2012, 2, 156–169. [Google Scholar] [CrossRef] [PubMed]
- Mateus, L.; Stollenwerk, N.; Zambrini, J.C. Stochastic Models in Population Biology: From Dynamic Noise to Bayesian Description and Model Comparison for Given Data Sets. Int. J. Comput. Math. 2013, 90, 2161–2173. [Google Scholar] [CrossRef]
- Mateus, L.; Masoero, D.; Rocha, F.; Aguiar, M.; Skwara, U.; Ghaffari, P.; Zambrini, J.C.; Stollenwerk, N. Epidemiological models in semiclassical approximation: An analytically solvable model as test case. In Proceedings of the 14th International Conference on Computational and Mathematical Methods in Science and Engineering, CMMSE 2014, Cadiz, Spain, 3–7 July 2014; ISBN 978-84-616-9216-3. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).