Unexpected Infection Spikes in a Model of Respiratory Syncytial Virus Vaccination
Abstract
:1. Introduction
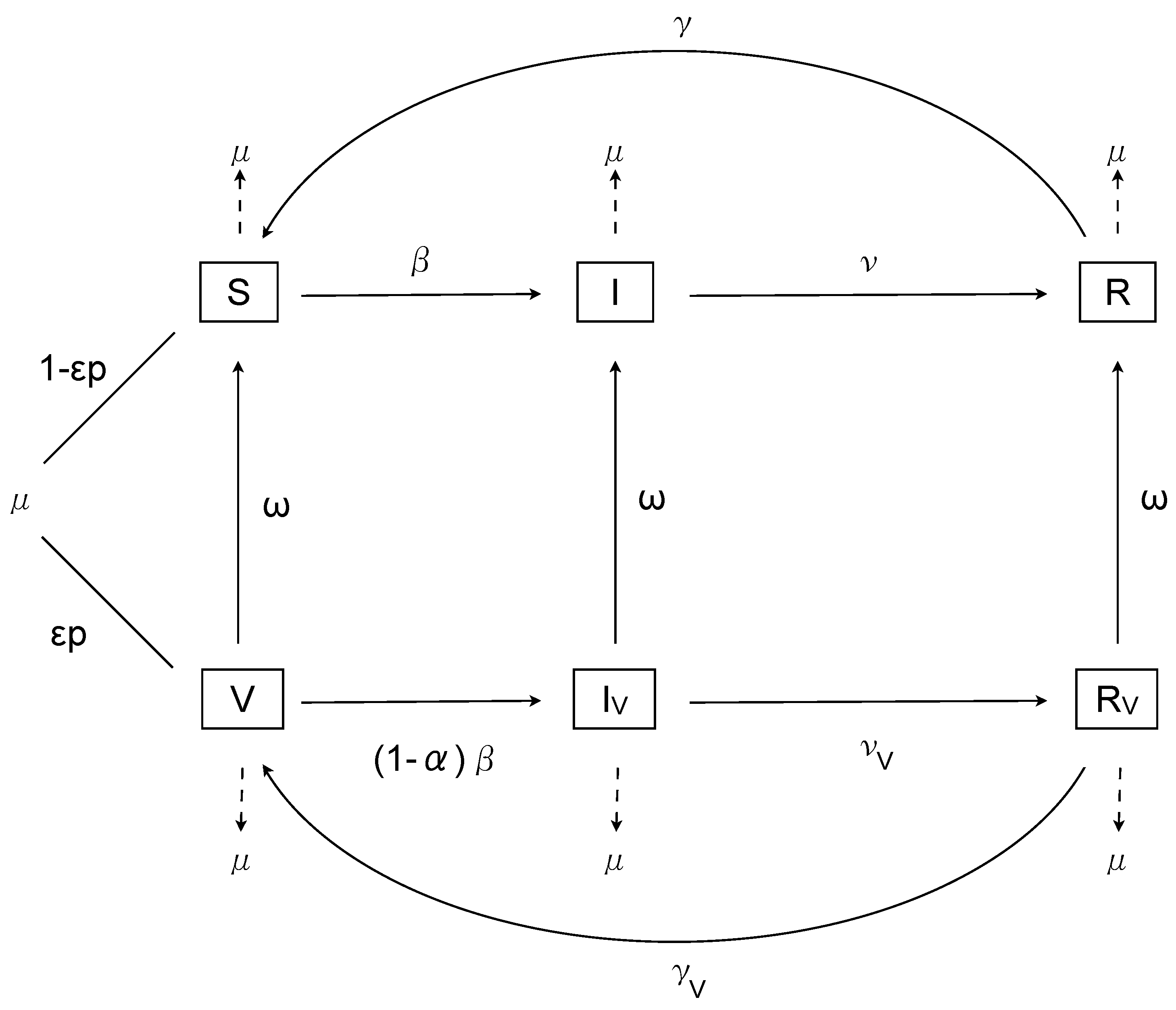
2. The Nonimpulsive Model
3. Analysis
Constant Transmission
- and
- is a local minimum.
4. The Impulsive Model
4.1. Impulsive Analysis
4.2. Susceptible Individuals
4.3. Vaccinated Individuals
4.4. Infected Individuals
5. Numerical Simulations
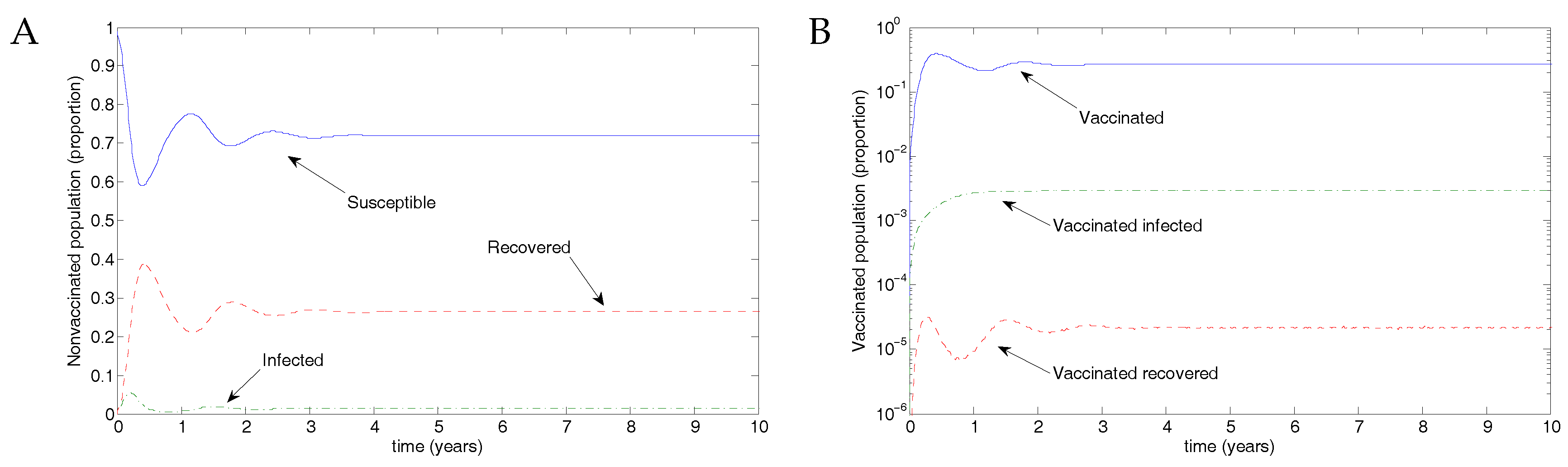
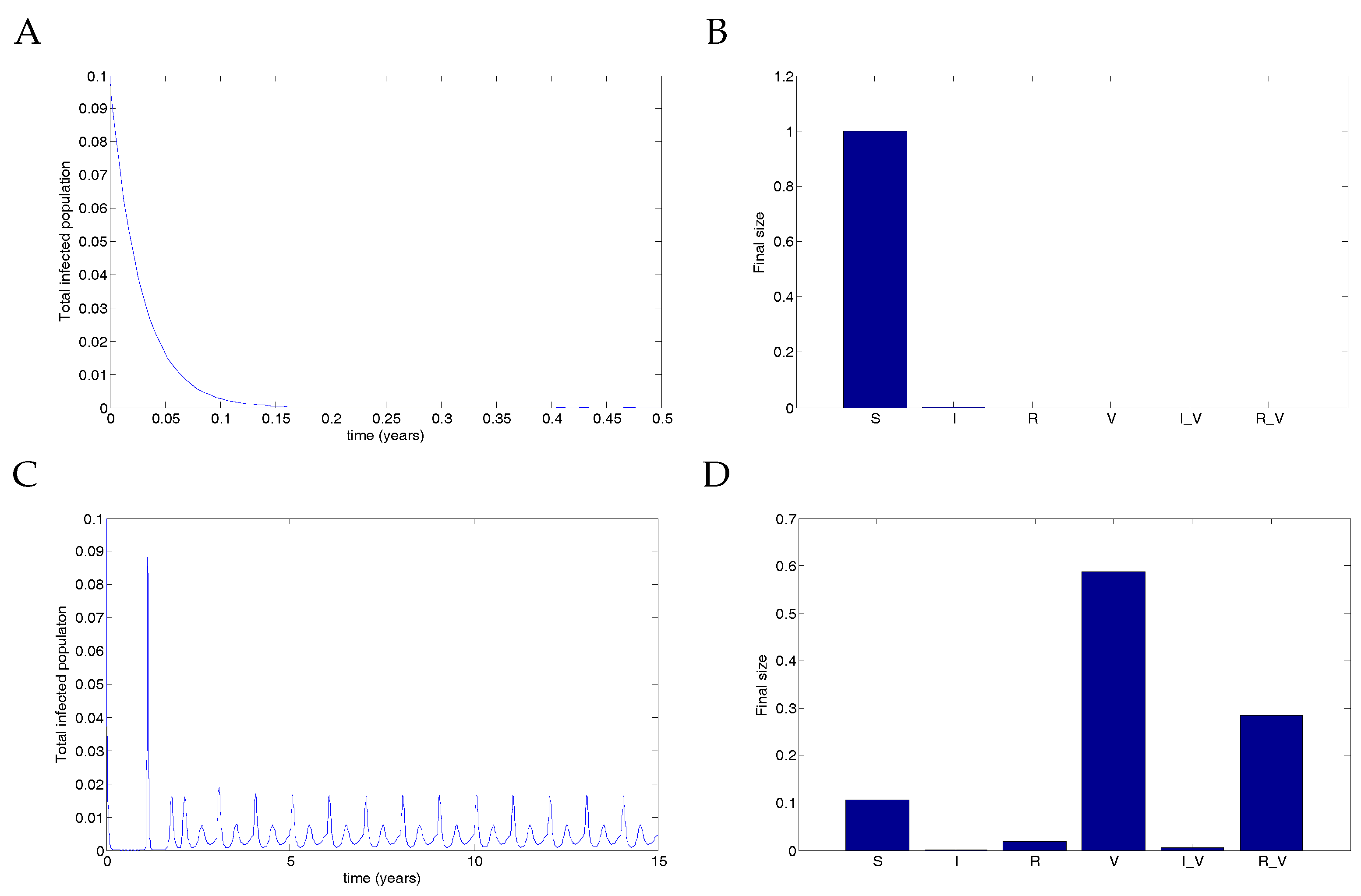
5.1. The Nonimpulsive Model
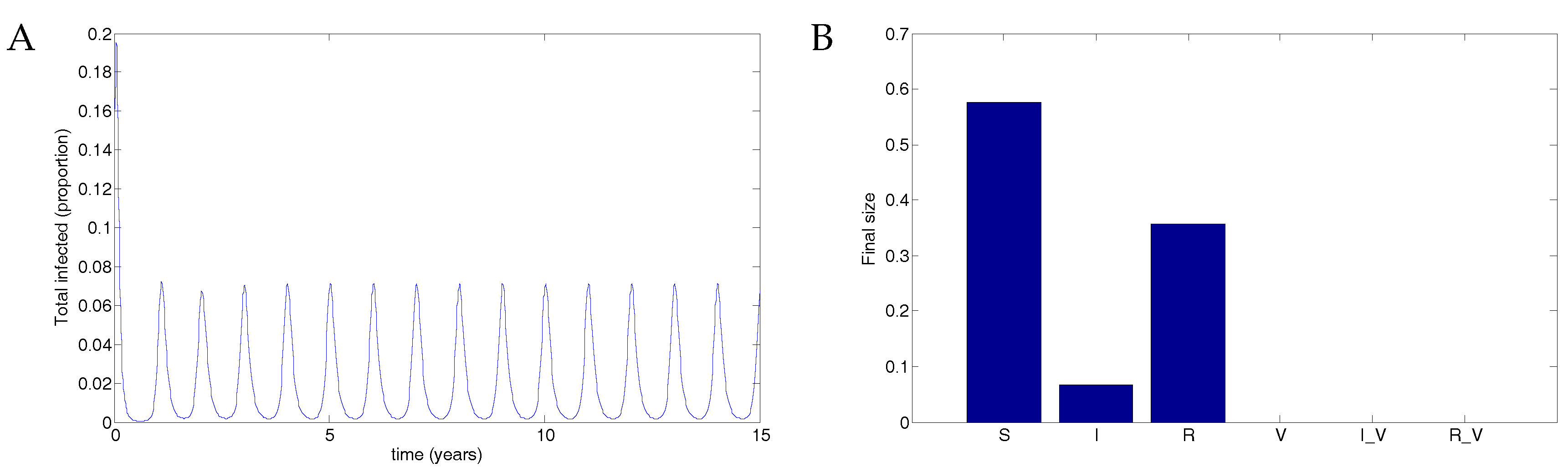
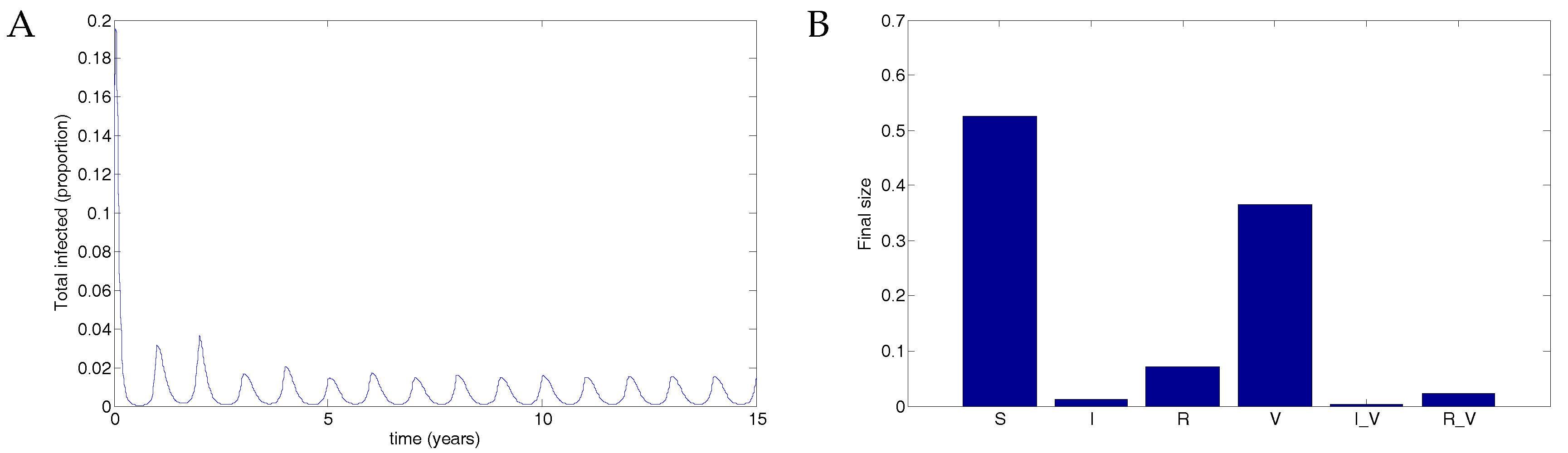
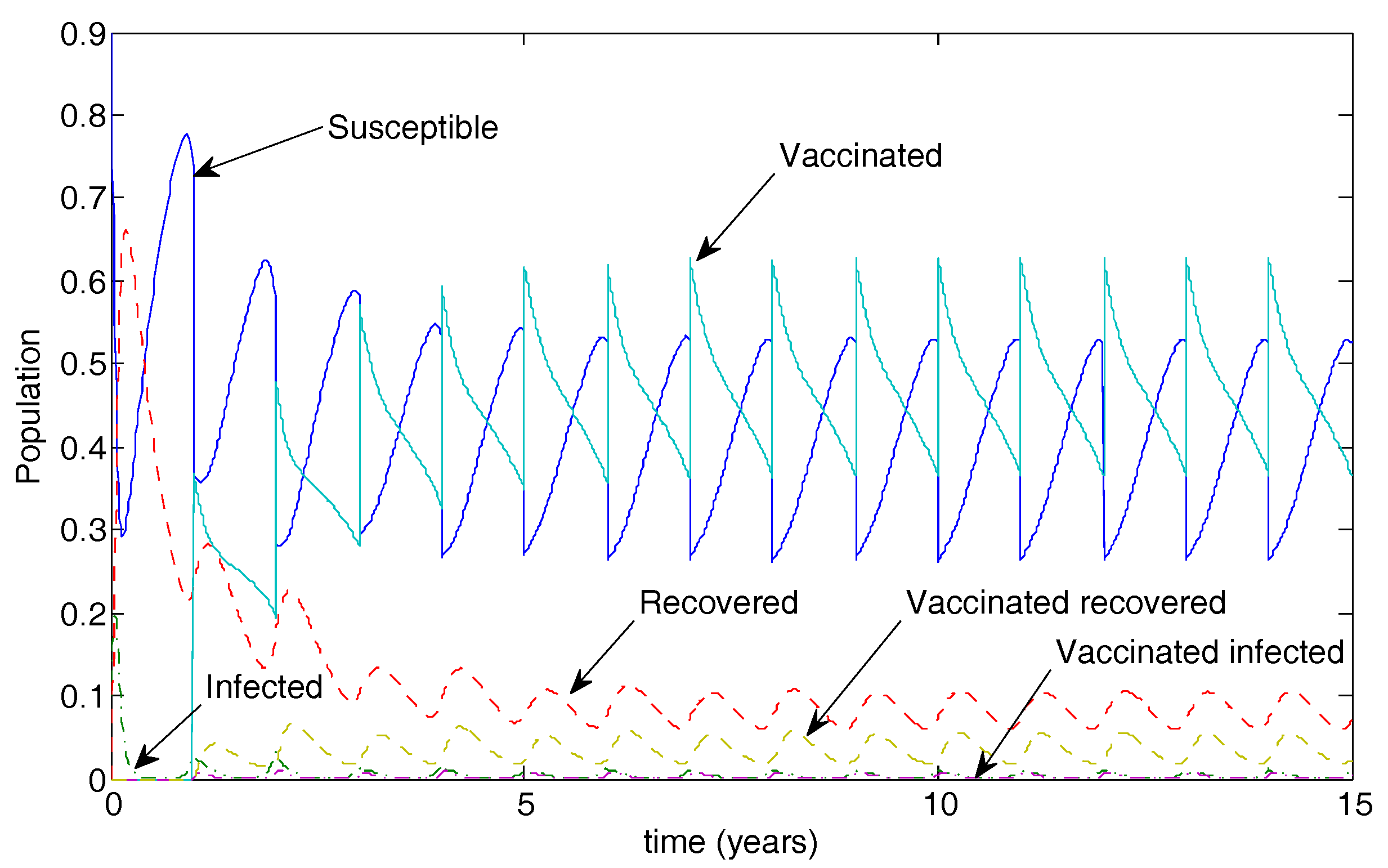
5.2. The Impulsive Model
6. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nair, H.; Nokes, D.J.; Gessner, B.D.; Dherani, M.; Madhi, S.A.; Singleton, R.J.; O’Brien, K.L.; Roca, A.; Wright, P.F.; Bruce, N.; et al. Global burden of acute lower respiratory infections due to respiratory syncytial virus in young children: A systematic review and meta-analysis. Lancet 2010, 375, 1545–1555. [Google Scholar] [CrossRef]
- Hall, C.B. Respiratory syncytial virus. In Textbook of Paediatric Infectious Diseases, 1st ed.; Feigin, R.D., Cherry, J.D., Eds.; W. B. Saunders Company: Philadelphia, PA, USA; London, UK, 1981; Chapter 28—Viral; Volume II, pp. 1247–1267. [Google Scholar]
- Sorce, L.R. Respiratory syncytial virus: from primary care to critical care. J. Pediatr. Health Care 2009, 23, 101–108. [Google Scholar] [CrossRef] [PubMed]
- McNamara, P.S.; Smyth, R.L. The pathogenesis of respiratory syncytial virus disease in childhood. Br. Med. Bull. 2002, 61, 13–28. [Google Scholar] [CrossRef] [PubMed]
- Wang, E.E.; Law, B.J. Respiratory syncytial virus infection in pediatric patients. Semin. Pediatr. Infect. Dis. 1998, 9, 146–153. [Google Scholar] [CrossRef]
- Weber, M.W.; Mulholland, E.K.; Greenwood, B.M. Respiratory syncytial virus infection in tropical and developing countries. Trop. Med. Int. Health 1998, 3, 268–280. [Google Scholar] [CrossRef] [PubMed]
- Haynes, L.M. Progress and Challenges in RSV Prophylaxis and Vaccine Development. J. Infect. Dis. 2013, 208 (Suppl. 3), S177–S183. [Google Scholar] [CrossRef] [PubMed]
- Yorita, K.L.; Holman, R.C.; Steiner, C.A.; Effler, P.V.; Miyamura, J.; Forbes, S.; Anderson, L.J.; Balaraman, V. Severe bronchiolitis and respiratory syncytial virus among young children in Hawaii. Pediatr. Infect. Dis. J. 2007, 26, 1081–1088. [Google Scholar] [CrossRef] [PubMed]
- Tregoning, J.S.; Schwarze, J. Respiratory viral infections in infants: Causes, clinical symptoms, virology, and immunology. Clin. Microbiol. Rev. 2010, 23, 74–98. [Google Scholar] [CrossRef] [PubMed]
- Domachowske, J.B.; Rosenberg, H.F. Respiratory Syncytial Virus Infection: Immune Response, Immunopathogenesis, and Treatment. Clin. Microbiol. Rev. 1999, 12, 298–309. [Google Scholar] [PubMed]
- Sullender, W.M. Respiratory syncytial virus genetic and antigenic diversity. Clin. Microbiol. Rev. 2000, 13, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Brandenburg, A.H.; Groen, J.; van Steensel-Moll, H.A.; Claas, E.C.; Rothbarth, P.H.; Neijens, H.J.; Osterhaus, A.D. Respiratory syncytial virus specific serum antibodies in infants under six months of age: Limited serological response upon infection. J. Med. Virol. 1997, 52, 97–104. [Google Scholar] [CrossRef]
- Meng, J.; Stobart, C.C.; Hotard, A.L.; Moore, M.L. An overview of respiratory syncytial virus. PLoS Pathog. 2014, 10, e1004016. [Google Scholar] [CrossRef] [PubMed]
- Cane, P.A. Molecular epidemiology of respiratory syncytial virus. Rev. Med. Virol. 2001, 11, 103–116. [Google Scholar] [CrossRef] [PubMed]
- Henderson, F.W.; Collier, A.M.; Clyde, W.A., Jr.; Denny, F.W. Respiratory-Syncytial-Virus Infections, Reinfection and Immunity: A Prospective, Longitudinal Study in Young Children. N. Engl. J. Med. 1979, 300, 530–534. [Google Scholar] [CrossRef] [PubMed]
- La Via, W.; Marks, M.; Stutman, H. Respiratory syncytial virus puzzle: Clinical features, pathophysiology, treatment, and prevention. J. Pediatr. 1992, 121, 503–510. [Google Scholar] [CrossRef]
- Hardelid, P.; Pebody, R.; Andrews, N. Mortality caused by influenza and respiratory syncytial virus by age group in England and Wales 1999–2010. Influenza Respir. Viruses 2013, 7, 35–45. [Google Scholar] [CrossRef] [PubMed]
- Van Asten, L.; van den Wijngaard, C.; van Pelt, W.; van de Kassteele, J.; Meijer, A.; van der Hoek, W.; Kretzschmar, M.; Koopmans, M. Mortality attributable to 9 common infections: Significant effect of influenza A, respiratory syncytial virus, influenza B, norovirus, and parainfluenza in elderly persons. J. Infect. Dis. 2012, 206, 628–639. [Google Scholar] [CrossRef] [PubMed]
- Han, L.L.; Alexander, J.P.; Anderson, L.J. Respiratory syncytial virus pneumonia among the elderly: An assessment of disease burden. J. Infect. Dis. 1999, 179, 25–30. [Google Scholar] [CrossRef] [PubMed]
- Hall, C.B. Respiratory syncytial virus and parainfluenza virus. N. Engl. J. Med. 2001, 344, 1917–1928. [Google Scholar] [CrossRef] [PubMed]
- Panozzo, C.A.; Fowlkes, A.L.; Anderson, L.J. Variation in timing of respiratory syncytial virus outbreaks: Lessons from national surveillance. Pediatr. Infect. Dis. J. 2007, 26 (Suppl. 11), S41–S45. [Google Scholar] [CrossRef] [PubMed]
- Avendano, L.F.; Ange, M.; Larran, C. Surveillance for Respiratory Syncytial Virus in Infants Hospitalized for Acute Lower Respiratory Infection in Chile (1989 to 2000). J. Clin. Microbiol. 2003, 41, 4879–4882. [Google Scholar] [CrossRef] [PubMed]
- Mlinaric-Galinovic, G.; Welliver, R.C.; Vilibic-Cavlek, T.; Ljubin-Sternak, S.; Drazenovic, V.; Galinovic, I.; Tomic, V. The biennial cycle of respiratory syncytial virus outbreaks in Croatia. Virol. J. 2008, 5, 18. [Google Scholar] [CrossRef] [PubMed]
- Terletskaia-Ladwig, E.; Enders, G.; Schalasta, G.; Enders, M. Defining the timing of respiratory syncytial virus (RSV) outbreaks: An epidemiological study. BMC Infect. Dis. 2005, 5. [Google Scholar] [CrossRef] [PubMed]
- Stensballe, L.G.; Devasundaram, J.K.; Simoes, E.A.F. Respiratory syncytial virus epidemics: The ups and downs of a seasonal virus. Pediatr. Infect. Dis. J. 2003, 22, S21–S32. [Google Scholar] [CrossRef] [PubMed]
- The IMpact-RSV Study Group. Palivizumab, a Humanized Respiratory Syncytial Virus Monoclonal Antibody, Reduces Hospitalization From Respiratory Syncytial Virus Infection in High-Risk Infants. Pediatrics 1998, 102, 531–537. [Google Scholar]
- Polack, F.P. The changing landscape of respiratory syncytial virus. Vaccine 2015, 33, 6473–6478. [Google Scholar] [CrossRef] [PubMed]
- Roberts, J.N.; Graham, B.S.; Karron, R.A.; Munoz, F.M.; Falsey, A.R.; Anderson, L.J.; Marshall, V.; Kim, S.; Beeler, J.A. Challenges and opportunities in RSV vaccine development: meeting report from FDA/NIH workshop. Vaccine 2016, 34, 4843–4849. [Google Scholar] [CrossRef] [PubMed]
- RSV Vaccine and mAb Snapshot. Available online: http://www.path.org/vaccineresources/files/RSV-snapshot-December2016.pdf (accessed on 13 January 2017).
- Weber, A.; Weber, M.; Milligan, P. Modeling epidemics caused by respiratory syncytial virus (RSV). Math. Biosci. 2001, 172, 95–113. [Google Scholar] [CrossRef]
- Leecaster, M.; Gesteland, P.; Greene, T.; Walton, N.; Gundlapalli, A.; Rolfs, R.; Byington, C.; Samore, M. Modeling the variations in pediatric respiratory syncytial virus seasonal epidemics. BMC Infect. Dis. 2011, 11, 105. [Google Scholar] [CrossRef] [PubMed]
- Moore, H.C.; Jacoby, P.; Hogan, A.B.; Blyth, C.C.; Mercer, G.N. Modelling the seasonal epidemics of Respiratory Syncytial Virus in young children. PLoS ONE 2014, 9, e100422. [Google Scholar] [CrossRef] [PubMed]
- Capistran, M.; Moreles, M.; Lara, B. Parameter estimation of some epidemic models. The case of recurrent epidemics caused by respiratory syncytial virus. Bull. Math. Biol. 2009, 71, 1890–1901. [Google Scholar] [CrossRef] [PubMed]
- Paynter, S.; Yakob, L.; Simões, E.A.F.; Lucero, M.G.; Tallo, V.; Nohynek, H.; Ware, R.S.; Weinstein, P.; Williams, G.; et al. Using mathematical transmission modelling to investigate drivers of respiratory syncytial virus seasonality in children in the Philippines. PLoS ONE 2014, 9, e90094. [Google Scholar] [CrossRef] [PubMed]
- White, L.J.; Mandl, J.N.; Gomes, M.G.M.; Bodley-Tickell, A.T.; Cane, P.A.; Perez-Brena, P.; Aguilar, J.C.; Siqueira, M.M.; Portes, S.A.; Straliotto, S.M.; et al. Understanding the transmission dynamics of respiratory syncytial virus using multiple time series and nested models. Math. Biosci. 2007, 209, 222–239. [Google Scholar] [CrossRef] [PubMed]
- Arenas, A.J.; González-Parra, G.; Jódar, L. Randomness in a mathematical model for the transmission of respiratory syncytial virus. Math. Comput. Simul. 2010, 80, 971–981. [Google Scholar] [CrossRef]
- Meijboom, M.J.; Rozenbaum, M.H.; Benedictus, A.; Luytjes, W.; Kneyber, M.C.J.; Wilschut, J.C.; Hak, E.; Postma, M.J. Cost-effectiveness of potential infant vaccination against respiratory syncytial virus infection in The Netherlands. Vaccine 2012, 30, 4691–4700. [Google Scholar] [CrossRef] [PubMed]
- Bos, J.M.; Rietveld, E.; Moll, H.A.; Steyerberg, E.W.; Luytjes, W.; Wilschut, J.C.; de Groot, R.; Postma, M.J. The use of health economics to guide drug development decisions: Determining optimal values for an RSV-vaccine in a model-based scenario-analytic approach. Vaccine 2007, 25, 6922–6929. [Google Scholar] [CrossRef] [PubMed]
- Acedo, L.; Díez-Domingo, J.; Moraño, J.-A.; Villanueva, R.-J. Mathematical modelling of respiratory syncytial virus (RSV): Vaccination strategies and budget applications. Epidemiol. Infect. 2010, 138, 853–860. [Google Scholar] [CrossRef] [PubMed]
- Acedo, L.; Moraño, J.-A.; Díez-Domingo, J. Cost analysis of a vaccination strategy for respiratory syncytial virus (RSV) in a network model. Math. Comput. Model. 2010, 52, 1016–1022. [Google Scholar] [CrossRef]
- Kinyanjui, T.M.; House, T.A.; Kiti, M.C.; Cane, P.A.; Nokes, D.J.; Medley, G.F. Vaccine induced herd immunity for control of respiratory syncytial virus disease in a low-income country setting. PLoS ONE 2015, 10, e0138018. [Google Scholar] [CrossRef] [PubMed]
- Poletti, P.; Merler, S.; Ajelli, M.; Manfredi, P.; Munywoki, P.K.; Nokes, J.D.; Melegaro, A. Evaluating vaccination strategies for reducing infant respiratory syncytial virus infection in low-income settings. BMC Med. 2015, 13, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Yamin, D.; Jones, F.K.; DeVincenzo, J.P.; Gertler, S.; Kobiler, O.; Townsend, J.P.; Galvani, A.P. Vaccination strategies against respiratory syncytial virus. Proc. Natl. Acad. Sci. USA 2016, 113, 13239–13244. [Google Scholar] [CrossRef] [PubMed]
- Heffernan, J.; Smith, R.J.; Wahl, L.M. Perspectives on the basic reproductive ratio. J. R. Soc. Interface 2005, 2, 281–293. [Google Scholar] [CrossRef] [PubMed]
- Bainov, D.; Simeonov, P. Systems with Impulsive Effect; Ellis Horwood Ltd.: Chichester, UK, 1989. [Google Scholar]
- Bainov, D.; Simeonov, P. Impulsive Differential Equations: Periodic Solutions and Applications; Longman Scientific and Technical: London, UK, 1993. [Google Scholar]
- Bainov, D.; Simeonov, P. Impulsive Differential Equations: Asymptotic Properties of the Solutions; World Scientific: London, UK, 1995. [Google Scholar]
- Lakshmikantham, V.; Bainov, D.; Simeonov, P. Theory of Impulsive Differential Equations; World Scientific: London, UK, 1989. [Google Scholar]
- Church, K.; Smith?, R. Analysis of piecewise-continuous extensions of periodic linear impulsive differential equations with fixed, strictly inhomogeneous impulses. Dyn. Contin. Discret. Impuls. Syst. Ser. B: Appl. Algorithms 2014, 21, 101–119. [Google Scholar]
- Smith?, R.J.; Schwartz, E.J. Predicting the potential impact of a Cytotoxic T-Lymphocyte HIV vaccine: How often should you vaccinate and how strong should the vaccine be? Math. Biosci. 2008, 212, 180–187. [Google Scholar] [CrossRef] [PubMed]
- Hogan, A.B.; Glass, K.; Moore, H.C.; Anderssen, R.S. Age structures in mathematical models for infectious diseases, with a case study of Respiratory Syncytial Virus. In Applications + Practical Conceptualization + Mathematics = Fruitful Innovation, Proceedings of the Forum of Mathematics for Industry 2014; Springer: New York, NY, USA, 2015; Volume 11, pp. 105–116. [Google Scholar]
- Piedra, P.; Munoz, F. The significance of transplacental antibody against respiratory syncytial virus. J. Infect. Dis. 2014, 210, 1526–1528. [Google Scholar] [CrossRef] [PubMed]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smith, R.J.; Hogan, A.B.; Mercer, G.N. Unexpected Infection Spikes in a Model of Respiratory Syncytial Virus Vaccination. Vaccines 2017, 5, 12. https://doi.org/10.3390/vaccines5020012
Smith RJ, Hogan AB, Mercer GN. Unexpected Infection Spikes in a Model of Respiratory Syncytial Virus Vaccination. Vaccines. 2017; 5(2):12. https://doi.org/10.3390/vaccines5020012
Chicago/Turabian StyleSmith, Robert J., Alexandra B. Hogan, and Geoffry N. Mercer. 2017. "Unexpected Infection Spikes in a Model of Respiratory Syncytial Virus Vaccination" Vaccines 5, no. 2: 12. https://doi.org/10.3390/vaccines5020012
APA StyleSmith, R. J., Hogan, A. B., & Mercer, G. N. (2017). Unexpected Infection Spikes in a Model of Respiratory Syncytial Virus Vaccination. Vaccines, 5(2), 12. https://doi.org/10.3390/vaccines5020012




