A Big Data Optimization Approach for Estimating the Time-Dependent Effectiveness Profiles Against Hospitalization for Double- and Single-Dose Schemes: Study Case, COVID-19 in Elderly Mexicans
Abstract
1. Introduction
2. Methodology
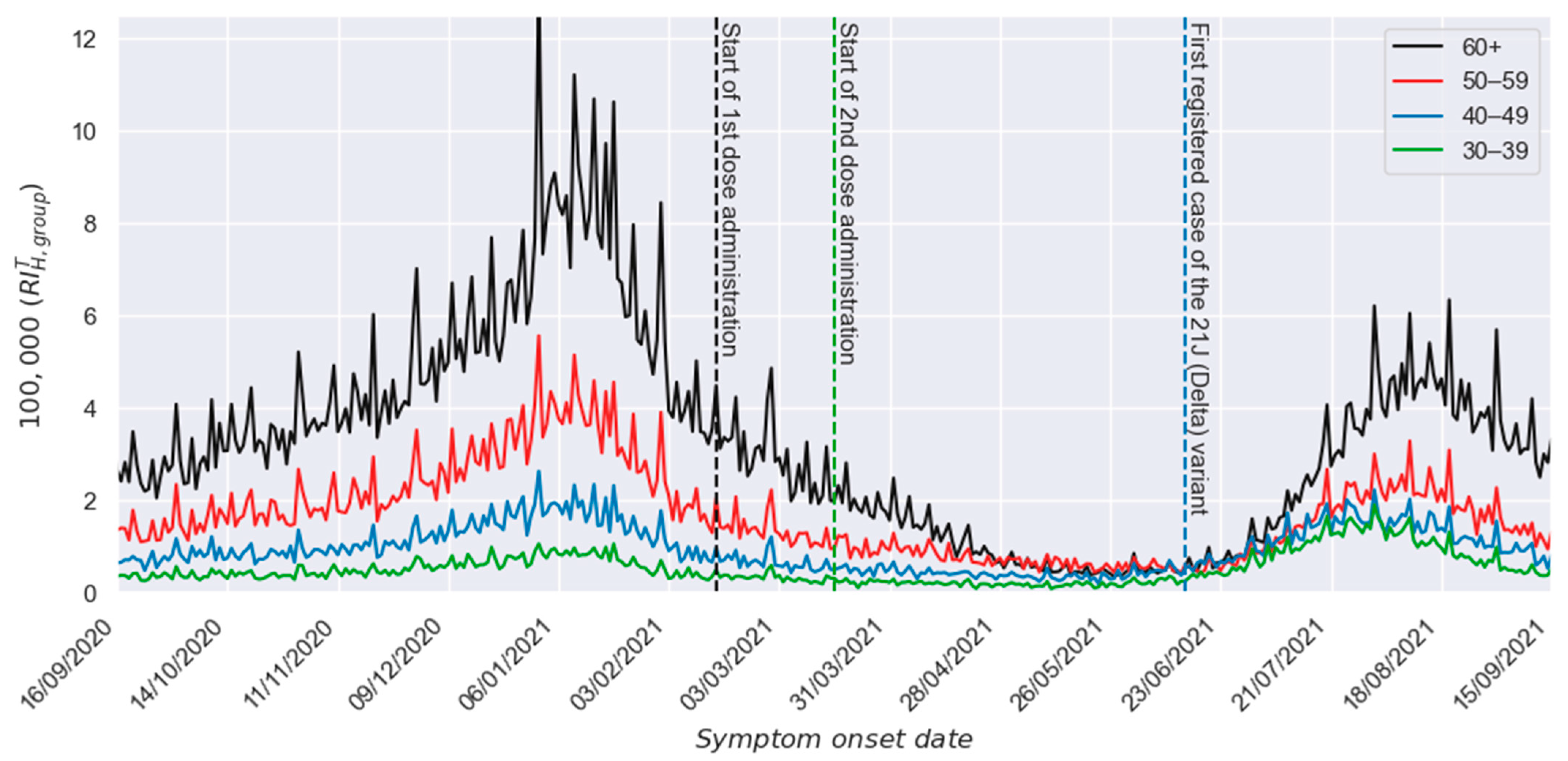
2.1. Required Real-World Profiles
2.1.1. The Vaccination Profile
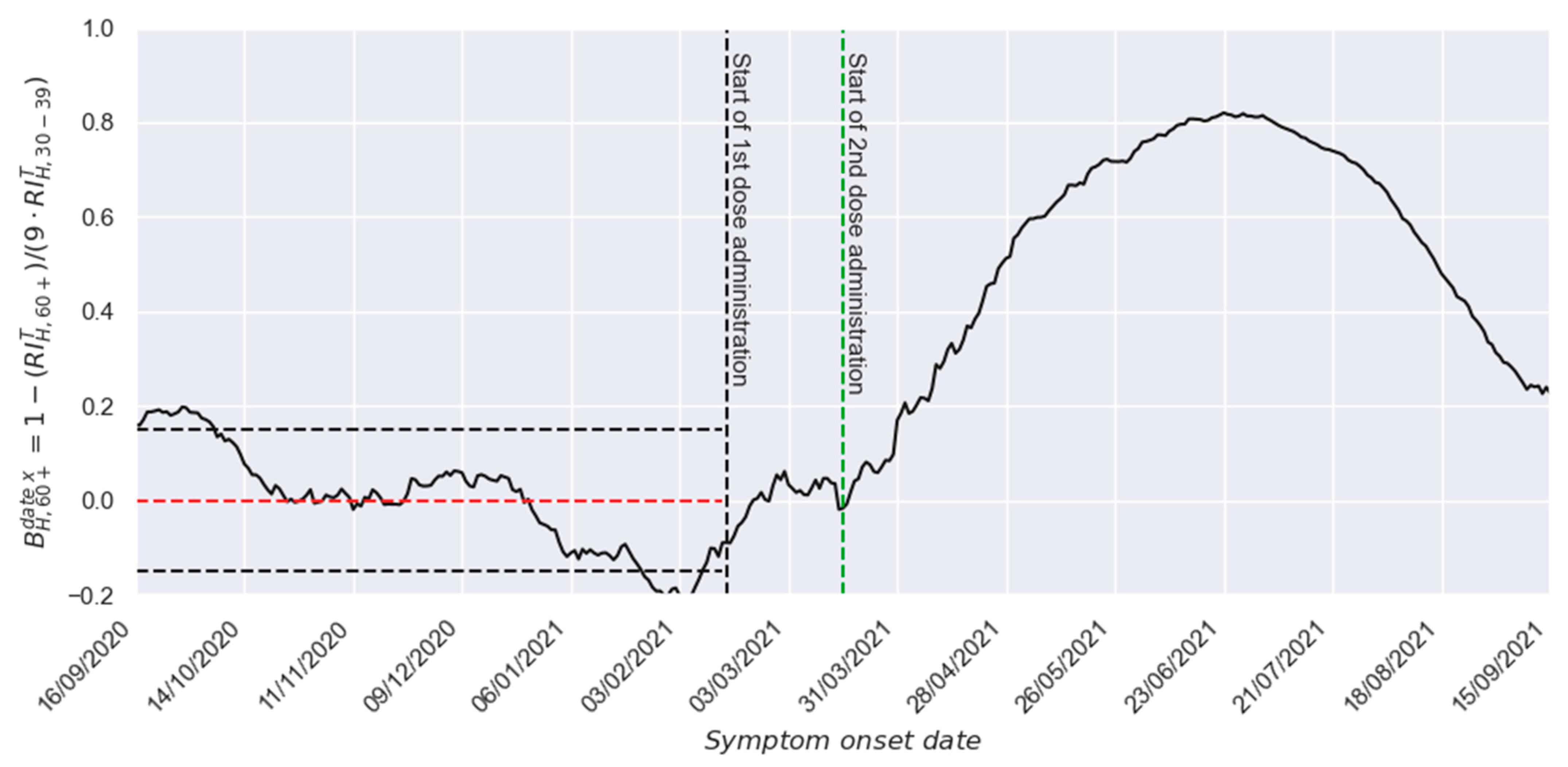
2.1.2. The Beneficial Effect Profile
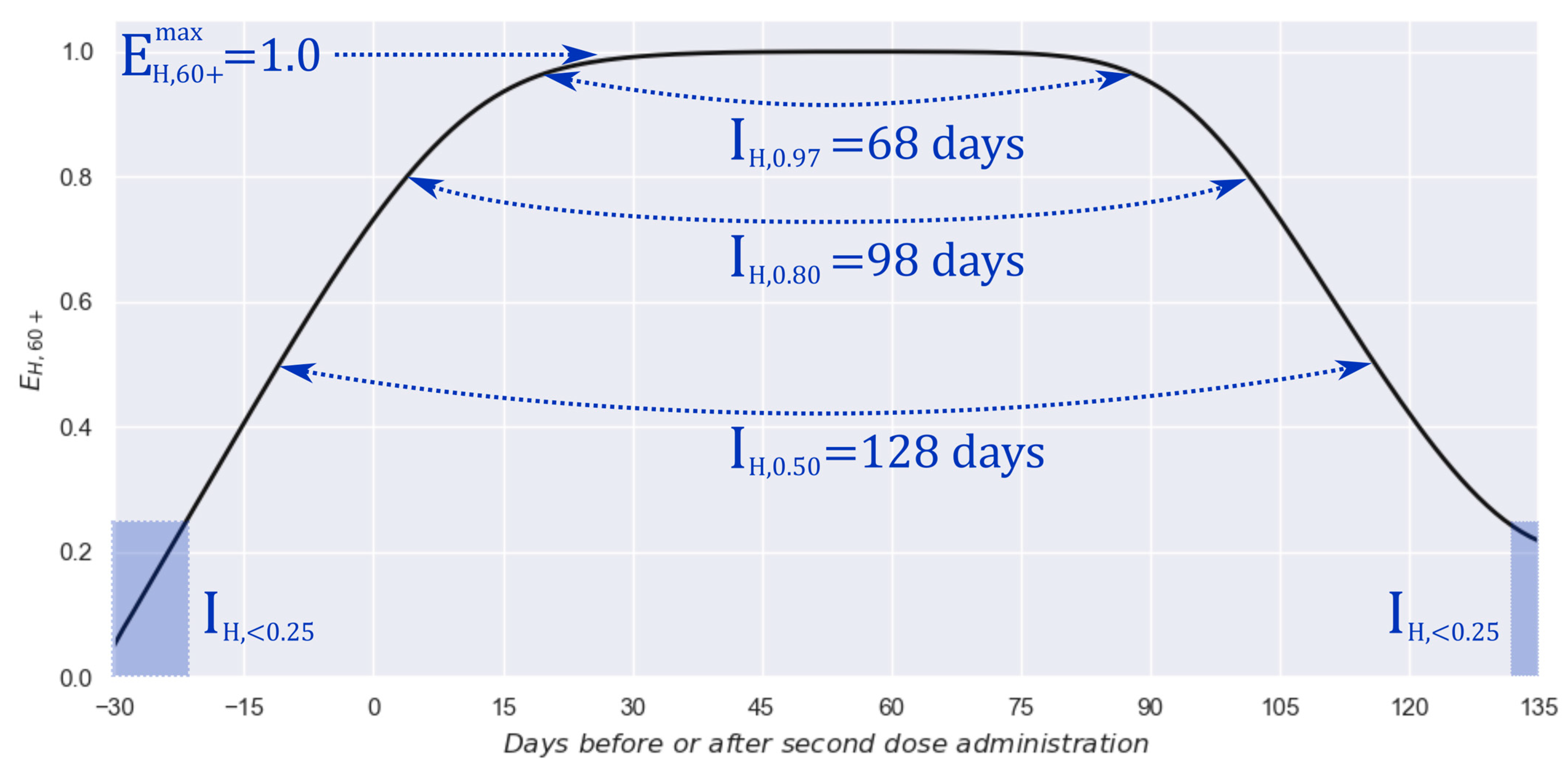
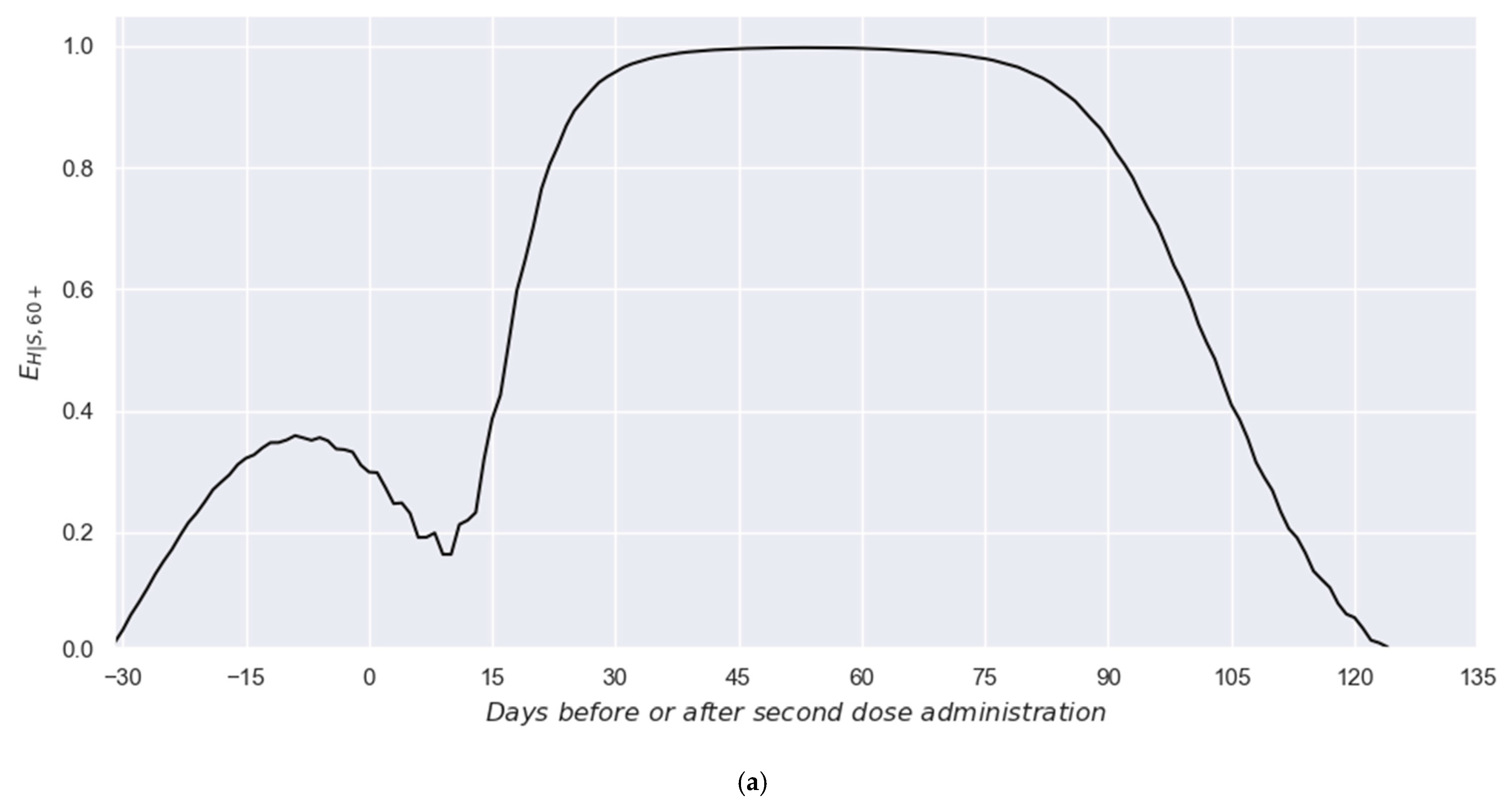
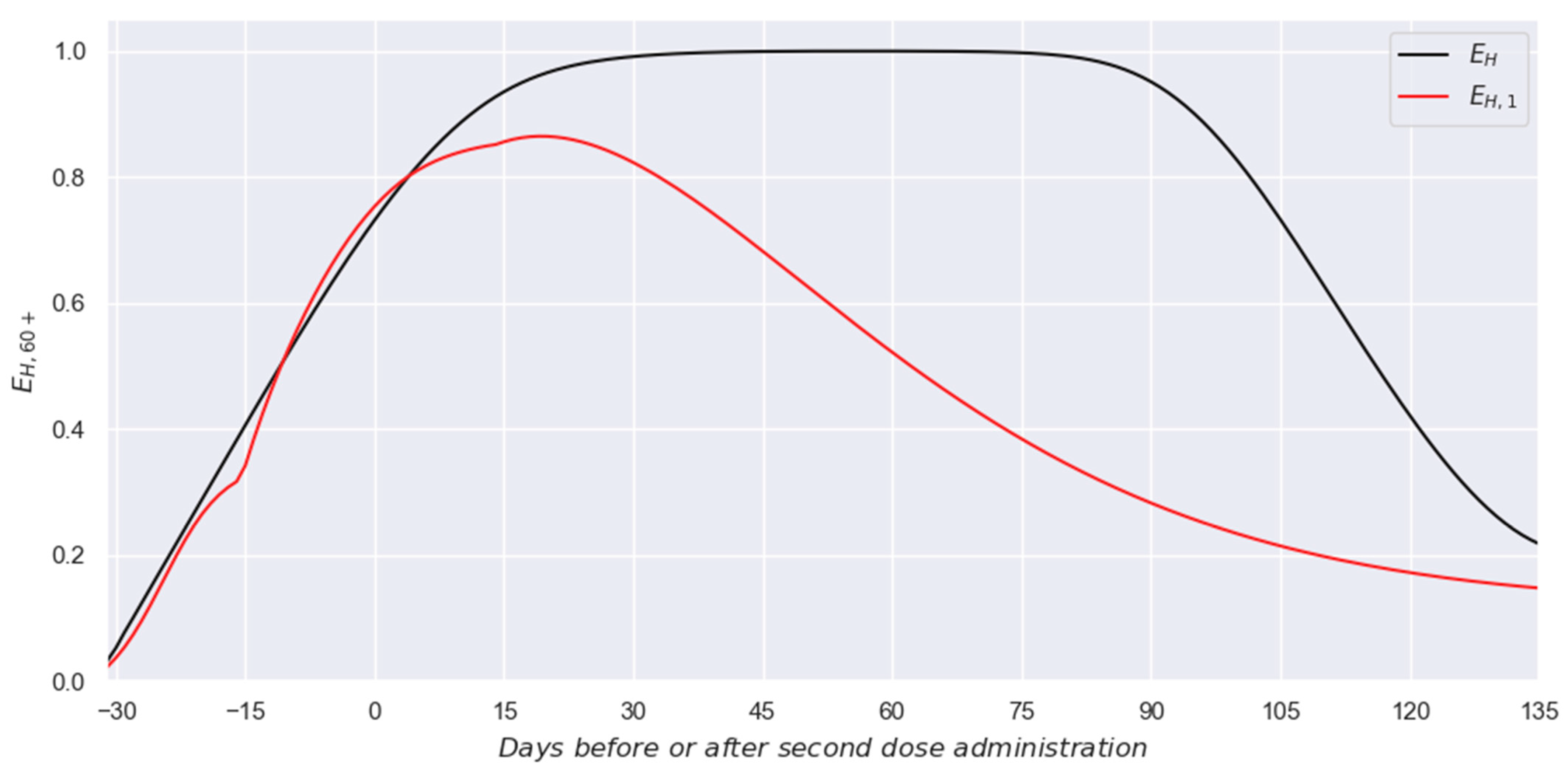
3. Results
3.1. Two-Dose Scheme
3.2. Single-Dose Schemes
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hussain, A.; Yang, H.; Zhang, M.; Liu, Q.; Alotaibi, G.; Irfan, M.; He, H.; Chang, J.; Liang, X.-J.; Weng, Y.; et al. mRNA vaccines for COVID-19 and diverse diseases. J. Control Release 2022, 345, 314–333. [Google Scholar] [PubMed]
- Zhang, M.; Hussain, A.; Yang, H.; Zhang, J.; Liang, X.-J.; Huang, Y. mRNA-based modalities for infectious disease management. Nanoresearch 2023, 16, 672–691. [Google Scholar] [CrossRef] [PubMed]
- Polack, F.P.; Thomas, S.J.; Kitchin, N.; Absalon, J.; Gurtman, A.; Lockhart, S.; Perez, J.L.; Pérez Marc, G.; Moreira, E.D.; Zerbini, C.; et al. Safety and efficacy of the BNT162b2 mRNA COVID-19 vaccine. N. Engl. J. Med. 2020, 383, 2603–2615. [Google Scholar] [PubMed]
- Falsey, A.R.; Sobieszczyk, M.E.; Hirsch, I.; Sproule, S.; Robb, M.L.; Corey, L.; Neuzil, K.M.; Hahn, W.; Hunt, J.; Mulligan, M.J.; et al. Phase 3 safety and efficacy of AZD1222 (ChAdOx1 nCoV-19) COVID-19 vaccine. N. Engl. J. Med. 2021, 385, 2348–2360. [Google Scholar]
- Sadoff, J.; Gray, G.; Vandebosch, A.; Cárdenas, V.; Shukarev, G.; Grinsztejn, B.; Goepfert, P.A.; Truyers, C.; Fennema, H.; Spiessens, B.; et al. Safety and efficacy of single-dose Ad26.COV2.S vaccine against COVID-19. N. Engl. J. Med. 2021, 384, 2187–2201. [Google Scholar]
- El Sahly, H.M.; Baden, L.R.; Essink, B.; Doblecki-Lewis, S.; Martin, J.M.; Anderson, E.J.; Campbell, T.B.; Clark, J.; Jackson, L.A.; Fichtenbaum, C.J.; et al. Efficacy of the mRNA-1273 SARS-CoV-2 vaccine at completion of blinded phase. N. Engl. J. Med. 2021, 385, 1774–1785. [Google Scholar]
- Tanriover, M.D.; Doğanay, H.L.; Akova, M.; Güner, H.R.; Azap, A.; Akhan, S.; Köse, Ş.; Erdinç, F.Ş.; Akalın, E.H.; Tabak, Ö.F.; et al. Efficacy and safety of an inactivated whole-virion SARS-CoV-2 vaccine (CoronaVac): Interim results of a double-blind, randomised, placebo-controlled, phase 3 trial in Turkey. Lancet 2021, 398, 213–222. [Google Scholar]
- Ella, R.; Reddy, S.; Blackwelder, W.; Potdar, V.; Yadav, P.; Sarangi, V.; Aileni, V.K.; Kanungo, S.; Rai, S.; Reddy, P.; et al. Efficacy, safety, and lot-to-lot immunogenicity of an inactivated SARS-CoV-2 vaccine (BBV152): Interim results of a randomised, double-blind, controlled, phase 3 trial. Lancet 2021, 398, 2173–2184. [Google Scholar]
- Heath, P.T.; Galiza, E.P.; Baxter, D.N.; Boffito, M.; Browne, D.; Burns, F.; Chadwick, D.R.; Clark, R.; Cosgrove, C.; Galloway, J.; et al. Safety and efficacy of NVX-CoV2373 COVID-19 vaccine. N. Engl. J. Med. 2021, 385, 1172–1183. [Google Scholar]
- Chemaitelly, H.; Tang, P.; Hasan, M.R.; AlMukdad, S.; Yassine, H.M.; Benslimane, F.M.; Al Khatib, H.A.; Coyle, P.; Ayoub, H.H.; Al Kanaani, Z.; et al. Waning of BNT162b2 vaccine protection against SARS-CoV-2 infection in Qatar. N. Engl. J. Med. 2021, 385, e83. [Google Scholar] [CrossRef]
- Tartof, S.Y.; Slezak, J.M.; Fischer, H.; Hong, V.; Ackerson, B.K.; Ranasinghe, O.N.; Frankland, T.B.; Ogun, O.A.; Zamparo, J.M.; Gray, S.; et al. Effectiveness of mRNA BNT162b2 COVID-19 vaccine up to 6 months in a large integrated health system in the USA: A retrospective cohort study. Lancet 2021, 398, 1407–1416. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.-Y.; Gu, Y.; Wheeler, B.; Young, H.; Holloway, S.; Sunny, S.-K.; Moore, Z.; Zeng, D. Effectiveness of COVID-19 vaccines over a 9-month period in North Carolina. N. Engl. J. Med. 2022, 386, 933–941. [Google Scholar] [CrossRef] [PubMed]
- Rosenberg, E.S.; Dorabawila, V.; Easton, D.; Bauer, U.E.; Kumar, J.; Hoen, R.; Hoefer, D.; Wu, M.; Lutterloh, E.; Conroy, M.B.; et al. COVID-19 vaccine effectiveness in New York State. N. Engl. J. Med. 2022, 386, 116–127. [Google Scholar] [CrossRef] [PubMed]
- Fowlkes, A.; Gaglani, M.; Groover, K.; These, M.S.; Tyner, H.; Ellingson, K.; HEROES-RECOVER Cohorts. Effectiveness of COVID-19 vaccines in preventing SARS-CoV-2 infection among frontline workers before and during B.1.617.2 (Delta) variant predominance—Eight U.S. locations, December 2020–August 2021. Morb. Mortal. Wkly. Rep. 2021, 70, 1167–1169. [Google Scholar] [CrossRef]
- Nanduri, S.; Pilishvili, T.; Derado, G.; Soe, M.M.; Dollard, P.; Wu, H.; Li, Q.; Bagchi, S.; Dubendris, H.; Link-Gelles, R.; et al. Effectiveness of Pfizer-BioNTech and Moderna Vaccines in Preventing SARS-CoV-2 Infection among nursing home residents before and during widespread circulation of the SARS-CoV-2 B.1.617.2 (Delta) Variant—National Healthcare Safety Network, March 1–August 1, 2021. Morb. Mortal. Wkly. Rep. 2021, 70, 1163–1166. [Google Scholar]
- Self, W.H.; Tenforde, M.W.; Rhoads, J.P.; Gaglani, M.; Ginde, A.A.; Douin, D.J.; Olson, S.M.; Talbor, H.K.; Casey, J.D.; Mohr, N.M.; et al. Comparative effectiveness of Moderna, Pfizer-BioNTech, and Janssen (Johnson & Johnson) vaccines in preventing COVID-19 hospitalizations among adults without immunocompromising conditions—United States, March-August 2021. Morb. Mortal. Wkly. Rep. 2021, 70, 1337–1343. [Google Scholar]
- Tenforde, M.W.; Self, W.H.; Naiori, E.A.; Ginde, A.A.; Douin, D.J.; Olson, S.M.; Talbot, H.K.; Casey, J.D.; Mohr, N.M.; Zepeski, A.; et al. Sustained effectiveness of Pfizer-BioNTech and Moderna vaccinees against COVID-19 associated hospitalizations among adults-United States March-July 2021. Morb. Mortal. Wkly. Rep. 2021, 70, 1156–1162. [Google Scholar] [CrossRef]
- WHO. Prequalification of Medical Products. Vaccines. Available online: https://extranet.who.int/prequal/vaccines (accessed on 23 December 2024).
- WHO. Regulation and Prequalification. Available online: https://www.who.int/teams/regulation-prequalification/eul/covid-19 (accessed on 23 December 2024).
- González-Sánchez, O.A.; González-Ortiz, L.J.; Sánchez-Peña, M.J.; Gutiérrez-Pulido, H.; Cervantes, O.; Márquez-Sandoval, F.; Hernández-Bello, J.; Casillas, N.; Muñoz-Valle, J.F. A novel approach to obtain vaccine effectiveness continuous profiles. Example case: COVID-19 in elderly Mexicans. Vaccines 2023, 11, 719. [Google Scholar] [CrossRef]
- González-Sánchez, O.A.; Zaldívar, D.; Cuevas, E.; González-Ortiz, L.J. Mathematical optimization strategy for effectiveness profile estimation in two-dose vaccines and its use in designing improved vaccination strategies focused on pandemic containment. Vaccines 2024, 12, 81. [Google Scholar] [CrossRef]
- Presentaciones de las Conferencias de Prensa 2021. Available online: https://www.gob.mx/salud/documentos/presentaciones-de-las-conferencias-de-prensa-2021 (accessed on 23 December 2024).
- Shioda, K.; Breskin, A.; Harati, P.; Chamberlain, A.T.; Komura, T.; Lopman, B.A.; Rogawski-McQuade, E.T. Comparative effectiveness of alternative intervals between first and second doses of the mRNA COVID-19 vaccines. Nat. Commun. 2024, 15, 1214. [Google Scholar] [CrossRef]
- COVID-19 MÉXICO Comunicado Técnico Diario. Available online: https://www.gob.mx/cms/uploads/attachment/file/680207/2021.11.04_17h00_ComunicadoTecnicoDiario_Covid19__4_.pdf (accessed on 23 December 2024).
- Datos Abiertos. Available online: https://datosabiertos.salud.gob.mx/gobmx/salud/datos_abiertos/historicos/2021/12/datos_abiertos_covid19_25.12.2021.zip (accessed on 23 December 2024).
- Genomic Epidemiology of SARS-CoV-2 with Subsampling Focused Globally Since Pandemic Start. Available online: https://nextstrain.org/ncov/gisaid/global/all-time?dmax=2021-09-15&dmin=2021-04-01&f_country=Mexico (accessed on 20 March 2025).
- Hyndman, R.J. Moving averages. In International Encyclopedia of Statistical Science, 1st ed.; Lovric, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 866–869. [Google Scholar]
- Pegu, A.; O‘Connell, S.E.; Schmidt, S.D.; O‘Dell, S.; Talana, C.A.; Lai, L.; Albert, J.; Anderson, E.; Bennett, H.; Corbett, K.S.; et al. Durability of mRNA-1273 vaccine–induced antibodies against SARS-CoV-2 variants. Science 2021, 373, 1372–1377. [Google Scholar] [CrossRef] [PubMed]
- van Gils, M.J.; Lavell, A.; van der Straten, K.; Appelman, B.; Bontjer, I.; Poniman, M.; Burger, J.A.; Oomen, M.; Bouhuijs, J.H.; van Vught, L.A.; et al. Antibody responses against SARS-CoV-2 variants induced by four different SARS-CoV-2 vaccines in health care workers in the Netherlands: A prospective cohort study. PLoS Med. 2022, 19, e1003991. [Google Scholar] [CrossRef] [PubMed]
- Suthar, M.S.; Arunachalam, P.S.; Hu, M.; Reis, N.; Trisal, M.; Raeber, O.; Chinthrajah, S.; Davis-Gardner, M.E.; Manning, K.; Mudvari, P.; et al. Durability of immune responses to the BNT162b2 mRNA vaccine. Med 2022, 3, 25–27. [Google Scholar] [CrossRef]
- Levin, E.G.; Lustig, Y.; Cohen, C.; Fluss, R.; Indenbaum, V.; Amit, S.; Doolman, R.; Asraf, K.; Mendelson, E.; Ziv, A.; et al. Waning immune humoral response to BNT162b2 COVID-19 vaccine over 6 months. N. Engl. J. Med. 2021, 385, e84. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Jain, M.; Saihjpal, V.; Singh, N.; Singh, S.B. An Overview of variants and advancements of PSO algorithm. Appl. Sci. 2022, 12, 8392. [Google Scholar] [CrossRef]
- Cuevas, E.; Rodríguez, A. Metaheuristic Computation with MATLAB®, 1st ed.; CRC Press: Boca Raton, FL, USA, 2020; ISBN 9780367438869. [Google Scholar]
- Satopää, V.; Albrecht, J.; Irwin, D.; Raghavan, B. Finding a “Kneedle” in a Haystack: Detecting Knee Points in System Behavior. In Proceedings of the 31st International Conference on Distributed Computing Systems Workshops, Minneapolis, MN, USA, 20–24 June 2011; pp. 166–171. [Google Scholar]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers (EMEA Edition), 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2020; pp. 39–40. [Google Scholar]
- Microsoft Support. Define and Solve a Problem by Using Solver. Available online: https://support.microsoft.com/en-us/office/define-and-solve-a-problem-by-using-solver-5d1a388f-079d-43ac-a7eb-f63e45925040 (accessed on 27 April 2023).
- Facó, J.L.D. A Generalized Reduced Gradient Algorithm for Solving Large-Scale Discrete-Time Nonlinear Optimal Control Problems. IFAC Proc. Vol. 1989, 22, 45–50. [Google Scholar]
- Lasdon, L.S.; Fox, R.L.; Ratner, M.W. Nonlinear Optimization Using the Generalized Reduced Gradient Method. Rev. Fr. Autom. Inf. Rech. Oper. 1974, 8, 73–103. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Sánchez, Ó.A.; González-Ortiz, L.J.; Sánchez-Peña, M.J.; Gutiérrez-Pulido, H. A Big Data Optimization Approach for Estimating the Time-Dependent Effectiveness Profiles Against Hospitalization for Double- and Single-Dose Schemes: Study Case, COVID-19 in Elderly Mexicans. Vaccines 2025, 13, 363. https://doi.org/10.3390/vaccines13040363
González-Sánchez ÓA, González-Ortiz LJ, Sánchez-Peña MJ, Gutiérrez-Pulido H. A Big Data Optimization Approach for Estimating the Time-Dependent Effectiveness Profiles Against Hospitalization for Double- and Single-Dose Schemes: Study Case, COVID-19 in Elderly Mexicans. Vaccines. 2025; 13(4):363. https://doi.org/10.3390/vaccines13040363
Chicago/Turabian StyleGonzález-Sánchez, Óscar A., Luis Javier González-Ortiz, María Judith Sánchez-Peña, and Humberto Gutiérrez-Pulido. 2025. "A Big Data Optimization Approach for Estimating the Time-Dependent Effectiveness Profiles Against Hospitalization for Double- and Single-Dose Schemes: Study Case, COVID-19 in Elderly Mexicans" Vaccines 13, no. 4: 363. https://doi.org/10.3390/vaccines13040363
APA StyleGonzález-Sánchez, Ó. A., González-Ortiz, L. J., Sánchez-Peña, M. J., & Gutiérrez-Pulido, H. (2025). A Big Data Optimization Approach for Estimating the Time-Dependent Effectiveness Profiles Against Hospitalization for Double- and Single-Dose Schemes: Study Case, COVID-19 in Elderly Mexicans. Vaccines, 13(4), 363. https://doi.org/10.3390/vaccines13040363





