Modeling Hybridization Kinetics of Gene Probes in a DNA Biochip Using FEMLAB
Abstract
:1. Introduction
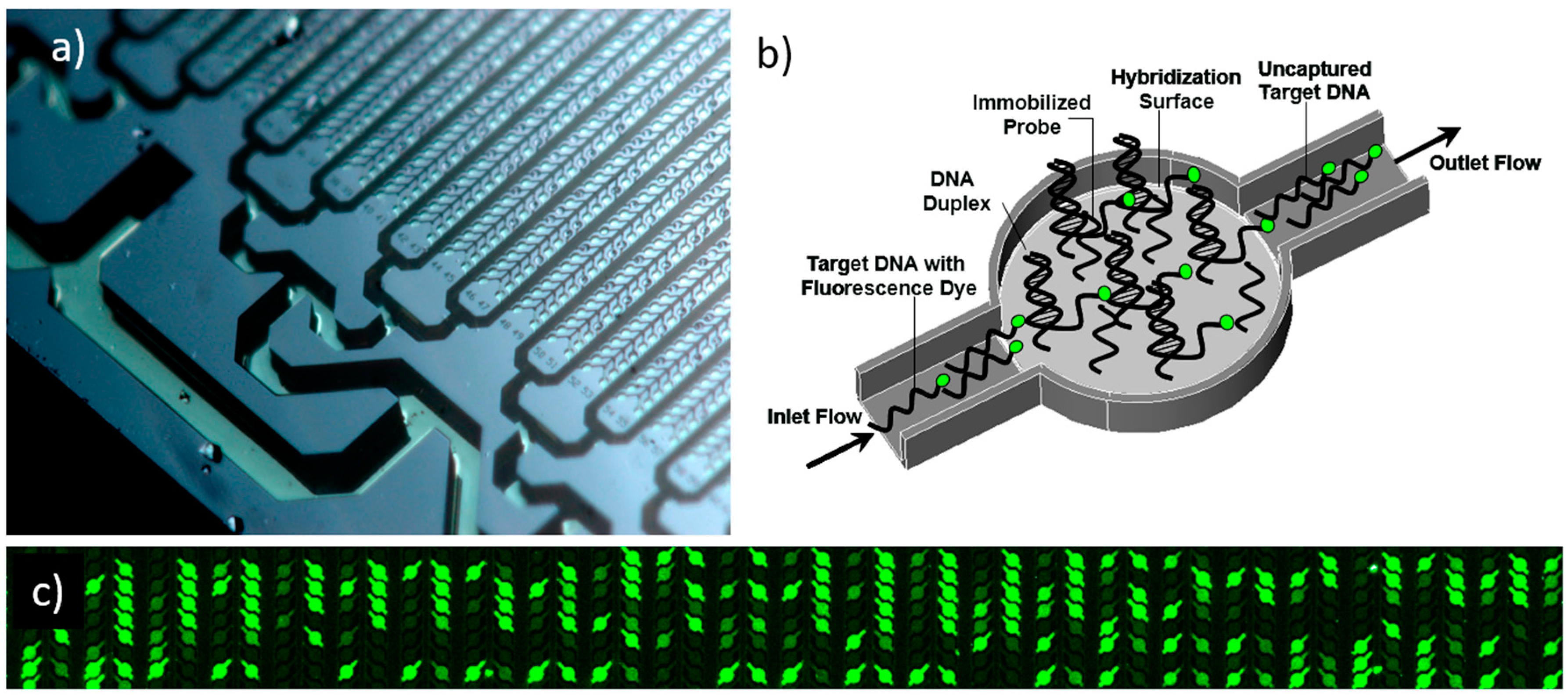
2. Materials and Methods
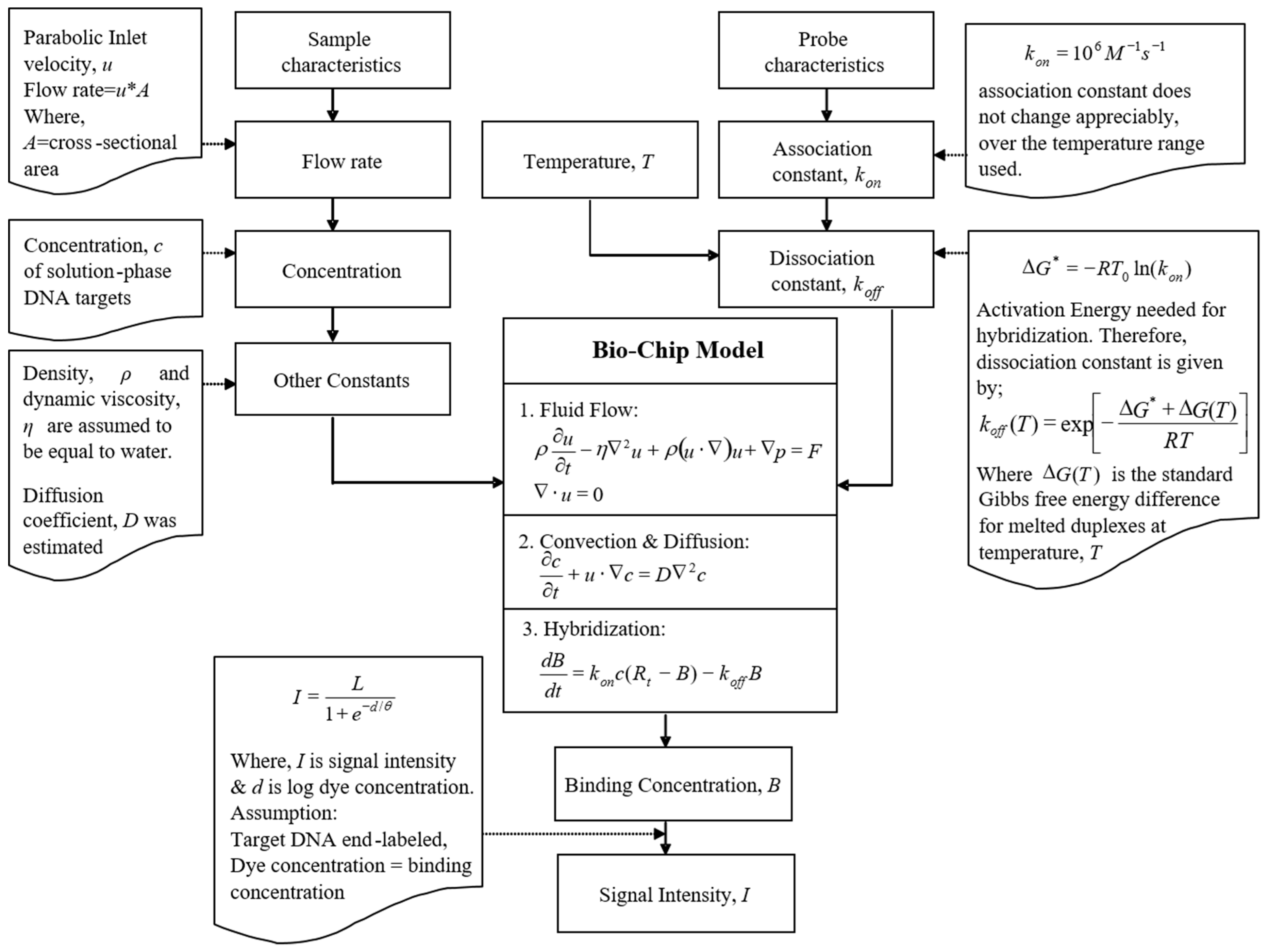
2.1. Mathematical Model
2.2. Numerical Simulations
2.3. Experimental Validation
3. Results and Discussion
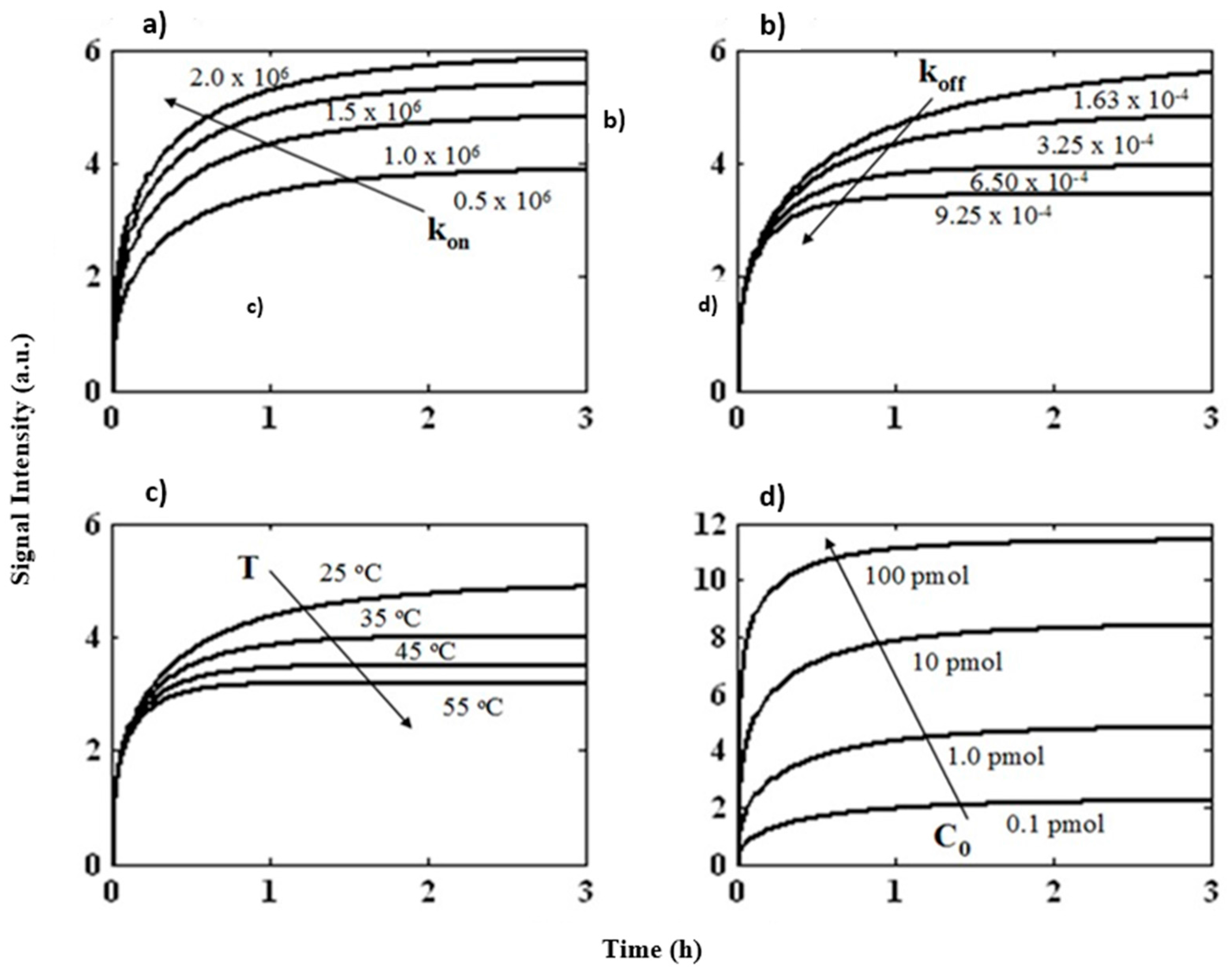
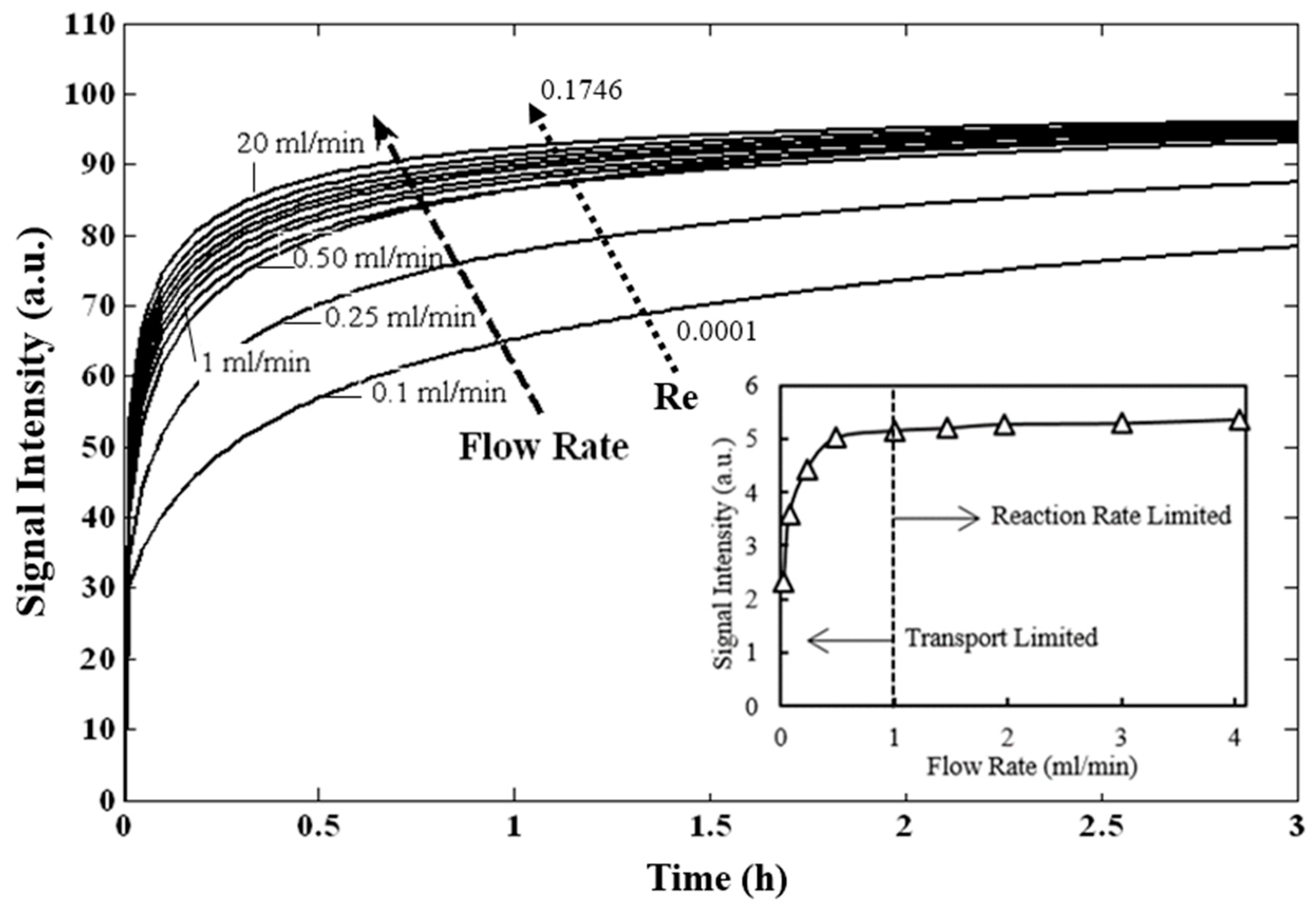
3.1. Theroretical Analysis
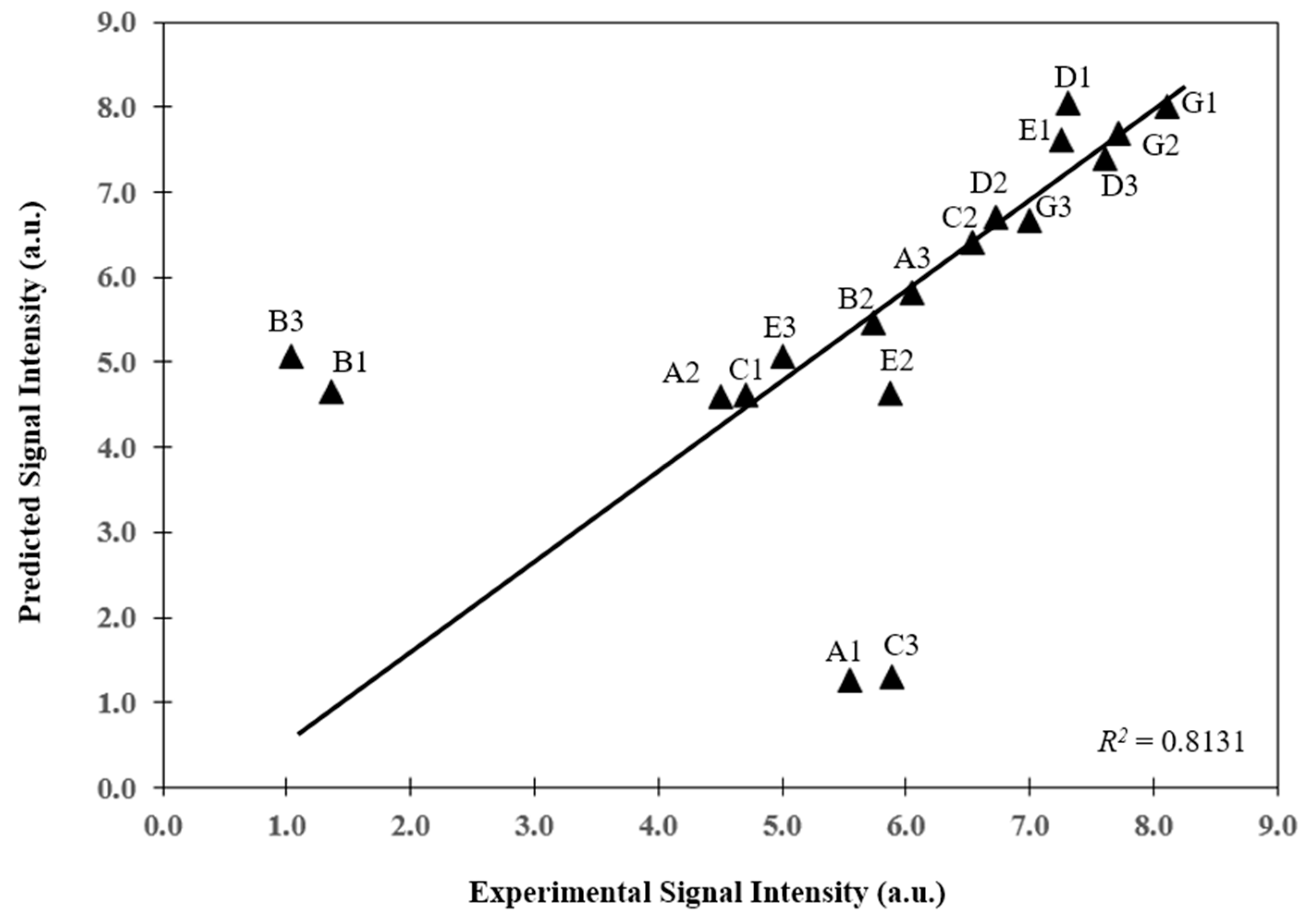
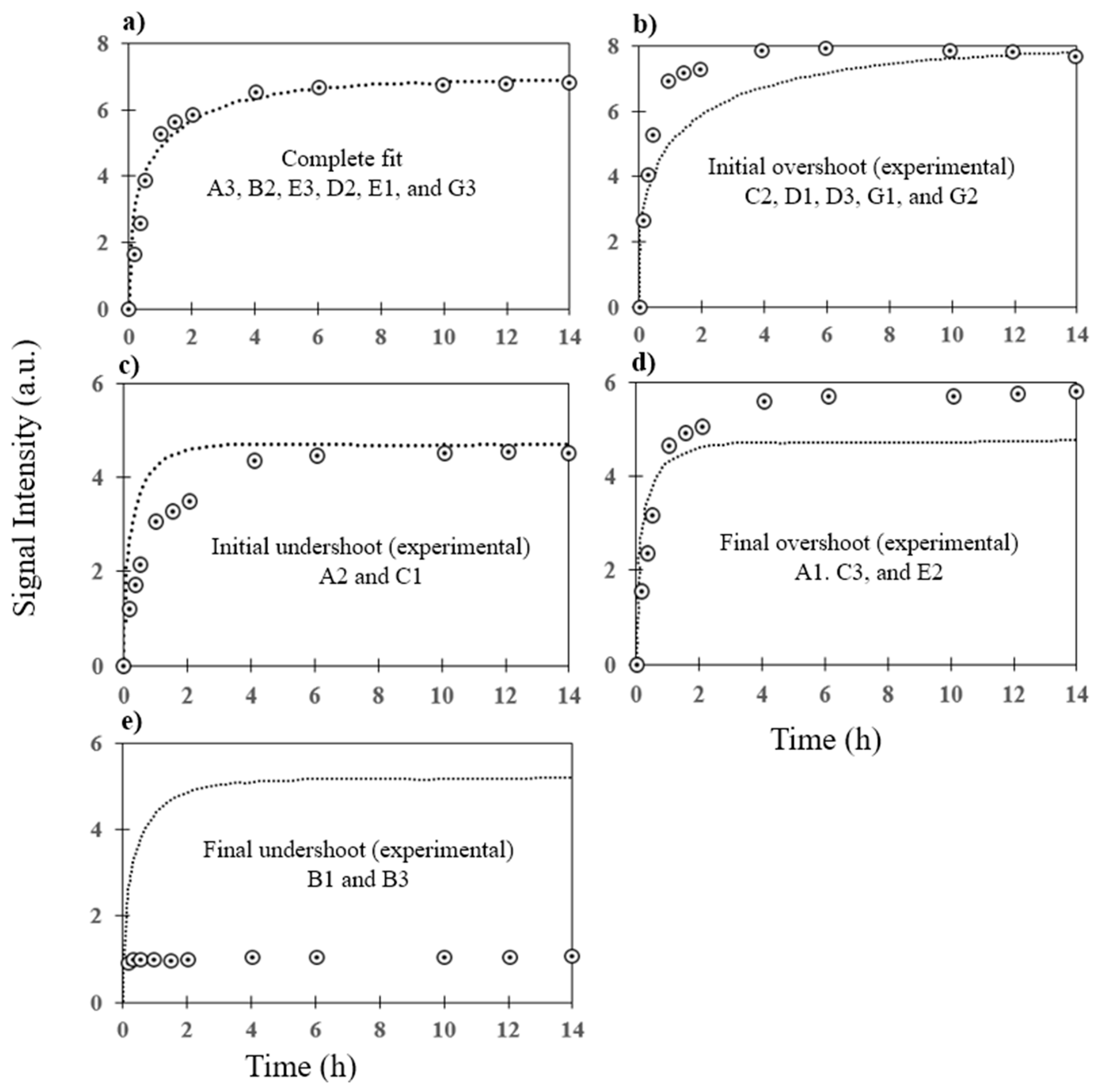
3.2. Prediction of Hybridization Kinetic Curves
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Warkiani, M.E.; Khoo, B.L.; Tan, D.S.-W.; Bhagat, A.A.S.; Lim, W.-T.; Yap, Y.S.; Lee, S.C.; Soo, R.A.; Han, J.; Lim, C.T. An ultra-high-throughput spiral microfluidic biochip for the enrichment of circulating tumor cells. Analyst 2014, 139, 3245–3255. [Google Scholar] [CrossRef] [PubMed]
- Weng, X. DNA hybridization assays on chip. In Encyclopedia of Microfluidics and Nanofluidics; Springer: New York, NY, USA, 2015; pp. 1–8. [Google Scholar]
- McDonagh, C.; Stranik, O.; Nooney, R.; MacCraith, B.D. Nanoparticle strategies for enhancing the sensitivity of fluorescence-based biochips. Nanomedicine 2009, 4, 645–656. [Google Scholar] [CrossRef] [PubMed]
- Kim, O.; Lee, D.; Lee, A.C.; Kwoon, S. High sensitivity rare cell capturing biochip with separable microstructures. In Proceedings of the 2015 IEEE SENSORS, Busan, Korea, 1–4 November 2015; pp. 1–3. [Google Scholar]
- Monserud, J.H.; Schwartz, D.K. Mechanisms of surface-mediated DNA hybridization mechanisms of surface-mediated DNA hybridization. ACS Nano 2014, 8, 4488–4499. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Li, G.-L.; Hu, B.-X. Optimization of condition for biochip hybridization using cellulose ester membrane as a substrate. Chin. J. Biol. 2009, 22, 281–283. [Google Scholar]
- Jakubek, Y.A.; Cutler, D.J. A model of binding on DNA microarrays: Understanding the combined effect of probe synthesis failure, cross-hybridization, DNA fragmentation and other experimental details of affymetrix arrays. BMC Genom. 2012, 13, 737. [Google Scholar] [CrossRef] [PubMed]
- Rode, A.B.; Endoh, T.; Tateishi-Karimata, H.; Takahashi, S.; Sugimoto, N. Real-time monitoring of DNA hybridization kinetics on living cell surfaces. Chem. Commun. 2013, 49, 8444–8446. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, L.; Hagedorn, P.H.; Lindholm, M.W.; Lindow, M. A kinetic model explains why shorter and less affine enzyme-recruiting oligonucleotides can be more potent. Mol. Ther. Acids 2014, 3, e149. [Google Scholar] [CrossRef] [PubMed]
- Zhou, F.; Noor, M.O.; Krull, U.J. Luminescence resonance energy transfer-based nucleic acid hybridization assay on cellulose paper with upconverting phosphor as donors. Anal. Chem. 2014, 86, 2719–2726. [Google Scholar] [CrossRef] [PubMed]
- Erickson, D.; Li, D.; Krull, U.J. Modeling of DNA hybridization kinetics for spatially resolved biochips. Anal. Biochem. 2003, 317, 186–200. [Google Scholar] [CrossRef]
- Bishop, J.; Blair, S.; Chagovetz, A.M. A competitive kinetic model of nucleic acid surface hybridization in the presence of point mutants. Biophys. J. 2006, 90, 831–840. [Google Scholar] [CrossRef] [PubMed]
- Gao, X. A flexible light-directed DNA chip synthesis gated by deprotection using solution photogenerated acids. Nucleic Acids Res. 2001, 29, 4744–4750. [Google Scholar] [CrossRef] [PubMed]
- Gardete, S.; Tomasz, A. Mechanisms of vancomycin resistance in Staphylococcus aureus. J. Clin. Investig. 2014, 124, 2836–2840. [Google Scholar] [CrossRef] [PubMed]
- Sabouni, F.; Movahedi, Z.; Mahmoudi, S.; Pourakbari, B.; Keshavarz Valian, S.; Mamishi, S. High frequency of vancomycin resistant Enterococcus faecalis in children: An alarming concern. J. Prev. Med. Hyg. 2016, 57, E201–E204. [Google Scholar] [PubMed]
- Lu, N.; Hu, Y.; Zhu, L.; Yang, X.; Yin, Y.; Lei, F.; Zhu, Y.; Du, Q.; Wang, X.; Meng, Z.; et al. DNA microarray analysis reveals that antibiotic resistance-gene diversity in human gut microbiota is age related. Sci. Rep. 2014, 4, 4302. [Google Scholar] [CrossRef] [PubMed]
- Frye, J.G.; Lindsey, R.L.; Rondeau, G.; Porwollik, S.; Long, F.; McClelland, M.; Jackson, C.R.; Englen, M.D.; Meinersmann, R.J.; Berrang, M.E.; et al. Development of a DNA microarray to detect antimicrobial resistance genes identified in the National Center for Biotechnology Information database. Microb. Drug Resist. 2010, 16, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.M.Y.; Henihan, G.; Macdonald, D.; Michalowski, A.; Templeton, K.; Gibb, A.P.; Schulze, H.; Bachmann, T.T. Rapid electrochemical detection of New Delhi metallo-beta-lactamase genes to enable point-of-care testing of carbapenem-resistant enterobacteriaceae. Anal. Chem. 2015, 87, 7738–7745. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Peng, J.; Yu, X.; Zhang, S.; Zhou, B.; Jiang, D.; Chen, J.; Ding, B.; Zhu, B.; Li, Y. A color-reaction-based biochip detection assay for RIF and INH resistance of clinical mycobacterial specimens. J. Microbiol. Biotechnol. 2015, 26, 180–189. [Google Scholar] [CrossRef] [PubMed]
- Zimenkov, D.V.; Kulagina, E.V.; Antonova, O.V.; Zhuravlev, V.Y.; Gryadunov, D.A. Simultaneous drug resistance detection and genotyping of Mycobacterium tuberculosis using a low-density hydrogel microarray. J. Antimicrob. Chemother. 2016, 71, 1520–1531. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Cai, S.; Hong, A.; You, Q.; Yu, P.; Sheng, N.; Srivannavit, O.; Muranjan, S.; Rouillard, J.M.; Xia, Y.; et al. Microfluidic PicoArray synthesis of oligodeoxynucleotides and simultaneous assembling of multiple DNA sequences. Nucleic Acids Res. 2004, 32, 5409–5417. [Google Scholar] [CrossRef] [PubMed]
- Miller, S.M.; Tourlousse, D.M.; Stedtfeld, R.D.; Baushke, S.W.; Herzog, A.B.; Wick, L.M.; Rouillard, J.M.; Gulari, E.; Tiedje, J.M.; Hashsham, S.A. In situ-synthesized virulence and marker gene biochip for detection of bacterial pathogens in water. Appl. Environ. Microbiol. 2008, 74, 2200–2209. [Google Scholar] [CrossRef] [PubMed]
- Chan, V.; Graves, D.J.; McKenzie, S.E. The biophysics of DNA hybridization with immobilized oligonucleotide probes. Biophys. J. 1995, 69, 2243–2255. [Google Scholar] [CrossRef]
- Yin, Y.; Zhao, X.S. Kinetics and dynamics of DNA hybridization. Acc. Chem. Res. 2011, 44, 1172–1181. [Google Scholar] [CrossRef] [PubMed]
- Heule, M.; Manz, A. Sequential DNA hybridisation assays by fast micromixing. Lab Chip 2004, 4, 506–511. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Tong, W.; Su, Z.; Han, T.; Han, J.; Puri, R.K.; Fang, H.; Frueh, F.W.; Goodsaid, F.M.; Guo, L.; et al. Microarray scanner calibration curves: characteristics and implications. BMC Bioinform. 2005, 6, S11. [Google Scholar] [CrossRef] [PubMed]
- Wick, L.M.; Rouillard, J.M.; Whittam, T.S.; Gulari, E.; Tiedje, J.M.; Hashsham, S.A. On-chip non-equilibrium dissociation curves and dissociation rate constants as methods to assess specificity of oligonucleotide probes. Nucleic Acids Res. 2006, 34, e26. [Google Scholar] [CrossRef] [PubMed]
- Ouldridge, T.E.; Sulc, P.; Romano, F.; Doye, J.P.K.; Louis, A.A. DNA hybridization kinetics: zippering, internal displacement and sequence dependence. Nucleic Acids Res. 2013, 41, 8886–8895. [Google Scholar] [CrossRef] [PubMed]
- Rao, A.N.; Grainger, D.W. Biophysical properties of nucleic acids at surfaces relevant to microarray performance. Biomater. Sci. 2014, 2, 436–471. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Wolf, L.K.; Georgiadis, R.M. Secondary structure effects on DNA hybridization kinetics: a solution versus surface comparison. Nucleic Acids Res. 2006, 34, 3370–3377. [Google Scholar] [CrossRef] [PubMed]
- Glazer, M.I.; Fidanza, J.A.; McGall, G.H.; Trulson, M.O.; Forman, J.E.; Frank, C.W. Kinetics of oligonucleotide hybridization to DNA probe arrays on high-capacity porous silica substrates. Biophys. J. 2007, 93, 1661–1676. [Google Scholar] [CrossRef] [PubMed]
- Weng, X.; Jiang, H.; Li, D. Microfluidic DNA hybridization assays. Microfluid Nanofluidics 2011, 11, 367–383. [Google Scholar] [CrossRef]
- Horny, M.-C.; Lazerges, M.; Siaugue, J.-M.; Pallandre, A.; Rose, D.; Bedioui, F.; Deslouis, C.; Haghiri-Gosnet, A.-M.; Gamby, J. Electrochemical DNA biosensors based on long-range electron transfer: investigating the efficiency of a fluidic channel microelectrode compared to an ultramicroelectrode in a two-electrode setup. Lab Chip 2016, 16, 4373–4381. [Google Scholar] [CrossRef] [PubMed]
- Bailey, L.E.; Kanazawa, K.K.; Bhatara, G.; Tyndall, G.W.; Kreiter, M.; Knoll, W.; Frank, C.W. Multistep adsorption of perfluoropolyether HardDisk lubricants onto amorphous carbon substrates from solution. Langmuir 2001, 17, 8145–8155. [Google Scholar] [CrossRef]
| Probe ID | Probe Sequence | ΔG a | GC b | Tm c |
|---|---|---|---|---|
| vanA-1 | ATCTTTCGTATTCATCAGGAAG | −14.3 | 36.4% | 61.8 |
| vanA-2 | GAAAAAGGCTCTGAAAACGCAGTT | −18.5 | 41.7% | 62.8 |
| vanA-3 | CGTTATCCCCGTATGATGGC | −16.2 | 55.0% | 60.9 |
| vanB-1 | ATGAATAGAATAAAAGTCGCAA | −13.3 | 27.3% | 52.3 |
| vanB-2 | GGCTGCGATATTCAAAGCTCCG | −18.7 | 54.5% | 65.8 |
| vanB-3 | TATATCGGGTGCTTGGATGCAGAGG | −21.1 | 52.0% | 67.7 |
| vanC-1 | GCCTTATGTATGAACAAATGGCT | −16.4 | 39.1% | 58.1 |
| vanC-2 | GATGGCTGTATCCAAGGACTGCTTG | −20.4 | 52.0% | 65.8 |
| vanC-3 | CCTCAAAAGGGATCACTAAAGTCAC | −18.0 | 44.0% | 60.2 |
| vanD-1 | TTATATTGGAATCACAAAATCCGGCG | −18.9 | 38.5% | 66.1 |
| vanD-2 | GAGGCCGTTACCGGGAGTGGGTAGG | −24.3 | 68.0% | 72.3 |
| vanD-3 | TTTTTTAAGATTCATCAGGAACACAGCCGGA | −25.1 | 38.7% | 70.5 |
| vanE-1 | AGGGACAAGACCTACAAAAAGTCGA | −19.3 | 44.0% | 62.2 |
| vanE-2 | CCGAATGAGGCAGGCTCATCAAAAG | −20.9 | 52.0% | 69.3 |
| vanE-3 | GGAATTAGCAAGGTAGAACGAAAAA | −17.1 | 36.0% | 59.9 |
| vanG-1 | TACCAGGCTTTACCTCGCACAGTCG | −22.4 | 56.0% | 68.0 |
| vanG-2 | AAAGCTCTGGGCTGTTCGGGTTTTT | −21.5 | 48.0% | 68.3 |
| vanG-3 | ATTGGTCTATCGTTCTCCCAAATGT | −18.4 | 40.0% | 61.8 |
| Flowrate (mL/min) | 0.01 | 0.1 | 0.25 | 0.5 | 1 | 2 | 20 |
|---|---|---|---|---|---|---|---|
| Velocity (m/s) | 6.03 × 10−6 | 6.03 × 10−5 | 1.51 × 10−4 | 3.01 × 10−4 | 6.03 × 10−4 | 1.21 × 10−3 | 1.21 × 10−2 |
| Re | 0.0001 | 0.0009 | 0.0022 | 0.0044 | 0.0087 | 0.0175 | 0.1746 |
| Pe | 1.16 | 11.63 | 29.07 | 58.15 | 116.30 | 232.60 | 2325.95 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munir, A.; Waseem, H.; Williams, M.R.; Stedtfeld, R.D.; Gulari, E.; Tiedje, J.M.; Hashsham, S.A. Modeling Hybridization Kinetics of Gene Probes in a DNA Biochip Using FEMLAB. Microarrays 2017, 6, 9. https://doi.org/10.3390/microarrays6020009
Munir A, Waseem H, Williams MR, Stedtfeld RD, Gulari E, Tiedje JM, Hashsham SA. Modeling Hybridization Kinetics of Gene Probes in a DNA Biochip Using FEMLAB. Microarrays. 2017; 6(2):9. https://doi.org/10.3390/microarrays6020009
Chicago/Turabian StyleMunir, Ahsan, Hassan Waseem, Maggie R. Williams, Robert D. Stedtfeld, Erdogan Gulari, James M. Tiedje, and Syed A. Hashsham. 2017. "Modeling Hybridization Kinetics of Gene Probes in a DNA Biochip Using FEMLAB" Microarrays 6, no. 2: 9. https://doi.org/10.3390/microarrays6020009
APA StyleMunir, A., Waseem, H., Williams, M. R., Stedtfeld, R. D., Gulari, E., Tiedje, J. M., & Hashsham, S. A. (2017). Modeling Hybridization Kinetics of Gene Probes in a DNA Biochip Using FEMLAB. Microarrays, 6(2), 9. https://doi.org/10.3390/microarrays6020009






