t-Test at the Probe Level: An Alternative Method to Identify Statistically Significant Genes for Microarray Data
Abstract
:1. Introduction
2. Methodology
3. Results
3.1. Sensitivity
3.2. Robustness
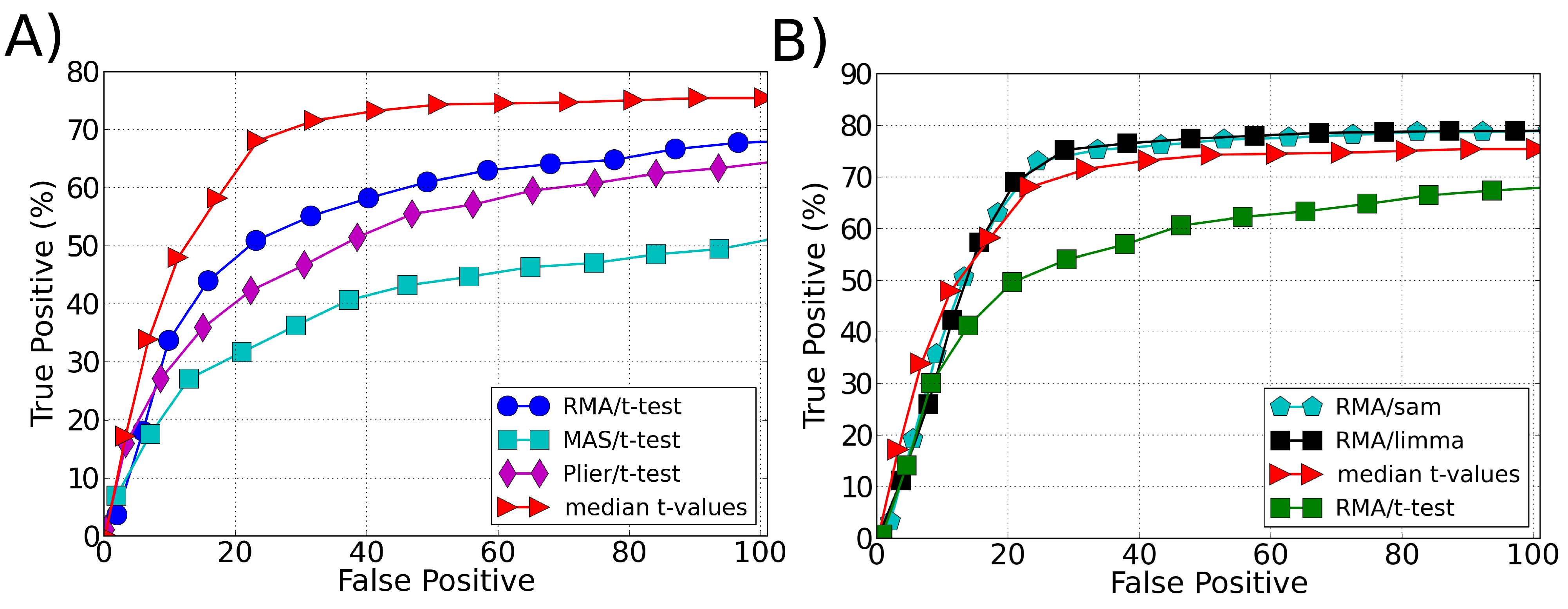
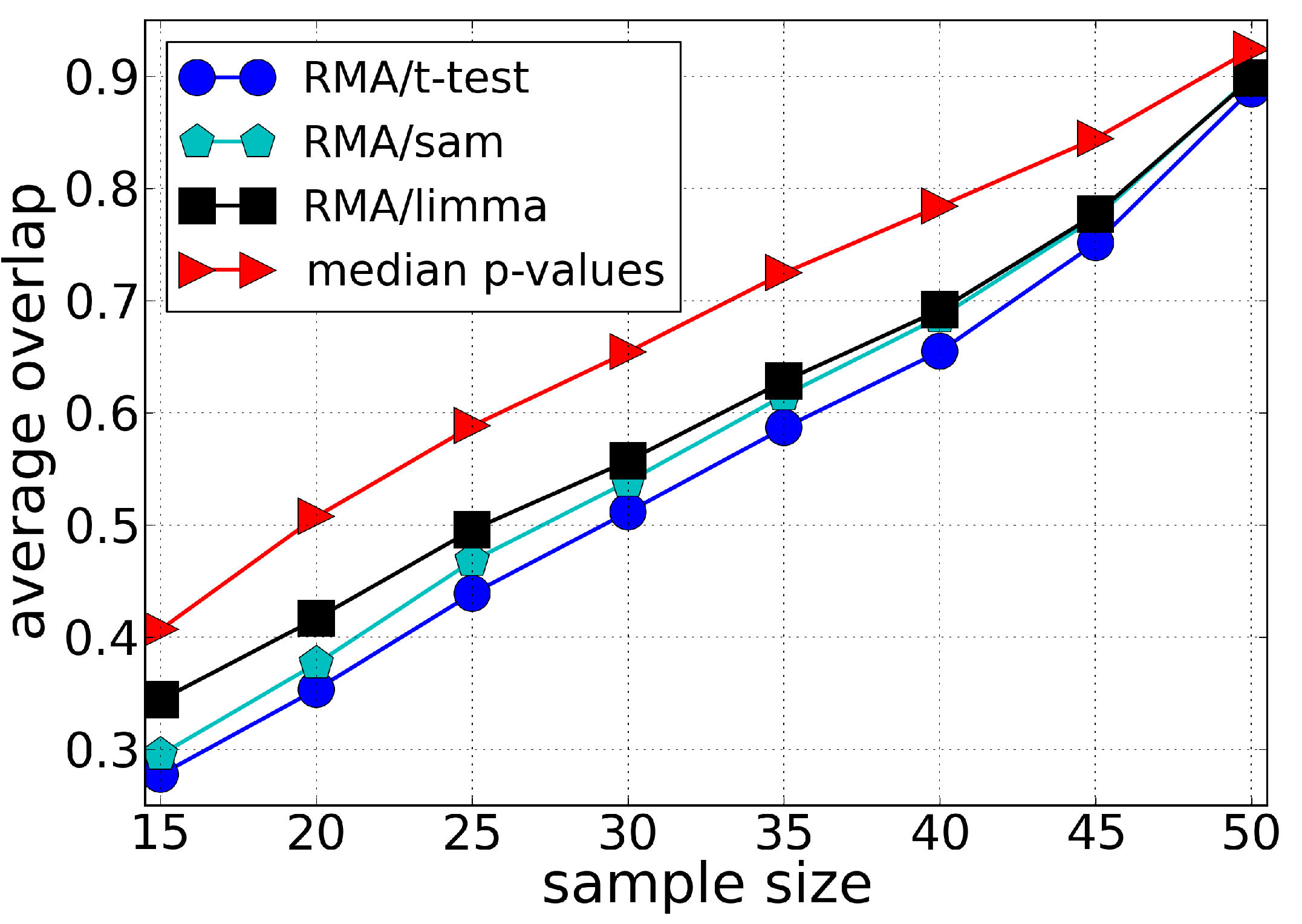
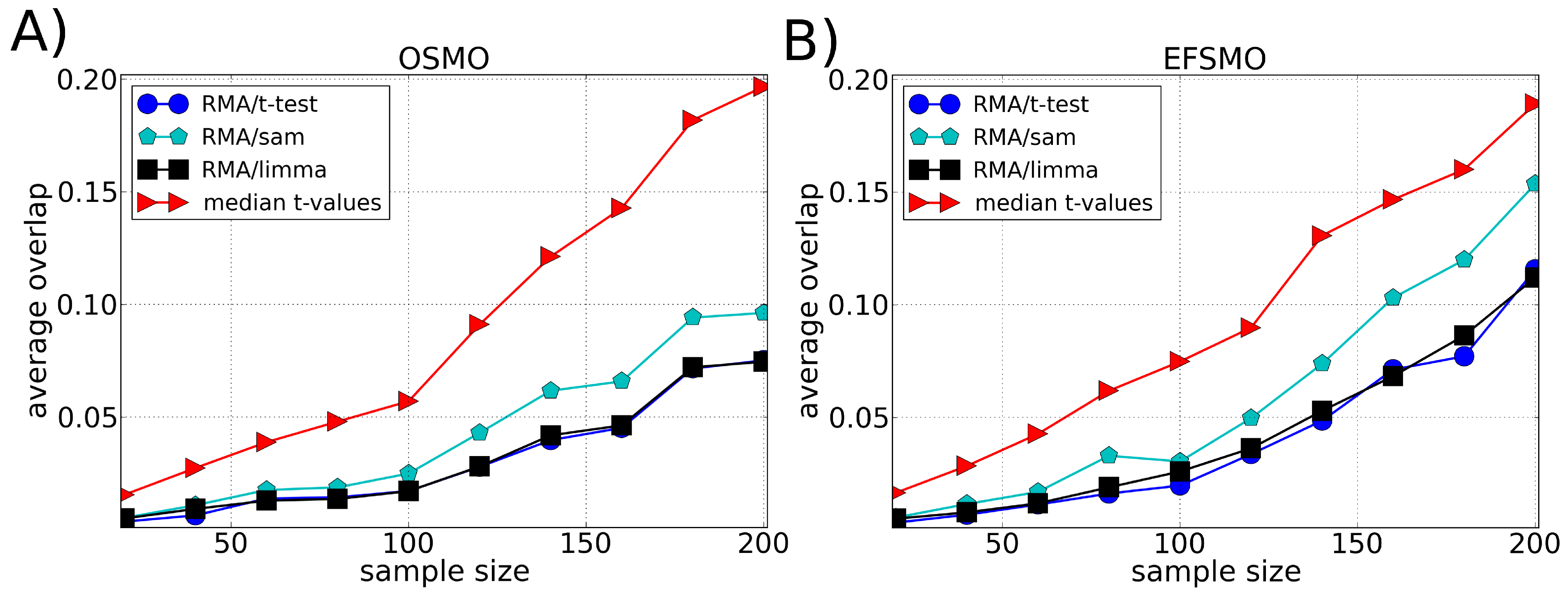
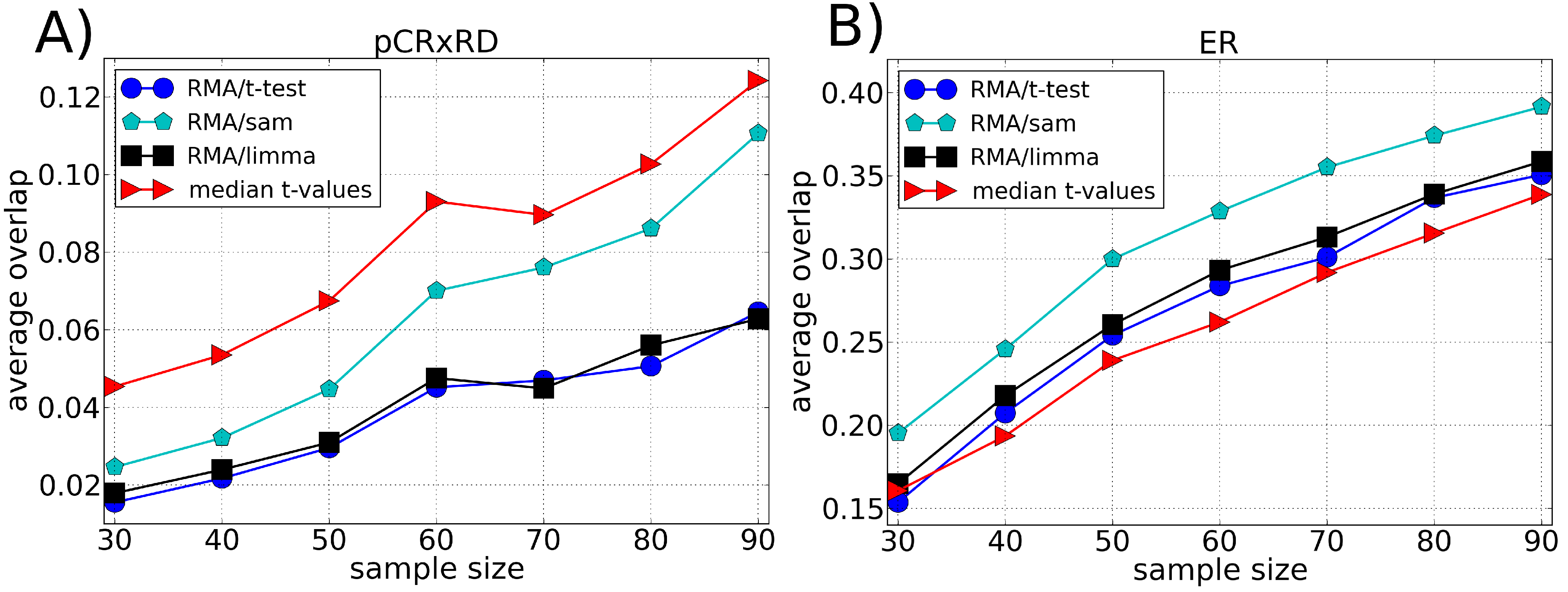
4. Discussion
Acknowledgments
Author Contributions
Appendices
| gene/exp | 1–3 | 4–6 | 7–9 | 10–12 | 13–15 | 16–18 | 19–21 | 22–24 | 25–27 | 28–30 | 31–33 | 34–36 | 37–39 | 40–42 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1–3 | 0 | 0.125 | 0.25 | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 |
| 4–6 | 0.125 | 0.25 | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 0 |
| 7–9 | 0.25 | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 0 | 0.125 |
| 10–12 | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 0 | 0.125 | 0.25 |
| 13–15 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 0 | 0.125 | 0.25 | 0.5 |
| 16–18 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 0 | 0.125 | 0.25 | 0.5 | 1 |
| 19–21 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 0 | 0.125 | 0.25 | 0.5 | 1 | 2 |
| 22–24 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 0 | 0.125 | 0.25 | 0.5 | 1 | 2 | 4 |
| 25–27 | 16 | 32 | 64 | 128 | 256 | 512 | 0 | 0.125 | 0.25 | 0.5 | 1 | 2 | 4 | 8 |
| 28–30 | 32 | 64 | 128 | 256 | 512 | 0 | 0.125 | 0.25 | 0.5 | 1 | 2 | 4 | 8 | 16 |
| 31–33 | 64 | 128 | 256 | 512 | 0 | 0.125 | 0.25 | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 |
| 34–36 | 128 | 256 | 512 | 0 | 0.125 | 0.25 | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
| 37–39 | 256 | 512 | 0 | 0.125 | 0.25 | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
| 40–42 | 512 | 0 | 0.125 | 0.25 | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
| Dataset | Training Set | Validation Set | ||||
|---|---|---|---|---|---|---|
| Number of Samples | Positive | Negative | Number of Samples | Positive | Negative | |
| Breast Cancer (pCR) | 130 | 33 | 97 | 100 | 15 | 85 |
| Breast Cancer (ER) | 130 | 80 | 50 | 100 | 61 | 39 |
| Multiple Myeloma (OS-MO) | 340 | 51 | 289 | 214 | 27 | 187 |
| Multiple Myeloma (EFS-MO) | 340 | 84 | 256 | 214 | 34 | 180 |
Conflicts of Interest
References
- Ein-Dor, L.; Kela, I.; Getz, G.; Givol, D.; Domany, E. Outcome signature genes in breast cancer: Is there a unique set? Bioinformatics 2005, 21, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Ein-Dor, L.; Zuk, O.; Domany, E. Thousands of samples are needed to generate a robust gene list for predicting outcome in cancer. Proc. Natl. Acad. Sci. USA 2006, 103, 5923–5928. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Wong, W.H. Model-based analysis of oligonucleotide arrays: Expression index computation and outlier detection. Proc. Natl. Acad. Sci. USA 2001, 98, 31–36. [Google Scholar] [CrossRef] [PubMed]
- Irizarry, R.A.; Hobbs, B.; Collin, F.; Beazer-Barclay, Y.D.; Antonellis, K.J.; Scherf, U.; Speed, T.P. Exploration, normalization, and summaries of high density oligonucleotide array probe level data. Biostatistics 2003, 4, 249–264. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z. A review of statistical methods for preprocessing oligonucleotide microarrays. Stat. Methods Med. Res. 2009, 18, 533–541. [Google Scholar] [PubMed]
- Guide to Probe Logarithmic Intensity Error (Plier) Estimation. Available online: http://www.affy metrix.com/support/technical/technotes/plier_technote.pdf (accessed on 1 November 2012).
- Shi, L.; Tong, W.; Fang, H.; Scherf, U.; Han, J.; Puri, R.K.; Frueh, F.W.; Goodsaid, F.M.; Guo, L.; Su, Z.; et al. Cross-platform comparability of microarray technology: Intra-platform consistency and appropriate data analysis procedures are essential. BMC Bioinform. 2005, 6, eS12. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Reid, L.H.; Jones, W.D.; Shippy, R.; Warrington, J.A.; Baker, S.C.; Collins, P.J.; de Longueville, F.; Kawasaki, E.S.; Lee, K.Y.; et al. The MicroArray Quality Control (MAQC) project shows inter- and intraplatform reproducibility of gene expression measurements. Nat. Biotechnol. 2006, 24, 1151–1161. [Google Scholar] [CrossRef] [PubMed]
- Allison, D.B.; Cui, X.; Page, G.P.; Sabripour, M. Microarray data analysis: From disarray to consolidation and consensus. Nat. Rev. Genet. 2006, 7, 55–65. [Google Scholar] [CrossRef] [PubMed]
- Jeanmougin, M.; de Reynies, A.; Marisa, L.; Paccard, C.; Nuel, G.; Guedj, M. Should we abandon the t-test in the analysis of gene expression microarray data: A comparison of variance modeling strategies. PLoS One 2010, 5, e0012336. [Google Scholar] [CrossRef] [PubMed]
- Tusher, V.G.; Tibshirani, R.; Chu, G. Significance analysis of microarrays applied to the ionizing radiation response. Proc. Natl. Acad. Sci. USA 2001, 98, 5116–5121. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Hwang, J.; Qiu, J.; Blades, N.; Churchill, G. Improved statistical tests for differential gene expression by shrinking variance components estimates. Biostatistics 2005, 6, 59–75. [Google Scholar] [CrossRef] [PubMed]
- Wright, G.W.; Simon, R.M. A random variance model for detection of differential gene expression in small microarray experiments. Bioinformatics 2003, 19, 2448–2455. [Google Scholar] [CrossRef] [PubMed]
- Smyth, G.K. Linear models and empirical Bayes methods for assessing differential expression in microarray experiments. Stat. Appl. Genet. Mol. Biol. 2004, 3, e3. [Google Scholar] [CrossRef] [PubMed]
- Zeisel, A.; Amir, A.; Kostler, W.J.; Domany, E. Intensity dependent estimation of noise in microarrays improves detection of differentially expressed genes. BMC Bioinform. 2010, 11, e400. [Google Scholar] [CrossRef] [PubMed]
- Baldi, P.; Long, A.D. A Bayesian framework for the analysis of microarray expression data: Regularized t-test and statistical inferences of gene changes. Bioinformatics 2001, 17, 509–519. [Google Scholar] [CrossRef] [PubMed]
- Stevens, J.R.; Bell, J.L.; Aston, K.I.; White, K.L. A comparison of probe-level and probeset models for small-sample gene expression data. BMC Bioinform. 2010, 11, e281. [Google Scholar] [CrossRef] [PubMed]
- Lemieux, S. Probe-level linear model fitting and mixture modeling results in high accuracy detection of differential gene expression. BMC Bioinform. 2006, 7, e391. [Google Scholar] [CrossRef] [PubMed]
- Barrera, L.; Benner, C.; Tao, Y. Leveraging two-way probe-level block design for identifying differential gene expression with high-density oligonucleotide arrays. BMC Bioinform. 2004, 14, 1–14. [Google Scholar]
- Astrand, M.; Mostad, P.; Rudemo, M. Empirical Bayes models for multiple probe type microarrays at the probe level. BMC Bioinform. 2008, 9, e156. [Google Scholar] [CrossRef] [PubMed]
- Chu, J.T. On the distribution of the sample median. Ann. Math. Stat. 1955, 26, 112–116. [Google Scholar] [CrossRef]
- Latin Square Data for Expression Algorithm Assessment. Available online: http://www.affymetrix.com/support/technical/sample_data/datasets.affx (accessed on 1 November 2012).
- Cope, L.M.; Irizarry, R.A.; Jaffee, H.A.; Wu, Z.; Speed, T.P. A benchmark for Affymetrix GeneChip expression measures. Bioinformatics 2004, 20, 323–331. [Google Scholar] [CrossRef] [PubMed]
- Bolstad, B.M.; Irizarry, R.A.; Astrand, M.; Speed, T.P. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics 2003, 19, 185–193. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Campbell, G.; Jones, W.D.; Campagne, F.; Wen, Z.; Walker, S.J.; Su, Z.; Chu, T.M.; Goodsaid, F.M.; Pusztai, L.; et al. The MicroArray Quality Control (MAQC)-II study of common practices for the development and validation of microarray-based predictive models. Nat. Biotechnol. 2010, 28, e827. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, S.A.; Staunton, J.E.; Silverman, L.B.; Pieters, R.; den Boer, M.L.; Minden, M.D.; Sallan, S.E.; Lander, E.S.; Golub, T.R.; Korsmeyer, S.J. MLL translocations specify a distinct gene expression profile that distinguishes a unique leukemia. Nat. Genet. 2002, 30, 41–47. [Google Scholar] [CrossRef] [PubMed]
- Golub, T.R.; Slonim, D.K.; Tamayo, P.; Huard, C.; Gaasenbeek, M.; Mesirov, J.P.; Coller, H.; Loh, M.; Downing, J.R.; Caligiuri, M.A.; et al. Molecular Classification of Cancer: Class Discovery and Class Prediction by Gene Expression Monitoring. Science 1999, 286, 531–537. [Google Scholar] [CrossRef] [PubMed]
- Gyorffy, B.; Molnar, B.; Lage, H.; Szallasi, Z.; Eklund, A.C. Evaluation of microarray preprocessing algorithms based on concordance with RT-PCR in clinical samples. PLoS One 2009, 4, e0005645. [Google Scholar] [CrossRef] [PubMed]
- Therneau, T.M.; Ballman, K.V. What does PLIER really do? Cancer Inform. 2008, 6, 423–431. [Google Scholar] [PubMed]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Boareto, M.; Caticha, N. t-Test at the Probe Level: An Alternative Method to Identify Statistically Significant Genes for Microarray Data. Microarrays 2014, 3, 340-351. https://doi.org/10.3390/microarrays3040340
Boareto M, Caticha N. t-Test at the Probe Level: An Alternative Method to Identify Statistically Significant Genes for Microarray Data. Microarrays. 2014; 3(4):340-351. https://doi.org/10.3390/microarrays3040340
Chicago/Turabian StyleBoareto, Marcelo, and Nestor Caticha. 2014. "t-Test at the Probe Level: An Alternative Method to Identify Statistically Significant Genes for Microarray Data" Microarrays 3, no. 4: 340-351. https://doi.org/10.3390/microarrays3040340
APA StyleBoareto, M., & Caticha, N. (2014). t-Test at the Probe Level: An Alternative Method to Identify Statistically Significant Genes for Microarray Data. Microarrays, 3(4), 340-351. https://doi.org/10.3390/microarrays3040340




