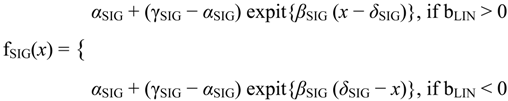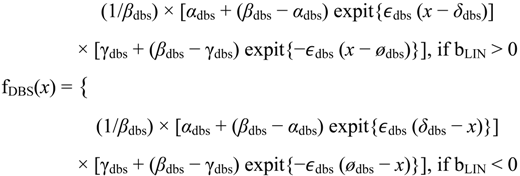1. Introduction
Many gene expression experiments involve serial measurements in response to a varying condition, such as temperature, oxygen availability, time, drug concentration, levels of pollutants, and exposures to ultraviolet light. Often investigators want to compare the time varying response between two scenarios, such as two species or two drugs. For this comparative analysis, we developed an algorithm to fit biologically relevant curves to serial response measurements from each gene, identify pairs of curves that fit well, and compare these curves under the two scenarios in terms of heteromorphy (different curves), heterochrony (different transition times) and heterometry (different magnitudes). In the context of ontogeny, Yanai
et al. [
1] introduced the concepts of heteromorphy and heterochrony in gene expression curves as analogs to tissue-level heteromorphy (different sizes of developing organs) and heterochrony (movement of modules in anatomy and physiology). In other comparative gene expression settings heteromorphy and heterochrony in gene expression curves can also provide insight into biological processes. The purpose of this methodology is to compare gene expression patterns in two settings, as guided by biologically relevant models. To simplify this discussion, we consider time as the time varying condition.
The fitting part of the algorithm involves the following models: flat, linear, sigmoid, double sigmoid [
2], and generalized double sigmoid [
3]. The flat and linear models yield flat and linear response curves, respectively. The sigmoid model yields a sigmoid curve (two steady states with an intermediate transition following a logistic function), a hockey stick curve (sigmoid curve missing one steady state) or a transition curve (sigmoid missing two steady states). The double sigmoid is the product of two sigmoid models; it yields an impulse curve (with a peak or trough) or step curve (with an intermediate-level plateau). The generalized double sigmoid curve adds an additional parameter to the double sigmoid model and yields analogous impulse+ curve or step+ curves. We also characterized all the curves, except for flat, as either trending upward or downward or having a downward or upward impulse.
The aforementioned response curves are biologically relevant, as opposed to polynomial curves of degree two or greater, which generally have little biological basis. Flat curves represent a steady state. Linear curves represent the constant addition or subtraction of reacting components. Sigmoid curves model the addition or subtraction of reacting components from one steady state to another steady state. Sigmoid curves also arise in transcription factor binding [
4,
5]. Impulse and impulse+ curves represent a temporary increase or decrease in reacting components that resolves into a new steady state [
1]. Step and step+ curves represent an intermediate-level steady state amid a monotonically increasing or decreasing number of reacting components.
Although there is a large literature on the fitting of response curves to sequential gene expression measurements in dose-response and short time series studies [
6,
7,
8,
9,
10], there has been little work on the comparative analysis of response curves. A notable exception is Sivriver,
et al. [
3] who fit and compared generalized double sigmoid response curves under two stimuli. A major concern of Sivriver
et al. [
3] was overfitting. Overfitting means that a model has so many parameters relative to time points that chance deviations from the true model strongly influence the model fit and lead to poor predictions at time points not used in model fitting. Here overfitting is particularly a concern for two reasons. First the generalized double sigmoid and double sigmoid models have a large number of parameters relative to the number of time points. Second the investigation of over ten thousands genes implies a much higher probability of substantial chance deviations in the response curves for some genes than if only a few genes were studied. Sivriver,
et al. [
3] tackled the problem of overfitting by pooling data from multiple genes with similar generalized double sigmoid response curves. Because we focus on heterochrony and heterometry, which would be diluted by pooling, we developed a different approach to reduce overfitting that does not involve pooling. In our approach we evaluated model fits at different times from those used to fit the model. In particular we fit biologically relevant curves to every other response (first, third, fifth, …) and evaluated the fits at the remaining responses (second, fourth, sixth, …), providing an empirical investigation of model fit. Because we used seven points for model fitting and seven points for model evaluation, we needed at least 14 points to adequately fit and evaluate the generalized double sigmoid model, which has seven parameters.
For illustration, we applied our algorithm to mean gene expression levels (averaged over three technical replicates and three specimens) for 11,299 genes at 14 development times in two species of frogs,
X.laevis and
X.tropicalis. [
1]. We found some interesting examples of heteromorphy and heterochrony that will hopefully spur new research. However, the main contribution of this paper is a method for identifying the most interesting changes in pairs of biologically relevant shapes for gene expression curves in comparative studies.
2. Identifying Biologically Relevant Response Curves that Fit Well
As noted by Forster [
11] standard methods of model selection (such as likelihood ratio tests, the Akaike Information Criterion (AIC), the Bayesian Information Criterion, and Minimum Description Length [
11,
12,
13]) minimize the discrepancy between predicted and observed results at the
same time points used to fit the model. In the spirit of Forster [
11] and with the emphasis on reducing overfitting, we were instead interested in minimizing the discrepancy between predicted and observed results at
different time points than used to fit the model. Similarly, Chechik and Koller [
2] evaluated double sigmoid fits at a single point that was left out of the fitting procedure. We considered every other point as left-out in order to examine discrepancy between observed and predicted results over the entire range of times.
Consider a single gene. Let yj denote the jth observed response and xj denote the jth observed time. We fit the model to responses {y1, y3, y5, y7, y9, y11, y13} at times {x1, x3, x5, x7, x9, x11, x13}. We call {(x1, y1), (x3, y3), (x5, y5), (x7, y7), (x9, y9), (x11, y11)} the fitted points. We evaluate the model at {(x2, y2), (x4, y4), (x6, y6), (x8, y8), (x10, y10), (x12, y12)}, which we call the evaluation points Let {f(x2), f(x4), f(x6), f(x8), f(x10), f(x12), f(x14)}denote the predicted responses of a particular model corresponding to the evaluation points.
We needed a measure of how well the predicted responses fit the observed evaluation points. One measure considered was the mean squared error (MSE). The problem with using MSE is that it depends on the absolute sizes of responses, so two genes could have the same MSE’s for comparing predicted and observed responses, yet visually one may fit well and the other fit poorly. To circumvent this problem we introduced the Relative Prediction Error (RPE), which is the square root of the MSE of the predicted response divided by the difference between the largest and smallest predicted responses, expressed as a percentage. The reason for using the square root is to put the measure on the same scale as the responses, analogous to using a standard deviation instead of a variance. The reason for dividing by the range of responses is to make small deviations between predicted and observed response relative to the entire shape of the curve, which leads to a visually satisfying measure. Let
J ={2, 4, 6, 8, 10, 12, 14} index the evaluation points. Mathematically we write RPE for our situation with 14 time points as
The formula for RPE can be readily modified for more than 14 points. Based on a visual inspection of curves with different values of RPE, we decided that a threshold of 10% was a reasonable indicator of a good fit. To put the idea of a threshold RPE into perspective, note that a likelihood ratio test comparing observed and fitted counts typically also involves a threshold, namely a 5% type I error.
When comparing predicted and observed results at
different time points than used to fit the model, Forster [
11] evaluated the fit of the model without considering the complexity of the model. A rationale is that an evaluation at different time points than used for fitting inherently penalizes for complexity that leads to overfitting. Nevertheless, visual inspection suggests that parsimony is desirable for characterizing curves based on their fits to the evaluation points. For characterizing parsimony using the evaluation points we allow a 5% leeway in terms of RPE for a curve with fewer parameters than the curve with smallest RPE. In other words, if a response curve has fewer parameters than the response curve with smallest RPE, we prefer the response curve with fewer parameters if its RPE is less than or equal to the smallest RPE plus 5% We chose the value of 5% based on visual inspection of many curves.
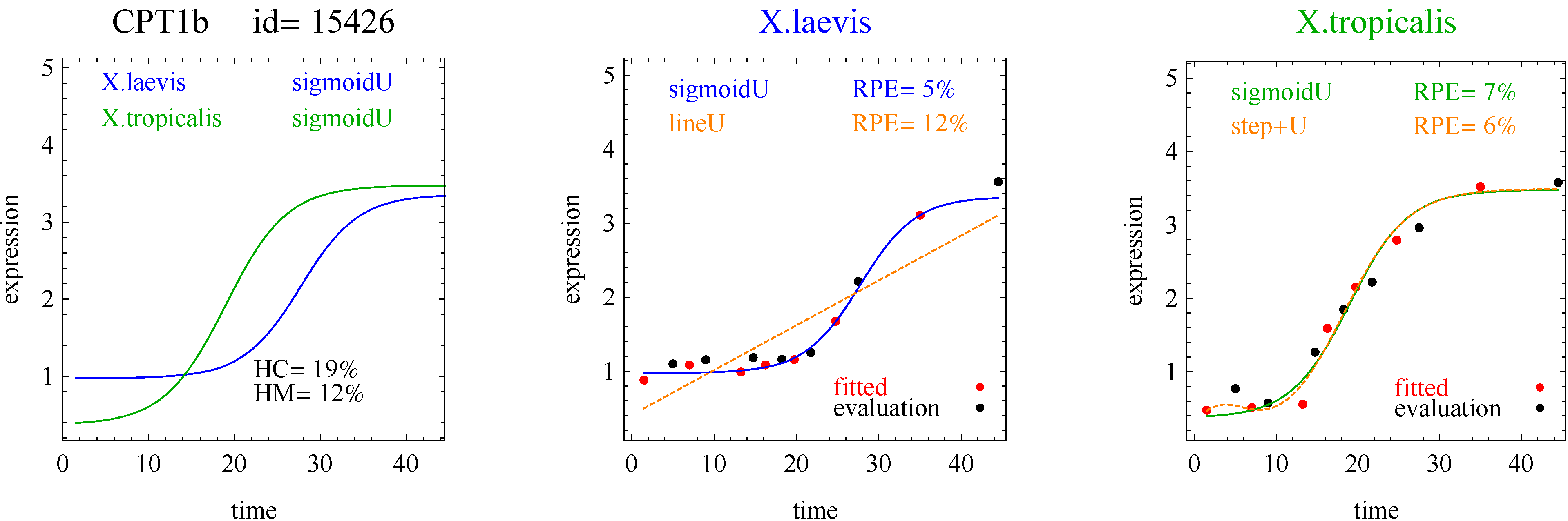
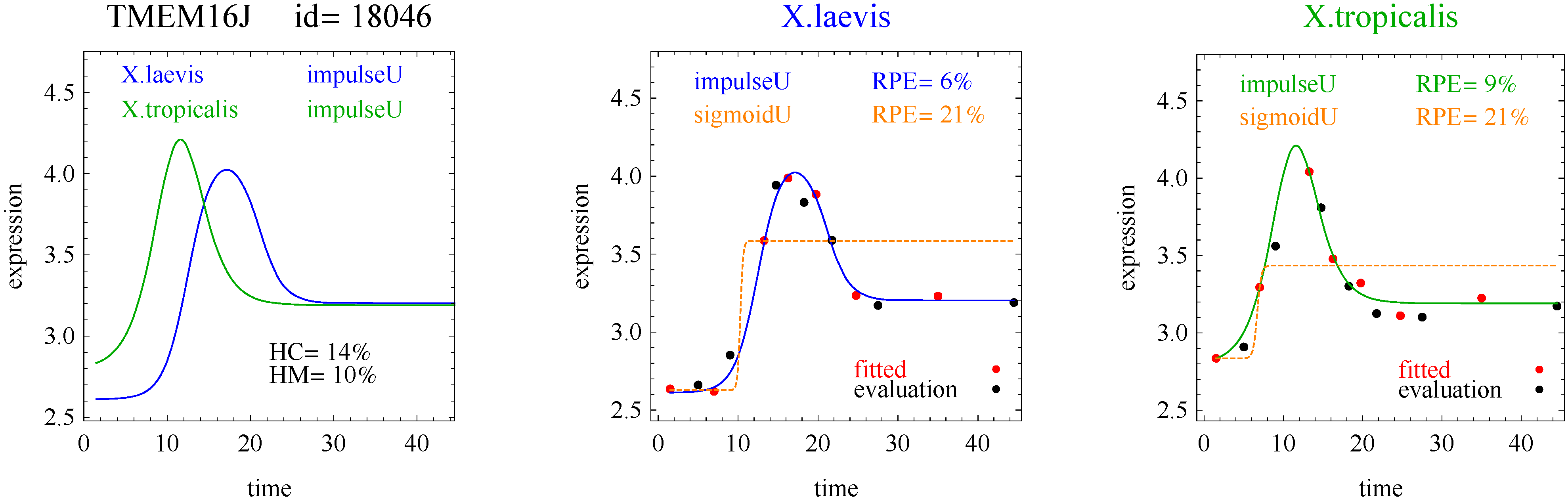
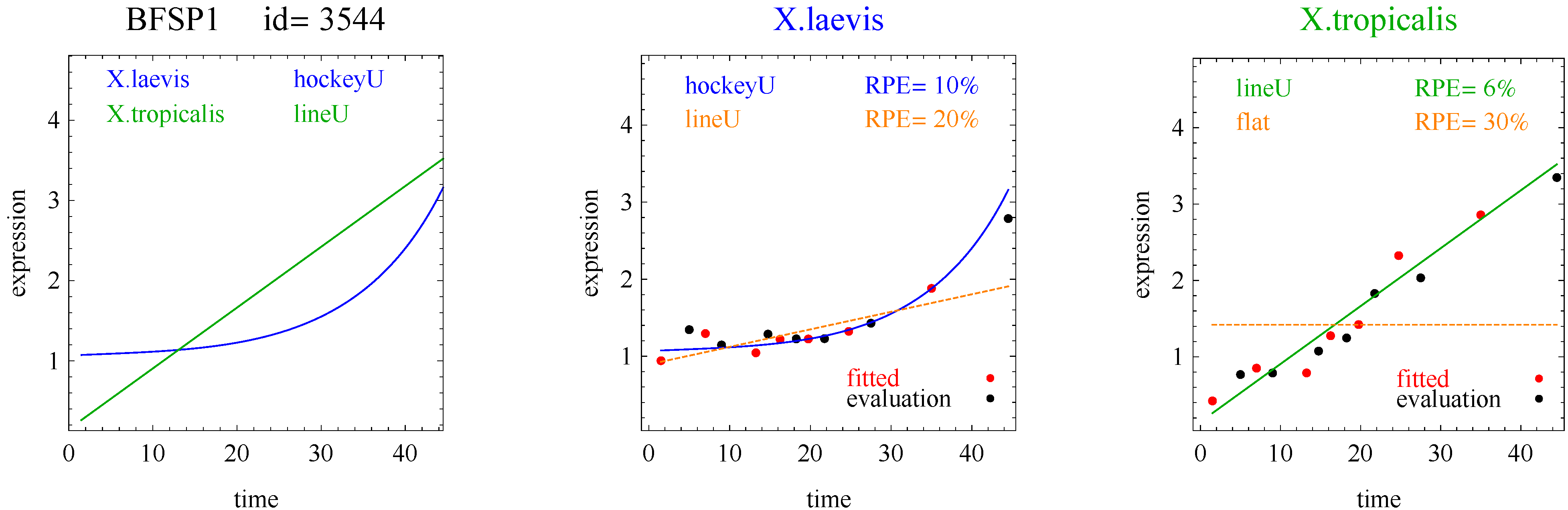
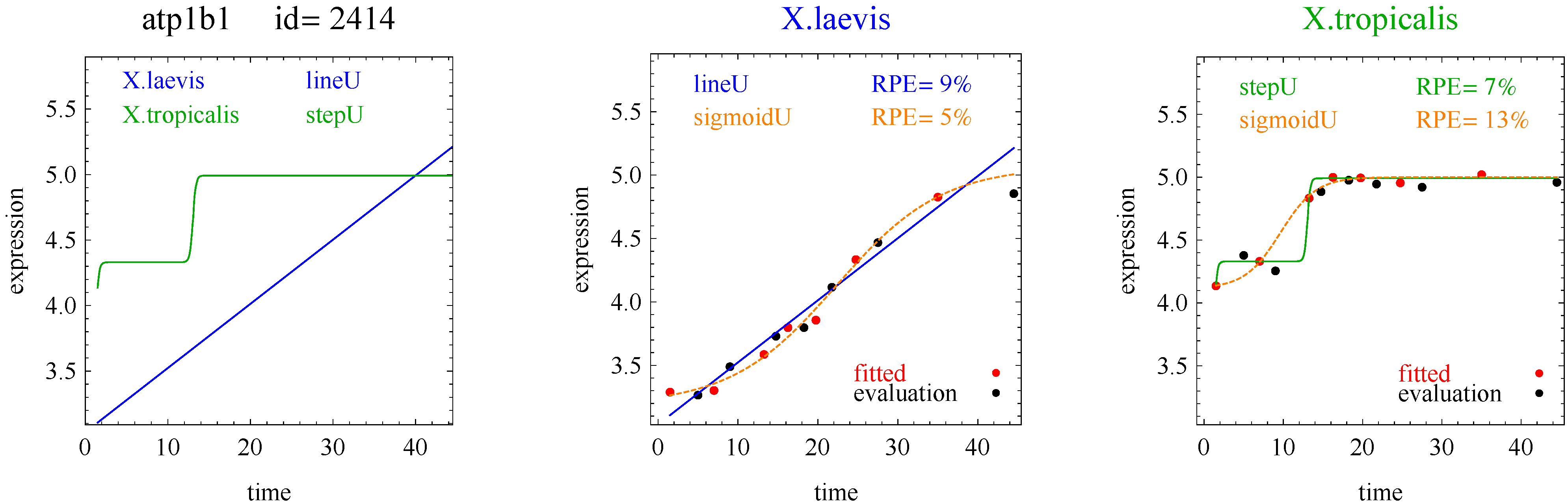
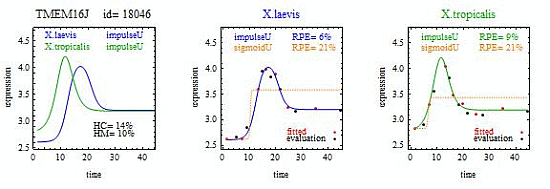
To introduce the curve selection algorithm, consider the following two hypothetical examples for a single gene. In the first example, suppose the RPE’s for flat, lineU, sigmoidU, impulseU, and impulse+U curves are 30%, 12%, 11%, 8%, and 9%, respectively (as explained in the next section, the “U” designates upward trend).
Step 1. In this first example the best fitting curve is impulseU because it has the smallest RPE, namely 8%. Because this RPE of 8% is less than or equal to the 10% RPE threshold for a good fit, we consider impulseU a good fit and investigate a more parsimonious curve in Step 2. Otherwise, if this RPE were greater than 10%, we would not report a response curve for this gene.
Step 2. In this first example, lineU and sigmoidU satisfy the 5% RPE leeway requirement, both having an RPE ≤ 8% + 5% = 13%. Because lineU has fewer parameters than sigmoidU, we select lineU as the reported response curve.
In the second hypothetical example, suppose the RPE’s for flat, lineU, sigmoidU, impulseU, and impulse+U curves are 30%, 22%, 14%, 8%, 9%, respectively.
Step 1. In this second example, the best fitting curve is impulseU because it has the smallest RPE, namely 8%. Because it is a good fit with RPE < 10%, we investigate a more parsimonious model in Step 2.
Step 2. In this second example, no curve with fewer parameters than impulseU satisfies the 5% RPE leeway requirement. Therefore we select impulseU as the reported response curve. However, for purposes of comparison, we identify the curve with the next fewest parameters than impulseU, namely sigmoidU.
We formalize the curve selection algorithm as follows.
Step 1. Let Curve A denote the response curve with the smallest RPE, which we denote RPEA. In the first example Curve A is impulseU. If RPEA > 10%, report no curve; otherwise proceed to Step 2.
Step 2. We identify a Curve B as follows. Let CurveSetB denote the set of response curves with fewer parameters than Curve A. In the first example CurveSetB = {flat, lineU, sigmoidU}. Let CurveSubsetB denote a subset of response curves in CurveSetB such that RPE ≤ RPEA + 5%. In the first example CurveSubsetB is {lineU, sigmoidU}. If CurveSubsetB is the empty set, we identify Curve B as the curve with the most parameters in CurveSetB (sigmoidU in the second example) but select Curve A as the reported curve. If CurveSubsetB is not empty we identify Curve B as the curve in CurveSubsetB with the fewest parameters (lineU in the first example) and select Curve B as the reported curve.
When we report a pair of response curves for a gene, we require that each response curve in the pair yield a good fit to the data with RPEA ≤ 10%. The curve reported for each gene in the pair is either Curve A or Curve B, whichever was selected via the curve selection algorithm.
In our application to frog data, the 5% RPE leeway agreed well with the sign of the change in AIC, where AIC = 7 log [Σ
j in J {
yj −
f(xj)}
2/7] + 2 × (number of parameters). Although this is a non-standard use of AIC because it applies to evaluation points instead of fitted points, it is still instructive.
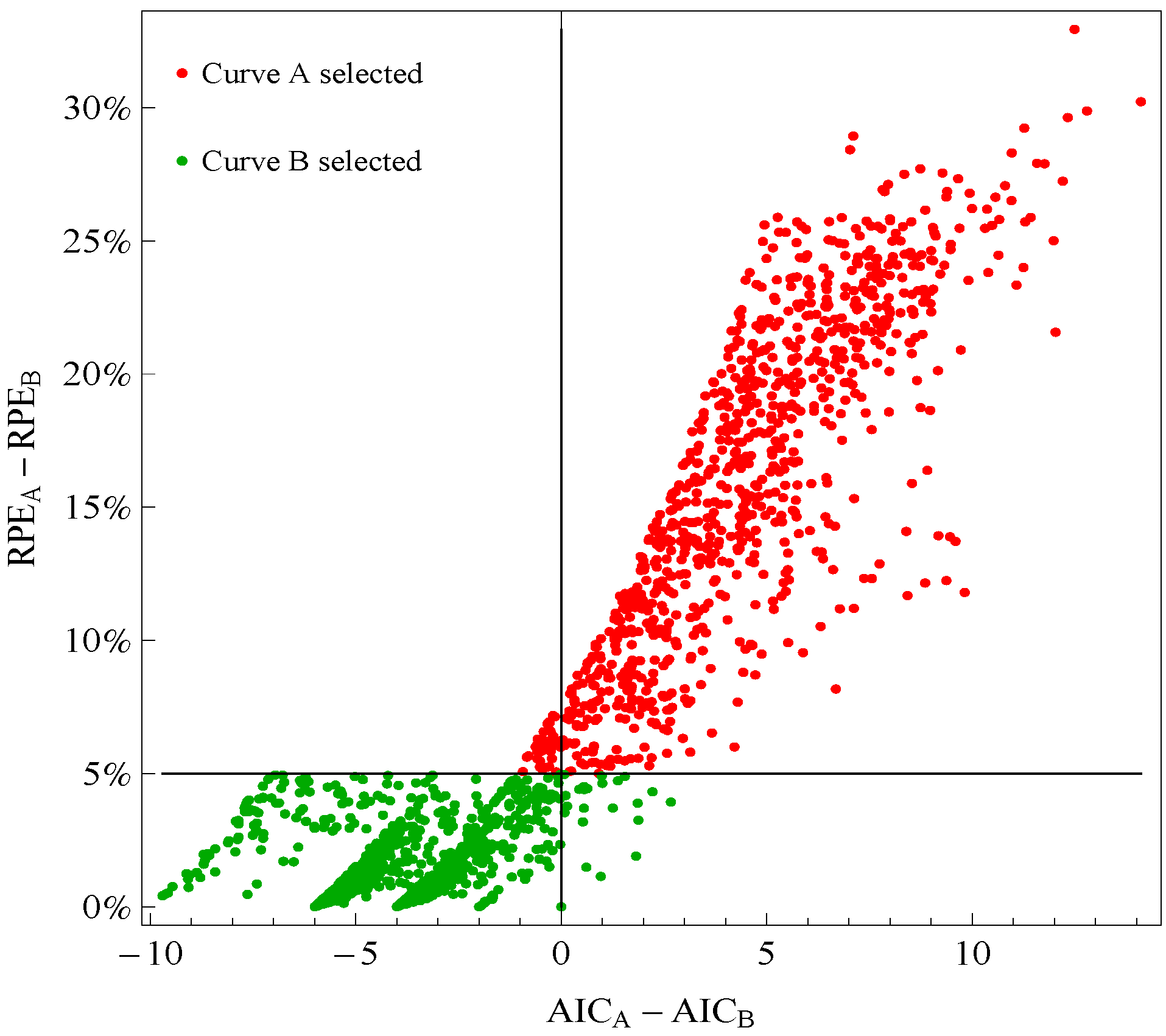
Figure 1 plots points for genes with good fitting models in both species of frogs. The points labeled Curve A (Curve B) selected correspond to reporting Curve A (Curve B) in the curve selection algorithm. Most Curve A selected points, which require RPE
A − RPE
B > 5%, correspond to AIC
A − AIC
B > 0 (the upper right quadrant). Most Curve B selected points, which require RPE
A − RPE
B ≤ 5%, correspond to AIC
A − AIC
B ≤ 0 (the lower left quadrant).
Figure 1.
Comparison of a change in relative prediction error (RPE) with a change in Akaike Information Criterion (AIC) among response curve pairs. The red points corresponding to Curve A require RPEA− RPEB ≤ 5% (so are above the horizontal 5% line) The green points corresponding to Curve B require RPEA − RPEB ≤ 5% (so are below the horizontal 5% line). A value of AICA − AICB ≤ 0 (so on the left of vertical line) would indicate selection of Curve B.
Figure 1.
Comparison of a change in relative prediction error (RPE) with a change in Akaike Information Criterion (AIC) among response curve pairs. The red points corresponding to Curve A require RPEA− RPEB ≤ 5% (so are above the horizontal 5% line) The green points corresponding to Curve B require RPEA − RPEB ≤ 5% (so are below the horizontal 5% line). A value of AICA − AICB ≤ 0 (so on the left of vertical line) would indicate selection of Curve B.