Evaluating Alternative Correction Methods for Multiple Comparison in Functional Neuroimaging Research
Abstract
1. Introduction
The Present Study
2. Materials and Methods
2.1. Subjects and Materials
2.2. Procedures
2.2.1. fMRI Data Reanalysis
2.2.2. Noise-Added Image Creation for Evaluation
2.2.3. Statistical Assessment of Consistency
3. Results
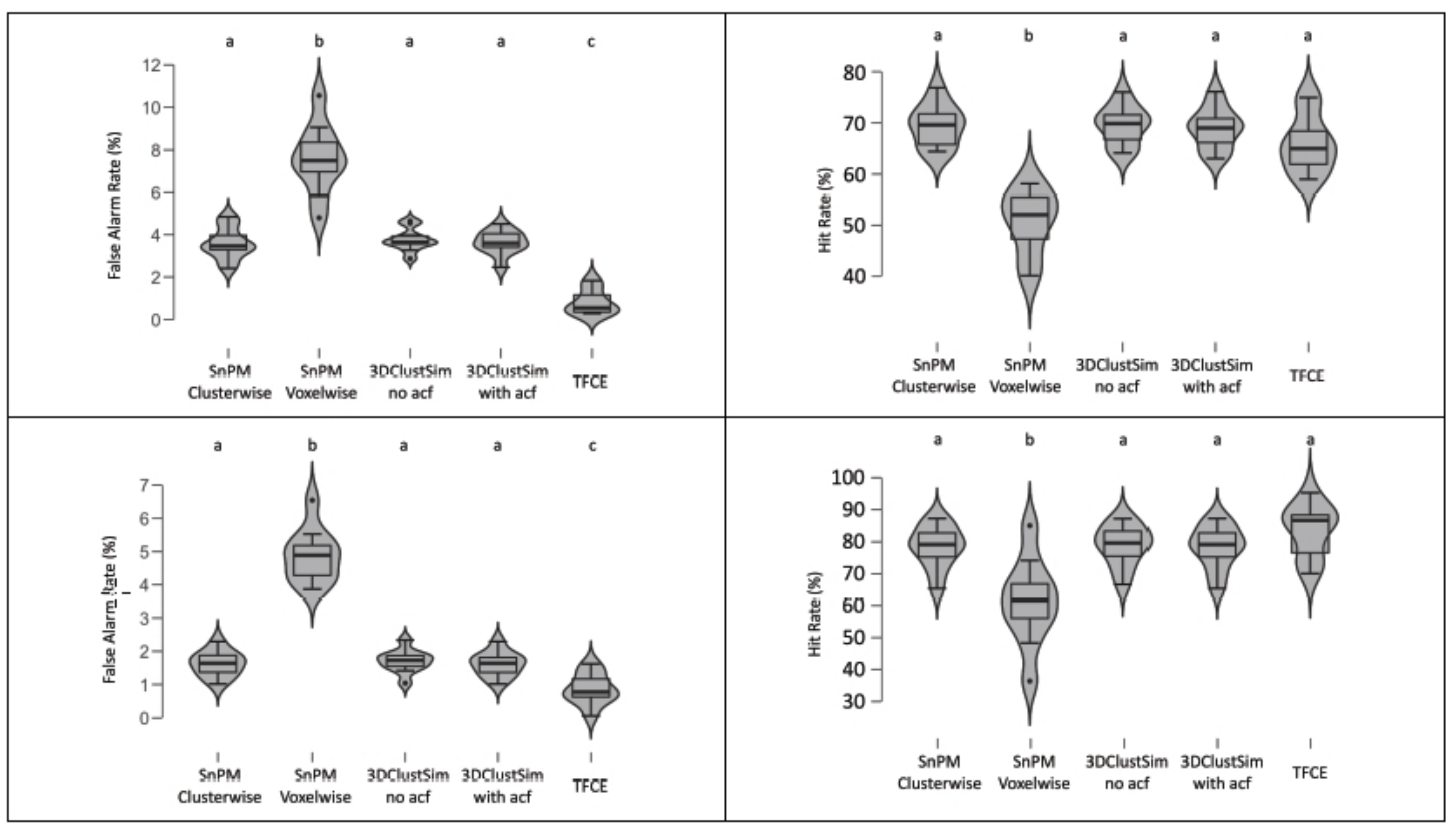
3.1. Thresholding Results with Different Methods
3.2. Comparing Consistency Outcomes between SnPM, 3DClustSim, and TFCE
4. Discussion
Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SnPM | Statistical non-Parametric Mapping |
| TFCE | Threshold Free Cluster Enhancement |
| SPM | Statistical Parametric Mapping |
| FSL | FMRIB Software Library |
| AFNI | Analysis of Functional NeuroImages |
| FWE | Family-Wise Error |
| RFT | Random Field Theory |
| FDR | False Discovery Rate |
| UAHPC | University of Alabama High-Performance Computing |
| ResMS | Residual Mean Squares |
References
- Bennett, C.M.; Miller, M.B.; Wolford, G.L. Neural correlates of interspecies perspective taking in the post-mortem Atlantic Salmon: An argument for multiple comparisons correction. NeuroImage 2009, 47, S125. [Google Scholar] [CrossRef]
- Nichols, T.; Hayasaka, S. Controlling the family-wise error rate in functional neuroimaging: A comparative review. Stat. Methods Med. Res. 2003, 12, 419–446. [Google Scholar] [CrossRef] [PubMed]
- Genovese, C.R.; Lazar, N.A.; Nichols, T. Thresholding of statistical maps in functional neuroimaging using the false discovery rate. NeuroImage 2002, 15, 870–878. [Google Scholar] [CrossRef] [PubMed]
- Cox, R.W.; Chen, G.; Glen, D.R.; Reynolds, R.C.; Taylor, P.A. fMRI clustering and false-positive rates. Proc. Natl. Acad. Sci. USA 2017, 114, E3370–E3371. [Google Scholar] [CrossRef] [PubMed]
- Slotnick, S.D. Resting-state fMRI data reflects default network activity rather than null data: A defense of commonly employed methods to correct for multiple comparisons. Cogn. Neurosci. 2017, 8, 141–143. [Google Scholar] [CrossRef] [PubMed]
- Nichols, T.E.; Eklund, A.; Knutsson, H. A defense of using resting-state fMRI as null data for estimating false positive rates. Cogn. Neurosci. 2017, 8, 144–149. [Google Scholar] [CrossRef] [PubMed]
- Eklund, A.; Nichols, T.E.; Knutsson, H. Cluster failure: Why fMRI inferences for spatial extent have inflated false-positive rates. Proc. Natl. Acad. Sci. USA 2016, 113, 7900–7905. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Glenn, A.L. Evaluating methods of correcting for multiple comparisons implemented in SPM12 in social neuroscience fMRI studies: an example from moral psychology. Soc. Neurosci. 2018, 13, 257–267. [Google Scholar] [CrossRef] [PubMed]
- Poldrack, R.A. Inferring mental states from neuroimaging data: From reverse inference to large-scale decoding. Neuron 2011, 72, 692–697. [Google Scholar] [CrossRef]
- Lieberman, M.D.; Cunningham, W.A. Type I and Type II error concerns in fMRI research: Re-balancing the scale. Soc. Cogn. Affect. Neurosci. 2009, 4, 423–428. [Google Scholar] [CrossRef]
- Nichols, T.; Holmes, A.P. Nonparametric permutation tests for functional neuroimaging: A primer with examples. Hum. Brain Mapp. 2002, 15, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.M.; Nichols, T.E. Threshold-free cluster enhancement: Addressing problems of smoothing, threshold dependence and localisation in cluster inference. NeuroImage 2009, 44, 83–98. [Google Scholar] [CrossRef] [PubMed]
- Cox, R.W.; Chen, G.; Glen, D.R.; Reynolds, R.C.; Taylor, P.A. FMRI Clustering in AFNI: False-Positive Rates Redux. Brain Connect. 2017, 7, 152–171. [Google Scholar] [CrossRef] [PubMed]
- Cox, R.W. AFNI: Software for Analysis and Visualization of Functional Magnetic Resonance Neuroimages. Comput. Biomed. Res. 1996, 29, 162–173. [Google Scholar] [CrossRef] [PubMed]
- Nichols, T. Multiple testing corrections, nonparametric methods, and random field theory. NeuroImage 2012, 62, 811–815. [Google Scholar] [CrossRef] [PubMed]
- Nichols, T.E. Statistical nonParametric Mapping—Manual; University of Warwick: Coventry, England, UK, 2014. [Google Scholar]
- National Institute of Mental Health. AFNI Program: 3dClustSim; National Institute of Mental Health: Bethesda, MD, USA, 2017.
- Winkler, A.M.; Ridgway, G.R.; Webster, M.A.; Smith, S.M.; Nichols, T.E. Permutation inference for the general linear model. NeuroImage 2014, 92, 381–397. [Google Scholar] [CrossRef] [PubMed]
- Thornton, M.A. MatlabTFCE. 2016. Available online: http://markallenthornton.com/blog/matlab-tfce/ (accessed on 11 August 2019).
- Cox, R.W. Equitable Thresholding and Clustering. Brain Connect. 2019. [Google Scholar] [CrossRef]
- Han, H. Neural correlates of moral sensitivity and moral judgment associated with brain circuitries of selfhood: a meta-analysis. J. Moral. Educ. 2017, 46, 97–113. [Google Scholar] [CrossRef]
- Han, H.; Park, J. Using SPM 12’s Second-level Bayesian Inference Procedure for fMRI Analysis: Practical Guidelines for End Users. Front. Neuroinform. 2018, 12, 1. [Google Scholar] [CrossRef]
- Greene, J.D.; Sommerville, R.B.; Nystrom, L.E.; Darley, J.M.; Cohen, J.D. An fMRI investigation of emotional engagement in moral judgment. Science 2001, 293, 2105–2108. [Google Scholar] [CrossRef]
- Han, H.; Chen, J.; Jeong, C.; Glover, G.H. Influence of the cortical midline structures on moral emotion and motivation in moral decision-making. Behav. Brain Res. 2016, 302, 237–251. [Google Scholar] [CrossRef] [PubMed]
- DeYoung, C.G.; Shamosh, N.A.; Green, A.E.; Braver, T.S.; Gray, J.R. Intellect as distinct from openness: Differences revealed by fMRI of working memory. J. Pers. Soc. Psychol. 2009, 97, 883–892. [Google Scholar] [CrossRef] [PubMed]
- Kragel, P.A.; Kano, M.; Van Oudenhove, L.; Ly, H.G.; Dupont, P.; Rubio, A.; Delon-Martin, C.; Bonaz, B.L.; Manuck, S.B.; Gianaros, P.J.; et al. Generalizable representations of pain, cognitive control, and negative emotion in medial frontal cortex. Nat. Neurosci. 2018, 21, 283–289. [Google Scholar] [CrossRef] [PubMed]
- Jo, H.J.; Saad, Z.S.; Simmons, W.K.; Milbury, L.A.; Cox, R.W. Mapping sources of correlation in resting state FMRI, with artifact detection and removal. Neuroimage 2010, 52, 571–582. [Google Scholar] [CrossRef] [PubMed]
- Greene, J.D.; Nystrom, L.E.; Engell, A.D.; Darley, J.M.; Cohen, J.D. The neural bases of cognitive conflict and control in moral judgment. Neuron 2004, 44, 389–400. [Google Scholar] [CrossRef] [PubMed]
- Glover, G.H.; Li, T.Q.; Ress, D. Image-based method for retrospective correction of physiological motion effects in fMRI: RETROICOR. Magn. Reson. Med. 2000, 44, 162–167. [Google Scholar] [CrossRef]
- Chang, C.; Glover, G.H. Relationship between respiration, end-tidal CO2, and BOLD signals in resting-state fMRI. NeuroImage 2009, 47, 1381–1393. [Google Scholar] [CrossRef] [PubMed]
- Gorgolewski, C. NeuroVault. 2015. Available online: https://neurovault.org/ (accessed on 11 August 2019).
- Cognitive and Affective Neuroscience Lab at University of Colorado Boulder. fMRI Dataset. 2019. Available online: https://canlabweb.colorado.edu/files/MFC_Generalizability.tar.gz (accessed on 11 August 2019).
- Woo, C.W.; Krishnan, A.; Wager, T.D. Cluster-extent based thresholding in fMRI analyses: Pitfalls and recommendations. NeuroImage 2014, 91, 412–419. [Google Scholar] [CrossRef]
- Triantafyllou, C.; Hoge, R.D.; Wald, L.L. Effect of spatial smoothing on physiological noise in high-resolution fMRI. Neuroimage 2006, 32, 551–557. [Google Scholar] [CrossRef]
- Friman, O.; Cedefamn, J.; Lundberg, P.; Borga, M.; Knutsson, H. Detection of neural activity in functional MRI using canonical correlation analysis. Magn. Reson. Med. 2001, 45, 323–330. [Google Scholar] [CrossRef]
- Zarahn, E.; Aguirre, G.; D’Esposito, M. Empirical Analyses of BOLD fMRI Statistics. Neuroimage 1997, 5, 179–197. [Google Scholar] [CrossRef]
- Olszowy, W.; Aston, J.; Rua, C.; Williams, G.B. Accurate autocorrelation modeling substantially improves fMRI reliability. Nat. Commun. 2019, 10, 1220. [Google Scholar] [CrossRef]
- Gopinath, K.; Krishnamurthy, V.; Lacey, S.; Sathian, K. Accounting for Non-Gaussian Sources of Spatial Correlation in Parametric Functional Magnetic Resonance Imaging Paradigms II: A Method to Obtain First-Level Analysis Residuals with Uniform and Gaussian Spatial Autocorrelation Function and Independent and I. Brain Connect. 2018, 8, 10–21. [Google Scholar] [CrossRef]
- National Institute of Mental Health. AFNI Program: 3dFWHMx; National Institute of Mental Health: Bethesda, MD, USA, 2019. [Google Scholar]
- Brost, M. Correlated Gaussian Noise. 2008. Available online: https://www.mathworks.com/matlabcentral/fileexchange/21156-correlated-gaussian-noise (accessed on 11 August 2019).
- Han, H. Bayesian fMRI-SPM Evaluation. 2018. Available online: https://osf.io/jucgx/ (accessed on 11 August 2019).
- Kass, R.E.; Raftery, A.E. Bayes Factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Han, H.; Park, J.; Thoma, S.J. Why Do We Need to Employ Bayesian Statistics in Studies of Moral Education? J. Moral Educ. 2018. [Google Scholar] [CrossRef]
- Benjamin, D.J.; Berger, J.O.; Johannesson, M.; Nosek, B.A.; Wagenmakers, E.J.; Berk, R.; Bollen, K.A.; Brembs, B.; Brown, L.; Camerer, C.; et al. Redefine statistical significance. Nat. Hum. Behav. 2018, 2, 6–10. [Google Scholar] [CrossRef]
- Wagenmakers, E.J.; Marsman, M.; Jamil, T.; Ly, A.; Verhagen, J.; Love, J.; Selker, R.; Gronau, Q.F.; Smira, M.; Epskamp, S.; et al. Bayesian inference for psychology. Part I: Theoretical advantages and practical ramifications. Psychon. Bull. Rev. 2017. [Google Scholar] [CrossRef]
- Wagenmakers, E.J.; Love, J.; Marsman, M.; Jamil, T.; Ly, A.; Verhagen, J.; Selker, R.; Gronau, Q.F.; Dropmann, D.; Boutin, B.; et al. Bayesian inference for psychology. Part II: Example applications with JASP. Psychon. Bull. Rev. 2017. [Google Scholar] [CrossRef]
- Pernet, C.; Latinus, M.; Nichols, T.; Rousselet, G. Cluster-based computational methods for mass univariate analyses of event-related brain potentials/fields: A simulation study. J. Neurosci. Methods 2015, 250, 85–93. [Google Scholar] [CrossRef]
- Desmond, J.E.; Glover, G.H. Estimating sample size in functional MRI (fMRI) neuroimaging studies: statistical power analyses. J. Neurosci. Methods 2002, 118, 115–128. [Google Scholar] [CrossRef]
- Drost, E.A. Validity and Reliability in Social Science Research. Educ. Res. Perspect. 2011, 38, 105–123. [Google Scholar]
- Hahn, A.D.; Rowe, D.B. Physiologic noise regression, motion regression, and TOAST dynamic field correction in complex-valued fMRI time series. Neuroimage 2012, 59, 2231–2240. [Google Scholar] [CrossRef]
| Correction Method | Number of Surviving Voxels | |
|---|---|---|
| Moral psychology fMRI data | ||
| SnPM voxel-wise p < 0.05 (FWE) | 860 | |
| SnPM cluster-wise p < 0.05 (FWE) | cluster-forming p < 0.001 | 14,945 |
| 3DClustSim cluster-wise p < 0.05 | cluster-forming p < 0.001 | 15,659 |
| 3DClustSim (acf) cluster-wise p < 0.05 | cluster-forming p < 0.001 | 15,273 |
| TFCE | corrected p < 0.05 | 32,272 |
| Working memory fMRI data | ||
| SnPM voxel-wise p < 0.05 (FWE) | 820 | |
| SnPM cluster-wise p < 0.05 (FWE) | cluster-forming p < 0.001 | 15,291 |
| 3DClustSim cluster-wise p < 0.05 | cluster-forming p < 0.001 | 15,426 |
| 3DClustSim (acf) cluster-wise p < 0.05 | cluster-forming p < 0.001 | 15,291 |
| TFCE | corrected p < 0.05 | 20,403 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Glenn, A.L.; Dawson, K.J. Evaluating Alternative Correction Methods for Multiple Comparison in Functional Neuroimaging Research. Brain Sci. 2019, 9, 198. https://doi.org/10.3390/brainsci9080198
Han H, Glenn AL, Dawson KJ. Evaluating Alternative Correction Methods for Multiple Comparison in Functional Neuroimaging Research. Brain Sciences. 2019; 9(8):198. https://doi.org/10.3390/brainsci9080198
Chicago/Turabian StyleHan, Hyemin, Andrea L. Glenn, and Kelsie J. Dawson. 2019. "Evaluating Alternative Correction Methods for Multiple Comparison in Functional Neuroimaging Research" Brain Sciences 9, no. 8: 198. https://doi.org/10.3390/brainsci9080198
APA StyleHan, H., Glenn, A. L., & Dawson, K. J. (2019). Evaluating Alternative Correction Methods for Multiple Comparison in Functional Neuroimaging Research. Brain Sciences, 9(8), 198. https://doi.org/10.3390/brainsci9080198






