Optimization of the Navigated TMS Mapping Algorithm for Accurate Estimation of Cortical Muscle Representation Characteristics
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects and the nTMS Mapping Procedure
2.2. Data Analysis
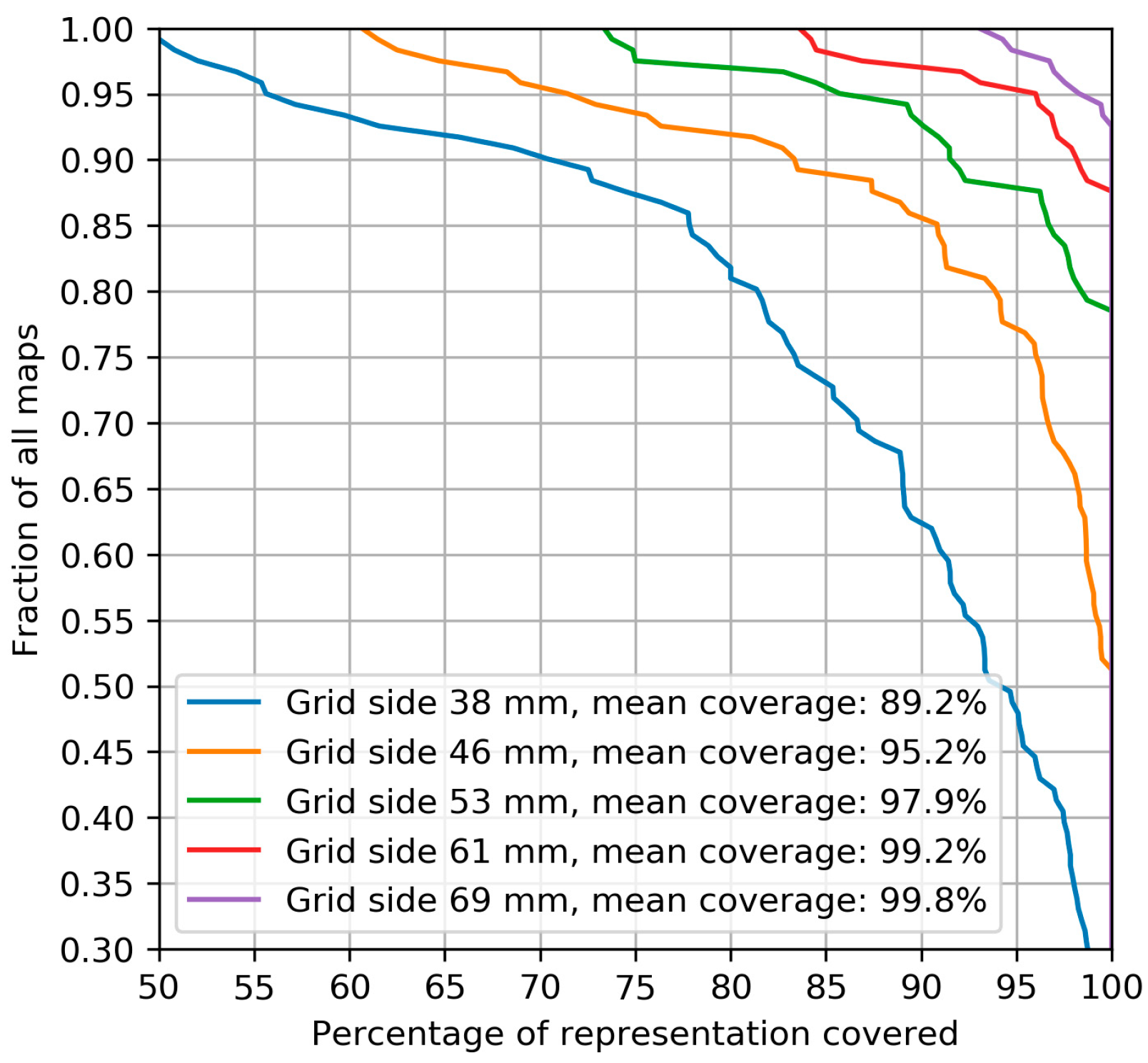
2.2.1. Muscle Representation Coverage by Grids of Different Sizes
2.2.2. Muscle Representation Parameters
- The area of the cells with a mean MEP above 50 µV;
- The area of the cells with a maximum MEP above 50 µV (or, equivalently, the area of the cells with at least one suprathreshold MEP);
- The area of the cells with more than half suprathreshold MEPs;
- The area weighted by the mean MEP amplitude (amplitude-weighted area, also known as map volume [17]);
- The area weighted by the probability of a suprathreshold MEP (probability-weighted area);
- The COG with the weights defined as the mean amplitudes in each grid cell;
- The COG with the weights defined as the maximal amplitudes in each grid cell;
- The COG with the weights defined as the probabilities of suprathreshold MEPs in each grid cell.
2.2.3. Simulation of Mapping with Different Numbers of Stimuli Using Bootstrapping
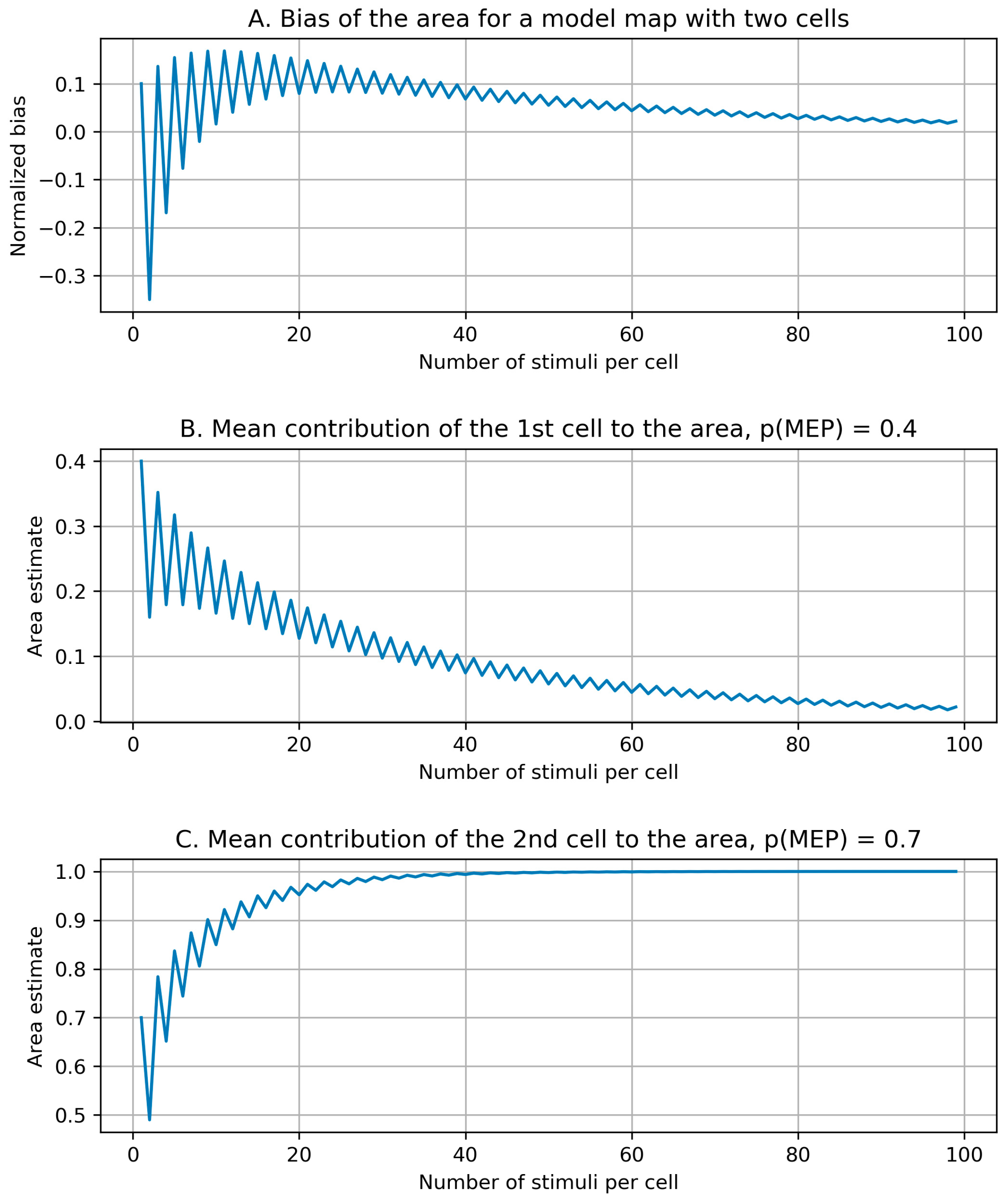
2.2.4. Bias of the Area and Weighted Area
2.2.5. Within-Session Variability of the Area and Weighted Area
2.2.6. Between-Session Variability of the Area and Weighted Area
2.2.7. Sensitivity of the Protocol to Changes between Sessions
2.2.8. Accuracy of the Center of Gravity
3. Results
3.1. Muscle Representation Coverage by Grids of Different Sizes
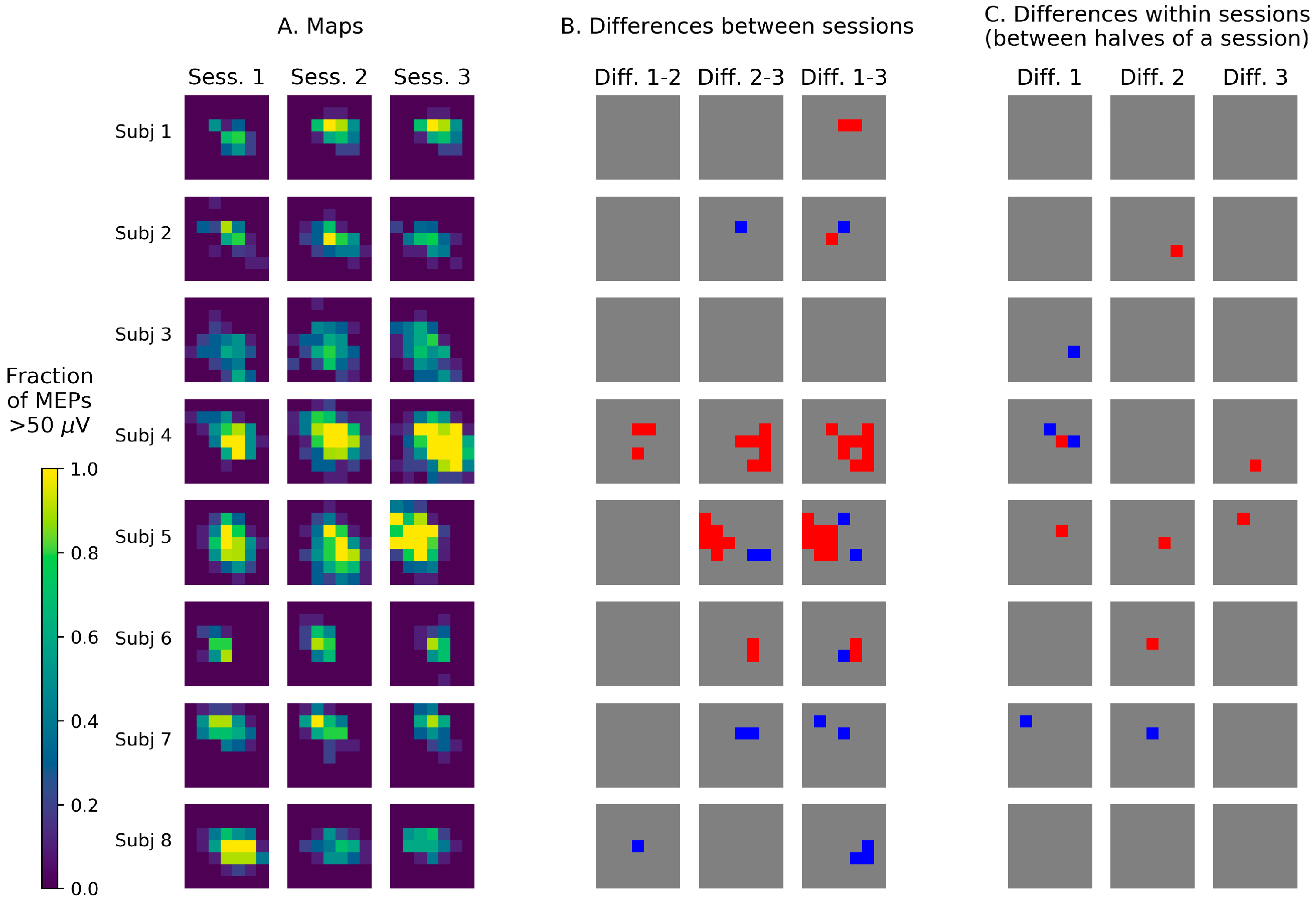
3.2. Visualization of TMS Maps Obtained with a Stimulation Grid
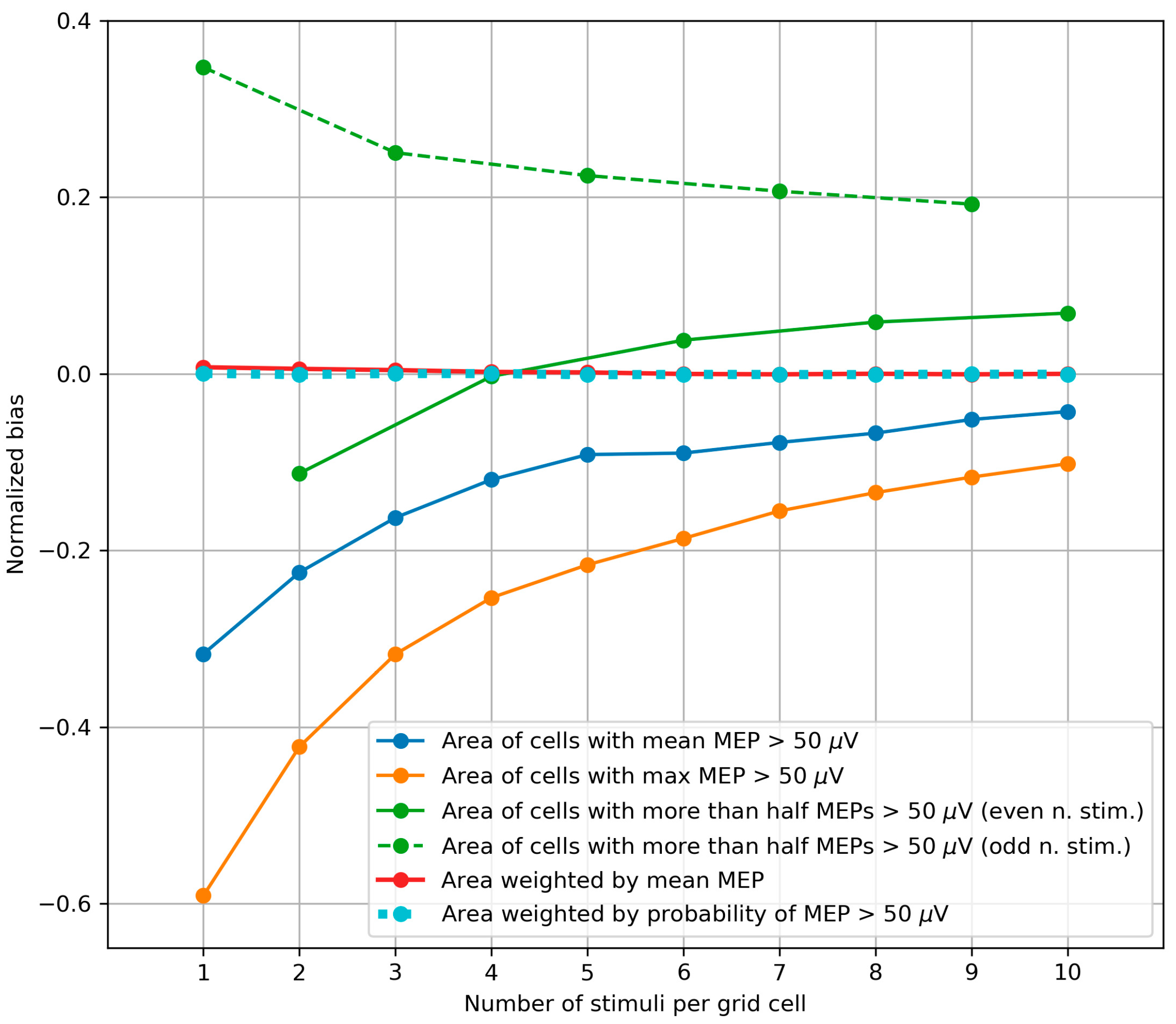
3.3. Bias of the Area and Weighted Area
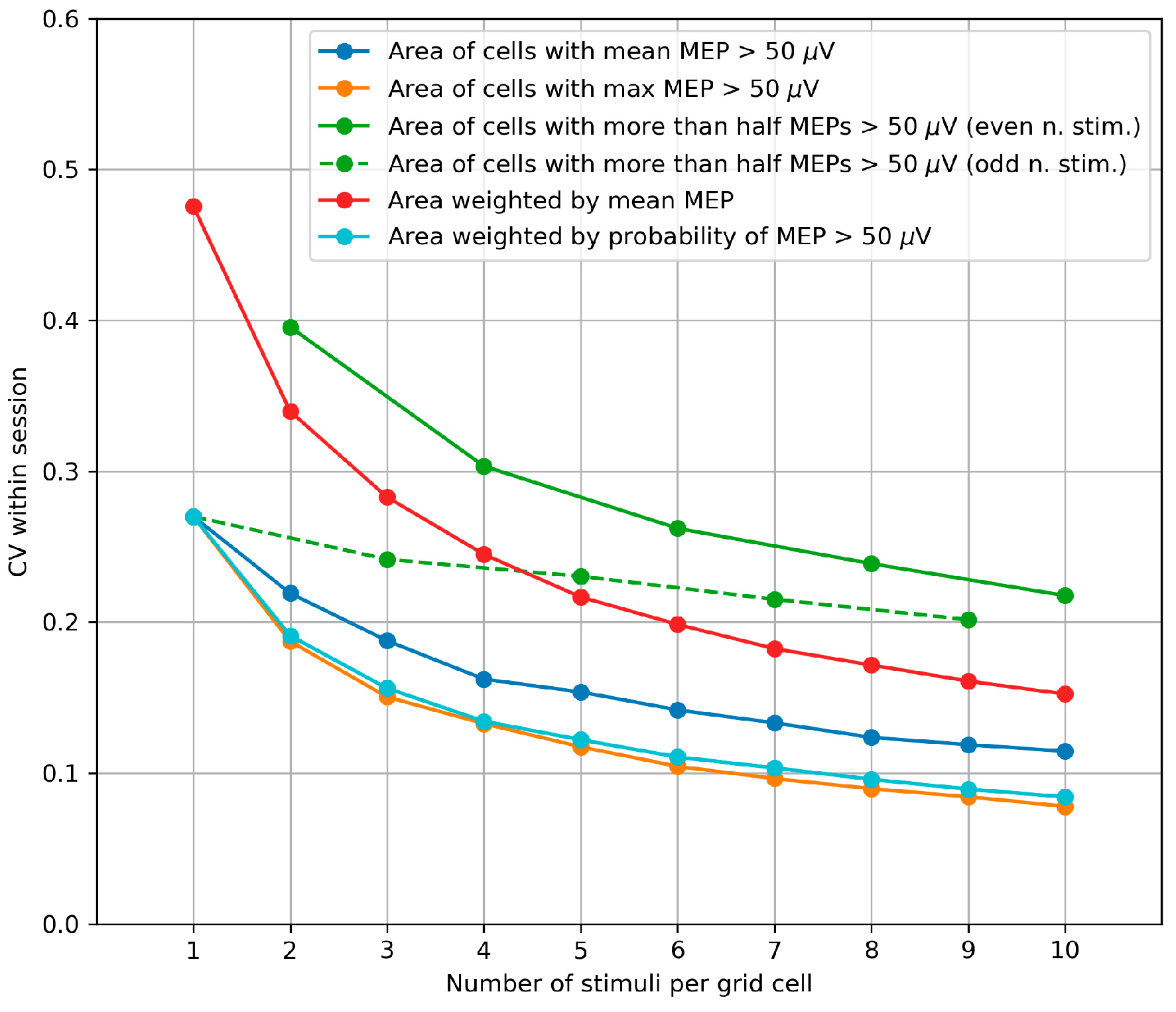
3.4. Within-Session Variability of the Area and Weighted Area
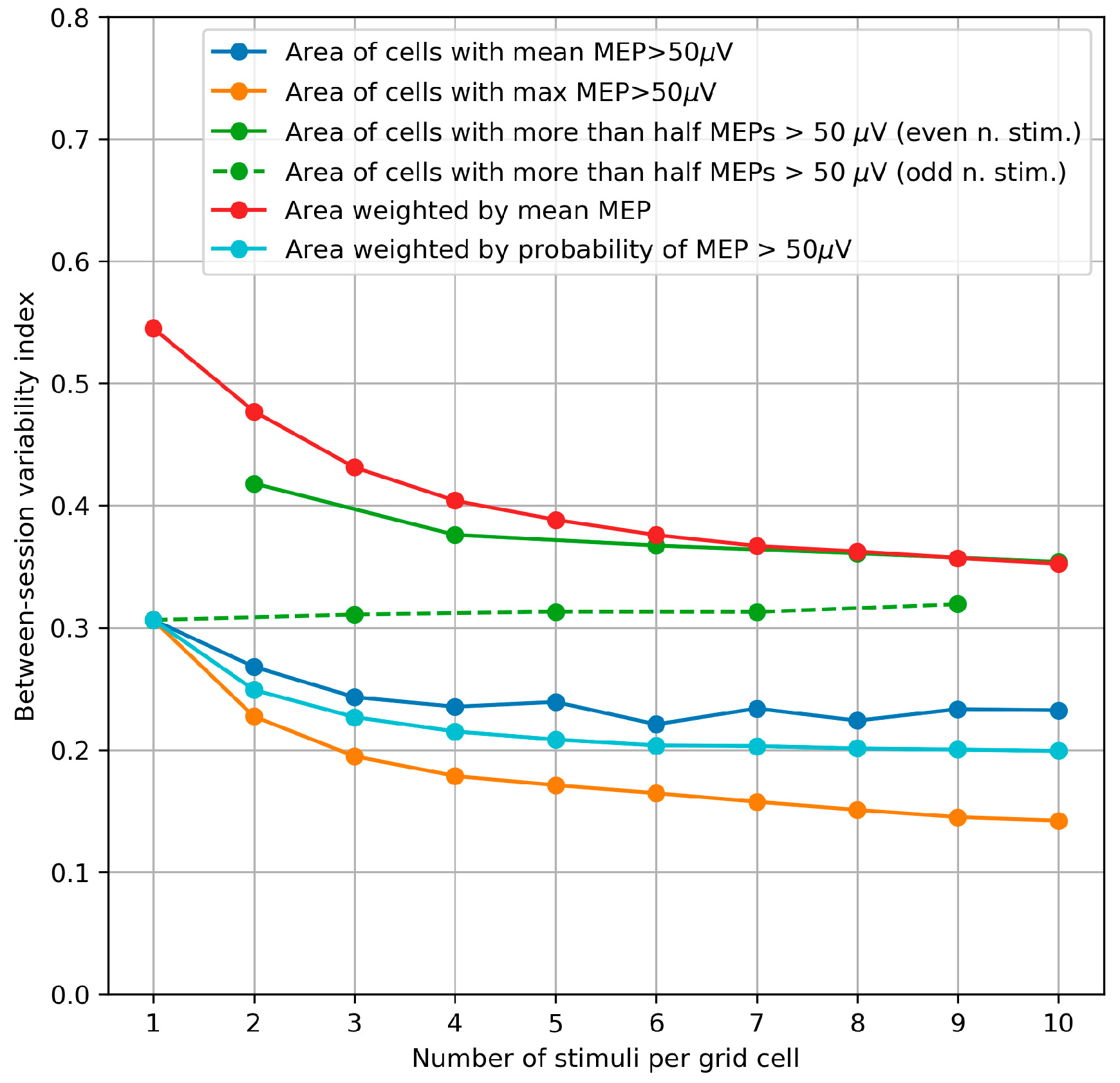
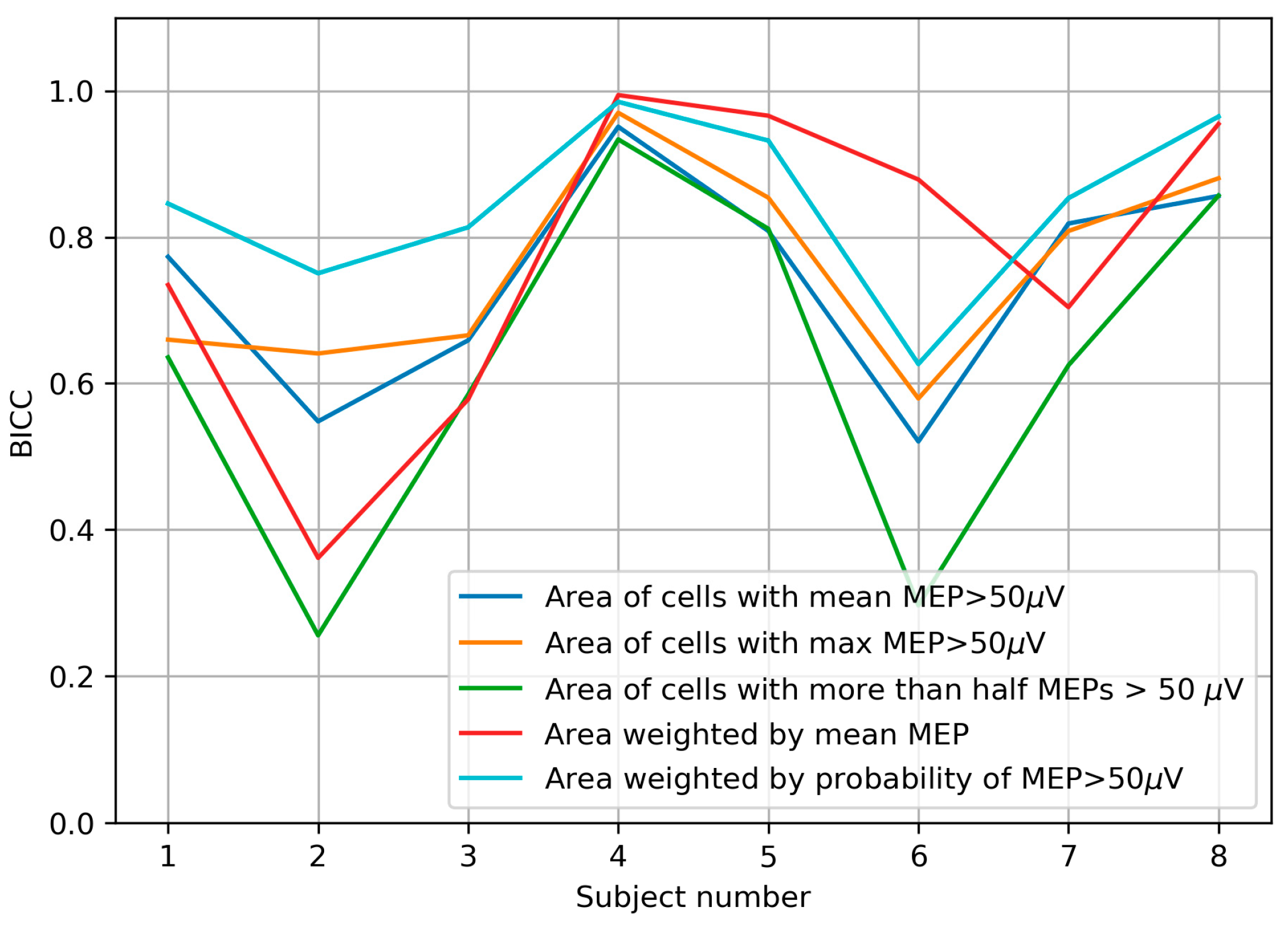
3.5. Between-Session Variability of the Area and Weighted Area
3.6. Sensitivity of the Protocol to Changes between Sessions
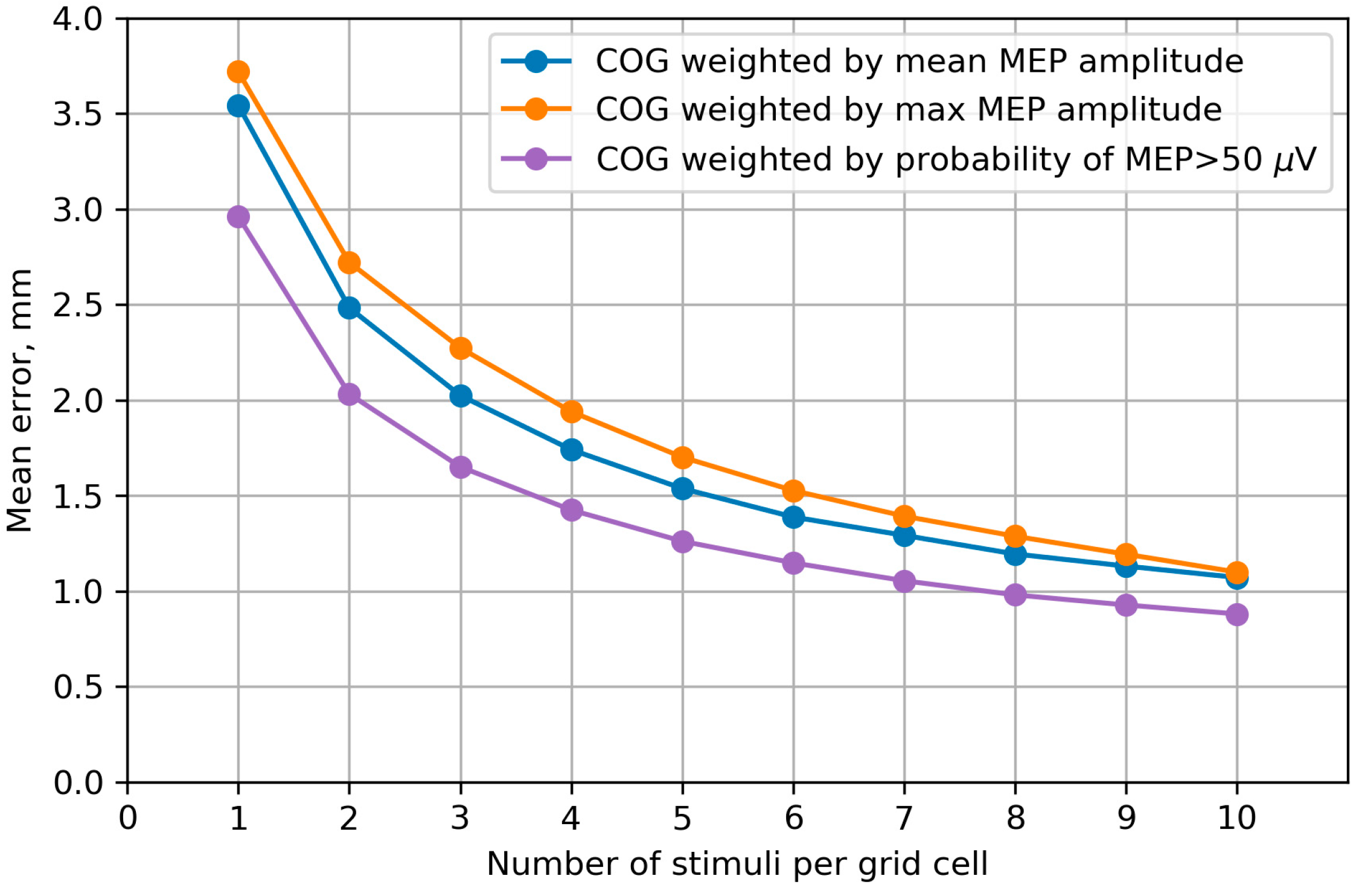
3.7. Accuracy of the Center of Gravity
4. Discussion
4.1. Muscle Representation Coverage by Grids of Different Sizes
4.2. Visualization of TMS Maps Obtained with a Stimulation Grid
4.3. Bias of the Area and Weighted Area
4.4. Within-Session Variability of the Area and Weighted Area
4.5. Between-Session Variability of the Area and Weighted Area
4.6. Sensitivity of the Protocol to Changes between Sessions
4.7. Accuracy of the Center of Gravity
4.8. Limitations
5. Conclusions
Data and Code Availability
Author Contributions
Funding
Conflicts of Interest
Appendix A. Formulas for the Muscle Representation Parameters
- The area of the grid cells with the mean MEP amplitude above 50 µV:Here, is the area of a grid cell, and is the number of cells for which where represents the MEP amplitudes obtained in a cell, and is the amplitude threshold (50 μV). The number of the averaged amplitudes is the number of stimuli per cell , which was equal to ten in our experimental maps and ranged from one to ten in the bootstrapping-generated maps.
- The area of the cells with the maximum MEP above 50 µV (or, equivalently, the area of the cells with at least one suprathreshold MEP):where is the number of cells for which
- The area of the cells with more than half suprathreshold MEPs:where is the number of cells for which more than half of the stimuli produced amplitudes
- The area weighted by the mean MEP amplitude (amplitude-weighted area):
- The area weighted by the probability of a suprathreshold MEP (probability-weighted area);where is the fraction of all the amplitudes in a cell that are greater than
- The COG with the weights defined as the mean amplitudes in each grid cell:where is the position vector of a cell, is the mean MEP amplitude in this cell.
- The COG with the weights defined as the maximal amplitudes in each grid cell;
- The COG with the weights defined as the probabilities of suprathreshold MEPs in each grid cell.
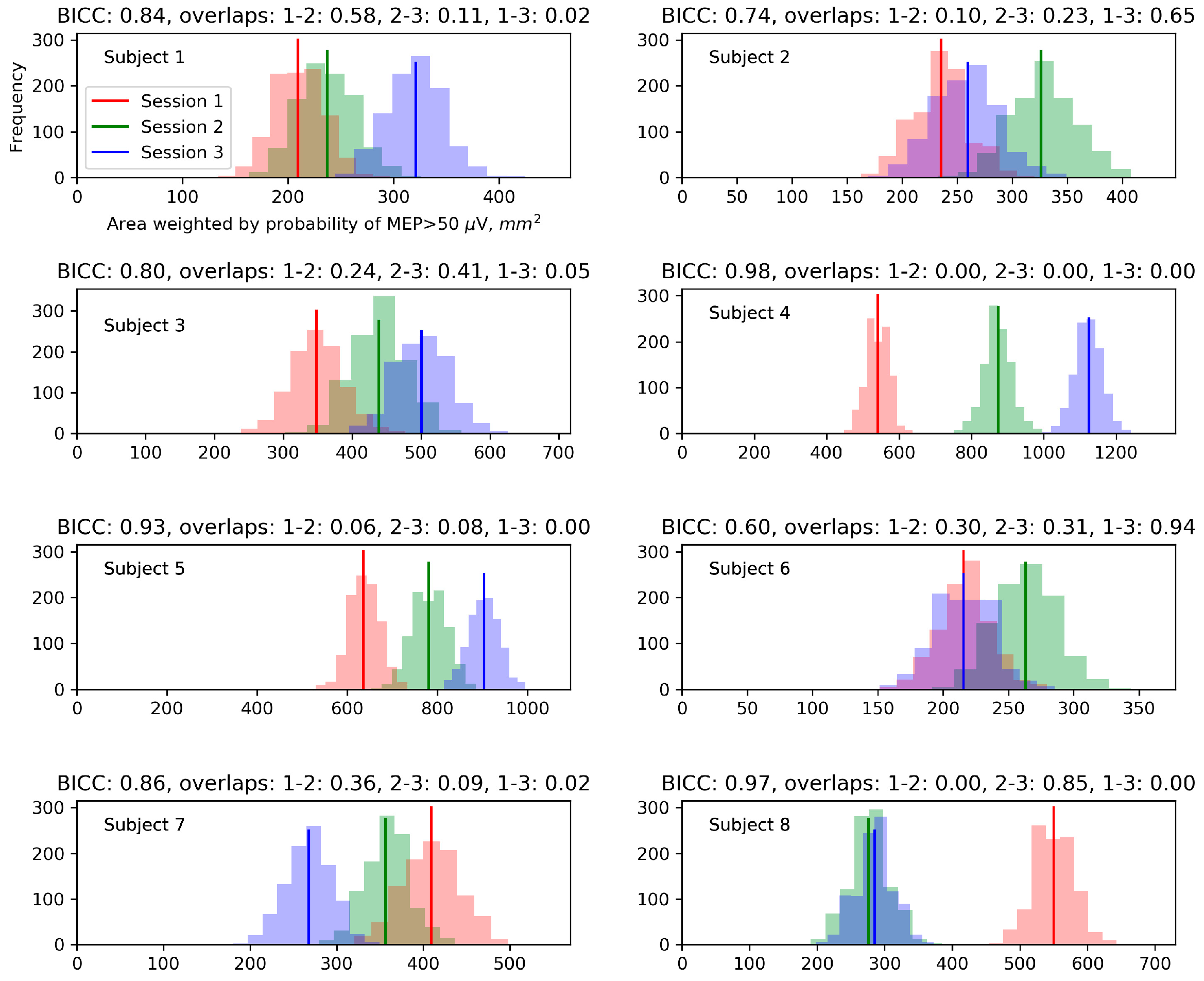
Appendix B. Biases of the Area and Weighted Area for the Individual Maps
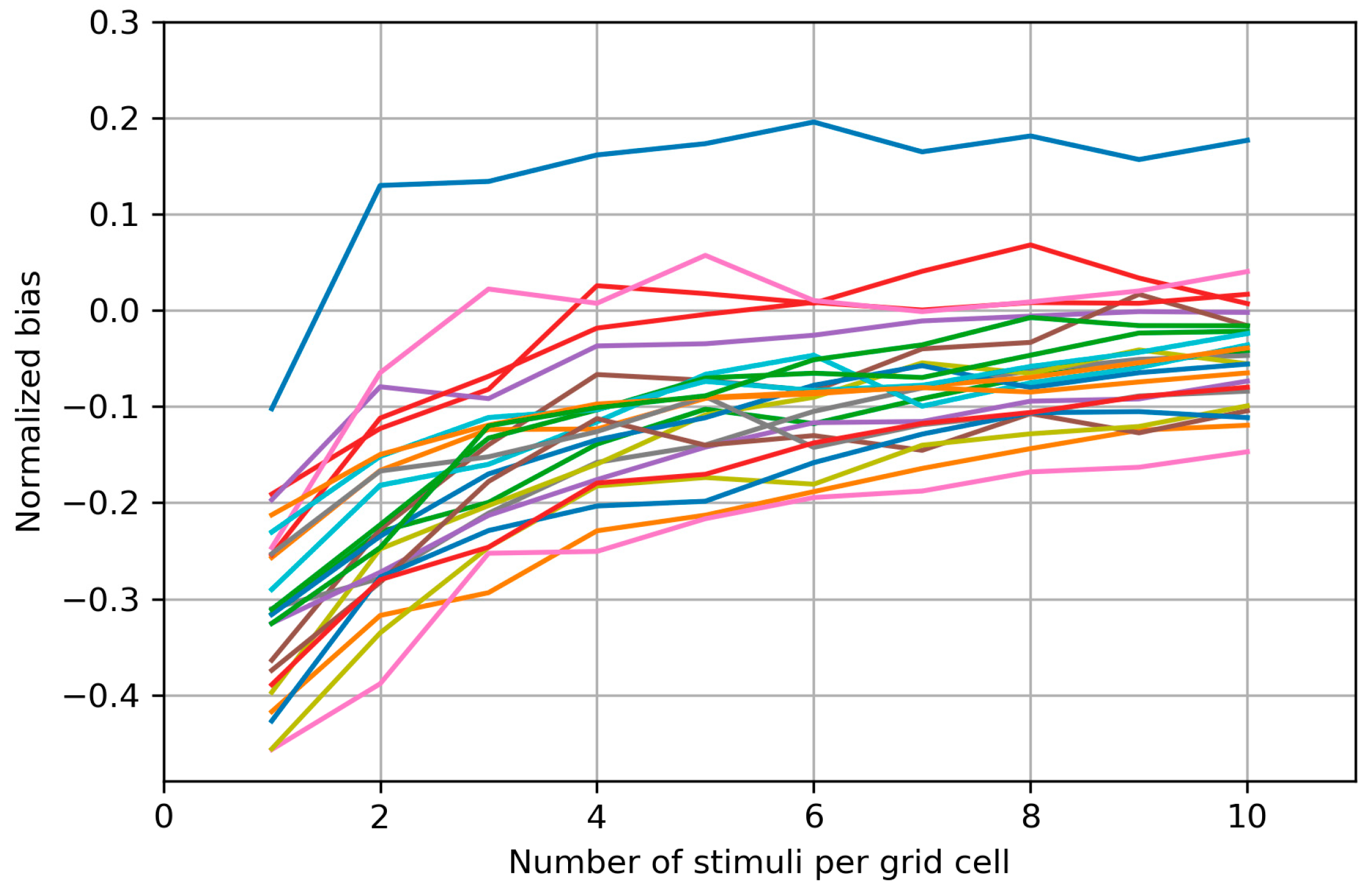
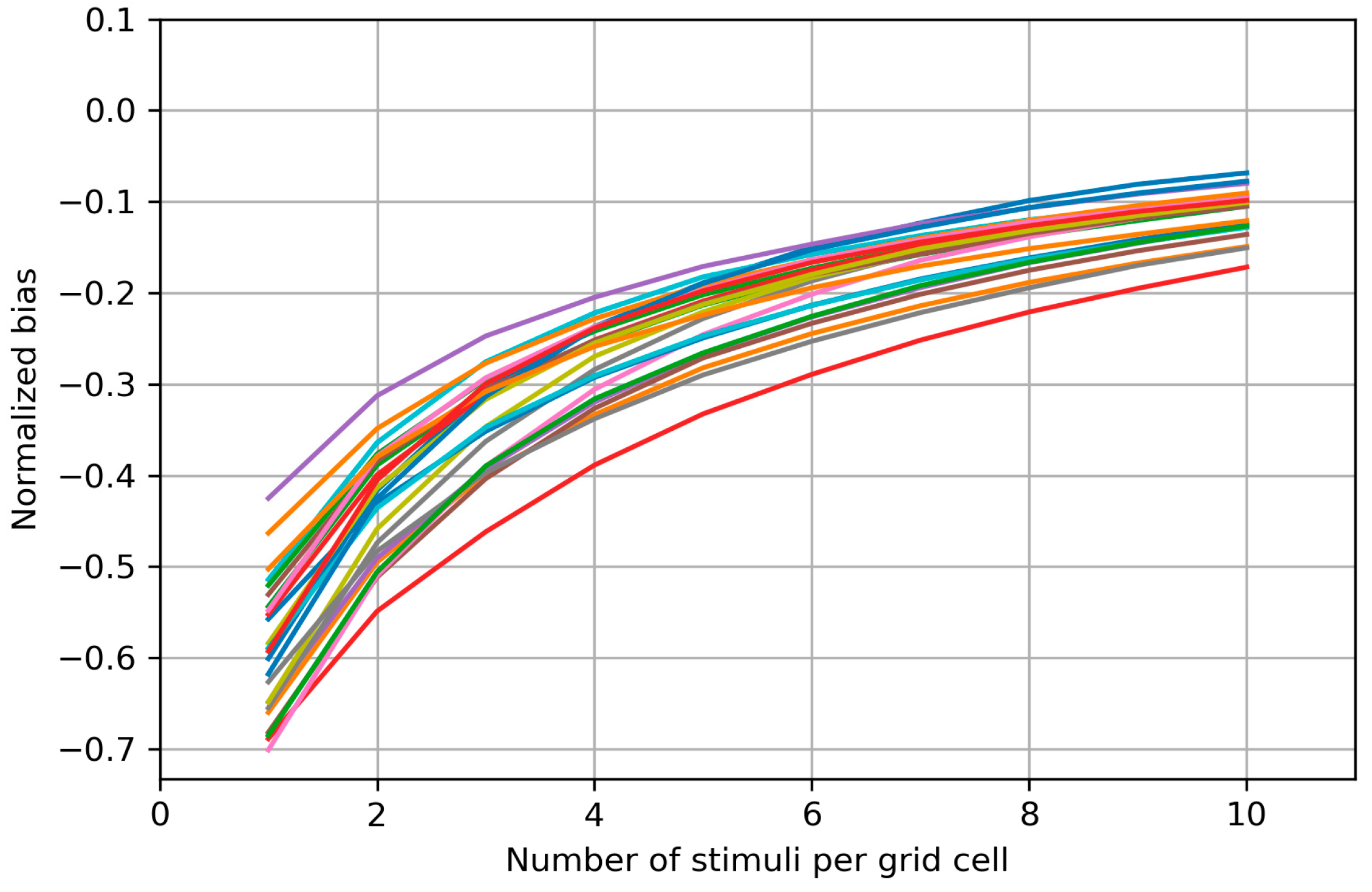
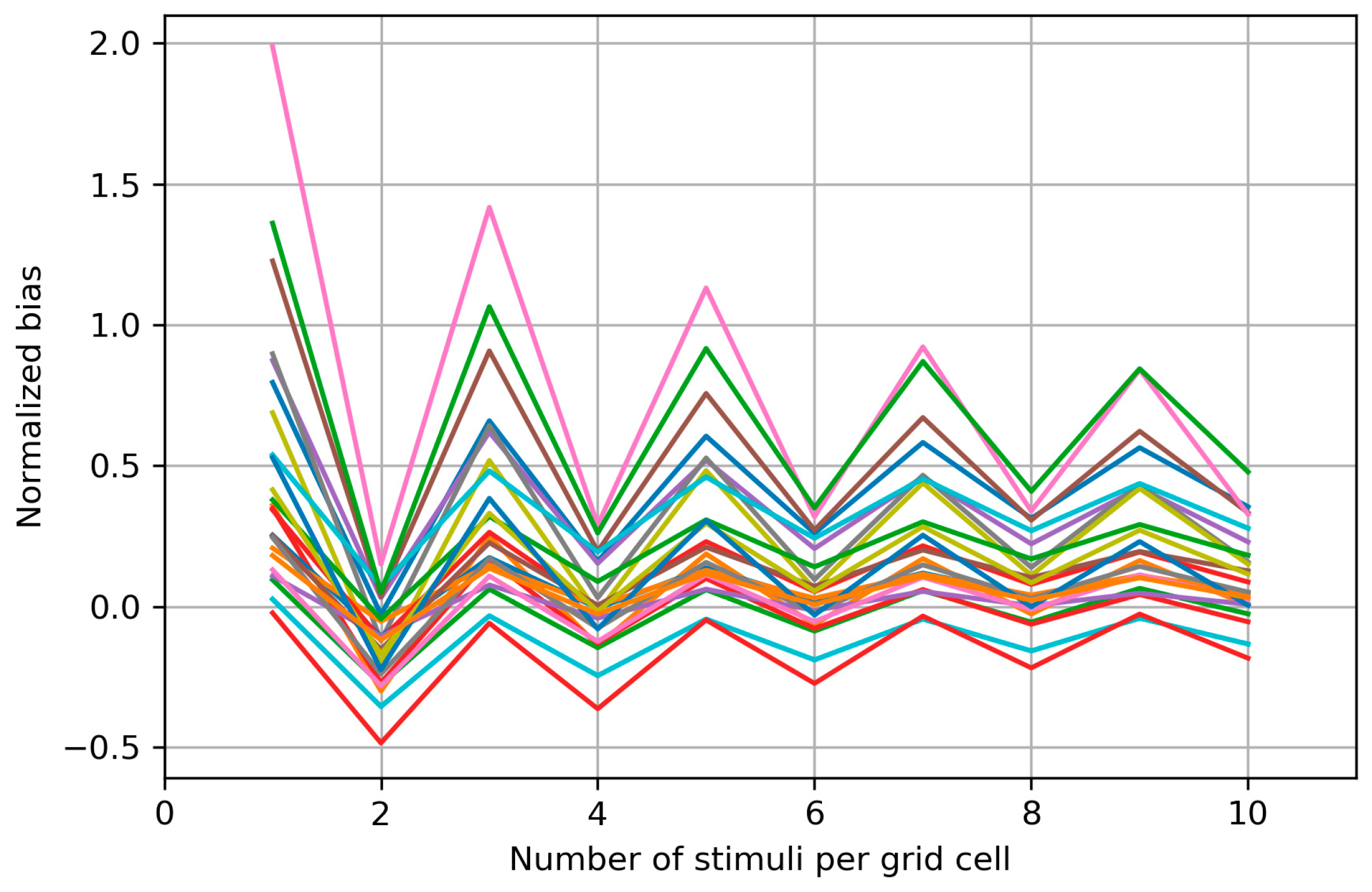
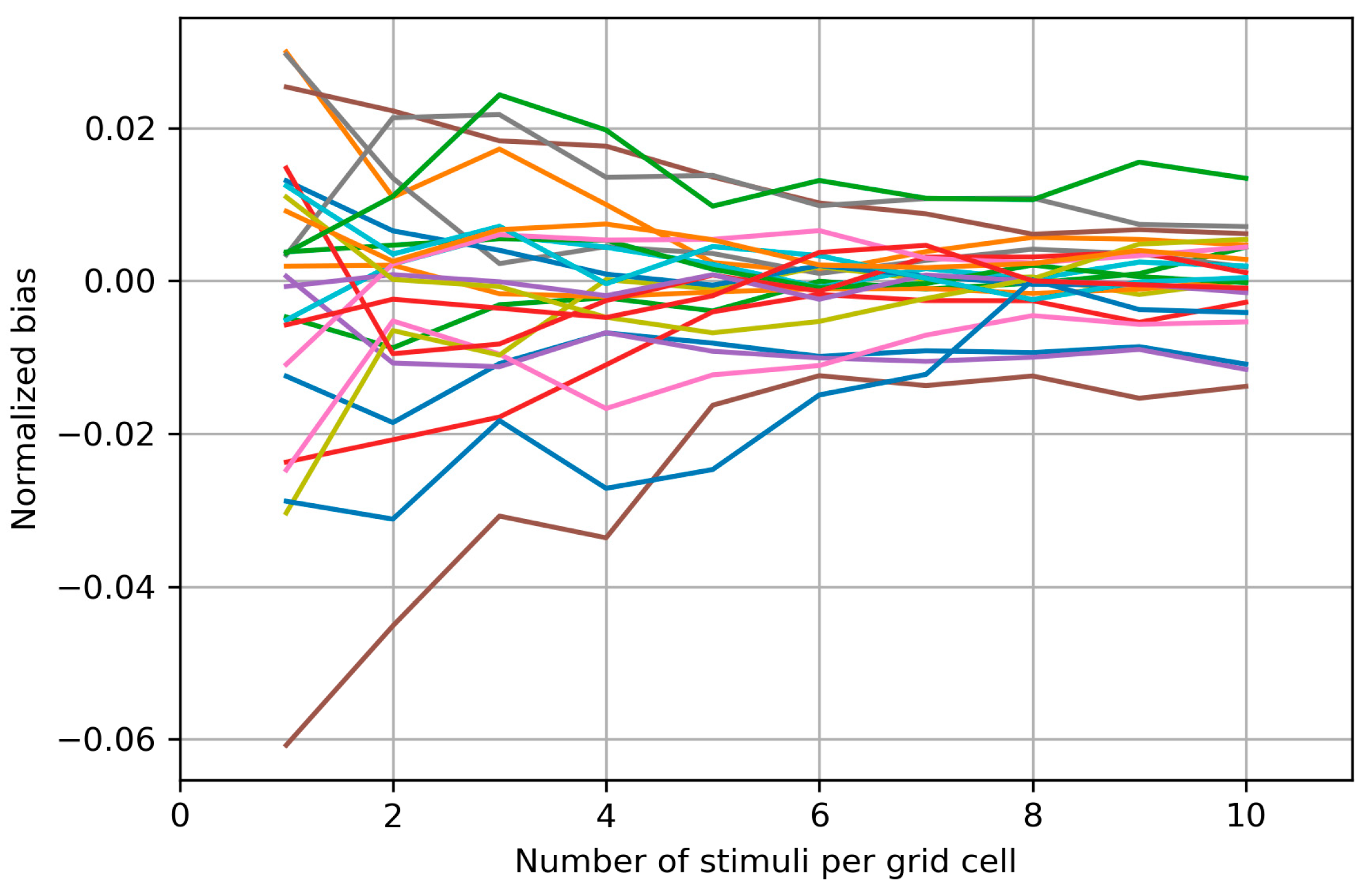
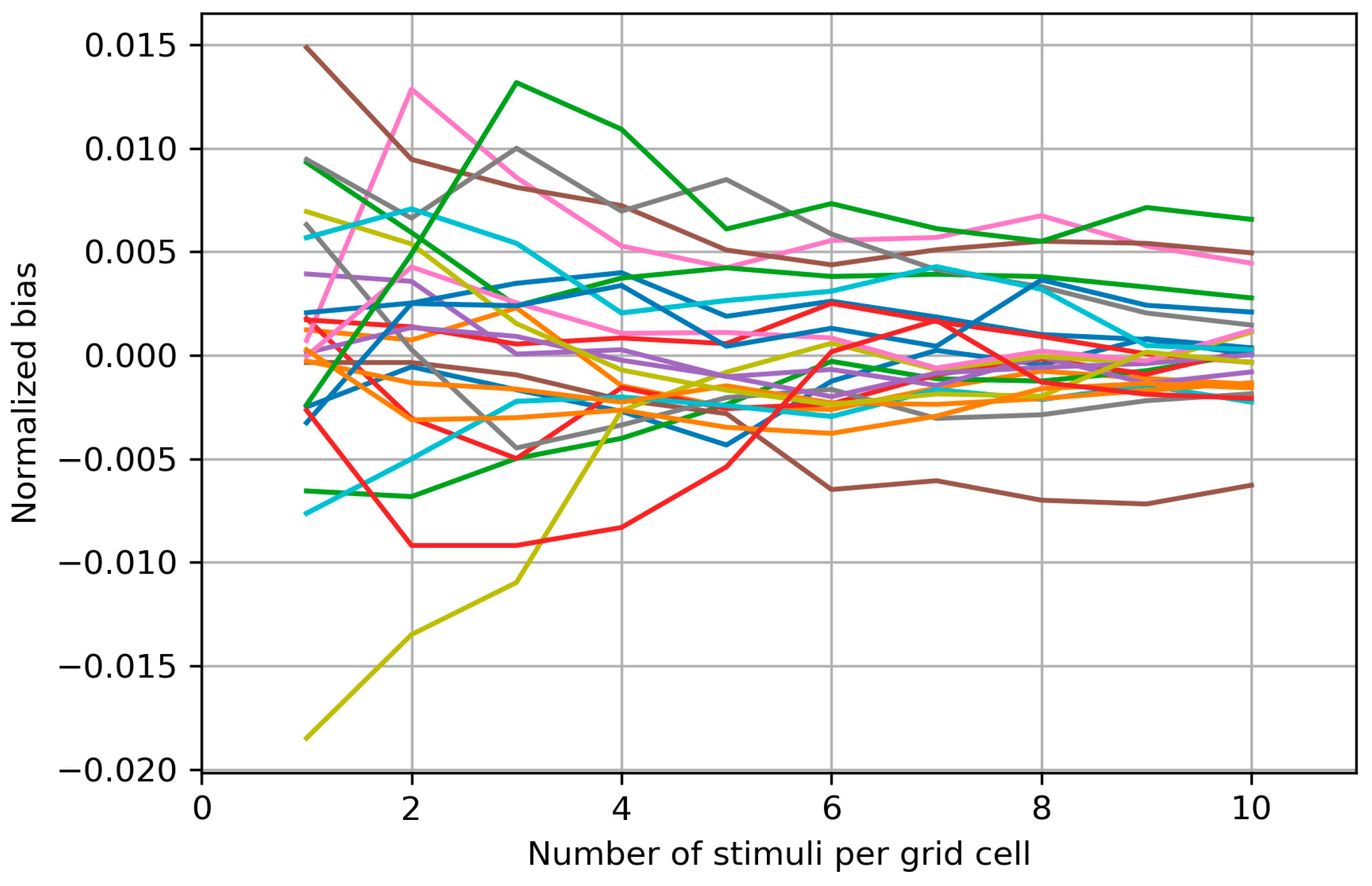
Appendix C. Bias Structure of the Area of the Cells with More than Half Suprathreshold MEPs
Appendix D. Resting Motor Threshold Values
| Subject Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| RMT | 37 | 30 | 31 | 41 | 41 | 31 | 27 | 35 |
References
- Rotenberg, A.; Horvath, J.C.; Pascual-Leone, A. Transcranial Magnetic Stimulation; Humana Press: New York, NY, USA, 2014; ISBN 978-1-4939-0878-3. [Google Scholar]
- Wittenberg, G.F. Experience, cortical remapping, and recovery in brain disease. Neurobiol. Dis. 2010, 37, 252–258. [Google Scholar] [CrossRef]
- Di Lazzaro, V.; Ziemann, U. The contribution of transcranial magnetic stimulation in the functional evaluation of microcircuits in human motor cortex. Front. Neural Circuits 2013, 7, 18. [Google Scholar] [CrossRef]
- Tarapore, P.E.; Tate, M.C.; Findlay, A.M.; Honma, S.M.; Mizuiri, D.; Berger, M.S.; Nagarajan, S.S. Preoperative multimodal motor mapping: A comparison of magnetoencephalography imaging, navigated transcranial magnetic stimulation, and direct cortical stimulation. J. Neurosurg. 2012, 117, 354–362. [Google Scholar] [CrossRef] [PubMed]
- Picht, T.; Frey, D.; Thieme, S.; Kliesch, S.; Vajkoczy, P. Presurgical navigated TMS motor cortex mapping improves outcome in glioblastoma surgery: A controlled observational study. J. Neurooncol. 2016, 126, 535–543. [Google Scholar] [CrossRef] [PubMed]
- Ziemann, U.; Ilić, T.V.; Jung, P. Chapter 3 Long-term potentiation (LTP)-like plasticity and learning in human motor cortex—Investigations with transcranial magnetic stimulation (TMS). Suppl. Clin. Neurophysiol. 2006, 59, 19–25. [Google Scholar]
- Boudreau, S.A.; Lontis, E.R.; Caltenco, H.; Svensson, P.; Sessle, B.J.; Struijk, L.N.A.; Arendt-Nielsen, L. Features of cortical neuroplasticity associated with multidirectional novel motor skill training: A TMS mapping study. Exp. Brain Res. 2013, 225, 513–526. [Google Scholar] [CrossRef] [PubMed]
- Pascual-Leone, A.; Nguyet, D.; Cohen, L.G.; Brasil-Neto, J.P.; Cammarota, A.; Hallett, M. Modulation of muscle responses evoked by transcranial magnetic stimulation during the acquisition of new fine motor skills. J. Neurophysiol. 1995, 74, 1037–1045. [Google Scholar] [CrossRef] [PubMed]
- Raffin, E.; Siebner, H.R. Use-Dependent Plasticity in Human Primary Motor Hand Area: Synergistic Interplay Between Training and Immobilization. Cereb. Cortex 2019, 29, 356–371. [Google Scholar] [CrossRef] [PubMed]
- Lüdemann-Podubecká, J.; Nowak, D.A. Mapping cortical hand motor representation using TMS: A method to assess brain plasticity and a surrogate marker for recovery of function after stroke? Neurosci. Biobehav. Rev. 2016, 69, 239–251. [Google Scholar] [CrossRef]
- Schabrun, S.M.; Stinear, C.M.; Byblow, W.D.; Ridding, M.C. Normalizing Motor Cortex Representations in Focal Hand Dystonia. Cereb. Cortex 2009, 19, 1968–1977. [Google Scholar] [CrossRef] [PubMed]
- Freund, P.; Rothwell, J.; Craggs, M.; Thompson, A.J.; Bestmann, S. Corticomotor representation to a human forearm muscle changes following cervical spinal cord injury. Eur. J. Neurosci. 2011, 34, 1839–1846. [Google Scholar] [CrossRef] [PubMed]
- Cortes, M.; Thickbroom, G.W.; Elder, J.; Rykman, A.; Valls-Sole, J.; Pascual-Leone, A.; Edwards, D.J. The corticomotor projection to liminally-contractable forearm muscles in chronic spinal cord injury: A transcranial magnetic stimulation study. Spinal Cord 2017, 55, 362–366. [Google Scholar] [CrossRef] [PubMed]
- Chervyakov, A.V.; Bakulin, I.S.; Savitskaya, N.G.; Arkhipov, I.V.; Gavrilov, A.V.; Zakharova, M.N.; Piradov, M.A. Navigated transcranial magnetic stimulation in amyotrophic lateral sclerosis. Muscle Nerve 2015, 51, 125–131. [Google Scholar] [CrossRef] [PubMed]
- Liepert, J.; Graef, S.; Uhde, I.; Leidner, O.; Weiller, C. Training-induced changes of motor cortex representations in stroke patients. Acta Neurol. Scand. 2000, 101, 321–326. [Google Scholar] [CrossRef]
- Weiss, C.; Nettekoven, C.; Rehme, A.K.; Neuschmelting, V.; Eisenbeis, A.; Goldbrunner, R.; Grefkes, C. Mapping the hand, foot and face representations in the primary motor cortex—Retest reliability of neuronavigated TMS versus functional MRI. Neuroimage 2013, 66, 531–542. [Google Scholar] [CrossRef] [PubMed]
- Kraus, D.; Gharabaghi, A. Neuromuscular Plasticity: Disentangling Stable and Variable Motor Maps in the Human Sensorimotor Cortex. Neural Plast. 2016, 2016. [Google Scholar] [CrossRef]
- Pellegrini, M.; Zoghi, M.; Jaberzadeh, S. The effect of transcranial magnetic stimulation test intensity on the amplitude, variability and reliability of motor evoked potentials. Brain Res. 2018, 1700, 190–198. [Google Scholar] [CrossRef] [PubMed]
- Julkunen, P. Methods for estimating cortical motor representation size and location in navigated transcranial magnetic stimulation. J. Neurosci. Methods 2014, 232, 125–133. [Google Scholar] [CrossRef]
- Classen, J.; Knorr, U.; Werhahn, K.J.; Schlaug, G.; Kunesch, E.; Cohen, L.G.; Seitz, R.J.; Benecke, R. Multimodal output mapping of human central motor representation on different spatial scales. J. Physiol. 1998, 512, 163–179. [Google Scholar] [CrossRef]
- Kleim, J.A.; Kleim, E.D.; Cramer, S.C. Systematic assessment of training-induced changes in corticospinal output to hand using frameless stereotaxic transcranial magnetic stimulation. Nat. Protoc. 2007, 2, 1675–1684. [Google Scholar] [CrossRef]
- Uy, J.; Ridding, M.C.; Miles, T.S. Stability of maps of human motor cortex made with transcranial magnetic stimulation. Brain Topogr. 2002, 14, 293–297. [Google Scholar] [CrossRef] [PubMed]
- Corneal, S.F.; Butler, A.J.; Wolf, S.L. Intra- and intersubject reliability of abductor pollicis brevis muscle motor map characteristics with transcranial magnetic stimulation. Arch. Phys. Med. Rehabil. 2005, 86, 1670–1675. [Google Scholar] [CrossRef]
- McGregor, K.M.; Carpenter, H.; Kleim, E.; Sudhyadhom, A.; White, K.D.; Butler, A.J.; Kleim, J.; Crosson, B. Motor map reliability and aging: A TMS/fMRI study. Exp. Brain Res. 2012, 219, 97–106. [Google Scholar] [CrossRef] [PubMed]
- Ngomo, S.; Leonard, G.; Moffet, H.; Mercier, C. Comparison of transcranial magnetic stimulation measures obtained at rest and under active conditions and their reliability. J. Neurosci. Methods 2012, 205, 65–71. [Google Scholar] [CrossRef]
- Cavaleri, R.; Schabrun, S.M.; Chipchase, L.S. The number of stimuli required to reliably assess corticomotor excitability and primary motor cortical representations using transcranial magnetic stimulation (TMS): A systematic review and meta-analysis. Syst. Rev. 2017, 6, 48. [Google Scholar] [CrossRef] [PubMed]
- Forster, M.-T.; Limbart, M.; Seifert, V.; Senft, C. Test-retest Reliability of Navigated Transcranial Magnetic Stimulation of the Motor Cortex. Oper. Neurosurg. 2014, 10, 51–56. [Google Scholar] [CrossRef] [PubMed]
- Schönfeldt-Lecuona, C.; Thielscher, A.; Freudenmann, R.W.; Kron, M.; Spitzer, M.; Herwig, U. Accuracy of stereotaxic positioning of transcranial magnetic stimulation. Brain Topogr. 2005, 17, 253–259. [Google Scholar] [CrossRef] [PubMed]
- Julkunen, P.; Säisänen, L.; Danner, N.; Niskanen, E.; Hukkanen, T.; Mervaala, E.; Könönen, M. Comparison of navigated and non-navigated transcranial magnetic stimulation for motor cortex mapping, motor threshold and motor evoked potentials. Neuroimage 2009, 44, 790–795. [Google Scholar] [CrossRef]
- Opitz, A.; Windhoff, M.; Heidemann, R.M.; Turner, R.; Thielscher, A. How the brain tissue shapes the electric field induced by transcranial magnetic stimulation. Neuroimage 2011, 58, 849–859. [Google Scholar] [CrossRef]
- Opitz, A.; Zafar, N.; Bockermann, V.; Rohde, V.; Paulus, W. Validating computationally predicted TMS stimulation areas using direct electrical stimulation in patients with brain tumors near precentral regions. NeuroImage Clin. 2014, 4, 500–507. [Google Scholar] [CrossRef]
- Raffin, E.; Pellegrino, G.; Di Lazzaro, V.; Thielscher, A.; Siebner, H.R. Bringing transcranial mapping into shape: Sulcus-aligned mapping captures motor somatotopy in human primary motor hand area. Neuroimage 2015, 120, 164–175. [Google Scholar] [CrossRef] [PubMed]
- Zrenner, C.; Desideri, D.; Belardinelli, P.; Ziemann, U. Real-time EEG-defined excitability states determine efficacy of TMS-induced plasticity in human motor cortex. Brain Stimul. 2018, 11, 374–389. [Google Scholar] [CrossRef]
- Brasil-Neto, J.P.; McShane, L.M.; Fuhr, P.; Hallett, M.; Cohen, L.G. Topographic mapping of the human motor cortex with magnetic stimulation: Factors affecting accuracy and reproducibility. Electroencephalogr. Clin. Neurophysiol. 1992, 85, 9–16. [Google Scholar] [CrossRef]
- Thickbroom, G.W.; Byrnes, M.L.; Mastaglia, F.L. A model of the effect of MEP amplitude variation on the accuracy of TMS mapping. Clin. Neurophysiol. 1999, 110, 941–943. [Google Scholar] [CrossRef]
- Van De Ruit, M.; Perenboom, M.J.L.; Grey, M.J. TMS brain mapping in less than two minutes. Brain Stimul. 2015, 8, 231–239. [Google Scholar] [CrossRef]
- Novikov, P.A.; Nazarova, M.A.; Nikulin, V.V. TMSmap—Software for Quantitative Analysis of TMS Mapping Results. Front. Hum. Neurosci. 2018, 12, 239. [Google Scholar] [CrossRef] [PubMed]
- Pitkänen, M.; Kallioniemi, E.; Julkunen, P.; Nazarova, M.; Nieminen, J.O.; Ilmoniemi, R.J. Minimum-Norm Estimation of Motor Representations in Navigated TMS Mappings. Brain Topogr. 2017, 30, 711–722. [Google Scholar] [CrossRef]
- Sommer, M.; Alfaro, A.; Rummel, M.; Speck, S.; Lang, N.; Tings, T.; Paulus, W. Half sine, monophasic and biphasic transcranial magnetic stimulation of the human motor cortex. Clin. Neurophysiol. 2006, 117, 838–844. [Google Scholar] [CrossRef]
- Kammer, T.; Beck, S.; Thielscher, A.; Laubis-Herrmann, U.; Topka, H. Motor thresholds in humans: A transcranial magnetic stimulation study comparing different pulse waveforms, current directions and stimulator types. Clin. Neurophysiol. 2001, 112, 250–258. [Google Scholar] [CrossRef]
- Oldfield, R.C. The assessment and analysis of handedness: The Edinburgh inventory. Neuropsychologia 1971, 9, 97–113. [Google Scholar] [CrossRef]
- Krieg, S.M.; Lioumis, P.; Mäkelä, J.P.; Wilenius, J.; Karhu, J.; Hannula, H.; Savolainen, P.; Lucas, C.W.; Seidel, K.; Laakso, A.; et al. Protocol for motor and language mapping by navigated TMS in patients and healthy volunteers; workshop report. Acta Neurochir. (Wien). 2017, 159, 1187–1195. [Google Scholar] [CrossRef]
- Chernyavskiy, A.Y.; Sinitsyn, D.O.; Poydasheva, A.G.; Bakulin, I.S.; Suponeva, N.A.; Piradov, M.A. Accuracy of Estimating the Area of Cortical Muscle Representations from TMS Mapping Data using Voronoi Diagrams. Brain Topogr. 2019. under review. [Google Scholar]
- Jonker, Z.D.; Van Der Vliet, R.; Hauwert, C.M.; Gaiser, C.; Joke, H.M.; Van Der Geest, J.N.; Donchin, O.; Ribbers, G.M.; Frens, M.A.; Selles, R.W. TMS motor mapping: Comparing the absolute reliability of digital reconstruction methods to the golden standard. Brain Stimul. 2018, 12, 309–313. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap Methods: Another Look at the Jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Hollander, M.; Wolfe, D.A. Nonparametric Statistical Methods, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1999; ISBN 0471190454. [Google Scholar]
- Gehan, E.A. A Generalized Wilcoxon Test for Comparing Arbitrarily Singly-Censored Samples. Biometrika 1965, 52, 203. [Google Scholar] [CrossRef] [PubMed]
- Flandin, G.; Friston, K. Statistical parametric mapping (SPM). Scholarpedia 2008, 3, 6232. [Google Scholar] [CrossRef]
- McGraw, K.O.; Wong, S.P. Forming inferences about some intraclass correlation coefficients. Psychol. Methods 1996, 1, 30–46. [Google Scholar] [CrossRef]
- Wolf, S.L.; Butler, A.J.; Campana, G.I.; Parris, T.A.; Struys, D.M.; Weinstein, S.R.; Weiss, P. Intra-subject reliability of parameters contributing to maps generated by transcranial magnetic stimulation in able-bodied adults. Clin. Neurophysiol. 2004, 115, 1740–1747. [Google Scholar] [CrossRef] [PubMed]
- Goetz, S.M.; Luber, B.; Lisanby, S.H.; Peterchev, A.V. A novel model incorporating two variability sources for describing motor evoked potentials. Brain Stimul. 2014, 7, 541–552. [Google Scholar] [CrossRef] [PubMed]
- Cavaleri, R.; Schabrun, S.M.; Chipchase, L.S. The reliability and validity of rapid transcranial magnetic stimulation mapping. Brain Stimul. 2018, 11, 1291–1295. [Google Scholar] [CrossRef]
- Mortifee, P.; Stewart, H.; Schulzer, M.; Eisen, A. Reliability of transcranial magnetic stimulation for mapping the human motor cortex. Electroencephalogr. Clin. Neurophysiol. 1994, 93, 131–137. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sinitsyn, D.O.; Chernyavskiy, A.Y.; Poydasheva, A.G.; Bakulin, I.S.; Suponeva, N.A.; Piradov, M.A. Optimization of the Navigated TMS Mapping Algorithm for Accurate Estimation of Cortical Muscle Representation Characteristics. Brain Sci. 2019, 9, 88. https://doi.org/10.3390/brainsci9040088
Sinitsyn DO, Chernyavskiy AY, Poydasheva AG, Bakulin IS, Suponeva NA, Piradov MA. Optimization of the Navigated TMS Mapping Algorithm for Accurate Estimation of Cortical Muscle Representation Characteristics. Brain Sciences. 2019; 9(4):88. https://doi.org/10.3390/brainsci9040088
Chicago/Turabian StyleSinitsyn, Dmitry O., Andrey Yu. Chernyavskiy, Alexandra G. Poydasheva, Ilya S. Bakulin, Natalia A. Suponeva, and Michael A. Piradov. 2019. "Optimization of the Navigated TMS Mapping Algorithm for Accurate Estimation of Cortical Muscle Representation Characteristics" Brain Sciences 9, no. 4: 88. https://doi.org/10.3390/brainsci9040088
APA StyleSinitsyn, D. O., Chernyavskiy, A. Y., Poydasheva, A. G., Bakulin, I. S., Suponeva, N. A., & Piradov, M. A. (2019). Optimization of the Navigated TMS Mapping Algorithm for Accurate Estimation of Cortical Muscle Representation Characteristics. Brain Sciences, 9(4), 88. https://doi.org/10.3390/brainsci9040088





