Brain Connectivity Estimation Network for the Identification of Dementia
Abstract
1. Introduction
- The proposed BCEN is a flexible approach for inferring directional influences between brain regions.
- The employed graph pooling layer effectively captures critical substructures and helps to enhance the identification performance of neurological disorders.
- The estimated brain network generated by our method exhibits nonlinear interactions between brain regions, surpassing traditional linear approaches.
2. Related Work
2.1. Causality for Brain Network Estimation
2.2. Graph Neural Network for Brain Disorder Identification
3. Methodology
3.1. Brain Structure Inference
3.2. Hierarchical Graph Representation Learning
4. Experimental Setup
4.1. Data and Preprocessing
4.2. Model Training
5. Results
5.1. Comparison Methods
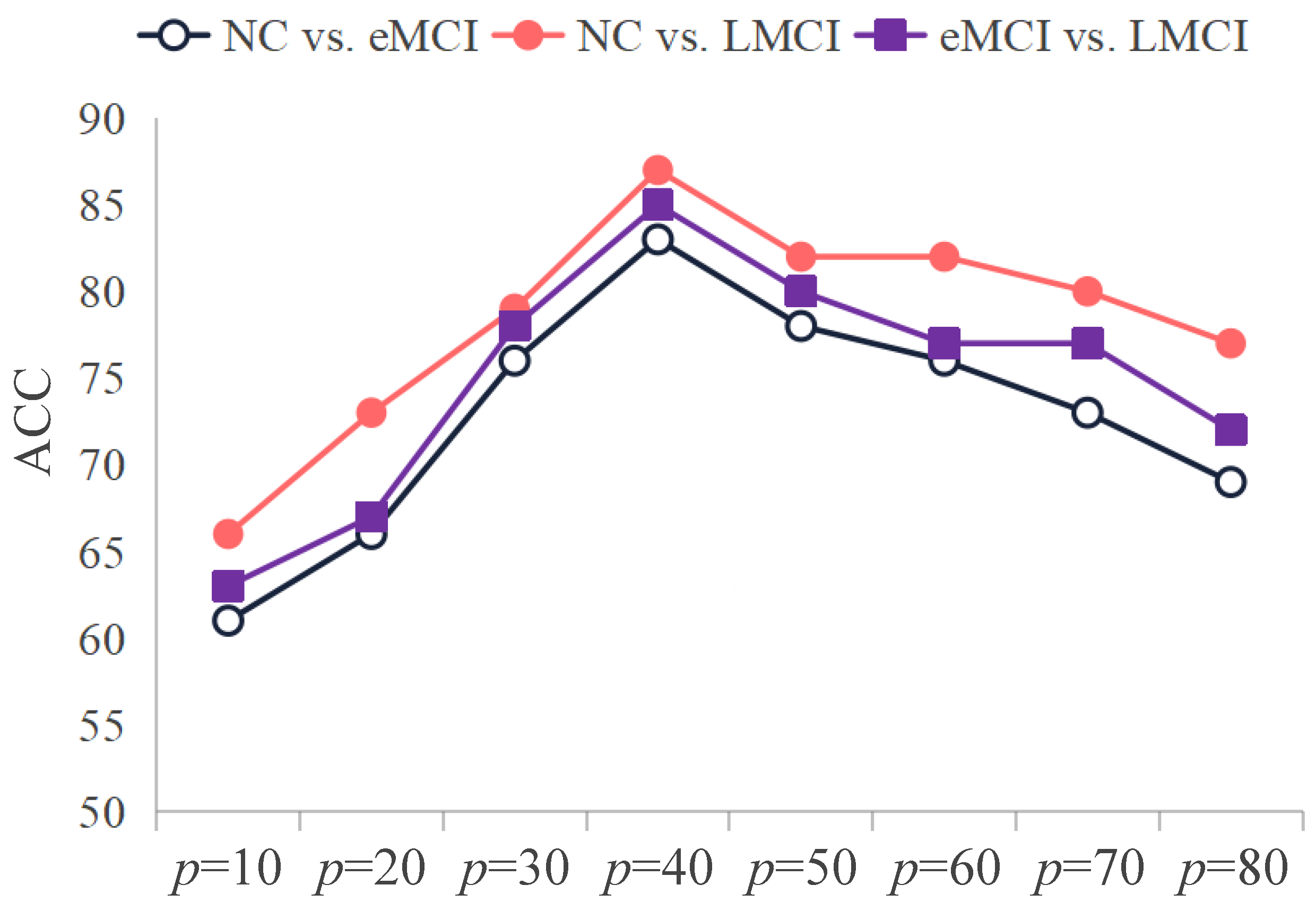
5.2. Experimental Results
5.3. Ablation Study
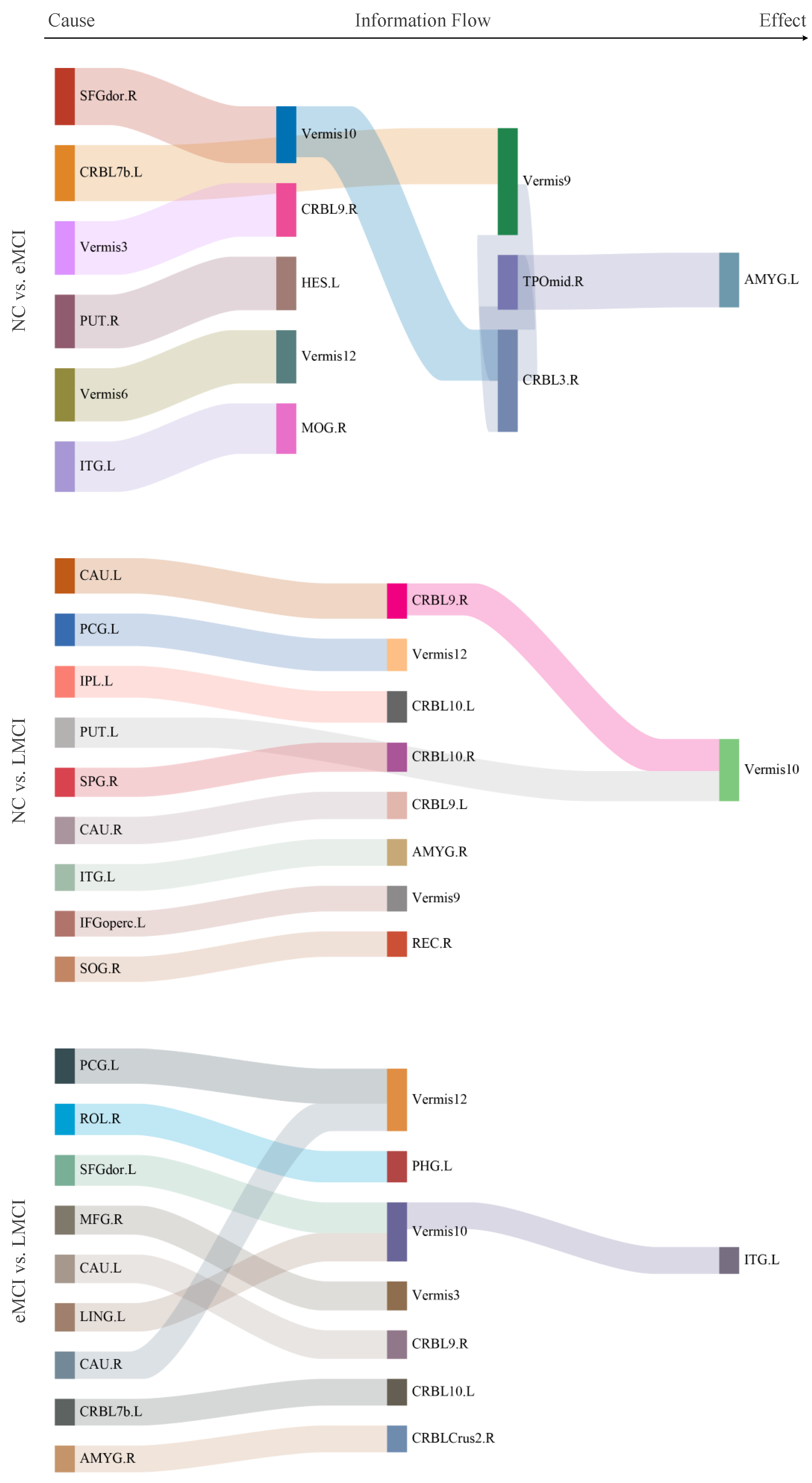
6. Discussion
Most Discriminative Patterns
7. Limitations and Future Work
7.1. Interpretability of Model Results
7.2. External Validation
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Better, M.A. Alzheimer’s disease facts and figures. Alzheimers Dement 2023, 19, 1598–1695. [Google Scholar]
- Steinmetz, J.D.; Seeher, K.M.; Schiess, N.; Nichols, E.; Cao, B.; Servili, C.; Cavallera, V.; Cousin, E.; Hagins, H.; Moberg, M.E.; et al. Global, regional, and national burden of disorders affecting the nervous system, 1990–2021: A systematic analysis for the Global Burden of Disease Study 2021. Lancet Neurol. 2024, 23, 344–381. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.W.; Kim, H.W.; Choe, Y.S.; Yang, H.S.; Lee, J.; Lee, H.; Yong, J.H.; Kim, D.; Lee, M.; Kang, D.W.; et al. A multimodal machine learning model for predicting dementia conversion in Alzheimer’s disease. Sci. Rep. 2024, 14, 12276. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, M.; Haughton, D.; Kazis, L.E. Transition of mild cognitive impairment to Alzheimer’s disease: Medications as modifiable risk factors. PLoS ONE 2024, 19, e0306270. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Xiao, X.; Yang, Y.; Yao, R.; Yang, Q.; Zhu, Y.; Yang, X.; Zhang, S.; Shen, L.; Jiao, B. The risk of Alzheimer’s disease and cognitive impairment characteristics in eight mental disorders: A UK Biobank observational study and Mendelian randomization analysis. Alzheimer’s Dement. 2024, 20, 4841–4853. [Google Scholar] [CrossRef]
- Luo, M.; He, Z.; Cui, H.; Ward, P.; Chen, Y.P.P.; Alzheimer’s Disease Neuroimaging Initiative. Dual attention based fusion network for MCI Conversion Prediction. Comput. Biol. Med. 2024, 182, 109039. [Google Scholar] [CrossRef]
- Ma, Y.; Mu, X.; Zhang, T.; Zhao, Y. MAFT-SO: A novel multi-atlas fusion template based on spatial overlap for ASD diagnosis. J. Biomed. Inform. 2024, 157, 104714. [Google Scholar] [CrossRef]
- Juan, Q.; Shiwan, T.; Yurong, S.; Jiabo, S.; Yu, C.; Shui, T.; Zhijian, Y.; Qing, L. Brain structural and functional abnormalities in affective network are associated with anxious depression. BMC Psychiatry 2024, 24, 533. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Q.; Yao, L.; He, N.; Tang, Y.; Chen, L.; Long, F.; Chen, Y.; Kemp, G.J.; Lui, S.; et al. Shared and differing functional connectivity abnormalities of the default mode network in mild cognitive impairment and Alzheimer’s disease. Cereb. Cortex 2024, 34, bhae094. [Google Scholar] [CrossRef]
- Yang, C.; Wang, X.K.; Ma, S.Z.; Lee, N.Y.; Zhang, Q.R.; Dong, W.Q.; Zang, Y.F.; Yuan, L.X. Abnormal functional connectivity of the reward network is associated with social communication impairments in autism spectrum disorder: A large-scale multi-site resting-state fMRI study. J. Affect. Disord. 2024, 347, 608–618. [Google Scholar] [CrossRef]
- Guo, H.; Huang, X.; Wang, C.; Wang, H.; Bai, X.; Li, Y. High-Order line graphs of fMRI data in major depressive disorder. Med. Phys. 2024, 51, 5535–5549. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, H.; Kim, M.; Teng, S.; Zhang, L.; Shen, D. Estimating functional brain networks by incorporating a modularity prior. Neuroimage 2016, 141, 399–407. [Google Scholar] [CrossRef] [PubMed]
- Koike, S.; Sakakibara, E.; Satomura, Y.; Sakurada, H.; Yamagishi, M.; Matsuoka, J.; Okada, N.; Kasai, K. Shared functional impairment in the prefrontal cortex affects symptom severity across psychiatric disorders. Psychol. Med. 2022, 52, 2661–2670. [Google Scholar] [CrossRef] [PubMed]
- Yu, R.; Qiao, L.; Chen, M.; Lee, S.W.; Fei, X.; Shen, D. Weighted graph regularized sparse brain network construction for MCI identification. Pattern Recognit. 2019, 90, 220–231. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Zhang, L.; Qiao, L.; Shen, D. Estimating sparse functional brain networks with spatial constraints for MCI identification. PLoS ONE 2020, 15, e0235039. [Google Scholar] [CrossRef]
- Kverková, K.; Marhounová, L.; Polonyiová, A.; Kocourek, M.; Zhang, Y.; Olkowicz, S.; Straková, B.; Pavelková, Z.; Vodička, R.; Frynta, D.; et al. The evolution of brain neuron numbers in amniotes. Proc. Natl. Acad. Sci. USA 2022, 119, e2121624119. [Google Scholar] [CrossRef]
- Wang, X.; Wang, R.; Li, F.; Lin, Q.; Zhao, X.; Hu, Z. Large-scale granger causal brain network based on resting-state fMRI data. Neuroscience 2020, 425, 169–180. [Google Scholar] [CrossRef]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econom. J. Econom. Soc. 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Su, R.; Yin, B.; Jing, J.; Xie, P.; Yuan, Y.; Han, Y.; Liang, Z.; Li, X. Information segregation and integration of aMCI based on genuine symbolic nonlinear Granger causality brain network. Biomed. Signal Process. Control 2024, 95, 106314. [Google Scholar] [CrossRef]
- Yi, C.; Zhang, J.; Weng, Z.; Chen, W.; Yao, D.; Li, F.; Cao, Z.; Li, P.; Xu, P. Nonparametric Dynamic Granger Causality based on Multi-Space Spectrum Fusion for Time-varying Directed Brain Network Construction. IEEE J. Biomed. Health Inform. 2024. [Google Scholar] [CrossRef]
- Sato, J.R.; Takahashi, D.Y.; Arcuri, S.M.; Sameshima, K.; Morettin, P.A.; Baccalá, L.A. Frequency domain connectivity identification: An application of partial directed coherence in fMRI. Hum. Brain Mapp. 2009, 30, 452–461. [Google Scholar] [CrossRef]
- Zhang, T.; Li, M.; Zhang, L.; Biswal, B.; Yao, D.; Xu, P. The time-varying network patterns in motor imagery revealed by adaptive directed transfer function analysis for fMRI. IEEE Access 2018, 6, 60339–60352. [Google Scholar] [CrossRef]
- Li, W.X.; Lin, Q.H.; Zhang, C.Y.; Han, Y.; Calhoun, V.D. A new transfer entropy method for measuring directed connectivity from complex-valued fMRI data. Front. Neurosci. 2024, 18, 1423014. [Google Scholar] [CrossRef]
- Frässle, S.; Harrison, S.J.; Heinzle, J.; Clementz, B.A.; Tamminga, C.A.; Sweeney, J.A.; Gershon, E.S.; Keshavan, M.S.; Pearlson, G.D.; Powers, A.; et al. Regression dynamic causal modeling for resting-state fMRI. Hum. Brain Mapp. 2021, 42, 2159–2180. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Wen, X.; Li, J.; Yao, L. A new dynamic Bayesian network approach for determining effective connectivity from fMRI data. Neural Comput. Appl. 2014, 24, 91–97. [Google Scholar] [CrossRef]
- Zhang, H.; Song, R.; Wang, L.; Zhang, L.; Wang, D.; Wang, C.; Zhang, W. Classification of brain disorders in rs-fMRI via local-to-global graph neural networks. IEEE Trans. Med. Imaging 2022, 42, 444–455. [Google Scholar] [CrossRef] [PubMed]
- Zheng, K.; Yu, S.; Chen, B. Ci-gnn: A granger causality-inspired graph neural network for interpretable brain network-based psychiatric diagnosis. Neural Netw. 2024, 172, 106147. [Google Scholar] [CrossRef]
- Bacciu, D.; Di Sotto, L. A non-negative factorization approach to node pooling in graph convolutional neural networks. In Proceedings of the AI* IA 2019—Advances in Artificial Intelligence: XVIIIth International Conference of the Italian Association for Artificial Intelligence, Rende, Italy, 19–22 November 2019; Proceedings 18. Springer: Cham, Switzerland, 2019; pp. 294–306. [Google Scholar]
- Xu, L.; Wu, X.; Chen, K.; Yao, L. Multi-modality sparse representation-based classification for Alzheimer’s disease and mild cognitive impairment. Comput. Methods Programs Biomed. 2015, 122, 182–190. [Google Scholar] [CrossRef]
- Jiao, Q.; Lu, G.; Zhang, Z.; Zhong, Y.; Wang, Z.; Guo, Y.; Li, K.; Ding, M.; Liu, Y. Granger causal influence predicts BOLD activity levels in the default mode network. Hum. Brain Mapp. 2011, 32, 154–161. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Gillies, D. Causality: Models, reasoning, and inference judea pearl. Br. J. Philos. Sci. 2001, 52, 613–622. [Google Scholar] [CrossRef]
- Peters, J.; Janzing, D.; Schölkopf, B. Elements of Causal Inference: Foundations and Learning Algorithms; The MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Jie, B.; Liu, M.; Shen, D. Integration of temporal and spatial properties of dynamic connectivity networks for automatic diagnosis of brain disease. Med Image Anal. 2018, 47, 81–94. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Zhou, F.; Frangi, A.F.; Cao, J.; Xiao, X.; Lei, Y.; Wang, T.; Lei, B. Graph convolution network with similarity awareness and adaptive calibration for disease-induced deterioration prediction. Med. Image Anal. 2021, 69, 101947. [Google Scholar] [CrossRef]
- Qiu, T.; Luo, X.; Shen, Z.; Huang, P.; Xu, X.; Zhou, J.; Zhang, M.; Alzheimer’s Disease Neuroimaging Initiative. Disrupted brain network in progressive mild cognitive impairment measured by eigenvector centrality mapping is linked to cognition and cerebrospinal fluid biomarkers. J. Alzheimer’s Dis. 2016, 54, 1483–1493. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zhang, H.; Gao, Y.; Wee, C.Y.; Li, G.; Shen, D.; Alzheimer’s Disease Neuroimaging Initiative. High-order resting-state functional connectivity network for MCI classification. Hum. Brain Mapp. 2016, 37, 3282–3296. [Google Scholar] [CrossRef]
- Khazaee, A.; Ebrahimzadeh, A.; Babajani-Feremi, A.; Alzheimer’s Disease Neuroimaging Initiative. Classification of patients with MCI and AD from healthy controls using directed graph measures of resting-state fMRI. Behav. Brain Res. 2017, 322, 339–350. [Google Scholar] [CrossRef]


| Group | NC | eMCI | LMCI |
|---|---|---|---|
| Male/Female | 28/39 | 32/45 | 50/20 |
| Age (mean ± STD) | 74.1 ± 6.2 | 71.2 ± 6.9 | 71.2 ± 8.3 |
| Classifier | Model | NC vs. eMCI | NC vs. LMCI | eMCI vs. LMCI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACC | SEN | SPE | F1 | ACC | SEN | SPE | F1 | ACC | SEN | SPE | F1 | ||
| RF | PC | 69.44 | 67.16 | 71.43 | 67.16 | 76.64 | 71.64 | 81.43 | 75.00 | 74.83 | 76.62 | 72.86 | 76.13 |
| SBN | 72.22 | 62.69 | 80.52 | 67.74 | 75.18 | 73.13 | 77.14 | 74.24 | 65.31 | 72.73 | 57.14 | 68.71 | |
| LRBN | 80.56 | 76.12 | 84.42 | 78.46 | 78.10 | 74.63 | 81.43 | 76.92 | 78.23 | 84.42 | 71.43 | 80.25 | |
| SLRBN | 69.44 | 59.70 | 77.92 | 64.52 | 78.10 | 77.61 | 78.57 | 77.61 | 64.63 | 76.62 | 51.43 | 69.41 | |
| GC | 80.56 | 70.15 | 89.61 | 77.05 | 81.75 | 77.61 | 85.71 | 80.62 | 65.31 | 68.83 | 61.43 | 67.52 | |
| mGC | 79.17 | 68.66 | 88.31 | 75.41 | 82.48 | 79.10 | 85.71 | 81.54 | 62.59 | 72.73 | 51.43 | 67.07 | |
| PDC | 75.69 | 77.61 | 74.03 | 74.82 | 78.83 | 73.13 | 84.29 | 77.17 | 69.39 | 71.43 | 67.14 | 70.97 | |
| DTF | 76.39 | 74.63 | 77.92 | 74.63 | 80.29 | 76.12 | 84.29 | 79.10 | 70.75 | 74.03 | 67.14 | 72.61 | |
| TE | 75.00 | 73.13 | 76.62 | 73.13 | 79.56 | 77.61 | 81.43 | 78.79 | 70.07 | 75.32 | 64.29 | 72.50 | |
| Ours | 81.25 | 76.12 | 85.71 | 79.07 | 83.21 | 77.61 | 88.57 * | 81.89 | 76.87 | 85.71 | 67.14 | 79.52 | |
| SVM | PC | 70.14 | 67.16 | 72.73 | 67.67 | 74.45 | 70.15 | 78.57 | 72.87 | 67.35 | 64.94 | 70.00 | 67.57 |
| SBN | 75.00 | 70.15 | 79.22 | 72.31 | 77.37 | 74.63 | 80.00 | 76.34 | 70.07 | 81.82 | 57.14 | 74.12 | |
| LRBN | 82.64 | 79.10 | 85.71 | 80.92 | 83.94 | 79.10 | 88.57 | 82.81 | 81.63 | 85.71 | 77.14 | 83.02 | |
| SLRBN | 73.61 | 70.15 | 76.62 | 71.21 | 76.64 | 74.63 | 78.57 | 75.76 | 65.31 | 81.82 | 47.14 | 71.19 | |
| GC | 80.56 | 79.10 | 81.82 | 79.10 | 80.29 | 79.10 | 81.43 | 79.70 | 69.39 | 74.03 | 64.29 | 71.70 | |
| mGC | 81.94 | 74.63 | 88.31 | 79.37 | 82.48 | 85.07 | 80.00 | 82.61 | 80.95 | 77.92 | 84.29 | 81.08 | |
| PDC | 75.69 | 77.61 | 74.03 | 74.82 | 79.56 | 76.12 | 82.86 | 78.46 | 71.43 | 75.32 | 67.14 | 73.42 | |
| DTF | 77.08 | 76.12 | 77.92 | 75.56 | 81.02 | 77.61 | 84.29 | 80.00 | 72.79 | 75.32 | 70.00 | 74.36 | |
| TE | 77.08 | 77.61 | 76.62 | 75.91 | 80.29 | 77.61 | 82.86 | 79.39 | 73.47 | 74.03 | 72.86 | 74.51 | |
| Ours | 83.33 | 79.10 | 87.01 | 81.54 | 85.40 * | 82.09 | 88.57 | 84.62 * | 82.99 * | 87.01 * | 78.57 | 84.28 | |
| HRGNN | PC | 75.69 | 73.13 | 77.92 | 73.68 | 76.64 | 82.09 | 71.43 | 77.46 | 71.43 | 66.23 | 77.14 | 70.83 |
| SBN | 78.47 | 71.64 | 84.42 | 75.59 | 78.10 | 82.09 | 74.29 | 78.57 | 75.51 | 84.42 | 65.71 | 78.31 | |
| LRBN | 79.86 | 76.12 | 83.12 | 77.86 | 81.02 | 76.12 | 85.71 | 79.69 | 79.59 | 84.42 | 74.29 | 81.25 | |
| SLRBN | 73.61 | 71.64 | 75.32 | 71.64 | 74.45 | 68.66 | 80.00 | 72.44 | 71.43 | 72.73 | 70.00 | 72.73 | |
| GC | 82.64 | 80.60 | 84.42 | 81.20 | 81.02 | 76.12 | 85.71 | 79.69 | 77.55 | 80.52 | 74.29 | 78.98 | |
| mGC | 81.94 | 77.61 | 85.71 | 80.00 | 83.21 | 79.10 | 87.14 | 82.17 | 78.23 | 83.12 | 72.86 | 80.00 | |
| PDC | 77.78 | 79.10 | 76.62 | 76.81 | 81.02 | 74.63 | 87.14 | 79.37 | 72.79 | 75.32 | 70.00 | 74.36 | |
| DTF | 79.86 | 79.10 | 80.52 | 78.52 | 80.29 | 76.12 | 84.29 | 79.10 | 74.83 | 74.03 | 75.71 | 75.50 | |
| TE | 78.47 | 76.12 | 80.52 | 76.69 | 81.75 | 77.61 | 85.71 | 80.62 | 75.51 | 75.32 | 75.71 | 76.32 | |
| Ours | 84.03 * | 82.09 * | 85.71 | 82.71 | 84.67 | 82.09 | 87.14 | 83.97 * | 83.67 * | 85.71 | 81.43 * | 84.62 * | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, J.; Xia, Z.; Zhang, W.; Zhao, L. Brain Connectivity Estimation Network for the Identification of Dementia. Brain Sci. 2025, 15, 975. https://doi.org/10.3390/brainsci15090975
Xi J, Xia Z, Zhang W, Zhao L. Brain Connectivity Estimation Network for the Identification of Dementia. Brain Sciences. 2025; 15(9):975. https://doi.org/10.3390/brainsci15090975
Chicago/Turabian StyleXi, Ji, Zhengwang Xia, Weiqi Zhang, and Li Zhao. 2025. "Brain Connectivity Estimation Network for the Identification of Dementia" Brain Sciences 15, no. 9: 975. https://doi.org/10.3390/brainsci15090975
APA StyleXi, J., Xia, Z., Zhang, W., & Zhao, L. (2025). Brain Connectivity Estimation Network for the Identification of Dementia. Brain Sciences, 15(9), 975. https://doi.org/10.3390/brainsci15090975







