The Projective Consciousness Model: Projective Geometry at the Core of Consciousness and the Integration of Perception, Imagination, Motivation, Emotion, Social Cognition and Action
Abstract
:1. Introduction
1.1. Consciousness as an Integrative Whole
1.2. The Subjective Perspective of Consciousness
1.3. Projective Geometry at the Core of Consciousness
1.4. General Positioning
2. Model
2.1. Motivation
2.2. Prerequisites
- for all ,
- , for all
2.3. MDP, POMDP and Active Inference
- S is the set of configurations of the environment;
- A is the collection of actions of the agent;
- is the transition probability, which captures the consequences of the action of the agent on the environment that changes from to ;
- ; it is the reward function for an action and two states thought of as and .
- O is the set of possible observations.
- Z is the observation kernel, , which specifies the probability of observing a particular observation given the current state and action.
- r is a reward function whose domain is ; .
- is defined as
- is defined as
2.3.1. Relation between POMDP and the Free Energy Principle
2.4. POMDP with Group-Structured State Space
- S is a G-space
- G is a subset of the set of actions A,
- For all ,
3. Results
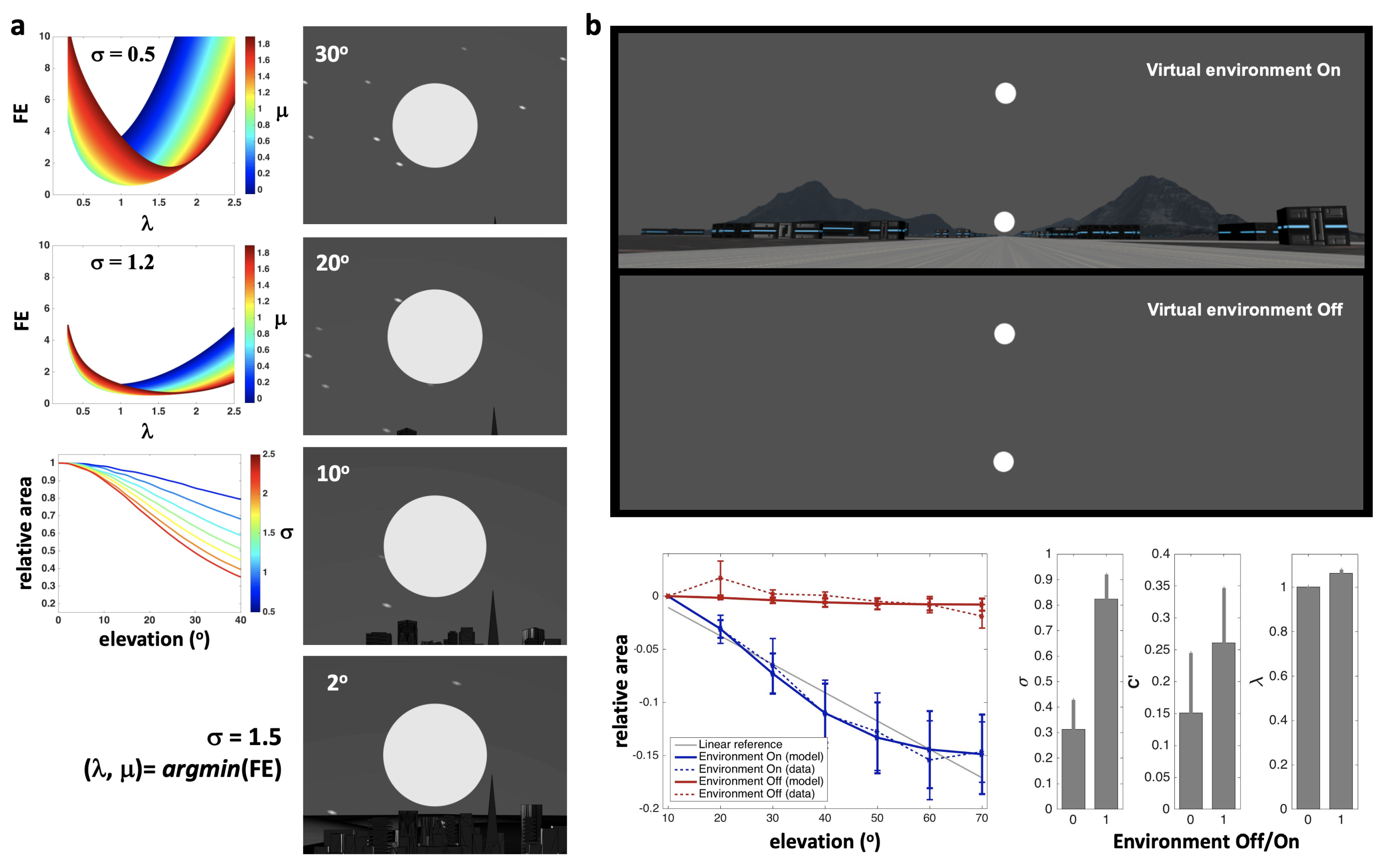
3.1. Perceptual Illusions
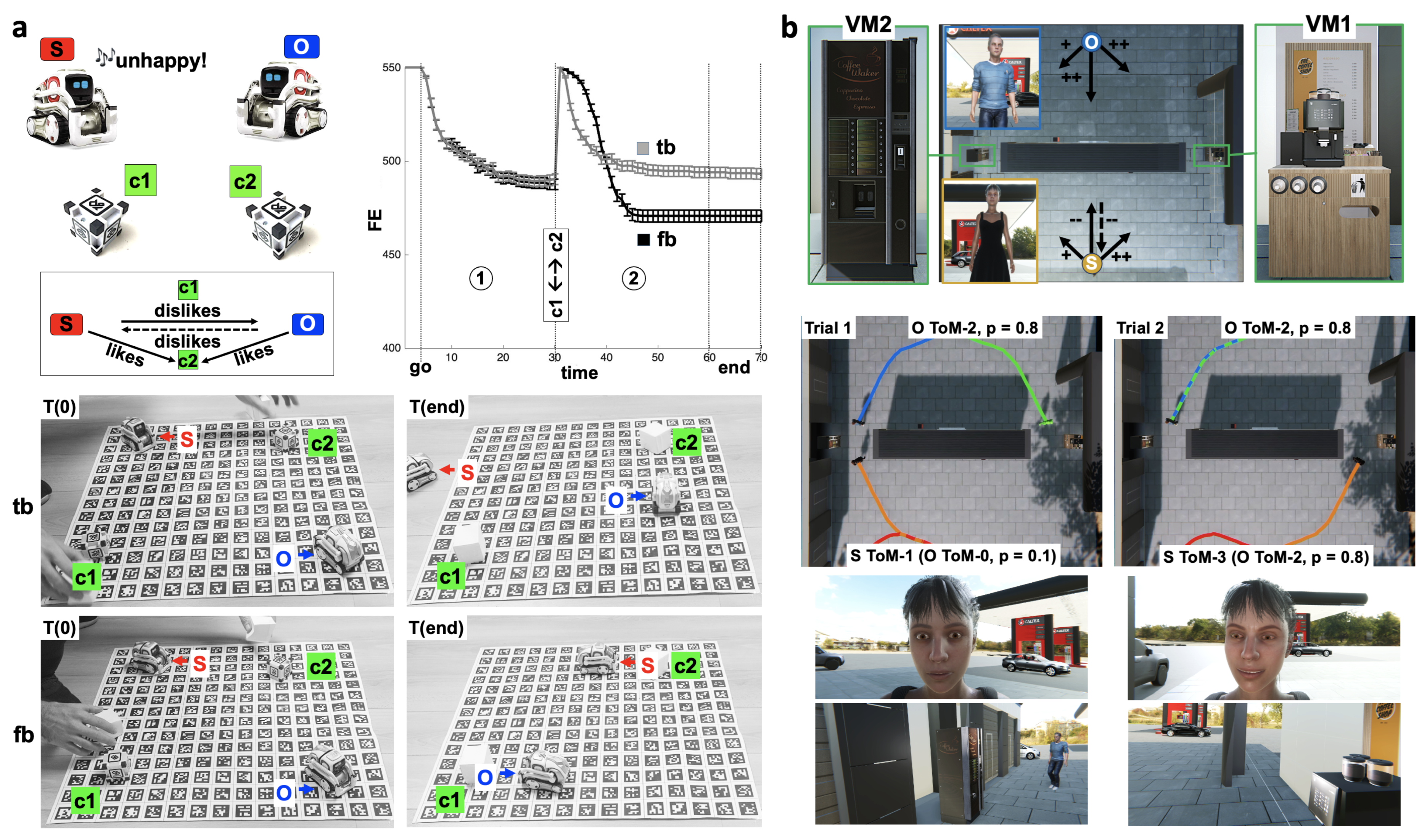
3.2. Imagination, Emotion, Drives, Social Cognition, and Adaptive Behaviors
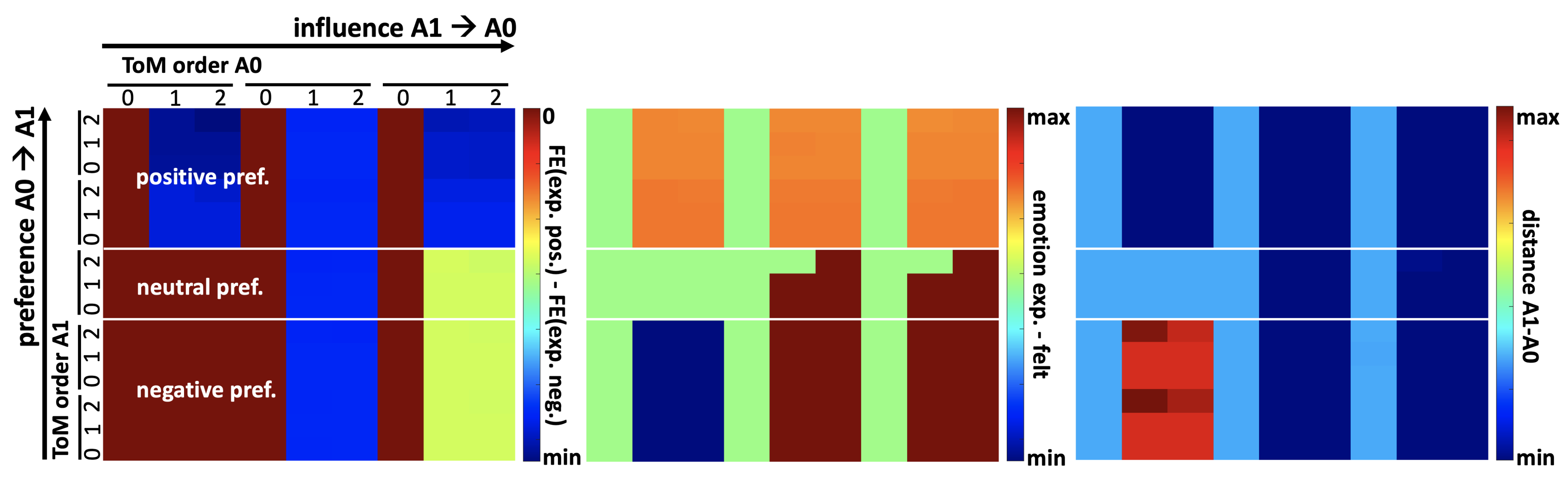
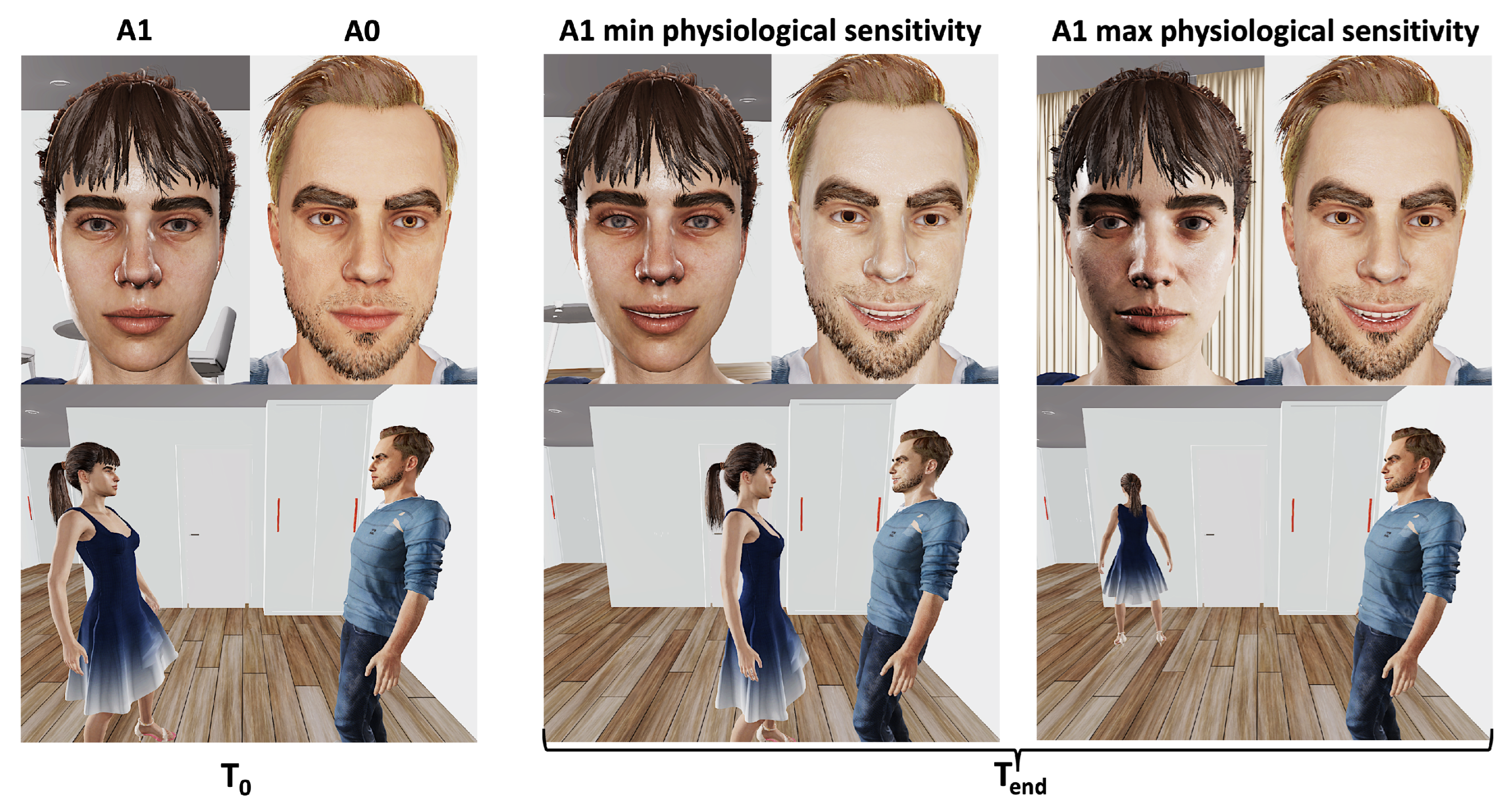
3.3. Application to Empathy, the Regulation of Emotion Expression, and the Control of Approach–Avoidance Behaviors
4. Discussion
4.1. Behavioral Science
4.2. Machine Learning
4.3. Human–Machine Interfaces and Interactions
4.4. The Neural Correlates of Consciousness
4.5. Pre-Reflective Self-Consciousness
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PCM | Projective Consciousness Model |
| NCC | Neural Correlates of Consciousness |
| IIT | Integrated Information Theory |
| GWT | Global Workspace Theory |
| GW | Global Workspace |
| ToM | Theory of Mind |
| FoC | Field of Consciousness |
| SP | Subjective Perspective |
| PGL | Projective General Linear |
| PT | Perspective Taking |
| L1PT | Level-1 Perspective Taking |
| L2PT | Level-2 Perspective Taking |
| 1PP | First Person Perspective |
| 3PP | Third Person Perspective |
| FE | Free Energy |
| FC | FoC Calibration |
| RL | Reinforcement Learning |
| SRL | State Reinforcement Learning |
| MDP | Markov Decision Process |
| POMDP | Partially Observable Markov Decision Process |
| I-POMDP | Interactive Partially Observable Markov Decision Process |
| 3D | Three-Dimensional |
References
- Seth, A.K.; Bayne, T. Theories of consciousness. Nat. Rev. Neurosci. 2022, 23, 439–452. [Google Scholar] [CrossRef]
- Crick, F.; Koch, C. Towards a neurobiological theory of consciousness. Semin. Neurosci. 1990, 2, 203. [Google Scholar]
- Tsuchiya, N.; Wilke, M.; Frässle, S.; Lamme, V.A. No-report paradigms: Extracting the true neural correlates of consciousness. Trends Cogn. Sci. 2015, 19, 757–770. [Google Scholar] [CrossRef] [PubMed]
- Northoff, G.; Lamme, V. Neural signs and mechanisms of consciousness: Is there a potential convergence of theories of consciousness in sight? Neurosci. Biobehav. Rev. 2020, 118, 568–587. [Google Scholar] [CrossRef] [PubMed]
- Merker, B.; Williford, K.; Rudrauf, D. The integrated information theory of consciousness: A case of mistaken identity. Behav. Brain Sci. 2022, 45, e41. [Google Scholar] [CrossRef] [PubMed]
- Rudrauf, D. Structure-function relationships behind the phenomenon of cognitive resilience in neurology: Insights for neuroscience and medicine. Adv. Neurosci. 2014, 2014, 462765. [Google Scholar] [CrossRef]
- Rudrauf, D.; Lutz, A.; Cosmelli, D.; Lachaux, J.P.; Le Van Quyen, M. From autopoiesis to neurophenomenology: Francisco Varela’s exploration of the biophysics of being. Biol. Res. 2003, 36, 27–65. [Google Scholar] [CrossRef]
- Tononi, G.; Boly, M.; Massimini, M.; Koch, C. Integrated information theory: From consciousness to its physical substrate. Nat. Rev. Neurosci. 2016, 17, 450–461. [Google Scholar] [CrossRef]
- Doerig, A.; Schurger, A.; Herzog, M.H. Hard criteria for empirical theories of consciousness. Cogn. Neurosci. 2021, 12, 41–62. [Google Scholar] [CrossRef]
- Baars, B. A Cognitive Theory of Consciousness; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Dehaene, S.; Lau, H.; Kouider, S. What is consciousness, and could machines have it? Science 2017, 358, 486–492. [Google Scholar] [CrossRef]
- Sergent, C.; Baillet, S.; Dehaene, S. Timing of the brain events underlying access to consciousness during the attentional blink. Nat. Neurosci. 2005, 8, 1391–1400. [Google Scholar] [CrossRef] [PubMed]
- Dehaene, S.; Changeux, J.P.; Naccache, L.; Sackur, J.; Sergent, C. Conscious, preconscious, and subliminal processing: A testable taxonomy. Trends Cogn. Sci. 2006, 10, 204–211. [Google Scholar] [CrossRef] [PubMed]
- Dehaene, S. Consciousness and the Brain: Deciphering How the Brain Codes Our Thoughts. J. Undergrad. Neurosci. Educ. 2014, 12, R5–R6. [Google Scholar]
- Wallace, R. CONSCIOUSNESS: A Mathematical Treatment of the Global Neuronal Workspace Model; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Boly, M.; Massimini, M.; Tsuchiya, N.; Postle, B.R.; Koch, C.; Tononi, G. Are the neural correlates of consciousness in the front or in the back of the cerebral cortex? Clinical and neuroimaging evidence. J. Neurosci. 2017, 37, 9603–9613. [Google Scholar] [CrossRef] [PubMed]
- Melloni, L.; Mudrik, L.; Pitts, M.; Bendtz, K.; Ferrante, O.; Gorska, U.; Hirschhorn, R.; Khalaf, A.; Kozma, C.; Lepauvre, A.; et al. An adversarial collaboration protocol for testing contrasting predictions of global neuronal workspace and integrated information theory. PLoS ONE 2023, 18, e0268577. [Google Scholar] [CrossRef]
- Lenharo, M. Decades-long bet on consciousness ends-and it’s philosopher 1, neuroscientist 0. Nature 2023, 619, 14–15. [Google Scholar] [CrossRef]
- Burgin, M. Theory of Information: Fundamentality, Diversity and Unification; World Scientific: Singapore, 2010; Volume 1. [Google Scholar]
- Burgin, M. Theory of Knowledge: Structures and Processes; World Scientific: Singapore, 2016; Volume 5. [Google Scholar]
- James, W.; Burkhardt, F.; Bowers, F.; Skrupskelis, I.K. The Principles of Psychology; Macmillan London: London, UK, 1890; Volume 1. [Google Scholar]
- Nagel, T. What is it like to be a bat? Philos. Rev. 1974, 83, 435–450. [Google Scholar] [CrossRef]
- Lehar, S.M. The World in Your Head: A Gestalt View of the Mechanism of Conscious Experience; Psychology Press: London, UK; Routledge: London, UK, 2003; Available online: https://philpapers.org/rec/LEHTWI (accessed on 8 July 2023).
- Merker, B. From probabilities to percepts A subcortical “global best estimate buffer” as locus of phenomenal experience. Being Time Dyn. Model. Phenomenal Exp. 2012, 88, 37. [Google Scholar]
- Rudrauf, D.; Bennequin, D.; Granic, I.; Landini, G.; Friston, K.; Williford, K. A mathematical model of embodied consciousness. J. Theor. Biol. 2017, 428, 106–131. [Google Scholar] [CrossRef]
- Amorim, M.A.; Trumbore, B.; Chogyen, P.L. Cognitive repositioning inside a desktop VE: The constraints introduced by first-versus third-person imagery and mental representation richness. Presence Teleoperators Virtual Environ. 2000, 9, 165–186. [Google Scholar] [CrossRef]
- Vogeley, K.; Fink, G.R. Neural correlates of the first-person-perspective. Trends Cogn. Sci. 2003, 7, 38–42. [Google Scholar] [CrossRef] [PubMed]
- David, N.; Bewernick, B.H.; Cohen, M.X.; Newen, A.; Lux, S.; Fink, G.R.; Shah, N.J.; Vogeley, K. Neural representations of self versus other: Visual-spatial perspective taking and agency in a virtual ball-tossing game. J. Cogn. Neurosci. 2006, 18, 898–910. [Google Scholar] [CrossRef] [PubMed]
- Mazzarella, E.; Ramsey, R.; Conson, M.; Hamilton, A. Brain systems for visual perspective taking and action perception. Soc. Neurosci. 2013, 8, 248–267. [Google Scholar] [CrossRef] [PubMed]
- Capozzi, F.; Cavallo, A.; Furlanetto, T.; Becchio, C. Altercentric intrusions from multiple perspectives: Beyond dyads. PLoS ONE 2014, 9, e114210. [Google Scholar] [CrossRef]
- Merleau-Ponty, M. Phenomenology of Perception; Translated by Colin Smith; Motilal Banarsidass: New Delhi, India, 2005; p. 487. [Google Scholar]
- Varela, F. Principles of Biological Autonomy; Appleton & Lange: New York, NY, USA, 1979; p. 701. [Google Scholar]
- Riva, G. The neuroscience of body memory: From the self through the space to the others. Cortex 2018, 104, 241–260. [Google Scholar] [CrossRef]
- McHugh, L.; Stewart, I. The Self and Perspective Taking: Contributions and Applications from Modern Behavioral Science; New Harbinger Publications: Oakland, CA, USA, 2012. [Google Scholar]
- Ciompi, L. Affects as Central Organising and Integrating Factors a New Psychosocial/Biological Model of the Psyche. Br. J. Psychiatry 1991, 159, 97–105. [Google Scholar] [CrossRef]
- Baron-Cohen, S. Joint-attention deficits in autism: Towards a cognitive analysis. Dev. Psychopathol. 1989, 1, 185–189. [Google Scholar] [CrossRef]
- Kalbe, E.; Grabenhorst, F.; Brand, M.; Kessler, J.; Hilker, R.; Markowitsch, H.J. Elevated emotional reactivity in affective but not cognitive components of theory of mind: A psychophysiological study. J. Neuropsychol. 2007, 1, 27–38. [Google Scholar] [CrossRef]
- Baron-Cohen, S. Precursors to a theory of mind: Understanding attention in others. In Natural Theories of Mind: Evolution, Development and Simulation of Everyday Mindreading; Whiten, A., Byrne, R., Eds.; Basil Blackwell Oxford: Oxford, UK, 1991; Volume 1, pp. 233–251. [Google Scholar]
- Wimmer, H.; Perner, J. Beliefs about beliefs: Representation and constraining function of wrong beliefs in young children’s understanding of deception. Cognition 1983, 13, 103–128. [Google Scholar] [CrossRef]
- Lamm, C.; Batson, C.D.; Decety, J. The neural substrate of human empathy: Effects of perspective-taking and cognitive appraisal. J. Cogn. Neurosci. 2007, 19, 42–58. [Google Scholar] [CrossRef]
- Berthoz, A.; Thirioux, B. A spatial and perspective change theory of the difference between sympathy and empathy. Paragrana 2010, 19, 32–61. [Google Scholar] [CrossRef]
- Seth, A.K.; Suzuki, K.; Critchley, H.D. An interoceptive predictive coding model of conscious presence. Front. Psychol. 2012, 2, 395. [Google Scholar] [CrossRef] [PubMed]
- Damasio, A.R. The Feeling of What Happens: Body and Emotion in the Making of Consciousness; Houghton Mifflin Harcourt: Boston, MA, USA, 1999. [Google Scholar]
- Blanke, O. Multisensory brain mechanisms of bodily self-consciousness. Nat. Rev. Neurosci. 2012, 13, 556–571. [Google Scholar] [CrossRef] [PubMed]
- Seth, A.K. Consciousness: The last 50 years (and the next). Brain Neurosci. Adv. 2018, 2, 2398212818816019. [Google Scholar] [CrossRef] [PubMed]
- Seth, A.K.; Hohwy, J. Elusive phenomenology, counterfactual awareness, and presence without mastery. Cogn. Neurosci. 2014, 5, 127–128. [Google Scholar]
- Seth, A.K. Presence, objecthood, and the phenomenology of predictive perception. Cogn. Neurosci. 2015, 6, 111–117. [Google Scholar] [CrossRef] [PubMed]
- Revonsuo, A. Consciousness as a Biological Phenomenon; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Chella, A.; Manzotti, R. Machine consciousness: A manifesto for robotics. Int. J. Mach. Conscious. 2009, 1, 33–51. [Google Scholar] [CrossRef]
- Manzotti, R.; Chella, A. Good old-fashioned artificial consciousness and the intermediate level fallacy. Front. Robot. 2018, 5, 39. [Google Scholar] [CrossRef]
- Flavell, J.H.; Everett, B.A.; Croft, K.; Flavell, E.R. Young children’s knowledge about visual perception: Further evidence for the Level 1–Level 2 distinction. Dev. Psychol. 1981, 17, 99. [Google Scholar] [CrossRef]
- Flavell, J.H. Thinking and Seeing: Visual Metacognition in Adults and Children; MIT Press: Cambridge, MA, USA, 2004; pp. 13–36. [Google Scholar]
- Michelon, P.; Zacks, J.M. Two kinds of visual perspective taking. Percept. Psychophys. 2006, 68, 327–337. [Google Scholar] [CrossRef]
- Amorim, M.A. “What is my avatar seeing?”: The coordination of “out-of-body” and “embodied” perspectives for scene recognition across views. Vis. Cogn. 2003, 10, 157–199. [Google Scholar] [CrossRef]
- Surtees, A.; Samson, D.; Apperly, I. Unintentional perspective-taking calculates whether something is seen, but not how it is seen. Cognition 2016, 148, 97–105. [Google Scholar] [CrossRef] [PubMed]
- Piaget, J.; Inhelder, B. The Child’s Concept of Space; Routledge & Paul: London, UK, 1956. [Google Scholar]
- Emery, N.J. The eyes have it: The neuroethology, function and evolution of social gaze. Neurosci. Biobehav. Rev. 2000, 24, 581–604. [Google Scholar] [CrossRef] [PubMed]
- Butterfill, S.A.; Apperly, I.A. How to construct a minimal theory of mind. Mind Lang. 2013, 28, 606–637. [Google Scholar] [CrossRef]
- Quesque, F.; Rossetti, Y. What do theory-of-mind tasks actually measure? Theory and practice. Perspect. Psychol. Sci. 2020, 15, 384–396. [Google Scholar] [CrossRef]
- Vestner, T.; Balsys, E.; Over, H.; Cook, R. The self-consistency effect seen on the Dot Perspective Task is a product of domain-general attention cueing, not automatic perspective taking. Cognition 2022, 224, 105056. [Google Scholar] [CrossRef]
- Kulke, L.; Johannsen, J.; Rakoczy, H. Why can some implicit Theory of Mind tasks be replicated and others cannot? A test of mentalizing versus submentalizing accounts. PLoS ONE 2019, 14, e0213772. [Google Scholar] [CrossRef]
- Heyes, C. Submentalizing: I am not really reading your mind. Perspect. Psychol. Sci. 2014, 9, 131–143. [Google Scholar] [CrossRef]
- Williford, K.; Bennequin, D.; Friston, K.; Rudrauf, D. The projective consciousness model and phenomenal selfhood. Front. Psychol. 2018, 9, 2571. [Google Scholar] [CrossRef]
- Rudrauf, D.; Debbané, M. Building a cybernetic model of psychopathology: Beyond the metaphor. Psychol. Inq. 2018, 29, 156–164. [Google Scholar] [CrossRef]
- Rudrauf, D.; Bennequin, D.; Williford, K. The moon illusion explained by the projective consciousness model. J. Theor. Biol. 2020, 507, 110455. [Google Scholar] [CrossRef] [PubMed]
- Rudrauf, D.; Sergeant-Perthuis, G.; Belli, O.; Tisserand, Y.; Serugendo, G.D.M. Modeling the subjective perspective of consciousness and its role in the control of behaviours. J. Theor. Biol. 2022, 534, 110957. [Google Scholar] [CrossRef] [PubMed]
- Rudrauf, D.; Sergeant-Perhtuis, G.; Tisserand, Y.; Monnor, T.; De Gevigney, V.; Belli, O. Combining the Projective Consciousness Model and Virtual Humans for immersive psychological research: A proof-of-concept simulating a ToM assessment. ACM Trans. Interact. Intell. Syst. 2023, 13, 1–31. [Google Scholar] [CrossRef]
- Williford, K.; Bennequin, D.; Rudrauf, D. Pre-Reflective Self-Consciousness & Projective Geometry. Rev. Philos. Psychol. 2022, 13, 365–396. [Google Scholar]
- Sergeant-Perthuis, G.; Rudrauf, D.; Ognibene, D.; Tisserand, Y. Action of the Euclidean versus Projective group on an agent’s internal space in curiosity driven exploration: A formal analysis. arXiv 2023, arXiv:2304.00188. [Google Scholar]
- Rabeyron, T.; Finkel, A. Consciousness, Free Energy and Cognitive Algorithms. Front. Psychol. 2020, 11, 1675. [Google Scholar] [CrossRef]
- Friston, K. The free-energy principle: A unified brain theory? Nat. Rev. Neurosci. 2010, 11, 127–138. [Google Scholar] [CrossRef]
- Friston, K.; FitzGerald, T.; Rigoli, F.; Schwartenbeck, P.; Pezzulo, G. Active inference: A process theory. Neural Comput. 2017, 29, 1–49. [Google Scholar] [CrossRef]
- Friston, K.; Samothrakis, S.; Montague, R. Active inference and agency: Optimal control without cost functions. Biol. Cybern. 2012, 106, 523–541. [Google Scholar] [CrossRef]
- Friston, K.; Rigoli, F.; Ognibene, D.; Mathys, C.; Fitzgerald, T.; Pezzulo, G. Active inference and epistemic value. Cogn. Neurosci. 2015, 6, 187–214. [Google Scholar] [CrossRef]
- Gmytrasiewicz, P.J.; Doshi, P. A Framework for Sequential Planning in Multi-Agent Settings. J. Artif. Int. Res. 2005, 24, 49–79. [Google Scholar] [CrossRef]
- Woodward, M.P.; Wood, R.J. Learning from Humans as an I-POMDP. arXiv 2012, arXiv:cs.RO/1204.0274. [Google Scholar]
- Lang, S. Algebra; Springer Science & Business Media: Berlin, Germany, 2012; Volume 211. [Google Scholar]
- Yang, Y.; Wang, J. An Overview of Multi-Agent Reinforcement Learning from Game Theoretical Perspective. arXiv 2021, arXiv:cs.MA/2011.00583. [Google Scholar]
- Kurniawati, H. Partially Observable Markov Decision Processes and Robotics. Annu. Rev. Control. Robot. Auton. Syst. 2022, 5, 253–277. [Google Scholar] [CrossRef]
- Todorov, E. General duality between optimal control and estimation. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 4286–4292. [Google Scholar] [CrossRef]
- Todorov, E. Linearly-solvable Markov decision problems. In Advances in Neural Information Processing Systems; Schölkopf, B., Platt, J., Hoffman, T., Eds.; MIT Press: Boston, MA, USA, 2006; Volume 19. [Google Scholar]
- Teghtsoonian, R.; Frost, R.O. The effects of viewing distance on fear of snakes. J. Behav. Ther. Exp. Psychiatry 1982, 13, 181–190. [Google Scholar] [CrossRef]
- Moscovici, S.; Faucheux, C. Social influence, conformity bias, and the study of active minorities. In Advances in Experimental Social Psychology; Elsevier: Amsterdam, The Netherlands, 1972; Volume 6, pp. 149–202. [Google Scholar]
- Baron-Cohen, S.; Leslie, A.M.; Frith, U. Does the autistic child have a “theory of mind”. Cognition 1985, 21, 37–46. [Google Scholar] [CrossRef] [PubMed]
- Leslie, A.M.; Frith, U. Autistic children’s understanding of seeing, knowing and believing. Br. J. Dev. Psychol. 1988, 6, 315–324. [Google Scholar] [CrossRef]
- Tisserand, Y.; Aylett, R.; Mortillaro, M.; Rudrauf, D. Real-time simulation of virtual humans’ emotional facial expressions, harnessing autonomic physiological and musculoskeletal control. In Proceedings of the 20th ACM International Conference on Intelligent Virtual Agents, Virtual, 20–22 October 2020; pp. 1–8. [Google Scholar]
- Ekman, P.; Friesen, W.V. Facial action coding system. Environ. Psychol. Nonverbal Behav. 1978, 1, 1–8. [Google Scholar]
- Lesort, T.; Díaz-Rodríguez, N.; Goudou, J.F.; Filliat, D. State representation learning for control: An overview. Neural Netw. 2018, 108, 379–392. [Google Scholar] [CrossRef]
- Kelly, J.W.; Avraamides, M.N. Cross-sensory transfer of reference frames in spatial memory. Cognition 2011, 118, 444–450. [Google Scholar] [CrossRef]
- Sander, D.; Grafman, J.; Zalla, T. The human amygdala: An evolved system for relevance detection. Rev. Neurosci. 2003, 14, 303–316. [Google Scholar] [CrossRef] [PubMed]
- Kitanishi, T.; Ito, H.T.; Hayashi, Y.; Shinohara, Y.; Mizuseki, K.; Hikida, T. Network mechanisms of hippocampal laterality, place coding, and goal-directed navigation. J. Physiol. Sci. 2017, 67, 247–258. [Google Scholar] [CrossRef] [PubMed]
- Andrews-Buckner, R.; Hanna, J.; Schacter, D. The brain’s default network: Anatomy, function, and relevance to disease. Ann. N. Y. Acad. Sci. 2008, 1124, 1–38. [Google Scholar] [CrossRef] [PubMed]
- Andersen, R.A. Multimodal integration for the representation of space in the posterior parietal cortex. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1997, 352, 1421–1428. [Google Scholar] [CrossRef]
- Bartolomeo, P.; Chokron, S. Orienting of attention in left unilateral neglect. Neurosci. Biobehav. Rev. 2002, 26, 217–234. [Google Scholar] [CrossRef]
- Hassabis, D.; Maguire, E.A. Deconstructing episodic memory with construction. Trends Cogn. Sci. 2007, 11, 299–306. [Google Scholar] [CrossRef]
- Vossel, S.; Mathys, C.; Stephan, K.E.; Friston, K.J. Cortical coupling reflects Bayesian belief updating in the deployment of spatial attention. J. Neurosci. 2015, 35, 11532–11542. [Google Scholar] [CrossRef]
- Mesmoudi, S.; Perlbarg, V.; Rudrauf, D.; Messe, A.; Pinsard, B.; Hasboun, D.; Cioli, C.; Marrelec, G.; Toro, R.; Benali, H.; et al. Resting state networks’ corticotopy: The dual intertwined rings architecture. PLoS ONE 2013, 8, e67444. [Google Scholar] [CrossRef]
- Nigro, G.; Neisser, U. Point of view in personal memories. Cogn. Psychol. 1983, 15, 467–482. [Google Scholar] [CrossRef]
- Berntsen, D.; Rubin, D.C. Emotion and vantage point in autobiographical. Cogn. Emot. 2006, 20, 1193–1215. [Google Scholar] [CrossRef]
- Philippi, C.L.; Duff, M.C.; Denburg, N.L.; Tranel, D.; Rudrauf, D. Medial PFC damage abolishes the self-reference effect. J. Cogn. Neurosci. 2012, 24, 475–481. [Google Scholar] [CrossRef]
- Küçüktaş, S.; St Jacques, P.L. How shifting visual perspective during autobiographical memory retrieval influences emotion: A change in retrieval orientation. Front. Hum. Neurosci. 2022, 16, 928583. [Google Scholar] [CrossRef]
- Ford, J.H.; Kensinger, E.A. The role of the amygdala in emotional experience during retrieval of personal memories. Memory 2019, 27, 1362–1370. [Google Scholar] [CrossRef]
- Jitsuishi, T.; Yamaguchi, A. Characteristic cortico-cortical connection profile of human precuneus revealed by probabilistic tractography. Sci. Rep. 2023, 13, 1936. [Google Scholar] [CrossRef]
- Gunia, A.; Moraresku, S.; Vlček, K. Brain mechanisms of visuospatial perspective-taking in relation to object mental rotation and the theory of mind. Behav. Brain Res. 2021, 407, 113247. [Google Scholar] [CrossRef]
- Lyu, D.; Stieger, J.R.; Xin, C.; Ma, E.; Lusk, Z.; Aparicio, M.K.; Werbaneth, K.; Perry, C.M.; Deisseroth, K.; Buch, V.; et al. Causal evidence for the processing of bodily self in the anterior precuneus. Neuron 2023, 111, 2502–2512. [Google Scholar] [CrossRef]
- Philippi, C.L.; Tranel, D.; Duff, M.; Rudrauf, D. Damage to the default mode network disrupts autobiographical memory retrieval. Soc. Cogn. Affect. Neurosci. 2015, 10, 318–326. [Google Scholar] [CrossRef]
- Pang, J.C.; Aquino, K.M.; Oldehinkel, M.; Robinson, P.A.; Fulcher, B.D.; Breakspear, M.; Fornito, A. Geometric constraints on human brain function. Nature 2023, 618, 566–574. [Google Scholar] [CrossRef]
- Northoff, G.; Zilio, F. Temporo-spatial Theory of Consciousness (TTC)–Bridging the gap of neuronal activity and phenomenal states. Behav. Brain Res. 2022, 424, 113788. [Google Scholar] [CrossRef]
- Northoff, G.; Smith, D. The subjectivity of self and its ontology: From the world–brain relation to the point of view in the world. Theory Psychol. 2022, 33, 485–514. [Google Scholar] [CrossRef]
- Mashour, G.A.; Palanca, B.J.; Basner, M.; Li, D.; Wang, W.; Blain-Moraes, S.; Lin, N.; Maier, K.; Muench, M.; Tarnal, V.; et al. Recovery of consciousness and cognition after general anesthesia in humans. Elife 2021, 10, e59525. [Google Scholar] [CrossRef] [PubMed]
- Damasio, A. Self Comes to Mind: Constructing the Conscious Brain by Antonio Damasio; Pantheon Books: New York, NY, USA, 2010; p. 367. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rudrauf, D.; Sergeant-Perthuis, G.; Tisserand, Y.; Poloudenny, G.; Williford, K.; Amorim, M.-A. The Projective Consciousness Model: Projective Geometry at the Core of Consciousness and the Integration of Perception, Imagination, Motivation, Emotion, Social Cognition and Action. Brain Sci. 2023, 13, 1435. https://doi.org/10.3390/brainsci13101435
Rudrauf D, Sergeant-Perthuis G, Tisserand Y, Poloudenny G, Williford K, Amorim M-A. The Projective Consciousness Model: Projective Geometry at the Core of Consciousness and the Integration of Perception, Imagination, Motivation, Emotion, Social Cognition and Action. Brain Sciences. 2023; 13(10):1435. https://doi.org/10.3390/brainsci13101435
Chicago/Turabian StyleRudrauf, David, Grégoire Sergeant-Perthuis, Yvain Tisserand, Germain Poloudenny, Kenneth Williford, and Michel-Ange Amorim. 2023. "The Projective Consciousness Model: Projective Geometry at the Core of Consciousness and the Integration of Perception, Imagination, Motivation, Emotion, Social Cognition and Action" Brain Sciences 13, no. 10: 1435. https://doi.org/10.3390/brainsci13101435
APA StyleRudrauf, D., Sergeant-Perthuis, G., Tisserand, Y., Poloudenny, G., Williford, K., & Amorim, M.-A. (2023). The Projective Consciousness Model: Projective Geometry at the Core of Consciousness and the Integration of Perception, Imagination, Motivation, Emotion, Social Cognition and Action. Brain Sciences, 13(10), 1435. https://doi.org/10.3390/brainsci13101435






