Imputing the Number of Responders from the Mean and Standard Deviation of CGI-Improvement in Clinical Trials Investigating Medications for Autism Spectrum Disorder
Abstract
:1. Introduction
2. Methods
2.1. Dataset
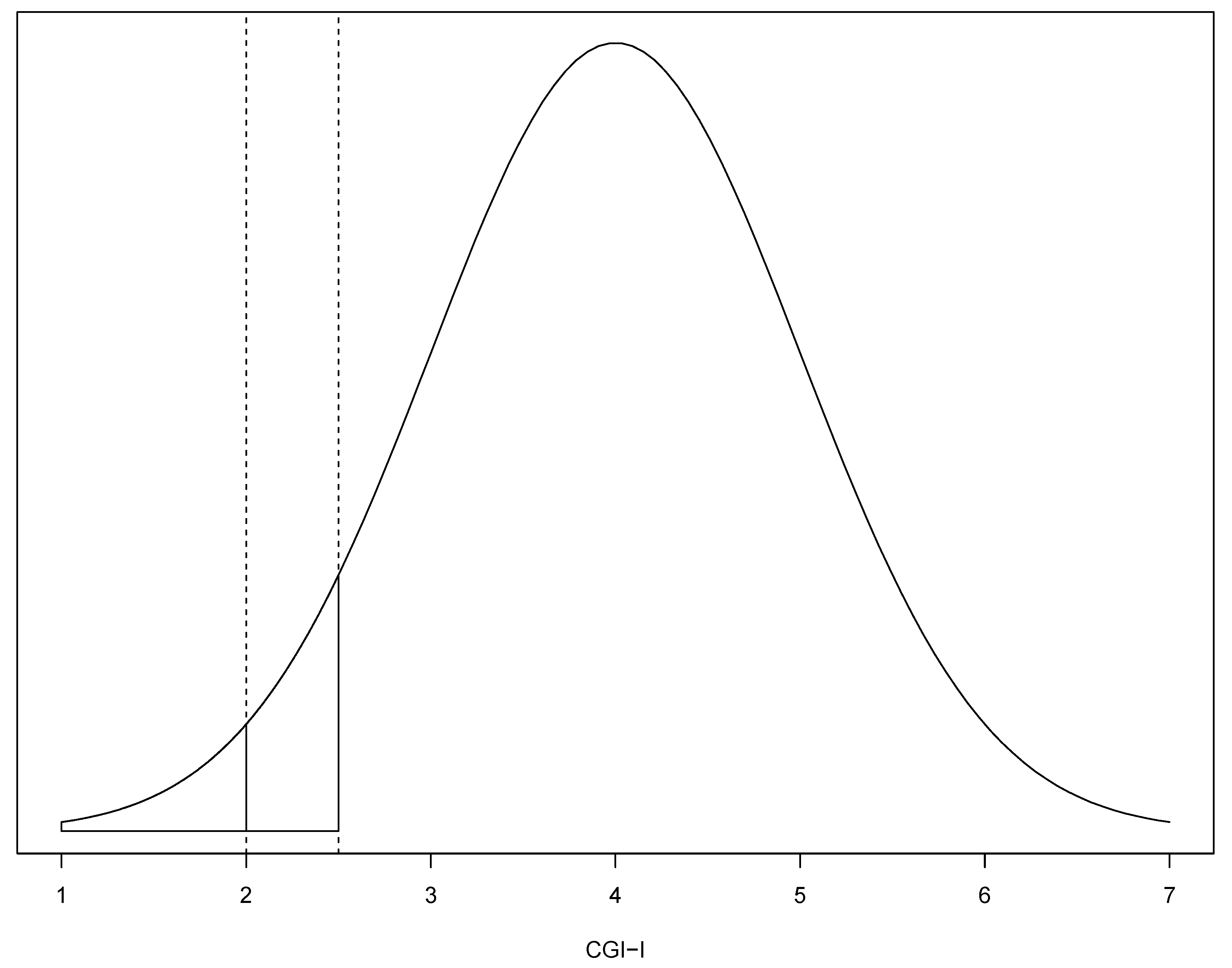
2.2. Imputation Method
2.3. Assessment of Performance of the Imputation Method
2.3.1. Concordance Correlation Coefficient (CCC)
2.3.2. Predictive Accuracy and Linear Regression Model
2.3.3. Limits of Agreement and Bland–Altman Analysis
2.4. Meta-Analysis
3. Results
3.1. Responder Rates
3.2. Odds Ratios
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Díaz-Caneja, C.M.; State, M.W.; Hagerman, R.J.; Jacquemont, S.; Marín, O.; Bagni, C.; Umbricht, D.; Simonoff, E.; De Andrés-Trelles, F.; Kaale, A.; et al. A white paper on a neurodevelopmental framework for drug discovery in autism and other neurodevelopmental disorders. Eur. Neuropsychopharmacol. 2021. [Google Scholar] [CrossRef]
- Tromans, S.; Adams, C. Brief Report: Autism Spectrum Disorder: A Comprehensive Survey of Randomized Controlled Trials. J. Autism. Dev. Disord. 2018, 48, 3228–3232. [Google Scholar] [CrossRef] [PubMed]
- Scahill, L.; Aman, M.G.; Lecavalier, L.; Halladay, A.K.; Bishop, S.L.; Bodfish, J.W.; Grondhuis, S.; Jones, N.; Horrigan, J.P.; Cook, E.H.; et al. Measuring repetitive behaviors as a treatment endpoint in youth with autism spectrum disorder. Autism 2013, 19, 38–52. [Google Scholar] [CrossRef] [PubMed]
- Anagnostou, E.; Jones, N.; Huerta, M.; Halladay, A.K.; Wang, P.; Scahill, L.; Horrigan, J.P.; Kasari, C.; Lord, C.; Choi, D.; et al. Measuring social communication behaviors as a treatment endpoint in individuals with autism spectrum disorder. Autism 2014, 19, 622–636. [Google Scholar] [CrossRef] [PubMed]
- McConachie, H.; Parr, J.R.; Glod, M.; Hanratty, J.; Livingstone, N.; Oono, I.P.; Robalino, S.; Baird, G.; Beresford, B.; Charman, T.; et al. Systematic review of tools to measure outcomes for young children with autism spectrum disorder. Health Technol. Assess. 2015, 19, 1–506. [Google Scholar] [CrossRef]
- Guy, W. ECDEU Assessment Manual for Psychopharmacology; US Department of Health and Welfare: Washington, DC, USA, 1976; pp. 534–537.
- Choque Olsson, N.; Bolte, S. Brief report: “Quick and (not so) dirty” assessment of change in autism: Cross-cultural reliability of the Developmental Disabilities CGAS and the OSU autism CGI. J. Autism. Dev. Disord. 2014, 44, 1773–1778. [Google Scholar] [CrossRef] [PubMed]
- Aman, M.G.; Novotny, S.; Samango-Sprouse, C.; Lecavalier, L.; Leonard, E.; Gadow, K.D.; King, B.H.; Pearson, D.A.; Gernsbacher, M.A.; Chez, M. Outcome measures for clinical drug trials in autism. CNS Spectr. 2004, 9, 36–47. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Provenzani, U.; Fusar-Poli, L.; Brondino, N.; Damiani, S.; Vercesi, M.; Meyer, N.; Rocchetti, M.; Politi, P. What are we targeting when we treat autism spectrum disorder? A systematic review of 406 clinical trials. Autism 2020, 24, 274–284. [Google Scholar] [CrossRef]
- King, B.H.; Hollander, E.; Sikich, L.; McCracken, J.T.; Scahill, L.; Bregman, J.D.; Donnelly, C.L.; Anagnostou, E.; Dukes, K.; Sullivan, L.; et al. Lack of efficacy of citalopram in children with autism spectrum disorders and high levels of repetitive behavior: Citalopram ineffective in children with autism. Arch. Gen. Psychiatry 2009, 66, 583–590. [Google Scholar] [CrossRef] [Green Version]
- Busner, J.; Targum, S.D. The clinical global impressions scale: Applying a research tool in clinical practice. Psychiatry 2007, 4, 28–37. [Google Scholar]
- Furukawa, T.A.; Cipriani, A.; Barbui, C.; Brambilla, P.; Watanabe, N. Imputing response rates from means and standard deviations in meta-analyses. Int. Clin. Psychopharmacol. 2005, 20, 49–52. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Samara, M.T.; Spineli, L.M.; Furukawa, T.A.; Engel, R.R.; Davis, J.M.; Salanti, G.; Leucht, S. Imputation of response rates from means and standard deviations in schizophrenia. Schizophr. Res. 2013, 151, 209–214. [Google Scholar] [CrossRef]
- Siafis, S.; Çıray, O.; Schneider-Thoma, J.; Bighelli, I.; Krause, M.; Rodolico, A.; Ceraso, A.; Deste, G.; Huhn, M.; Fraguas, D.; et al. Placebo response in pharmacological and dietary supplement trials of autism spectrum disorder (ASD): Systematic review and meta-regression analysis. Mol. Autism 2020, 11, 66. [Google Scholar] [CrossRef] [PubMed]
- Siafis, S.; Çıray, O.; Wu, H.; Schneider-Thoma, J.; Bighelli, I.; Krause, M.; Rodolico, A.; Ceraso, A.; Deste, G.; Huhn, M.; et al. Pharmacological and dietary supplement treatments for autism spectrum disorder: A systematic review and network meta-analysis. 2021; In preparation. [Google Scholar]
- Liddell, T.M.; Kruschke, J.K. Analyzing ordinal data with metric models: What could possibly go wrong? J. Exp. Soc. Psychol. 2018, 79, 328–348. [Google Scholar] [CrossRef] [Green Version]
- Lin, L.I. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]
- Schwarzer, G.; Chemaitelly, H.; Abu-Raddad, L.J.; Rücker, G. Seriously misleading results using inverse of Freeman-Tukey double arcsine transformation in meta-analysis of single proportions. Res. Synth. Methods 2019, 10, 476–483. [Google Scholar] [CrossRef] [Green Version]
- DerSimonian, R.; Laird, N. Meta-analysis in clinical trials revisited. Contemp. Clin. Trials 2015, 45, 139–145. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: https://www.r-project.org/ (accessed on 22 March 2021).
- Stevenson, M.; Nunes, T.; Heuer, C.; Marshall, J.; Sanchez, J.; Thornton, R.; Reiczigel, J.; Robison-Cox, J.; Sebastiani, P.; Solymos, P. epiR: Tools for the Analysis of Epidemiological Data. R Package Version 2.0.17. 2020. Available online: https://cran.r-project.org/package=epiR (accessed on 22 March 2021).
- Viechtbauer, W. Conducting meta-analyses in R with the metafor package. J. Stat. Softw. 2010, 36, 1–48. [Google Scholar] [CrossRef] [Green Version]
- Balduzzi, S.; Rücker, G.; Schwarzer, G. How to perform a meta-analysis with R: A practical tutorial. Evid. Based Ment. Health 2019, 22, 153–160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wickham, H.; Averick, M.; Bryan, J.; Chang, W.; McGowan, L.D.A.; François, R.; Grolemund, G.; Hayes, A.; Henry, L.; Hester, J. Welcome to the Tidyverse. J. Open Source Softw. 2019, 4, 1686. [Google Scholar] [CrossRef]
- Furukawa, T.A.; Akechi, T.; Wagenpfeil, S.; Leucht, S. Relative indices of treatment effect may be constant across different definitions of response in schizophrenia trials. Schizophr. Res. 2011, 126, 212–219. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Johnston, B.C.; Alonso-Coello, P.; Friedrich, J.O.; Mustafa, R.A.; Tikkinen, K.A.O.; Neumann, I.; Vandvik, P.O.; Akl, E.A.; Da Costa, B.R.; Adhikari, N.K.; et al. Do clinicians understand the size of treatment effects? A randomized survey across 8 countries. Cmaj 2016, 188, 25–32. [Google Scholar] [CrossRef] [Green Version]
- Higgins, J.P.T.; Thomas, J.; Chandler, J.; Cumpston, M.; Li, T.; Page, M.J.; Welch, V.A. Cochrane Handbook for Systematic Reviews of Interventions; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Meister, R.; Von Wolff, A.; Kriston, L. Odds ratios of treatment response were well approximated from continuous rating scale scores for meta-analysis. J. Clin. Epidemiol. 2015, 68, 740–751. [Google Scholar] [CrossRef] [PubMed]
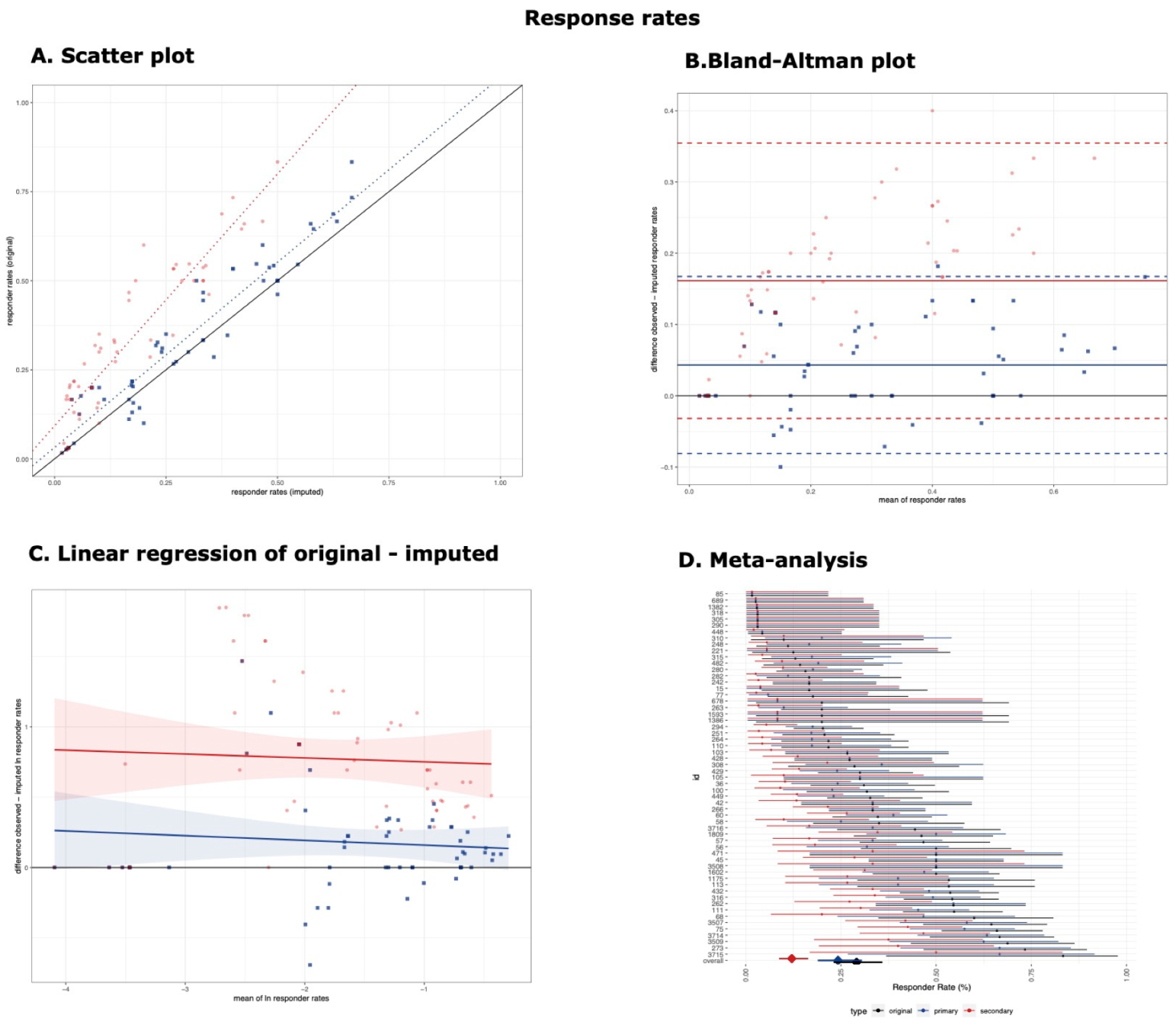
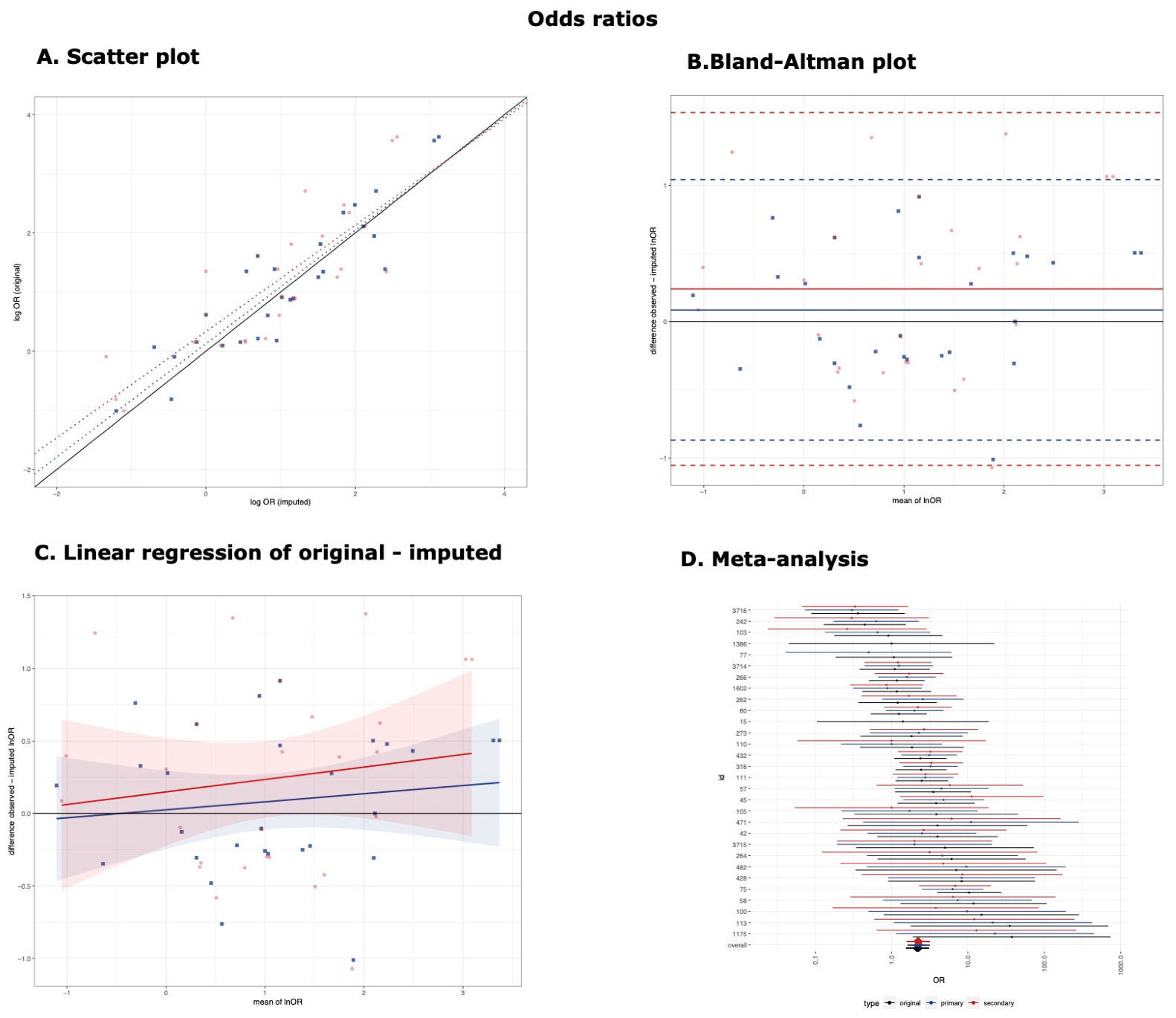
| Agreement | Predictive Accuracy | Bias | |||||
|---|---|---|---|---|---|---|---|
| Number of Observations (k) | CCC (95% CI) | β (95% CI) of Original (Y) and Imputed (X) | R2 (%) | MSE | Bias and 95% Limits of Agreement | β (95% CI) of Difference (Y) and Mean (X) | |
| Responder Rates (Original 58 Observations) | |||||||
| Primary Threshold | 58 | 0.93 (0.89–0.96) | 1.04 (0.95, 1.13) | 90.86 | 0.063 | 4.32% (−8.1%, 16.74%) | −0.034 (−0.135, 0.068) * |
| Secondary Threshold | 58 | 0.59 (0.48−0.69) | 1.41 (1.26, 1.57) | 85.01 | 0.0813 | 16.15% (−3.18%, 35.47%) | −0.028 (−0.177, 0.121) * |
| Log OR (Original 30 Observations) | |||||||
| Primary Threshold | 28 | 0.91 (0.81, 0.95) | 0.96 (0.78, 1.14) | 82.03% | 0.495 | 0.09 (−0.87, 1.04) | 0.06 (−0.120, 0.231) |
| Secondary Threshold | 27 | 0.81 (0.63, 0.91) | 0.90 (0.65, 1.15) | 67.85% | 0.664 | 0.24 (−1.05, 1.53) | 0.086 (−0.164, 0.334) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siafis, S.; Rodolico, A.; Çıray, O.; Murphy, D.G.; Parellada, M.; Arango, C.; Leucht, S. Imputing the Number of Responders from the Mean and Standard Deviation of CGI-Improvement in Clinical Trials Investigating Medications for Autism Spectrum Disorder. Brain Sci. 2021, 11, 908. https://doi.org/10.3390/brainsci11070908
Siafis S, Rodolico A, Çıray O, Murphy DG, Parellada M, Arango C, Leucht S. Imputing the Number of Responders from the Mean and Standard Deviation of CGI-Improvement in Clinical Trials Investigating Medications for Autism Spectrum Disorder. Brain Sciences. 2021; 11(7):908. https://doi.org/10.3390/brainsci11070908
Chicago/Turabian StyleSiafis, Spyridon, Alessandro Rodolico, Oğulcan Çıray, Declan G. Murphy, Mara Parellada, Celso Arango, and Stefan Leucht. 2021. "Imputing the Number of Responders from the Mean and Standard Deviation of CGI-Improvement in Clinical Trials Investigating Medications for Autism Spectrum Disorder" Brain Sciences 11, no. 7: 908. https://doi.org/10.3390/brainsci11070908
APA StyleSiafis, S., Rodolico, A., Çıray, O., Murphy, D. G., Parellada, M., Arango, C., & Leucht, S. (2021). Imputing the Number of Responders from the Mean and Standard Deviation of CGI-Improvement in Clinical Trials Investigating Medications for Autism Spectrum Disorder. Brain Sciences, 11(7), 908. https://doi.org/10.3390/brainsci11070908






