FARCI: Fast and Robust Connectome Inference
Abstract
:1. Introduction
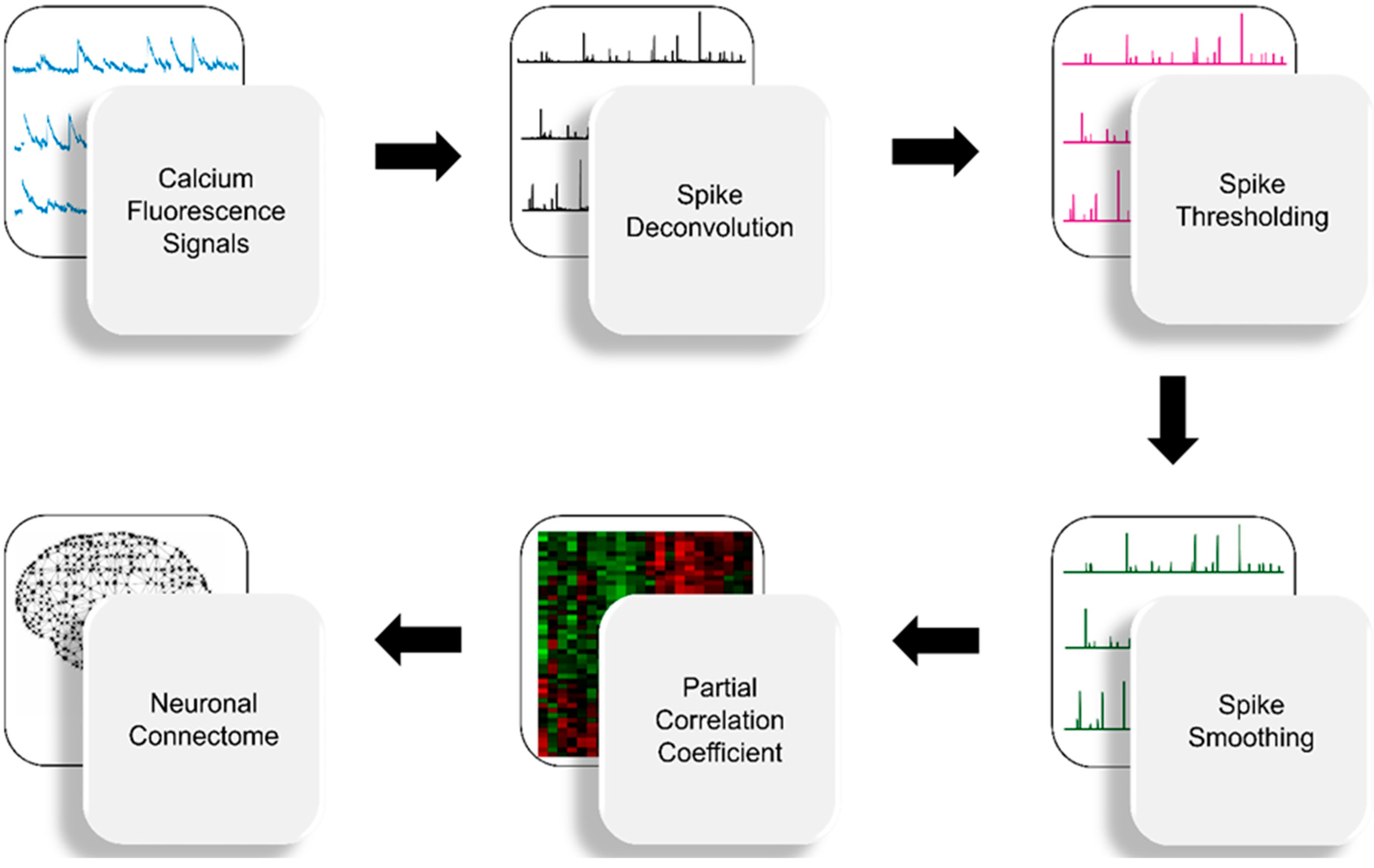
2. Materials and Methods
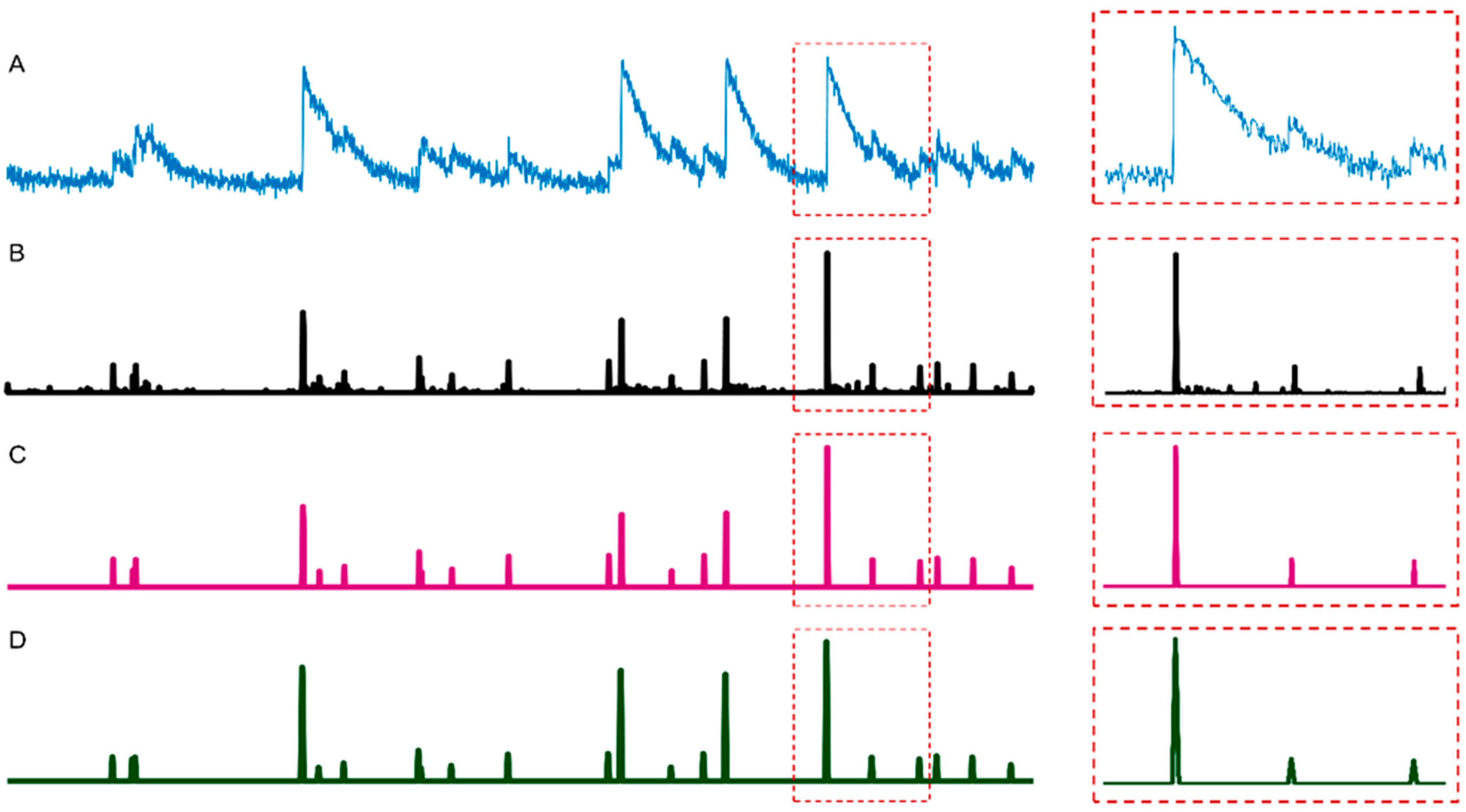
2.1. Spike Deconvolution
2.2. Spike Thresholding
2.3. Spike Smoothing
2.4. Partial Correlation Statistics
2.5. Performance Evaluation
2.6. Performance Comparison
3. Results
3.1. Neuronal Spike Deconvolution
3.2. Binarization of Neuronal Spikes
3.3. Neuronal Spike Thresholding
3.4. Neuronal Spike Smoothing
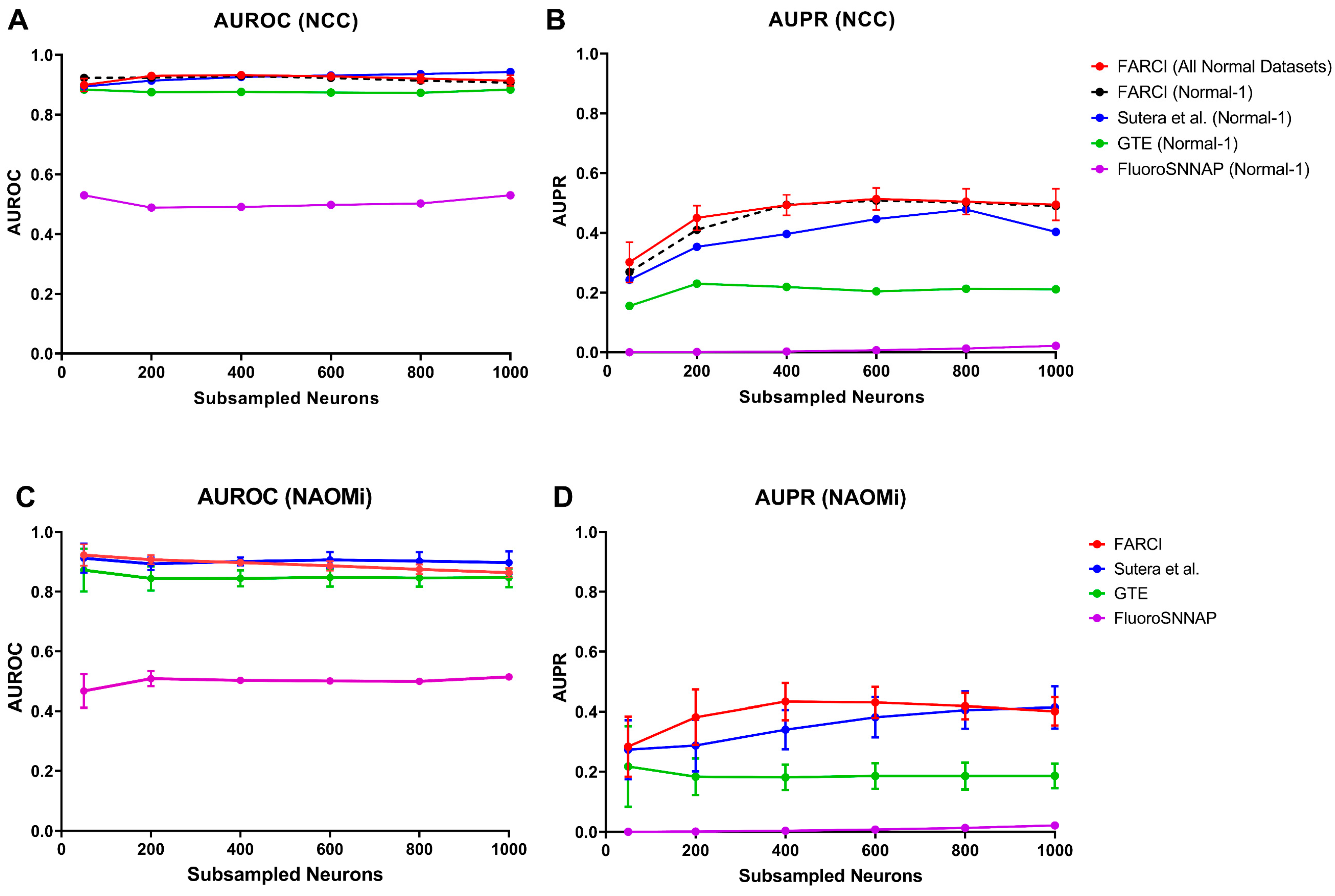
3.5. FARCI Performance
3.6. Missing Neurons
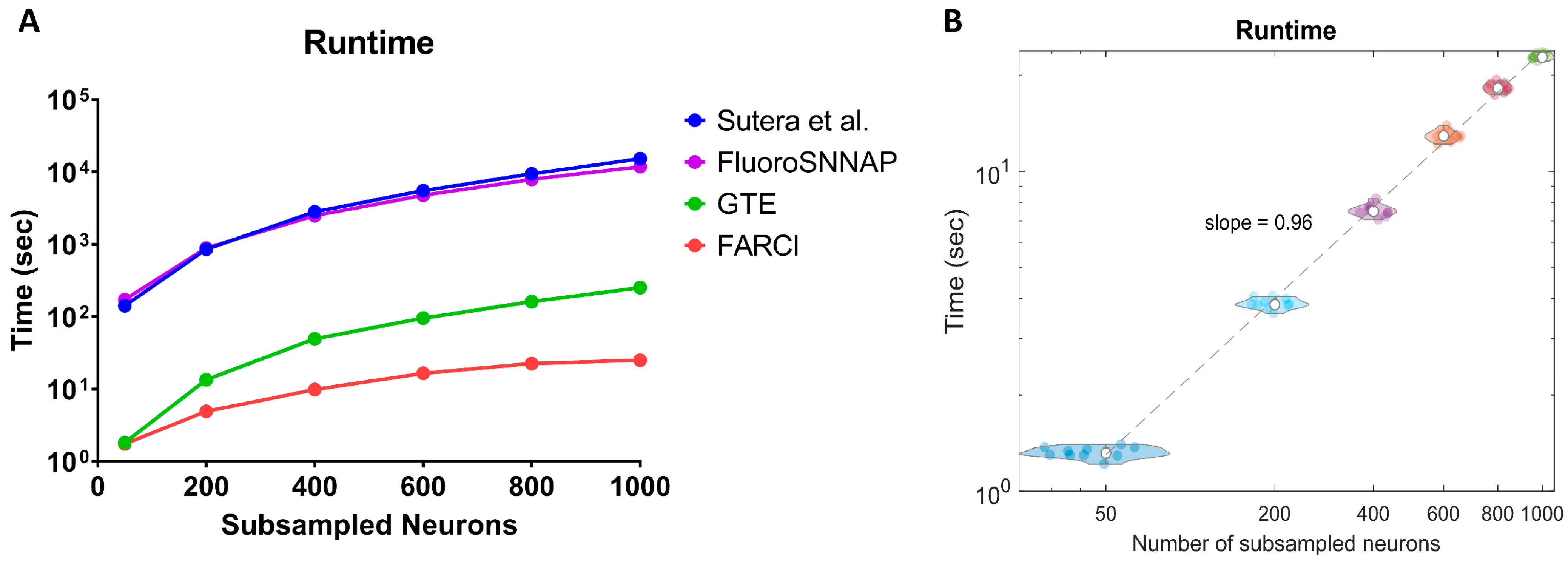
3.7. Computational Speed
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bennett, S.H.; Kirby, A.J.; Finnerty, G.T. Rewiring the Connectome: Evidence and Effects. Neurosci. Biobehav. Rev. 2018, 88, 51–62. [Google Scholar] [CrossRef]
- Sotiropoulos, S.N.; Zalesky, A. Building Connectomes Using Diffusion MRI: Why, How and But. NMR Biomed. 2019, 32, e3752. [Google Scholar] [CrossRef] [Green Version]
- Sporns, O.; Tononi, G.; Kötter, R. The Human Connectome: A Structural Description of the Human Brain. PLoS Comput. Biol. 2005, 1, 245–251. [Google Scholar] [CrossRef] [PubMed]
- Kasthuri, N.; Hayworth, K.J.; Berger, D.R.; Schalek, R.L.; Conchello, J.A.; Knowles-Barley, S.; Lee, D.; Vázquez-Reina, A.; Kaynig, V.; Jones, T.R.; et al. Saturated Reconstruction of a Volume of Neocortex. Cell 2015, 162, 648–661. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peters, A.J.; Chen, S.X.; Komiyama, T. Emergence of Reproducible Spatiotemporal Activity during Motor Learning. Nature 2014, 510, 263–267. [Google Scholar] [CrossRef]
- Magrans de Abril, I.; Yoshimoto, J.; Doya, K. Connectivity Inference from Neural Recording Data: Challenges, Mathematical Bases and Research Directions. Neural Netw. 2018, 102, 120–137. [Google Scholar] [CrossRef]
- Hwang, E.J.; Dahlen, J.E.; Hu, Y.Y.; Aguilar, K.; Yu, B.; Mukundan, M.; Mitani, A.; Komiyama, T. Disengagement of Motor Cortex from Movement Control during Long-Term Learning. Sci. Adv. 2019, 5, eaay0001. [Google Scholar] [CrossRef] [Green Version]
- Alivisatos, A.P.; Andrews, A.M.; Boyden, E.S.; Chun, M.; Church, G.M.; Deisseroth, K.; Donoghue, J.P.; Fraser, S.E.; Lippincott-Schwartz, J.; Looger, L.L.; et al. Nanotools for Neuroscience and Brain Activity Mapping. ACS Nano 2013, 7, 1850–1866. [Google Scholar] [CrossRef]
- Jercog, P.; Rogerson, T.; Schnitzer, M.J. Large-Scale Fluorescence Calcium-Imaging Methods for Studies of Long-Term Memory in Behaving Mammals. Cold Spring Harb. Perspect. Biol. 2016, 8, 21824–21825. [Google Scholar] [CrossRef] [Green Version]
- Peters, A.J.; Lee, J.; Hedrick, N.G.; O’Neil, K.; Komiyama, T. Reorganization of Corticospinal Output during Motor Learning. Nat. Neurosci. 2017, 20, 1133–1141. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Makino, H.; Ren, C.; Liu, H.; Kim, A.N.; Kondapaneni, N.; Liu, X.; Kuzum, D.; Komiyama, T. Transformation of Cortex-Wide Emergent Properties during Motor Learning. Neuron 2017, 94, 880–890.e8. [Google Scholar] [CrossRef] [PubMed]
- Berens, P.; Freeman, J.; Deneux, T.; Chenkov, N.; McColgan, T.; Speiser, A.; Macke, J.H.; Turaga, S.C.; Mineault, P.; Rupprecht, P.; et al. Community-Based Benchmarking Improves Spike Rate Inference from Two-Photon Calcium Imaging Data. PLoS Comput. Biol. 2018, 14, e1006157. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sutera, A.; Joly, A.; François-Lavet, V.; Qiu, Z.A.; Louppe, G.; Ernst, D.; Geurts, P.; Battaglia, D.; Guyon, I.; Lemaire, V.; et al. Simple Connectome Inference from Partial Correlation Statistics in Calcium Imaging. J. Mach. Learn. Res. 2015, 46, 23–35. [Google Scholar]
- Orlandi, J.G.; Stetter, O.; Soriano, J.; Geisel, T.; Battaglia, D. Transfer Entropy Reconstruction and Labeling of Neuronal Connections from Simulated Calcium Imaging. PLoS ONE 2014, 9, e98842. [Google Scholar] [CrossRef] [Green Version]
- Stetter, O.; Battaglia, D.; Soriano, J.; Geisel, T. Model-Free Reconstruction of Excitatory Neuronal Connectivity from Calcium Imaging Signals. PLoS Comput. Biol. 2012, 8, 1002653. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Romaszko, L. Signal Correlation Prediction Using Convolutional Neural Networks. In Proceedings of the Neural Connectomics Workshop, Nancy, France, 15 September 2014; Springer: Cham, Switzerland, 2015; pp. 45–56. [Google Scholar]
- Orlandi, J.G.; Ray, B.; Battaglia, D.; Lemaire, V.; Statnikov AlexanderStatnikov, A.; Stetter, O.; Soriano, J.; Guyon, I.; Orlandi, J.; Ray, B.; et al. First Connectomics Challenge: From Imaging to Connectivity. In Proceedings of the Neural Connectomics Workshop, Nancy, France, 15 September 2014; Volume 46, pp. 1–22. [Google Scholar]
- Song, A.; Gauthier, J.L.; Pillow, J.W.; Tank, D.W.; Charles, A.S. Neural Anatomy and Optical Microscopy (NAOMi) Simulation for Evaluating Calcium Imaging Methods. J. Neurosci. Methods 2021, 358, 109173. [Google Scholar] [CrossRef]
- Patel, T.P.; Man, K.; Firestein, B.L.; Meaney, D.F. Automated Quantification of Neuronal Networks and Single-Cell Calcium Dynamics Using Calcium Imaging. J. Neurosci. Methods 2015, 243, 26–38. [Google Scholar] [CrossRef] [Green Version]
- Deneux, T.; Kaszas, A.; Szalay, G.; Katona, G.; Lakner, T.; Grinvald, A.; Rózsa, B.; Vanzetta, I. Accurate Spike Estimation from Noisy Calcium Signals for Ultrafast Three-Dimensional Imaging of Large Neuronal Populations in Vivo. Nat. Commun. 2016, 7, 12190. [Google Scholar] [CrossRef]
- Rupprecht, P.; Carta, S.; Hoffmann, A.; Echizen, M.; Blot, A.; Kwan, A.C.; Dan, Y.; Hofer, S.B.; Kitamura, K.; Helmchen, F.; et al. A Database and Deep Learning Toolbox for Noise-Optimized, Generalized Spike Inference from Calcium Imaging. Nat. Neurosci. 2021, 24, 1324–1337. [Google Scholar] [CrossRef]
- Friedrich, J.; Zhou, P.; Paninski, L. Fast Online Deconvolution of Calcium Imaging Data. PLoS Comput. Biol. 2017, 13, e1005423. [Google Scholar] [CrossRef] [Green Version]
- Pachitariu, M.; Stringer, C.; Harris, K.D. Robustness of Spike Deconvolution for Neuronal Calcium Imaging. J. Neurosci. 2018, 38, 7976–7985. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stringer, C.; Pachitariu, M. Computational Processing of Neural Recordings from Calcium Imaging Data. Curr. Opin. Neurobiol. 2019, 55, 22–31. [Google Scholar] [CrossRef]
- Cowden, D.J. The Multiple-Partial Correlation Coefficient. J. Am. Stat. Assoc. 1952, 47, 442. [Google Scholar] [CrossRef]
- Vogelstein, J.T.; Watson, B.O.; Packer, A.M.; Yuste, R.; Jedynak, B.; Paninskik, L. Spike Inference from Calcium Imaging Using Sequential Monte Carlo Methods. Biophys. J. 2009, 97, 636–655. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eppler, J.M.; Helias, M.; Muller, E.; Diesmann, M.; Gewaltig, M.O. PyNEST: A Convenient Interface to the NEST Simulator. Front. Neuroinform. 2009, 2, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gewaltig, M.-O.; Diesmann, M. NEST (NEural Simulation Tool). Scholarpedia 2007, 2, 1430. [Google Scholar] [CrossRef]
- Hawkes, A.G. Spectra of Some Self-Exciting and Mutually Exciting Point Processes. Biometrika 1971, 58, 83–90. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective Dynamics of ‘Small-World’ Networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Davis, J.; Goadrich, M. The Relationship between Precision-Recall and ROC Curves. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; Volume 148, pp. 233–240. [Google Scholar] [CrossRef] [Green Version]
- Receiver Operating Characteristic (ROC). Curve or Other Performance Curve for Classifier Output—MATLAB Perfcurve. Available online: https://www.mathworks.com/help/stats/perfcurve.html (accessed on 9 September 2021).
- Schrynemackers, M.; Küffner, R.; Geurts, P. On Protocols and Measures for the Validation of Supervised Methods for the Inference of Biological Networks. Front. Genet. 2013, 4, 262. [Google Scholar] [CrossRef] [Green Version]
- Saito, T.; Rehmsmeier, M. The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Hernandez, O.; Chrapkiewicz, R.; Shai, A.; Wagner, M.J.; Zhang, Y.; Wu, C.H.; Li, J.Z.; Inoue, M.; Gong, Y.; et al. Kilohertz Two-Photon Brain Imaging in Awake Mice. Nat. Methods 2019, 16, 1119–1122. [Google Scholar] [CrossRef] [PubMed]
- Hodgkin, A.L.; Huxley, A.F. A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Vanwalleghem, G.; Constantin, L.; Scott, E.K. Calcium Imaging and the Curse of Negativity. Front. Neural Circuits 2021, 14, 607391. [Google Scholar] [CrossRef] [PubMed]
- Meamardoost, S.; Bhattacharya, M.; Hwang, E.; Komiyama, T.; Mewes, C.; Wang, L.; Zhang, Y.; Gunawan, R. FARCI: Fast and Robust Connectome Inference. bioRxiv 2020. [Google Scholar] [CrossRef]


| Networks | # of Neurons | Description |
|---|---|---|
| small (6 datasets) | 100 | six connectomes with 100 neurons |
| normal (4 datasets) | 1000 | four connectomes with 1000 neurons |
| normal3-highrate | 1000 | normal-3 connectome with a higher neuronal firing frequency |
| normal4-lownoise | 1000 | normal-4 connectome with a higher signal-to-noise ratio |
| highcc | 1000 | a connectome of 1000 neurons with a higher clustering coefficient |
| lowcc | 1000 | a connectome of 1000 neurons with a lower clustering coefficient |
| highcon | 1000 | a connectome of 1000 neurons with a higher average connectivity |
| lowcon | 1000 | a connectome of 1000 neurons with a lower average connectivity |
| AUROC | AUPR | |||||
|---|---|---|---|---|---|---|
| Filter | Small (n = 6) | Normal (n = 4) | Others (n = 6) | Small (n = 6) | Normal (n = 4) | Others (n = 6) |
| Neuronal Spikes | 0.871 ± 0.058 | 0.892 ± 0.002 | 0.905 ± 0.030 | 0.543 ± 0.097 | 0.335 ± 0.005 | 0.347 ± 0.067 |
| Spikes + Binarization | 0.563 ± 0.055 | 0.653 ± 0.006 | 0.647 ± 0.069 | 0.189 ± 0.021 | 0.042 ± 0.002 | 0.050 ± 0.021 |
| Spikes + Thresholding | 0.876 ± 0.051 | 0.882 ± 0.003 | 0.895 ± 0.040 | 0.620 ± 0.096 | 0.408 ± 0.012 | 0.421 ± 0.114 |
| Spikes + Smoothing | 0.891 ± 0.035 | 0.908 ± 0.002 | 0.917 ± 0.025 | 0.538 ± 0.056 | 0.330 ± 0.004 | 0.346 ± 0.053 |
| FARCI | 0.916 ± 0.031 | 0.908 ± 0.002 | 0.918 ± 0.032 | 0.741 ± 0.067 | 0.491 ± 0.003 | 0.497 ± 0.100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meamardoost, S.; Bhattacharya, M.; Hwang, E.J.; Komiyama, T.; Mewes, C.; Wang, L.; Zhang, Y.; Gunawan, R. FARCI: Fast and Robust Connectome Inference. Brain Sci. 2021, 11, 1556. https://doi.org/10.3390/brainsci11121556
Meamardoost S, Bhattacharya M, Hwang EJ, Komiyama T, Mewes C, Wang L, Zhang Y, Gunawan R. FARCI: Fast and Robust Connectome Inference. Brain Sciences. 2021; 11(12):1556. https://doi.org/10.3390/brainsci11121556
Chicago/Turabian StyleMeamardoost, Saber, Mahasweta Bhattacharya, Eun Jung Hwang, Takaki Komiyama, Claudia Mewes, Linbing Wang, Ying Zhang, and Rudiyanto Gunawan. 2021. "FARCI: Fast and Robust Connectome Inference" Brain Sciences 11, no. 12: 1556. https://doi.org/10.3390/brainsci11121556
APA StyleMeamardoost, S., Bhattacharya, M., Hwang, E. J., Komiyama, T., Mewes, C., Wang, L., Zhang, Y., & Gunawan, R. (2021). FARCI: Fast and Robust Connectome Inference. Brain Sciences, 11(12), 1556. https://doi.org/10.3390/brainsci11121556








