Adaptive Dual Extended Kalman Filter Based on Variational Bayesian Approximation for Joint Estimation of Lithium-Ion Battery State of Charge and Model Parameters
Abstract
:1. Introduction
2. Battery Modeling
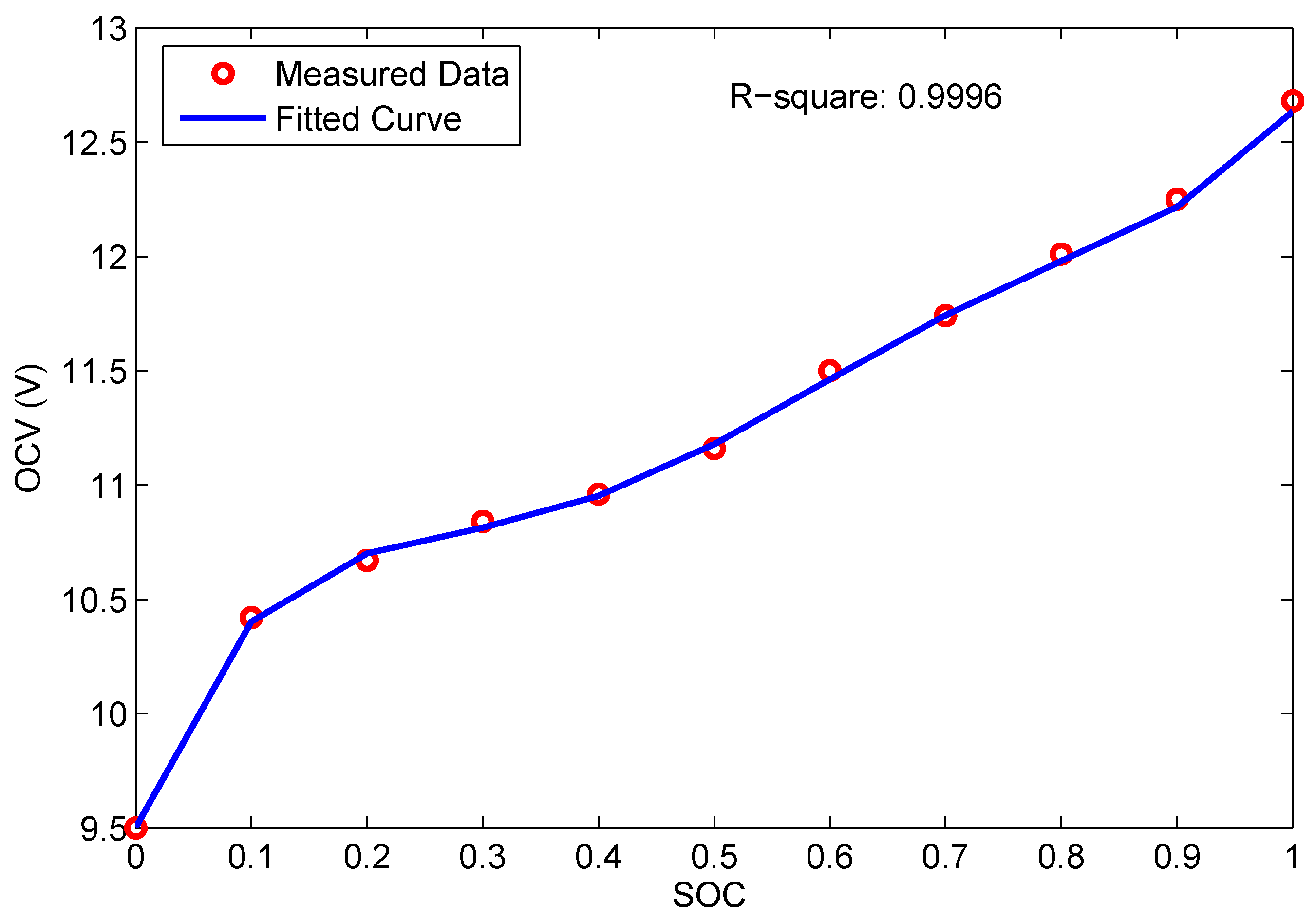
2.1. Battery Model
2.2. Definition of State of Charge
2.3. State-Space Model
2.3.1. State Space Model for SOC Estimation
2.3.2. State Space Model for Battery Parameter Estimation
3. Variational Bayesian Approximation-Based Adaptive Kalman Filter Algorithm
4. Variational Bayesian Approximation-Based Adaptive Dual Extended Kalman Filter
| Algorithm 1: VB-ADEKF. |
| (1) Initialization: , , , , , , , , , (2) Prediction: where , and , are the inverse gamma distribution parameters of the measurement noise covariance, and are the scale factors. (3) Update: the update of VB-ADEKF utilizes iterate filtering framework. First set: , , , For , iterate the following N (N denotes iterated times) steps: Measurement variances: State estimate and its covariance: Battery parameters estimate and its covariance: Parameters for the measurement noise variances estimation: End for. And set , , , , , |
5. Experimental Verification and Analysis
5.1. Experimental Settings
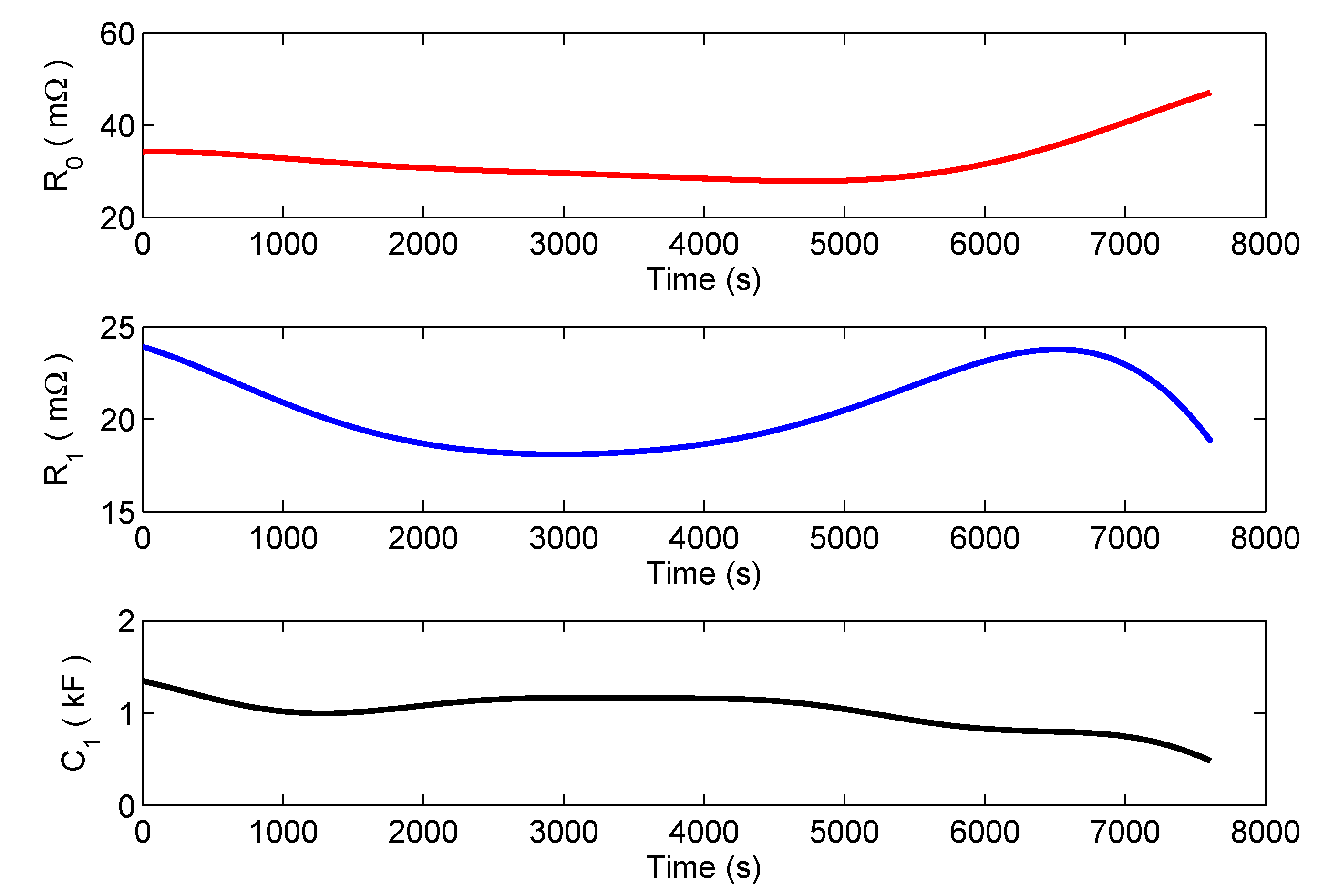
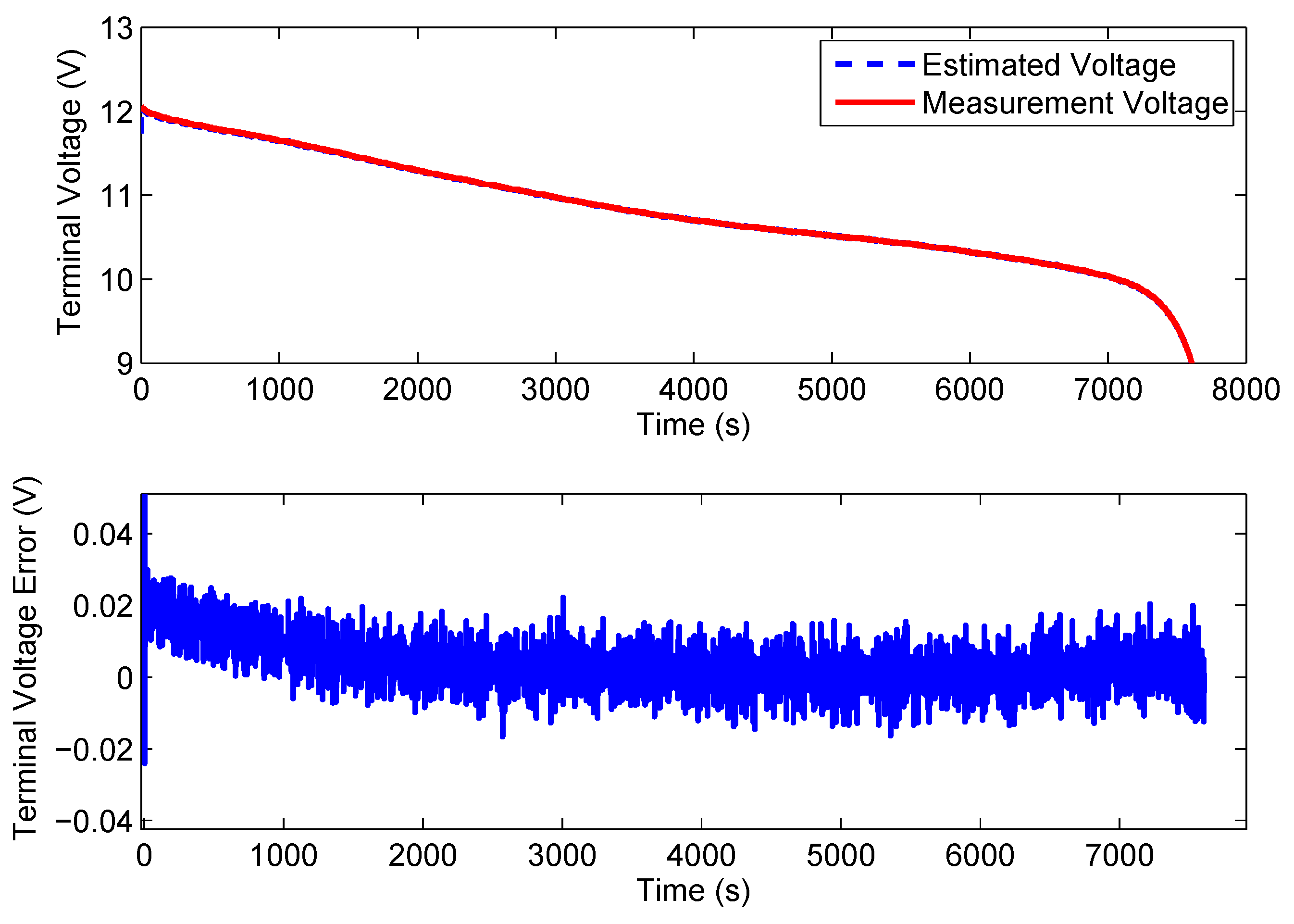
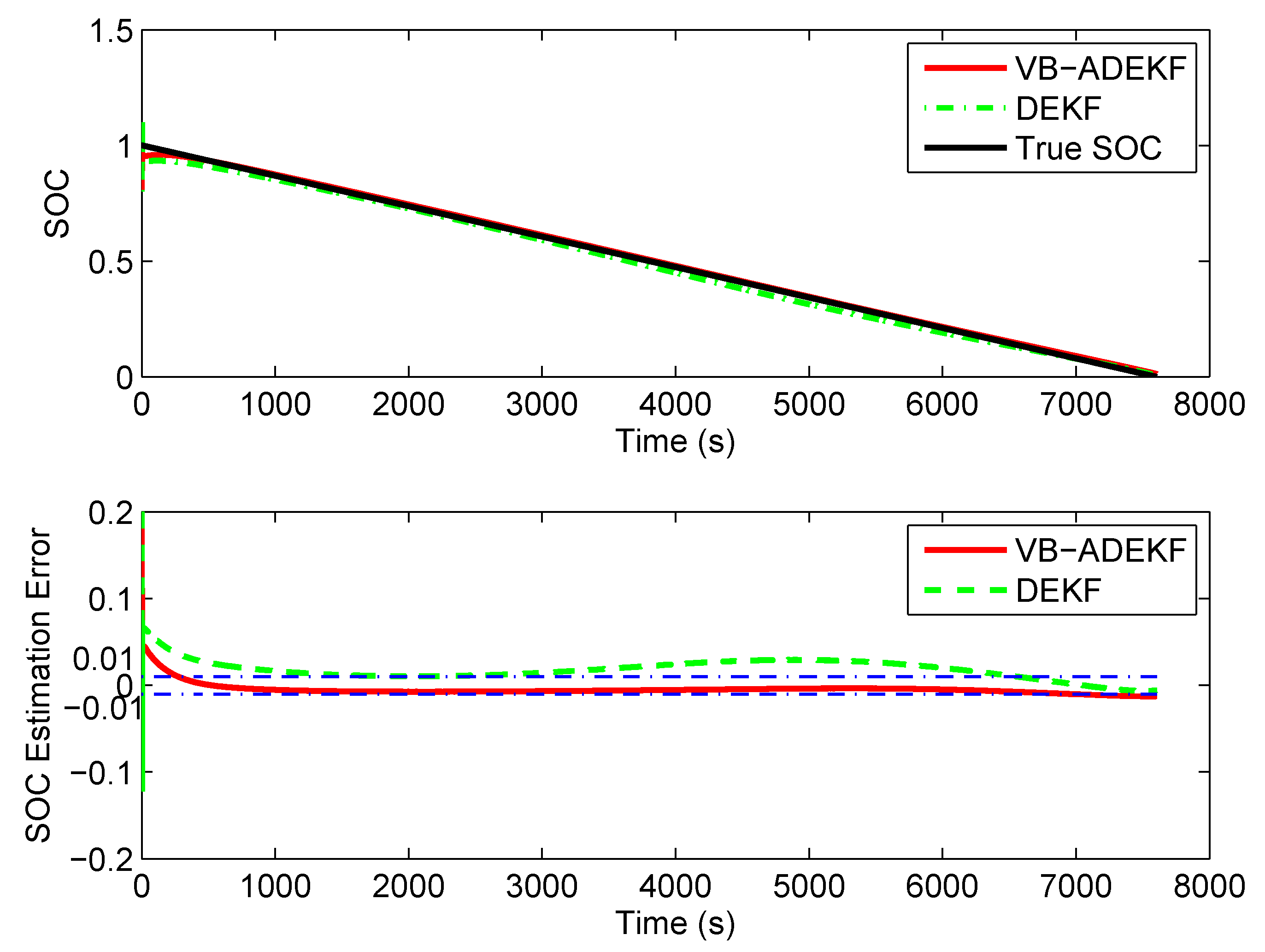
5.2. Constant Current Discharge Test
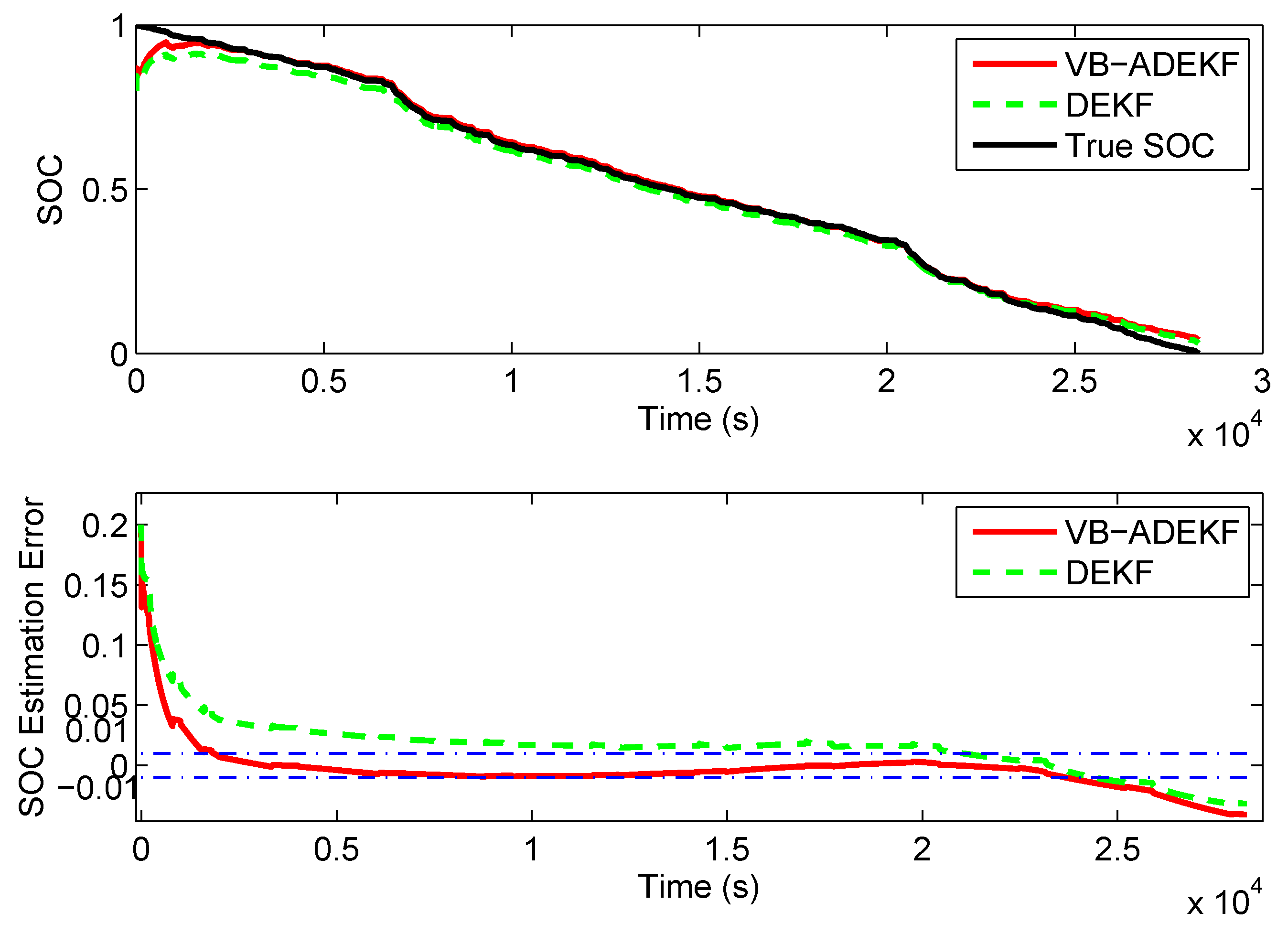
5.3. Pulse Current Discharge Test
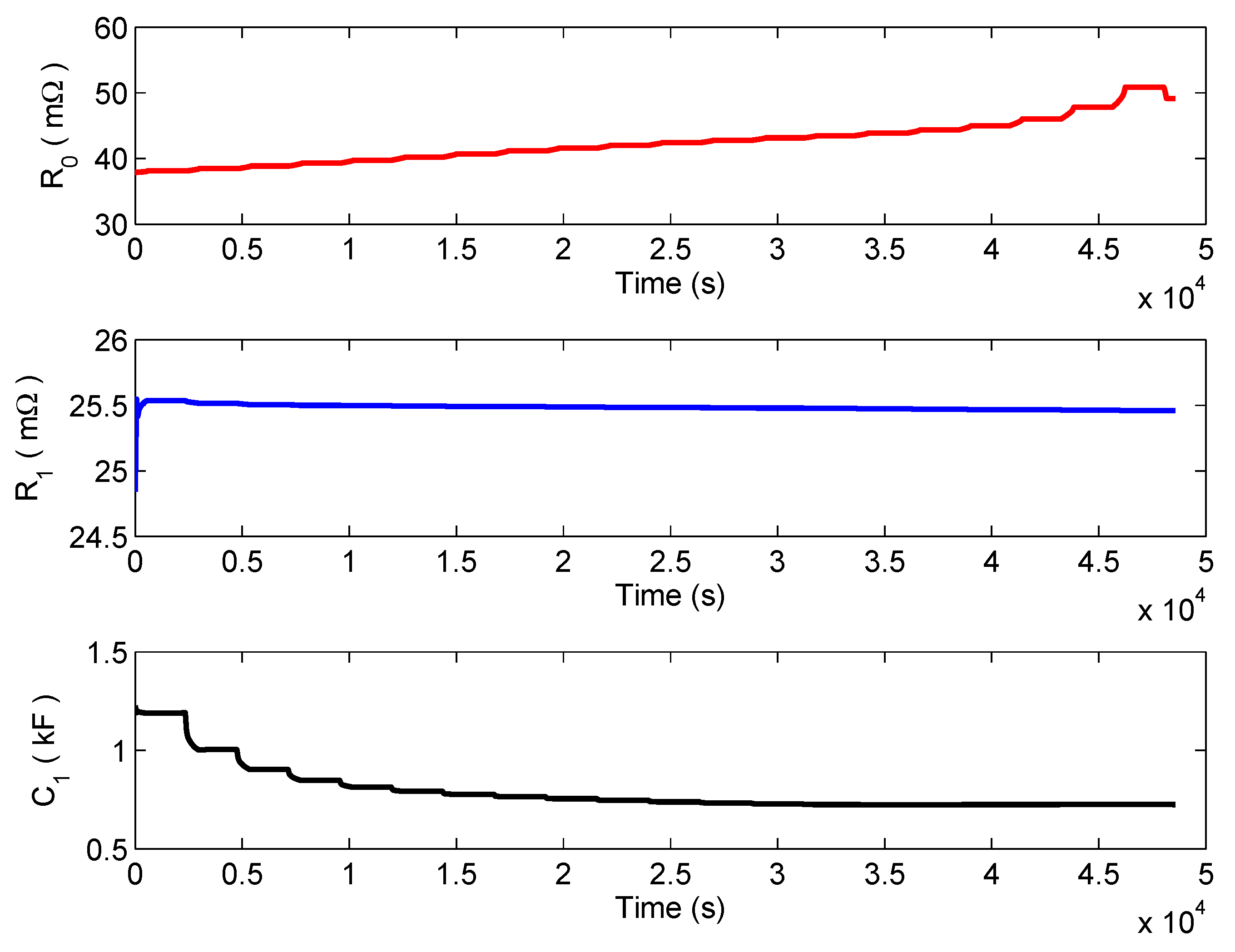
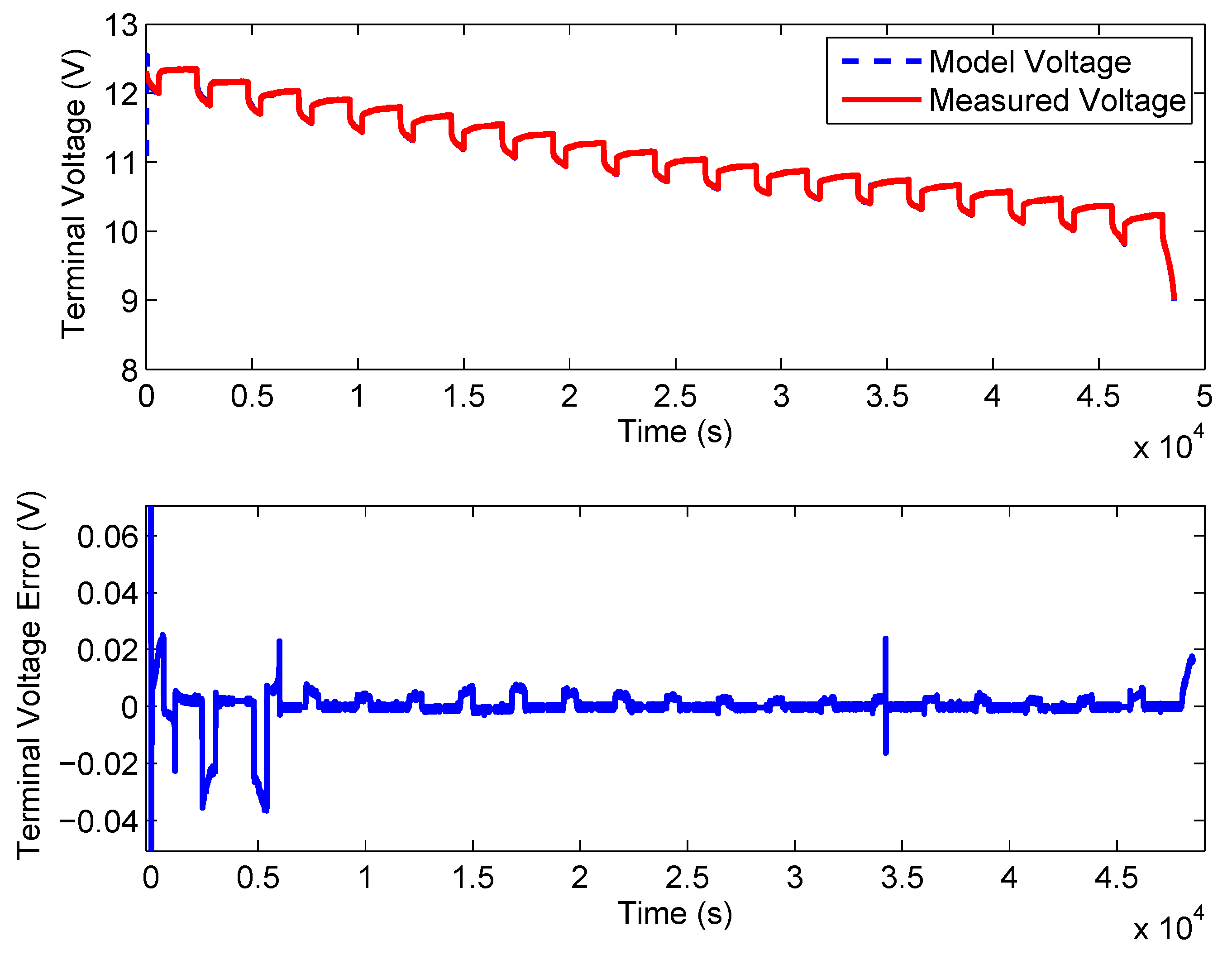
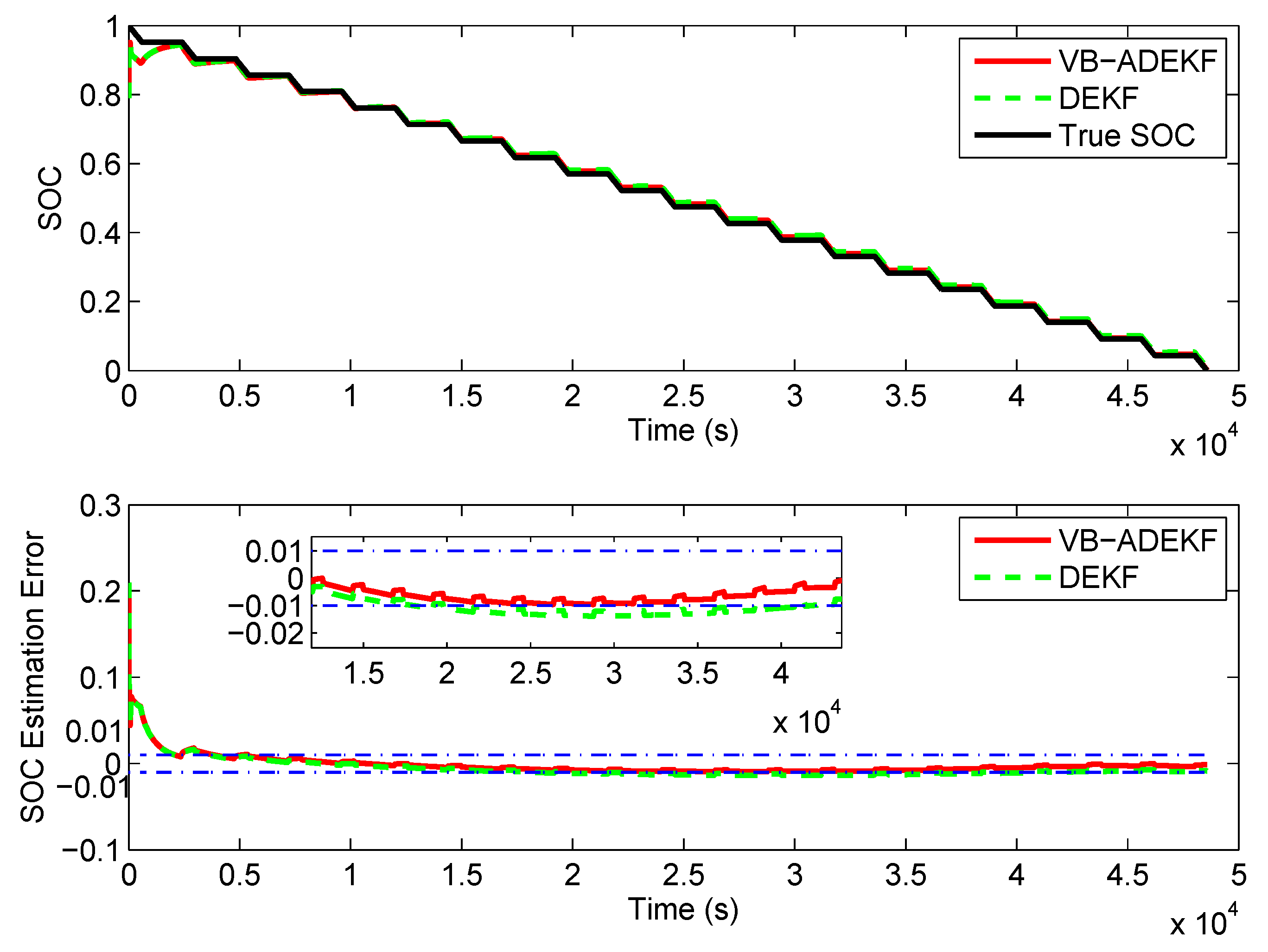
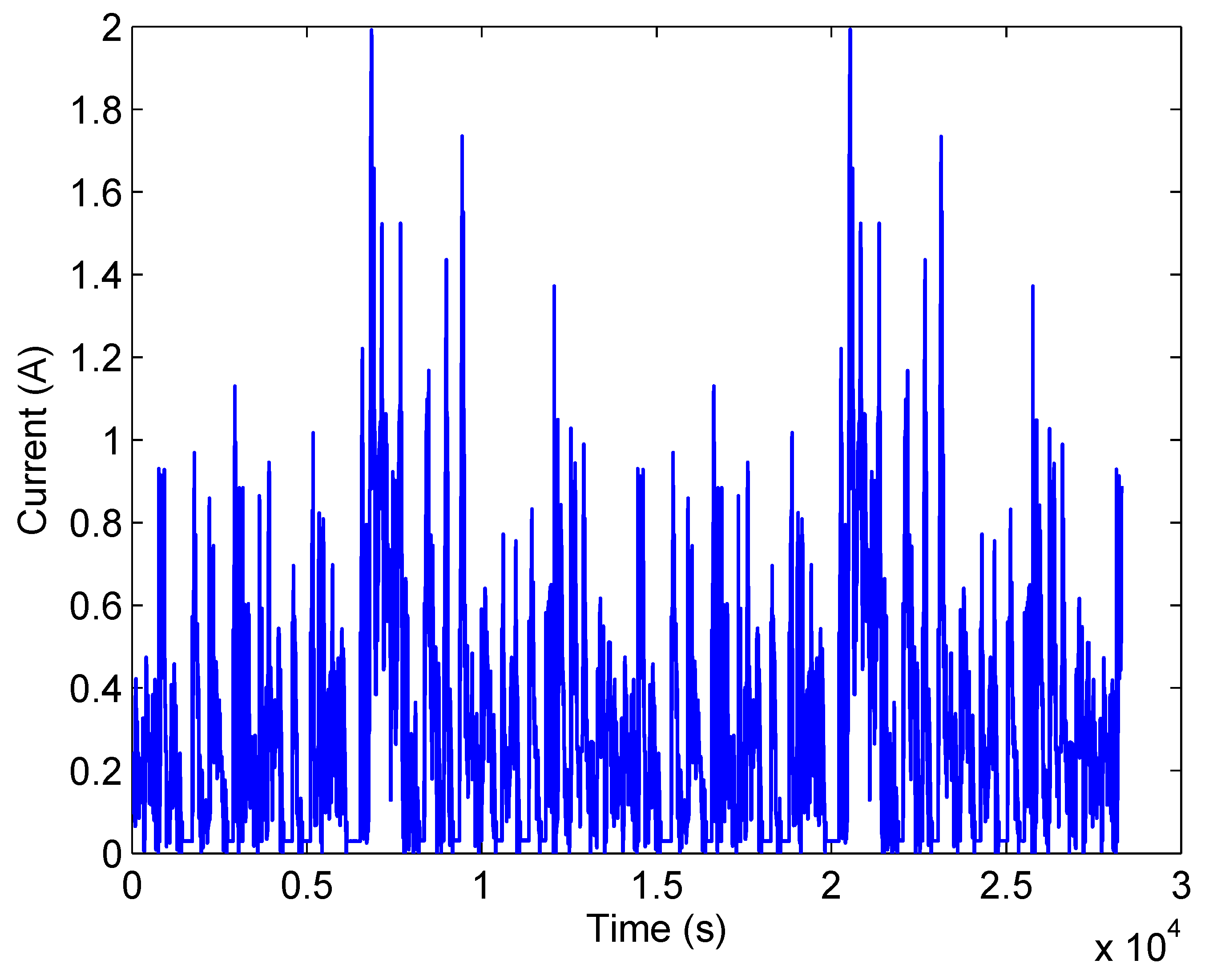
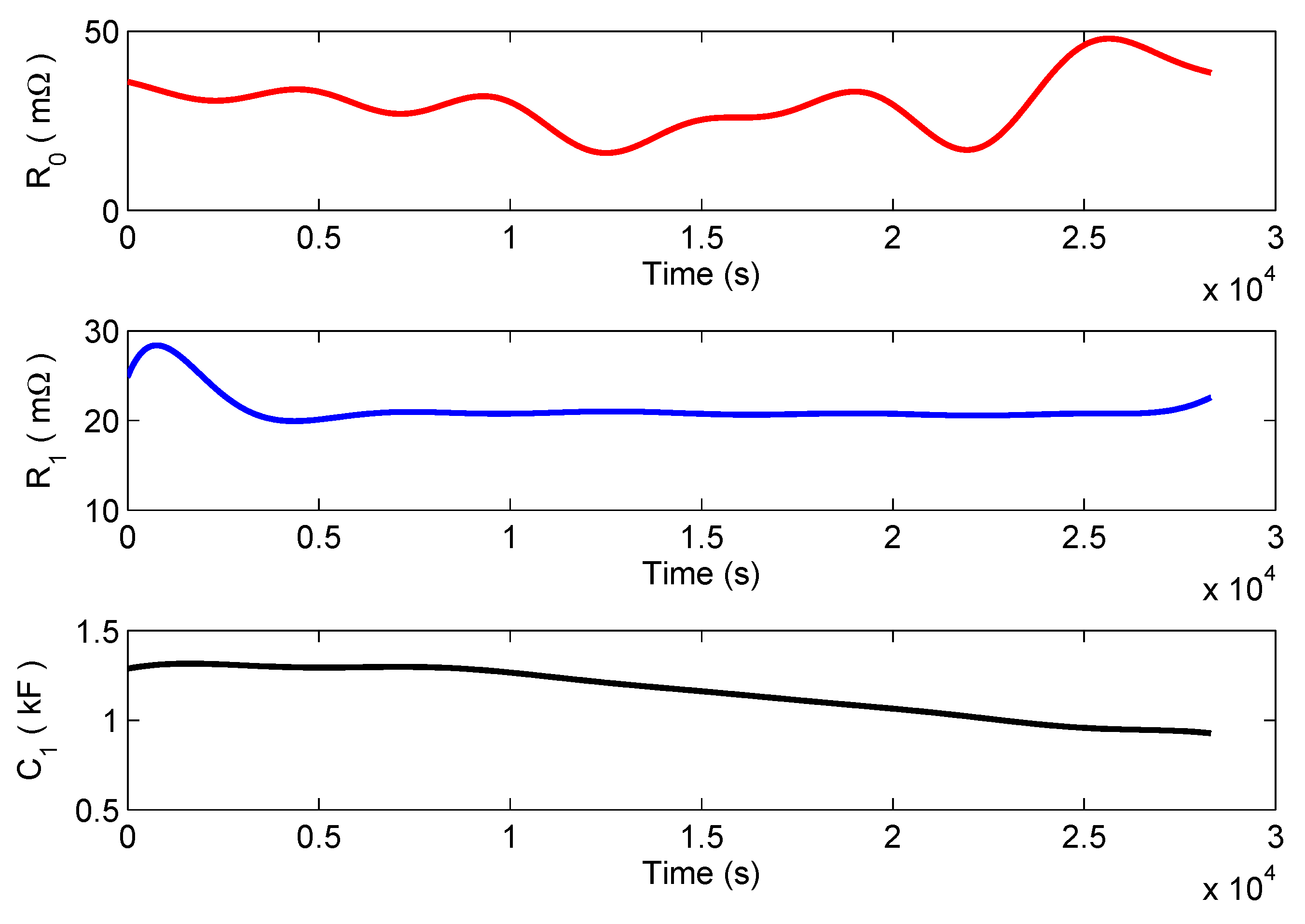
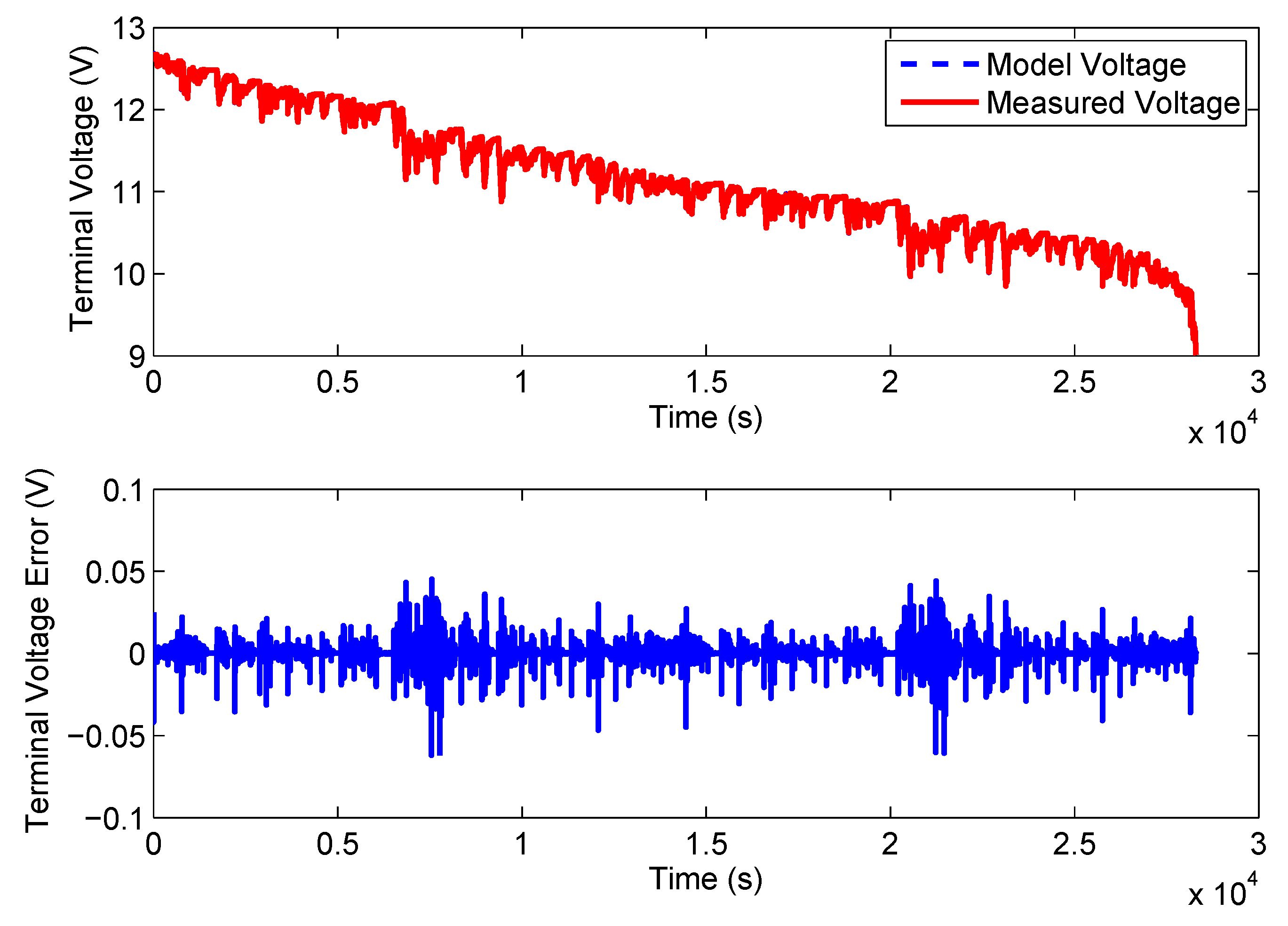
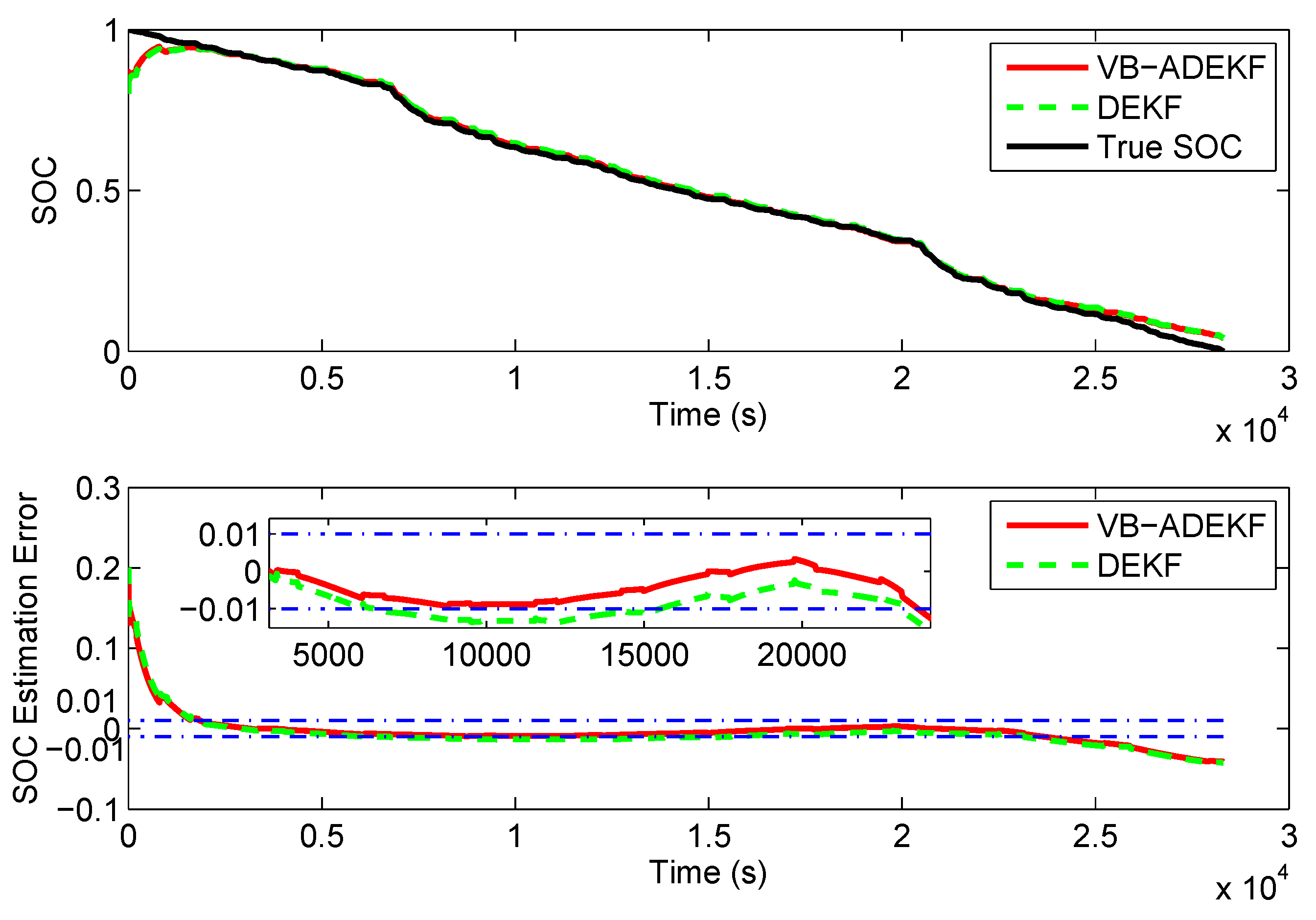
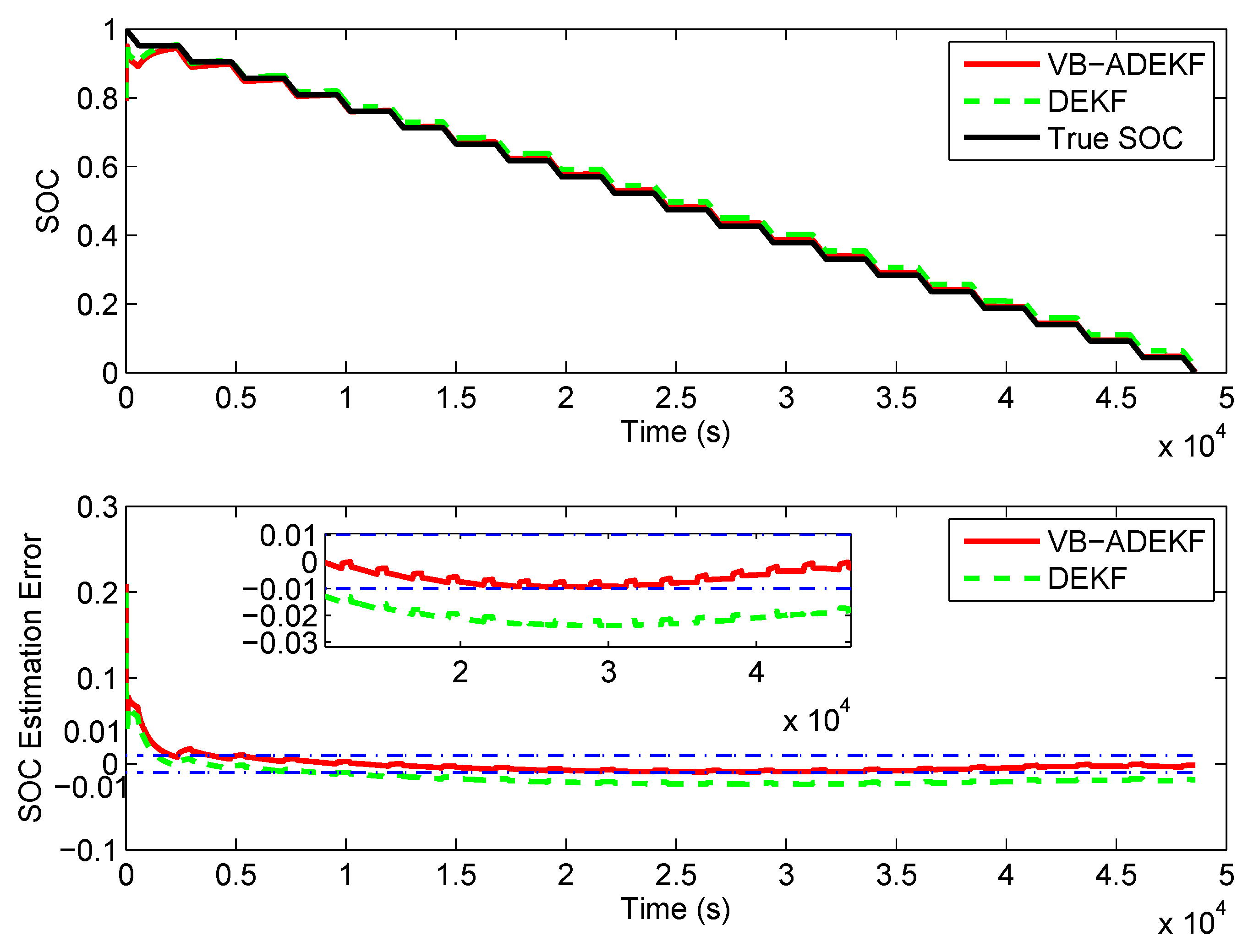
5.4. UDDS Test
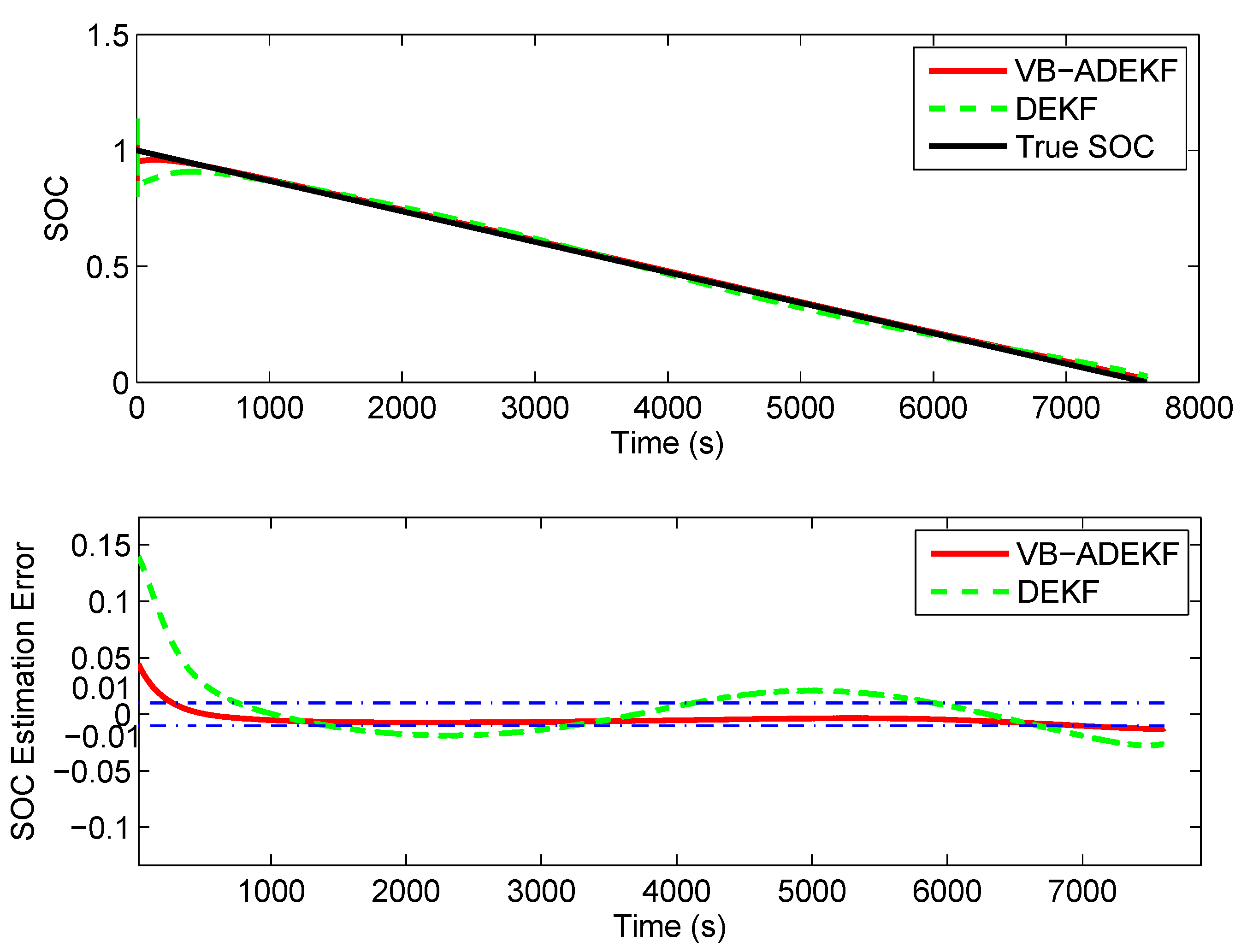
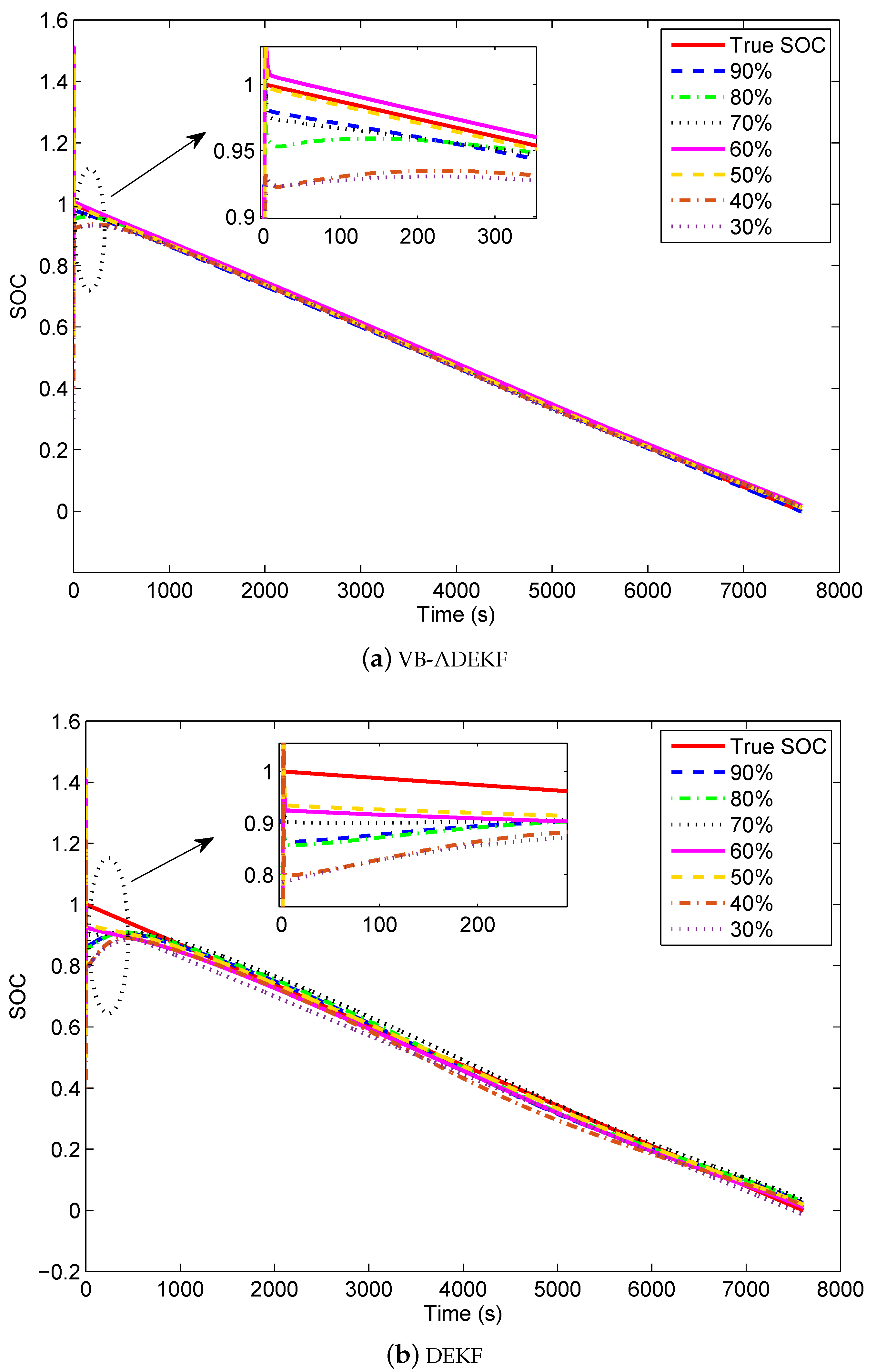
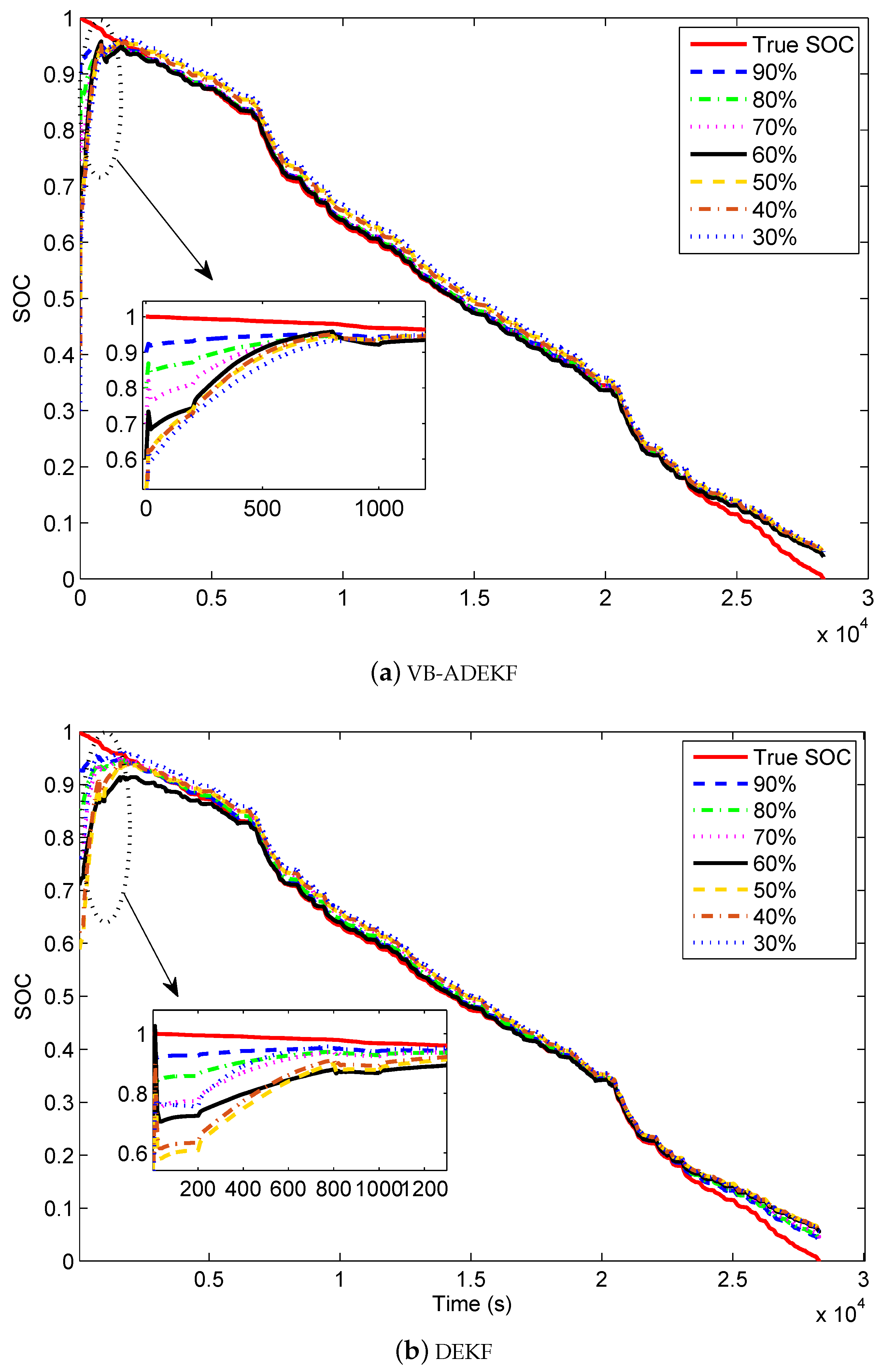
5.5. Convergence Ability with Initial SOC Error
5.6. Effect of Mistuning
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AEKF | Adaptive Extended Kalman Filter |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| ALS | Autocovariance Least Squares |
| ASRUKF | Adaptive Square Root Unscented Kalman Filter |
| AUKF | Adaptive Unscented Kalman Filter |
| BMS | Battery Management System |
| CC | Coulomb Counting |
| CKF | Cubature Kalman Filter |
| DEKF | Dual Extended Kalman Filter |
| EKF | Extended Kalman Filter |
| EV | Electric Vehicle |
| FFRLS | Forgetting-Factor Recursive Least-Squares |
| FL | Fuzzy Logic |
| KF | Kalman Filter |
| KL | Kullback–Leibler |
| MM | Multiple Model |
| NN | Neural Network |
| OCV | Open Circuit Voltage |
| RC | Resistor–Capacitor |
| SOC | State Of Charge |
| SVM | Support Vector Machine |
| UDDS | Urban Dynamometer Driving Schedule |
| UKF | Unscented Kalman Filter |
| VB | Variational Bayesian |
References
- Pan, H.; Lü, Z.; Lin, W.; Li, J.; Chen, L. State of charge estimation of lithium-ion batteries using a grey extended Kalman filter and a novel open-circuit voltage model. Energy 2017, 138, 764–775. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for Li-ion batteries using neural network modeling and unscented Kalman filter-based error cancellation. Int. J. Electr. Power Energy Syst. 2014, 62, 783–791. [Google Scholar] [CrossRef]
- Zhao, W.; Kong, X.; Wang, C. Combined estimation of the state of charge of a lithium battery based on a back-propagation- adaptive Kalman filter algorithm. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2018, 232, 357–366. [Google Scholar] [CrossRef]
- Charkhgard, M.; Farrokhi, M. State-of-charge estimation for lithium-ion batteries using neural networks and EKF. IEEE Trans. Ind. Electron. 2010, 57, 4178–4187. [Google Scholar] [CrossRef]
- Singh, P.; Vinjamuri, R.; Wang, X.; Reisner, D. Design and implementation of a fuzzy logic-based state-of-charge meter for Li-ion batteries used in portable defibrillators. J. Power Sources 2006, 162, 829–836. [Google Scholar] [CrossRef]
- Cai, C.H.; Du, D.; Liu, Z.Y. Battery state-of-charge (SOC) estimation using adaptive neuro-fuzzy inference system (ANFIS). In Proceedings of the 12th IEEE International Conference on Fuzzy Systems, St Louis, MO, USA, 25–28 May 2003; pp. 1068–1073. [Google Scholar]
- Awadallah, M.A.; Venkatesh, B. Accuracy improvement of SOC estimation in lithium-ion batteries. J. Energy Storage 2016, 6, 95–104. [Google Scholar] [CrossRef]
- Hu, J.N.; Hu, J.J.; Lin, H.B.; Li, X.P.; Jiang, C.L.; Qiu, X.H.; Li, W.S. State-of-charge estimation for batterymanagement system using optimized support vectormachine for regression. J. Power Sources 2014, 269, 682–693. [Google Scholar] [CrossRef]
- Sheng, H.; Xiao, J. Electric vehicle state of charge estimation: Nonlinear correlation and fuzzy support vector machine. J. Power Sources 2015, 281, 131–137. [Google Scholar] [CrossRef]
- Wu, X.; Mi, L.; Tan, W.; Qin, J.L.; Zhao, M.N. State of charge (SOC) estimation of Ni-MH battery based on least square support vector machines. Adv. Mater. Res. 2011, 211, 1204–1209. [Google Scholar] [CrossRef]
- Chen, Z.; Fu, Y.; Mi, C.C. State of charge estimation of lithium-ion batteries in electric drive vehicles using extended Kalman filtering. IEEE Trans. Veh. Technol. 2013, 62, 1020–1030. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Zhang, X.; Sun, F.; Fan, J. State-of-charge estimation of the Lithium-ion battery using an adaptive extended Kalman filter based on an improved Thevenin model. IEEE Trans. Veh. Technol. 2011, 60, 1461–1469. [Google Scholar]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for electric vehicle batteries using unscented kalman filtering. Microelectron. Reliab. 2013, 53, 840–847. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Gong, J. A multi-model probability SOC fusion estimation approach using an improved adaptive unscented Kalman filter technique. Energy 2017, 141, 1402–1415. [Google Scholar] [CrossRef]
- Peng, S.; Chen, C.; Shi, H.; Yao, Z. State of charge estimation of battery energy storage systems based on adaptive unscented Kalman filter with a noise statistics estimator. IEEE Access 2017, 5, 13202–13212. [Google Scholar] [CrossRef]
- Zeng, Z.; Tian, J.; Li, D.; Tian, Y. An online state of charge estimation algorithm for lithium-ion batteries using an improved adaptive cubature Kalman filter. Energies 2018, 11, 59. [Google Scholar] [CrossRef]
- Xiong, R.; Zhang, Y.; He, H.; Zhou, X.; Pecht, M. A double-scale, particle filtering, energy state prediction algorithm for lithium-ion batteries. IEEE Trans. Ind. Electron. 2018, 65, 1526–1538. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Chen, Z. A method for state-of-charge estimation of LiFePO4 batteries at dynamic currents and temperatures using particle filter. J. Power Sources 2015, 279, 306–311. [Google Scholar] [CrossRef]
- Nejad, S.; Gladwin, D.T.; Stone, D.A. On-chip implementation of extended kalman filter for adaptive battery states monitoring. In Proceedings of the 42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 5513–5518. [Google Scholar]
- Cai, M.; Chen, W.; Tan, X. Battery state-of-charge estimation based on a dual unscented Kalman filter and fractional variable-order model. Energies 2017, 10, 1577. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, C.; Zhang, X. State-of-charge estimation of the lithium-ion battery system with time-varying parameter for hybrid electric vehicles. Control Theory Appl. IET 2014, 8, 160–167. [Google Scholar] [CrossRef]
- Charkhgard, M.; Zarif, M.H. Design of adaptive H∞ filter for implementing on state of- charge estimation based on battery state-of-charge-varying modelling. IET Power Electron. 2015, 8, 1825–1833. [Google Scholar] [CrossRef]
- Yu, Q.; Xiong, R.; Lin, C.; Shen, W.; Deng, J. Lithium-ion battery parameters and state-of-charge joint estimation based on H-infinity and unscented Kalman filters. IEEE Trans. Veh. Technol. 2017, 66, 8693–8701. [Google Scholar] [CrossRef]
- Liu, S.; Cui, N.; Zhang, C. An adaptive square root unscented Kalman filter approach for state of charge estimation of lithium-ion batteries. Energies 2017, 10, 1345. [Google Scholar]
- El Din, M.S.; Abdel-Hafez, M.F.; Hussein, A.A. Enhancement in Li-ion battery cell state-of-charge estimation under uncertain model statistics. IEEE Trans. Veh. Technol. 2016, 65, 4608–4618. [Google Scholar] [CrossRef]
- Sarkka, S.; Nummenmaa, A. Recursive noise adaptive Kalman filtering by variational Bayesian approximations. IEEE Trans. Autom. Control 2009, 54, 596–600. [Google Scholar] [CrossRef]
- Li, K.; Chang, L.; Hu, B. A variational Bayesian-based unscented Kalman filter with both adaptivity and robustness. IEEE Sens. J. 2016, 16, 6966–6976. [Google Scholar] [CrossRef]
- Sun, J.; Zhou, J.; Li, X.R. State estimation for systems with unknown inputs based on variational Bayes method. In Proceedings of the 15th International Conference on Information Fusion, Singapore, 9–12 July 2012; pp. 983–990. [Google Scholar]
- Hou, J.; Yang, Y.; Gao, T. Variational Bayesian based adaptive shifted Rayleigh filter for bearings-only tracking in clutters. Sensors 2019, 19, 1512. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Fatehi, A.; Huang, B. Robust estimation of ARX models with time varying time delays using variational Bayesian approach. IEEE Trans. Cybern. 2018, 48, 532–542. [Google Scholar] [CrossRef]
- Wang, Q.; Kang, J.; Tan, Z.; Luo, M. An online method to simultaneously identify the parameters and estimate states for lithium ion batteries. Electrochim. Acta 2018, 289, 376–388. [Google Scholar] [CrossRef]



| 137.40 |
| Constant Current Test | Pulse Current Test | UDDS Test | ||||
|---|---|---|---|---|---|---|
| DEKF | VB-ADEKF | DEKF | VB-ADEKF | DEKF | VB-ADEKF | |
| Maximum Absolute Error | ||||||
| Mean Absolute Error | ||||||
| Convergence Time | 335 s | 10 s | 698 s | 690 s | 675 s | 603 s |
| Initial SOC Values | ||||||||
|---|---|---|---|---|---|---|---|---|
| 90% | 80% | 70% | 60% | 50% | 40% | 30% | ||
| Constant current test | DEKF | 341 | 335 | 331 | 425 | 262 | 468 | 483 |
| VB-ADEKF | 2 | 10 | 9 | 10 | 12 | 135 | 157 | |
| Pulse current test | DEKF | 596 | 698 | 1020 | 1253 | 1238 | 1820 | 2121 |
| VB-ADEKF | 410 | 690 | 629 | 776 | 918 | 943 | 1115 | |
| UDDS test | DEKF | 383 | 675 | 718 | 1133 | 1420 | 1890 | 2085 |
| VB-ADEKF | 359 | 603 | 610 | 612 | 695 | 658 | 783 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, J.; Yang, Y.; He, H.; Gao, T. Adaptive Dual Extended Kalman Filter Based on Variational Bayesian Approximation for Joint Estimation of Lithium-Ion Battery State of Charge and Model Parameters. Appl. Sci. 2019, 9, 1726. https://doi.org/10.3390/app9091726
Hou J, Yang Y, He H, Gao T. Adaptive Dual Extended Kalman Filter Based on Variational Bayesian Approximation for Joint Estimation of Lithium-Ion Battery State of Charge and Model Parameters. Applied Sciences. 2019; 9(9):1726. https://doi.org/10.3390/app9091726
Chicago/Turabian StyleHou, Jing, Yan Yang, He He, and Tian Gao. 2019. "Adaptive Dual Extended Kalman Filter Based on Variational Bayesian Approximation for Joint Estimation of Lithium-Ion Battery State of Charge and Model Parameters" Applied Sciences 9, no. 9: 1726. https://doi.org/10.3390/app9091726
APA StyleHou, J., Yang, Y., He, H., & Gao, T. (2019). Adaptive Dual Extended Kalman Filter Based on Variational Bayesian Approximation for Joint Estimation of Lithium-Ion Battery State of Charge and Model Parameters. Applied Sciences, 9(9), 1726. https://doi.org/10.3390/app9091726





