New Four Points Initialization for Digital Image Correlation in Metal-Sheet Strain Measurements

Abstract

Nowadays, the deformation measurement in metal sheets is important for industries such as the automotive and aerospace industries during its mechanical stamping processes. In this sense, Digital Image Correlation (DIC) has become the most relevant measurement technique in the field of experimental mechanics. This is mainly due to its versatility and low-cost compared with other techniques. However, traditionally, DIC global image registration implemented in software, such as MATLAB 2018, did not find the complete perspective transformation needed successfully and with high precision, because those algorithms use an image registration of the type “afine” or “similarity”, based on a 2D information. Therefore, in this paper, a DIC initialization method is presented to estimate the surface deformation of metal sheets used in the bodywork automotive industry. The method starts with the 3D points reconstruction from a stereoscopic digital camera system. Due to the problem complexity, it is first proposed that the user indicates four points, belonging to reference marks of a “Circle grid”. Following this, an automatic search is performed among the nearby marks, as far as one desires to reconstruct it. After this, the local DIC is used to verify that those are the correct marks. The results show reliability by reason of the high coincidence of marks in experimental cases. We also consider that the quality of mark stamping, lighting, and the initial conditions also contribute to trustworthy effects.

1. Introduction

The quality control of mechanical stamping is a need in modern industries. Engineers are always looking to improve the mechanical work optimization. Specifically, in the mechanical industry of metal-sheets manufacture, it is necessary to know their mechanical properties to use them in the most suitable way [1,2]. In this industry, the material properties such as Young’s modulus, Poisson’s ratio, anisotropic plastic ratio parameters and others are required for improving the design and manufacture processes by finite element analyses. On the other hand, the most commonly used method for finding the material properties is a tensile test with a strain-gauge type extensometer. However, the results from the extensometer are not applicable to measure the strain at a local point and the onset of diffuse necking. In contrast, the Digital Image Correlation (DIC) method is a state-of-the-art technique that can be used for an accurate strain measurement of material properties [3]. DIC has become a very popular technique in mechanics, particularly for measurement materials deformation without contact. It is an economic and versatile method which also offers a big amount of experimental data [4]. As digital cameras technology constantly improves in terms of resolution, lenses and frames per second (FPS), this technique allows covering a wide range of scale in space and time. DIC in stereo systems even reach non-planar cases, very common in the industry, meaning the three-dimensional reconstruction and access to volumetric data about the material and structure behavior through time. Nonetheless, the use of DIC data to validate models in a quantitative way or to identify with precision several constitutive parameters, remains an open problem. One of the reasons for this is the complicate compromise between the measuring resolution and the large space for the measuring to be done. A second reason is the state of the frontiers. A third reason is that the measured displacements are not directly compared with common simulations. Of course, there are several efforts presenting promising results, as well as [5], a work analyzing the damage in a super pression aerostatic balloon (SPB) used by the Japanese Aerospace Exploration Agency (JAXA) during the insufflate prove. The expansion, when it is not uniform, generates a concentration of stress and makes the balloon explode. They proved a new method called the Simplified Digital Image Correlation Method (SiDIC), in a rubber balloon, to verify if the SPB could be measured. The SiDIC identified in a correct way the non-deformed region even though the deformation was not precise.

Below, a brief historical background of DIC is given. An open code 3D-DIC Toolbox for MATLAB, the one implemented algorithm for multiple cameras, inspired by biomechanics, was reported in [6]. They were verified using the Multiple Digital Image Correlation Method (MultiDIC) and low-cost hardware. In [7], a quick method to correlate digital images (3D-DIC) was proposed to implement real-time measuring. Two improvements came up: the development of an efficient algorithm of the inverse composition of Gauss-Newton (IC-GN) with parallel computing to avoid redundant calculation, and an efficient IC-GN algorithm which was used to reach a speed of 10 frames/second with a resolution of 5000 points per frame. For validation, the displacement field of a four-point bending beam was determined by the real-time 3D-DIC. The experimental results were verified in traditional Chinese medicine. In the publication of [8], a procedure was developed to generate a sequence of intermediate synthetic images for a gradual following of the transformation of the pixel’s subset between the two external configurations. An adequate distortion function of image was defined in the whole image through adopting an algorithm based in characteristics and followed by a scheme of interpolation based in non-uniform rational B-spline (NURBS). This allowed a fast and trustworthy estimation of the initial deformation parameters for the refinement phase after the DIC analysis, and tests were made on aluminum plates. Document [9] proposed a method of deconvolution to recover the real fields of displacement and tension of their counterparts provided by local DIC. The proposed algorithm could be considered an extension of the Van Cittert deconvolution, based on the small tension assumption. The authors claimed an improvement on the fine details in displacement and tension maps, as well as in space resolution. The guidelines to evaluate the precision and resolution of the 2D analysis under the patronage of the Society of Experimental Mechanics were reported in [10].

On the other hand, algorithms to map relative displacements of the deformed material points in opposition to non-deformed material by using DIC were reported in [11,12]. The current possibilities for the DIC scale allows the study of deformation on different levels, from meters to the nanoscale [13,14], with the condition of recording it correctly, following a known pattern like a circle grid or square grid. Additionally, studies have looked at how different systems behave, like biological materials [15,16,17,18], metallic alloys [19,20,21], memory-shape alloys [22,23], porous metals [24,25,26], polymers [27] and polymeric foams [28]. A key step in the process of DIC image tracking is the definition of the initial assumption, for the non-linear optimization routine aimed at finding the parameters that describe the transformation of the subset of pixels. This initialization can be very challenging and possibly fail when it comes to pairs of highly deformed images, such as those obtained from two angled views of non-planar objects. For example, in Figure 1, it can be seen how the global DIC cannot exactly match the circle mark to measure the strain. This was performed with the MATLAB function called “imregcorr”, which was reported in [29].

As can be observed from the preceding discussion, there still is the question of whether it is possible to improve the DIC accurateness. In brief, these previous works highlight the need for developing a systematic approach for achieving this goal, which to the author’s awareness has not yet been stated. Therefore, in this paper we propose the use of a mark-search as an initial condition and of DIC as the system to verify the point-pairing. We propose the use of a mark-search as an initial condition and the use of DIC as the system to verify the point-pairing, because the number of mechanical part images are plentiful, the search for features to measure is very broad, as a result of which providing the initial conditions is necessary to fully automate the process gradually. The lack of a correct initial condition generates slowness and inaccurateness in current implementations of DIC. An appropriate initial condition is especially useful to know the material properties, specifically, its deformation curve and characterization zones such as: elastic, inelastic and rupture [30]. The proposed method in this work is applied to galvanized steel sheet, used in the outside bodywork of a pickup truck at 620 µm-thick and 96.5 µ hardness. Figure 2 shows the surface view of the material obtained from a metallographic microscope model:AX @ 200X, Company: Carl Zeiss AG, Jena, Turinga, Germany. It is necessary to mention that the experiments presented in this paper were all made for the automotive industry sector.

2. Theoretical Bases

The dimensional estimation using stereoscopic vision systems was described in detail by Tsai in [31], who quantitatively concluded that the accuracy and precision relied on the distance between the camera and the object to be measured, as well as the resolution of the cameras used. Stereoscopic vision is a technique frequently used to locate points in three dimensions (3D) based on points in two or more 2D images [6,32]. To achieve a stereoscopic point triangulation, it is necessary to calibrate both cameras. In this paper, we used the PinHole model, which is described by Equation (1) [33]:

$$s\tilde{m}=A\left[R|t\right]\tilde{M}=\left[\begin{array}{ccc}{f}_x& c& u_0\\ 0& f_y& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}|\begin{array}{c}{t}_x\\ t_y\\ t_z\end{array}\right]\tilde{M}=\left[\begin{array}{ccc}{m}_{11}& m_{12}& m_{13}\\ m_{21}& m_{22}& m_{23}\\ m_{31}& m_{32}& m_{33}\end{array}\begin{array}{c}{m}_{14}\\ m_{24}\\ m_{34}\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$

(1)

since s is the number that defines the scale of the objects with respect to their real size in the image, $\mathrm{and}\left[R|t\right]$ is the matrix of extrinsic parameters of the camera that describe the rigid transformation (rotation and translation) between the coordinate system of the camera and the coordinate system of an object outside the camera. A is the matrix of intrinsic parameters that describes the position of the center of the image in pixels $(u_0,v_0)$, and the ratio of the size of the pixel $\left(fx,fy\right)$ has units expressed in $\frac{pixels}{meters}$ in the axes $x$ and $y$ regarding the focal distance between the entrance hole of the light and the matrix of the light sensors of the camera. Parameter c describes the asymmetry of the two axes of a pixel where a zero expresses an angle of 90 degrees. On the other hand, the entry M = $\tilde{M}=\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$ is a 3D point $\left(x,y,z\right)$ in homogeneous coordinates of the scene or object expressed in meters in its own coordinate system, and $\tilde{m}=\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]$ is the corresponding 2D point in the image expressed in pixels $\left(u,v\right)$. Finally, the correction of the lens distortion is made with a polynomial based on the idea that the distortion changes as a circumference, as in Equations (2) and (3):

$$\breve{u}=u+\left(u-u_0\right)\left[k_1\left(x^2+y^2\right)+k_2{\left(x^2+y^2\right)}^2\right]$$

(2)

$$\breve{v}=v+\left(v-v_0\right)\left[k_1\left(x^2+y^2\right)+k_2{\left(x^2+y^2\right)}^2\right]$$

(3)

Subsequently, to achieve a stereoscopic calibration, the translation vector that joins each camera reference system is calculated [34,35]. The point position in three dimensions can be estimated from the coordinates in two dimensions and the Equation (4) [33,36,37,38]:

$$\left[\begin{array}{c}\begin{array}{ccc}u{m}_{31}-m_{11}& u{m}_{32}-m_{12}& u{m}_{33}-m_{13}\\ v{m}_{31}-m_{21}& v{m}_{32}-m_{22}& v{m}_{33}-m_{23}\end{array}\\ \begin{array}{ccc}u\prime m{\prime }_{31}-m{\prime }_{11}& u\prime m{\prime }_{32}-m{\prime }_{12}& u\prime m{\prime }_{33}-m{\prime }_{13}\\ v\prime m{\prime }_{31}-m{\prime }_{21}& v\prime m{\prime }_{32}-m{\prime }_{22}& v\prime m{\prime }_{33}-m{\prime }_{23}\end{array}\end{array}\right]\left[\begin{array}{c}\widehat{x}\\ \widehat{y}\\ \widehat{z}\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}{m}_{14}-u{m}_{34}\\ m_{24}-v{m}_{34}\end{array}\\ \begin{array}{c}m{\prime }_{14}-u\prime m{\prime }_{34}\\ m{\prime }_{24}-v\prime m{\prime }_{34}\end{array}\end{array}\right]$$

(4)

where $\left(u,v\right)$ and $\left(u\prime ,v\prime \right)$ are the coordinates of the paired points of the left and right cameras that correspond to the 3D point to be reconstructed. The scalars $m_{ij}$ are obtained by multiplying the intrinsic and extrinsic parameters of the left camera $A\left[R|t\right]$; in an analogous way, the scalars $m{\prime }_{ij}$ are obtained by multiplying the intrinsic and extrinsic parameters of the right chamber $A\prime \left[R\prime |t\prime \right]$.

2.1. Normalized Cross Correlation (NCC)

Points matching, which consists of locating a point (photographed from different positions) in the left photograph and in the right image, is necessary to carry out the triangulation process. 2D-DIC is used to correlate a given set of points in the two stereo views of the reference configuration and match these points along the sequence of images. The correlated image points that are set are used to reconstruct and track the 3D position of the material points of the ROI (region of interest) through time [6]. In the literature, there are several works that report using 2D-DIC to accomplish this process, because this technique is so meaningful for 3D point reconstruction based on 2D images. The first advantage is that cross correlation is equally simple to calculate. Once a coincidence for a patch in a typical position inside an image is achieved, the Fourier methods can be used to calculate the correlation in a fast way. The second advantage is that cross correlation is independent from translations and invariant in the scaling dominance of the intensity. Equation (5) presents the definition of a normalized cross correlation:

$$NCC=\frac{{{\displaystyle \sum }}_{\left(i,j\right)\in S}\left[f\left(u,v\right)-\overline{f}\right]\left[g\left(u,v\right)-\overline{g}\right]}{\sqrt{{{\displaystyle \sum }}_{\left(i,j\right)\in S}{\left[f\left(u,v\right)-\overline{f}\right]}^2{{\displaystyle \sum }}_{\left(i,j\right)\in S}{\left[g\left(u,v\right)-\overline{g}\right]}^2}}$$

(5)

Here, f and g are each the grayscale functions of the windows of the current image at a specific location (x, y). The functions $\overline{f}$ and $\overline{g}$ correspond to the gray scale mean of the reference image and the current subset.

2.2. Superficial Strain Estimation

To estimate the level of superficial strain, the engravings of speckle, circular or square marks on the sheet are used, which involves an electrochemical process in which an electrolyte is applied as a reagent on the surface of the sheet to engrave a thin pattern so that when the sheet is painted, the marking is imperceptible. The use of a circles pattern was chosen because it is considered a non-uniform mark deformation. In this proposed method, the facet sizes (window sizes) for the correlation function are defined by the distance between the circles’ centroids. The advantages and disadvantages of a circle pattern in contrast with a speckle pattern are show in

Table 1. The advantages and disadvantages of circle pattern versus speckle pattern.

Characteristics	Speckle Pattern	Circle Pattern
The normalized correlation matches well with the patterns.	YES	NO
Mark deformation is assumed as irregular.	NO	YES
A pixel can represent a mark.	Some cases	YES
Independence of the distance between the cameras and the specimen.	Some cases	YES

.

After the sheet is subjected to the sausage process, the circles are distorted in the form of ellipses and the distances between their centroids are modified; the latter are used in the digital images to determine the deformation states in the testing metal sheet. Figure 3a,b shows the changes of the circular grid with the deformation of the metal sheet. A simple way to estimate the deformation in the centroid of each ellipse is by averaging the distance with its four neighboring centroids ${\widehat{C}}_{k-1,l}$, ${\widehat{C}}_{k,l-1}$, ${\widehat{C}}_{k+1,l}$ and ${\widehat{C}}_{k,l+1}$, as expressed by Equation (6):

$$\Delta f_{k,l}=\frac{d\left({\widehat{C}}_{i,j},{\widehat{C}}_{i-1,l}\right)+d\left({\widehat{C}}_{i,j},{\widehat{C}}_{i,j-1}\right)+d\left({\widehat{C}}_{i,j},{\widehat{C}}_{i+1,j}\right)+d\left({\widehat{C}}_{i,j},{\widehat{C}}_{i,j+1}\right)}{4}$$

(6)

where $d\left(\left[\begin{array}{c}{x}_1\\ y_1\\ z_1\end{array}\right],\left[\begin{array}{c}{x}_2\\ y_2\\ z_2\end{array}\right]\right)=\sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2+{\left(z_1-z_2\right)}^2}$.

3. Materials and Methods

3.1. Materials

To capture the images, a pair of Posilica GT 2750 (Allied vision, Exton, PA, USA) cameras with a sensitivity in the range of 400 nm to 670 nm as used. It has ethernet communication, a maximum capture rate of 33 fps, and resolution of 2750 to 2200 pixels at 230–250 lux. They were mounted on a metal structure that allows lighting control. Figure 4 shows the arrangement of the cameras, the light source and the metal test piece used to test the proposed method. LED lighting was chosen due to the contrast with the circles marked on the sheet: a blue LED of 640 nm, which coincides with the work [39]. To compare the dimensional measurements, a digital microscope (Jiusion 6-06814-24289-8) with a 100 μm scale was used.

3.2. Method

The proposed method has the purpose of measuring the surface deformation in a metal sheet specimen used for truck exteriors, and it was divided into ten stages from (a) to (j). The peculiarity of this procedure consists of the incorporation of an initial condition based on points normalization to perform the matching using 2D-DIC. The general procedure is as follows:

(a)

Stamping of known circle grid on the unformed metal sheet.

(b)

Deformation of the metal-sheet through the mechanical stamping process.

(c)

Calibration of cameras.

(d)

Illumination of the piece with LED blue light for measuring.

(e)

Capture of stereo images.

(f)

Selection of four landmarks.

(g)

Search for neighbor’s centroid.

(h)

Calculation of the NCC in the proposed neighborhood.

(i)

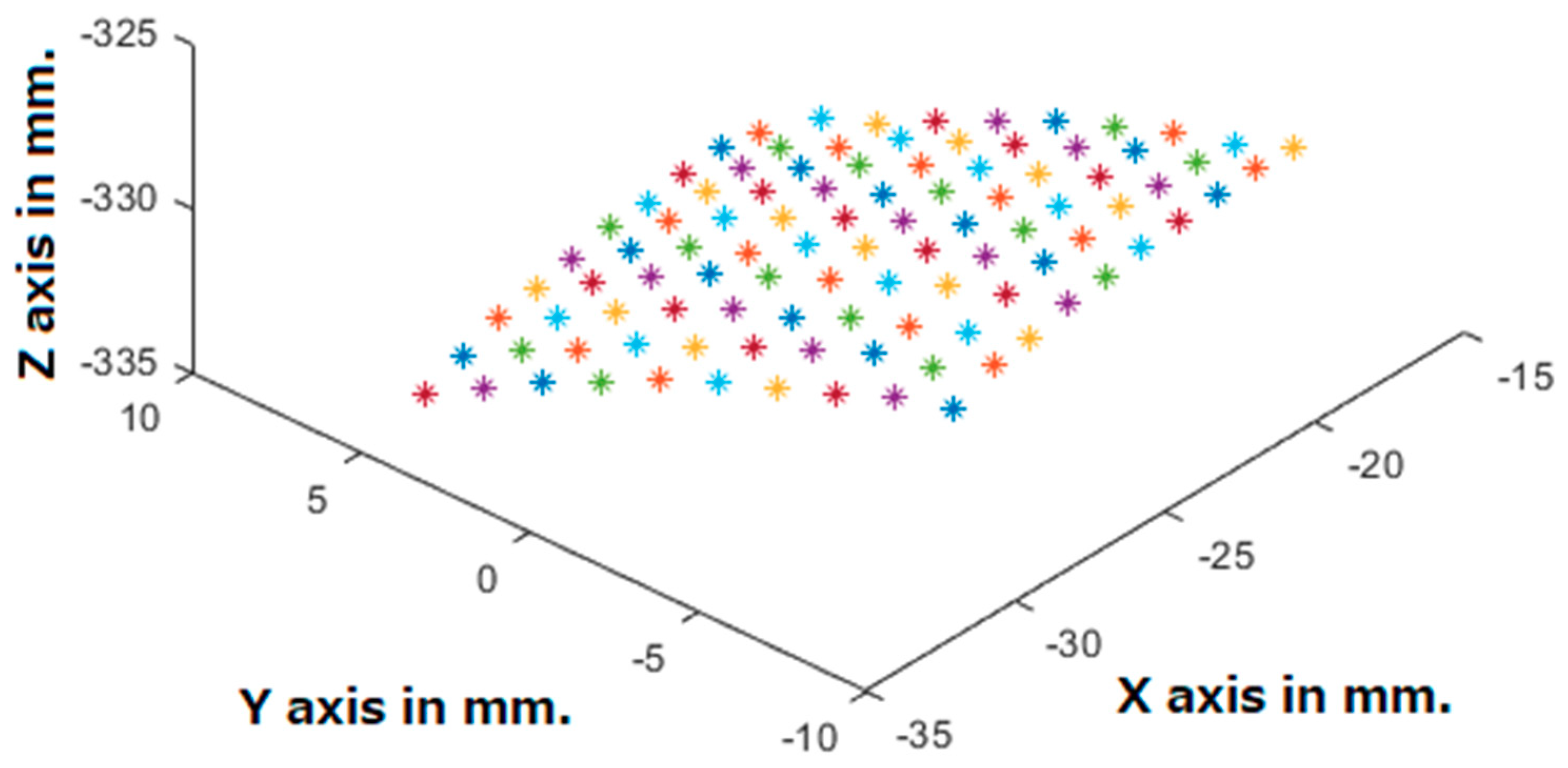
Triangulation of the points to obtain their position in 3D space.

(j)

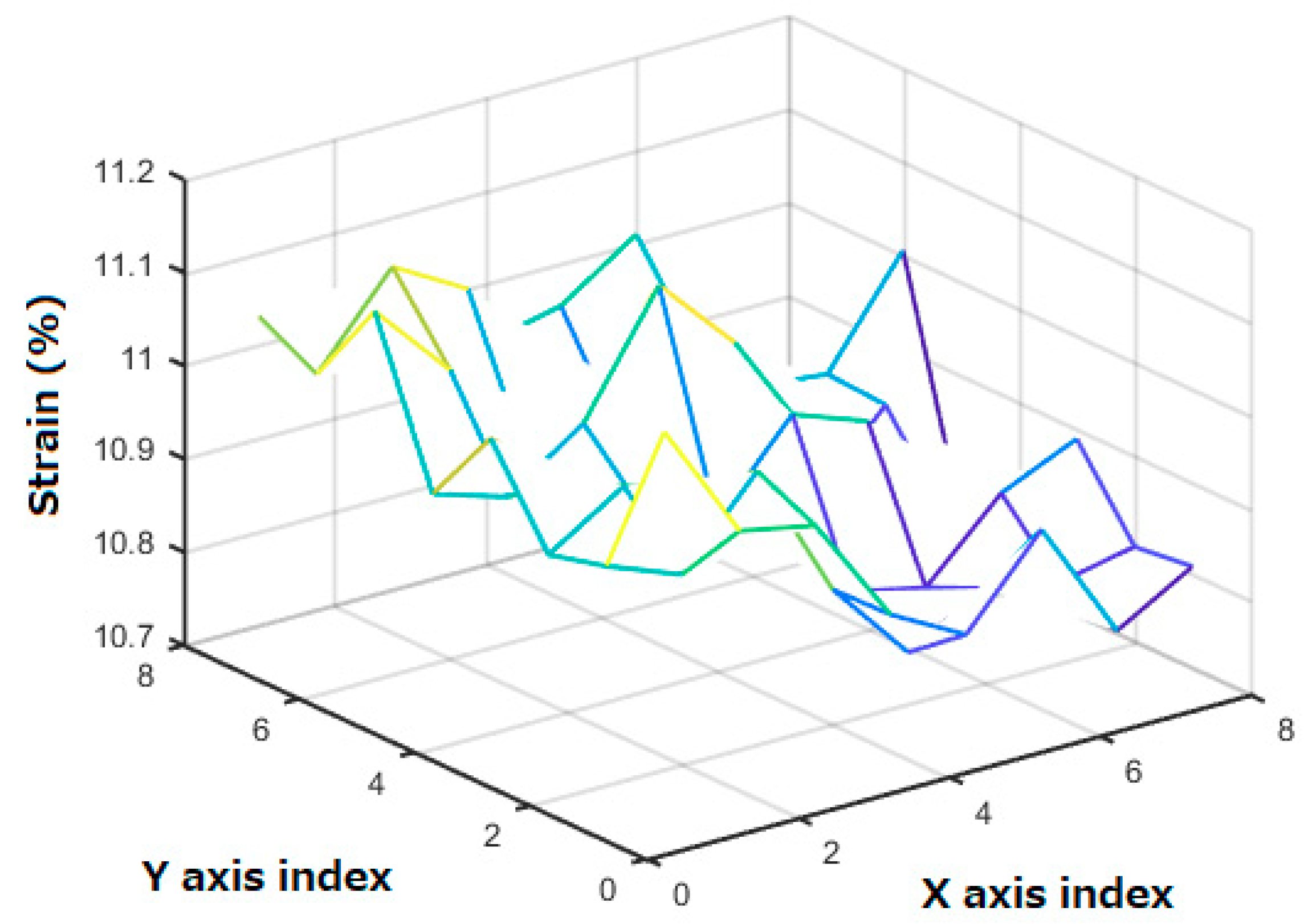
Strain estimation from averaging the centroids’ differences with the four neighbors using Equation (6).

The process includes the stamping of the known circle grid on the unformed metal sheet and the deformation of the sheet through the mechanical stamping process, because it is important to delimit the application of the proposed method.

The individual camera calibration can be performed with the “calib” function, while the stereoscopic calibration can be performed with the function “stereo_gui”. Both are from the library “Camera Calibration Toolbox for Matlab” published by Jean-Yves Bouguet [40]. The illumination can be performed through a blue LED set. It is important that the image capture is done with the calibrated camera system.

3.3. Four-Points Initialization

The construction of the 3D centroid mesh $CM=C_{i,j}$ of the deformed circles pattern begins with the process of obtaining the binarized image, which is detailed in Appendix A. After this, two clicks given on two consecutive ellipses of the left binarized image and two on the same circles of the right binarized image (Figure 5), allows for a knowledge of the distance and slope between two centroids of pseudo-ellipses.

The clicks do not necessarily have to be done on the centroids; it is only necessary that they are done on the two consecutives pseudo-ellipses. The selected points are referred to as $\left(x_{0,0}^{left}, y_{0,0}^{left}\right)$ and $\left(x_{1,0}^{left},y_{1,0}^{left}\right)$, while in the right image the points are $\left(x_{0,0}^{right},y_{0,0}^{right}\right)$ and $\left(x_{1,0}^{right},y_{1,0}^{right}\right)$. To work with discrete values, the values of each point, in each image, are rounded up because the computational functions give fractions of the pixels where the mouse is clicked via the computer. From the rounded coordinates provided by the user, the blob number $n{b}_i^s$ (considering a blob as a group of pixels with a connected connection equal to four) is retrieved to provide the coordinates of the centroid, also rounded; as an index of the tagged image (7).

$$n{b}_i^s=L^s\left({\tilde{x}}_{i,j}^s,{\tilde{y}}_{i,j}^s\right)$$

(7)

where $s$ can be the left or right side, and $L^s\left(x,y\right)$ is the labeled image as explained in Appendix A.

Next, the centroid of each blob $C_{i,j}^s$ is calculated using the statistical moments for 2D (8) with the help of Equations (9) and (10):

$$C_{i,j}^s=\left(x{c}_{i,j}^s,y{c}_{i,j}^s\right)=\left(\frac{m_{10}}{m_{00}},\frac{m_{01}}{m_{00}}\right)$$

(8)

$$m_{pq}={\displaystyle \sum }_{x=1}^k{\displaystyle \sum }_{y=1}^l{x}^p{y}^{q}B{O}^s\left(x,y\right)$$

(9)

$$B{O}^s\left(x,y\right)=\{\begin{array}{c}1si{L}^s\left(x,y\right)=n{b}_i^s\\ 0otherwise\end{array}$$

(10)

The distance and the slope between the two centroids in Equations (11) and (12) are calculated to initiate an iterative automatic process of estimation of the 2D position of blobs. The estimation of the next blob position from the information of the two clicks on each image $y{c}_{i+1,j}^s$, $y{c}_{i,j}^s$, $x{c}_{i+1,j}^s$ and $x{c}_{i,j}^s$:

$${\tilde{d}}_{g,h}^s=\sqrt{{\left(y{c}_{i+1,j}^s-y{c}_{i,j}^s\right)}^2+{\left(x{c}_{i+1,j}^s-x{c}_{i,j}^s\right)}^2}$$

(11)

$${\tilde{m}}_{g,h}^s=\frac{\left(y{c}_{i+1,j}^s-y{c}_{i,j}^s\right)}{\left(x{c}_{i+1,j}^s-x{c}_{i,j}^s\right)}$$

(12)

where g and h are the index of the distances and slopes matrixes.

From Equations (11) and (12), the pseudo-row of marks is estimated using Equations (13) and (14):

$${\widetilde{xc}}_{i+1,j}^s=x{c}_{i,j}^s+{\tilde{d}}_{g,h}^s\cos \left({\tilde{m}}_{g,h}^s\right)$$

(13)

$${\widetilde{yc}}_{i+1,j}^s=y{c}_{i,j}^s+{\tilde{d}}_{g,h}^s\cos \left({\tilde{m}}_{g,h}^s\right)$$

(14)

Meanwhile, to find the next row, Equations (15) and (16) are used:

$${\widetilde{xc}}_{i,j+1}^s=x{c}_{i,j}^s+{\tilde{d}}_{g,h}^s\cos \left({\tilde{m}}_{t-1}^s+\pi /2\right)$$

(15)

$${\widetilde{yc}}_{i,j+1}^s=x{c}_{i,j}^s+{\tilde{d}}_{g,h}^s\cos \left({\tilde{m}}_{t-1}^s+\pi /2\right)$$

(16)

The normalized cross-correlation (5) is used to ensure a good pairing of centroids. This drastically decreases the number of operations performed for the matching between the interest points and at the same time takes advantage of the reliability granted by the NCC. The Matlab code can be downloaded from https://sites.google.com/itcelaya.edu.mx/dic/.

4. Results

The results of a typical initialization of the DIC are displayed in Figure 6 to show an initialization comparison. The working conditions were: one facet of 21 × 21, the search for the maximum normalized correlation, one-pixel step, and 100 marks that were pre-selected in the left image.

To observe the behavior of the normalized correlation internally, the correlation between a left image ellipse against all the possible 21 × 21 facets of the right image was plotted to qualitatively locate the maximum peak of the correlation (Figure 7).

The engraving of light reference circles on the metal sheet resulted from an equidistance of 1.55 mm between the centroids when the metal sheet had not been deformed. The measurement made with a microscope is shown in Figure 8, where the before (Figure 8a) and after (Figure 8b) deformation is appreciated.

On the other hand, the calibration parameters of the right and left cameras, as well as the translation vector between both cameras are the following:

Intrinsic parameters of the left camera:

Focal length:  fc_left = [ 4139.77293   4125.08567 ] ± [ 262.92862   287.85915 ]

Principal point:  cc_left = [ 1386.44233   1290.81589 ] ± [ 145.82339   108.75101 ]

Skew:  alpha_c_left = [ 0.00000 ] ± [ 0.00000 ] => pixel angle = 90.00000 ± 0.00000 degrees

Distortion:  kc_left = [ −0.03826   −0.81032   −0.00495   −0.00231  0.00000 ] ± [ 0.15686   2.09125   0.00925   0.01010  0.00000 ]

Intrinsic parameters of the right camera:

Focal length:  fc_right = [ 4009.97898   4233.47842 ] ± [ 271.16800   339.84438 ]

Principal point:  cc_right = [ 1149.40996   962.27029 ] ± [ 198.63016   96.89436 ]

Skew:  alpha_c_right = [ 0.00000 ] ± [ 0.00000 ] => pixel angle = 90.00000 ± 0.00000 degrees

Distortion:   kc_right = [ −0.12949   0.25429   0.00496   0.02934  0.00000 ] ± [ 0.13731   0.93124   0.00825   0.01424   0.00000 ]

Extrinsic parameters (position of the right chamber with respect to the one on the left):

Rotation (In Rodrigues format):  om = [ −0.00856   0.37660   0.00093 ] ± [ 0.03213   0.04287   0.00594 ]

Translation vector:  T = [ −85.14492   33.53035   24.13032 ] ± [ 2.97387   1.09323   11.19968 ]

The results of the image processing step are shown in Figure 9. In the top row, the pair of stereo images before the area filter is presented, while in the row below, the images after the area filter application are reported.

We selected one hundred points to show the method´s accuracy in a space of 100 × 100 marks. To verify if each point matching was right, the local DIC was calculated for the proposed points estimated in the initialization stage. The best correspondence was in the same position projected by the four-point method. Figure 10 shows a case of the correlation using a window of 31 × 31 pixels on a zone of 21 × 21 pixels. The MATLAB function used for this aim was “corr2”.

Figure 11 shows the points matching of an area of 10 × 10 deformed circular marks. Those are the same taken to perform the 3D reconstruction. On one side, the detail of the points matching is shown with a zoom.

Figure 12 shows the three-dimensional reconstruction of the marks found and verified for the point matching stage. From the 3D reconstruction the strain was calculated using Equation (6), averaging the distances between the four neighboring marks of the mesh of circles of a radius of 0.5 mm and a separation between the centers of 2.55 mm. The strain estimated by the proposed method is shown in Figure 13.

The strains estimated in points having their four neighbors from a matrix of 100 × 100 were reduced to a matrix of 8 × 8. The values in

Table 2. Estimated strain (%) using the proposed method.

Position Indexes	j = 1	j = 2	j = 3	j = 4	j = 5	j = 6	j = 7	j = 8
i = 1	10.4623	10.334	10.2988	10.1945	10.2066	10.2369	10.1932	10.1931
i = 2	10.2814	10.2721	10.3268	10.2013	10.1416	10.2001	10.1461	10.209
i = 3	10.2739	10.3202	10.2906	10.2571	10.1665	10.1584	10.2454	10.2757
i = 4	10.3615	10.2886	10.2542	10.2351	10.3094	10.2866	10.2113	10.217
i = 5	10.2692	10.282	10.2885	10.4412	10.3556	10.2272	10.2494	10.158
i = 6	10.4365	10.3514	10.2451	10.4047	10.361	10.2592	10.3007	10.3751
i = 7	10.3587	10.4371	10.3885	10.1398	10.215	10.2778	10.1877	10.3029
i = 8	10.3664	10.3276	10.3599	10.2999	10.314	10.3569	10.2394	10.172

and

Table 3. Estimated strain (%) using a digital microscope.

Position Indexes	j = 1	j = 2	j = 3	j = 4	j = 5	j = 6	j = 7	j = 8
i = 1	11.2903	9.6774	9.3548	9.6774	8.871	8.0645	8.0645	7.2581
i = 2	10.4839	8.871	7.2581	8.0645	8.0645	5.6452	4.8387	5.6452
i = 3	6.4516	8.0645	8.5484	7.7419	6.4516	6.4516	6.4516	6.4516
i = 4	8.0645	9.6774	9.6774	7.2581	6.4516	6.4516	5.6452	6.4516
i = 5	8.0645	10.1613	10.1613	5.6452	5.6452	6.4516	5.6452	7.2581
i = 6	11.2903	11.2903	8.0645	7.2581	8.0645	10.4839	8.0645	10.9677
i = 7	13.7097	10.4839	8.871	8.871	8.871	9.6774	8.871	12.9032
i = 8	9.6774	6.4516	7.2581	8.0645	10.4839	7.2581	6.4516	8.871

were obtained with the stereoscopic vision system. From these results, it can be calculated that the average error in the experiment was, in this case, $ϵ=1.290878\%$ (0.019995 mm.). This takes into account a distance between the centroids of the marks of 1.55 mm, without deformation.

5. Discussion

The principal contribution of this work consists in the correct points-pairing between images (100%), in the specific case of almost-identical marks, to measure the deformation of a metal sheet with a small error. The method is semi-automatic due to the high complexity of the shown problem. This is evident when using the MATLAB function called “imregcorr” [41], and it is solved when the user indicates only two pairs of coinciding points. This works as an initial condition to begin a search of correspondent marks among the images. Basically, we noticed that the initial conditions of the search increased, in a notable way, the efficiency of the point-pairing system (with efficiency referring to the amount of paired marks, divided between the total of marks in the space of analysis). We assumed that the quality of the mark stamping, lighting, and the initial conditions, also contribute to trustworthy effects. According to the results, it can be observed that the correlation applied to the detection of deformed circular patterns (ellipses) is not ordered. This is because the objective of the construction of the pattern is to make the marks identical and that, in opposition to this, the correlation uses the differences between marks to emit a factor of similarity. The system was also compared with a manual deformation measurement using a microscope, which achieved a low sensitivity of the camera system and a displacement. This was due to the resolution of the camera system. In terms of processing time, it is well known that the correlation has a computational complexity of m²n² for an nxn image and an mxm template. Meanwhile, the proposed method depends on the number of points on the analyzed sheet; which is many times less than the number of pixels of an image, and it also depends on the distance between the camera and the printed sheet that is to be studied.

6. Conclusions

The proposed methodology solves the corresponding points-pairing for cases where multiple marks tend to be identical. This is one of the most complex and difficult problems DIC experiences in stereoscopic vision. The philosophical basis where most of points-pairing algorithms reside is the search for differences between the objects inside images. This goes against the goal of the Circle-grid of obtaining identical circles. The proposal in this work takes advantage of the characteristics of the problem to reduce its fallibility and to reach very important results, as well as the knowledge of an equal-points grid and a superficial deformation of less than 50%; which is of interest. The results are compared to the predetermined MATLAB function to show the advantages of this work´s proposal, which may be of use with a high degree of trustworthiness, thanks to the large amount of accurate correspondences. The processing time for the search in the initial conditions is relatively low because only distances, slopes and cosine functions are calculated. This way of solving the problem could be used in systems requiring patterns or points-grids, such as squares, hexagons and others. As a future work, we suggest to automatize in a total way the points´ correspondence without losing the gained benefits.