The Heisenberg equation for the number operator
, with the Hamiltonian
in Equation (
25),
has no exact solution, as mentioned above. Nevertheless, it allows one to retrieve the coefficients of the Taylor expansion for
,
being the derivatives of all orders provided by the iteration of Equation (
26) and
.
Equivalently, one can study the evolution of the states. The most general input state for an SHG process can be expanded over the basis of the number states as:
where
are suitable coefficients such that
. Given the evolution operator
, we get the output state from:
by suitably expanding
In particular, we focus on the evolution of Fock states and then generalize to any input state by expanding it like in Equation (
28), i.e.,
Both the Heisenberg (Equation (
27)) and the Schrödinger (Equation (
29)) pictures will be exploited in the following. In particular, in
Section 2.2.1, we need the expansion of the number operator to retrieve the first moment of the SH photon-number distribution. On the contrary, the conversion probabilities in
Section 2.2.2 are more easily computed by evolving the input state.
2.2.1. Photon-Number Distribution
Kozierowski and Tanaś in [
7] provided an expansion of the first moment of the output statistics
up to the fourth order as a function of the Glauber autocorrelation function of the input field. The Glauber autocorrelation function for the modes
and
is defined as follows [
12,
16]:
As shown in
Appendix A, it is possible to demonstrate that every order of the perturbative expansion of the output mean photon-number can be expressed as a linear combination of the Glauber autocorrelation functions in Equation (
32).
The theorem allows us to express the SH moments as convergent series over the order of the autocorrelation function of the fundamental field. In particular, we found out that up to the sixth order in
, the output mean value reads:
where
. For the sake of simplicity, we assumed
and replaced
with
.
Moreover, for the Fock state, the theorem provides a general expression for the asymptotic value of
as a function of
N (see
Appendix B), namely:
Note that, upon defining the conversion efficiency as:
we find from Equation (
34) that:
meaning that the conversion efficiency related to every single interaction is proportional to the input intensity. This fact will be relevant in the analysis of the evolution of the input light statistics.
Furthermore, note that, if
, Equation (
34) is a geometric series, and
.
The physical meaning of the coefficients in the perturbative terms of
can be pointed out by writing the autocorrelations in Equation (
33) for the Fock state as a function of
N:
for any given
K. Up to the sixth order in
, we have:
Note that the three terms in Equation (
37) represent the three different processes concurring in SHG. The first one
is related to the creation of
k SH photons from
N. This contribution comes from all and only the terms that in the expansion of
U in Equation (
29) are of the kind
. They correspond to pure up-conversion events, i.e., the creation of
SH photons from
N at each order
k.
Then, for
, we have the
αk terms, corresponding to the alternating creation and annihilation of SH photons. For the sake of simplicity, we name these as annihilation processes since, at variance with the former term, they consist of back-conversion events. For instance, for
k = 3, we have three different processes leading to a non-null value of
, which are the following: the creation process
(creation of three SH photons from
N after three interactions) and the annihilation processes
and
(creation of one SH photon from
N after three interactions). The last two provide the first and the second term in
α3 (Equation (
38)), respectively, and differ for the ordering of the operators only. In particular, both these processes lead to the same output state (|
N − c2, 1〉), but, in the first one, we have that an SH photon is created, annihilated, and then created again (each of these events happening in
N!/(
N − 2)! possible ways), while in the second one, two SH photons are created (which is likely to happen in
N!/(
N − 4)! equivalent configurations), and then, one of the two is down-converted in two photons of the fundamental field ((
N − 2)!/(
N − 4)! possible configurations).
Finally, if
k ≥ 2, the annihilation processes can interfere either with one another or with creation events, giving rise to the third kind of contribution (the
βk terms in Equation (
37)). This superposition happens whenever different processes lead to the same output state. For instance, for
k = 2, we find, together with the two-photon-creation process
(creation of two SH photons from
N after two interactions), the superposition
β2 of the one-photon-creation process
(creation of one SH photon from
N after one interaction) with the annihilation processes
and
mentioned above. Note that all of these three terms provide the output state
. More explicitly, the superposition of
with
corresponds to a term
in the Taylor expansion of
U. In particular, from that expansion, it is straightforward that the factor
contributes with an amplitude
, whereas
contributes with
. Similarly, the superposition of
with
is given by a term
, where
contributes with an amplitude
.
The role of these different contributions will be outlined in the following, in connection with the conversion probability and the evolution of the input light statistics.
2.2.2. Conversion Probability
Achieving an analytic expression for the probability of converting 2
k photons of the fundamental field into
l ≤
k SH photons is generally a hard task because the number of perturbative terms in the expansion of the SH state (see Equation (
29)) is generally not enough to recognize the convergence to a known analytic function. Moreover, there is no guarantee at all that such a function exists. However, there are some simple cases where a large number of perturbative orders (up to 30) can be retrieved and found to be the terms of the perturbative expansion of known analytical functions. In particular, this is the case if the input photon-number is small and
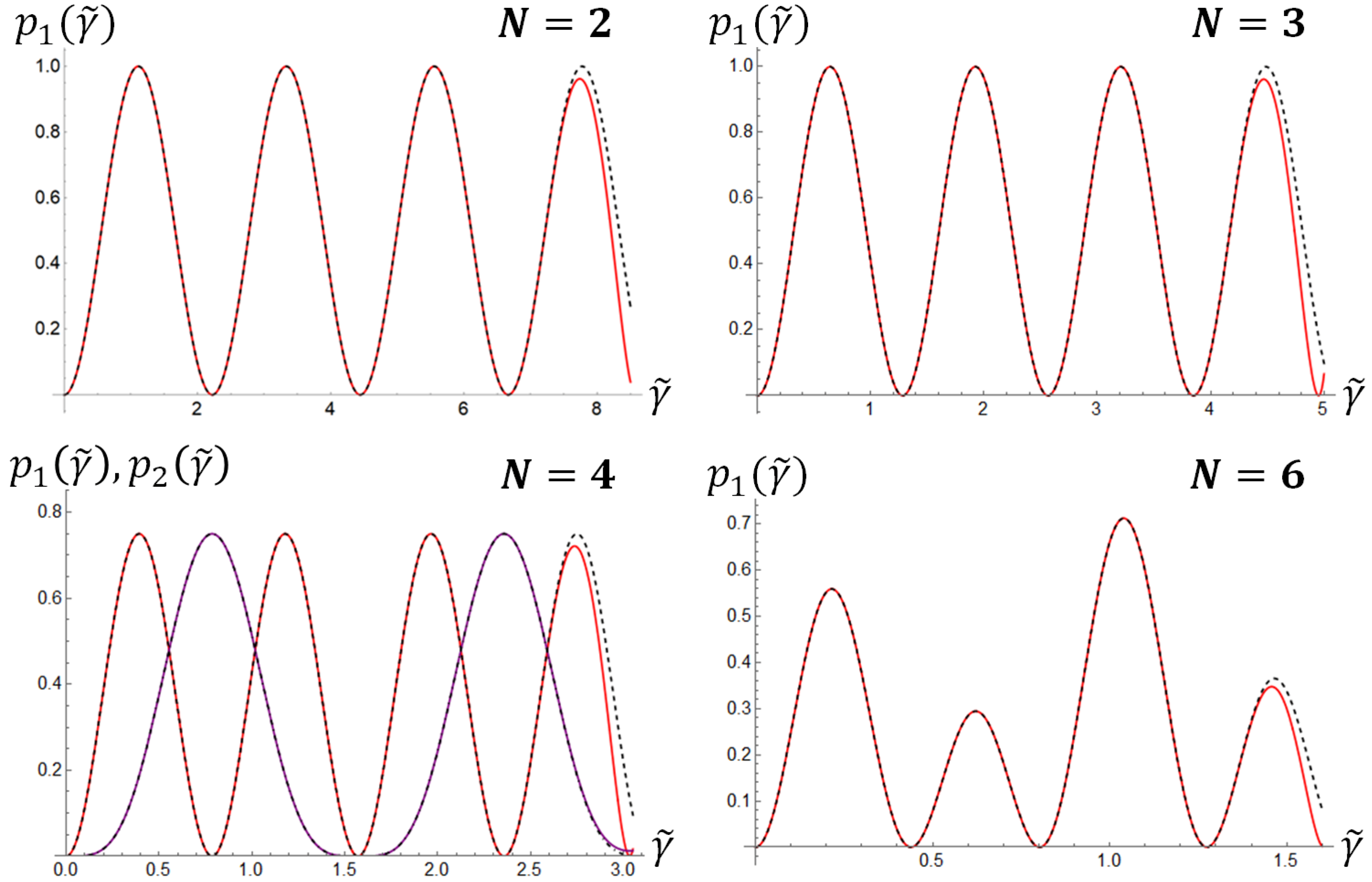
l = 1. We found out that the probability
of generating a single SH photon from 2 ≤
N < 6 input photons converges, up to the order 30, to a periodic function, i.e.,
where:
The interplay among multiple creation and annihilation processes and their superposition is periodic up to six input photons, as shown in
Figure 1. For
N ≥ 6, this is no longer true, but still,
converges to an analytic function. The reason for the aperiodic behavior of
for
N ≥ 6 is due to the contribution of a larger number of processes at every order, resulting in a squared sum of different periodic functions. The ratio between the periods of these functions turns out to be incommensurable, so that their sum is not a periodic function.
2.2.3. Statistics
Finally, we focus on the transformation of the statistics of the input field via SHG. We choose a particular input statistics by suitably setting the coefficients
cn of the input density matrix (
28). We investigate and compare the evolution of Fock, coherent, multithermal, and squeezed states. Moreover, we point out the role of the creation and annihilation processes together with their superpositions, outlined in Equation (
38) by comparing the autocorrelation function for SHG (blue solid lines in the plots) with the autocorrelation function for the process
(red dashed lines in the plots), only corresponding to the SH creation events. The latter is simply obtained by neglecting the
αk and
βk terms in Equation (
37). Since the conversion efficiency is proportional to the input photon-number (see Equation (
36)), we expect the annihilation processes and the superpositions to reduce the quantum correlations in the output state.
The moments of the output statistics are straightforward from:
In analogy with Equation (
33), the variance can be expressed as an expansion over the autocorrelation functions (
32) of the input field, which here we rename
:
It is possible to show that the autocorrelation function defined in Equation (
32) can be written as a function of the variance and of the mean value of the number operator, so that we can compute the autocorrelation function of the SH field through:
2.2.6. Multithermal State
The probability distribution of a multithermal state reads [
16]:
which is the discrete case of
P(
IF) (see Equation (
16)). The mean number
is the average boson number from the Bose–Einstein statistics [
20]. If
μ = 1, the well-known thermal distribution:
is retrieved. The computation of the mean value and the variance from Equation (
47) yields:
We note that the variance can be rewritten in terms of the mean value as
so that it is clear that, for large mode numbers, the statistics tends to a Poissonian distribution, as expected (see the final remarks in
Section 2.1). A generic input state with multithermal statistics is the mixed state
Here, we write explicitly the mean value and the variance of the output statistics since this case is amenable to a comparison with the classical one:
We remark that, at the lowest orders of
,
and
in Equations (
51) and (
52) exhibit the same dependence on the number of modes
μ and on the input mean value
N, which was retrieved in Equations (
18) and (
20) for the classical case.
Thus, at the first order, we find again the moments of a superthermal distribution. Furthermore, at higher orders, we still have that annihilation processes and superpositions result in a reduction of correlations, as we show in
Figure 3. The computation of the SH autocorrelation function yields:
In particular, if we compare the second panel of
Figure 3 with
Figure 2, we find again that if the number of modes is large, we end up with a Poissonian statistics. We remark that the contribution of the only creation processes (dashed red line) is significant to point out the effect of the back-conversion throughout the whole process, but that it has no particular physical meaning itself.
2.2.7. Squeezed State
A pure single-mode squeezed vacuum state is expanded over the number-state basis as follows [
13,
16]:
where
μ = cosh(
r),
ν =
eiθ sinh(
r),
θ and
r being respectively the phase and the squeezing parameter. For the sake of simplicity, we set
θ = 0. The autocorrelation function for a squeezed state is given by
We found that, for such an input state, the SH autocorrelation function reads:
Firstly, we remark that the zero order in Equation (
56) is the usual first approximation of the SH autocorrelation function, which is obtained through Equation (
43). It is provided by the first and second orders of the perturbative expansion of the moments, then it also contains the superposition processes
β2 (Equation (
37)). We note that, while for a multithermal state, this contribution does not apparently affect the output correlations (see
Figure 3),
Figure 4 shows that for a squeezed input state, these superposition processes help to increase correlations. This is why the zero order of the SH autocorrelation function is smaller if we omit the superposition processes (red dashed line in
Figure 4).
Moreover, we find that, at increasing input photon-number,
is reduced (compare the two panels in
Figure 4). The same result is found for the autocorrelation function of the squeezed state (see Equation (
55)), with the difference that the asymptotic value in the SH case is larger:
. The fact that this value is the same as that of the zero order of the autocorrelation computed in the absence of back-conversion processes (dashed red line in
Figure 4) is not accidental. From Equation (
36), we know that the conversion efficiency is asymptotically smaller for higher orders, and we have superpositions just for
k ≥ 2, so that their contribution is reduced as
N → ∞.
Finally, we point out that, in general, the multiple back-conversion events occurring for contribute to reducing correlations as usual.
The high fluctuations retrieved for this SH field are a signature of the quantum properties of both the input state and the SHG process: since the squeezed state is a superposition of pairs of photons (Equation (
54)) and the process always annihilates even numbers of pump photons, then SHG enhances the correlations of the input statistics.