Enhanced Digital Image Correlation Analysis of Ruptures with Enforced Traction Continuity Conditions Across Interfaces
Abstract
:1. Introduction
2. Monitoring Dynamic Shear Ruptures in the Laboratory
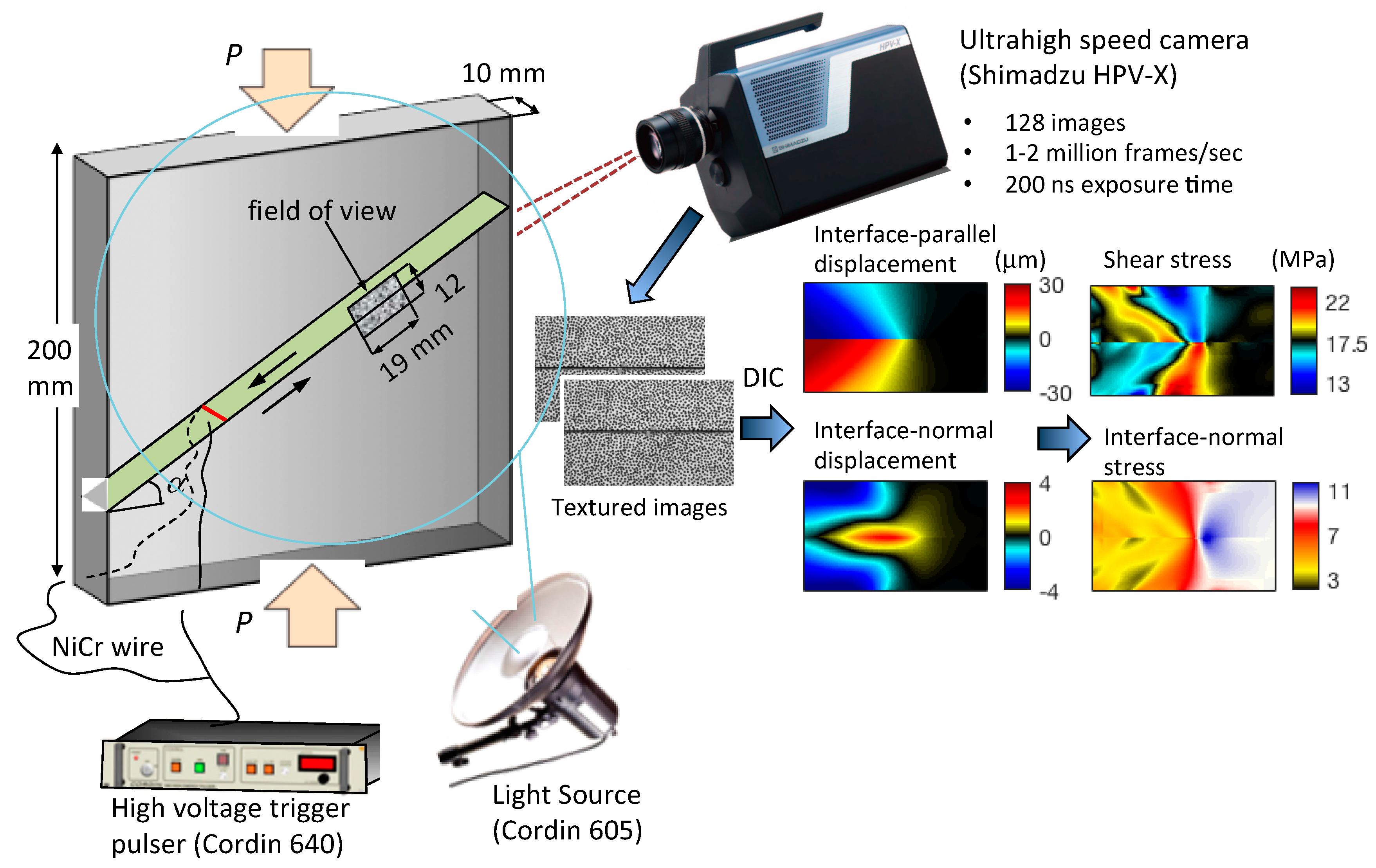
2.1. The Laboratory Setup
2.2. Digital Image Correlation to obtain Displacement Fields
2.3. Post-Processing of the Displacement Fields
3. A Post-Processing Algorithm to Enforce Traction Continuity along the Interface
3.1. Traction Continuity Conditions
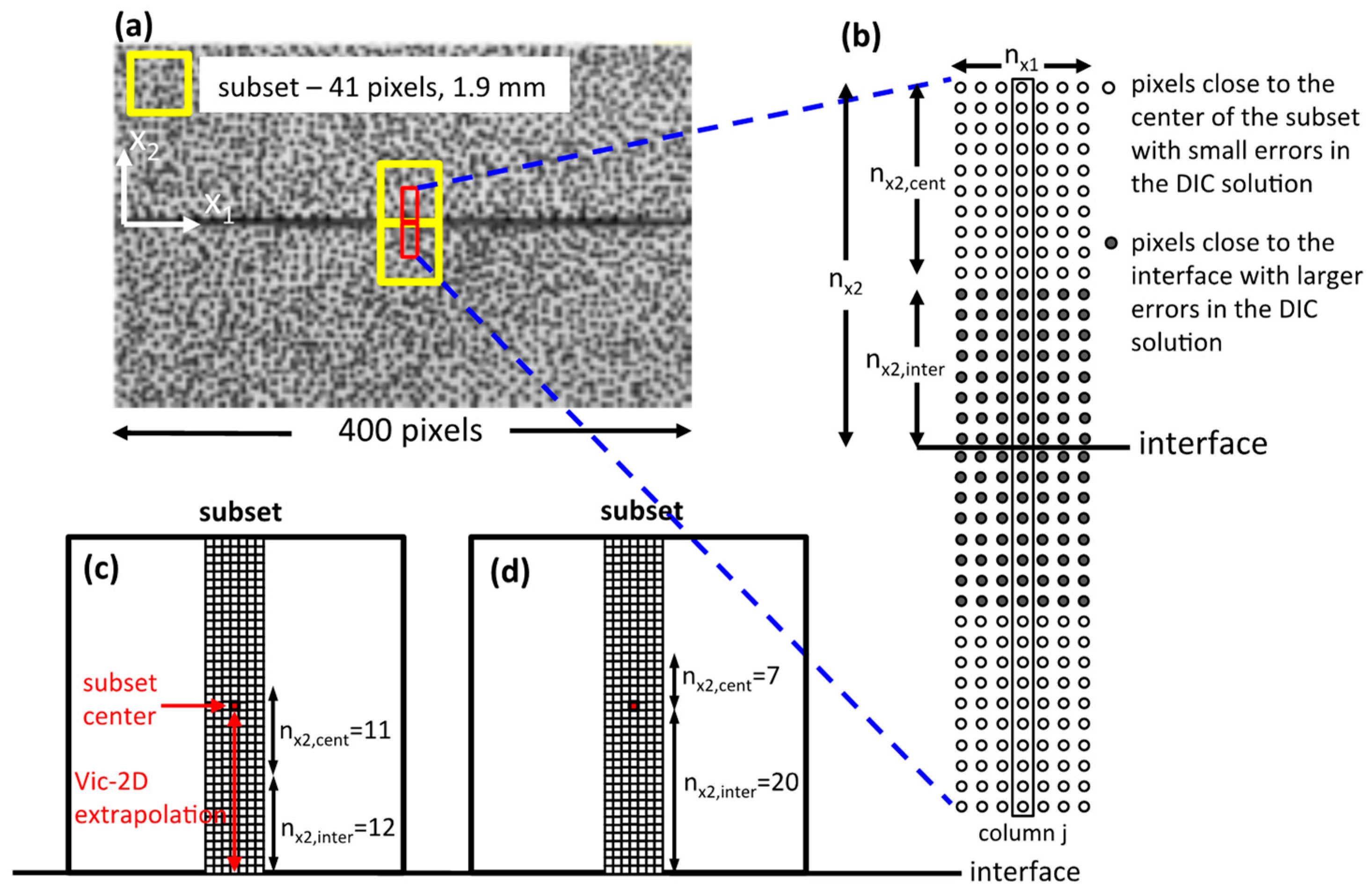
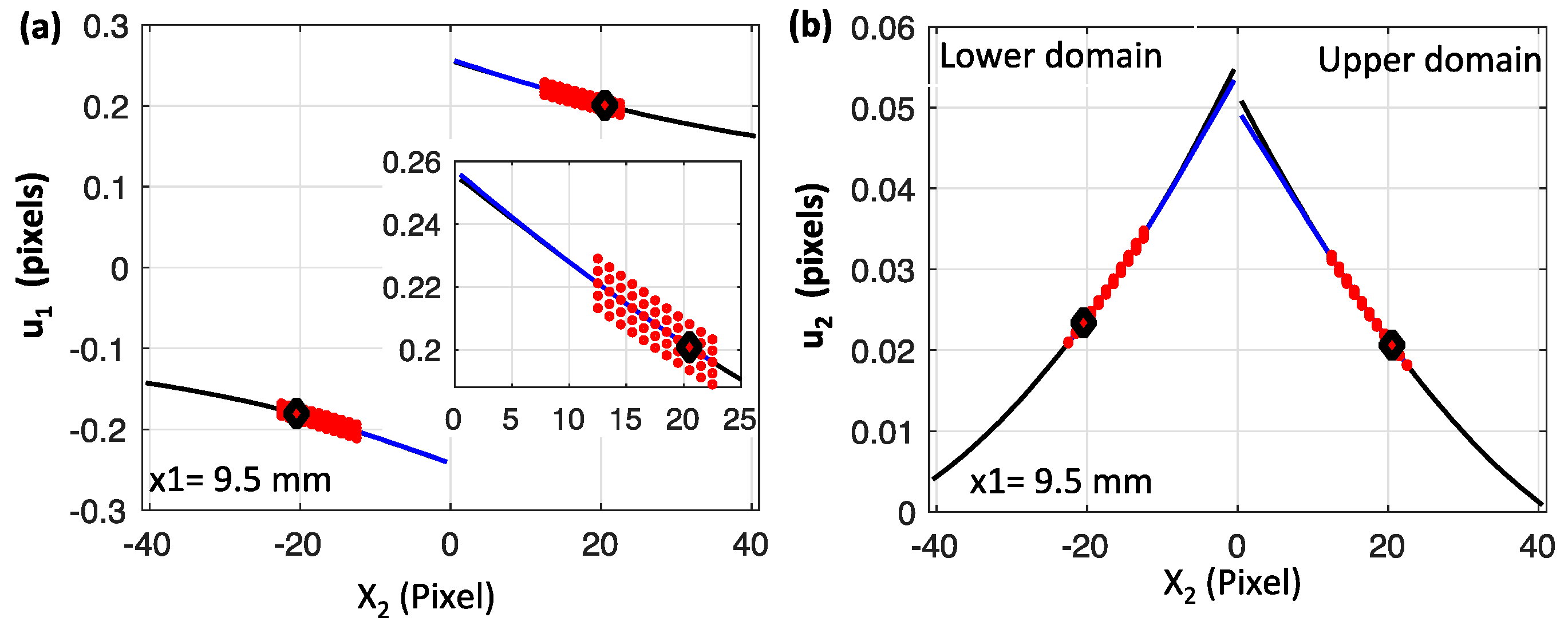
3.2. Approximating the Displacements with Local Polynomials
3.3. Inverting for the Polynomial Coefficients
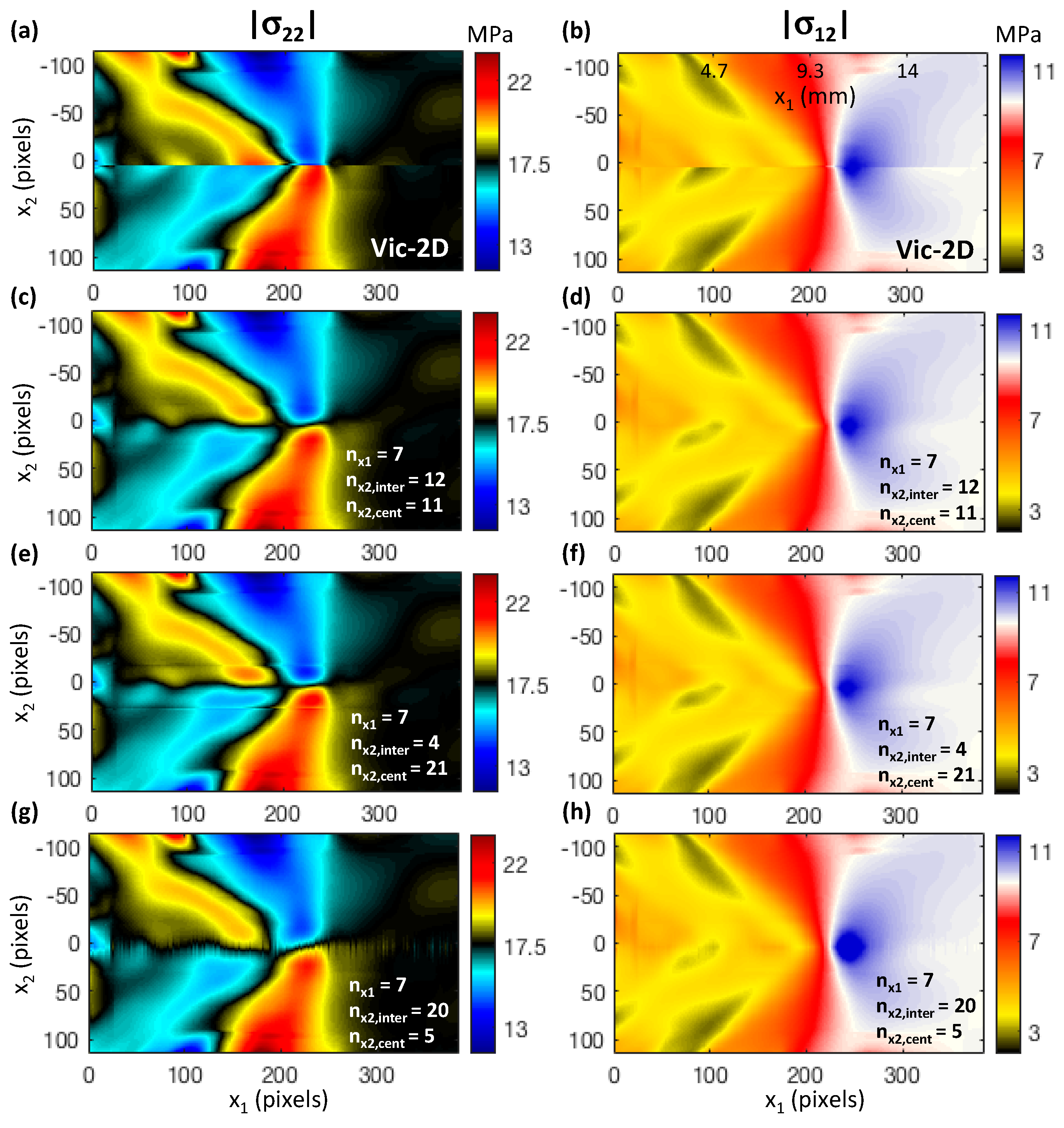
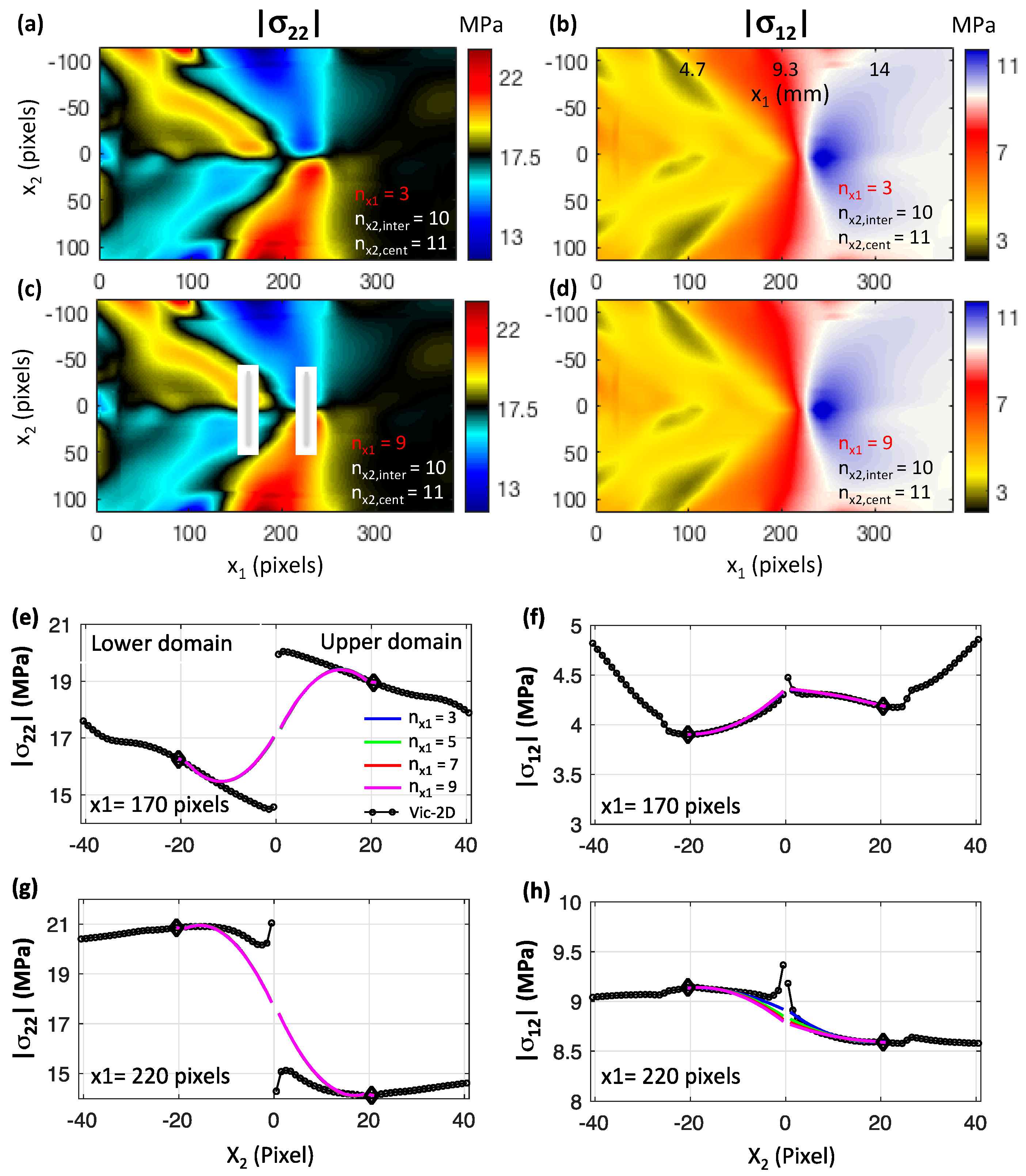
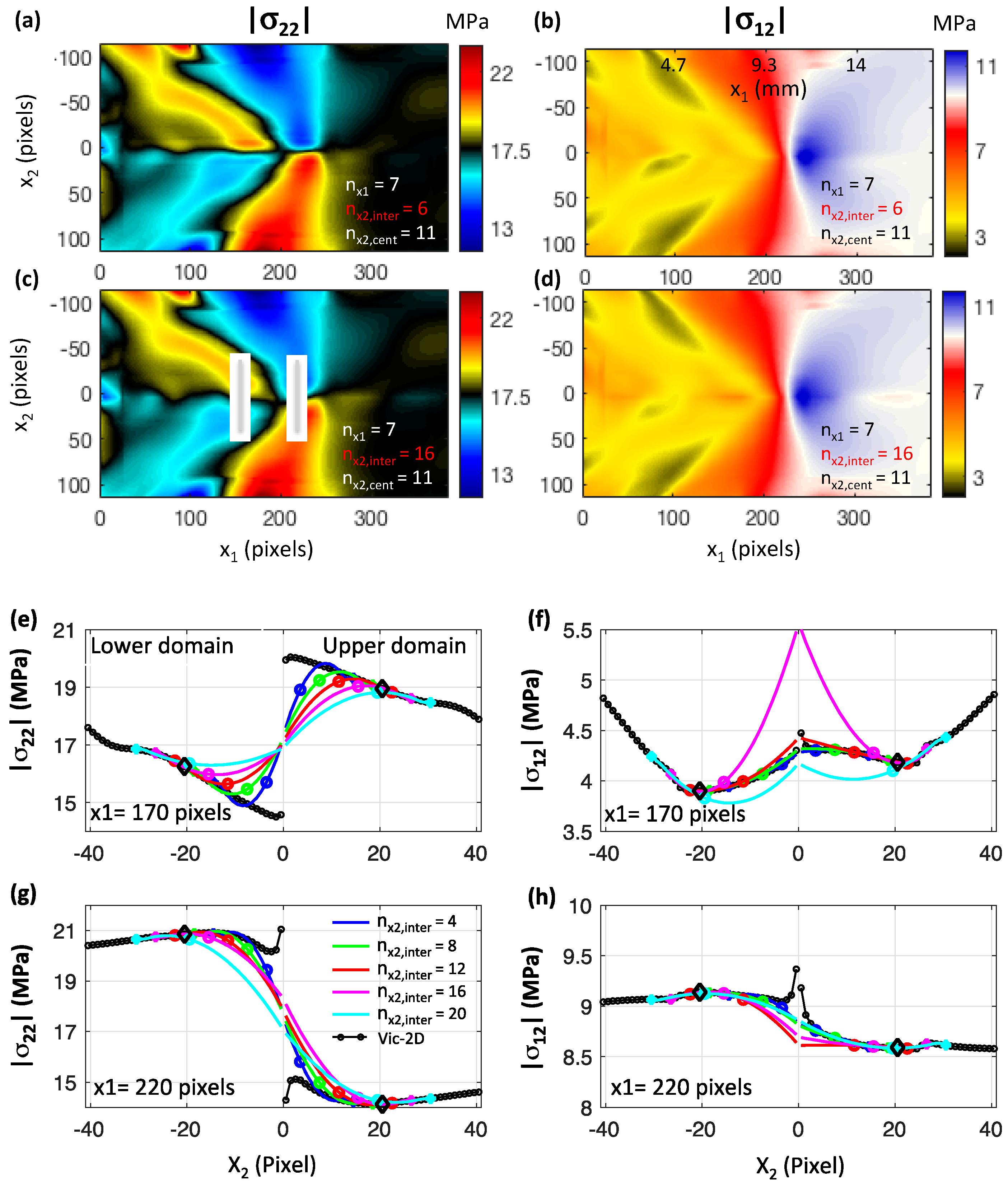
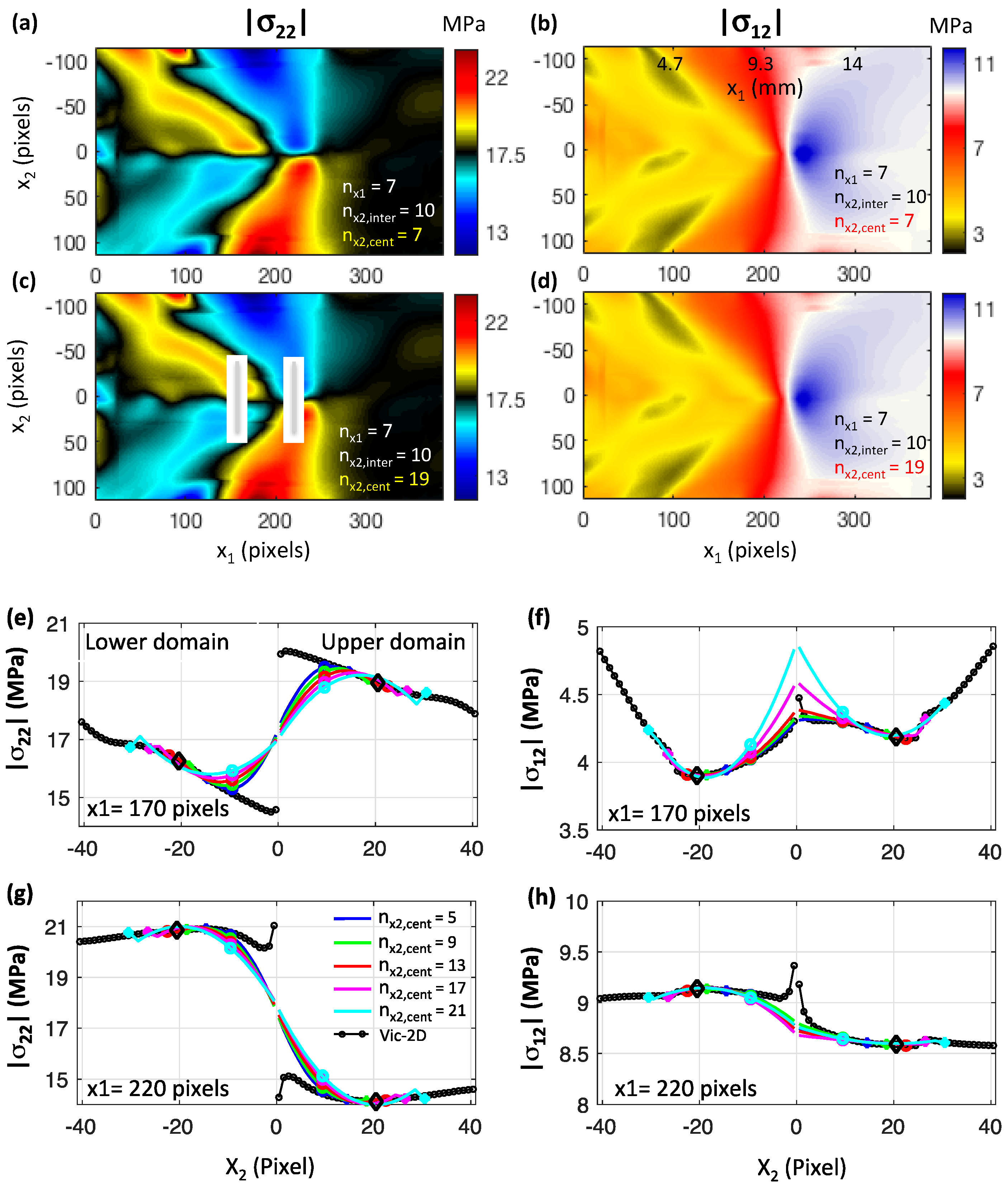
3.4. The Effects of the Geometrical Parameters of the Polynomial
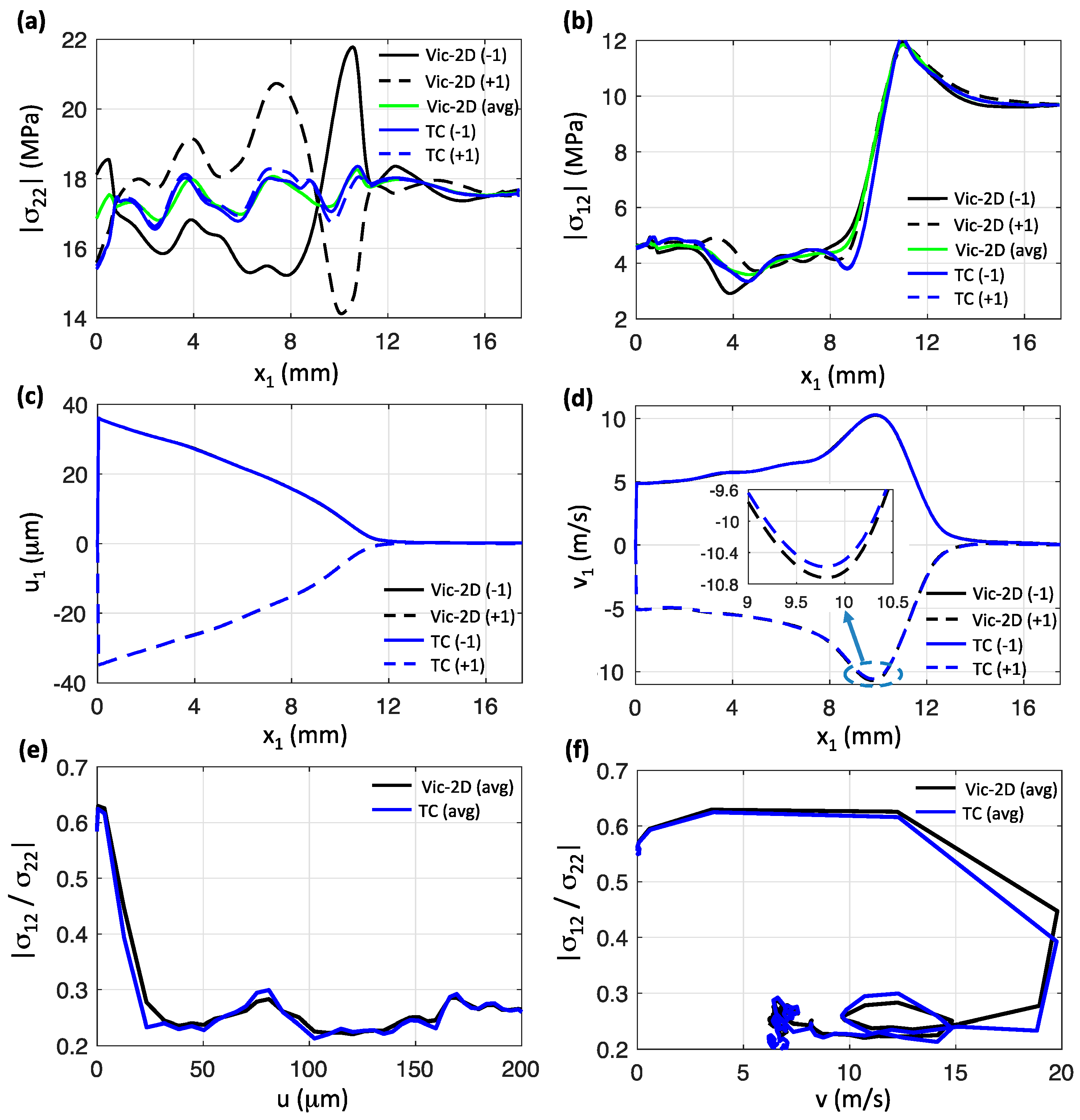
4. Implications for Friction Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rubino, V.; Rosakis, A.J.; Lapusta, N. Understanding dynamic friction through spontaneously evolving laboratory earthquakes. Nat. Commun. 2017, 8, 15991. [Google Scholar] [CrossRef] [PubMed]
- Gori, M.; Rubino, V.; Rosakis, A.J.; Lapusta, N. Pressure shock fronts formed by ultra-fast shear cracks in viscoelastic materials. Nat. Commun. 2018, 9, 4754. [Google Scholar]
- Rubino, V.; Rosakis, A.J.; Lapusta, N. Full-field ultrahigh-speed quantification of dynamic shear ruptures using digital image correlation. Exp. Mech. 2019, in press. [Google Scholar] [CrossRef]
- Sutton, M.A.; Orteu, J.J.; Schreier, H. Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications; Springer: New York, NY, USA, 2009. [Google Scholar]
- Hild, F.; Roux, S. Digital Image Correlation; Wiley-VCH: Weinheim, UK, 2012. [Google Scholar]
- Sutton, M.A.; Matta, F.; Rizos, D.; Ghorbani, R.; Rajan, S.; Mollenhauer, D.H.; Schreier, H.W.; Lasprilla, A.O. Recent Progress in Digital Image Correlation: Background and Developments since the 2013 W M Murray Lecture. Exp. Mech. 2017, 57, 1–30. [Google Scholar] [CrossRef]
- Hild, F.; Roux, S. Comparison of Local and Global Approaches to Digital Image Correlation. Exp. Mech. 2012, 52, 1503–1519. [Google Scholar] [CrossRef]
- Wang, B.; Pan, B. Subset-based local vs. finite element-based global digital image correlation: A comparison study. Theor. Appl. Mech. Lett. 2016, 6, 200–208. [Google Scholar] [CrossRef]
- Besnard, G.; Hild, F.; Roux, S. “Finite-element” displacement fields analysis from digital images: Application to Portevin-Le Châtelier bands. Exp. Mech. 2006, 46, 789–803. [Google Scholar] [CrossRef]
- Sun, Y.; Pang, J.H.; Wong, C.K.; Su, F. Finite element formulation for a digital image correlation method. Appl. Opt. 2005, 44, 7357–7363. [Google Scholar] [CrossRef]
- Sutton, M.A.; Wolters, W.J.; Peters, W.H.; Ranson, W.F.; McNeill, S.R. Determination of displacements using an improved digital correlation method. Image Vis. Comput. 1983, 1, 133–139. [Google Scholar] [CrossRef]
- Sutton, M.A.; Cheng, M.; Peters, W.H.; Chao, Y.J.; McNeill, S.R. Application of an optimized digital correlation method to planar deformation analysis. Image Vis. Comput. 1986, 4, 143–150. [Google Scholar] [CrossRef]
- Reu, P.L.; Toussaint, E.; Jones, E.; Bruck, H.A.; Iadicola, M.; Balcaen, R.; Turner, D.Z.; Siebert, T.; Lava, P.; Simonsen, M. DIC Challenge: Developing Images and Guidelines for Evaluating Accuracy and Resolution of 2D Analyses. Exp. Mech. 2018, 58, 1067–1099. [Google Scholar] [CrossRef]
- Rossi, M.; Lava, P.; Pierron, F.; Debruyne, D.; Sasso, M. Effect of DIC spatial resolution, noise and interpolation error on identification results with the VFM. Strain 2015, 51, 206–222. [Google Scholar] [CrossRef]
- Jin, H.; Bruck, H.A. Theoretical development for pointwise digital image correlation. Opt. Eng. 2005, 44, 067003. [Google Scholar] [CrossRef]
- Réthoré, J.; Hild, F.; Roux, S. Shear-band capturing using a multiscale extended digital image correlation technique. Comput. Methods Appl. Mech. Eng. 2007, 196, 5016–5030. [Google Scholar] [CrossRef]
- Réthoré, J.; Hild, F.; Roux, S. Extended digital image correlation with crack shape optimization. Int. J. Numer. Methods Eng. 2008, 73, 248–272. [Google Scholar] [CrossRef]
- Poissant, J.; Barthelat, F. A novel “subset splitting” procedure for digital image correlation on discontinuous displacement fields. Exp. Mech. 2010, 50, 353–364. [Google Scholar] [CrossRef]
- Nguyen, T.L.; Hall, S.A.; Vacher, P.; Viggiani, G. Fracture mechanisms in soft rock: Identification and quantification of evolving displacement discontinuities by extended digital image correlation. Tectonophysics 2011, 503, 117–128. [Google Scholar] [CrossRef]
- Tomicevic, Z.; Hild, F.; Roux, S.; Tomicevic, Z.; Hild, F.; Roux, S.; Image, M.D. Mechanics-Aided Digital Image Correlation. J. Strain Anal. Eng. Des. 2013, 48, 330–343. [Google Scholar] [CrossRef]
- Hassan, G.M.; Dyskin, A.; Macnish, C.; Pasternak, E.; Shufrin, I. Discontinuous Digital Image Correlation to reconstruct displacement and strain fields with discontinuities: Dislocation approach. Eng. Fract. Mech. 2018, 189, 273–292. [Google Scholar] [CrossRef]
- Hassan, G.M.; Macnish, C.; Dyskin, A. Extending Digital Image Correlation to Reconstruct Displacement and Strain Fields around Discontinuities in Geomechanical Structures under Deformation. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 5–9 January 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 710–717. [Google Scholar]
- Rubino, V.; Lapusta, N.; Rosakis, A.J.; Leprince, S.; Avouac, J.P. Static Laboratory Earthquake Measurements with the Digital Image Correlation Method. Exp. Mech. 2015, 55, 77–94. [Google Scholar] [CrossRef]
- Xia, K.; Rosakis, A.J.; Kanamori, H. Laboratory Earthquakes: The Sub-Rayleigh-to-Supershear. Science 2004, 303, 1859–1861. [Google Scholar] [CrossRef]
- Lu, X.; Lapusta, N.; Rosakis, A.J. Pulse-like and crack-like ruptures in experiments mimicking crustal earthquakes. Proc. Natl. Acad. Sci. USA 2007, 104, 18931–18936. [Google Scholar] [CrossRef] [PubMed]
- Rosakis, A.J.; Xia, K.; Lykotrafitis, G.; Kanamori, H. Dynamic shear rupture in frictional interfaces: Speeds, directionality, and modes. Treatise Geophys. 2007, 4, 153–192. [Google Scholar]
- Gabuchian, V.; Rosakis, A.J.; Bhat, H.S.; Madariaga, R.; Kanamori, H. Experimental evidence that thrust earthquake ruptures might open faults. Nature 2017, 545, 336–339. [Google Scholar] [CrossRef]
- Mello, M.; Bhat, H.S.; Rosakis, A.J.; Kanamori, H. Identifying the unique ground motion signatures of supershear earthquakes: Theory and experiments. Tectonophysics 2010, 493, 297–326. [Google Scholar] [CrossRef]
- Mello, M.; Bhat, H.S.; Rosakis, A.J.; Kanamori, H. Reproducing the supershear portion of the 2002 Denali earthquake rupture in laboratory. Earth Planet. Sci. Lett. 2014, 387, 89–96. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J. The Staircasing Effect in Neighborhood Filters and its Solution. IEEE Trans. Image Process. 2006, 15, 1499–1505. [Google Scholar] [CrossRef] [PubMed]
- Buades, A.; Coll, B.; Morel, J. Nonlocal Image and Movie Denoising. Int. J. Comput. Vis. 2008, 76, 123–139. [Google Scholar] [CrossRef]
- Rosakis, A.; Samudrala, O.; Coker, D. Cracks faster than the shear wave speed. Science 1999, 284, 1337–1340. [Google Scholar] [CrossRef] [PubMed]
- Rosakis, A.J. Intersonic shear cracks and fault ruptures. Adv. Phys. 2002, 51, 1189–1257. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tal, Y.; Rubino, V.; Rosakis, A.J.; Lapusta, N. Enhanced Digital Image Correlation Analysis of Ruptures with Enforced Traction Continuity Conditions Across Interfaces. Appl. Sci. 2019, 9, 1625. https://doi.org/10.3390/app9081625
Tal Y, Rubino V, Rosakis AJ, Lapusta N. Enhanced Digital Image Correlation Analysis of Ruptures with Enforced Traction Continuity Conditions Across Interfaces. Applied Sciences. 2019; 9(8):1625. https://doi.org/10.3390/app9081625
Chicago/Turabian StyleTal, Yuval, Vito Rubino, Ares J. Rosakis, and Nadia Lapusta. 2019. "Enhanced Digital Image Correlation Analysis of Ruptures with Enforced Traction Continuity Conditions Across Interfaces" Applied Sciences 9, no. 8: 1625. https://doi.org/10.3390/app9081625
APA StyleTal, Y., Rubino, V., Rosakis, A. J., & Lapusta, N. (2019). Enhanced Digital Image Correlation Analysis of Ruptures with Enforced Traction Continuity Conditions Across Interfaces. Applied Sciences, 9(8), 1625. https://doi.org/10.3390/app9081625




