Wind Loads on a Solar Panel at High Tilt Angles
Abstract
Featured Application
Abstract
1. Introduction
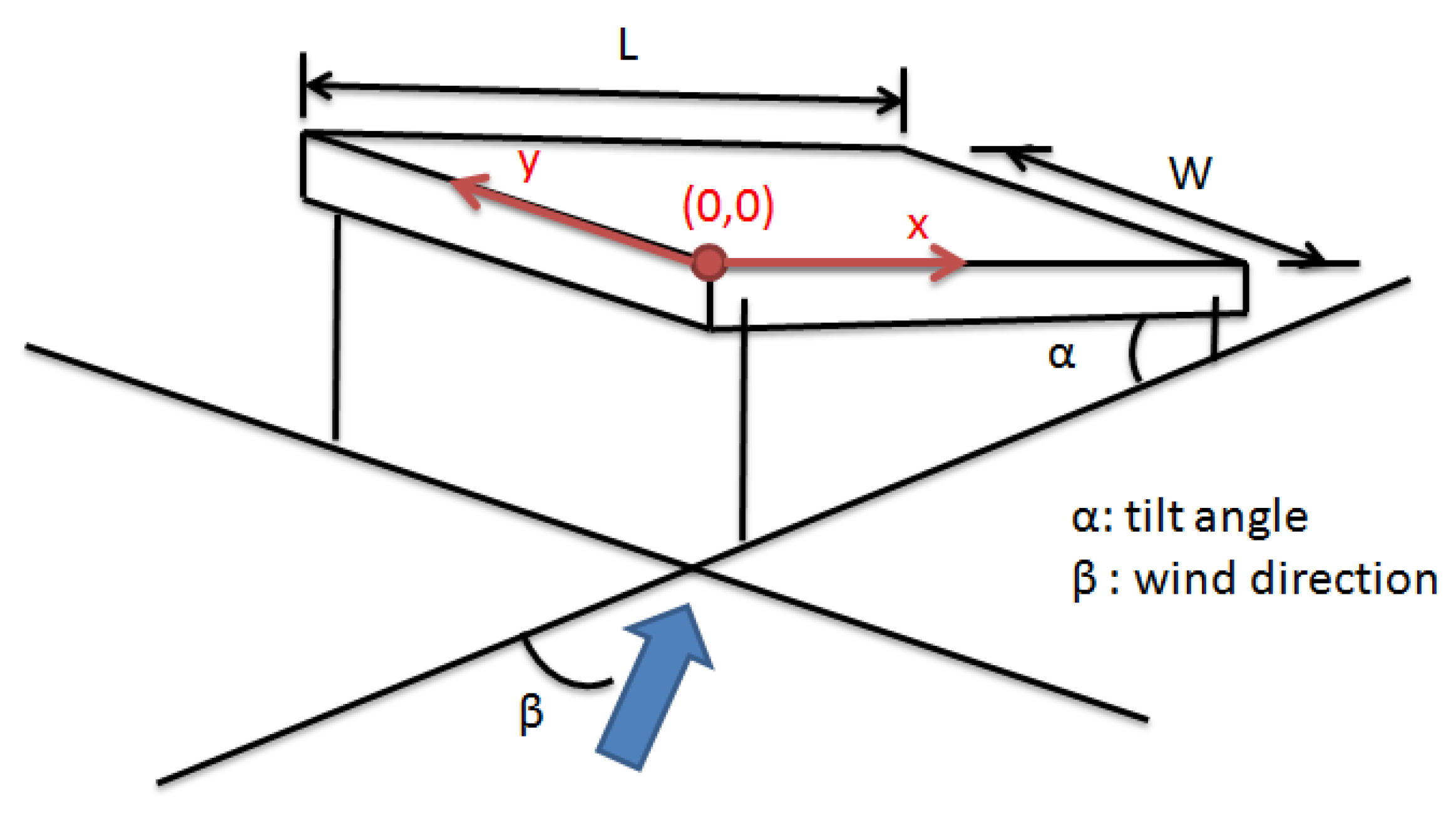
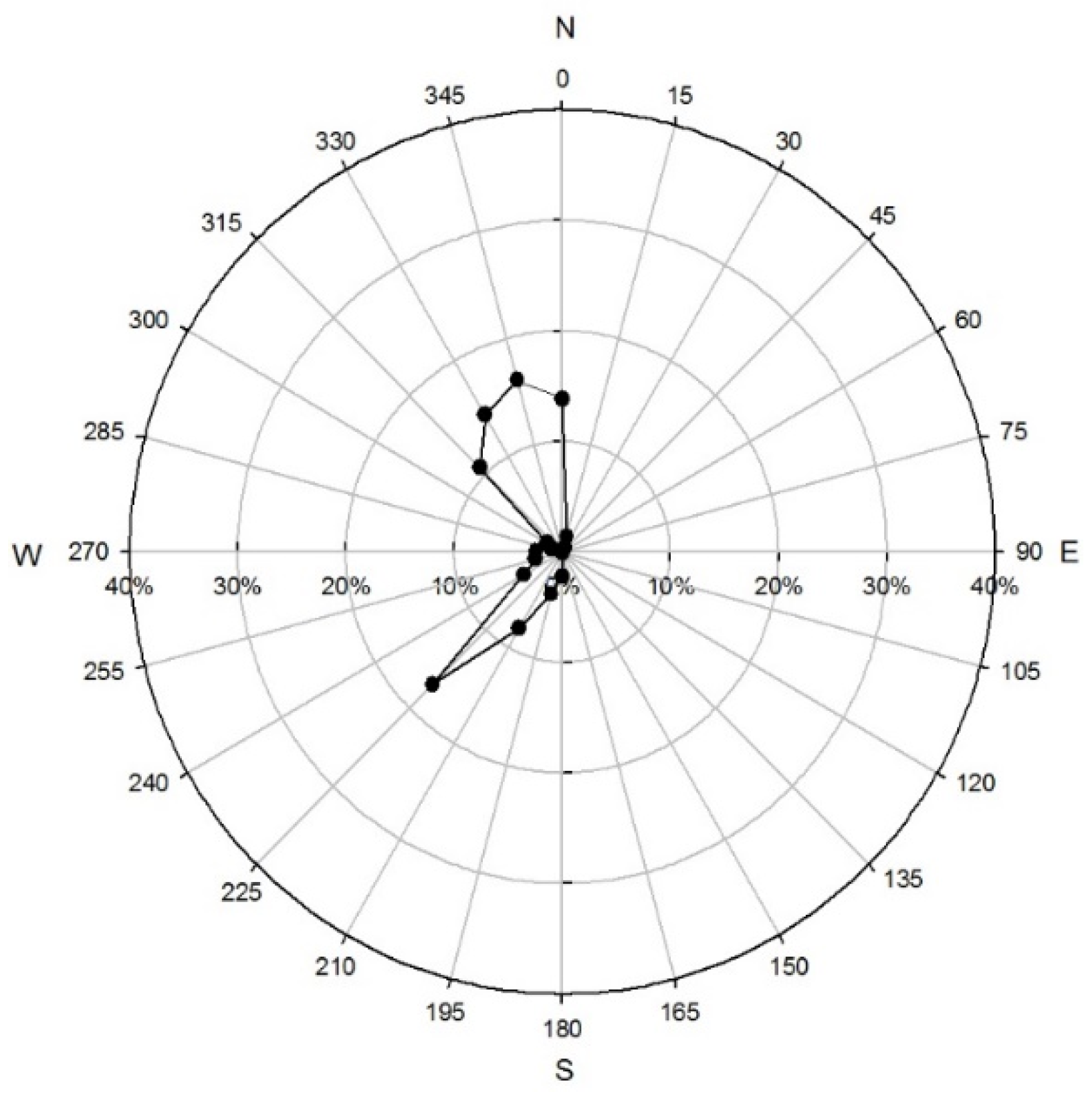
2. Experimental Setup
3. Results and Discussion
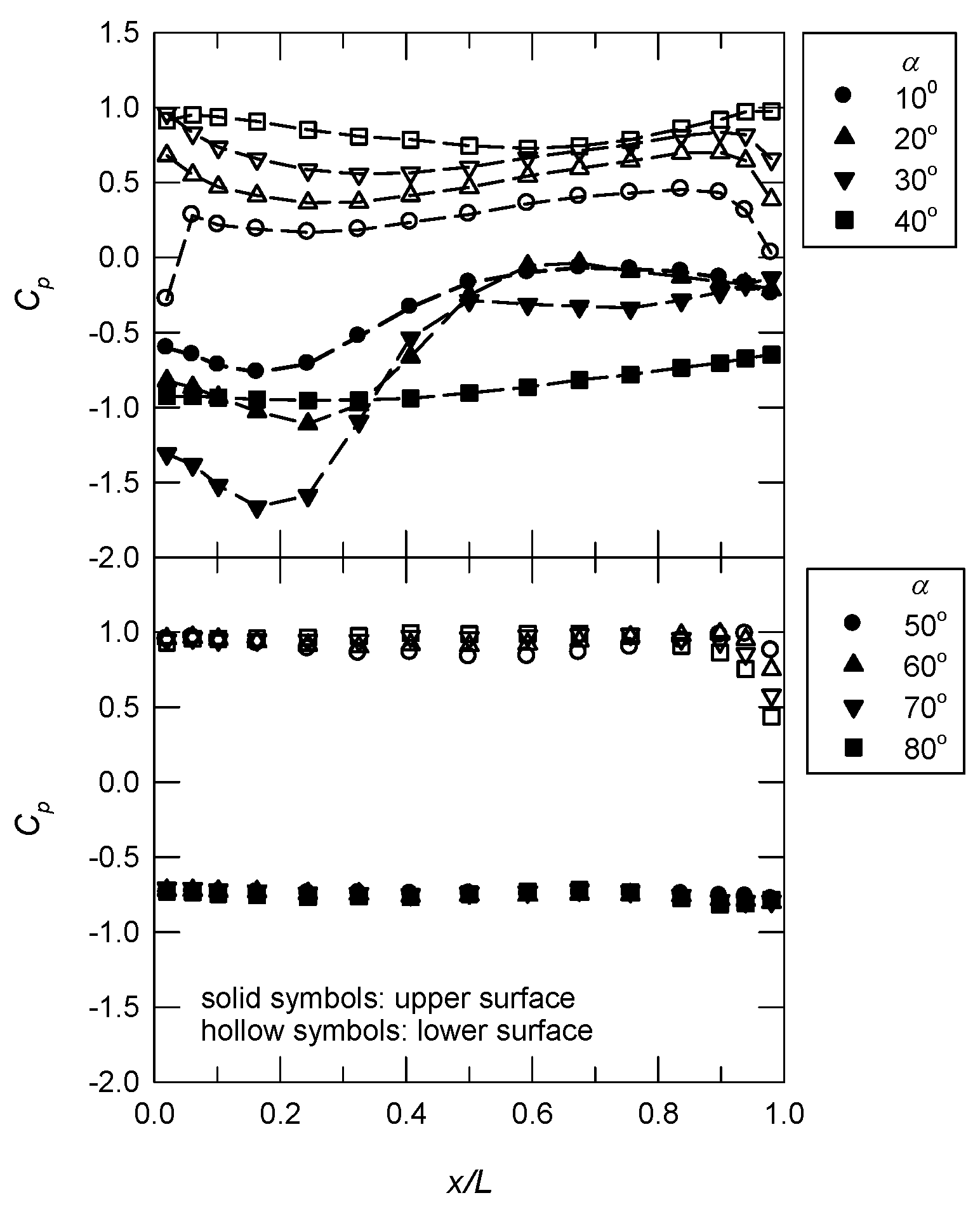
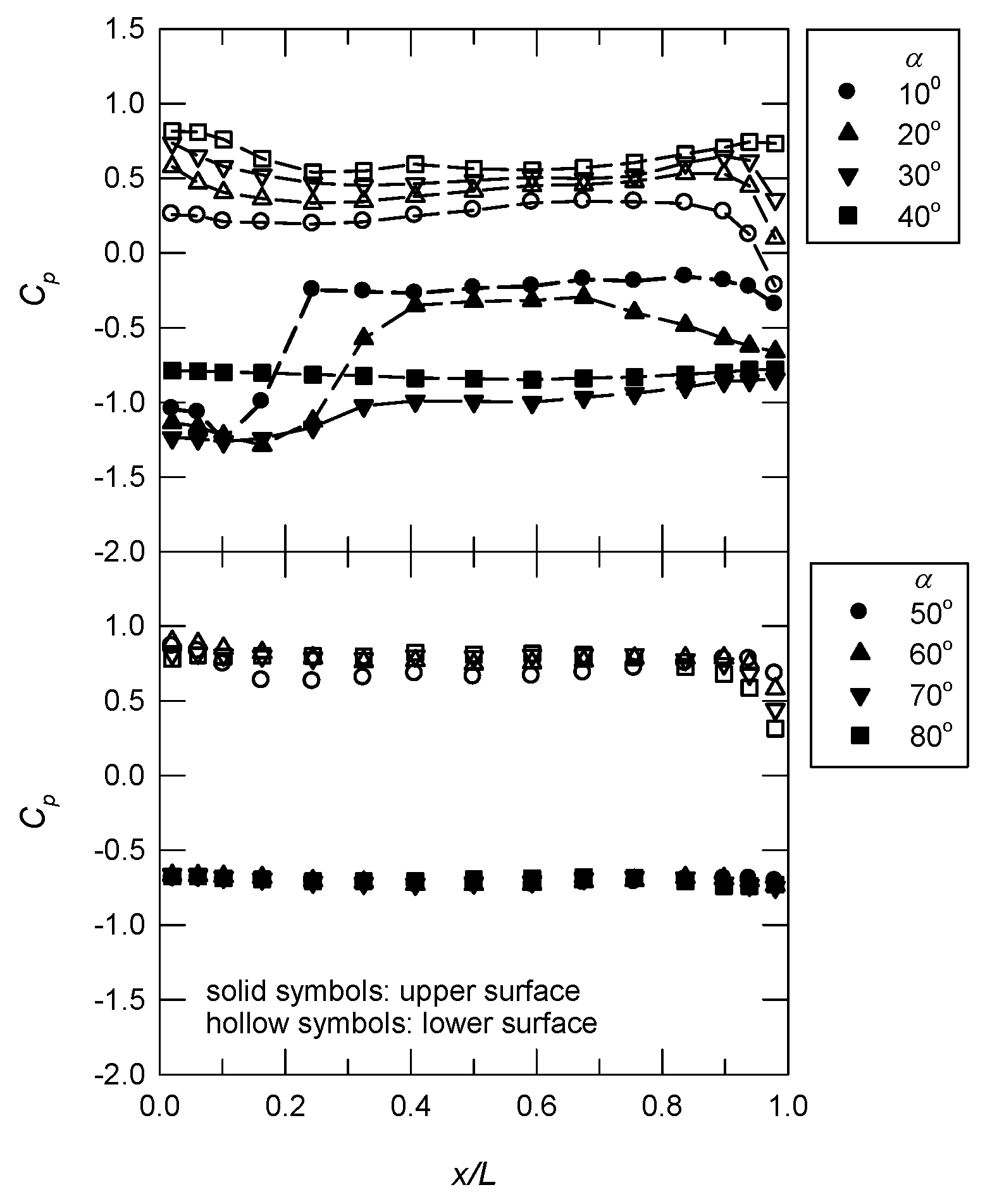
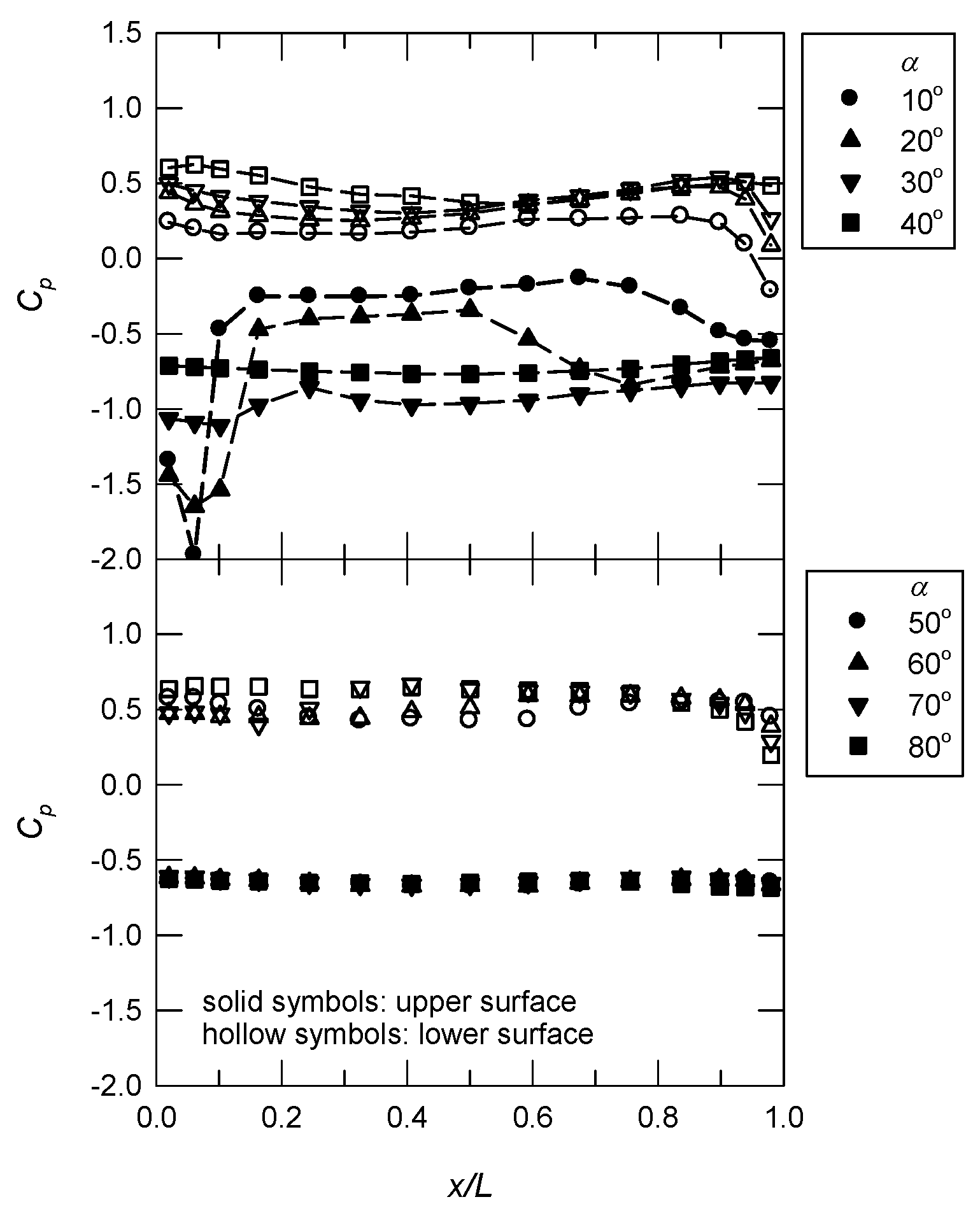
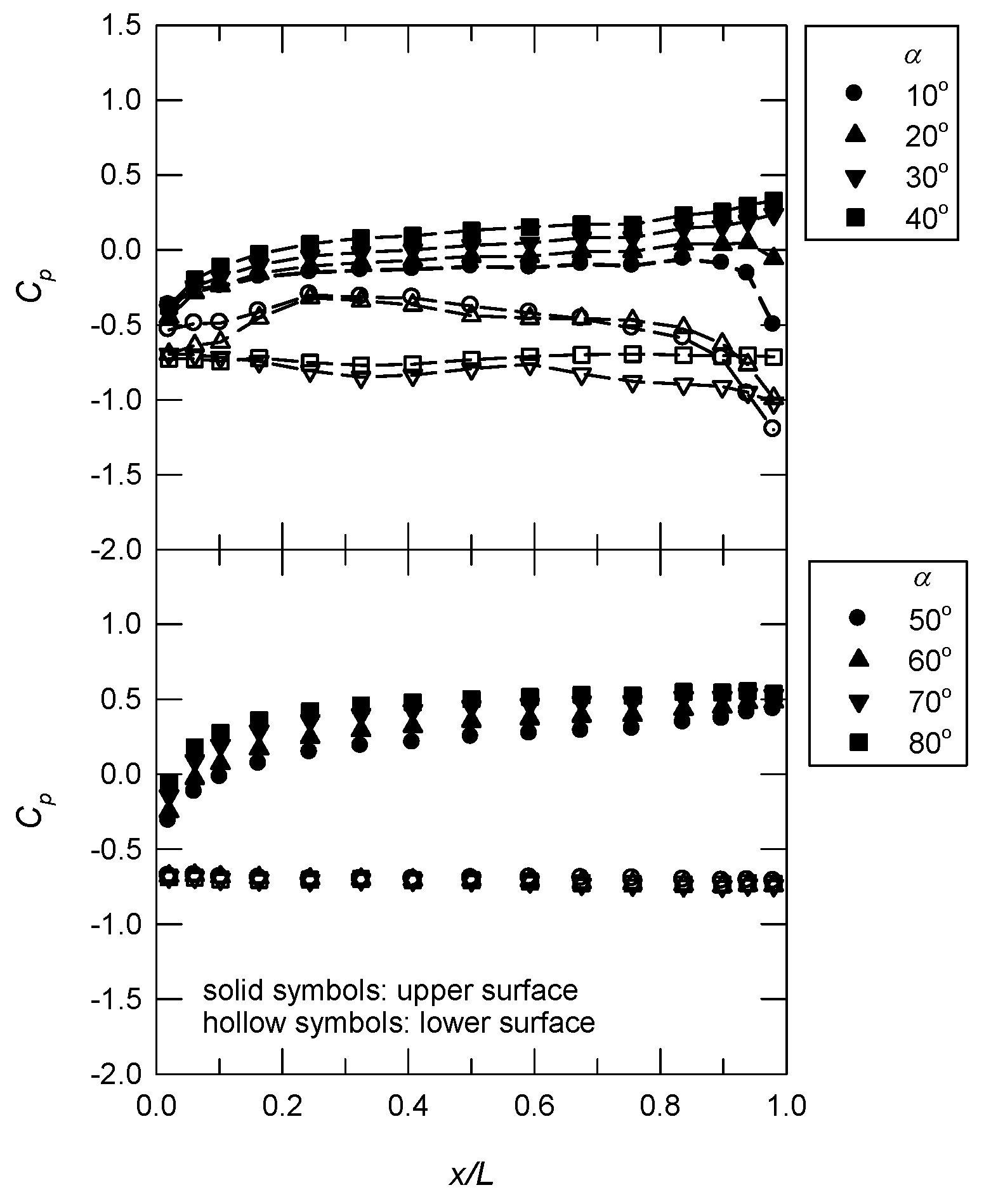
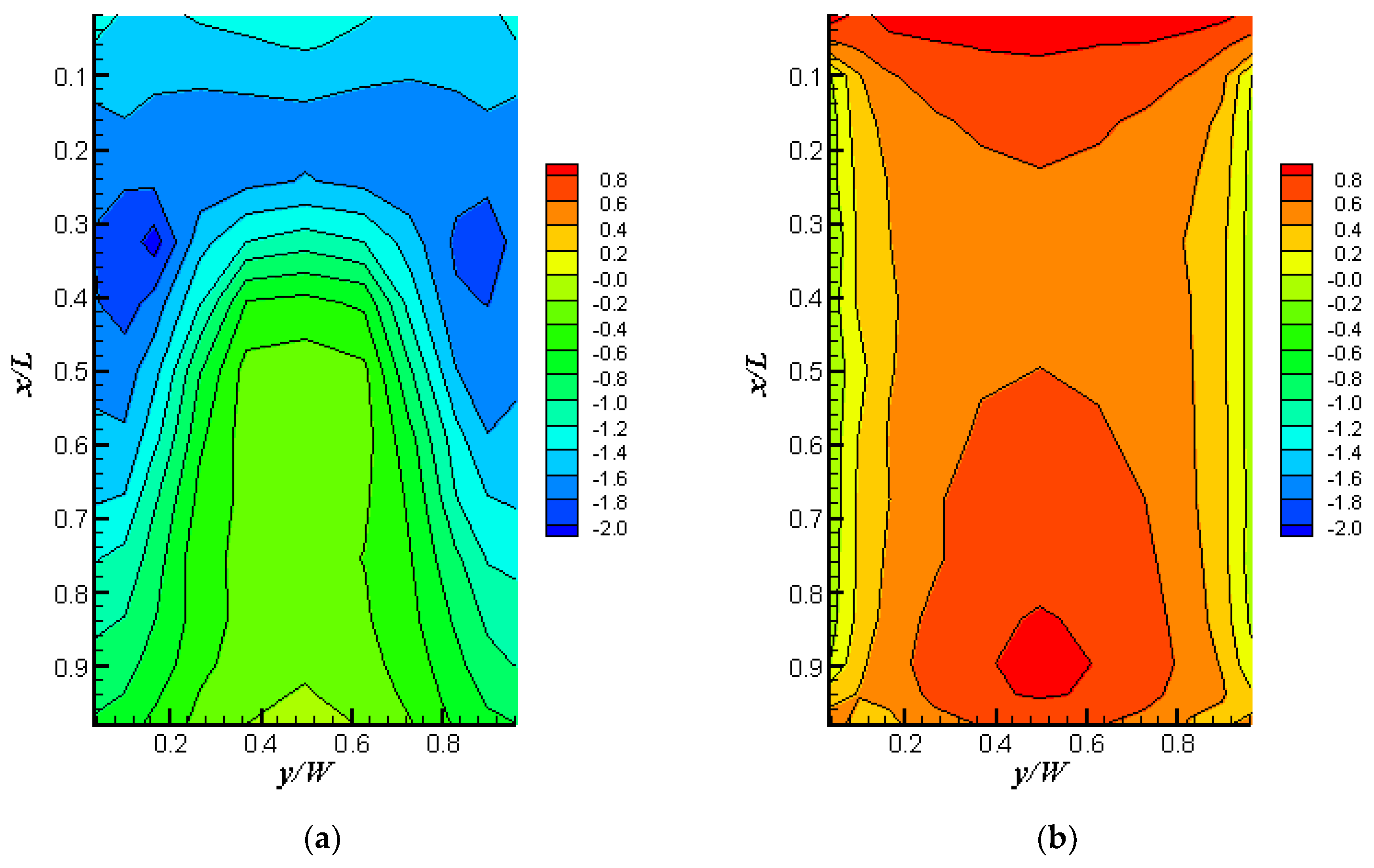
3.1. Longitudinal Pressure Distributions
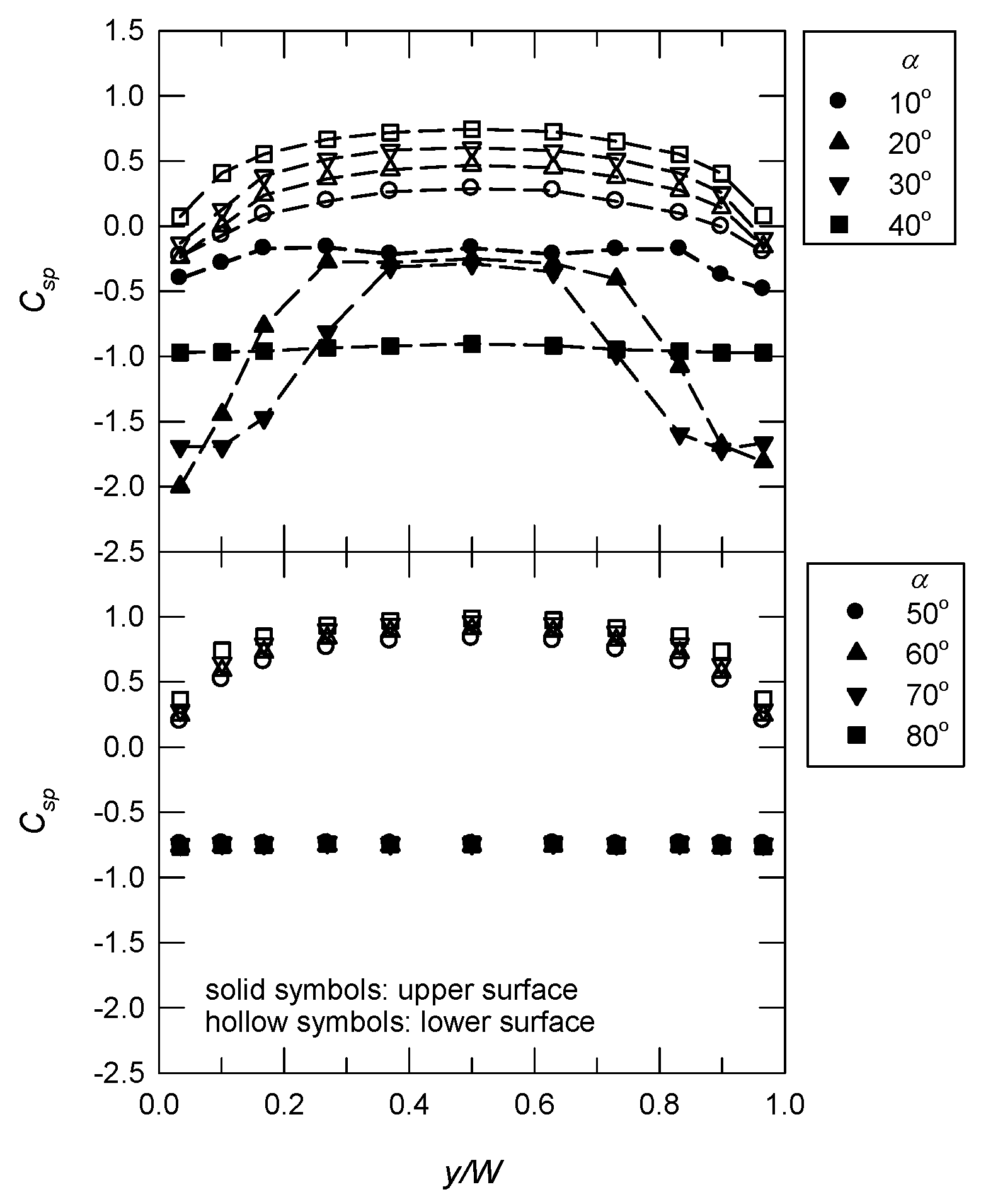
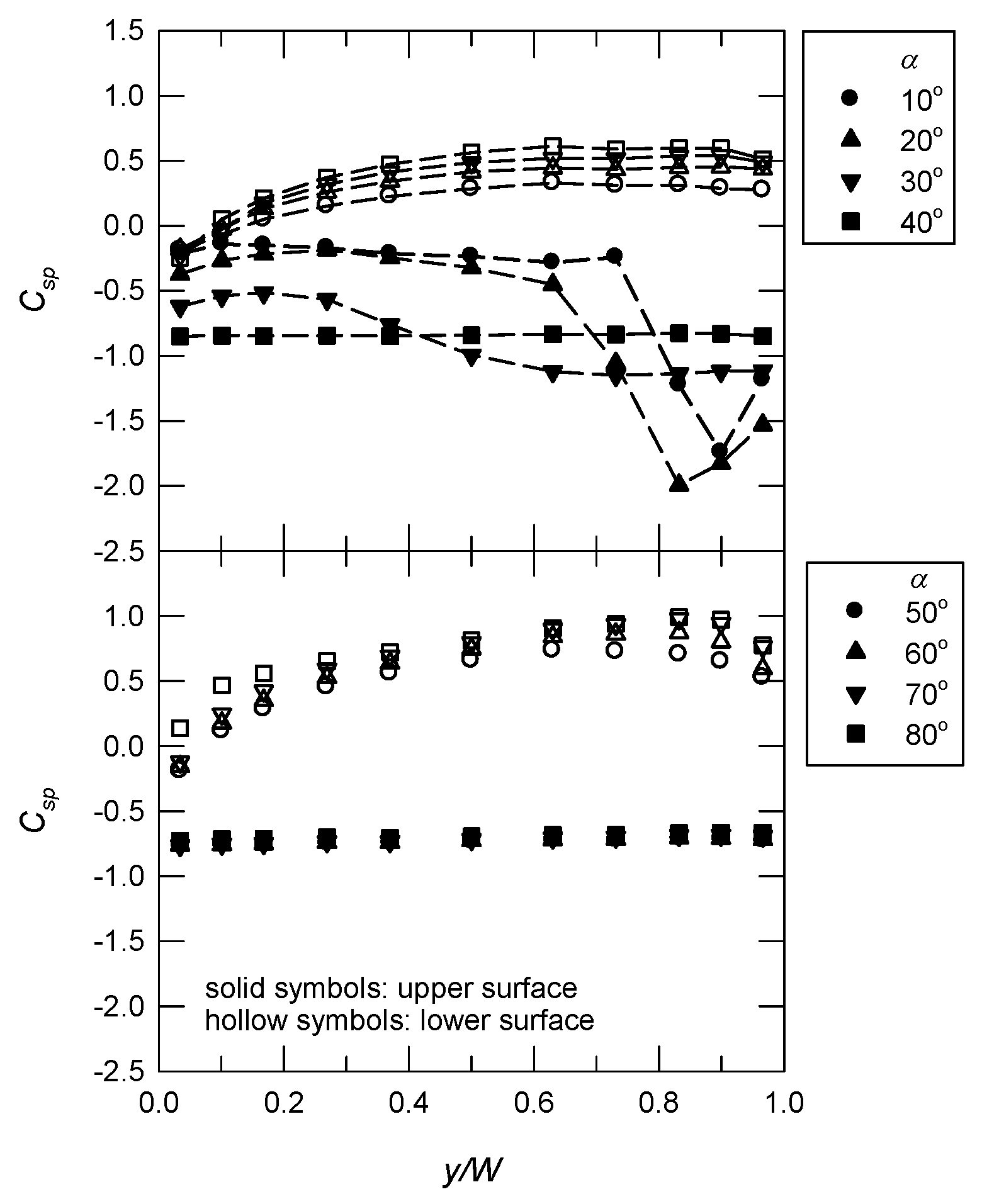
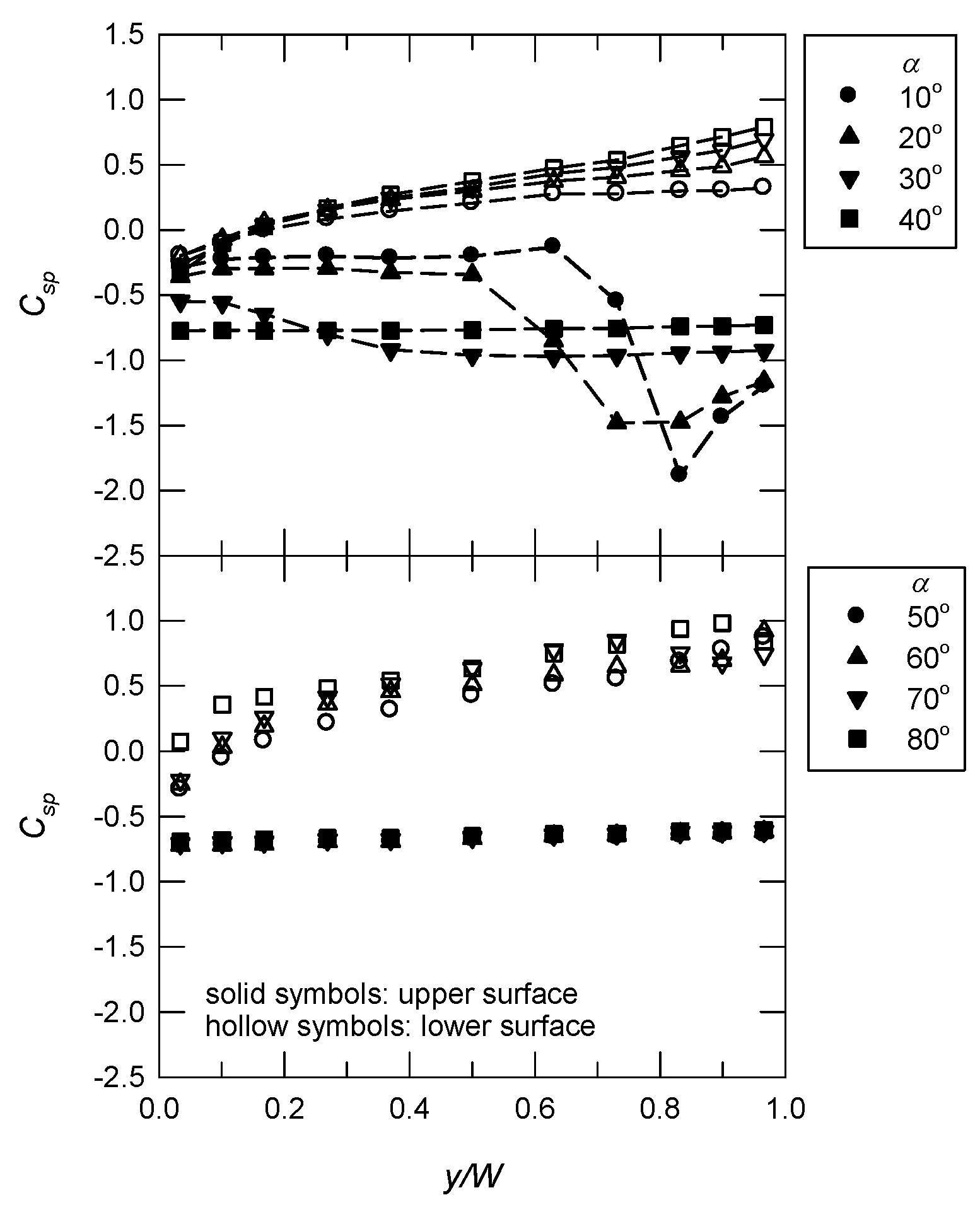
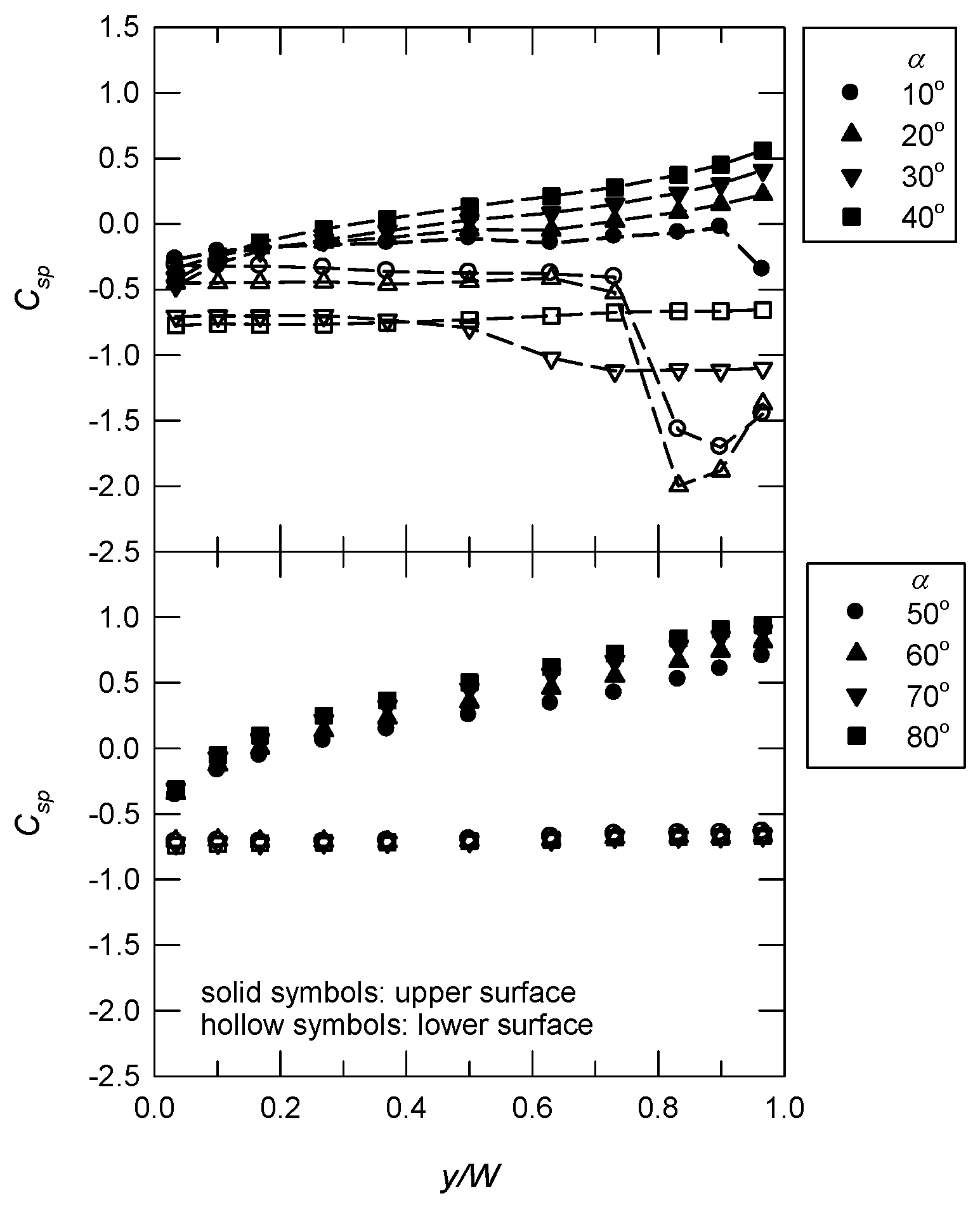
3.2. Spanwise Pressure Distributions
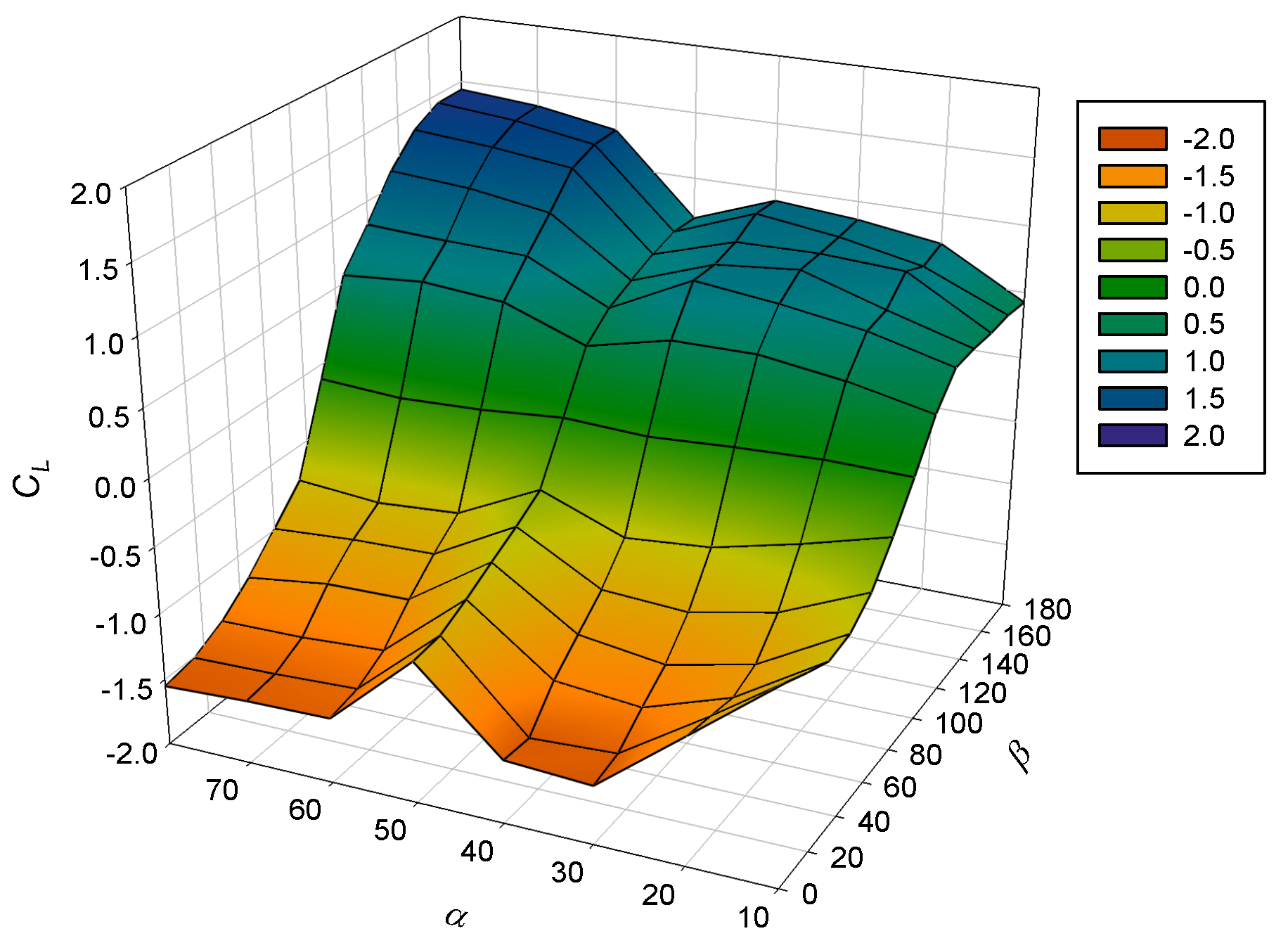
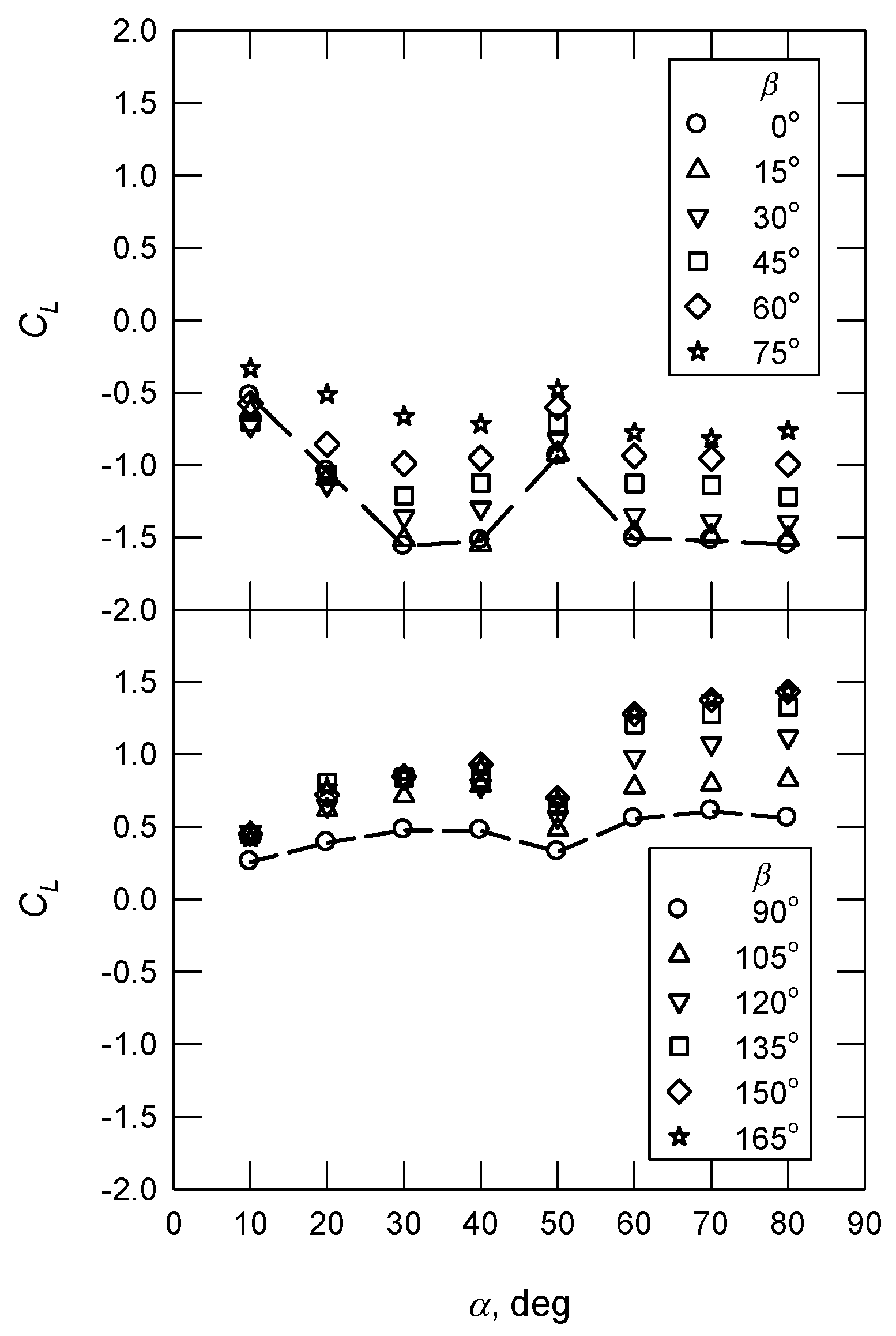
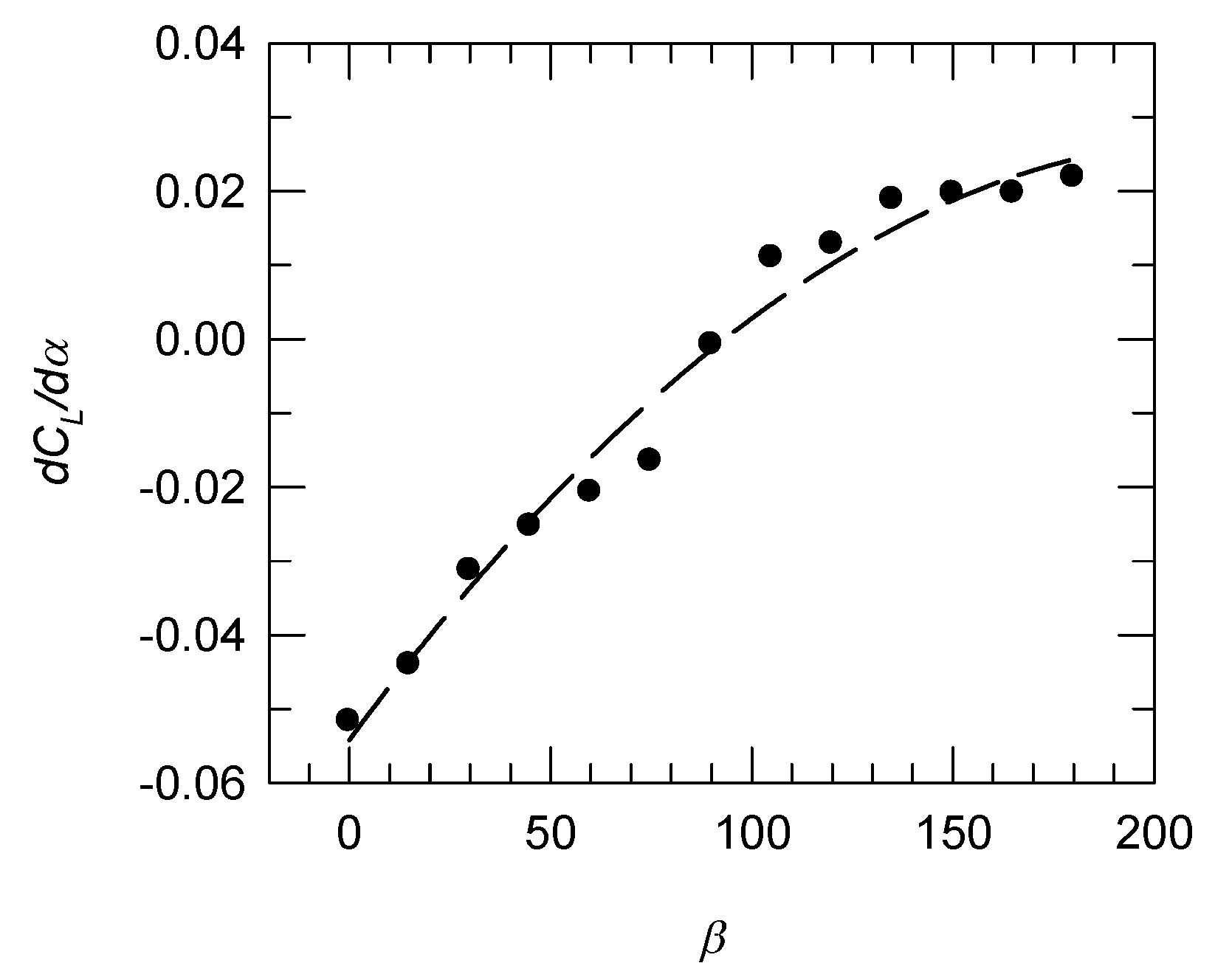
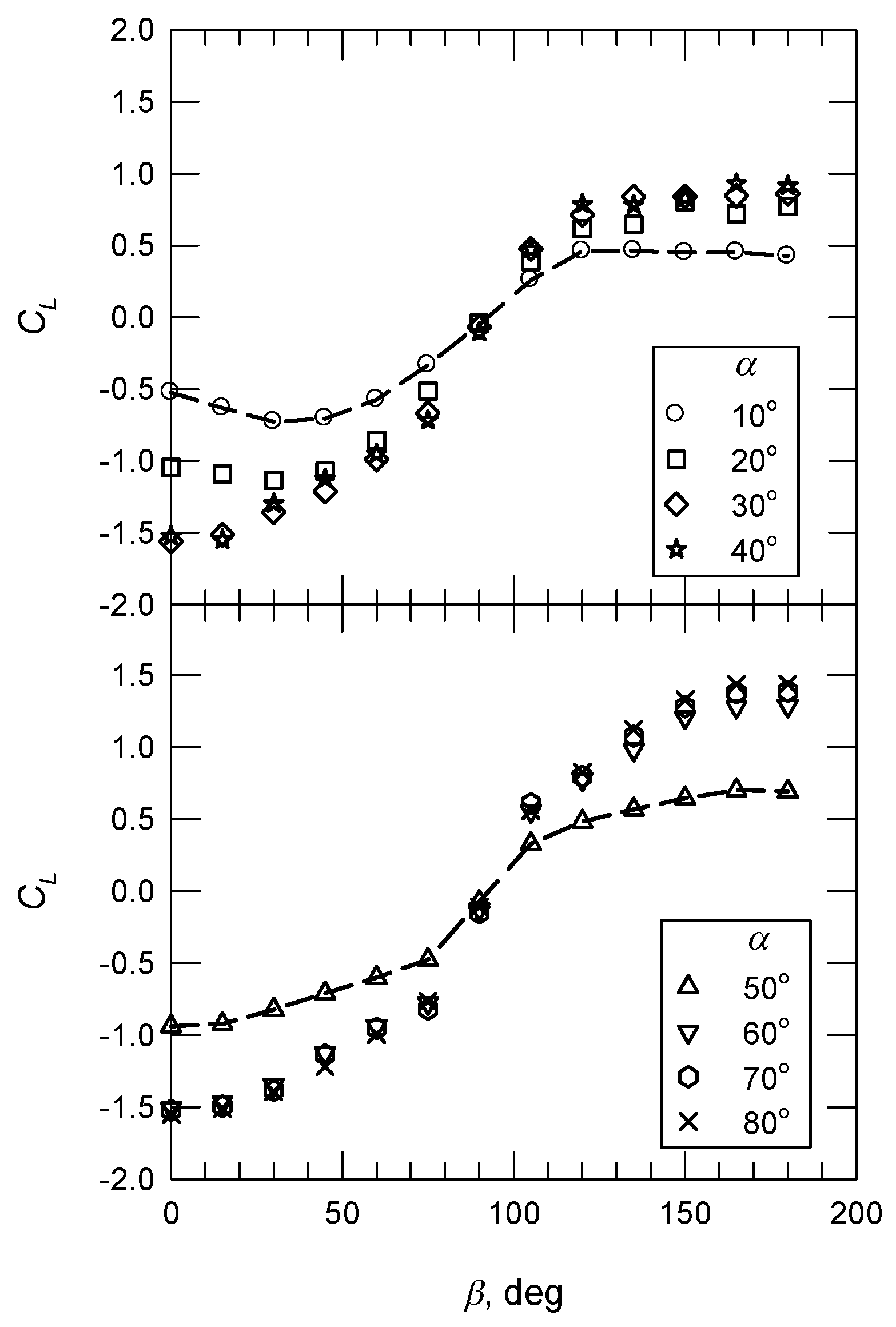
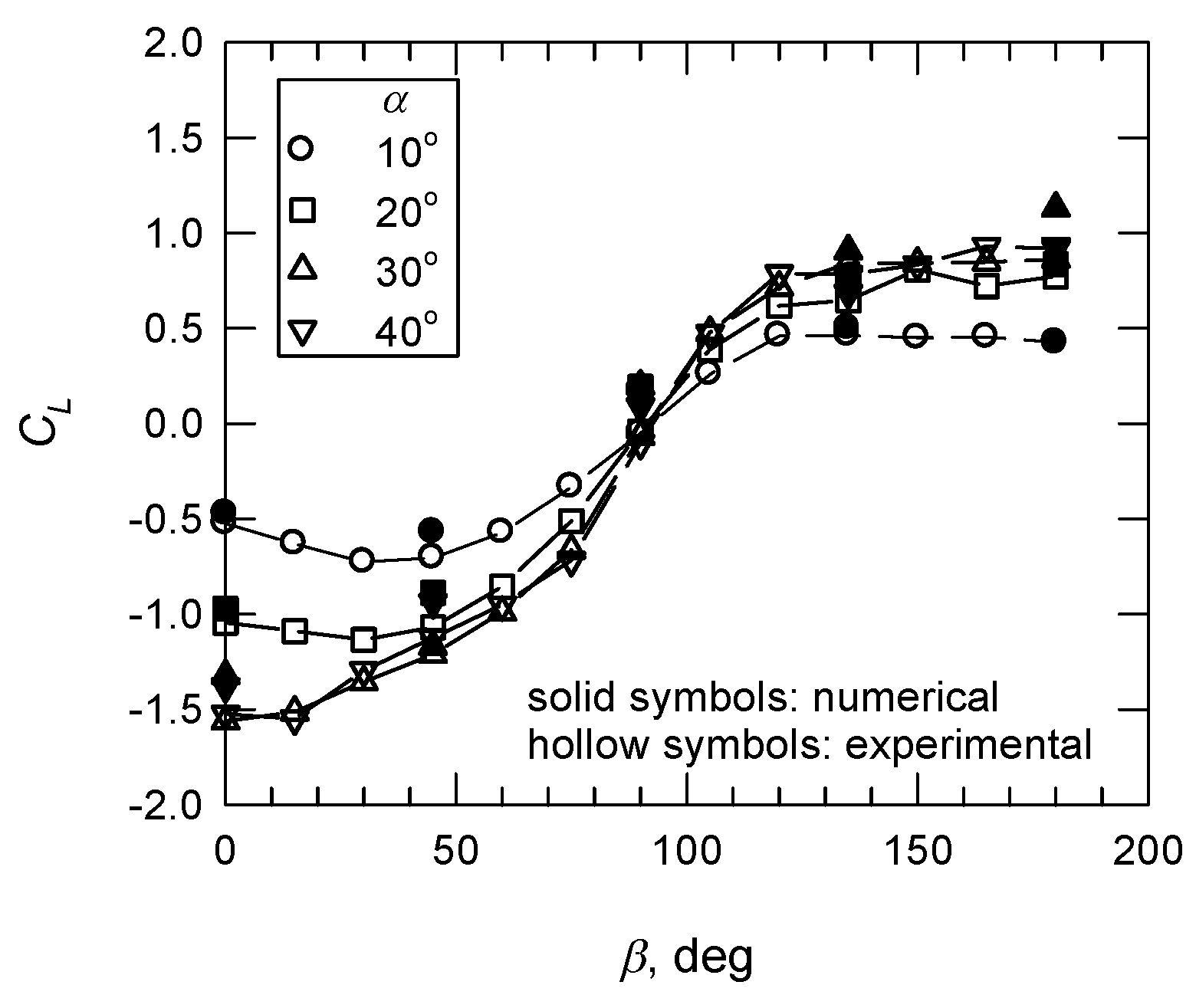
3.3. The Uplift Coefficient
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| CL | uplift coefficient |
| Cp | pressure coefficient in the longitudinal direction, (p–p∞)/q |
| Cp,low | pressure coefficient on the lower surface |
| Csp | pressure coefficient in the spanwise direction |
| Cp,up | pressure coefficient on the upper surface |
| L | length of tilted panel |
| p∞ | freestream static pressure |
| q | dynamic pressure |
| W | width of tilted panel |
| x | coordinate in the longitudinal direction |
| y | coordinate in the spanwise direction |
| α | angle of tilt |
| β | wind incidence angle |
| ΔCp | differential pressure, Cp,up − Cp,low |
References
- Mauthner, F.; Weiss, W.; Spörk-Dür, M. Solar Heat Worldwide; AEE-Institute for Sustainable Technologies: Gleisdorf, Austria, 2018. [Google Scholar]
- Trapani, K.; Santafe, M.R. A review of floating photovoltaics installations: 2007–2013. Prog. Photovolt. 2015, 23, 524–532. [Google Scholar] [CrossRef]
- Trapani, K.; Millar, D.L.; Smith, H.C. Novel offshore application of photovoltaics in comparison to conventional marine renewable energy technologies. Renew. Energy 2013, 50, 879–888. [Google Scholar] [CrossRef]
- Sahu, A.; Yadav, N.; Sudhakar, K. Floating photovoltaic power plant: A review. Renew. Sustain. Rev. 2016, 66, 815–824. [Google Scholar]
- Naeiji, A.; Raji, F.; Zisis, I. Wind loads on residential scale rooftop photovoltaic panels. J. Wind. Eng. Ind. Aerodyn. 2017, 168, 228–246. [Google Scholar] [CrossRef]
- Cao, J.; Yoshida, A.; Saha, P.K.; Tamura, Y. Wind loading characteristics of solar arrays mounted on flat roofs. J. Wind. Eng. Ind. Aerodyn. 2013, 123, 214–225. [Google Scholar] [CrossRef]
- Kopp, G.A.; Banks, D. Use of the Wind Tunnel Test Method for Obtaining Design Wind Loads on Roof-Mounted Solar Arrays. J. Struct. Eng. 2013, 139, 284–287. [Google Scholar] [CrossRef]
- Chung, K.-M.; Chang, K.-C.; Chou, C.-C. Wind loads on residential and large-scale solar collector models. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 59–64. [Google Scholar] [CrossRef]
- Stathopoulos, T.; Zisis, I.; Xypnitou, E. Local and overall wind pressure and force coefficients for solar panels. J. Wind. Eng. Ind. Aerodyn. 2014, 125, 195–206. [Google Scholar] [CrossRef]
- Chung, K.-M.; Chou, C.-C.; Chang, K.-C.; Chen, Y.-J. Effect of a vertical guide plate on the wind loading of an inclined flat plate. Wind. Struct. Int. J. 2013, 17, 537–552. [Google Scholar] [CrossRef]
- Aly, A.M. On the evaluation of wind loads on solar panels: The scale issue. Sol. Energy 2016, 135, 423–434. [Google Scholar] [CrossRef]
- Chou, C.-C.; Chung, K.-M.; Chang, K.-C. Wind Loads of Solar Water Heaters: Wind Incidence Effect. J. Aerodyn. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
- Chu, C.-R.; Tsao, S.-J. Aerodynamic loading of solar trackers on flat-roofed buildings. J. Wind. Eng. Ind. Aerodyn. 2018, 175, 202–212. [Google Scholar] [CrossRef]
- Jubayer, C.M.; Hangan, H. Numerical simulation of wind effects on a stand-alone ground mounted photovoltaic (PV) system. J. Wind. Eng. Ind. Aerodyn. 2014, 134, 56–64. [Google Scholar] [CrossRef]
- Radu, A.; Axinte, E. Wind forces on structures supporting solar collectors. J. Wind. Eng. Ind. Aerodyn. 1989, 32, 93–100. [Google Scholar] [CrossRef]
- Warsido, W.P.; Bitsuamlak, G.T.; Barata, J.; Chowdhury, A.G. Influence of spacing parameters on the wind loading of solar array. J. Fluids Struct. 2014, 48, 295–315. [Google Scholar] [CrossRef]
- Guo, M.; Zang, H.; Gao, S.; Chen, T.; Xiao, J.; Cheng, L.; Wei, Z.; Sun, G. Optimal tilt angle and orientation on photovoltaic modules using HS algorithm in different climates in China. Appl. Sci. 2017, 7, 1028. [Google Scholar] [CrossRef]
- Lau, K.; Tan, C.; Yatim, A. Effects of ambient temperatures, tilt angles, and orientations on hybrid photovoltaic/diesel systems under equatorial climates. Renew. Sustain. Rev. 2018, 81, 2625–2636. [Google Scholar] [CrossRef]
- Castellano, N.N.; Parra, J.A.G.; Valls-Guirado, J.; Manzano-Agugliaro, F. Optimal displacement of photovoltaic array’s rows using a novel shading model. Appl. Energy 2015, 144, 1–9. [Google Scholar] [CrossRef]
- ASCE 7-10. Minimum Design Loads for Buildings and Other Structures; American Society of Civil Engineers: Reston, VA, USA, 2010. [Google Scholar]
- Bender, W.; Waytuck, D.; Wang, S.; Reed, D. In situ measurement of wind pressure loadings on pedestal style rooftop photovoltaic panels. Eng. Struct. 2018, 163, 281–293. [Google Scholar] [CrossRef]
- Chung, K.-M.; Chen, Y.-J. Effect of High Blockage Ratios on Surface Pressures of an Inclined Flat Plate. J. Eng. Arch. 2016, 4, 1–16. [Google Scholar] [CrossRef][Green Version]
- Central Weather Bureau (CWB), Ministry of Transportation and Communication. Available online: https://www.cwb.gov. tw/V7/climate/marine_stat/wave.htm (accessed on 22 May 2018).
- Chung, K.M.; Chou, C.C.; Chang, K.C.; Chen, Y.J. Wind loads on a residential solar water heater. J. Chin. Inst. Eng. 2013, 36, 870–877. [Google Scholar] [CrossRef]
- Chung, K.; Chang, K.-C.; Liu, Y. Reduction of wind uplift of a solar collector model. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1294–1306. [Google Scholar] [CrossRef]
- Irwin, H.; Cooper, K.; Girard, R. Correction of distortion effects caused by tubing systems in measurements of fluctuating pressures. J. Wind Eng. Ind. Aerodyn. 1979, 5, 93–107. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new κ-ε eddy-viscosity model for high Reynolds number turbulent flows–Model development and validation. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chou, C.-C.; Chung, P.-H.; Yang, R.-Y. Wind Loads on a Solar Panel at High Tilt Angles. Appl. Sci. 2019, 9, 1594. https://doi.org/10.3390/app9081594
Chou C-C, Chung P-H, Yang R-Y. Wind Loads on a Solar Panel at High Tilt Angles. Applied Sciences. 2019; 9(8):1594. https://doi.org/10.3390/app9081594
Chicago/Turabian StyleChou, Chin-Cheng, Ping-Han Chung, and Ray-Yeng Yang. 2019. "Wind Loads on a Solar Panel at High Tilt Angles" Applied Sciences 9, no. 8: 1594. https://doi.org/10.3390/app9081594
APA StyleChou, C.-C., Chung, P.-H., & Yang, R.-Y. (2019). Wind Loads on a Solar Panel at High Tilt Angles. Applied Sciences, 9(8), 1594. https://doi.org/10.3390/app9081594





