Size-Dependent Free Vibrations of FG Polymer Composite Curved Nanobeams Reinforced with Graphene Nanoplatelets Resting on Pasternak Foundations
Abstract
1. Introduction
2. Effective Material Properties and Constitutive Relations
3. Solution Procedure
4. Numerical Results and Discussion
Comparison and Validation
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
References
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.Z.; Koratkar, N. Enhanced Mechanical Properties ofnanocomposites at low graphene content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Wang, Y.; Huang, Y.; Ma, Y.; Liu, Z.; Cai, J. Letter to the Editor Electromagnetic interference shielding of graphene/epoxy composites. Carbon N. Y. 2008, 47, 922–925. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y.; Lin, F. Nonlinear vibration of functionally graded graphene-reinforced composite laminated plates in thermal environments. Comput. Methods Appl. Mech. Eng. 2017, 319, 175–193. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, C.; Zhao, Z.; Yang, J. Buckling of Graphene Platelet Reinforced Composite Cylindrical Shell with Cutout. Int. J. Struct. Stab. Dyn. 2018, 18, 1850040. [Google Scholar] [CrossRef]
- Song, M.; Kitipornchai, S.; Yang, J. Free and forced vibrations of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Struct. 2017, 159, 579–588. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Eng. Struct. 2017, 140, 110–119. [Google Scholar] [CrossRef]
- Sahmani, S.; Aghdam, M.M. Nonlocal strain gradient beam model for nonlinear vibration of prebuckled and postbuckled multilayer functionally graded GPLRC nanobeams. Compos. Struct. 2017, 179, 77–88. [Google Scholar] [CrossRef]
- Zhao, Z.; Feng, C.; Wang, Y.; Yang, J. Bending and vibration analysis of functionally graded trapezoidal nanocomposite plates reinforced with graphene nanoplatelets (GPLs). Compos. Struct. 2017, 180, 799–808. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Nonlinear vibration and postbuckling of functionally graded graphene reinforced porous nanocomposite beams. Compos. Sci. Technol. 2017, 142, 235–245. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, C.; Zhao, Z.; Yang, J. Eigenvalue buckling of functionally graded cylindrical shells reinforced with graphene platelets (GPL). Compos. Struct. 2017. [Google Scholar] [CrossRef]
- Yang, B.; Kitipornchai, S.; Yang, Y.F.; Yang, J. 3D thermo-mechanical bending solution of functionally graded graphene reinforced circular and annular plates. Appl. Math. Model. 2017, 49, 69–86. [Google Scholar] [CrossRef]
- Kitipornchai, S.; Chen, D.; Yang, J. Free vibration and elastic buckling of functionally graded porous beams reinforced by graphene platelets. Mater. Des. 2017, 116, 656–665. [Google Scholar] [CrossRef]
- Song, M.; Yang, J.; Kitipornchai, S.; Zhu, W. Buckling and postbuckling of biaxially compressed functionally graded multilayer graphene nanoplatelet-reinforced polymer composite plates. Int. J. Mech. Sci. 2017, 131, 345–355. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear bending of polymer nanocomposite beams reinforced with non-uniformly distributed graphene platelets (GPLs). Compos. Part B Eng. 2017, 110, 132–140. [Google Scholar] [CrossRef]
- Gholami, R.; Ansari, R. Large deflection geometrically nonlinear analysis of functionally graded multilayer graphene platelet-reinforced polymer composite rectangular plates. Compos. Struct. 2017, 180, 760–771. [Google Scholar] [CrossRef]
- Song, M.; Yang, J.; Kitipornchai, S. Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Part B Eng. 2018, 134, 106–113. [Google Scholar] [CrossRef]
- Hosseini, S.A.H.; Rahmani, O. Free vibration of shallow and deep curved FG nanobeam via nonlocal Timoshenko curved beam model. Appl. Phys. A Mater. Sci. Process 2016, 122, 169. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. A nonlocal strain gradient refined beam model for buckling analysis of size-dependent shear-deformable curved FG nanobeams. Compos. Struct. 2017, 159, 174–182. [Google Scholar] [CrossRef]
- Rahmani, O.; Hosseini, S.A.H.; Hayati, H. Frequency analysis of curved nano-sandwich structure based on a nonlocal model. Mod. Phys. Lett. B 2016, 30, 1650136. [Google Scholar] [CrossRef]
- Hayati, H.; Hosseini, S.A.; Rahmani, O. Coupled twist–bending static and dynamic behavior of a curved single-walled carbon nanotube based on nonlocal theory. Microsyst. Technol. 2016. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Thermo-electro-mechanical bending behavior of sandwich nanoplate integrated with piezoelectric face-sheets based on trigonometric plate theory. Compos. Struct. 2017, 162, 108–122. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Effect of thermo-magneto-electro-mechanical fields on the bending behaviors of a three-layered nanoplate based on sinusoidal shear-deformation plate theory. J. Sandw. Struct. Mater. 2017. [Google Scholar] [CrossRef]
- Aya, S.A.; Tufekci, E. Modeling and analysis of out-of-plane behavior of curved nanobeams based on nonlocal elasticity. Compos. Part B Eng. 2017, 119, 184–195. [Google Scholar] [CrossRef]
- Hajianmaleki, M.; Qatu, M.S. Static and vibration analyses of thick, generally laminated deep curved beams with different boundary conditions. Compos. Part B Eng. 2012, 43, 1767–1775. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Nonlocal electro-thermo-mechanical analysis of a sandwich nanoplate containing a Kelvin–Voigt viscoelastic nanoplate and two piezoelectric layers. Acta Mech. 2017, 228, 475–493. [Google Scholar] [CrossRef]
- Arefi, M. Surface effect and non-local elasticity in wave propagation of functionally graded piezoelectric nano-rod excited to applied voltage. Appl. Math. Mech. 2016, 37, 289–302. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Transient sinusoidal shear deformation formulation of a size-dependent three-layer piezo-magnetic curved nanobeam. Acta Mech. 2017, 228, 3657–3674. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Comment on the paper “Exact solution of Eringen’s nonlocal integral model for bending of Bernoulli-Euler and Timoshenko beams” by meral Tuna & Mesut Kirca. Int. J. Eng. Sci. 2016, 109, 240–242. [Google Scholar] [CrossRef]
- Barretta, R.; Feo, L.; Luciano, R.; Marotti de Sciarra, F. Application of an enhanced version of the Eringen differential model to nanotechnology. Compos. Part B Eng. 2016, 96, 274–280. [Google Scholar] [CrossRef]
- Barretta, R.; Feo, L.; Luciano, R.; Marotti de Sciarra, F.; Penna, R. Functionally graded Timoshenko nanobeams: A novel nonlocal gradient formulation. Compos. Part B Eng. 2016, 100, 208–219. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Canadija, M.; Feo, L.; Luciano, R.; Marotti de Sciarra, F. A closed-form model for torsion of nanobeams with an enhanced nonlocal formulation. Compos. Part B Eng. 2017, 108, 315–324. [Google Scholar] [CrossRef]
- Barati, M.R.; Shahverdi, H. Vibration analysis of multi-phase nanocrystalline silicon nanoplates considering the size and surface energies of nanograins/nanovoids. Int. J. Eng. Sci. 2017, 119, 128–141. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Nonlocal elasticity in nanobeams: The stress-driven integral model. Int. J. Eng. Sci. 2017, 115, 14–27. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M.; Marotti de Sciarra, F. Constitutive boundary conditions and paradoxes in nonlocal elastic nano-beams. Int. J. Mech. Sci. 2017, 121, 151–156. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. On the dynamics of imperfect shear deformable microplates. Int. J. Eng. Sci. 2018, 133, 264–283. [Google Scholar] [CrossRef]
- Barretta, R.; Ali Faghidian, S.; Marotti de Sciarra, F. Stress-driven nonlocal integral elasticity for axisymmetric nano-plates. Int. J. Eng. Sci. 2019, 136, 38–52. [Google Scholar] [CrossRef]
- Barretta, R.; Marotti de Sciarra, F. Constitutive boundary conditions for nonlocal strain gradient elastic nano-beams. Int. J. Eng. Sci. 2018, 130, 187–198. [Google Scholar] [CrossRef]
- Faghidian, S.A. Reissner stationary variational principle for nonlocal strain gradient theory of elasticity. Eur. J. Mech. A Solids 2018, 70, 115–126. [Google Scholar] [CrossRef]
- Asadi, H. Numerical simulation of the fluid-solid interaction for CNT reinforced functionally graded cylindrical shells in thermal environments. Compos. Struct. 2017, 138, 214–224. [Google Scholar] [CrossRef]
- Asadi, H.; Souri, M.; Wang, Q. A numerical study on flow-induced instabilities of supersonic FG-CNT reinforced composite flat panels in thermal environments. Compos. Struct. 2017, 171, 113–125. [Google Scholar] [CrossRef]
- Jouneghani, F.Z.; Dimitri, R.; Bacciocchi, M.; Tornabene, F. Free vibration analysis of functionally graded porous doubly-curved shells based on the First-order Shear Deformation Theory. Appl. Sci. 2017, 7, 1252. [Google Scholar] [CrossRef]
- Nejati, M.; Dimitri, R.; Tornabene, F.; Yas, M.H. Thermal buckling of nanocomposite stiffened cylindrical shells reinforced by functionally Graded wavy Carbon NanoTubes with temperature-dependent properties. Appl. Sci. 2017, 7, 1223. [Google Scholar] [CrossRef]
- Keleshteri, M.M.; Asadi, H.; Wang, Q. Postbuckling analysis of smart FG-CNTRC annular sector plates with surface-bonded piezoelectric layers using generalized differential quadrature method. Comput. Methods Appl. Mech. Eng. 2017, 325, 689–710. [Google Scholar] [CrossRef]
- Asadi, H.; Beheshti, A.R. On the nonlinear dynamic responses of FG-CNTRC beams exposed to aerothermal loads using thord-order piston theory. Acta Mech. 2018, 229, 2413–2430. [Google Scholar] [CrossRef]
- Keleshteri, M.M.; Asadi, H.; Wang, Q. On the snap-through instability of post-buckled FG-CNTRC rectangula plates with intergated piezoelectric layers. Comput. Method. Appl. Mech. Eng. 2018, 331, 53–71. [Google Scholar] [CrossRef]
- Malikan, M.; Dimitri, R.; Tornabene, F. Effect of sinusoidal corrugated geometries on the vibrational response of viscoelastic nanoplates. Appl. Sci. 2018, 8, 1432. [Google Scholar] [CrossRef]
- Jouneghani, F.Z.; Dimitri, R.; Tornabene, F. Structural response of porous FG nanobeams under hygro-thermo-mechanical loadings. Compos. Part B Eng. 2018, 152, 71–78. [Google Scholar] [CrossRef]
- Malikan, M.; Nguyen, V.B.; Tornabene, F. Damped forced vibration analysis of single-walled carbon nanotubes resting on viscoelastic foundation in thermal environment using nonlocal strain gradient theory. Eng. Sci. Technol. Int. J. 2018, 21, 778–786. [Google Scholar] [CrossRef]
- Jalaei, M.H.; Dimitri, R.; Tornabene, F. Dynamic stability of temperature-dependent graphene sheet embedded in an elastomeric medium. Appl. Sci. 2019, 9, 887. [Google Scholar] [CrossRef]
- Guzmán de Villoria, R.; Miravete, A. Mechanical model to evaluate the effect of the dispersion in nanocomposites. Acta Mater. 2007, 55, 3025–3031. [Google Scholar] [CrossRef]
- Shi, Z.; Zhang, T. Bending analysis of a piezoelectric curved actuator with a generally graded property for the piezoelectric parameter. Smart Mater. Struct. 2008, 17, 45018. [Google Scholar] [CrossRef]
- Arefi, M.; Rahimi, G.H. Application of shear deformation theory for two dimensional electro-elastic analysis of a FGP cylinder. Smart Struct. Syst. 2014, 13, 1–24. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J Appl. Phys. 1983, 54, 4703. [Google Scholar] [CrossRef]
- Arefi, M.; Zenkour, A.M. Employing sinusoidal shear deformation plate theory for transient analysis of three layers sandwich nanoplate integrated with piezo-magnetic face-sheets. Smart Mater. Struct. 2016, 25, 115040. [Google Scholar] [CrossRef]
- Arefi, M.; Kiani, M.; Zenkour, A.M. Size-dependent free vibration analysis of a three-layered exponentially graded nano-/micro-plate with piezomagnetic face sheets resting on Pasternak’s foundation via MCST. J. Sandw. Struct. Mater. 2017, 1–32. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Faghidian, S.A.; Luciano, R.; Marotti de Sciarra, F. Nonlocal strain gradient exact solutions for functionally graded inflected nano-beams. Compos. Part B Eng. 2019, 164, 667–674. [Google Scholar] [CrossRef]
- Ganapathi, M.; Merzouki, T.; Polit, O. Vibration study of curved nanobeams based on nonlocal higher-order shear deformation theory using finite element approach. Compos. Struct. 2018, 184, 821–838. [Google Scholar] [CrossRef]
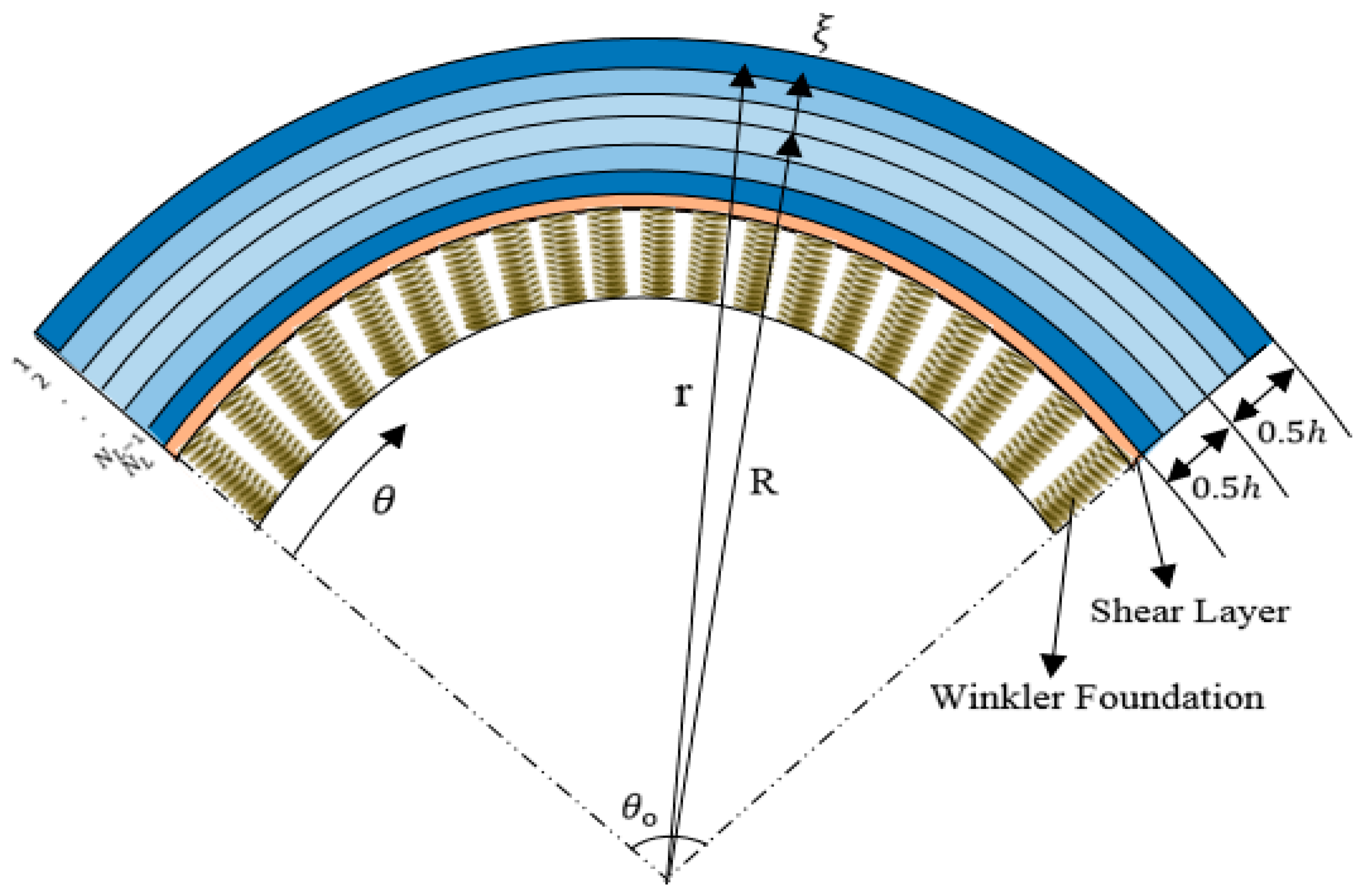
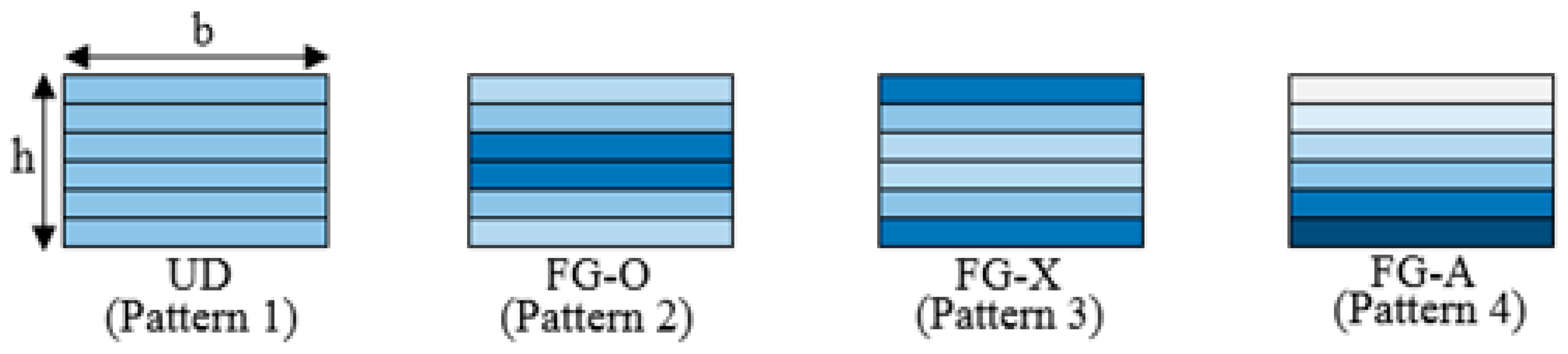
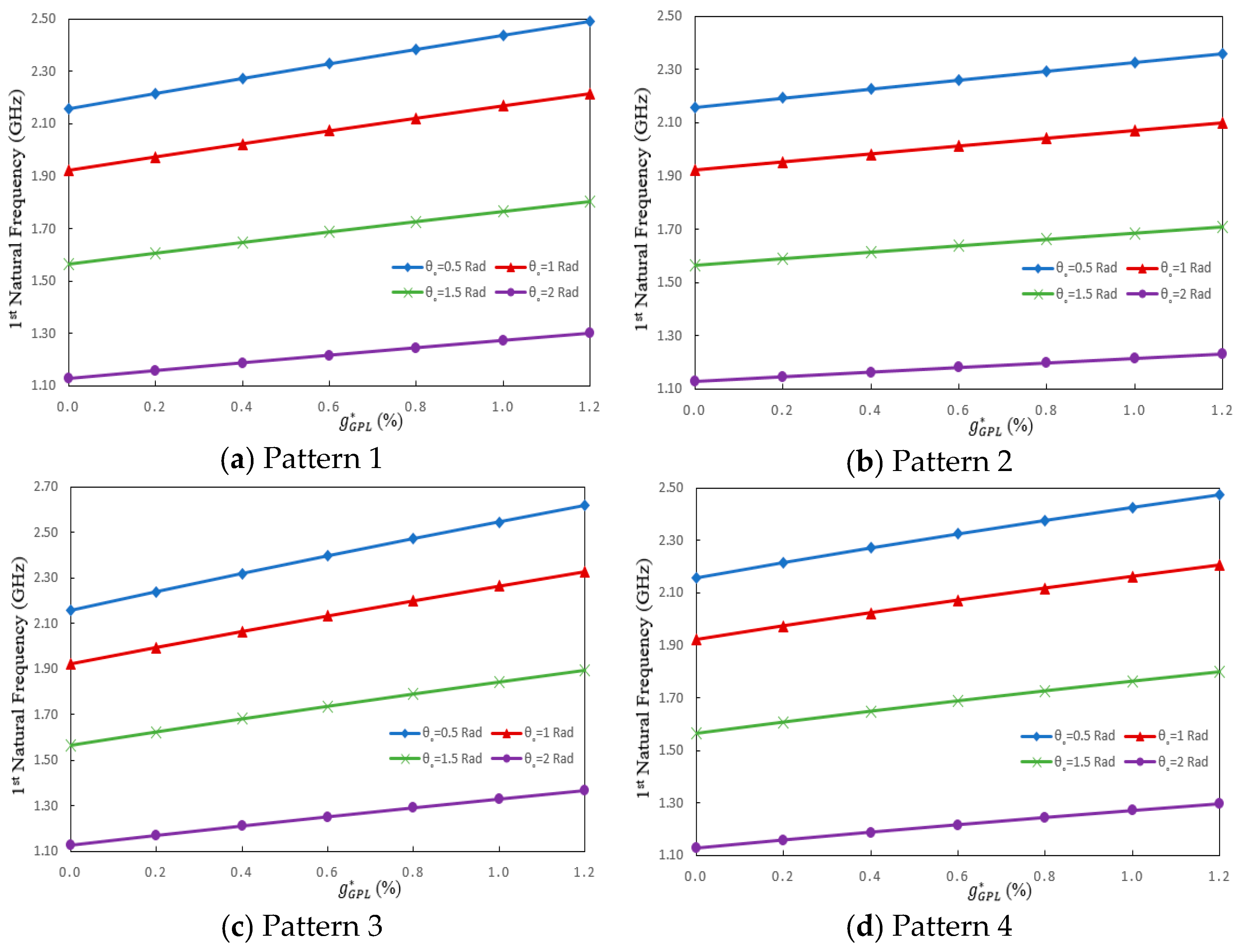
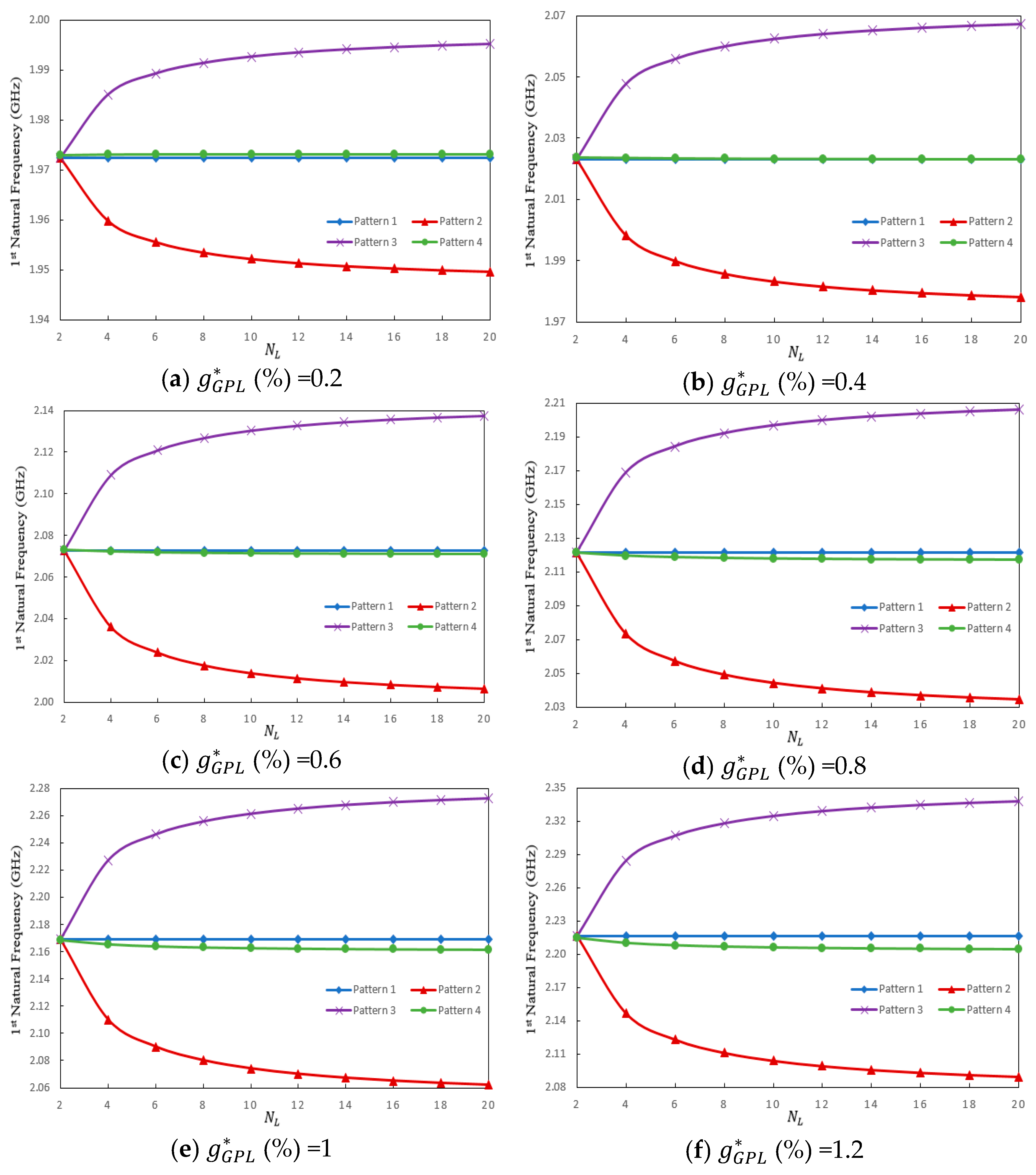
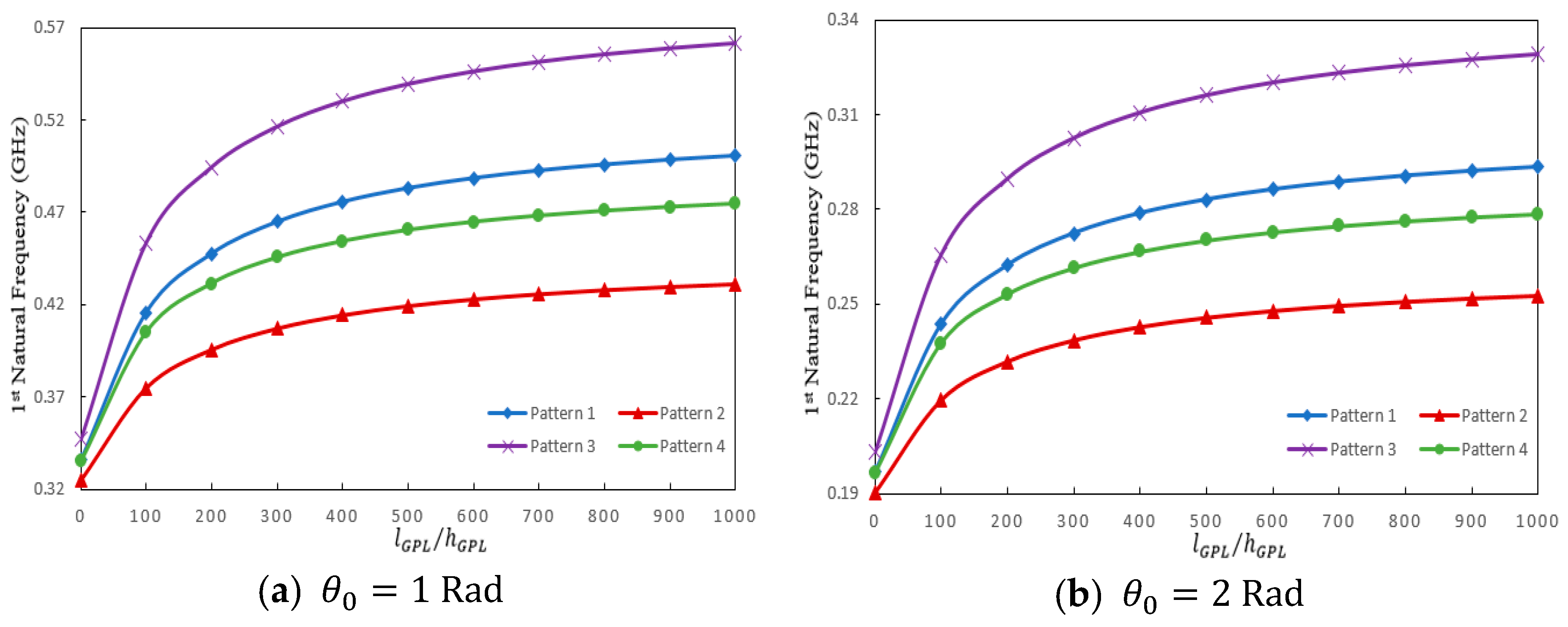
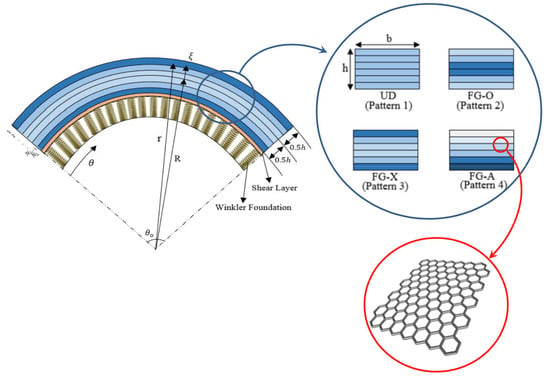
| Boundary Conditions | ||
|---|---|---|
| S-S | ||
| C-S | ||
| C-C |
| Ref. [17] | Present | Ref. [17] | Present | Ref. [17] | Present | Ref. [17] | Present | Ref. [17] | Present | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | i = 1 | 4.56009 | 4.5739 | 4.35045 | 4.3630 | 4.1673 | 4.1788 | 4.00549 | 4.0161 | 3.86118 | 3.8710 |
| i = 2 | 23.7375 | 23.7852 | 20.0993 | 20.1213 | 17.7444 | 17.7547 | 16.0611 | 16.0652 | 14.7808 | 14.7813 | |
| i = 3 | 53.2817 | 53.3129 | 38.7745 | 38.7229 | 31.9762 | 31.9116 | 27.8325 | 27.7665 | 24.9704 | 24.9058 | |
| 20 | i = 1 | 4.66754 | 4.6710 | 4.45296 | 4.4563 | 4.2655 | 4.2687 | 4.09987 | 4.1029 | 3.95216 | 3.9551 |
| i = 2 | 25.0039 | 25.0155 | 21.1716 | 21.1794 | 18.6911 | 18.6969 | 16.9179 | 16.9226 | 15.5694 | 15.5734 | |
| i = 3 | 58.3285 | 58.3342 | 42.4472 | 42.4407 | 35.0050 | 34.9964 | 30.4689 | 30.4600 | 27.3356 | 27.3269 | |
| 50 | i = 1 | 4.72079 | 4.7215 | 4.50376 | 4.5045 | 4.31416 | 4.3150 | 4.14665 | 4.1475 | 3.99725 | 3.9981 |
| i = 2 | 25.5362 | 25.5382 | 21.6223 | 21.6251 | 19.0889 | 19.0919 | 17.2780 | 17.2810 | 15.9008 | 15.9037 | |
| i = 3 | 60.4005 | 60.4016 | 43.9551 | 43.9589 | 36.2484 | 36.2525 | 31.5512 | 31.5551 | 28.3067 | 28.3104 | |
| S-S Boundary Conditions | C-C Boundary Conditions | ||||
|---|---|---|---|---|---|
| Ref. [40] | Present | Ref. [40] | Present | ||
| 10 | 0 | 8.2006 | 8.2141 | 25.8678 | 26.0937 |
| 1 | 7.8236 | 7.8366 | 24.3792 | 24.4961 | |
| 2 | 7.4942 | 7.5057 | 23.1083 | 23.1601 | |
| 3 | 7.2032 | 7.2134 | 22.0084 | 22.0212 | |
| 4 | 6.9437 | 6.9527 | 21.0456 | 21.0353 | |
| 20 | 0 | 8.2922 | 8.2955 | 37.0381 | 37.0333 |
| 1 | 7.9110 | 7.9138 | 34.7887 | 34.7932 | |
| 2 | 7.5779 | 7.5803 | 32.8611 | 32.9158 | |
| 3 | 7.2837 | 7.2858 | 31.1899 | 31.3129 | |
| 4 | 7.0213 | 7.0231 | 29.7263 | 29.9234 | |
| Boundary Condition | Boundary Condition | |||||
|---|---|---|---|---|---|---|
| S-S | C-S | C-C | S-S | C-S | C-C | |
| 0.0 | 2.2360 | 6.9765 | 8.9273 | 2.3185 | 7.3241 | 9.3883 |
| 0.5 | 2.2358 | 6.9751 | 8.9258 | 2.3182 | 7.3227 | 9.3867 |
| 1.0 | 2.2349 | 6.9709 | 8.9214 | 2.3173 | 7.3183 | 9.3821 |
| 1.5 | 2.2336 | 6.9640 | 8.9140 | 2.3159 | 7.3111 | 9.3743 |
| 2.0 | 2.2316 | 6.9544 | 8.9037 | 2.3139 | 7.3010 | 9.3634 |
| 2.5 | 2.2292 | 6.9421 | 8.8905 | 2.3113 | 7.2880 | 9.3495 |
| 3.0 | 2.2262 | 6.9271 | 8.8744 | 2.3082 | 7.2723 | 9.3326 |
| 3.5 | 2.2226 | 6.9096 | 8.8555 | 2.3046 | 7.2539 | 9.3128 |
| 4.0 | 2.2186 | 6.8895 | 8.8339 | 2.3004 | 7.2328 | 9.2900 |
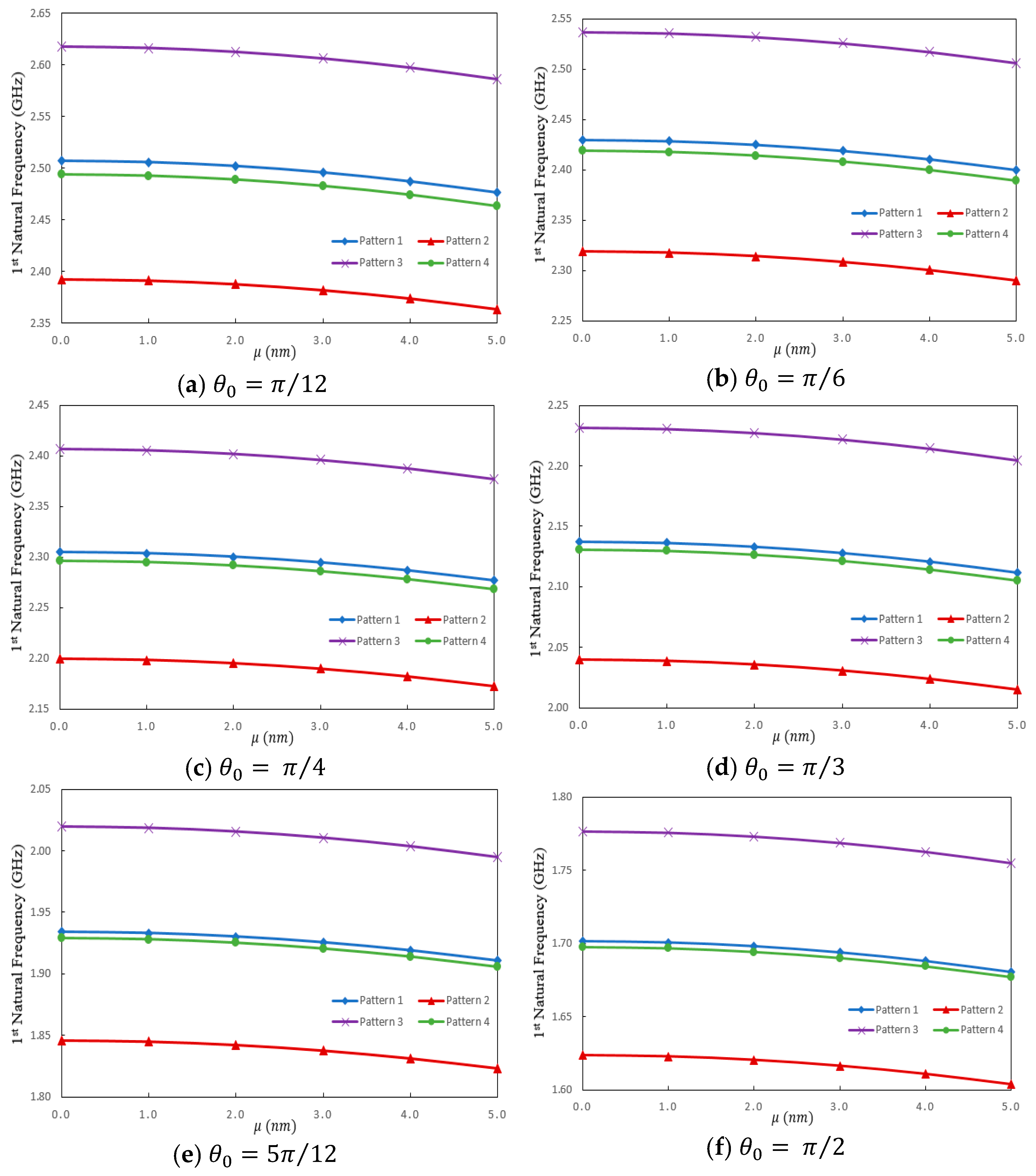
| Pattern of Multilayer | Boundary Condition | |||
|---|---|---|---|---|
| S-S | C-S | C-C | ||
| Pattern 1 | 2.5058 | 5.7430 | 6.9190 | |
| Pattern 2 | 2.3910 | 5.5456 | 6.7041 | |
| Pattern 3 | 2.6163 | 5.9357 | 7.1293 | |
| Pattern 4 | 2.4923 | 5.7200 | 6.8935 | |
| Pattern 1 | 2.4283 | 7.4648 | 9.5336 | |
| Pattern 2 | 2.3173 | 7.3183 | 9.3821 | |
| Pattern 3 | 2.5356 | 7.6117 | 9.6868 | |
| Pattern 4 | 2.4174 | 7.4543 | 9.5225 | |
| 3 | 3.5 | 4 | 4.5 | 5 | ||
|---|---|---|---|---|---|---|
| 10 | m = 1 | 53.6075 | 54.0087 | 54.3011 | 54.5226 | 54.6958 |
| m = 2 | 100.9296 | 102.9847 | 104.6266 | 105.9049 | 106.8881 | |
| m = 3 | 139.5596 | 142.0667 | 144.4766 | 146.7824 | 148.9747 | |
| 11 | m = 1 | 53.7027 | 54.0769 | 54.3521 | 54.5621 | 54.7271 |
| m = 2 | 102.6704 | 104.3787 | 105.7134 | 106.7410 | 107.5308 | |
| m = 3 | 144.1770 | 146.4964 | 148.7037 | 150.7876 | 152.7349 | |
| 12 | m = 1 | 53.7911 | 54.1410 | 54.4004 | 54.5996 | 54.7571 |
| m = 2 | 104.1203 | 105.5133 | 106.5874 | 107.4125 | 108.0505 | |
| m = 3 | 148.4306 | 150.5309 | 152.4963 | 154.3126 | 155.9658 | |
| 13 | m = 1 | 53.8735 | 54.2012 | 54.4461 | 54.6354 | 54.7858 |
| m = 2 | 105.3043 | 106.4268 | 107.2889 | 107.9545 | 108.4744 | |
| m = 3 | 152.2553 | 154.0912 | 155.7658 | 157.2676 | 158.5904 | |
| 14 | m = 1 | 53.9504 | 54.2578 | 54.4894 | 54.6695 | 54.8133 |
| m = 2 | 106.2589 | 107.1599 | 107.8544 | 108.3958 | 108.8240 | |
| m = 3 | 155.5631 | 157.0872 | 158.4328 | 159.6003 | 160.5981 | |
| 15 | m = 1 | 54.0224 | 54.3113 | 54.5305 | 54.7020 | 54.8397 |
| m = 2 | 107.0251 | 107.7501 | 108.3140 | 108.7588 | 109.1154 | |
| m = 3 | 158.2723 | 159.4621 | 160.4807 | 161.3424 | 162.0661 | |
| 0 | 1 | 2 | 3 | 4 | 5 | ||
|---|---|---|---|---|---|---|---|
| m = 1 | 2.6176 | 2.6163 | 2.6125 | 2.6061 | 2.5972 | 2.5859 | |
| m = 2 | 10.4115 | 10.3910 | 10.3302 | 10.2313 | 10.0974 | 9.9329 | |
| m = 3 | 22.9623 | 22.8610 | 22.5649 | 22.0960 | 21.4861 | 20.7716 | |
| m = 1 | 2.5369 | 2.5356 | 2.5319 | 2.5257 | 2.5171 | 2.5061 | |
| m = 2 | 10.3316 | 10.3112 | 10.2509 | 10.1527 | 10.0199 | 9.8564 | |
| m = 3 | 22.8853 | 22.7843 | 22.4891 | 22.0217 | 21.4138 | 20.7012 | |
| m = 1 | 2.4064 | 2.4053 | 2.4017 | 2.3958 | 2.3877 | 2.3773 | |
| m = 2 | 10.1994 | 10.1793 | 10.1197 | 10.0228 | 9.8916 | 9.7302 | |
| m = 3 | 22.7573 | 22.6568 | 22.3632 | 21.8983 | 21.2936 | 20.5849 | |
| m = 1 | 2.2318 | 2.2307 | 2.2274 | 2.2219 | 2.2143 | 2.2047 | |
| m = 2 | 10.0164 | 9.9967 | 9.9382 | 9.8429 | 9.7140 | 9.5555 | |
| m = 3 | 22.5790 | 22.4793 | 22.1878 | 21.7264 | 21.1261 | 20.4227 | |
| m = 1 | 2.0194 | 2.0184 | 2.0155 | 2.0105 | 2.0037 | 1.9949 | |
| m = 2 | 9.7847 | 9.7654 | 9.7082 | 9.6151 | 9.4891 | 9.3342 | |
| m = 3 | 22.3512 | 22.2524 | 21.9638 | 21.5067 | 20.9122 | 20.2157 | |
| m = 1 | 1.7765 | 1.7756 | 1.7730 | 1.7686 | 1.7626 | 1.7549 | |
| m = 2 | 9.5067 | 9.4879 | 9.4323 | 9.3418 | 9.2193 | 9.0687 | |
| m = 3 | 22.0750 | 21.9774 | 21.6921 | 21.2404 | 20.6529 | 19.9646 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arefi, M.; Bidgoli, E.M.-R.; Dimitri, R.; Tornabene, F.; Reddy, J.N. Size-Dependent Free Vibrations of FG Polymer Composite Curved Nanobeams Reinforced with Graphene Nanoplatelets Resting on Pasternak Foundations. Appl. Sci. 2019, 9, 1580. https://doi.org/10.3390/app9081580
Arefi M, Bidgoli EM-R, Dimitri R, Tornabene F, Reddy JN. Size-Dependent Free Vibrations of FG Polymer Composite Curved Nanobeams Reinforced with Graphene Nanoplatelets Resting on Pasternak Foundations. Applied Sciences. 2019; 9(8):1580. https://doi.org/10.3390/app9081580
Chicago/Turabian StyleArefi, Mohammad, Elyas Mohammad-Rezaei Bidgoli, Rossana Dimitri, Francesco Tornabene, and J. N. Reddy. 2019. "Size-Dependent Free Vibrations of FG Polymer Composite Curved Nanobeams Reinforced with Graphene Nanoplatelets Resting on Pasternak Foundations" Applied Sciences 9, no. 8: 1580. https://doi.org/10.3390/app9081580
APA StyleArefi, M., Bidgoli, E. M.-R., Dimitri, R., Tornabene, F., & Reddy, J. N. (2019). Size-Dependent Free Vibrations of FG Polymer Composite Curved Nanobeams Reinforced with Graphene Nanoplatelets Resting on Pasternak Foundations. Applied Sciences, 9(8), 1580. https://doi.org/10.3390/app9081580