Water Jacket Systems for Temperature Control of Petri Dish Cell Culture Chambers

Abstract

Water jacket systems are routinely used to control the temperature of Petri dish cell culture chambers. Despite their widespread use, the thermal characteristics of such systems have not been fully investigated. In this study, we conducted a comprehensive set of theoretical, numerical and experimental analyses to investigate the thermal characteristics of Petri dish chambers under stable and transient conditions. In particular, we investigated the temperature gradient along the radial axis of the Petri dish under stable conditions, and the transition period under transient conditions. Our studies indicate a radial temperature gradient of 3.3 °C along with a transition period of 27.5 min when increasing the sample temperature from 37 to 45 °C for a standard 35 mm diameter Petri dish. We characterized the temperature gradient and transition period under various operational, geometric, and environmental conditions. Under stable conditions, reducing the diameter of the Petri dish and incorporating a heater underneath the Petri dish can effectively reduce the temperature gradient across the sample. In comparison, under transient conditions, reducing the diameter of the Petri dish, reducing sample volume, and using glass Petri dish chambers can reduce the transition period.

1. Introduction

Temperature is a major environmental parameter that affects cellular processes, ranging from enzyme activities and trafficking of signaling receptors across the membrane to gene expression, survival, signaling, proliferation, and differentiation of cells [1,2,3,4]. Temperature can also affect several physical properties of cells, including the fluidity and permeability of the plasma membrane, organization of the cytoskeleton, and the morphology and stiffness of cells [5,6].

Petri dish cell culture chambers are routinely used in biomedical laboratories for various in vitro studies. In particular, Petri dish chambers are useful for monitoring the response of cells using various microscopic techniques. Petri dish chambers are placed on the microscope stage, and are exposed to the surrounding environment, which generally has a temperature of 20–25 °C. This demonstrates the need for temperature control systems to set the temperature of Petri dish chambers to ensure the cultured cells are maintained at their physiological temperature, i.e., 37 °C for human cells.

Microscopes with integrated incubation chambers have been used to control the temperature of the sample within the Petri dish [7,8,9]. Temperature control is facilitated by circulating warm air through a relatively large chamber that encloses the microscope stage. Despite their widespread application, the chamber occupies a large volume, which also limits access to the sample. Temperature control is generally limited to heating, and is associated with long temperature transition periods due to the large volume of the air enclosed within the chamber.

These limitations have inspired researchers to introduce alternative methods to control the temperature of samples. These include objective heaters, in which a flexible heating element is wrapped around the microscope objective to heat the air surrounding the Petri dish [10,11]. Using a similar principle, objective coolers have been introduced, in which water tubes are wrapped around the microscope objective [12,13,14]. Despite their simplicity, the distance between the objective and the Petri dish (which depends on the objective magnification) limits the accuracy and results in quick changes in temperature. Infrared heaters, enabled by emitting laser beams into the sample, have also been used to heat the sample [15].

Heating stages are also used for heating the sample [16,17,18]. These heaters consist of circular metallic rings with a large aperture in the middle to accommodate the Petri dish and are heated by the Joule heating effect after applying a small voltage. The metallic heating ring can be reconfigured to facilitate heating of multi-well plates. Implementing supplementary equipment to adjust carbon dioxide and humidity levels facilitates miniaturized cell incubation chambers [19,20,21]. In comparison, cooling stages, also known as cooling chambers or water jackets, are used for both heating and cooling samples. These heat exchangers consist of circular or square metallic chambers that recirculate temperature-controlled water with an aperture in the middle to insert the Petri dish. The temperature of the recirculating water is controlled using heating elements or Peltier heat sinks. Despite their simplicity and high degree of controllability, the heat transfer across a stationary sample inside a Petri dish is dominated by conduction (diffusion), which leads to relatively large temperature gradients across the sample and long temperature transition periods, as will be comprehensively discussed here.

An alternative solution is to provide a constant flow of liquid through the Petri dish to reduce the dominance of diffusion. This can be achieved by inserting a channel-shaped silicon structure (also known as Petri dish perfusion inserts) inside the Petri dish to drive the cell culture medium between the inlet/outlet ports of the channel [22,23]. In this case, the Petri dish is effectively converted into a perfusion chamber. The temperature of the sample can be controlled by inserting the Petri dish inside a heating stage or water jacket, or directly by heating/cooling the sample before it enters the channel. In both cases, heat dissipation across the moving sample is dominated by convection, which leads to uniform temperature profiles and short transition periods. This is particularly useful for long-term cellular assays, in which the cells need to be perfused with fresh cell culture media, and the cellular waste needs to be constantly withdrawn from the sample. However, the problems associated with assembling and interfacing a silicon insert might make these solutions less attractive for short-term cellular assays. Furthermore, the flow of liquid can induce shear stress on the cells cultured in the Petri dish, causing undesired cellular events [24].

Here, we conduct a comprehensive set of theoretical, numerical and experimental analyses to investigate the thermal characteristics of Petri dish chambers under various stable (fixed temperature) and dynamic (varying temperatures) conditions. In particular, we studied the temperature distribution along the radial axis of the Petri dish under stable conditions as well as the transition period of the sample temperature under dynamic conditions. Our results show a temperature gradient of 3.3 °C along the radial axis of the Petri dish and a transition period of 27.5 min when increasing the sample temperature from 37 to 45 °C for a 35 mm-diameter Petri dish. These characteristics are caused by the dominance of the conductive heat transfer inside the sample and the consistent convective heat loss across the free surface of the Petri dish. We analyzed the effect of various operational, geometric, and environmental conditions on the temperature distribution and transition period of samples, and suggest some solutions to reduce these two parameters.

2. Materials and Methods

2.1. The Structure of the Water Jacket System

Figure 1 shows the water jacket system investigated in our study, which consisted of a circular aluminum water jacket, a polystyrene Petri dish, and a rubber washer. The other components of the system, including the pump, reservoirs, and connecting tubes are not shown or considered in our study.

The water jacket was made of aluminum, due to its low density (2700 kg/m³), high thermal conductivity (237 W/mK), and good chemical stability following anodization. The polystyrene Petri dish investigated here had a diameter of 35 mm and a wall thickness of 1 mm, and is filled with a water-based biological sample up to 50% of its volume. A rubber washer with a thickness of 0.5 mm was placed between the water jacket and the Petri dish to provide mechanical stability and minimize undesired vibrations caused by recirculating water through the water jacket chamber. The rubber washer had a higher thermal conductivity compared to air and, therefore, reduced the temperature drop between the water jacket and Petri dish.

2.2. Experimental Prototype

A custom-built experimental prototype was fabricated to verify the accuracy of numerical simulations under reference static and dynamic thermal conditions. The experimental prototype included a (i) 35 mm polystyrene Petri dish for storing the sample, (ii) a 0.5 mm thick rubber washer surrounding the Petri dish, (iii) a water jacket for controlling the temperature of the sample inside the Petri dish, (iv) a water reservoir equipped with heating elements for regulating the temperature of the water recirculating through the system, (v) a thermocouple for monitoring the temperature of water inside the water reservoir, (vi) a peristaltic pump along with Teflon tubing for recirculation of hot water, and (vii) an infrared camera for monitoring the temperature across the Petri dish.

The water jacket was made of aluminum with an external diameter of 55 mm, an internal diameter of 36 mm, a height of 10 mm, and a thickness of 1 mm, as presented in Figure S1. The water jacket was equipped with inlet/outlet ports with an internal diameter of 3 mm to recirculate water. The water reservoir consisted of a stainless steel cylindrical container with an internal volume of 200 mL. A Nichrome heating element with an electrical resistance of 13.77 Ω/m was immersed in the water reservoir. Applying a DC current of 3 A to the wire resulted in the water inside the reservoir reaching a stable temperature of 55 °C within 30 min. The temperature of the water inside the reservoir was constantly monitored using a K-type thermocouple (TC Measurement & Control Pty Ltd). The water was recirculated through the system using a peristaltic pump with an integrated geared motor (Welco, WPM1-P3-AA). Operating the pump at 12 V resulted in a flow rate of 60 mL/min. The pump was interfaced with the water jacket using Teflon tubes (Bohlender™ PTFE tubing, ID = 4.35 mm, OD = 6.35 mm). The temperature of the Petri dish and the water jacket was monitored in real-time using a thermal imaging camera (FLIR systems, Thermo Vision A320, Sweden) interfaced with ThermaCAM researcher software.

2.3. Theoretical Model Describing the Heat Transfer Inside the Petri Dish

The heat transfer within the water jacket system is governed by convection through the water jacket facilitated by the temperature change between the inlet/outlet ports to compensate for the free convection at the surfaces of the system, which are exposed to the surrounding air. The heat transfer between the water jacket chamber and the Petri dish is facilitated by conduction via the sidewalls and the rubber washer. Similarly, heat transfer across the radial axis of the Petri dish is facilitated by conduction via the sample as well as the thin surface of the Petri dish (Figure 1).

In this regard, the sample inside the Petri dish behaves as a heat sink [25,26,27]. Ignoring the temperature gradient along the height of the sample, the temperature distribution along the radial axis of the Petri dish can be expressed using the following simplified differential equation:

$$\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right)=\frac{h_{air}}{k_{sample }{H}_{sample}}\left(T- T_{air}\right)$$

(1)

$${\frac{\partial T}{\partial r}|}_{r=0}=0$$

(2)

$${T|}_{r=R_{petri dish}}=T_{side wall }$$

(3)

where, r, R_{Petri dish}, and H_sample are the location along the radial axis radius, Petri dish radius, and sample height inside the Petri dish, respectively, h_air is the free convection heat transfer coefficient, T_air is the ambient temperature, T_{side wall} is the temperature of the sample along the side walls of the Petri dish, and k_sample is the thermal conductivity of the sample. Solving this equation, the temperature profile along the radial axis of the Petri dish is obtained as below, in which BesselJ is the Bessel function of the first kind:

$$T\left(r\right)= T_{air}+\frac{\mathrm{BesselJ}\left(0,\alpha r\right)}{\mathrm{BesselJ}\left(0,\alpha R_{Petri dish}\right)} \left( T_{side wall }-T_{air}\right)$$

(4)

$$\alpha =\sqrt{\frac{h_{air}}{k_{sample }{H}_{sample}}}$$

(5)

2.4. Computational Fluid Dynamics (CFD) Simulations

A comprehensive set of CFD simulations were conducted to analyze the thermal performance of the water jacket system under various geometric, operational, and environmental conditions. Simulations were conducted in three dimensions under both steady state (stable) and unsteady state (transient) conditions, using ANSYS Fluent software.

The differential equations governing mass balance, momentum, and energy for the water stored inside the water jacket chamber (as given in Equations (6)–(8)) are solved. For the other components of the system, including the water jacket structure, the sample stored inside the Petri dish, the Petri dish structure, and the washer surrounding the Petri dish, only the energy balance equation (as given in Equations (9)–(12)) is solved, as there is no flow within these components.

Water recirculating through the water chamber:

$$\nabla \cdot \overrightarrow{U}=0$$

(6)

$${\rho }_{water}(\overrightarrow{U}\cdot \nabla )\overrightarrow{U}=-\nabla P+{\mu }_{water}{\nabla }^2\overrightarrow{U}$$

(7)

$${(\rho c_p)}_{water}\left(\frac{\partial T}{\partial t}+(\overrightarrow{U}\cdot \nabla )T\right)=k_{water}{\nabla }^{2}T$$

(8)

Water jacket walls:

$${\left(\rho c_p\right)}_{jacket}=k_{jacket}{\nabla }^{2}T$$

(9)

Sample inside the Petri dish:

$${\left(\rho c_p\right)}_{sample}=k_{sample }{\nabla }^{2}T$$

(10)

Petri dish walls:

$${\left(\rho c_p\right)}_{Petri dish}=k_{Petri dish }{\nabla }^{2}T$$

(11)

Rubber washer:

$${\left(\rho c_p\right)}_{washer}=k_{washer }{\nabla }^{2}T$$

(12)

where U and P are the velocity and pressure of the liquid, T is temperature, and ρ, µ, c_p, and k are the density, dynamic viscosity, heat capacity, and thermal conductivity of the fluid or solid components, respectively. The thermos-physical properties used in the above equations are summarized in Table S1.

The boundary conditions include a fixed flow rate and temperature at the inlet of the water jacket and fixed pressure and fully developed temperature at the outlet of the water chamber. The no-slip boundary condition is applied at the internal surfaces of the water chamber. The temperatures and heat fluxes are coupled at all internal surfaces of the system. The free convection boundary condition was applied across all external surfaces of the system, which are exposed to the surrounding environment, as given below:

External surfaces of the system:

$$k_{surface}\frac{\partial T}{\partial n}=h_{air}(T-T_{air})$$

(13)

where n is the vector normal to the surface, as schematically shown in Figure 1.

Geometry was created and divided into fine elements using Gambit software. The mesh generated involved a combination of structured and unstructured elements.

3. Results and Discussion

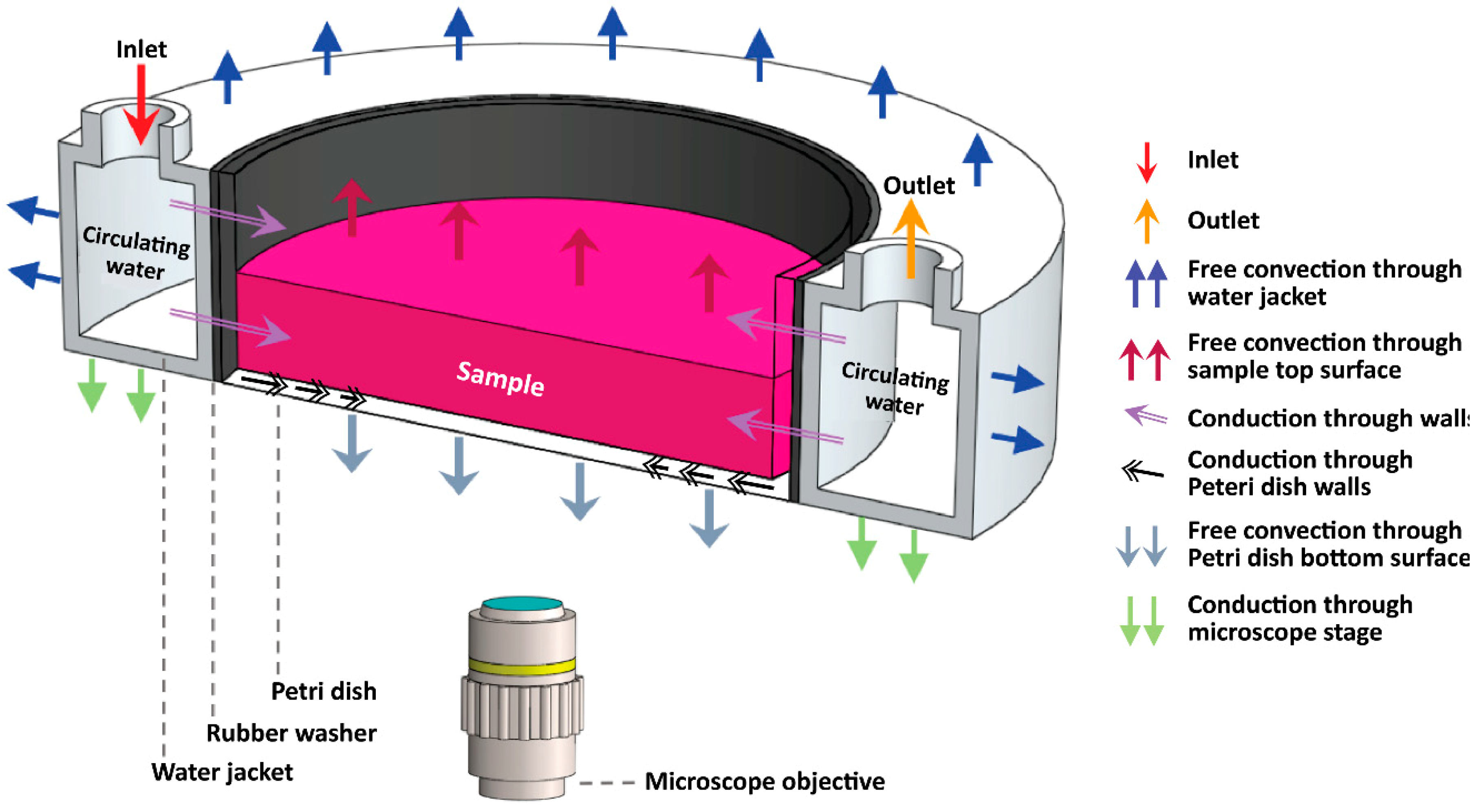
3.1. Thermal Analysis of the Water Jacket under Static Reference Conditions

First, we investigate the thermal performance of the water jacket system under steady-state reference conditions. The reference condition was defined as water temperature at the inlet port of the water jacket, T_water@inlet = 39 °C; water flow rate through the water jacket, Q_water = 60 mL/min; free convection coefficient, h_air = 10 W/m²K; ambient temperature, T_air = 20 °C; Petri dish external diameter, D_{Petri dish} = 35 mm; target sample temperature, T_sample = 37 °C; and volume ratio of the sample inside the Petri dish, V_sample = 50%. Furthermore, the Petri dish was made of polystyrene, and a rubber washer was inserted between the water jacket and the Petri dish, as shown in Figure 1.

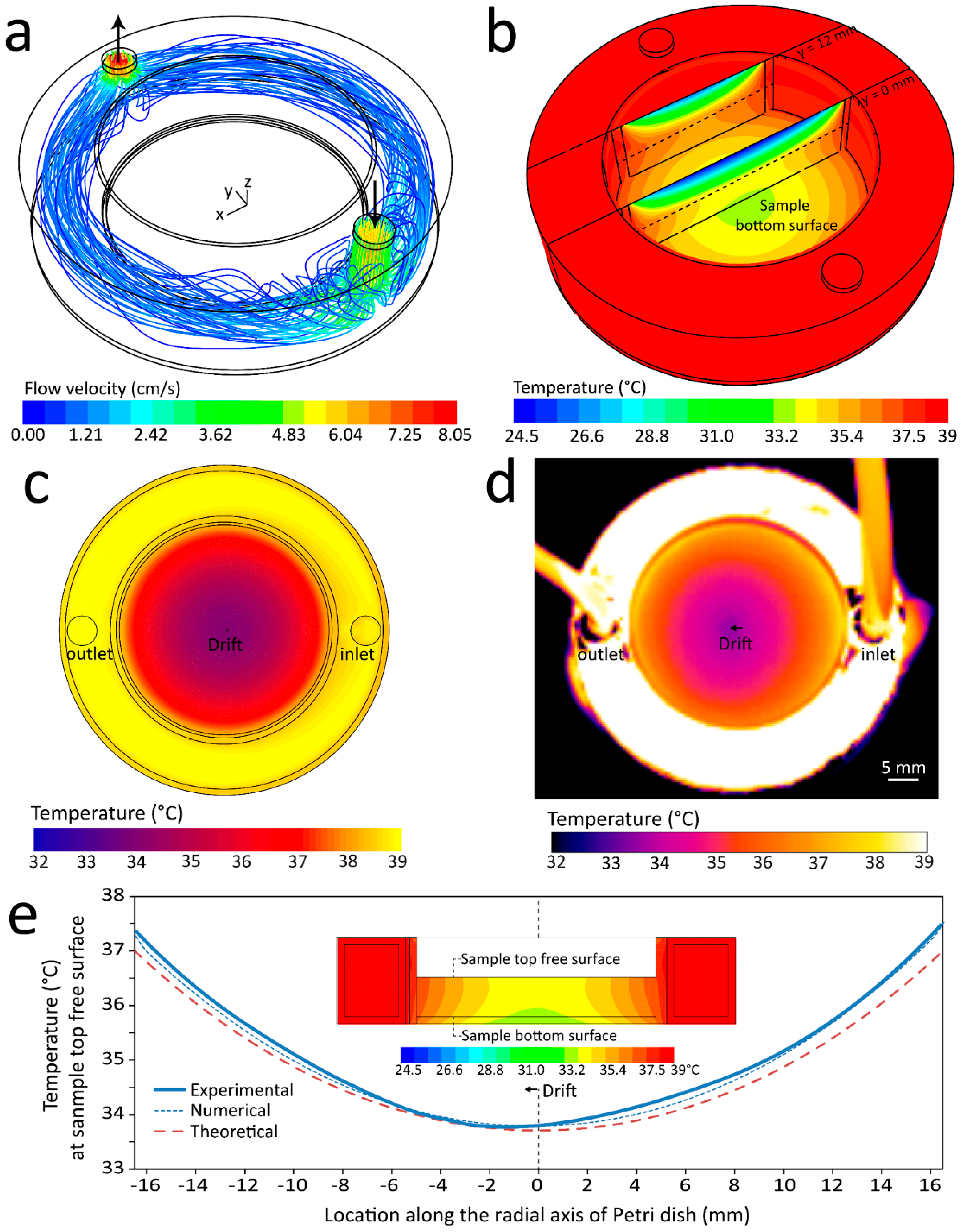
Figure 2a shows the flow streamlines of the water circulating through the water jacket chamber, colored by the magnitude of the flow velocity. The results were obtained at the reference water flow rate of 60 mL/min, as described above. The Reynolds number for recirculating water was ~50, reflecting the laminar nature of the recirculating flow at this rate. The flow streamlines were highly ordered across the water jacket due to the laminar flow characteristics, except at the inlet region where flow was not fully developed. A total pressure drop of 4.5 Pa was obtained along the water jacket cylinder (excluding the connecting tubes).

Figure 2b presents the temperature contours across the system. The simulations revealed an almost uniform temperature distribution across the water jacket surface, which was due to the dominance of forced convection. In contrast, a large temperature gradient was obtained along the radial axis of the Petri dish (from the side walls toward the middle), which was due to the dominance of conduction and the free convection heat loss across the free surfaces of the Petri dish, as defined in Equation (13). This free convection heat loss caused a temperature gradient along the height of the Petri dish. The filled level of the sample inside the Petri dish is shown by a dashed line.

Experimental measurements were also conducted to further investigate the temperature gradient along the radial axis of the Petri dish. We took advantage of a thermal imaging camera to monitor the temperature distribution across the top free surface of the system. Figure 2c,d present the temperature contours at the top free surface of the system obtained by numerical simulations and thermal imaging, respectively. The results confirmed the existence of a temperature gradient along the radial axis of the Petri dish. Interestingly, the lowest temperature was not located at the center of the Petri dish, and instead drifted toward the colder side of the water jacket (toward the outlet port), which is attributed to the temperature drop of the water while passing through the water jacket. The numerical simulations predicted this drift as 0.4 mm, whereas the thermal imaging recorded this drift as 1.9 mm.

Figure 2e compares the temperature profiles along the radial axis of the Petri dish (parallel with the inlet/outlet ports axis) obtained from experimental, numerical and theoretical analyses. Good agreement was observed between the experimental and numerical results, both indicating the maximum temperature gradient along the radial axis of the Petri dish as 3.78 °C. The theoretical model calculated this value as 3.29 °C. The inset shows the temperature contours at the middle cross section of the Petri dish, obtained by numerical simulations. Simulations revealed that the maximum temperature gradient along the bottom surface of the Petri dish reduces to 3.28 °C (corresponding to 37 °C along the sidewalls, which decreased to 33.72 °C in the middle of the Petri dish). Given the biological organisms existing in the sample (such as cells) generally settle to the bottom surface of the Petri dish, the temperature at this surface was referred to as T_sample. In particular, we investigated the variations of T_sample along the radial axis of the Petri dish under different conditions.

3.2. Analyzing the Effect of Recirculating Water and Surrounding Air Parameters

Next, we characterize the thermal performance of the system with respect to the flow rate and temperature of the recirculating water (serving as the heat source), as well as the temperature and free convection coefficient of the surrounding air (serving as the heat sink), as discussed below.

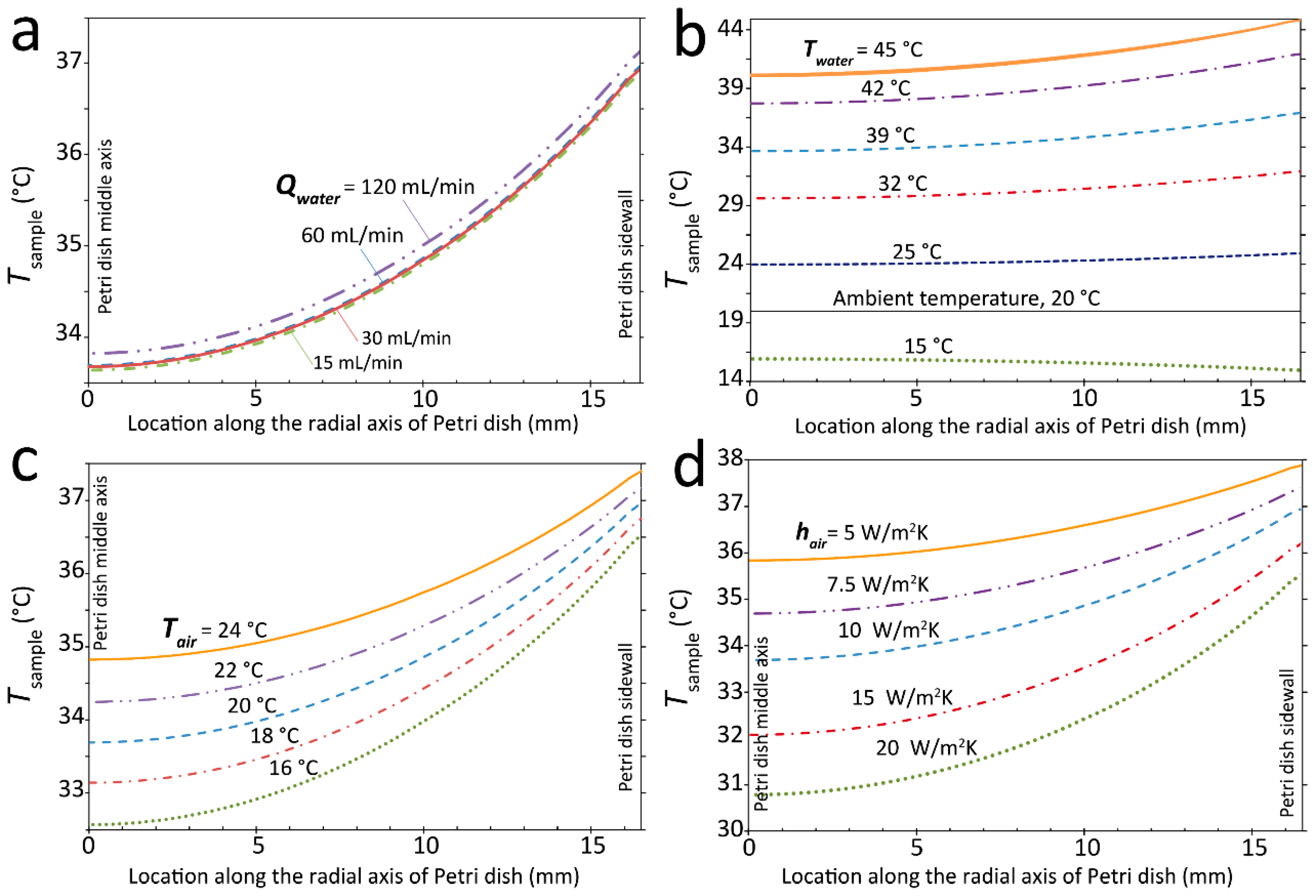
Water flow rate: Figure 3a shows the temperature profile across the bottom surface of the Petri dish (referred to as T_sample) when varying the flow rate of the water recirculating through the water jacket (Q_water) from 15 to 120 mL/min. The temperature contours across the middle cross-section of the Petri dish at various water flow rates are presented in Figure S2. Increase of Q_water enhanced the convective heat transfer through the water jacket. However, the majority of the heat left via the outlet port of the water jacket without being injected into the Petri dish. Under these conditions, despite increasing the average temperature of the sample inside the Petri dish, the magnitude of the temperature gradient along the radial axis of the Petri dish did not change significantly.

Water inlet temperature:Figure 3b presents the temperature profile across the Petri dish when changing the temperature of the water entering the water jacket (T_water@inlet) from 15 to 45 °C. The temperature contours at various water inlet temperatures are presented in Figure S3. Increase of T_water@inlet enhanced the conductive heat injected into the Petri dish via its sidewalls, which consequently increased the temperature gradient along the radial axis of the Petri dish. Decrease of T_water@inlet below the ambient temperature reversed the conductive heat from the sample into the water jacket, leading to negative temperature gradients along the radial axis of the Petri dish.

Ambient temperature:Figure 3c shows the temperature profile across the Petri dish when varying the temperature of surrounding air (T_air) from 24 to 16 °C. The temperature contours at various ambient temperatures are presented in Figure S4. Decrease of T_air enhanced the convective heat losses at the free surfaces of the Petri dish, and consequently increased the temperature gradient along the radial axis of the Petri dish.

Convection coefficient:Figure 3d presents the temperature profile across the Petri dish when changing the free convection coefficient of surrounding air (h_air) from 5 to 20 W/m²K. The temperature contours at various convection coefficients are presented in Figure S5. Increase of h_air enhanced the convective heat losses at the free surfaces of the Petri dish and, accordingly, increased the temperature gradient along the radial axis of the Petri dish.

3.3. Analyzing the Effect of Petri Dish Parameters

Next, we investigate the thermal performance of the water jacket system with respect to the diameter of the Petri dish, volume of the sample stored inside the Petri dish, material of the Petri dish, and incorporation of an integrated heater as discussed below.

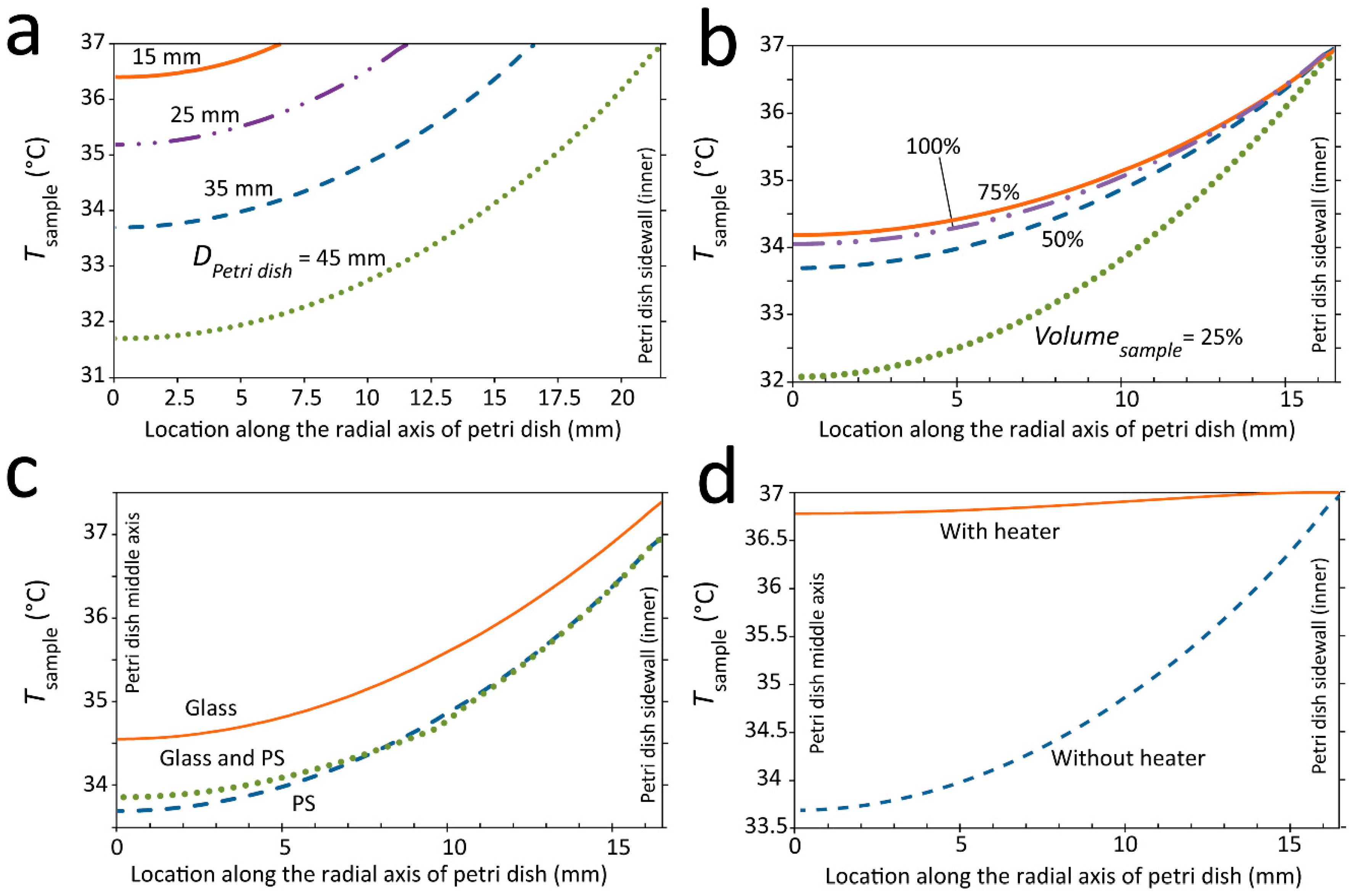
Petri dish diameter:Figure 4a shows the temperature profile across the radial axis of the Petri dish when varying the diameter of the Petri dish (D_{Petri dish}) from 15 to 45 mm. The temperature contours across the middle cross-section of the Petri dish at various Petri dish diameters are presented in Figure S6. The amount of heat transferred into the Petri dish is proportional to the surface area of the side walls, and therefore proportional to D_{Petri dish}. However, the amount of heat lost through the bottom and top surfaces of the Petri dish is proportional to the surface area of these surfaces and, therefore, proportional to $D_{Petri dish}^2$. Hence, decrease of D_{Petri dish} reduced the ratio of heat loss to heat gain, leading to a more uniform temperature profile across the Petri dish.

Sample volume:Figure 4b presents the temperature profile when varying the volume of sample inside the Petri dish (V_sample) from 25% to 100%. The temperature contours at various sample volumes are presented in Figure S7. Decrease of V_sample reduced the height of the sample, and consequently enhanced the conductive loss through the sample. This in turn increased the temperature gradient along the radial axis of the Petri dish.

Petri dish material:Figure 4c shows the temperature profile against the material of the Petri dish with the associated temperature contours presented in Figure S8. The higher thermal conductivity of glass compared to that of polystyrene (0.3 vs. 0.15 W/mk) facilitated the conductive heat transfer across the bottom surface of the Petri dish, and consequently reduced the temperature gradient along the radial axis of the Petri dish. It should be noted that changing the material of the water jacket from aluminum to stainless steel did not change the temperature profile of the sample inside the Petri dish.

Heater integration:Figure 4d presents the temperature profile following the integration of a heater underneath the Petri dish. The heater consisted of a 100 µm thick glass substrate coated with ITO (indium tin oxide) that released 187 mW of thermal power uniformly across the bottom surface of the Petri dish with the associated temperature contour presented in Figure S9. The heater compensated the convective heat loss at the free surfaces of the Petri dish, and decreased the temperature gradient along the radial axis of the Petri dish to ~0.4 °C.

3.4. Analyzing the Effect of Water Jacket Geometry

Furthermore, we investigate the effect of the water jacket geometry on the thermal performance of the system, as discussed here.

Square water jacket:Figure 5a shows the temperature contours of the system using a square water jacket. The temperature contours are similar to those of the reference circular water jacket presented in Figure 2b. However, the extended external surfaces of a square water jacket increased the convective loss across those surfaces. The inlet water temperature was increased from 39 °C with the circular water jacket to 39.1 °C to compensate for those extra losses. The flow streamlines presented in Figure S10 were similar to those of the reference circular water jacket presented in Figure 2a. A total pressure drop of 4.5 Pa was observed between the inlet/outlet ports of the square jacket, which was similar to that obtained for the circular water jacket.

Semi-circular water jacket:Figure 5b presents the temperature contours obtained for the semi-circular water jacket. Compared to the reference circular water jacket presented in Figure 2b, the semi-circular jacket produced an asymmetric temperature profile with a larger temperature gradient along the radial axis of the Petri dish. Despite a large temperature gradient, no buoyancy-driven flows were observed inside the Petri dish. The flow streamlines presented in Figure S11 are similar to those of the reference circular water jacket presented in Figure 2a.

Figure 5c compares the temperature profiles along the radial axis of Petri dish at z = 1 mm obtained with circular and square water jackets. Both jackets produced symmetrical temperature profiles with almost similar temperature gradients of 3.28 and 3.29 °C obtained across the Petri dish, respectively. In contrast, the semi-circular water jacket produced an asymmetrical temperature profile with an impressive temperature gradient of 12 °C. Such a large temperature gradient might be of particular interest for researchers studying the sensitivity of cells to medium temperature, as presented in Figure 5b.

3.5. Comparison of Temperature Gradients across a Petri Dish under Different Stable Conditions

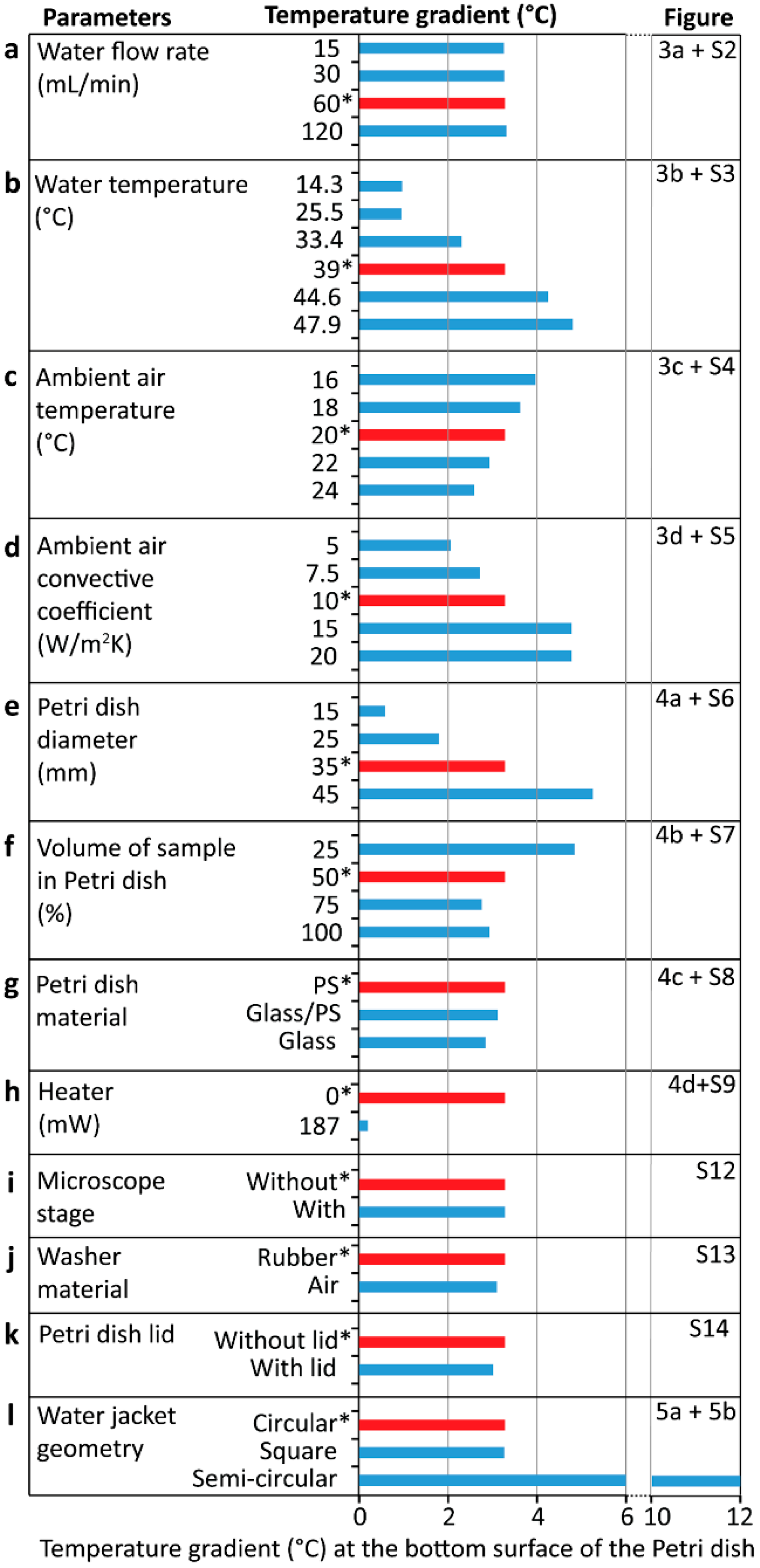
Figure 6 compares the magnitude of the temperature gradient along the radial axis of the Petri dish (z = 1 mm) for all stable cases presented in Figure 2, Figure 3, Figure 4 and Figure 5. We also investigated the effect of microscope stage, washer material, and Petri dish lid on the thermal characteristics of the water jacket system, as presented in Figures S12–S14. It should be noted that a lid is usually inserted on the Petri dish in order to maintain sterility of the sample, which is a crucial condition for cell culture. A quick look at this figure reveals that the following five parameters, including the (i) flow rate of the water recirculating through the water jacket, (ii) Petri dish material, (iii) placing of the Petri dish on a microscope stage, (iv) washer material, and (v) inserting a lid onto the Petri dish, did not change the temperature gradient significantly. In contrast, the following seven parameters significantly changed the temperature gradient across the sample, as summarized below:

Water inlet temperature: Increase of water inlet temperature from 25 to 45 °C increased the temperature gradient from 1 to 4.4 °C, as presented in Figure 3b and Figure S3. Interestingly, similar temperature gradients were obtained for water inlet temperatures of 15 °C (5 °C colder than ambient) and 25 °C (5 °C hotter than ambient), which clearly indicates the dependence of the temperature gradient on the ambient temperature.

Ambient temperature: Decrease of ambient temperature from 24 to 16 °C increased the temperature gradient from 2.4 to 4 °C, as presented in Figure 3c and Figure S4.

Free convection coefficient: Increase of free convection coefficient occurred at the free surfaces of the system from 5 to 20 W/m²K increased the temperature gradient from 2.1 to 4.3 °C, as presented in Figure 3d and Figure S5.

Petri dish diameter: Decrease of the Petri dish diameter from 45 to 15 mm (50% filled in all cases) decreased the temperature gradient from 5.1 to 0.9 °C, as presented in Figure 4a and Figure S6.

Sample volume: Increase of the volume of the sample inside the Petri dish from 25% to 75% (for a 35 mm diameter Petri dish) decreased the temperature gradient from 4.2 to 2.9 °C, as presented in Figure 4b and Figure S7. A slightly higher temperature gradient was obtained when increasing the sample volume from 75% to 100%, which was attributed to higher convective loss at the top surface of the Petri dish due to higher thermal conductivity of water compared to air.

Water jacket geometry: A semi-circular water jacket led to an asymmetric temperature profile with a temperature gradient of 12 °C, the highest value obtained in our investigations, as presented in Figure 5b.

Integrated heater: Integrating a heater underneath the Petri dish led to a uniform temperature across the sample with a temperature gradient of 0.2 °C, the lowest in our investigations, as presented in Figure 4d and Figure S9.

3.6. Thermal Analysis of the Water Jacket under Transient Conditions

We also investigated the thermal performance of the water jacket system under transient conditions. The inlet water temperature was increased from 39 to 48.5 °C to raise the sample temperature at the side walls from 37 to 45 °C.

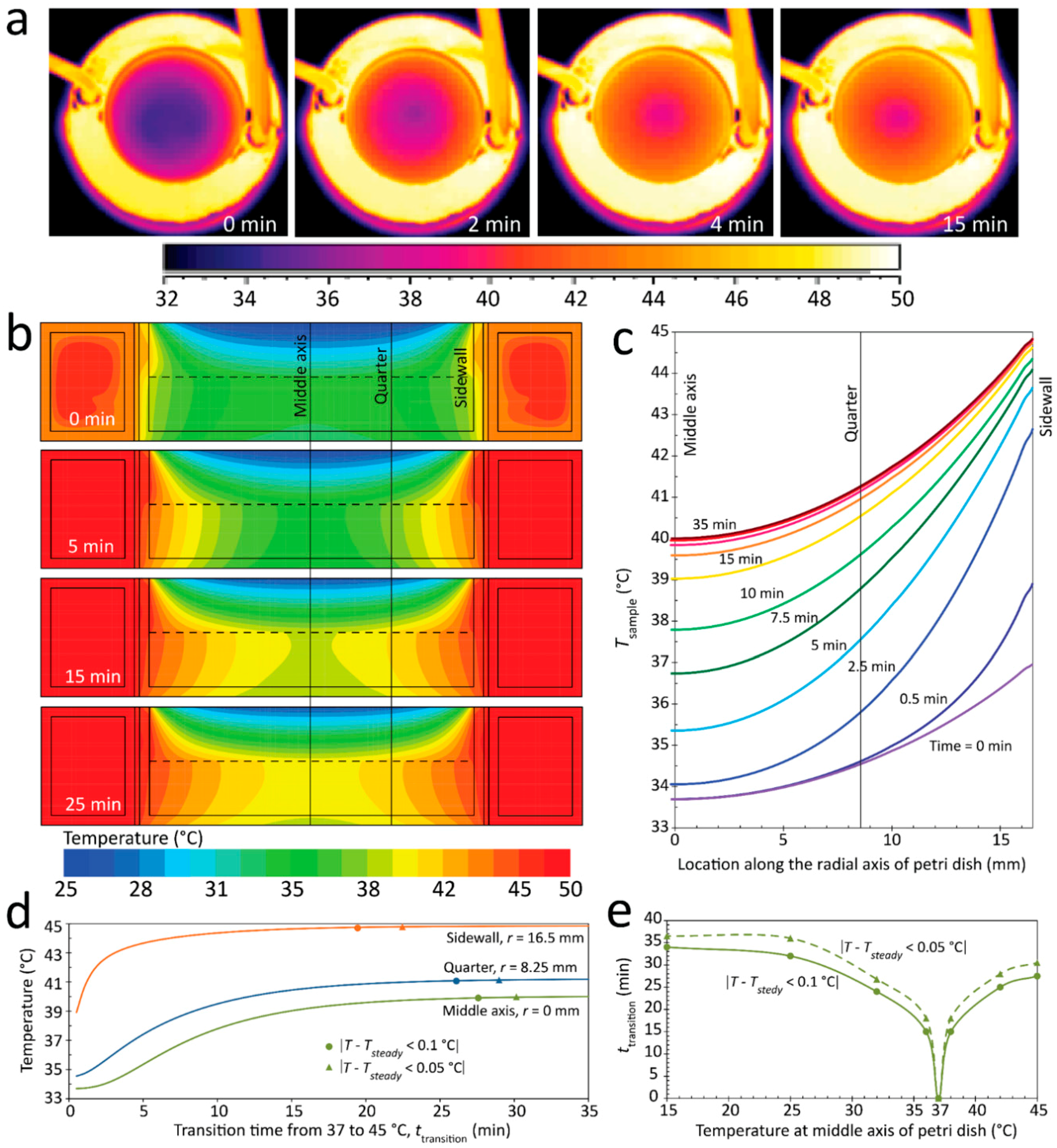
An infrared thermal imaging camera was utilized to monitor the temperature distribution at the top surface of the water jacket system over a period of 30 min. Supplementary Movie 1 presents the transient temperatures over the first 15 min of the process. Figure 7a presents the experimental temperature contours at four snapshots, corresponding to 0.5, 2, 4 and 15 min. Our measurements revealed the rapid temperature change of the sample in the first few minutes of the process, which can be clearly seen by comparing the size of the cold region at the middle of the Petri dish that is colored in purple. The system reached its steady-state conditions within ~25 min.

Figure 7b shows the temperature contours of the system 0.5, 5, 15, and 25 min after the inlet water temperature was increased. Simulations revealed that the temperature of the water recirculating through the water jacket reaches steady-state conditions in less than 1 min due to the dominance of forced convection. In contrast, the temperature of the sample inside the Petri dish reached steady-state conditions in >25 min due to dominance of conduction. The detailed temperature contours from 0 to 35 min are presented in Figure S15.

Figure 7c compares the dynamic temperature profiles along the radial axis of the Petri dish at different time steps ranging from 0 to 35 min before the entire system reached steady-state conditions. The simulations revealed that the rate of temperature change reduces toward the end of the process, which is in line with our experiments. For example, while the middle region of the Petri dish experienced a temperature rise of ~5.5 °C from 0 to 15 min, it only experienced a temperature rise of ~1 °C from 15 to 35 min.

Figure 7d further investigates the temporal temperature changes at the three representative locations of the Petri dish, including the middle, quarter, and sidewall axes, as shown in Figure 7c. The sidewall region, influenced by convection heat exchange through the sidewalls of the Petri dish, experienced a relatively quick temperature rise. Alternatively, the middle region, influenced by conductive heat exchange, experienced a relatively slow temperature rise. The quarter region, although symmetrically located between the sidewall and middle regions, was more influenced by the conduction mechanism.

Next, we defined the following two criteria to assess the “transition period,” or the amount of time required to obtain new steady state conditions across these three regions, in which T_steady is the target steady-state temperature at each of those regions when the sample temperature is set to 45 °C.

$$\left|T-T_{steady}\right|<0.1°\mathrm{C}$$

(14)

$$\left|T-T_{steady}\right|<0.05°\mathrm{C}$$

(15)

Using the first criteria, the “transition periods” across the sidewall, quarter, and middle regions were 19, 26, and 27 min, respectively, as shown by the circles in Figure 7d. In comparison, using the second criteria, the “transition period” across the sidewall, quarter, and middle regions increased to 22, 28.5, and 30.5 min, respectively, as shown by the triangles in Figure 7d.

Figure 7e shows the “transition period” based on the middle region of the Petri dish for different transient conditions obtained from both criteria defined in Equations (14) and (15). These transient conditions include three “heating” cases set to increase the temperature of the sample from 37 to 38, 42 and 45 °C, and four “cooling” cases set to decrease the temperature of the sample from 37 to 36, 32, 25, and 15 °C, as presented in Figures S16–S18. The simulations revealed that the “transition period” depended on the magnitude of the temperature change, defined as $\Delta T$. For example, using the first criterion, the “transition period” can be described as $t_{transition}=15.232 \Delta T^{0.291}$ for the “heating” cases and $t_{transition}=16.026 \Delta T^{0.253}$ for the “cooling” cases. Interestingly, the transition period was almost symmetrical with respect to the initial temperature of the sample, as shown for the cases of 37 ± 1 °C and 37 ± 5 °C. More interestingly, the “transition period” for the case of 37 ± 1 °C was 15 min, indicating the ineffectiveness of the water jacket system for handling small temperature changes.

3.7. Comparison of Sample ‘Transition Period’ under Different Dynamic Conditions

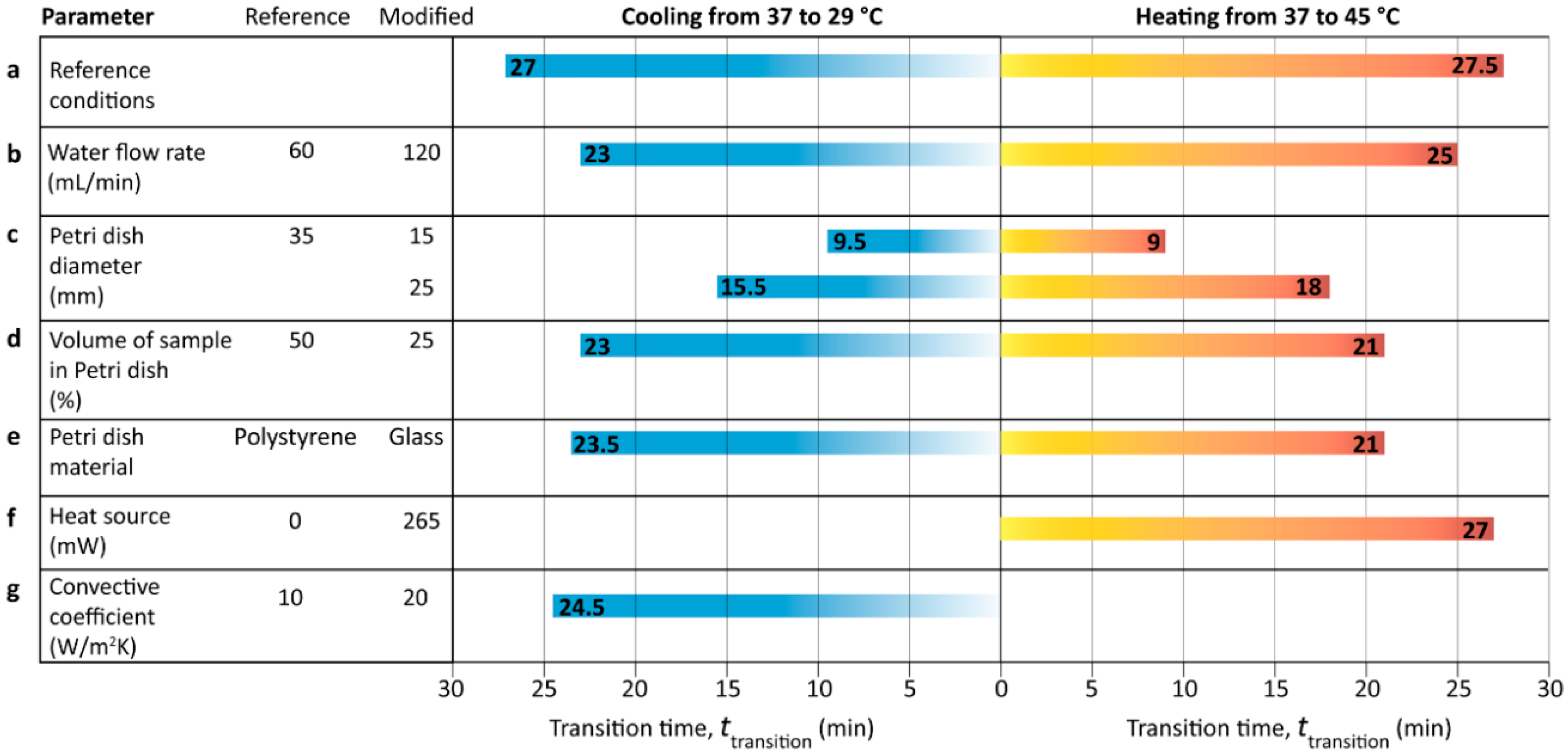
The transient simulations were further extended to analyze the transition period of the sample using different strategies and based on Equation (14), as summarized in Figure 8. Simulations were conducted under the 37 ± 8 °C condition, corresponding to the heating (37 to 45 °C) and cooling (37 to 29 °C) cases. The detailed transient temperature contours corresponding to the different cases are presented in Figures S19–S25. No significant differences were observed between the transition period of the heating and cooling cases, which is in line with our findings shown in Figure 7e.

Based on our results, the strategies can be categorized into three groups according to their effectiveness for shortening the transition period, as discussed below:

Group one: doubling the flow rate of recirculating water, integrating the heater underneath the Petri dish, and doubling the localized convective heat transfer coefficient at the bottom surface of the Petri dish (by placing a small fan) shortened the transition period by ~10%. The integrated heating system described here operates by setting the water inlet temperature to 45.7 °C, and the heater power to 265 mW, under which the sample temperature reaches 45 °C under steady state conditions, and the temperature gradient across the Petri dish decreases to 0.5 °C, as presented in Figure S9. Despite its effectiveness under stable conditions, the integrated heating system is unable to reduce the “transition period” of the sample significantly. This suggests a more holistic approach by varying the water inlet temperature and the heater power to reduce the response time of the sample while producing a low temperature gradient across the sample and avoiding overheating of the sample.

Group two: reducing the sample volume inside the Petri dish to 25%, and using a glass Petri dish instead of a polystyrene dish shortened the “transition period” by ~20%.

Group three: reducing the Petri dish diameter to 25 mm shortened the “transition period” by ~30%, and more interestingly, further reducing the Petri dish diameter to 15 mm shortened the “transition period” by ~60%.

4. Conclusions

In this study, we investigated the thermal characteristics of a water jacket system used for temperature control of Petri dish cell culture chambers. In particular, we studied the temperature distribution across samples under stable conditions and the transition period of samples under dynamic conditions. Under stable reference conditions, the temperature gradient along the radial axis of a 35 mm diameter Petri dish was 3.28 °C. Under dynamic conditions, the transition period of a 35 mm Petri dish, which is the amount of time required to increase the sample temperature from 37 to 45 °C, was 27.5 min. These results indicate the limited capability of a conventional water jacket system for creating uniform temperature profiles and rapid temperature changes across a sample.

We studied the role of various operational, geometric, and environmental conditions on the temperature distribution and transition period of the sample. Our results suggest that reducing the diameter of the Petri dish and incorporating a heater underneath the Petri dish were the two most effective solutions for reducing the temperature gradient across the sample under stable conditions. For example, reducing Petri dish diameter to 25 and 15 mm decreased the temperature gradient to 1.8 and 0.6 °C, respectively, whereas integrating a heater with an input power of 187 mW decreased the temperature gradient to 0.2 °C. Our results also suggest that reducing the diameter of the Petri dish, reducing sample volume, and using glass Petri dish chambers were the three most effective solutions for reducing the transition period of the sample under dynamic conditions. For example, reducing the Petri dish diameter to 25 and 15 mm decreased the transition period to 18 and 9.5 min, respectively, in comparison reducing the sample volume to 25% and using a glass Petri dish both decreased the transition period to 21 min. These results were obtained when heating the sample from 37 to 45 °C with almost similar transition periods obtained when cooling from 37 to 29 °C.

Future work includes developing more accurate numerical models to consider (i) sample evaporation in long-term experiments, (ii) convective instabilities driven by Marangoni and buoyancy-driven flows caused by the inhomogeneous concentrations of species [28], (iii) presence of high-density cultured cells and (iv) presence of miniaturized self-sufficient devices for passive/active release of chemicals [29] or encapsulation of cells inside droplets [30].