Abstract
The complex dispersion relations along the main symmetry directions of two-dimensional finite size periodic arrangements of resonant or non-resonant scatterers are recovered by using an extension of the SLaTCoW (Spatial LAplace Transform for COmplex Wavenumber) method. This method relies on the analysis of the spatial Laplace transform instead of the usual spatial Fourier transform of the measured wavefield in the frequency domain. We apply this method to finite dimension square periodic arrangements of both rigid and resonant scatterers embedded in air, i.e., to finite size sonic crystals and finite size acoustic metamaterials, respectively. The main hypothesis considered in this work is the mirror symmetry of the finite structure with respect to its median axis along the analyzed direction. However, we show that the method is robust enough to provide excellent results even if this hypothesis is not fully satisfied. Effectively, a minor asymmetry could be considered as a side effect when the structure is large enough because Laplace transforming the field along the main symmetry directions also implies averaging the field in the perpendicular one. The calculated complex dispersion relations are in excellent agreement with those obtained by an already validated technique, like the Extended Plane Wave Expansion (EPWE). The methodology employed in this work is intended to be directly used for the experimental characterization of real 2D periodic and resonant systems.
1. Introduction
Periodic structures or locally resonant systems, also known as metamaterials, have revolutionized the control of waves these last years [1,2]. The main physical properties of these structured media, as for example the opening of band gaps [3,4], the slow wave frequency band [5,6], or the spatial filtering [7], among others, can be directly derived from the complex dispersion relation [8,9,10,11,12]. In addition to dispersive effects, wave attenuation can be caused by factors such as geometric attenuation or intrinsic material loss (e.g., heat or viscous dissipation). In all cases, wave attenuation can be interpreted in terms of complex wavenumbers, which are functions of the angular frequency via a complex dispersion relation . The real part of the wavenumber translates the propagative (dispersive) properties of the system while its imaginary part is related to the attenuation. This rich but sometimes hardly to interpret information is of crucial relevance for the design of metamaterial-based devices. Therefore, the recovery of the complex dispersion relation, i.e., the measurement or calculation of both the dispersion and the attenuation of waves in a finite system is of utmost importance in wave physics and material science, since it provides insightful information on the tested system also allowing the characterization of the effective properties of the material.
Several methods have been proposed during these last years to calculate the complex dispersion relation of waves in discrete or continuous systems. The extended plane wave expansion [9,10] or methods based on Multiple Scattering Theory (MST) [13,14] are efficient tools to evaluate the complex dispersion relation in non-resonant structures made of scatterers of simple geometry. Numerical approaches are more relevant [15] when the scatterer geometry is more complicated or the scatterers are resonant.
Recently, the SLaTCoW (Spatial LAplace Transform for COmplex Wavenumber) [11,12] method has been proposed as a general procedure for the recovery of the complex dispersion relation. It has been successfully applied to several systems of different kind, such as Lamb-like modes in lossy materials in the low kHz regime, elastic waves in a Duralumin plate in the MHz regime at the Zero-Group Velocity (ZGV) point, surface acoustic waves in a two-dimensional microscale granular crystal adhered to a substrate near 100 MHz [11] and also spoof surface acoustic waves at a lossy resonant metasurface [12]. The method is based on the spatial Laplace transform (LT) instead of the usual spatial Fourier transform (FT) of the measured wavefield in the frequency domain. The LT, providing information on both the real and imaginary parts of the wavenumber, is analyzed by minimizing a correctly chosen cost function. The complex wavenumbers (as well as the complex amplitudes) of the modes are reconstructed even when they are interacting one with another or overlapping. Moreover, the SLaTCoW method is particularly suitable for the experimental characterization of real periodic systems of finite-size (resonant or non-resonant), which, while exhibiting similar properties as systems of infinite extent such as band gaps [16,17,18] or other dispersive effects [19,20], can not be experimentally characterized using methods considering infinite structures, such as EPWE, MST or solving an eigenvalue problem using the Finite Element Method (FEM).
In this work, we present an advanced version of the SLaTCoW method to characterize the complex dispersion relation of two-dimensional systems. We apply this methodology to both periodic media as Sonic Crystals (SC) and locally resonant acoustic materials. The article is organized as follows. The methodology and the extension of the method is presented Section 2. Section 3 depicts the different two-dimensional configurations the methodology is applied to. Finally, results are provided and validated in Section 4. Numerical reconstructions from finite size two-dimensional systems agree well with complex dispersion relation calculated from analytical techniques. A summary and the concluding remarks are given in Section 5.
2. Methods
2.1. SLatCoW
The SLatCow method relies on the analysis of the spatial LT of the acoustic field in the frequency domain. The analysis is performed in the linear harmonic regime at the circular frequency with the implicit time dependence . For two-dimensional problems, the pressure field is recorded on a surface map of dimensions and , as depicted in Figure 1. The excitation is assumed to take the form of a plane incident wave along the positive x-axis. Therefore, the pressure field takes the form
where is the complex amplitude of the m-th mode, is the complex wavenumber of the m-th mode, is the set of modes, and is the gate function equal to 1 when and equal to 0 elsewhere. For the sake of explanation the dependence is further dropped.
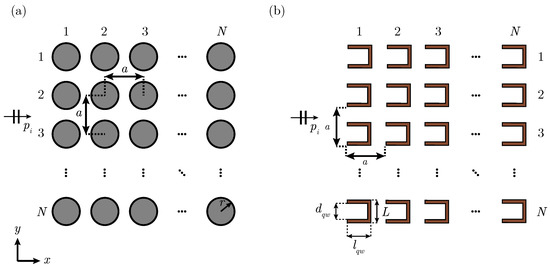
Figure 1.
Set-up of the numerical experiments used to calculate the complex dispersion relation: (a) 2D SC composed of cylindrical scatterers arranged in a square lattice. (b) 2D Metamaterial composed of QWRs.
The complex wavenumber is also defined as , with and are two component vectors, one along the x-axis and the other along the y-axis. Please note that along the specific direction , , with and ensuring that Equation (1) only involves forward propagating waves along positive . Applying the usual spatial FT only enables the recovery of . In order to recover both real and imaginary parts of , a spatial LT is applied to denoted , where is a complex valued vector , with and being two component vectors, again one along the x-axis and the other along the y-axis. The spatial LT takes the form
In what follows, we are only interested in specific directions, namely and , obtained by rotating the structure in the area . For a structure of infinite lateral extent, i.e., along the y-direction, the continuity of the real part of the is ensured between the outer and the inner domain. In the present case of finite lateral dimensions, every modes are excited because of wave diffraction by the edges. Fixing ensures that we are only looking for modes propagating along the x-axis. Nevertheless, the LT reduces in the general case to . Considering a symmetric structure with respect to excited by a plane wave along the x-axis ensures that , [21]. Therefore, the two dimensional LT reduces to
Please note that the symmetry is ensured in the case depicted in Figure 1a along both directions and , while it is only ensured along the direction in the case depicted in Figure 1b. Along the direction, the symmetry condition is not satisfied because of the rotation of the quarter-wavelength resonator (QWR) openings. Nevertheless, this will be considered and proven as a side effect in what follows. Note also that Laplace transforming along the y-direction for consists in averaging the pressure field measured along this axis or alternatively Fourier transforming the field with . The problem becoming also independent from y, we drop the x dependence on both and , so as and .
The spatial LT of the field therefore reduces to a form close to the one used in Ref. [11]. The recovery of is performed in a very similar way for each frequency by minimizing the following cost function
where is the spatial LT of the measured field , and and are, respectively, the theoretical amplitude and phase of the m-th mode. The minimization is performed under constraints with the Nelder-Mead simplex algorithm (® Matlab function ).
2.2. Spatial Sampling Criteria for Dispersion Relation Recovery
As stated previously, the SLaTCoW method relies on analyzing the pressure field in the complex wavenumber and frequency domains (). Hence, a double transformation of the acoustic pressure is needed to apply the method. First, time to frequency () through the temporal FT, then space to wavenumber () through the spatial LT. While the temporal FT is not limited by or independent from the spatial periodicity of the structure, the spatial LT greatly depends on both the size of the structure, i.e., the number of periodic elements, and the spatial sampling of the acoustic field. To illustrate this, we consider a spatial signal as represented in Figure 2a and applied successively a temporal and a spatial FT. By analogy with temporal signals and following basic sampling theory, the resolution in -space is determined by the length of the signal, , where with the spatial sampling and N the number of samples of the spatial signal. Lets consider now a finite size one-dimensional periodic structure with lattice constant a formed by alternating two different materials, as depicted in Figure 2b. From the Nyquist-Shannon sampling theorem [22] and considering periodicity in -space, the spatial sampling rate has to be equal or greater than twice the highest wavenumber component, i.e., , where . As a result, the following condition for the spatial sampling should be satisfied to ensure that no information is lost when performing the FT. In summary, for a finite dimension periodic structure comprising a specific number of unit cells and assuming that the wavefield is measured at a single point per periodic element, the number of these periodic elements (unit cells) determines the number of points and hence the resolution in the -space as follows
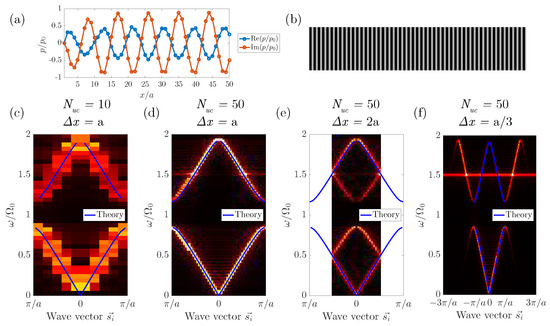
Figure 2.
(a) Example of real and imaginary parts of the spatial pressure signal along the multilayer structure at the normalized frequency . (b) Periodic multilayer structure composed of periodic elements, combining two artificial materials with different acoustic properties. (c–f) Double FT of the pressure field and dispersion relation of the multilayer structure considering different number of periodic elements and different values of the spatial sampling .
Figure 2c–f illustrates the effects of the variation of the number of periodic elements, and therefore of the spatial sampling used on the FT of the pressure field, used to evaluate the dispersion relation of the multilayer structure shown in Figure 2b. A double FT is applied to numerically simulated spatio-temporal acoustic pressure values, . Results are presented for positive and negative values of the wavenumber and are compared to the theoretical dispersion relation calculated using the Rytov formula [23]. Figure 2c,d analyze the influence of the number of unit cells on the double FT using the critical sampling rate . The total number of wavevector points in the -space is not high enough to extract accurate information to represent the dispersion relation in the case of a structure containing only . Please note that the number of points in the -space is distributed along the positive and negative parts of the wavenumber. Figure 2e,f show the consequences of spatially under-sampling and over-sampling, respectively. The former causes the FT to be folded, while the latter creates replicates of the FT. However, no gain in information is obtained by increasing the spatial sampling above its critical value. Please note that the wavenumber resolution can be artificially increased by zero-padding the spatial signal in the space domain, although no actual information will be extracted from this process.
3. Numerical Set-Up
Two different 2D periodic structures of finite sizes are considered in this study, as shown in Figure 1. Both structures are composed of rigid scatterers arranged in a square lattice with a lattice constant m, embedded in air, where . The SC shown in Figure 1a consists of cylindrical rigid scatterers with radius m. The second periodic system is a metamaterial consisting of square scatterers with QWRs, as shown in Figure 1b. The geometric parameters of the resonator are its external side length, m, and internal dimensions, m and m. See Refs. [24,25] for specific details on the resonators. The host medium in both cases is air, with density and speed of sound kg/m3 and m/s, respectively.
Numerical experiments are carried out using FEM. A scattering problem in the frequency domain is solved for the two structures described previously. The excitation is an incident plane wave traveling along the positive x-axis. Perfectly matched layers are considered surrounding the numerical domain to approximate the Sommerfeld radiation condition. Following the spatial sampling criteria for periodic structures introduced in Section 2.2, the acoustic pressure is recorded at multiple positions separated by the lattice constant, , giving rise to a total of measurement points. Please note that the structures presented in Figure 1 are used to calculate the complex dispersion relation along the X direction. To retrieve the dispersion relation along the M direction both structures are rotated by 45 degrees while the incident plane wave is unchanged, i.e., remains traveling along the positive x-axis. Note also that the spatial sampling in this case is modified accordingly, .
4. Results
4.1. Complex Dispersion Relation. SLaTCoW vs. EPWE
We start by considering a reference case which consists in a classical SC of finite size composed of 21 × 21 rigid cylinders arranged in a square lattice and embedded in air, where no losses are considered. In this situation, the imaginary part of the wavenumber is non-zero only because of the evanescent modes created within the band gap. To validate the results obtained using SLaTCoW, we make use of EPWE [9,10], an already established technique that allows us to retrieve both the real and imaginary parts of the wavenumber for non-resonant periodic structures of simple geometries.
Figure 3 illustrates the complex band structure of the finite SC presented in Figure 1 using SLaTCoW and the one obtained using EPWE for an infinite SC with the same geometrical and physical properties. The imaginary part of the wavenumber is shown in the right (left) panel in the X (M) direction, while the real part of the wavevector for both directions is shown in the central panel. Both the real and imaginary parts of the wavenumber show an excellent agreement with the EPWE calculations for both directions of symmetry. Moreover, the typical signature of the Bragg interference on the imaginary part of the wavevector is captured, with a maximum attenuation at the Bragg frequency and smooth variations from this point to the upper and lower limits of the band gap. Minor differences are noted in the band gap frequency range along the M direction, where the imaginary part of the wavenumber using SLaTCoW is slightly lower than the one obtained using EPWE. Small differences are also noticed on the real part of the wavenumber in that frequency range. Both are therefore attributed to the finite size of the SC used for SLaTCoW calculations.
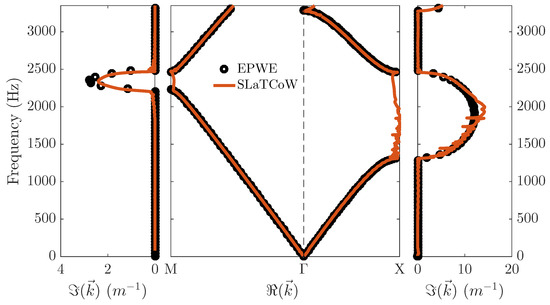
Figure 3.
Complex dispersion relation for a SC composed of rigid cylinders arranged in a square lattice. Numerical results obtained for a finite structure are compared to the ones obtained using EPWE for the same periodic structure having infinite size.
4.2. Complex Dispersion Relation of a 2D Periodic Resonant System
We then focus on the dispersion relation of the 2D acoustic metamaterial of finite size. Specifically, we consider the structure shown in Figure 1b, i.e., a periodic system composed of QWRs arranged in a square lattice embedded in air. Both lossless and lossy cases are considered with visco-thermal losses considered solely inside the QWR resonators [24,25]. Figure 4 shows the complex dispersion relation results of the 2D acoustic metamaterial. The real part of the wavenumber is shown in the central panel and results obtained using SLaTCoW are compared to those obtained solving an eigenvalue problem using the FEM over an infinite periodic structure with the same geometric and physical characteristics. Please note that the dispersion relation of the host medium alone, i.e., the air in this case, is also plotted in gray dashed lines.
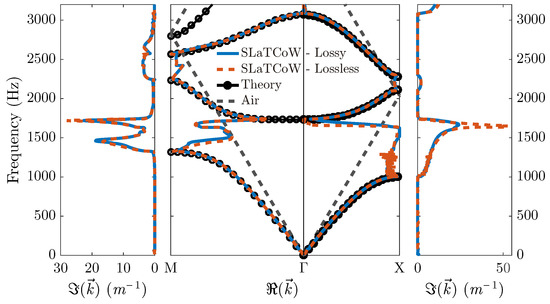
Figure 4.
Complex dispersion relation for a periodic resonant system formed by QWRs. Numerical simulations using an infinite structure and solving the corresponding eigenvalue problem in FEM are compared to the results obtained applying SLatCoW from numerical data using a finite structure.
Results show an excellent agreement for all the propagative bands between the results obtained using SLaTCoW and FEM for both X and M directions. However, differences are noticed in between the propagative bands, where the eigenvalue problem does not possess real solution. Effectively, no real solution satisfy the problem for a periodic system of infinite extent. Moreover, acoustic modes corresponding to the air medium are also recovered via the SLaTCoW method, because the structure under analysis is of finite size and excited by a plane incident wave initially propagating in a homogeneous medium. Their magnitude are much smaller than those of periodic structure modes and decrease rapidly with the number of unit cells of the finite structure. In the band gap frequency range, air modes become more significant, because no propagative mode in the periodic system exists. They are detected by the algorithm as for example along the M direction around 1500 Hz. This prompts a reduction of the imaginary part of the wavenumber at a small range of frequencies within the resonant gap. A closer look to X results for both lossless and lossy cases, indicate the typical characteristics of resonant and Bragg gaps when the air modes are not detected. The attenuation peak of the resonant band gap (around 1600 Hz) is greatly reduced when the visco-thermal losses are accounted for in the QWRs. On the other hand, the attenuation is unaltered between lossless and lossy cases for the Bragg gap (around 2200 Hz), because the losses are only considered inside the resonators and not in the host medium.
5. Conclusions
We have presented a methodology to calculate the complex dispersion relation of 2D periodic resonant and non-resonant systems of finite-size via a slight modification of the SLaTCoW method presented in Ref. [11]. By assuming the finite size structures to be mirror symmetric with respect to their median axes along the analyzed direction, the SLaTCoW method is extended to a two-dimensional problem allowing for the calculation of the dispersive and attenuation properties of the system at specific symmetry directions, namely X and M. To properly record the necessary acoustic pressure, which happens to be distributed in a surface map to account for 2D structures, a basic spatial sampling criteria applicable to periodic structures is provided and discussed. Two periodic structures with different properties are considered in the study. First, we validated the results provided by the present methodology by comparing them to those obtained via a well-established technique, the EPWE, exhibiting an excellent agreement for both the real and imaginary parts of the wavevector for the two symmetry directions. Then, we show the potential of the methodology to analyze a 2D acoustic metamaterial including QWRs and accounting for visco-thermal losses. The obtained results also show an excellent agreement with an already validated technique for the real part of the dispersion relation and clearly manifest the typical signature of resonant and Bragg gaps in the imaginary part of the wavenumber. Limitations related to the appearance of air modes in the dispersion results, due to the finite size of the structure and its excitation by plane incident waves are also discussed. As shown in Refs. [11,12] this method is applicable to systems of different kind, at different frequency ranges, and should also be applicable for other type of waves, such as TE and TM modes for electromagnetic waves, where there is a close similarity with the 2D acoustic wave equation. Finally, the methodology presented in this work is intended to directly serve for the experimental characterization of real 2D periodic and resonant systems.
Author Contributions
Conceptualization, A.C., V.R.-G., J.P.G. Methodology, A.C., V.R.-G., J.P.G.; Original Draft Preparation, A.C., V.R.-G., J.P.G.; Writing Review & Editing, A.C., V.R.-G., J.P.G.; Supervision, A.C., V.R.-G., J.P.G., Numerical simulations: A.C.
Funding
This article is based on work from COST Action DENORMS CA15125, supported by COST (European Cooperation in Science and Technology).
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.; Yang, Z.; Chan, C.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nat. Mater. 2006, 5, 452–456. [Google Scholar] [CrossRef] [PubMed]
- Bradley, C.E. Acoustic Bloch Wave Propagation in a Periodic Waveguide; Technical Report of Applied Research Laboratories, Report No. ARL-TR-91-19; The University of Texas at Austin: Austin, TX, USA, 1991. [Google Scholar]
- Sugimoto, N.; Horioka, T. Dispersion characteristics of sound waves in a tunnel with an array of helmholtz resonators. J. Acoust. Soc. Am. 1995, 97, 1446. [Google Scholar] [CrossRef]
- Theocharis, G.; Richoux, O.; García, V.R.; Merkel, A.; Tournat, V. Limits of slow sound propagation and transparency in lossy, locally resonant periodic structures. New J. Phys. 2014, 16, 093017. [Google Scholar] [CrossRef]
- Groby, J.-P.; Huand, W.; Lardeau, A.; Aurégan, Y. The use of slow sound to design simple sound absorbing materials. J. Appl. Phys. 2015, 117, 124903. [Google Scholar] [CrossRef]
- Romero-García, V.; Picó, R.; Cebrecos, A.; Staliunas, K.; Sánchez-Morcillo, V.J. Angular Band Gaps in Sonic Crystals: Evanescent Waves and Spatial Complex Dispersion Relation. J. Vib. Acoust. 2013, 135, 041012. [Google Scholar] [CrossRef]
- Philippe, F.D.; Roux, P.; Cassereau, D. Iterative high-resolution wavenumber inversion applied to broadband acoustic data. IEEE Trans. Ultrason. Ferroelectr. Frequency Control 2008, 55, 2306–2311. [Google Scholar] [CrossRef]
- Laude, V.; Achaoui, Y.; Benchabane, S.; Khelif, A. Evanescent Bloch waves and the complex band structure of phononic crystals. Phys. Rev. B 2009, 80, 092301. [Google Scholar] [CrossRef]
- Romero-García, V.; Sánchez-Pérez, J.V.; García-Raffi, L.M. Evanescent modes in sonic crystals: Complex dispersion relation and supercell approximation. J. Appl. Phys. 2010, 108, 044907. [Google Scholar] [CrossRef]
- Geslain, A.; Raetz, S.; Hirwia, M.; Ghamen, M.A.; Wallen, S.P.; Khanolkar, A.; Boechler, N.; Laurent, J.; Prada, C.; Duclos, A.; et al. Spatial Laplace transform for complex wavenumber recovery and its application to the analysis of attenuation in acoustic systems. J. Appl. Phys. 2016, 120, 135107. [Google Scholar] [CrossRef]
- Schwan, L.; Geslain, A.; Romero-García, V.; Groby, J.-P. Complex dispersion relation of surface acoustic waves at a lossy metasurface. Appl. Phys. Lett. 2017, 110, 051902. [Google Scholar] [CrossRef]
- Botten, L.; Nicorovici, N.; McPhedran, R.; de Sterke, C.; Asatryan, A. Photonic band structure calculations using scattering matrices. Phys. Rev. E 2001, 64, 046603. [Google Scholar]
- Poulton, C.G.; Movchan, A.B.; McPhedran, R.C.; Nicorovici, N.A.; Antipovy, A. Eigenvalue problems for doubly periodic elastic structures and phononic band gaps. Proc. R. Soc. A 2000, 456, 2543–2559. [Google Scholar] [CrossRef]
- Collet, M.; Ouisse, M.; Ichchou, M. A floquet-bloch decomposition of the elastodynamical equations: application to bi-dimensional wave’s dispersion computation of damped mechanical system. Int. J. Solids Struct. 2011, 48, 2837–2848. [Google Scholar] [CrossRef]
- García-Pablos, D.; Sigalas, M.; de Espinosa, F.R.M.; Torres, M.; Kafesaki, M.; García, N. Theory and experiments on elastic band gaps. Phys. Rev. Lett. 2000, 84, 4349–4352. [Google Scholar] [CrossRef] [PubMed]
- Montiel, F.; Chung, H.; Karimi, M.; Kessissoglou, N. An analytical and numerical investigation of acoustic attenuation by a finite sonic crystal. Wave Motion 2017, 70, 135–151. [Google Scholar] [CrossRef]
- Romero-García, V.; Krynkin, A.; García-Raffi, L.M.; Umnova, O.; Sánchez-Pérez, J.V. Multi-resonant scatterers in sonic crystals: Locally multi-resonant acoustic metamaterial. J. Sound Vib. 2013, 332, 184–198. [Google Scholar] [CrossRef]
- Yang, S.; Page, J.; Liu, Z.; Cowan, M.; Chan, C.; Sheng, P. Focusing of sound in a 3d phononic crystal. Phys. Rev. Lett. 2004, 93, 024301. [Google Scholar] [CrossRef] [PubMed]
- Sukhovich, A.; Jing, L.; Page, J.H. Negative refraction and focusing of ultrasound in two-dimensional phononic crystals. Phys. Rev. B 2008, 77, 014301. [Google Scholar] [CrossRef]
- Romero-García, V.; Sánchez-Pérez, J.V.; Garcia-Raffi, L.M. Evanescent waves and deaf bands in sonic crystals. AIP Adv. 2011, 1, 416011–416019. [Google Scholar] [CrossRef]
- Oppenheim, A.V. Discrete-Time Signal Processing; Pearson Education India: London, UK, 1999. [Google Scholar]
- Kosevich, A.M. Acoustics of Elastic Superlattices: Phonon Crystals, The Crystal Lattice: Phonons, Solitons, Dislocations, Superlattices, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006; Chapter 5; pp. 153–162. [Google Scholar]
- Lardeau, A.; Groby, J.-P.; Romero-García, V. Broadband transmission loss using the overlap of resonances in 3D sonic crystals. Crystals 2016, 6, 51. [Google Scholar] [CrossRef]
- Cavalieri, T.; Cebrecos, A.; Groby, J.-P.; Chaufour, C.; Romero-García, V. Three-dimensional multiresonant lossy sonic crystal for broadband acoustic attenuation: Application to train noise reduction. Appl. Acoust. 2019, 146, 1–8. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).