An Energy-Based Approach for Fatigue Life Estimation of Welded Joints without Residual Stress through Thermal-Graphic Measurement
Abstract
1. Introduction
2. Experimental Work
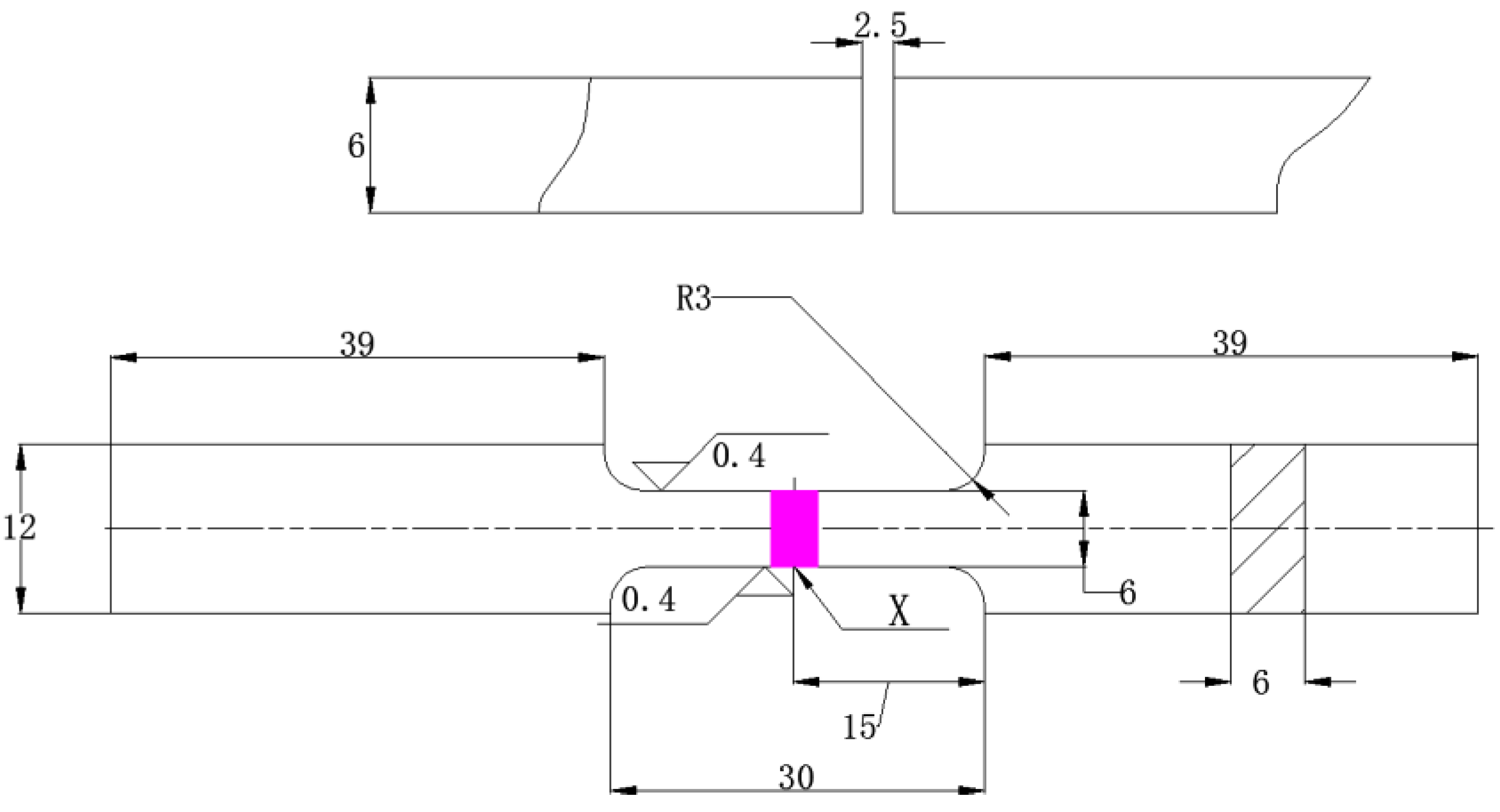
2.1. Specimen Preparation
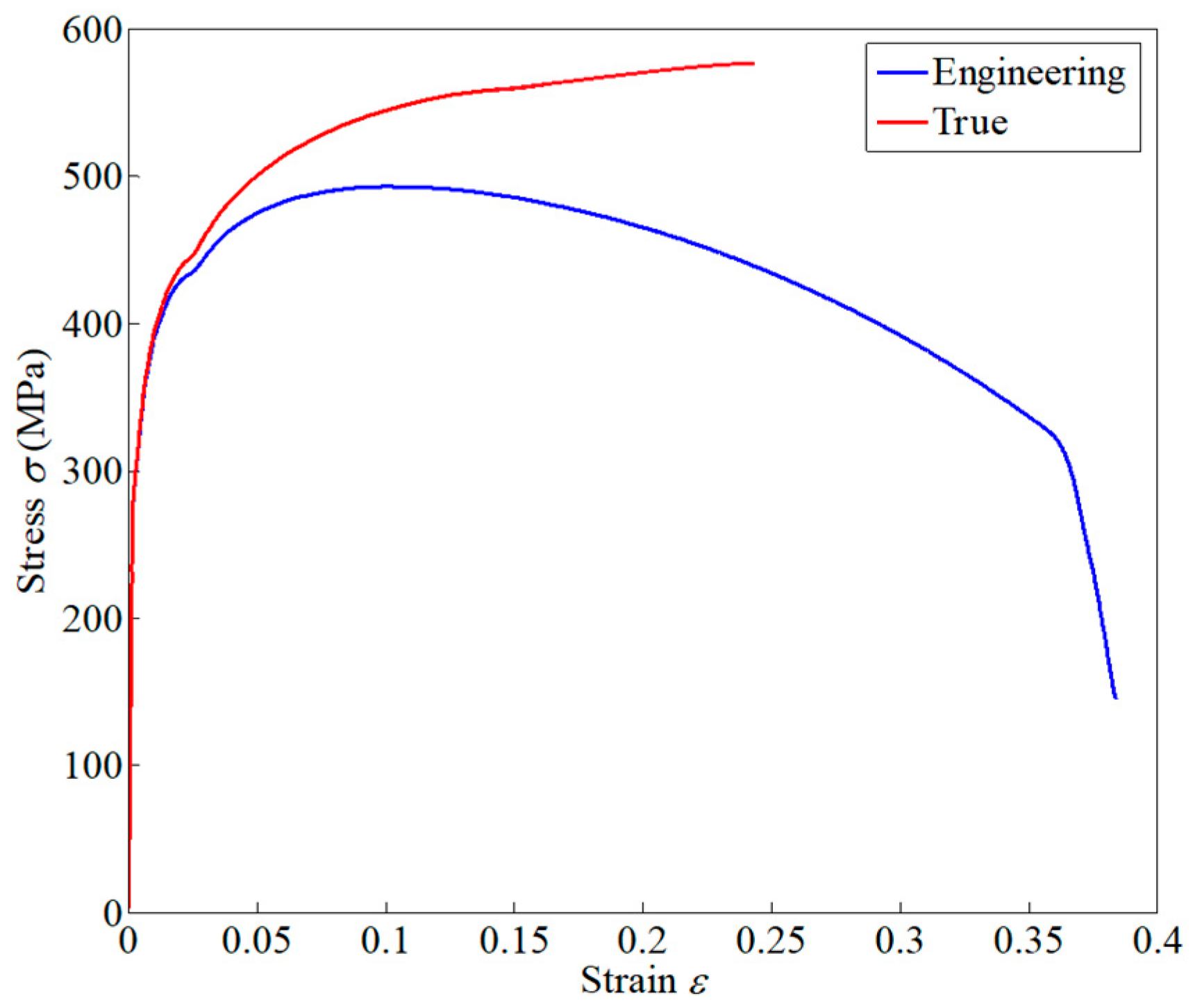
2.2. Monotonic Test
2.3. Cyclic Test
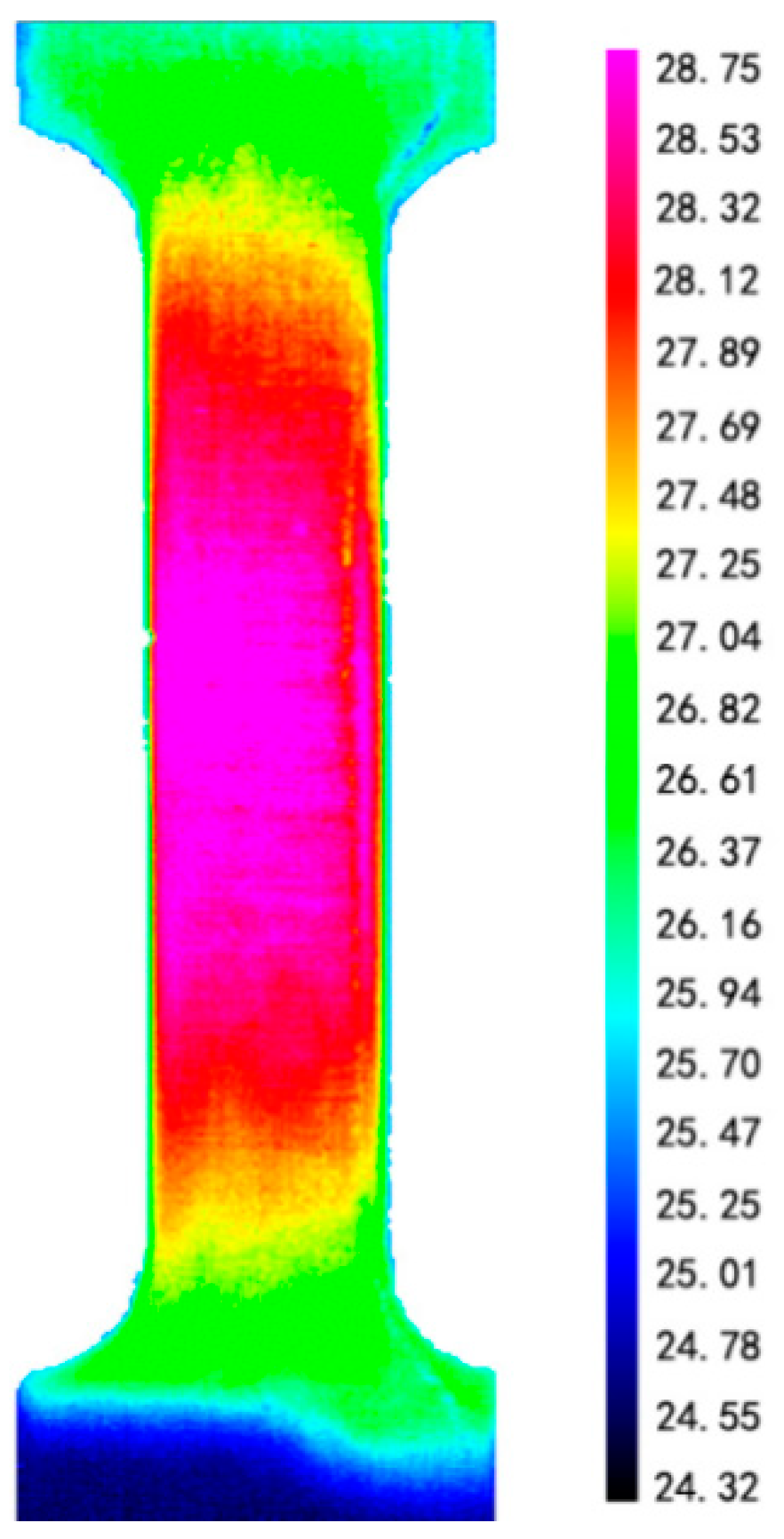
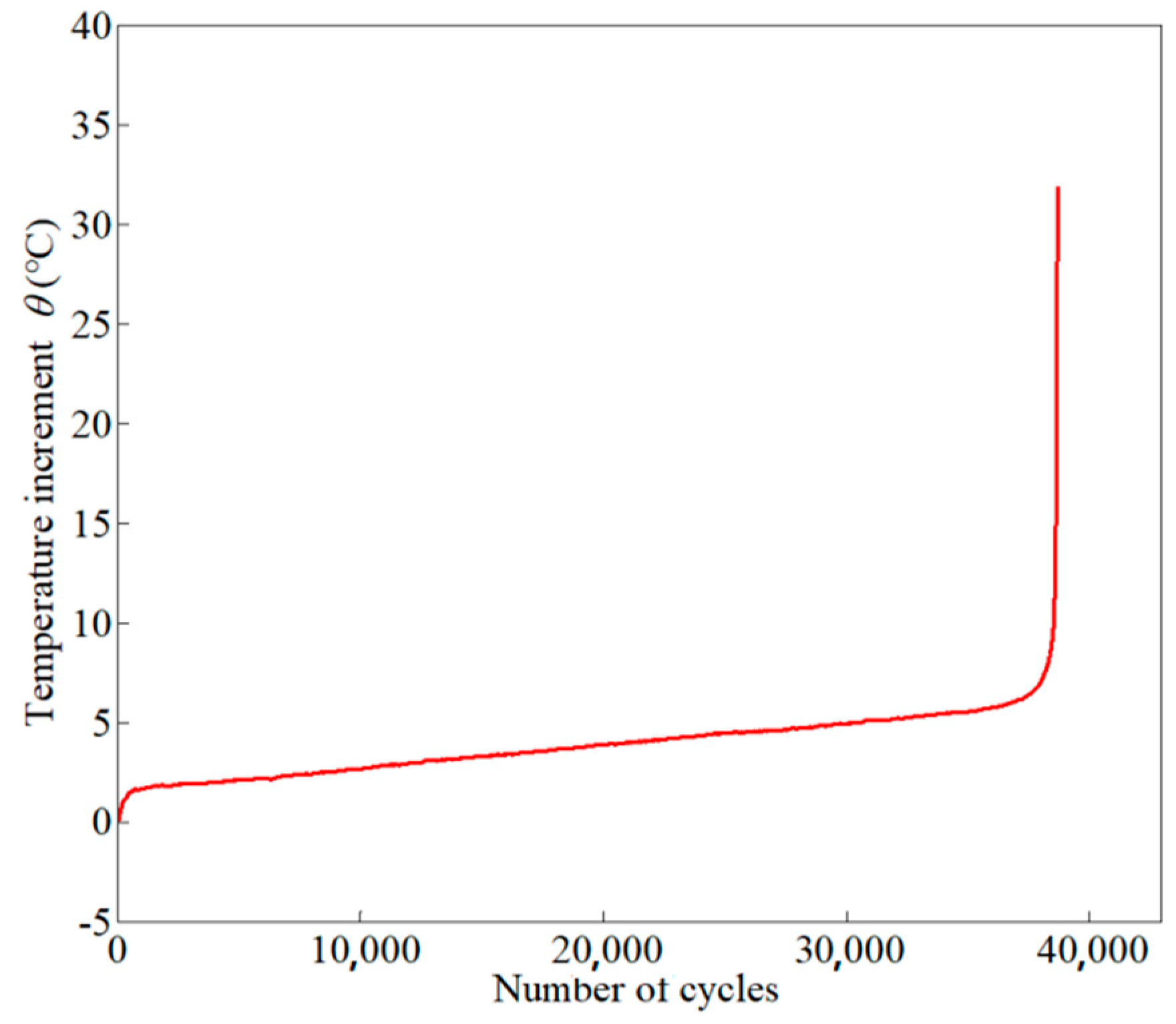
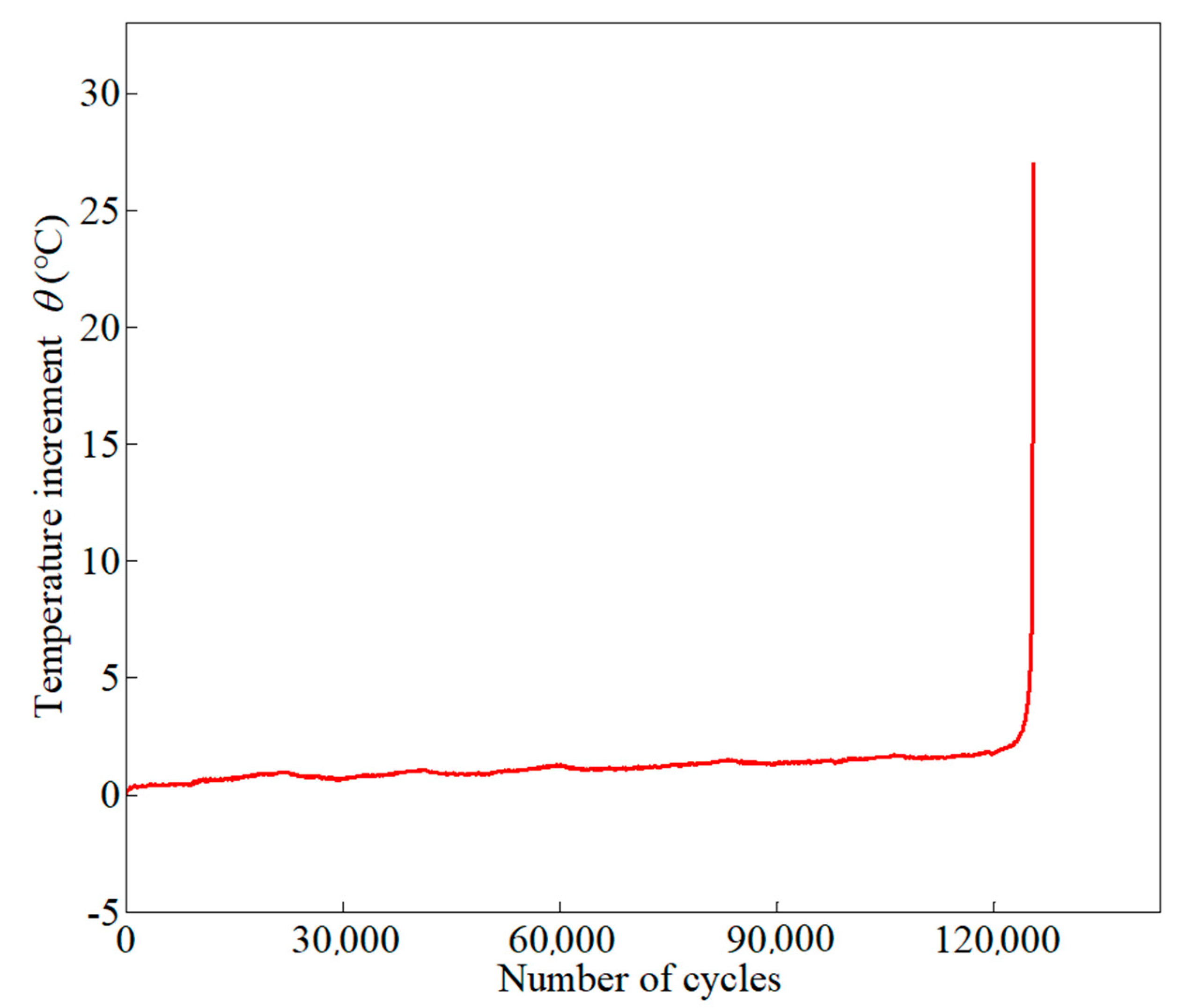
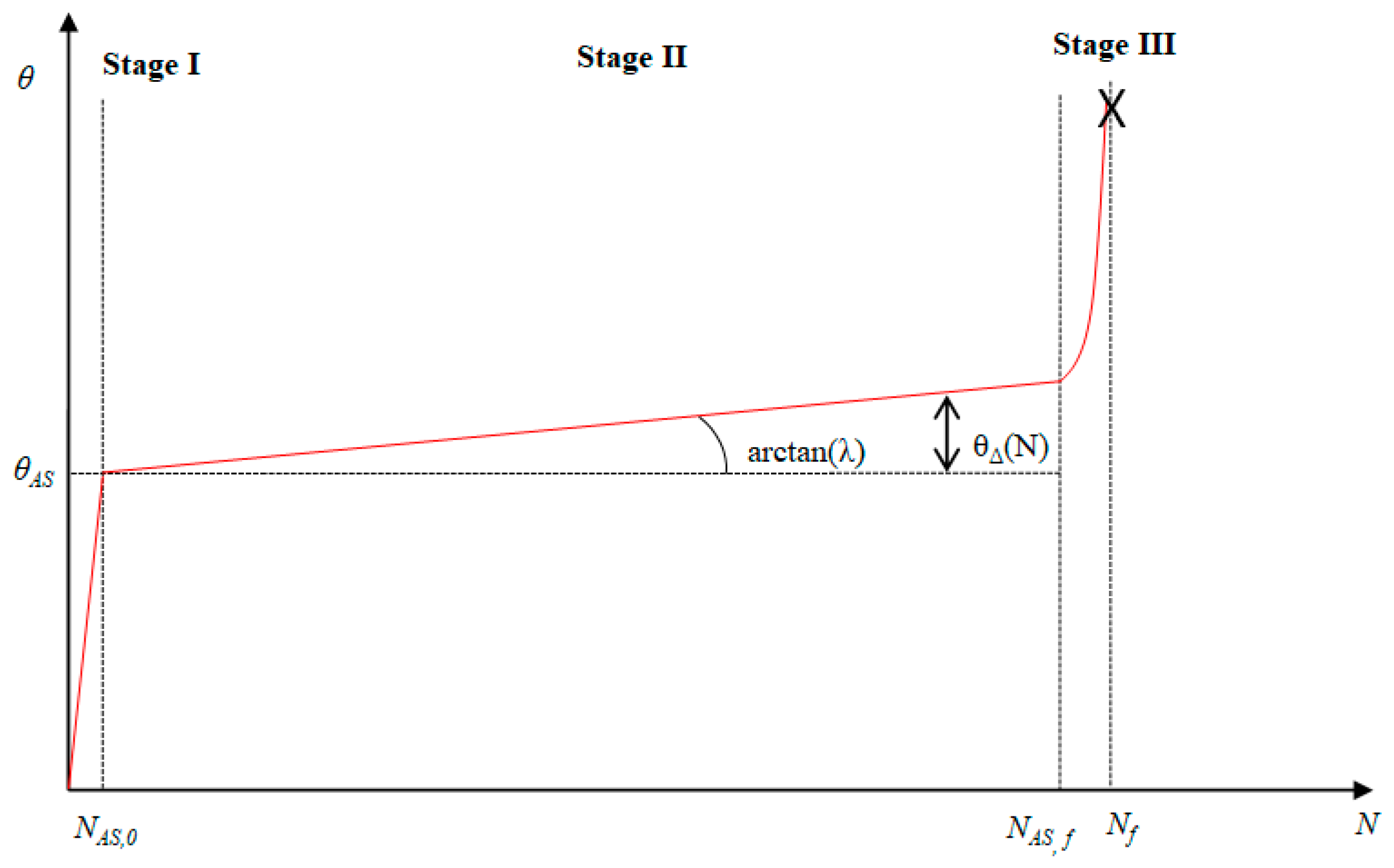
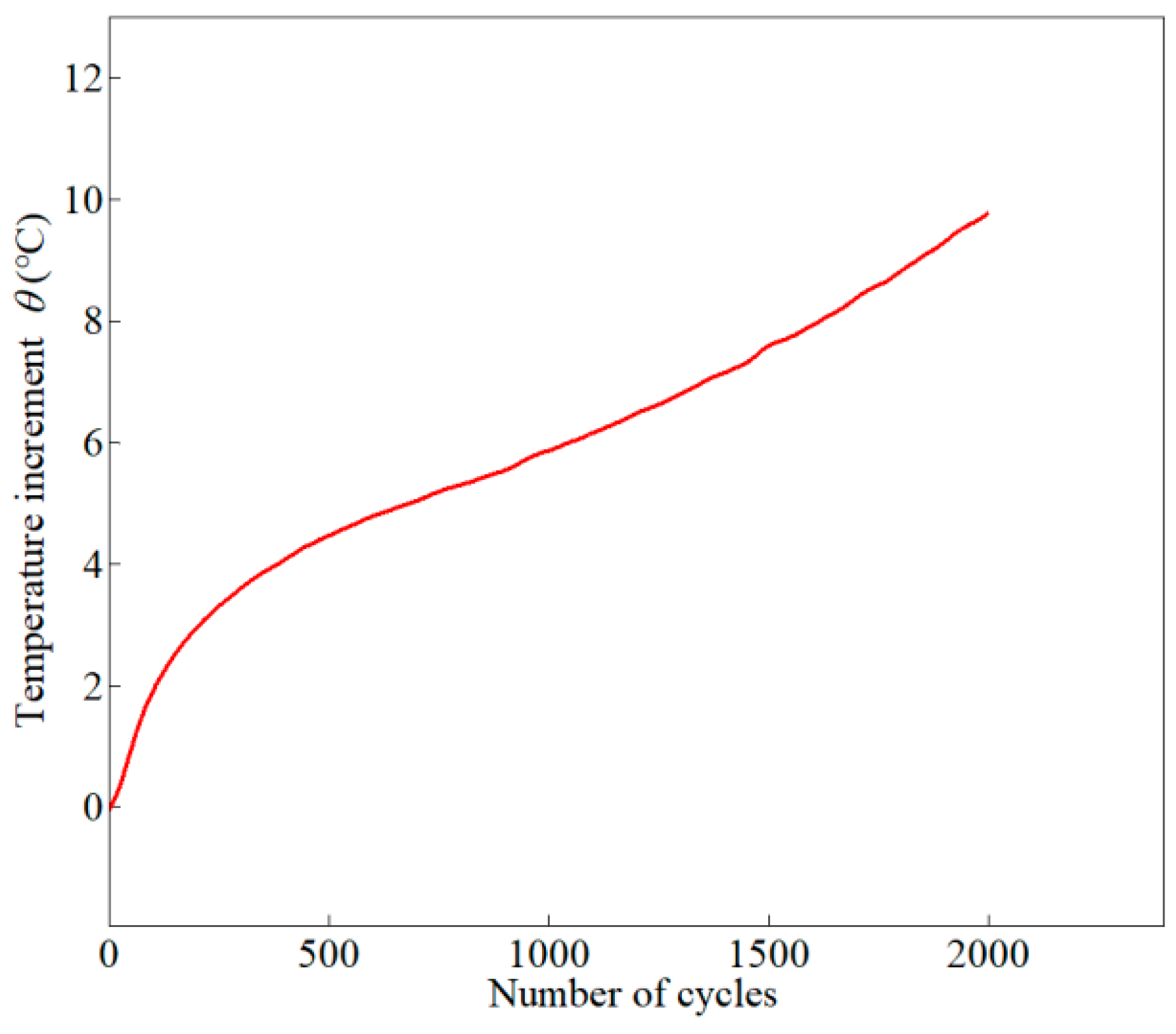
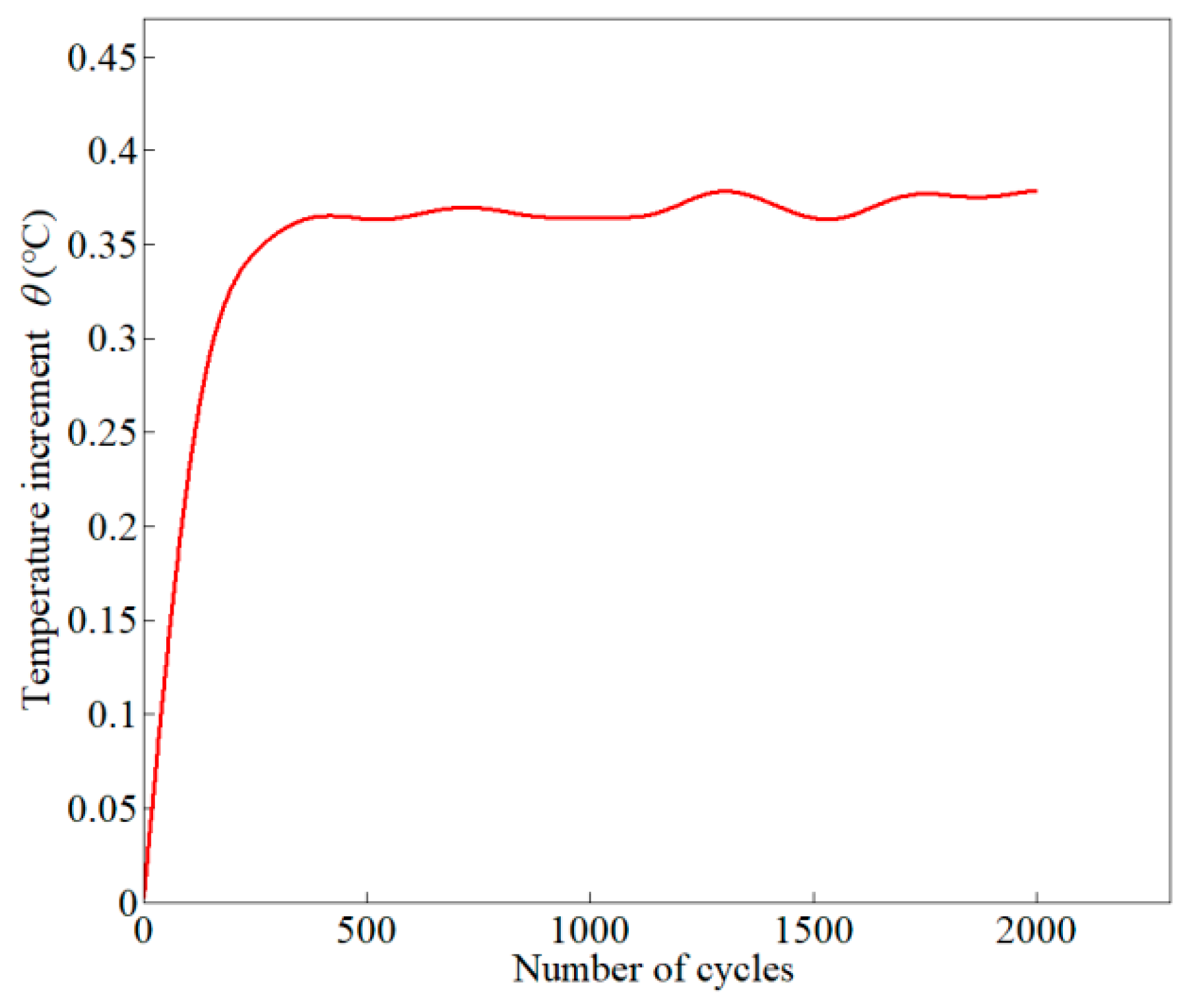
2.4. Thermal Evolution
3. An Energy-Based Fatigue Life Prediction Method
3.1. Intrinsic Dissipation
3.2. Energy-Based Fatigue Life Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shiozaki, T.; Yamaguchi, N.; Tamai, Y.; Hiramoto, J.; Ogawa, K. Effect of weld toe geometry on fatigue life of lap fillet welded ultra-high strength steel joints. Int. J. Fatigue 2018, 116, 409–420. [Google Scholar] [CrossRef]
- Costa, J.D.M.; Ferreira, J.A.M.; Abreu, L.P.M. Fatigue behavior of butt welded joints in a high strength steel. Procedia Eng. 2010, 2, 697–705. [Google Scholar] [CrossRef]
- Ma, L.L.; Wei, Y.H.; Hou, L.F.; Guo, C.L. Evaluation on fatigue performance and fracture mechanism of laser welded TWIP steel joint based on evolution of microstructure and micromechanical properties. J. Iron Steel Res. Int. 2016, 23, 677–684. [Google Scholar] [CrossRef]
- D’Angelo, L.; Nussbaumer, A. Estimation of fatigue S-N curves of welded joints using advanced probabilistic approach. Int. J. Fatigue 2017, 97, 98–113. [Google Scholar] [CrossRef]
- Ding, Y.L.; Song, Y.S.; Cao, B.Y.; Wang, G.X.; Li, A.Q. Full-range S-N fatigue life evaluation method for welded bridge structures considering hot-spot and welding residual stress. J. Bridge Eng. 2016, 21, 1–10. [Google Scholar] [CrossRef]
- Deng, C.; Liu, Y.; Gong, B.; Wang, D. Numerical implementation for fatigue assessment of butt joint improved by high frequency mechanical impact treatment: A structural hot spot stress approach. Int. J. Fatigue 2016, 92, 211–219. [Google Scholar] [CrossRef]
- Stenberg, T.; Barsoim, Z.; Balawi, S.O.M. Comparison of local stress based concepts- Effects of low- and high cycle fatigue and weld quality. Eng. Fail. Anal. 2015, 57, 323–333. [Google Scholar] [CrossRef]
- Schork, B.; Kucharczyk, P.; Madia, M.; Zerbst, U.; Hensel, J.; Bernhard, J.; Tchuindjang, D.; Kaffenberger, M.; Oechsner, M. The effect of the local and global weld geometry as well as material defects on crack initiation and fatigue strength. Eng. Fract. Mech. 2018, 198, 103–122. [Google Scholar] [CrossRef]
- Varvani-Farahani, A.; Kodric, T.; Ghahramani, A. A method of fatigue prediction in notched and un-notched components. J. Mater. Process. Technol. 2005, 169, 94–102. [Google Scholar] [CrossRef]
- Nykanen, T.; Mettanen, H.; Bjork, T.; Ahola, A. Fatigue assessment of welded joints under variable amplitude loading using a novel notch stress approach. Int. J. Fatigue 2017, 101, 177–191. [Google Scholar] [CrossRef]
- Gu, Z.; Mi, C.; Ding, Z.; Zhang, Y.; Liu, S.; Nie, D. An energy-based fatigue life prediction of a mining truck welded frame. J. Mech. Sci. Technol. 2016, 30, 3615–3624. [Google Scholar] [CrossRef]
- Berto, F.; Vinogradov, A.; Filippi, S. Application of the strain energy density approach in comparing different design solutions for improving the fatigue strength of load carrying shear welded joints. Int. J. Fatigue 2017, 101, 371–384. [Google Scholar] [CrossRef]
- Chapetti, M.D.; Jaureguizahar, L.F. Fatigue behavior prediction of welded joints by using an integrated fracture mechanics approach. Int. J. Fatigue 2012, 43, 43–53. [Google Scholar] [CrossRef]
- Meneghetti, G.; Ricotta, M. The use of the specific heat loss to analyze the low- and high-cycle fatigue behavior of plain and notched specimens made of a stainless steel. Eng. Fract. Mech. 2012, 81, 2–16. [Google Scholar] [CrossRef]
- Palumbo, D.; Galietti, U. Characterisation of steel welded joints by infrared thermographic methods. Quant. Infrared Thermogr. J. 2014, 11, 29–42. [Google Scholar] [CrossRef]
- Palumbo, D.; de Finis, R.; Ancona, F.; Galietti, U. Damage monitoring in fracture mechanics by evaluation of the heat dissipated in the cyclic plastic zone ahead of the crack tip with thermal measurement. Eng. Fract. Mech. 2017, 181, 65–76. [Google Scholar] [CrossRef]
- Luong, M.P. Fatigue limit evaluation of metals using an infrared thermographic technique. Mech. Mater. 1998, 28, 155–163. [Google Scholar] [CrossRef]
- La Roa, G.; Risitano, A. Thermographic methodology for rapid determination of the fatigue limit of materials and mechanical components. Int. J. Fatigue 2000, 22, 65–73. [Google Scholar] [CrossRef]
- Wang, X.G.; Crupi, V.; Jiang, C.; Guglielmino, E. Quantitative thermographic methodology for fatigue life assessment in a multiscale energy dissipation framework. Int. J. Fatigue 2015, 81, 249–256. [Google Scholar] [CrossRef]
- Wang, X.G.; Crupi, V.; Guo, X.L.; Zhao, Y.G. Quantitative thermographic methodology for fatigue assessment and stress measurement. Int. J. Fatigue 2010, 32, 1970–1976. [Google Scholar] [CrossRef]
- Corigliano, P.; Crupi, V.; Epasto, G.; Guglielmino, E.; Risitano, G. Fatigue life prediction of high strength steel welded joints by energy approach. Procedia Struct. Integr. 2016, 2, 2156–2163. [Google Scholar] [CrossRef]
- Crupi, V.; Gugliemino, E.; Maestro, M.; Marino, A. Fatigue analysis of butt welded AH36 steel joints: Thermographic method and design curve. Mar. Struct. 2009, 22, 373–386. [Google Scholar] [CrossRef]
- Guo, Q.; Guo, X.; Fan, J.; Syed, R.; Wu, C. An energy method for rapid evaluation of high-cycle fatigue parameters based on intrinsic dissipation. Int. J. Fatigue 2015, 80, 136–144. [Google Scholar] [CrossRef]
- Amiri, M.; Khonsari, M.M. Rapid determination of fatigue failure based on temperature evaluation: Fully reversed bending load. Int. J. Fatigue 2010, 32, 382–389. [Google Scholar] [CrossRef]
- Berthel, B.; Chrysochoos, A.; Wattrisse, B.; Galtier, A. Infrared image processing for the calorimetric analysis of fatigue phenomena. Exp. Mech. 2008, 48, 79–90. [Google Scholar] [CrossRef]
- Plekhov, O.A.; Saintier, N.; Palin-Luc, T.; Uvarov, S.V.; Naimark, O.B. Theoretical analysis, infrared and structural investigations of energy dissipation in metals under cyclic loading. Mater. Sci. Eng. A 2007, 462, 367–369. [Google Scholar] [CrossRef]
- Dumoulin, S.; Louche, H.; Hopperstad, O.S.; Børvik, T. Heat sources, energy storage and dissipation in high-strength steels: Experiments and modeling. Eur. J. Mech. 2010, 29, 461–474. [Google Scholar] [CrossRef]
- Wang, X.G.; Crupi, V.; Jiang, C.; Feng, E.S.; Guglielmino, E.; Wang, C.S. Energy-based approach for fatigue life prediction of pure copper. Int. J. Fatigue 2017, 104, 243–250. [Google Scholar] [CrossRef]



| Point 1 (MPa) | Point 2 (MPa) | Point 3 (MPa) |
|---|---|---|
| −14.55 ± 3.27 | −16.84 ± 12.51 | 5.09 ± 6.86 |
| Young’s Modulus (GPa) | 205 |
| Yield Strength (MPa) | 365 |
| Ultimate Tensile Strength (MPa) | 500 |
| (kg·m−3) | (J·kg−1·K−1) | (WK−1·m−1) | (s) | (Hz) |
|---|---|---|---|---|
| 7850 | 460 | 45.5 | 14.7~35.2 | 20 |
| −1 | 300 | 1.0091 × 109 |
| −1 | 260 | 0.9653 × 109 |
| Predicted Cycles | Experimental Cycles | ||
|---|---|---|---|
| −1 | 340 | 11,809 | 12,877 |
| −1 | 240 | 401,025 | 386,302 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mi, C.; Li, W.; Xiao, X.; Berto, F. An Energy-Based Approach for Fatigue Life Estimation of Welded Joints without Residual Stress through Thermal-Graphic Measurement. Appl. Sci. 2019, 9, 397. https://doi.org/10.3390/app9030397
Mi C, Li W, Xiao X, Berto F. An Energy-Based Approach for Fatigue Life Estimation of Welded Joints without Residual Stress through Thermal-Graphic Measurement. Applied Sciences. 2019; 9(3):397. https://doi.org/10.3390/app9030397
Chicago/Turabian StyleMi, Chengji, Wentai Li, Xuewen Xiao, and Filippo Berto. 2019. "An Energy-Based Approach for Fatigue Life Estimation of Welded Joints without Residual Stress through Thermal-Graphic Measurement" Applied Sciences 9, no. 3: 397. https://doi.org/10.3390/app9030397
APA StyleMi, C., Li, W., Xiao, X., & Berto, F. (2019). An Energy-Based Approach for Fatigue Life Estimation of Welded Joints without Residual Stress through Thermal-Graphic Measurement. Applied Sciences, 9(3), 397. https://doi.org/10.3390/app9030397





