Fatigue Performance of Tunnel Invert in Newly Designed Heavy Haul Railway Tunnel
Abstract
:1. Introduction
2. Mechanical Characteristics of the Heavy Haul Railway Tunnel Base
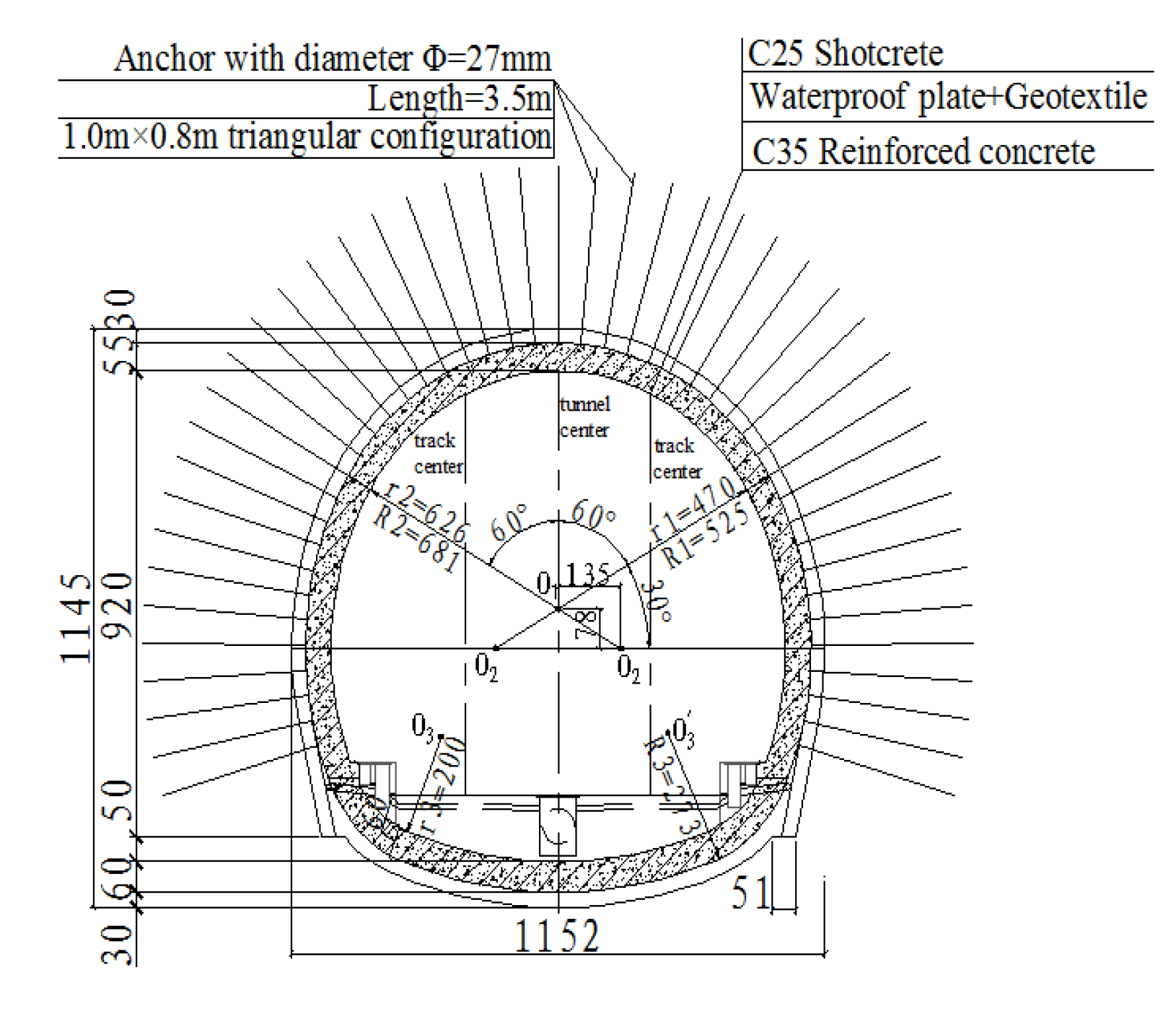
2.1. Engineering Background
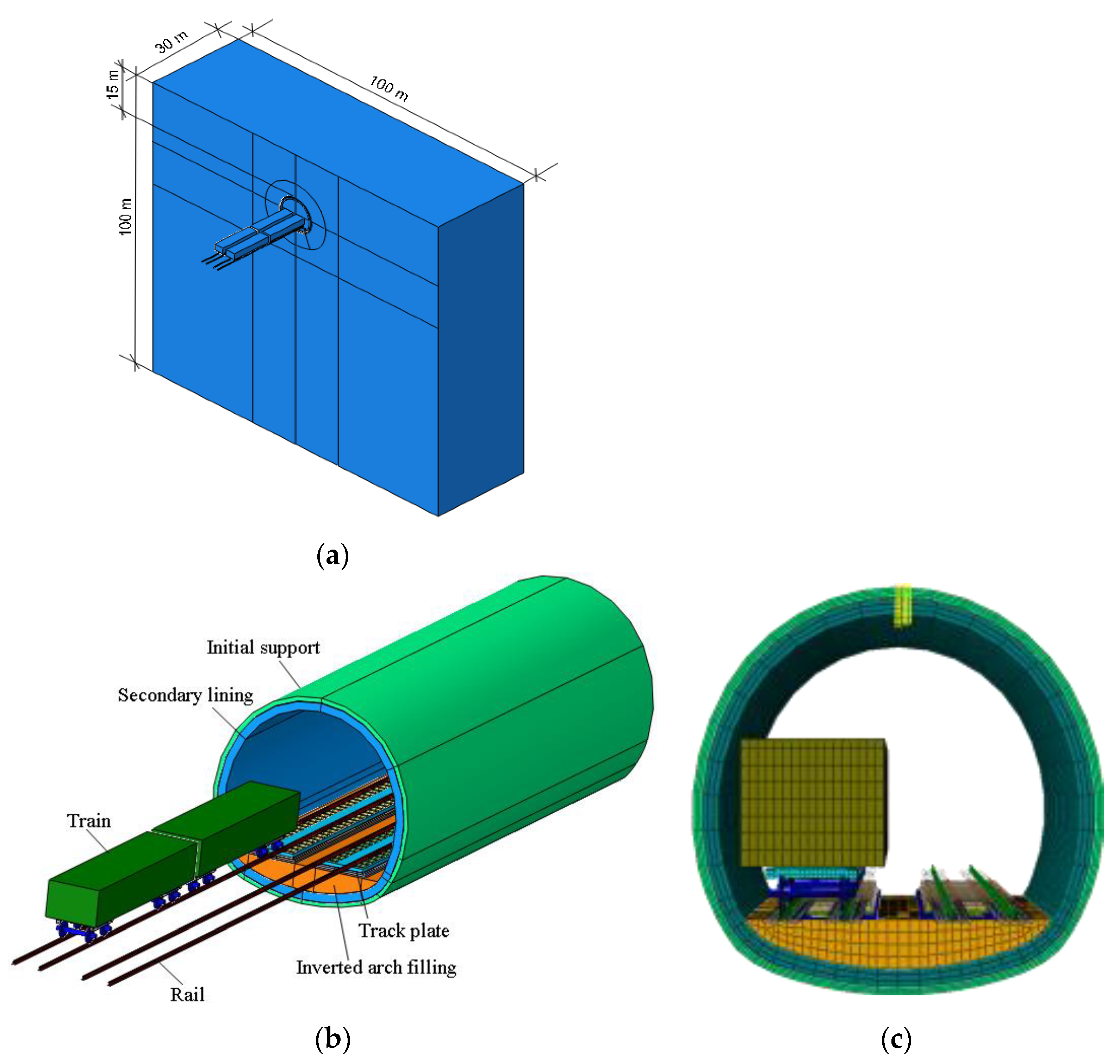
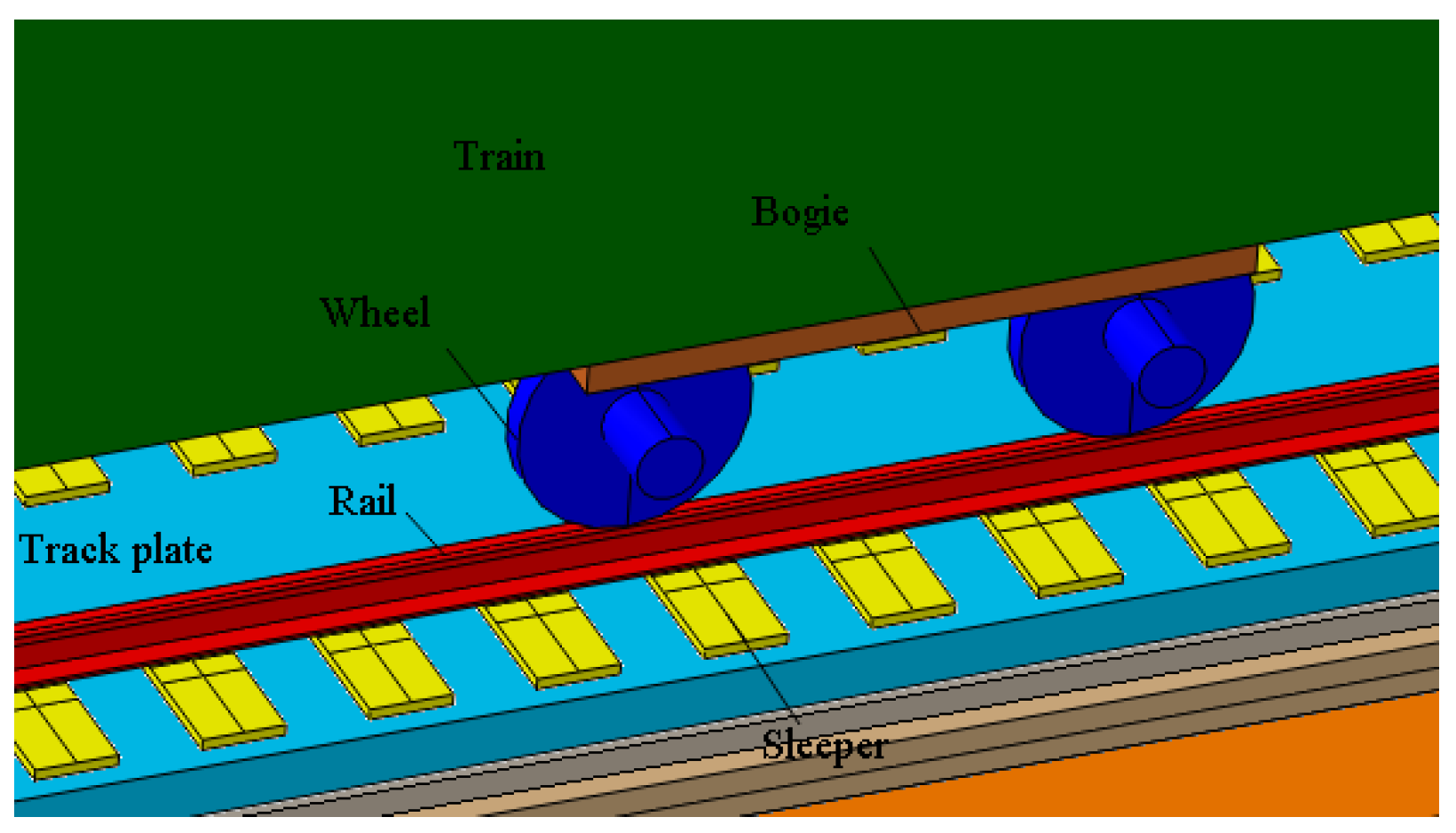
2.2. Numerical Model
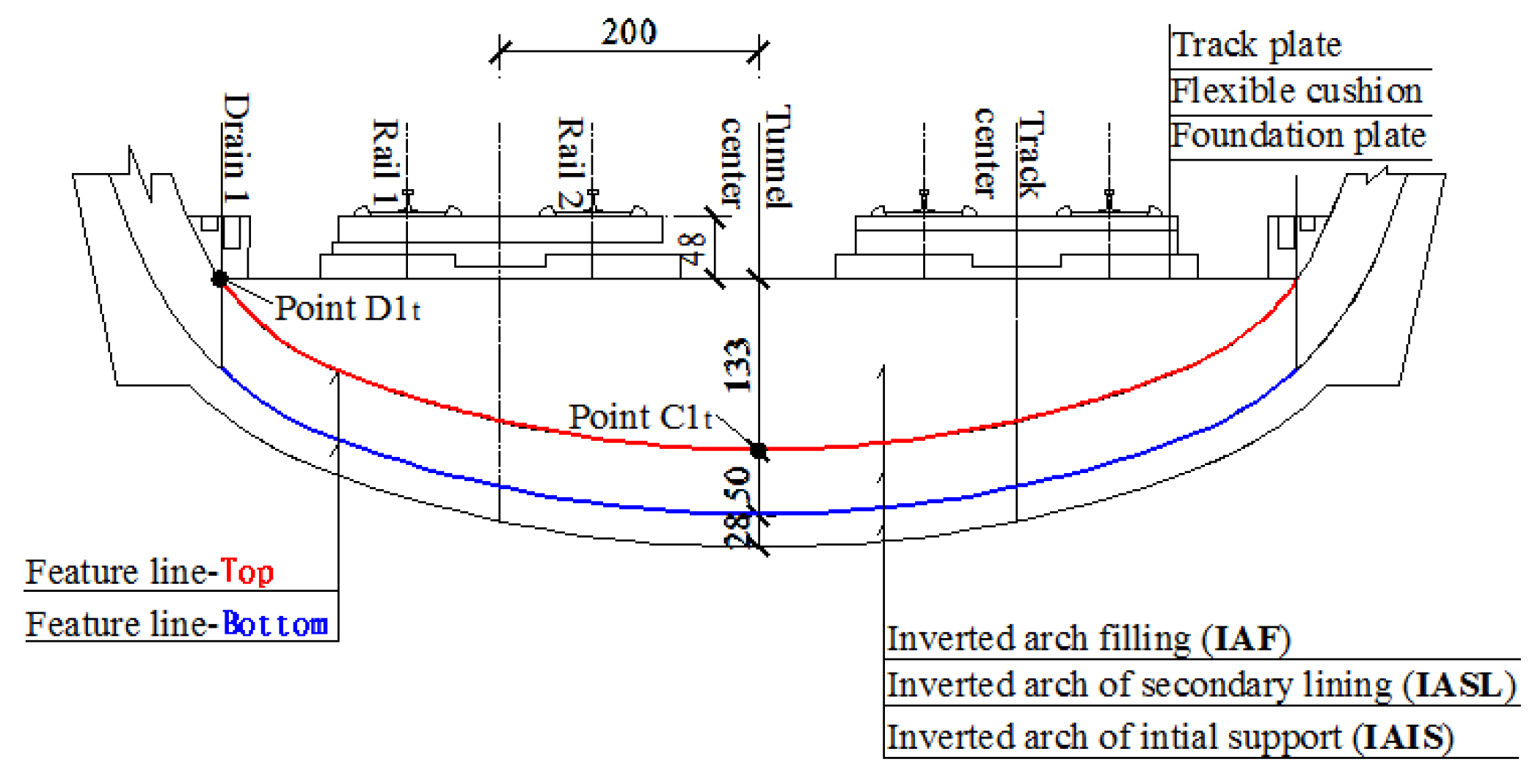
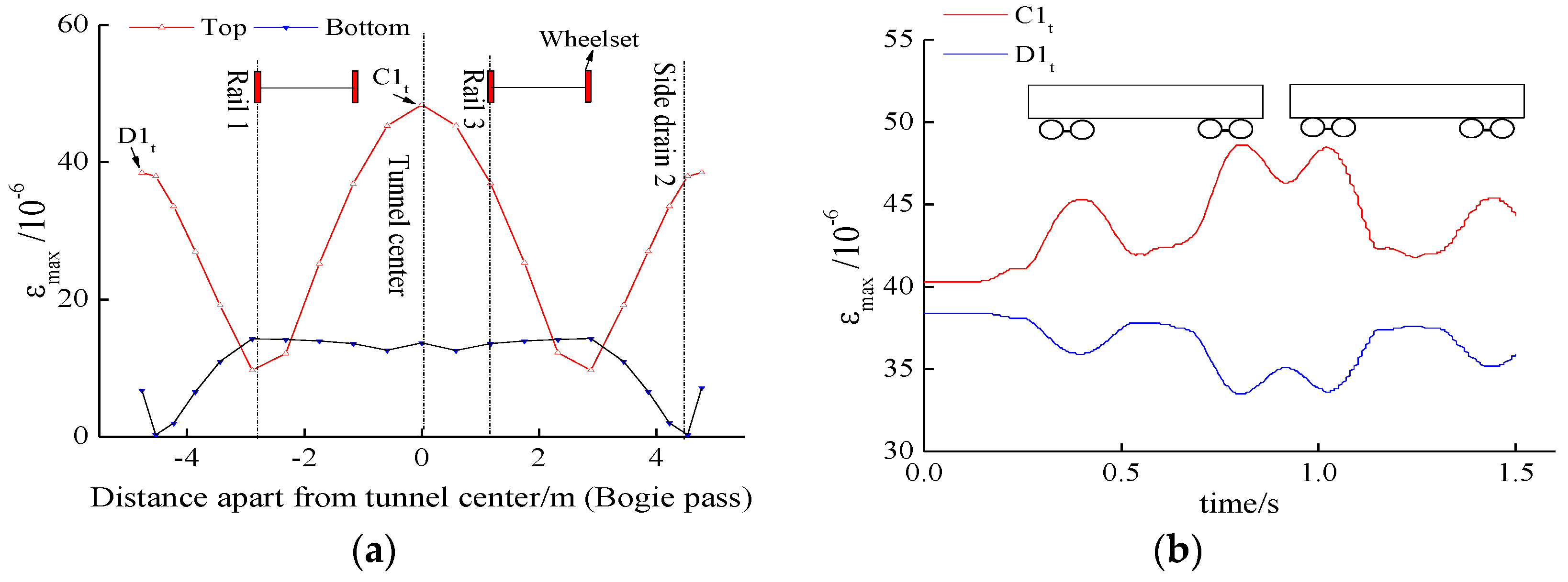
2.3. Feature Points and Feature Lines
3. Mechanical Characteristics
4. Fatigue Test of Tunnel Base Structures
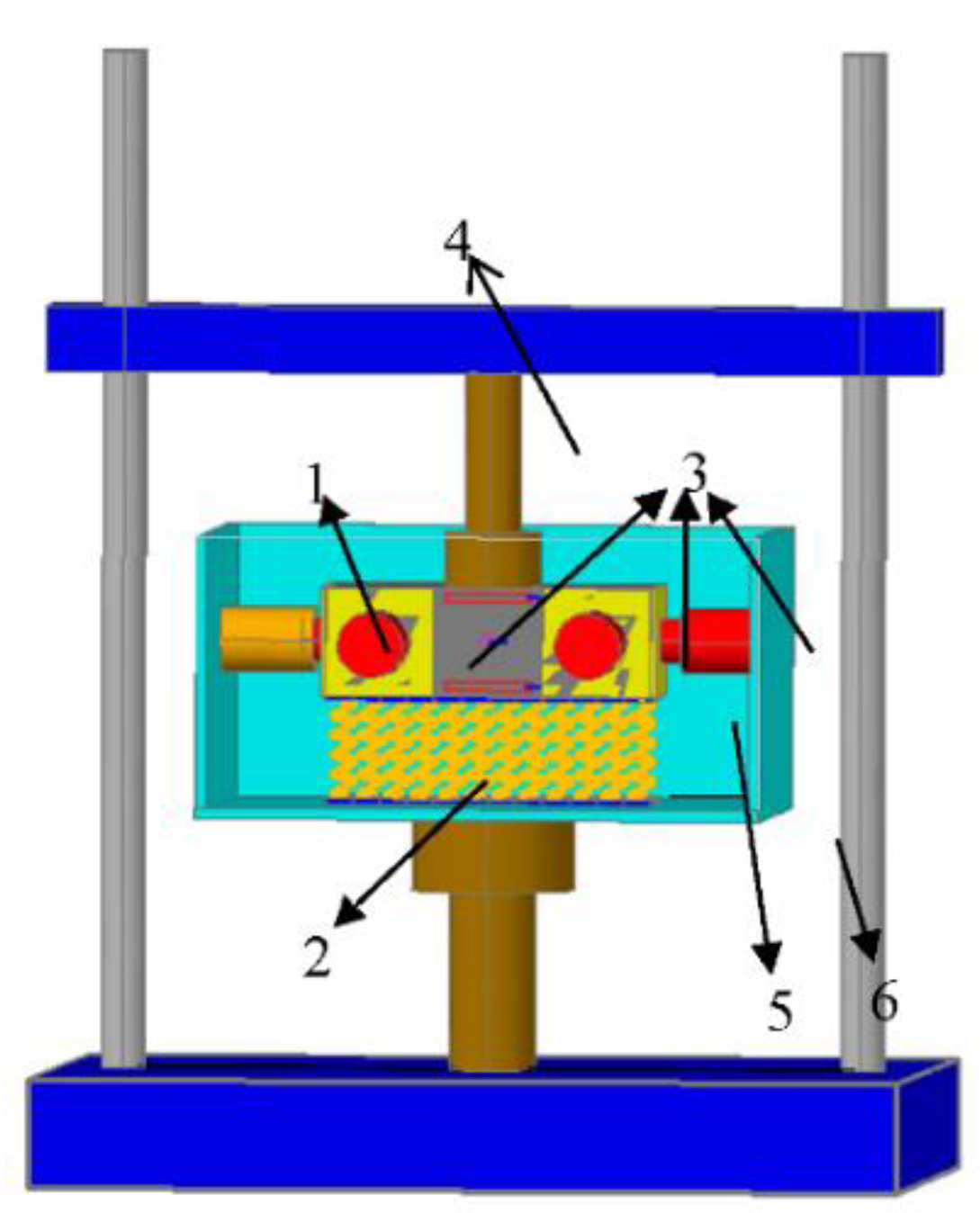
4.1. Fatigue Test System
4.2. Load Condition
4.3. Sensor Layout
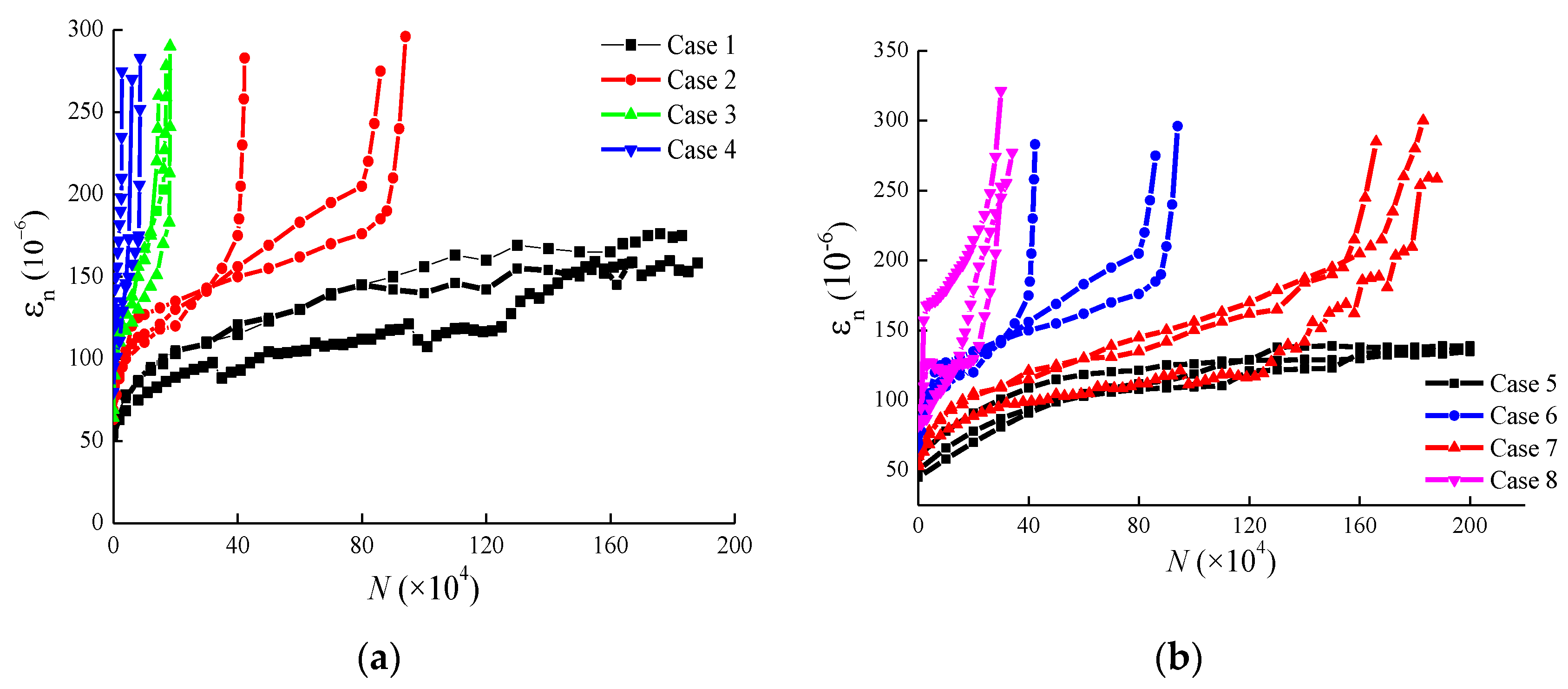
4.4. Strain Evolution
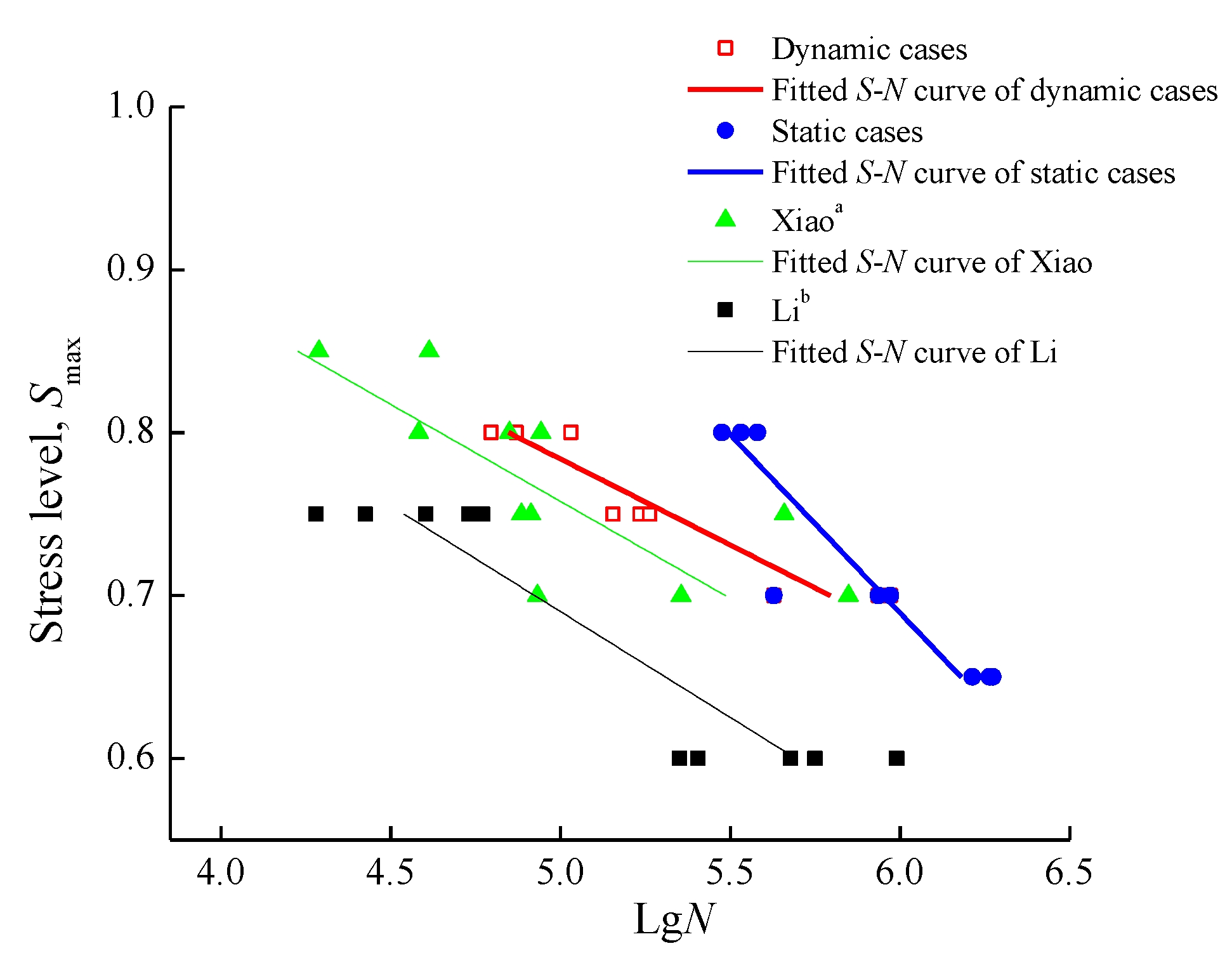
4.5. Fatigue Performance of Tunnel Basal Structures
5. Conclusions
- The top center was the position vulnerable to fatigue in the tunnel invert of the new line, which experienced high static and low dynamic stresses. Its static maximum principal strain was 40.3 × 10−6, which was caused by surrounding rock pressure, whereas the dynamic maximum principal strain caused by train load was 8.3 × 10−6.
- The tests results revealed that the fatigue life decreased as dynamic and static loads increased. Combined with the expression of the two-parameter S–N curve, an evolution model was proposed to characterize the fatigue behavior of the tunnel invert specimens.
- For the new line’s tunnel invert structures, fatigue failure would not occur within 2 million cycles. Any invert fracture within the design service life could be attributed to geological reasons or bedrock defects, rather than fatigue failure caused by dynamic train load.
Author Contributions
Funding
Conflicts of Interest
References
- Van Rickstal, F.; Van Gemert, D.; Bonheure, M. Fatigue testing of traffic tunnel panels. J. Perform. Constr. Fac. 1999, 13, 152–156. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.; Xie, W. Experimental Study of Dynamic Cumulative Damage Model for High Speed Railway Tunnel. Tunn. Constr. 2017, 37, 939–945. (In Chinese) [Google Scholar]
- Han, J.; Liu, W.; Wang, S.; Geert, D.S.; Sun, W.; Liang, Y. Carbonation reaction and microstructural changes of metro-tunnel segment concrete coupled with static and fatigue load. J. Mater. Civ. Eng. 2017, 29, 1943–5533. [Google Scholar] [CrossRef]
- Qian, W.; Qi, T.; Yi, H.; Liang, X.; Jin, Z.; Lei, B.; Li, Y.; Li, Z. Evaluation of structural fatigue properties of metro tunnel by model test under dynamic load of high-speed railway. Tunn. Undergr. Sp. Tech. 2019, 93, 103099. [Google Scholar] [CrossRef]
- Tian, B. Operation and development of railway heavy haul transport technology in the world. Roll. Stock 2015, 12, 10-19+5. [Google Scholar]
- Tian, Y. The Base Treatment Process with Grouting Resin in Datong-Qinhuangdao Railway Tunnels. Paper Collection of Heavy Haul Railway Transportation Technical Exchange; China Railway Society: Beijing, China, 2014; pp. 363–367. (In Chinese) [Google Scholar]
- Hu, Y. Current Status and Development Trend of Technology System for Railway Heavy Haul Transport in China. China Railw. Sci. 2015, 36, 1–10. (In Chinese) [Google Scholar]
- Niu, Y. The Heavy Haul Railway Tunnel Diseases Mechanism and Remediation Technology Research. Master’s Thesis, China Academy of Railway Sciences, Beijing, China, 2013. (In Chinese). [Google Scholar]
- Huang, Y. Research on Monitoring System and Reinforcement Treatment of Heavy Haul Railway Long Tunnel’s Bedding Diseases. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2015. (In Chinese). [Google Scholar]
- Yin, C.; Fu, B.; Ma, W. Analysis on Dynamic Stress of Tunnel Structure under Heavy Haul Train. China Railw. Sci. 2013, 34, 47–52. [Google Scholar]
- Xue, J. Analysis of the Influence of Tunnel Bottom Compactness on Structure Stress and Strengthening Measures under 30 t Axle Load Train. China Railw. Sci. 2015, 36, 90–95. (In Chinese) [Google Scholar]
- Liu, N.; Peng, L.; Shi, C.; Lei, M. Experimental and model study on dynamic behaviour and fatigue damage of tunnel invert. Constr. Build. Mater. 2016, 126, 777–784. [Google Scholar] [CrossRef]
- Zhang, Z.; Zeng, B.; Dai, C.; He, W. Study on Structural Service Performance of Heavy-Haul Railway Tunnel with Voided Base. Adv. Civ. Eng. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Nicholas, T.; Zuiker, J. On the use of the Goodman diagram for high cycle fatigue design. Int. J. Fract. 1996, 80, 219–235. [Google Scholar] [CrossRef]
- TB 10003-2016. Code for Design of Railway Tunnel; China Railway Publishing House: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Chappell, B. Deformational response in discontinua. Int. J. Rock Mech. Sci. Geomech. 1979, 4, 377–390. [Google Scholar] [CrossRef]
- Hernandez, Y.; Farfan, A.; De Assis, A. Three-dimensional analysis of excavation face stability of shallow tunnels. Tunn. Undergr. Sp. Tech. 2019, 92, 103062. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, J.; Du, Y. 3D consistent viscous-spring artificial boundary and viscous-spring boundary element. Gongcheng Lixue/Eng. Mech. 2007, 24, 31–37. [Google Scholar]
- GB/T 50081-2002. Standard for Test Method of Mechanical Properties on Ordinary Concrete; China Architecture and Building Press: Beijing, China, 2003. (In Chinese) [Google Scholar]
- Zhai, W.; Xia, H. Train-Track-Bridge of Train Track Bridge Dynamic Interaction: Theory and Engineering Application; Science Press: Beijing, China, 2011. [Google Scholar]
- Klausen, D. Concrete strength and damage due to frequently repeated loading. Darmstadt 1978. (In German) [Google Scholar]
- Oneschkow, N. Fatigue behaviour of high-strength concrete with respect to strain and stiffness. Int. J. Fatigue 2016, 87, 38–49. [Google Scholar] [CrossRef]
- Xiao, J.; Li, H.; Yang, Z. Fatigue behavior of recycled aggregate concrete under compression and bending cyclic loadings. Constr. Build. Mater. 2013, 38, 681–688. [Google Scholar] [CrossRef]
- Li, Y.; Che, H. A Study on the Cumulative Damage to Plain Concrete due to Flexural Fatigue. China Railw. Sci. 1998, 19, 52–59. (In Chinese) [Google Scholar]



| Material | Density (/kg/m3) | Elastic Modulus (GPa) | Poisson Ratio | Tensile Strength (MPa) | Compressive Strength (MPa) |
| Secondary lining (C35) | 2600 | 31.5 | 0.2 | 2.20 | 23.4 |
| Initial support (C25) | 2500 | 28.5 | 0.2 | 1.78 | 16.7 |
| Inverted arch filling (C25) | 2500 | 19.8 | 0.3 | 1.78 | 16.7 |
| Foundation plate (C30) | 2500 | 30 | 0.2 | 2.01 | 20.1 |
| Flexible cushion (C30) | 2200 | 20 | 0.2 | 2.01 | 20.1 |
| Track plate (C45) | 2700 | 33.5 | 0.2 | 2.51 | 29.6 |
| Rail and train | 7800 | 210 | 0.3 | 210 | 210 |
| Material | Density (/kg/m3) | Elastic modulus (GPa) | Poisson Ratio | Cohesion (kPa) | Internal Friction Angle (°) |
| V grade surrounding rock | 2100 | 0.50 | 0.33 | 80 | 25 |
| Position | Stiffness Coefficient (MN/m) | Damping (kN·s/m) | ||
|---|---|---|---|---|
| kx | ky | kz | cz | |
| Primary suspension | 6.0 | 10.0 | 35.0 | 5.0 |
| Secondary suspension | 5.3 | 5.3 | 6.6 | 5.0 |
| Material | Cement | Fine Aggregate | Coarse Aggregate | Fly Ash | Plasticizer | Water |
|---|---|---|---|---|---|---|
| kg/m³ | 277 | 747 | 1075 | 108 | 3.85 | 153 |
| Mechanical Parameters | Cube Specimens 150 × 150 × 150 mm | Rectangular Specimens 100 × 100 × 300 mm | |||
|---|---|---|---|---|---|
| Static Elastic Modulus E (GPa) | Compression Strength (MPa) | Dynamic Elastic Modulus E (GPa) | Bending Strength (MPa) | ||
| Value | 21.7 | 42.3 | 31.8 | 2.5 | 0.23 |
| Test Conditions | Constant Loads | Dynamic Load (kN) | ||
| Dynamic load conditions | Case 1 | Static load: 27 kN Lateral load: 1.5 kN | 1.6 | 0.65 |
| Case 2 | 2.4 | 0.70 | ||
| Case 3 | 3.6 | 0.75 | ||
| Case 4 | 4.5 | 0.80 | ||
| Test conditions | Constant loads | Static load (kN) | ||
| Static load conditions | Case 5 | Dynamic load: 2.4 kN Lateral load: 1.5 kN | 23 | 0.60 |
| Case 6 | 25 | 0.65 | ||
| Case 7 | 27 | 0.70 | ||
| Case 8 | 29 | 0.80 | ||
| Case | λ | α | β | γ | Case | λ | α | β | γ |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.7 | 1.5 | 1.01 | 0.18 | 6 | 0.7 | 2 | 1 | 0.17 |
| 3 | 0.7 | 1.4 | 1.01 | 0.2 | 7 | 0.6 | 1.4 | 1.01 | 0.15 |
| 4 | 0.8 | 1 | 1 | 0.25 | 8 | 0.5 | 1 | 1 | 0.14 |
| Test Conditions | Fatigue Life | ||||
|---|---|---|---|---|---|
| Test 1 | Test 2 | Test 3 | |||
| Case 1 | 0.65/56 × 10−6 | 0.056/16 × 10−6 | 1,661,391 | >2,070,000 | >2,030,000 |
| Case 2 | 0.70/68 × 10−6 | 0.082/28 × 10−6 | 937,982 | 863,045 | 424,988 |
| Case 3 | 0.75/74 × 10−6 | 0.118/34 × 10−6 | 142,565 | 171,412 | 182,940 |
| Case 4 | 0.80/85 × 10−6 | 0.143/45 × 10−6 | 62,348 | 73,915 | 107,242 |
| Case 5 | 0.60/52 × 10−6 | 0.082/28 × 10−6 | >2,000,000 | >2,000,000 | >2,000,000 |
| Case 6 | 0.65/56 × 10−6 | 0.082/28 × 10−6 | 1,873,947 | 1,632,586 | 1,836,432 |
| Case 7 | 0.70/68 × 10−6 | 0.082/28 × 10−6 | 937,982 | 863,045 | 424,988 |
| Case 8 | 0.80/84 × 10−6 | 0.082/28 × 10−6 | 339,625 | 298,581 | 380,517 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Peng, L.; Lei, M.; Shi, C.; Liu, N. Fatigue Performance of Tunnel Invert in Newly Designed Heavy Haul Railway Tunnel. Appl. Sci. 2019, 9, 5514. https://doi.org/10.3390/app9245514
Liu C, Peng L, Lei M, Shi C, Liu N. Fatigue Performance of Tunnel Invert in Newly Designed Heavy Haul Railway Tunnel. Applied Sciences. 2019; 9(24):5514. https://doi.org/10.3390/app9245514
Chicago/Turabian StyleLiu, Cong, Limin Peng, Mingfeng Lei, Chenghua Shi, and Ning Liu. 2019. "Fatigue Performance of Tunnel Invert in Newly Designed Heavy Haul Railway Tunnel" Applied Sciences 9, no. 24: 5514. https://doi.org/10.3390/app9245514
APA StyleLiu, C., Peng, L., Lei, M., Shi, C., & Liu, N. (2019). Fatigue Performance of Tunnel Invert in Newly Designed Heavy Haul Railway Tunnel. Applied Sciences, 9(24), 5514. https://doi.org/10.3390/app9245514






