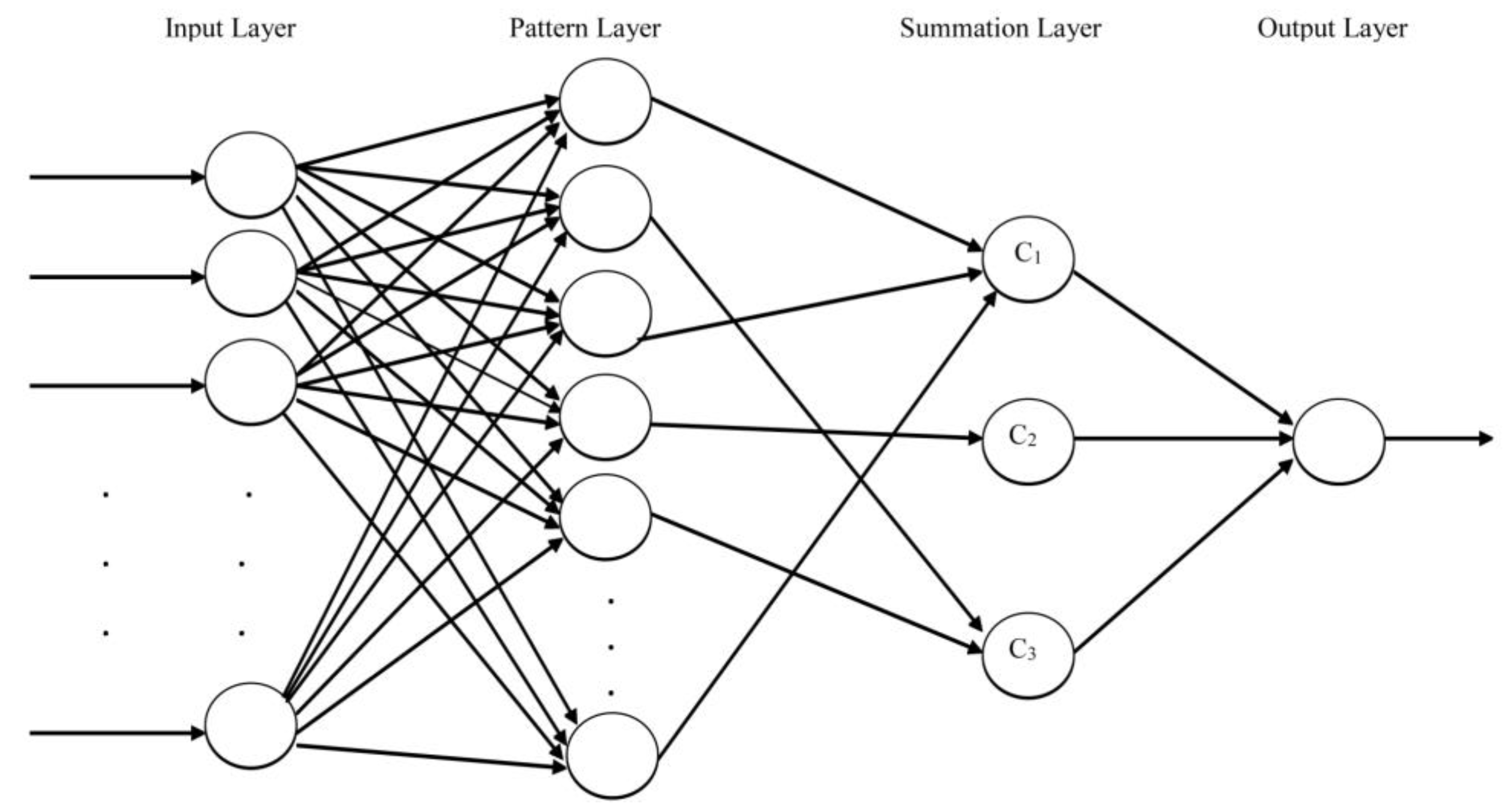
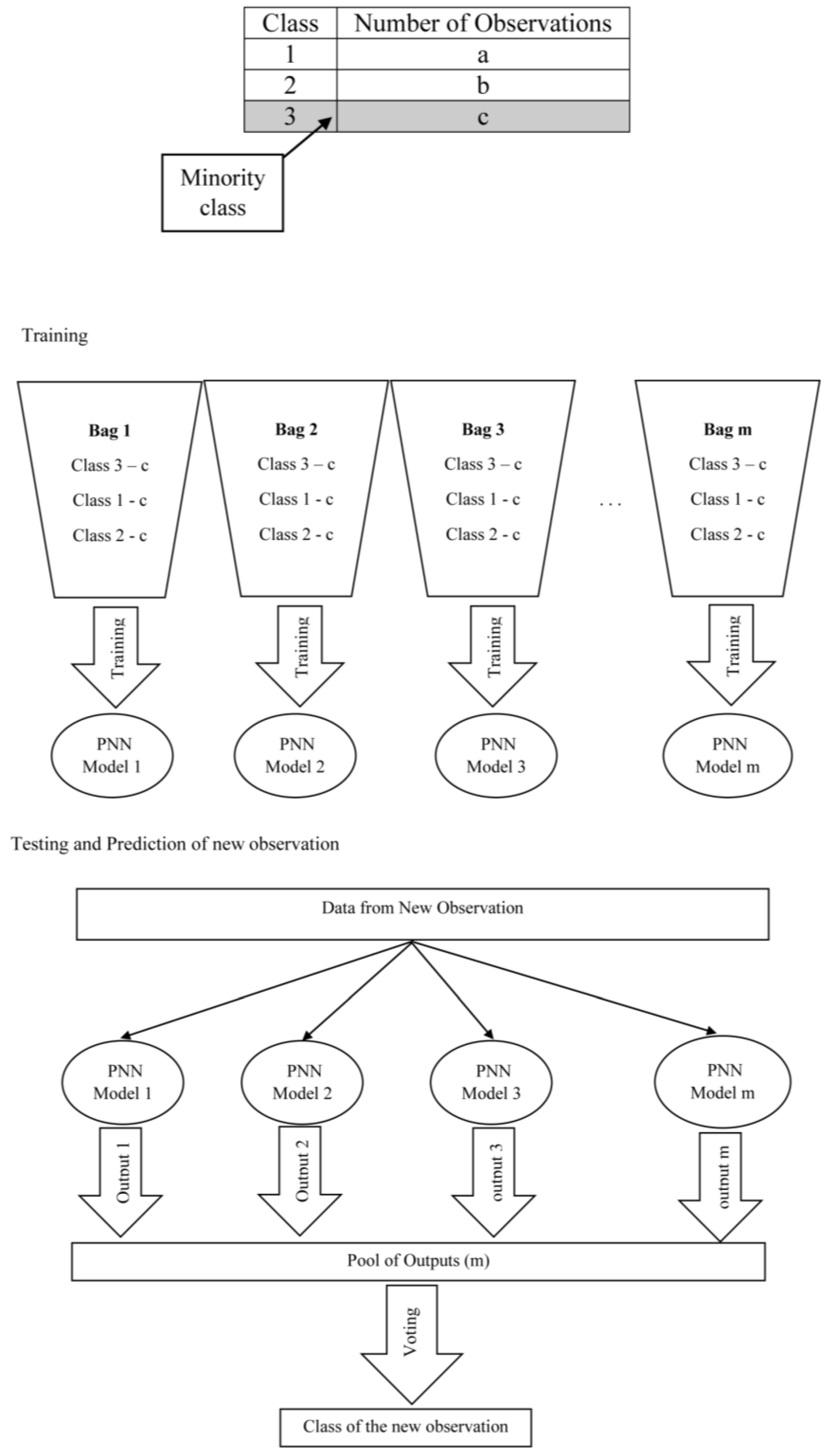
1. Introduction
Financial Markets play a major role in controlling dynamics of the world economy. Forecasting of financial markets has had great importance recently due to the rapid increase in the investments of financial markets in the past decades. The stock market is one of the leading financial markets in this regard due to the importance and interest of many stakeholders. The profitability of investing in financial markets is directly proportional to its predictability [
1,
2,
3,
4]. Efficient market hypothesis indicates that market prices fully reflect all available information, and “beating the market” is very difficult. Researchers found that the weak form of the efficient market hypothesis exists in the real world and suggested that prediction is possible using this weak form with a satisfactory degree of accuracy [
5,
6,
7]. On the other hand, movements of stock market index depend on combined impact factors such as news, civil unrest, natural disasters, psychological factors, inflation, etc. Most of these factors are immeasurable and/or intangible. Therefore, it is very difficult to identify and measure all the factors that affect stock markets. When considering the real world phenomena, it can be seen that all effects reflect on other financial markets and on other indices. Hence, it is worth to use inter-market influences in stock market predictions [
1,
2].
Different techniques have been used by researchers for financial market predictions, and time series models can be identified as one of the widely used techniques as shown in the literature [
8,
9,
10]. Even though they are capable of forecasting financial markets, the downside of the time series models are the assumptions associated with them such as constant variance, linear relationships and normality where most of the financial time series data do not agree with them. Furthermore, time series models used for financial market predictions exhibit less accuracy [
11]. Consequently, linear time series models are not capable enough to capture the non-linear dependencies in financial data. Development of machine learning techniques leads to improve the forecasting ability of financial markets. Machine learning techniques can be identified as apposite techniques to predict financial markets, which exhibit higher accuracy in predictions and can capture non-linear relationships. Many researches recently proved that machine learning techniques can be successfully used for forecasting financial markets with a satisfactory degree of accuracy [
2,
12,
13,
14,
15,
16].
Literature reveals that the directional prediction is more effective and leads to higher profits than the value prediction [
17,
18,
19]. Directional prediction is a classification problem. Probabilistic neural networks (PNN), support vector machines (SVM) and feedforward neural networks (FNN) can be recognized as the common machine learning techniques for the classification of future movements of stock market, and researchers revealed that the PNN is a powerful tool for classification problems as it shows higher accuracy in forecasting [
1,
18,
20,
21,
22]. Despite the fact that the PNN is a powerful tool in classification, the standard PNN algorithm encompasses some shortcomings such as not considering a joint distribution other than the Gaussian, as the distribution of input variables where, the real world financial data do not always follow Gaussian distribution [
23,
24,
25]. Conversely, a major issue associated with most of the real-world data sets is class imbalanced problem, which leads to reduce performance of classifiers [
26,
27,
28]. The standard PNN algorithm does not facilitate handling the multi-class imbalanced problem in the classification of cost sensitive data which is very frequent in reality [
26,
27,
28,
29].
Therefore, the main objective of this study is to improve the standard PNN model by introducing appropriate (multivariate) joint probability distribution for non-Gaussian input variables and embedding a feasible technique to handle multi-class imbalanced problem for cost sensitive data.
It is hard to find published evidences for the availability of a PNN algorithm which facilitates the incorporation of multivariate probability distribution other than the Gaussian distribution and handling multi-class imbalanced problem for cost sensitive data. This study will develop such a model to forecast the direction of a given stock market for any time period. The proposed model is capable of forecasting the direction of a given stock market index with a higher accuracy. The final outcome of this research will lead to provide quick, reliable forecast for a given stock market index, and it will help governments, financial institutes, stockbrokers, agents and investors to utilize their money effectively. Furthermore, findings of this research can be applied to handle classification problems in other research areas such as climate, weather, medical, agriculture, biology and marketing research.
Organization of the paper is as follows:
Section 2 contains materials and methods used in the study while all the results obtained are presented in
Section 3. Discussion of the study is in
Section 4 and
Section 5 concludes the paper.
4. Discussion
The main objective of this study is to improve the standard probabilistic neural network algorithm by introducing an appropriate multivariate distribution for non-Gaussian input variables and incorporating a feasible technique to handle multi-class imbalanced problem. This objective was further elaborated into finding the most suitable marginal distributions of the identified input variables, estimating parameters of multivariate distributions associated with these input variables and introducing a proper method to handle multi-class imbalanced problem. Comparisons of proposed and existing methods were carried out to assess the performance of proposed methods.
Preliminary analysis identified nine variables, lag 4 (i.e., return series four days back) of AORD index, lag 1 of oil index, lag 1 of gold index, lag 14 of cocoa index, lag 1 of GSPC index, lag 0 of exchange rate of Australian dollar to United States dollar (AUD-USD), lag 1 of AUD-USD, lag 8 of AUD-USD and lag 12 of AUD-USD exchange rates; four variables, lag 5 of GSPC index, lag 12 of oil index, lag 13 of gold index, lag 6 of cocoa index, and thirteen variables, lag 1 of ASPI index, lag 3 to lag 5 of ASPI index, lag 1 of oil index, lag 5 of oil index, lag 13 of oil index, lag 14 of oil index, lag 9 of gold index, lag 1 of GSPC index, lag 2 of GSPC index, lag 13 of GSPC index, lag 14 of GSPC index as potential inputs to PNN models with respect to three stock market indices AORD, GSPC and ASPI, respectively.
Different marginal distributions, normal distribution, lognormal distribution, inverse Gaussian distribution, levy distribution and Pareto distribution, were used to model return series of stock market indices and other financial markets under study, and inadequacies of all above mentioned distributions to model return series of considered financial indices were identified. Finally, scaled t distribution was identified as a more suitable distribution to model return series of financial indices and respective parameters are present in
Table 2. The shape parameter ν of the scaled t distribution can capture the fat tails of the fitted distributions. Smaller ν parameter estimates between 2 to 5 for all indices in
Table 2 indicate that the fat tails of the distributions are well captured by the fitted distributions. All estimated location parameters are small and around zero, which implies that the identified scaled t distributions are symmetric. It can be said that the fitted marginal distributions for return series of considered markets are suitable based on the estimated parameter values.
Adequacy of fitted distributions was assessed using probability-probability plots (p-p plots) and cumulative plots. All results confirm that the fitted scaled t distributions with respective parameters are suitable to model respective financial return series. Therefore, the scaled t distribution can be considered as a more suitable distribution to model return series of AORD, GSPC, ASPI, Amex oil, Amex gold, world cocoa indices and AUD-USD exchange rate.
Identifying most suitable multivariate distribution for input variables is a difficult task as the parameter estimation is associated with heavy mathematical calculations. Three parameter estimation techniques, batch approximation algorithm, local optimization method with matlab “fmincon” function and global optimization method with DSO algorithm, were considered in parameter estimation of multivariate distributions, and results show that the global optimization provides better results than the other two techniques.
The number of parameters to be estimated associated with each multivariate distribution varies with the number of potential input variables associated with them or the dimension of the multivariate distribution. Number of potential input variables\dimensions of considered three multivariate distributions of AORD, GSPC and ASPI and their related other markets are nine, four and thirteen, respectively. Past studies provide evidence for parameter estimation of multivariate distributions only up to four dimensions, and the global optimization technique considered in this study is able to estimate parameters of multivariate distributions with any dimension. The number of parameters to be estimated are ninety-one, twenty-one and one-hundred-and-eighty-three with respect to multivariate distributions associated with AORD, GSPC and ASPI and their related financial markets.
It is evident that the parameter estimates provided by the local optimization technique are ambiguous. This characteristic of the local optimization method is prominent due to its main disadvantage of excessive dependence on the initial parameters provided. As a solution, a global optimization technique, DSO algorithm, was considered, which does not require initial parameters and is a stable algorithm that provides solid solutions.
Results obtained from the global optimization method are much better than the parameters of the multivariate scaled t distributions of return series of AORD, GSPC and ASPI and those of their related financial indices. The discussion below is based on the results obtained from global optimization. The estimates of location parameters are small and around zero, and this implies that the multivariate distribution associated with AORD index and its related financial indices is central. The multivariate scaled t distribution of AORD series and related financial indices is less peaked and have fat tails as the estimated shape parameter is three. The multivariate distribution of GSPC index and related financial indices is symmetric, less peaked and has fat tails as the parameter estimates exhibits similar formation. Furthermore, the multivariate scaled t distribution of ASPI and related indices is central as the location parameters are around zero, less peaked as the shape parameter is three and has fat tails as the shape parameter is closer to unity. The parameter estimates of scale parameter Σ are alike values in each table, and it suggests that the markets have similar influence on the respective multivariate distributions.
Incorporating an appropriate multivariate distribution other than the Gaussian distribution as the distribution of input variables to the probabilistic neural network is one of the objectives of the study. Therefore, proposed PNN was implemented using matlab software, which facilitates considering the multivariate scaled t distribution as the distribution of input variables. To evaluate the performance of the proposed PNN, comparisons were carried out with the existing standard PNN implemented using matlab software. For budgetary convenience, the implemented matlab codes can be easily converted into an open source programming language like python.
Table 5 illustrates that the overall accuracy levels of standard probabilistic neural network model when forecasting the direction of stock indices AORD, GSPC and ASPI are 54.5%, 53.34% and 55.09%, respectively. Same data sets were used to evaluate the performance of proposed PNN model which consider multivariate scaled t distribution when calculating probabilities in the pattern layer. Overall accuracy of AORD index is 61.56% while GSPC and ASPI indices exhibit 63.04% and 63.47% corresponding accuracy when forecasting the direction using proposed PNN, and this implies an increase in overall accuracy of proposed PNN for all considered stock indices than that of standard PNN. These are acceptable and high percentages of accuracy with respect to financial market forecasting.
By referring
Table 5, it is noteworthy that the misclassification percentages when applying standard PNN for AORD series for Class 1, Class 2 and Class 3 are 70.59%, 4.67% and 61.25%. Very high misclassification percentages can be observed in Class 1 and Class 3, while a very low misclassification percentage can be observed in Class 2. Consequently, it is evident that the standard PNN model is biased towards one class against the other two classes in this scenario. Class imbalance ratio (IR) plays a significant role in controlling forecasting ability of PNN models.
Table 6 indicates that the IR of Class 1, Class 2 and Class 3 of AORD series are 0.2, 0.6 and 0.2, respectively. By comparing overall misclassification percentage and IR of each class of AORD index, it can be said that the standard PNN model is biased towards the majority class and forecasts most of the test set observations to the majority class. Similar behavior can be observed when comparing misclassification percentages and class imbalance ratios of classes in GSPC and ASPI indices. Results suggest that the performance of the existing probabilistic neural network model heavily depends on the class imbalanced ratio.
Correspondingly,
Table 5 indicates that the misclassification percentages among three classes of each index differ significantly when using the proposed PNN. Similar to the results of standard PNN, Class 2 exhibits a lower misclassification percentage than that of Class 1 and Class 3 when forecasting the direction of AORD, GSPC and ASPI indices using proposed PNN. Even though the proposed probabilistic neural network model outperforms the existing PNN model, it still suffers from the class imbalanced problem.
Findings described above highlight the necessity of an appropriate technique to handle class imbalanced problem in data sets. A technique called multi-class undersampling based bagging (MCUB) is proposed to handle the multi-class imbalanced problem persisting in data sets considered in the study. Both standard PNN and proposed PNN were embedded into the proposed MCUB technique separately for further investigations.
Overall accuracy of standard PNN model increases after introducing MCUB technique in forecasting the direction of GSPC and ASPI indices, and AORD index predictions exhibit a slight decrease in the overall performance with reference to
Table 5. After ingraining the proposed PNN to the proposed MCUB technique, an increase in overall accuracy can be observed with respect to all indices. Increase of two highly important types of misclassification percentages can be observed after introducing MCUB to standard PNN whereas two types of moderately important misclassification percentages have decreased in all indices. The crucial misclassification types of buy-sell and sell-buy signals have reduced considerably by the introduced ensemble technique in most of the circumstances, and misclassification percentages of buy-hold and sell-hold signals have been reduced in all the cases simultaneously in proposed PNN model. The remarkable fact is that the misclassification percentages among Class 1, Class 2 and Class 3 in forecasting the direction of each stock index when using both standard and proposed PNN models are very much similar. Accordingly, it is indisputable that the proposed ensemble technique, multi-class undersampling based bagging (MCUB), is able to unravel the multi-class imbalanced problem residing in the data sets.
Results in
Table 5 prove that the proposed MCUB technique is suitable to handle the multi-class imbalanced problem existing in probabilistic neural networks when classifying data. Hence, it is sensible to compare performance of standard PNN versus proposed PNN with MCUB technique. By referring to
Table 5, it can be said that the proposed PNN with multivariate scaled
t distribution as the joint distribution of input variables exhibits higher accuracy than that of standard PNN with respect to all considered stock indices. The balance between misclassification percentages among three classes has been enhanced when classifying using the proposed PNN. Misclassification percentages of most important buy-sell and sell-buy signals leading to critical losses have been decreased immensely by the proposed PNN. Slight increase in misclassification percentages of moderately important two misclassification types can be observed. Based on the aforesaid facts, performance improvements can be observed when classification is done using proposed PNN with MCUB in contrast to the standard PNN with MCUB. By considering the improved PNN model with MCUB introduced in the study, 66.37%, 67.02% and 70.12% accuracies can be observed in forecasting the direction of AORD, GSPC and ASPI indices respectively. It is generally accepted that these percentages are high enough to make profit from investments in financial markets.
To understand the generalization ability of the proposed PNN model, performance was evaluated for an updated data set which contains three months’ daily data just after the ending date of the data set used in the study.
Table 7 illustrates that the proposed model (proposed PNN with MCUB) is capable of forecasting the direction of all considered stock indices with similar accuracy for the novel data set. All types of misclassification percentages exhibit similar values when comparing corresponding values of the final proposed model. Therefore, it is evident that the proposed dynamic model is proficient to forecast the direction of a given stock market index for any given time period with higher accuracy.
Finally, this study identified an improved PNN model to forecast the direction of a given stock market index by incorporating a suitable non-Gaussian multivariate distribution for calculating probabilities and multi-class undersampling based bagging approach to overcome the class imbalanced problem.
Based on past studies, influences from few inter-market, other financial markets and world major commodities were considered in identifying potential inputs to the probabilistic neural network models. Other stock market indices, other financial markets and other commodities may have significant influence on the considered three stock indices. Even though the gross domestic product (GDP), interest rates, Treasury bill rates, etc., affect the stock market indices, they were not considered as potential inputs to the PNN models because of the non-availability of daily data corresponding to those variables. These facts can be identified as limitations of the study.
As a future study, the proposed dynamic model with multivariate scaled t distribution and multi-class undersampling based bagging technique can be used to build a computer intensive tool, an attractive, user friendly platform to support stakeholders in decision making. The proposed probabilistic neural network model can be used to forecast the direction of other financial indices like exchange rates, interest rates, Treasury bill rates, etc., with higher accuracy. Moreover, the proposed PNN can be used for classification purposes in other applications such as weather, biology, agriculture, medicine, image processing, natural language processing, marketing research, etc.
5. Conclusions
The scaled t distribution with three parameters, location parameter, scale parameter and shape parameter, is introduced as a more suitable distribution to model financial market returns.
Other multivariate distributions than the Gaussian distribution have not considered as the joint distribution of input variables in probabilistic neural networks. The proposed probabilistic neural network model facilitates considering the multivariate scaled t distribution as the distribution associated with input variables.
The proposed probabilistic neural network model outperforms the existing standard PNN model.
The proposed ensemble technique to handle multi-class imbalanced problem, multi-class undersampling based bagging (MCUB), is a novel approach and capable of handling multi-class imbalanced problem in probabilistic neural network models.
The improved PNN model with MCUB technique proposed in the study is competent to forecast the direction of stock market indices AORD, GSPC and ASPI with 66.37%, 67.02% and 70.12% accuracy, respectively, which are acceptable and high percentages of accuracy in financial market forecasting.
Performance evaluation was carried out for an updated data set, verifying the generalization ability of the proposed dynamic model to forecast the direction of a given stock market index for a similar time period with higher accuracy and profitability.
The proposed dynamic model is suitable for use in forecasting the direction of a given stock market index with higher accuracy.