New Satellite Selection Approach for GPS/BDS/GLONASS Kinematic Precise Point Positioning
Abstract
1. Introduction
2. PPP Mathematical Model and Satellite Selection Algorithms
2.1. Dual-Frequency Multi-GNSS PPP
2.2. Optimal DOP Algorithm
2.3. The Maximum Volume Algorithm
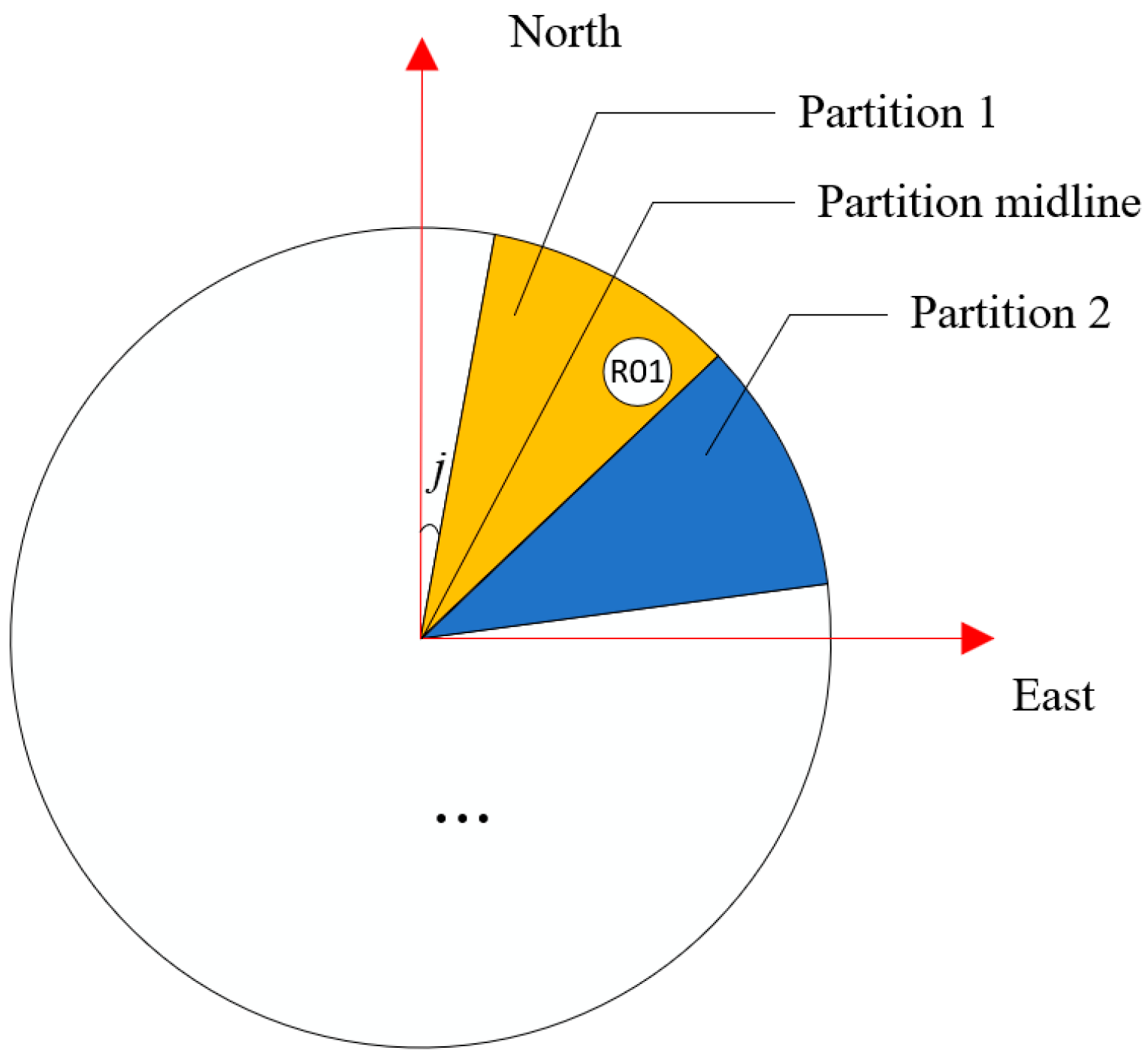
2.4. The Fast-Rotating Partition Satellite Selection Algorithm
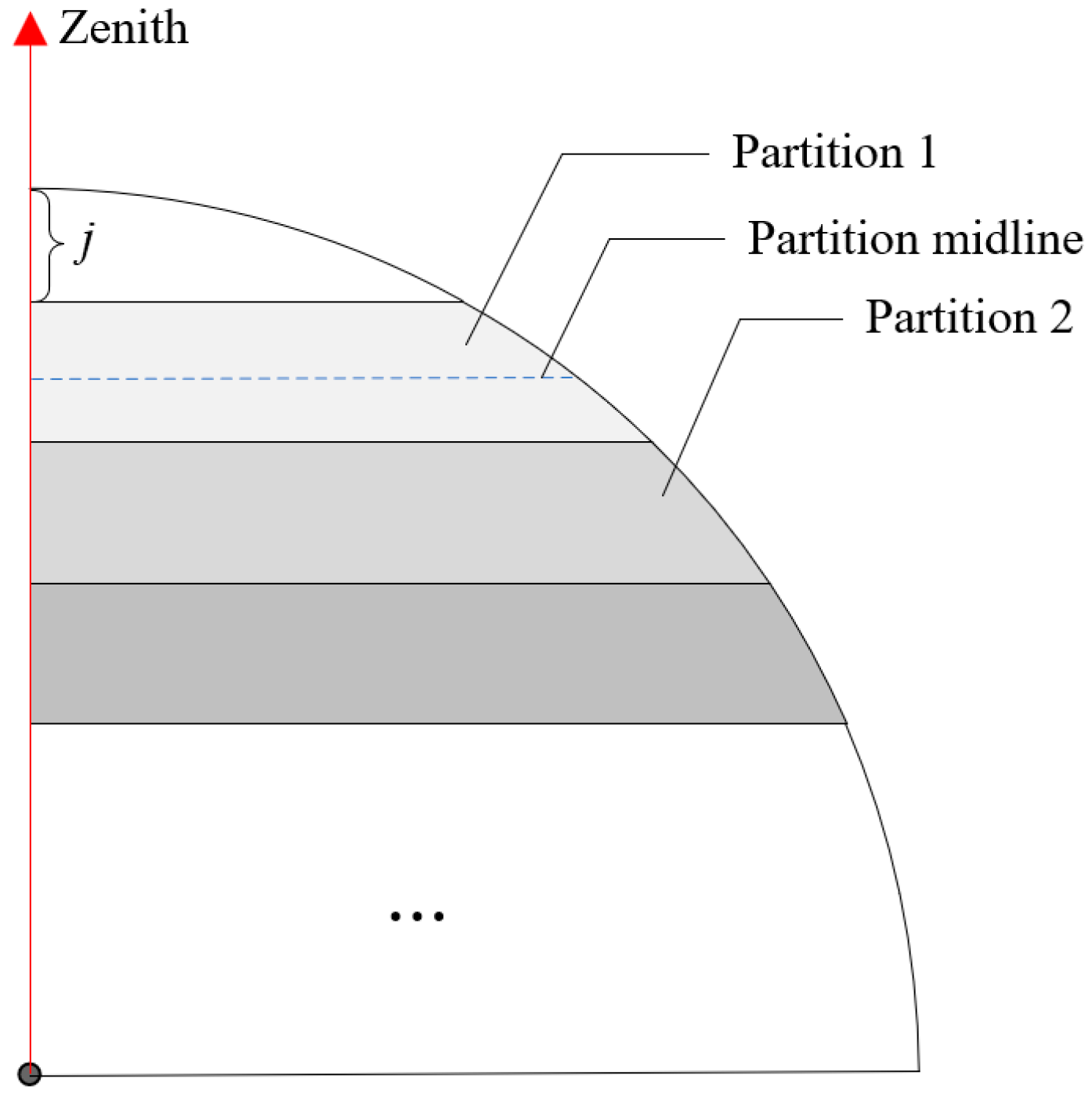
2.5. The Elevation Partition Satellite Selection Algorithm
3. Establishment of the NSS Model in Kinematic PPP
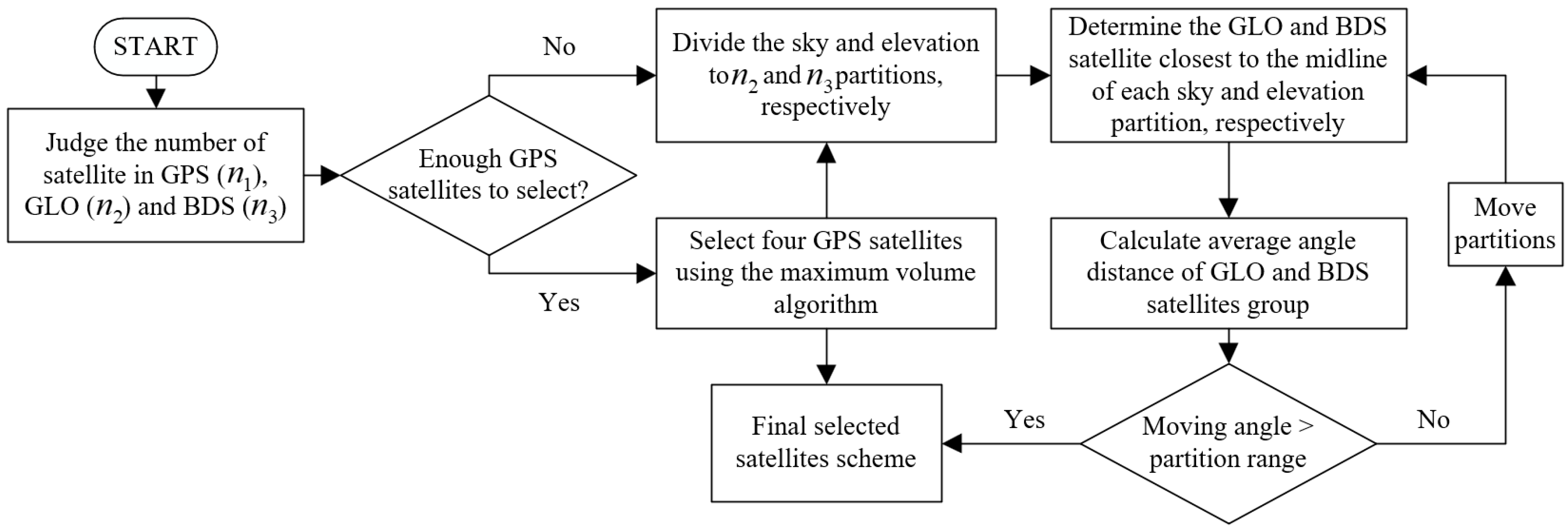
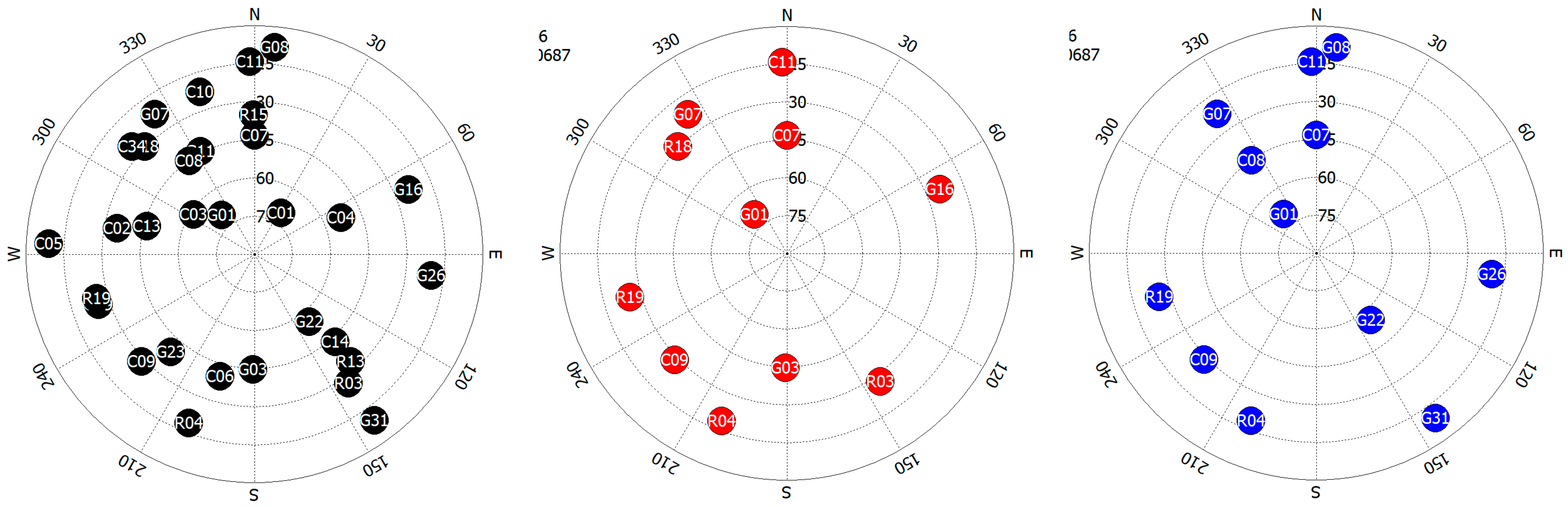
3.1. The Combination of Three Different Satellite Selection Algorithms
3.2. The Inheritance of Ambiguity
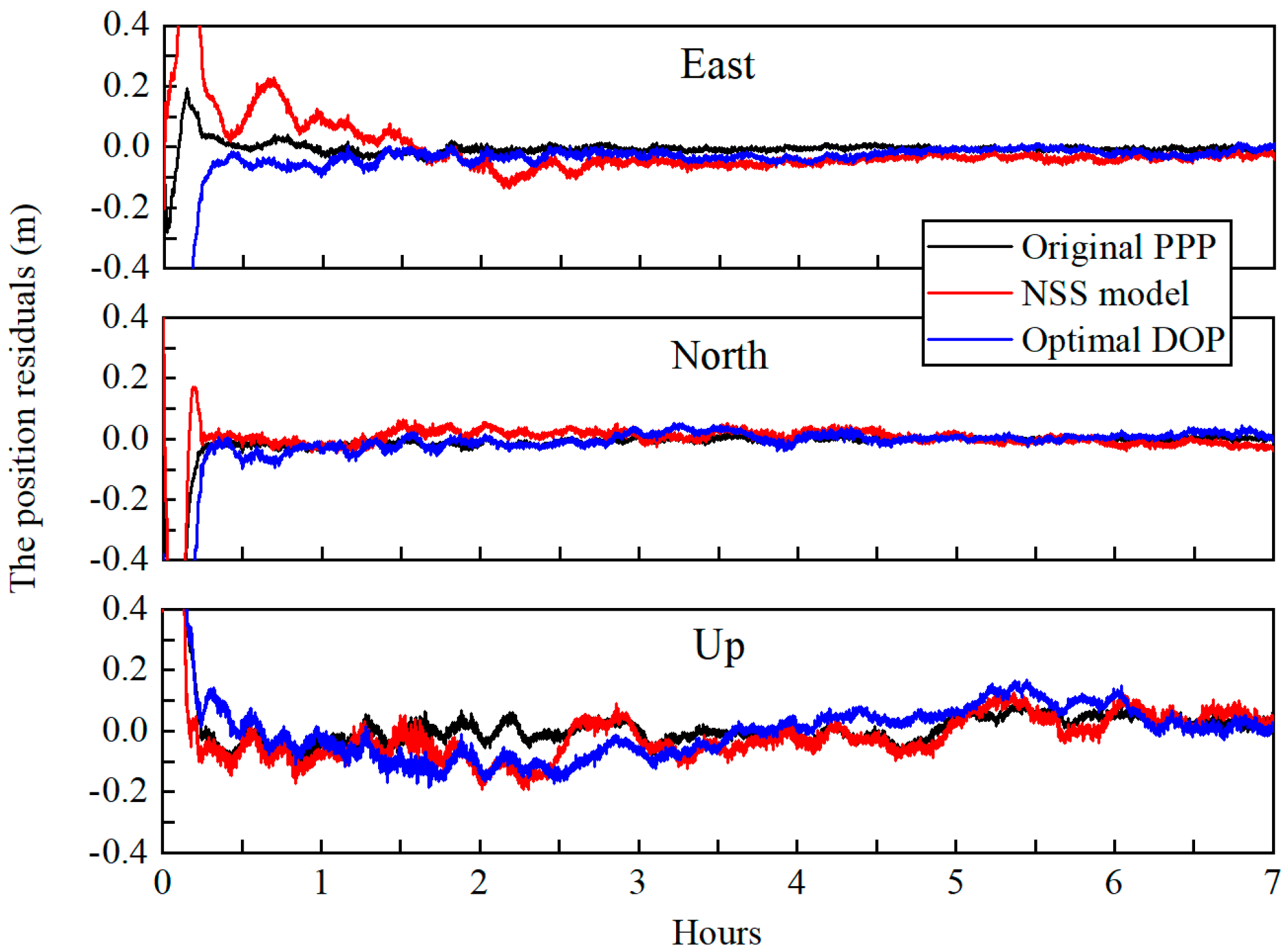
4. Test and Analysis
4.1. Time Complexity of the NSS Model
4.2. Positioning Accuracy of the NSS Model
4.2.1. The MGEX Data
4.2.2. The Measured Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alkan, R.M.; Saka, M.H.; Ozulu, İ.M.; İlçi, V. Kinematic Precise Point Positioning Using GPS and Glonass Measurements in Marine Environments. Measurement 2017, 109, 36–43. [Google Scholar] [CrossRef]
- Kouba, J.; Héroux, P. Precise Point Positioning Using IGS Orbit and Clock Products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Wang, L.; Li, Z.; Ge, M.; Neitzel, F.; Wang, Z.; Yuan, H. Validation and Assessment of Multi-GNSS Real-Time Precise Point Positioning in Simulated Kinematic Mode Using IGS Real-Time Service. Remote Sens. 2018, 10, 337. [Google Scholar] [CrossRef]
- Jiao, G.Q.; Song, S.L.; Ge, Y.L.; Su, K.; Liu, Y.Y. Assessment of BeiDou-3 and Multi-GNSS Precise Point Positioning Performance. Sensors 2019, 19, 2496. [Google Scholar] [CrossRef]
- Yasyukevich, Y.; Astafyeva, E.; Padokhin, A.; Ivanova, V.; Syrovatskii, S.; Podlesnyi, A. The 6 September 2017 X-Class Solar Flares and Their Impacts on the Ionosphere, GNSS, and HF Radio Wave Propagation. Space Weather Int. J. Res. Appl. 2018, 16, 1013–1027. [Google Scholar] [CrossRef]
- Jacobsen, K.S.; Andalsvik, Y.L. Overview of the 2015 St. Patrick’s day storm and its consequences for RTK and PPP positioning in Norway. J. Space Weather Space Clim. 2016, 6. [Google Scholar] [CrossRef]
- RISDE. Global Navigation Satellite System GLONASS—Interface Control Document, Version 5.1; Russian Institute of Space Device Engineering: Moscow, Russia, 2008. [Google Scholar]
- EU. European GNSS (Galileo) Open Service Signal in Space Interface Control Document; European Union: Brussels, Belgium, 2014. [Google Scholar]
- CSNO. BeiDou Navigation Satellite System Signal in Space Interface Control Document: Open Service Signal (Version 2.0); China Satellite Navigation Office: Beijing, China, 2013. [Google Scholar]
- CSNO. Report on the Development of BeiDou Navigation Satellite System (Version 2.2); China Satellite Navigation Office: Beijing, China, 2013. [Google Scholar]
- Alcay, S.; Yigit, C.O. Network based performance of GPS-only and combined GPS/GLONASS positioning under different sky view conditions. Acta Geod. Geophys. 2017, 52, 345–356. [Google Scholar] [CrossRef]
- Nie, Z.; Gao, Y.; Wang, Z.; Ji, S. A new method for satellite selection with controllable weighted PDOP threshold. Surv. Rev. 2016, 49, 285–293. [Google Scholar] [CrossRef]
- Kihara, M.; Okada, T. A Satellite Selection Method and Accuracy for the Global Positioning System. Navigation 1984, 31, 8–20. [Google Scholar] [CrossRef]
- Swaszek, P.F.; Hartnett, R.J.; Seals, K.C. Multi-Constellation GNSS: New Bounds on DOP and a Related Satellite Selection Process. In Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, OR, USA, 12–16 September 2016; pp. 228–235. [Google Scholar]
- Meng, F.; Wang, S.; Zhu, B. Research of Fast Satellite Selection Algorithm for Multi-constellation. Chin. J. Electron. 2016, 25, 1172–1178. [Google Scholar] [CrossRef]
- Blanco-Delgado, N.; Nunes, F.D. Satellite Selection Method for Multi-Constellation GNSS Using Convex Geometry. IEEE Trans. Veh. Technol. 2010, 59, 4289–4297. [Google Scholar] [CrossRef]
- Roongpiboonsopit, D.; Karimi, H.A. A Multi-Constellations Satellite Selection Algorithm for Integrated Global Navigation Satellite Systems. J. Intell. Transp. Syst. 2009, 13, 127–141. [Google Scholar] [CrossRef]
- Li, F.; Li, Z.; Gao, J.; Yao, Y. A Fast Rotating Partition Satellite Selection Algorithm Based on Equal Distribution of Sky. J. Navig. 2019, 72, 1053–1069. [Google Scholar] [CrossRef]
- Gao, X.; Dai, W.; Song, Z.; Cai, C. Reference satellite selection method for GNSS high-precision relative positioning. Geod. Geodyn. 2017, 8, 125–129. [Google Scholar] [CrossRef]
- Huang, P.P.; Rizos, C.; Roberts, C. Satellite selection with an end-to-end deep learning network. GPS Solut. 2018, 22, 108. [Google Scholar] [CrossRef]
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS: Principles and Applications, 2nd ed.; Artech House: Norwood, MA, USA, 2006. [Google Scholar]
- Li, Z.K.; Chen, F. Improving availability and accuracy of GPS/BDS positioning using QZSS for single receiver. Acta Geod. Geophys. 2017, 52, 95–109. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stuerze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS) —Achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.A.; Ge, M.R.; Li, P.; Wickert, J.; Schuh, H. Simultaneous estimation of GLONASS pseudorange inter-frequency biases in precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22. [Google Scholar] [CrossRef]
- Schönemann, E.; Becker, M.; Springer, T. A new Approach for GNSS Analysis in a Multi-GNSS and Multi-Signal Environment. J. Geod. Sci. 2011, 1, 204–214. [Google Scholar] [CrossRef]
- Odijk, D.; Zhang, B.C.; Khodabandeh, A.; Odolinski, R.; Teunissen, P.J.G. On the estimability of parameters in undifferenced, uncombined GNSS network and PPP-RTK user models by means of system theory. J. Geod. 2016, 90, 15–44. [Google Scholar] [CrossRef]
- Yan, X.; Yang, G.; Shi, J.; Xu, C. Carrier phase-based ionospheric observables using PPP models. Geod. Geodyn. 2017, 8, 17–23. [Google Scholar]
- Liu, T.; Yuan, Y.B.; Zhang, B.C.; Wang, N.B.; Tan, B.F.; Chen, Y.C. Multi-GNSS precise point positioning (MGPPP) using raw observations. J. Geod. 2017, 91, 253–268. [Google Scholar] [CrossRef]
- Guo, F.; Zhang, X.H.; Wang, J.L.; Ren, X.D. Modeling and assessment of triple-frequency BDS precise point positioning. J. Geod. 2016, 90, 1223–1235. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.; Li, W.; Jiang, X.; Wickert, J.; Schuh, H. GAMP: An open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22, 33. [Google Scholar] [CrossRef]
- Li, X.; Zus, F.; Lu, C.; Dick, G.; Ning, T.; Ge, M.; Wickert, J.; Schuh, H. Retrieving of atmospheric parameters from multi-GNSS in real time: Validation with water vapor radiometer and numerical weather model. J. Geophys. Res. Atmos. 2015, 120, 7189–7204. [Google Scholar] [CrossRef]
- Kazmierski, K.; Sosnica, K.; Hadas, T. Quality assessment of multi-GNSS orbits and clocks for real-time precise point positioning. GPS Solut. 2017, 22, 11. [Google Scholar] [CrossRef]
- Kazmierski, K.; Hadas, T.; Sosnica, K. Weighting of Multi-GNSS Observations in Real-Time Precise Point Positioning. Remote Sens. 2018, 10, 84. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X.; Guo, F. Ambiguity resolved precise point positioning with GPS and BeiDou. J. Geod. 2017, 91, 25–40. [Google Scholar] [CrossRef]
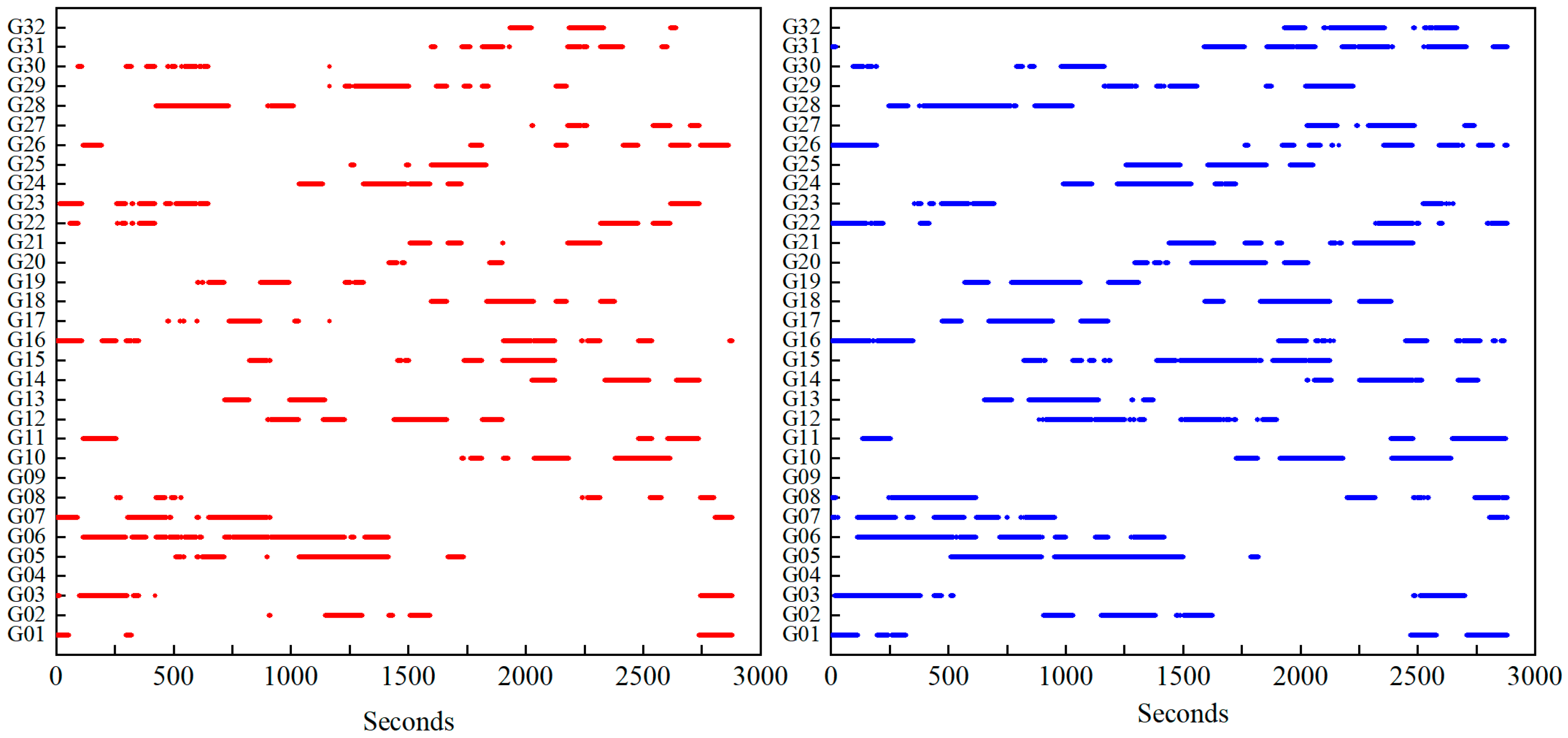
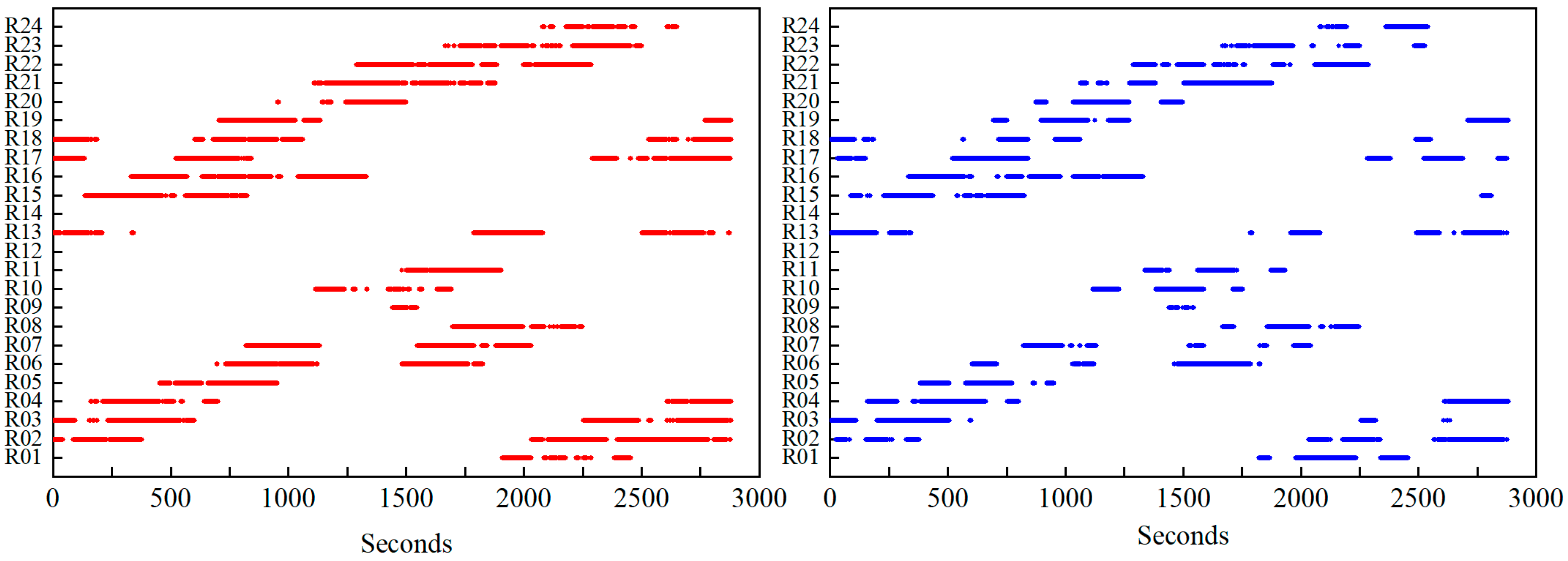

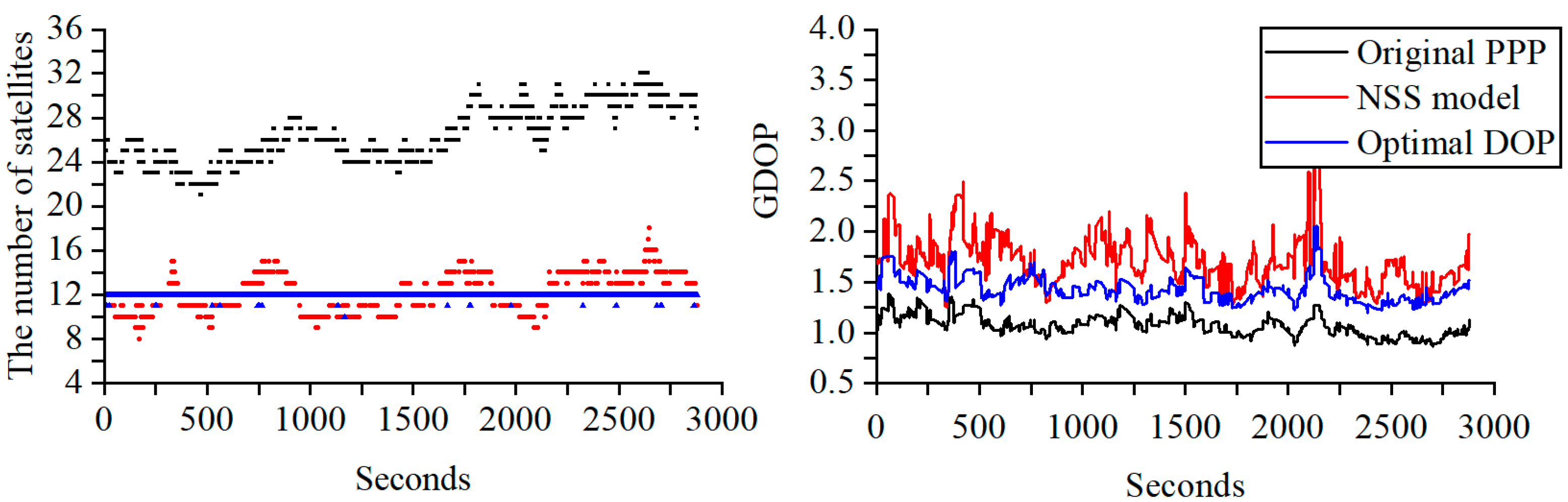
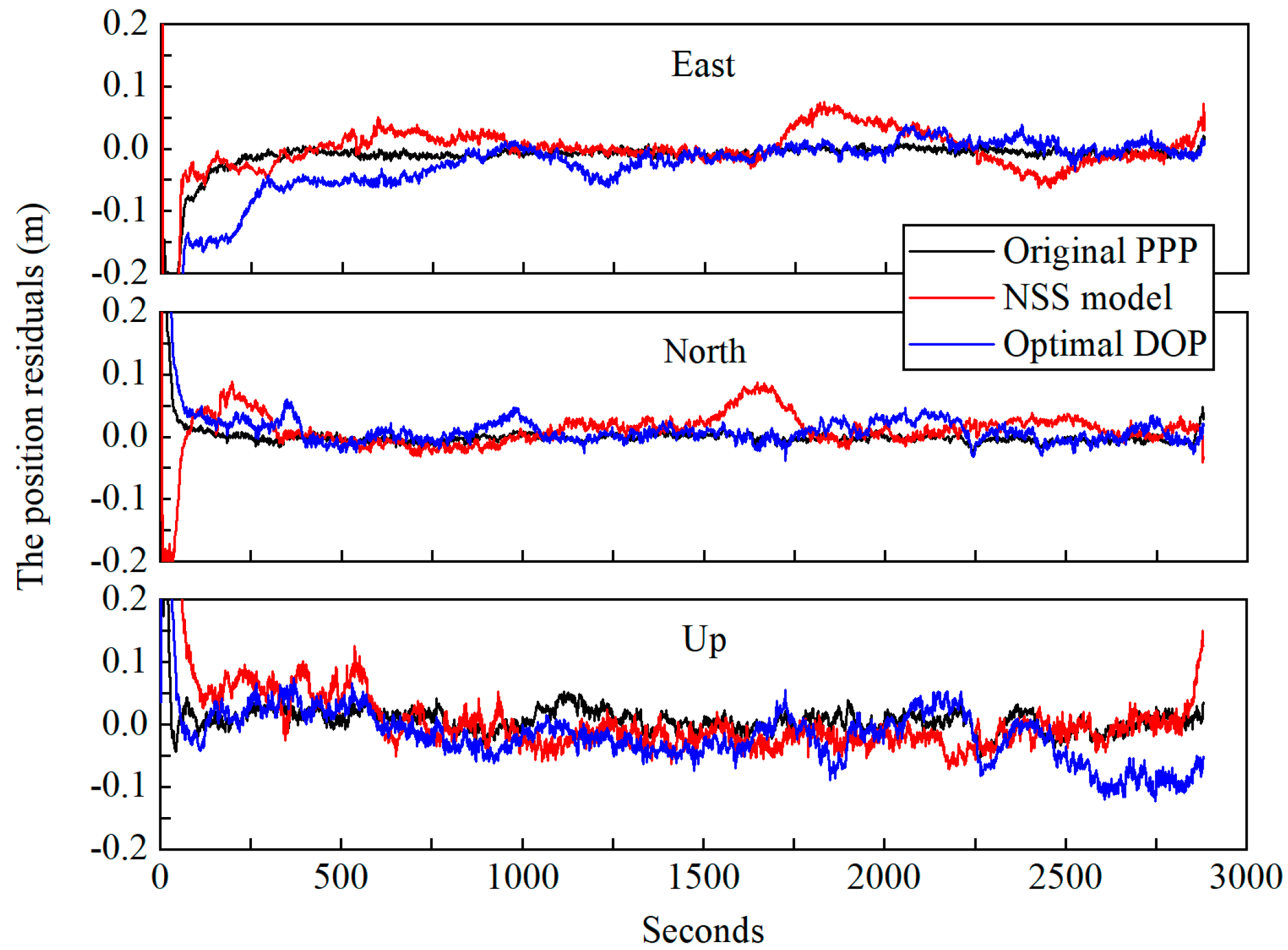

| Average Number of Visible Satellites at JFNG | ||||
|---|---|---|---|---|
| Number of Selected Satellites | G | GC | GR | GRC |
| 9 | 15 | 19 | 25 | |
| 4 | 126 | 1365 | 3876 | 12,650 |
| 5 | 126 | 3003 | 11,628 | 53,130 |
| 6 | 84 | 5005 | 27,132 | 177,100 |
| 7 | 6435 | 50,388 | 780,700 | |
| 8 | 6435 | 75,582 | 1,081,575 | |
| 9 | 5005 | 92,378 | 2,042,975 | |
| 10 | 3003 | 92,378 | 3,268,760 | |
| 11 | 75,582 | 4,457,400 | ||
| 12 | 50,388 | 5,200,300 | ||
| DARW | GMSD | KARR | MRO1 | XMIS | Mean | |
|---|---|---|---|---|---|---|
| Original PPP | 100% | 100% | 100% | 100% | 100% | 100% |
| NSS model | 46.0% | 48.3% | 45.0% | 45.4% | 43.0% | 45.5% |
| Optimal DOP | 45.8% | 51.1% | 45.4% | 46.8% | 43.9% | 46.6% |
| DARW | GMSD | KARR | MRO1 | XMIS | Mean | |
|---|---|---|---|---|---|---|
| Original PPP | 3.6 | 2.7 | 2.9 | 3.1 | 2.8 | 3.0 |
| NSS model | 7.8 | 8.7 | 6.4 | 8.7 | 7.2 | 7.8 |
| Optimal DOP | 8.6 | 5.3 | 8.3 | 6.2 | 8.1 | 7.3 |
| Original PPP | NSS Model | Improved | |
|---|---|---|---|
| DARW | 130.440 | 62.823 | 51.8% |
| GMSD | 78.570 | 45.342 | 42.3% |
| KARR | 112.436 | 62.214 | 44.7% |
| MRO1 | 103.957 | 60.057 | 42.2% |
| XMIS | 112.781 | 60.924 | 46.0% |
| Mean | 107.637 | 58.272 | 45.9% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Gao, J.; Li, Z.; Li, F.; Chen, C.; Wang, Y. New Satellite Selection Approach for GPS/BDS/GLONASS Kinematic Precise Point Positioning. Appl. Sci. 2019, 9, 5280. https://doi.org/10.3390/app9245280
Yang L, Gao J, Li Z, Li F, Chen C, Wang Y. New Satellite Selection Approach for GPS/BDS/GLONASS Kinematic Precise Point Positioning. Applied Sciences. 2019; 9(24):5280. https://doi.org/10.3390/app9245280
Chicago/Turabian StyleYang, Liu, Jingxiang Gao, Zengke Li, Fangchao Li, Chao Chen, and Yifan Wang. 2019. "New Satellite Selection Approach for GPS/BDS/GLONASS Kinematic Precise Point Positioning" Applied Sciences 9, no. 24: 5280. https://doi.org/10.3390/app9245280
APA StyleYang, L., Gao, J., Li, Z., Li, F., Chen, C., & Wang, Y. (2019). New Satellite Selection Approach for GPS/BDS/GLONASS Kinematic Precise Point Positioning. Applied Sciences, 9(24), 5280. https://doi.org/10.3390/app9245280






