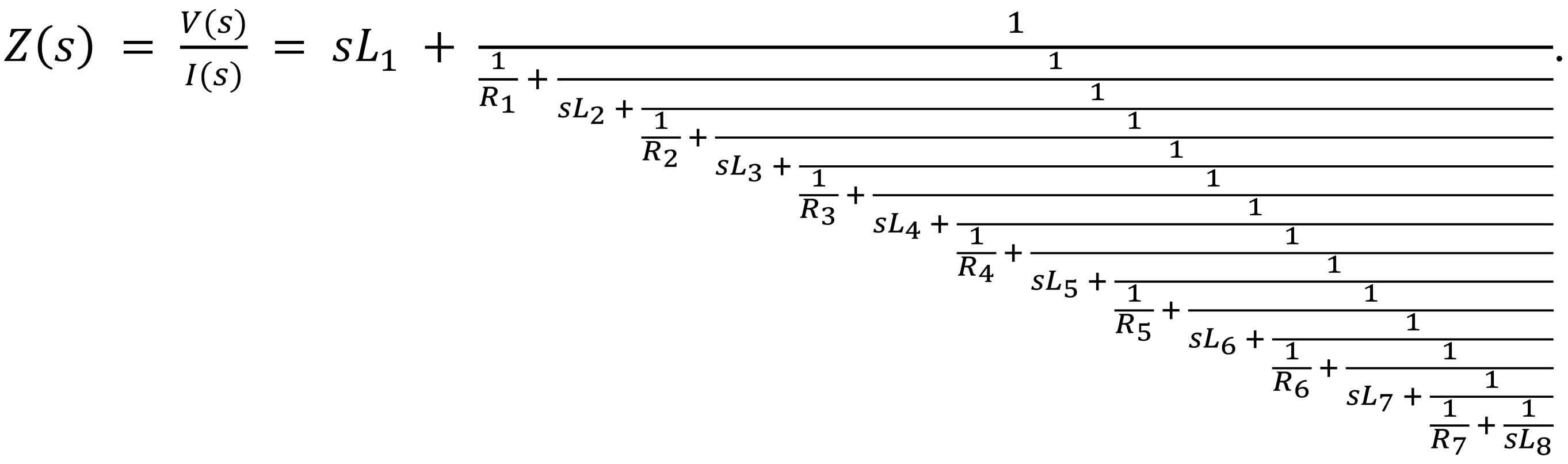
Figure 1.
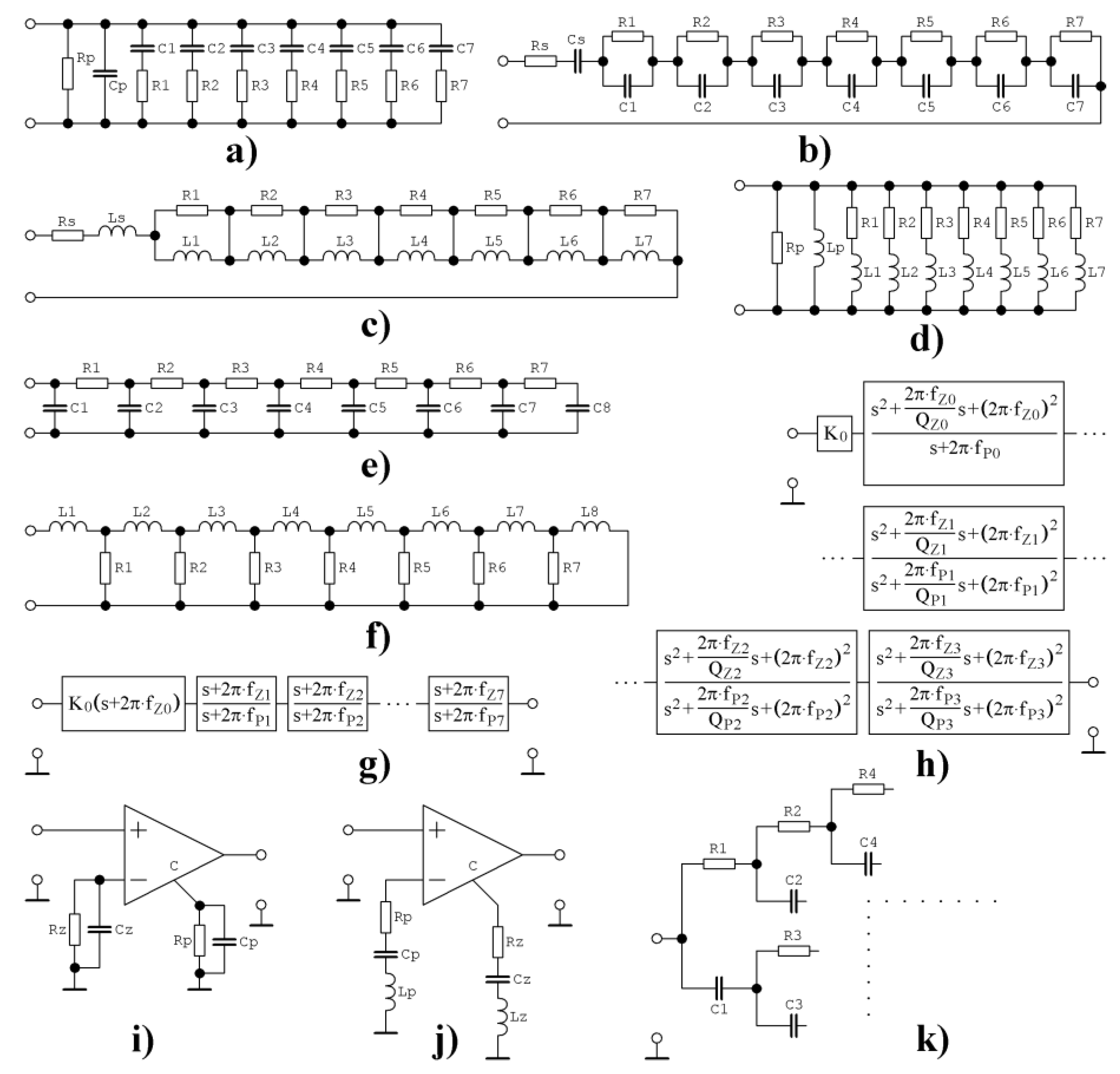
Gallery of a fundamental passive circuit implementations of seventh-order approximations of constant phase elements (CPEs): (a) parallel-series RC ladder, (b) equivalent series-parallel RC structure, (c) series-parallel RL network, (d) equivalent parallel-series RL structure, (e) simplified transmission line for fractional-order (FO) admittance realization, (f) simplified transmission line for FO impedance realization, (g) FO two-port realization using first-order filtering sections, (h) FO two-port realization using second-order filtering sections, (i) active CPE realization using knowledge of zeroes and poles of the impedance function, (j) active CPE realization based on knowledge of significant frequencies and quality factors of impedance function, and (k) fragment of RC tree structure.
Figure 1.
Gallery of a fundamental passive circuit implementations of seventh-order approximations of constant phase elements (CPEs): (a) parallel-series RC ladder, (b) equivalent series-parallel RC structure, (c) series-parallel RL network, (d) equivalent parallel-series RL structure, (e) simplified transmission line for fractional-order (FO) admittance realization, (f) simplified transmission line for FO impedance realization, (g) FO two-port realization using first-order filtering sections, (h) FO two-port realization using second-order filtering sections, (i) active CPE realization using knowledge of zeroes and poles of the impedance function, (j) active CPE realization based on knowledge of significant frequencies and quality factors of impedance function, and (k) fragment of RC tree structure.
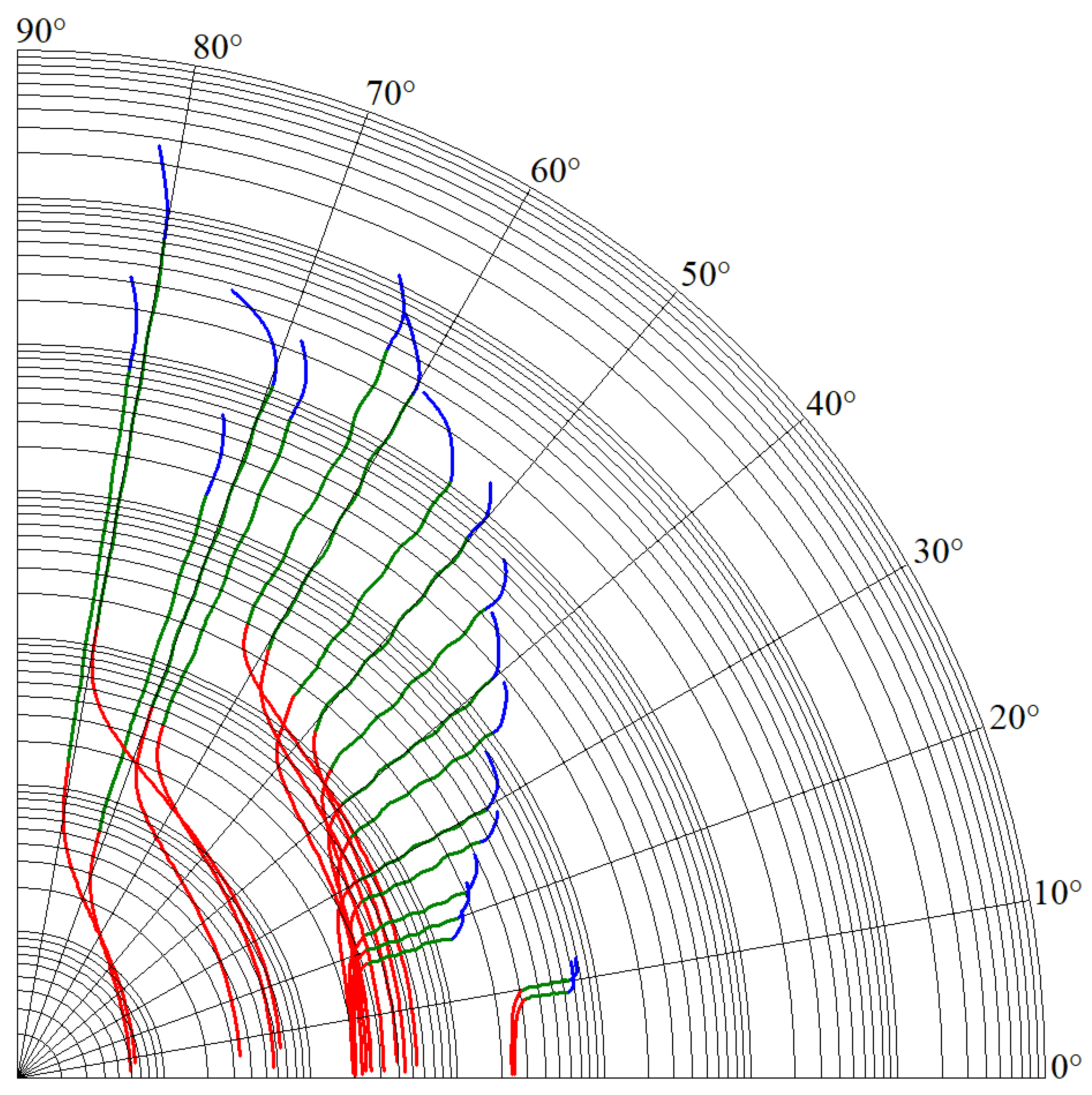
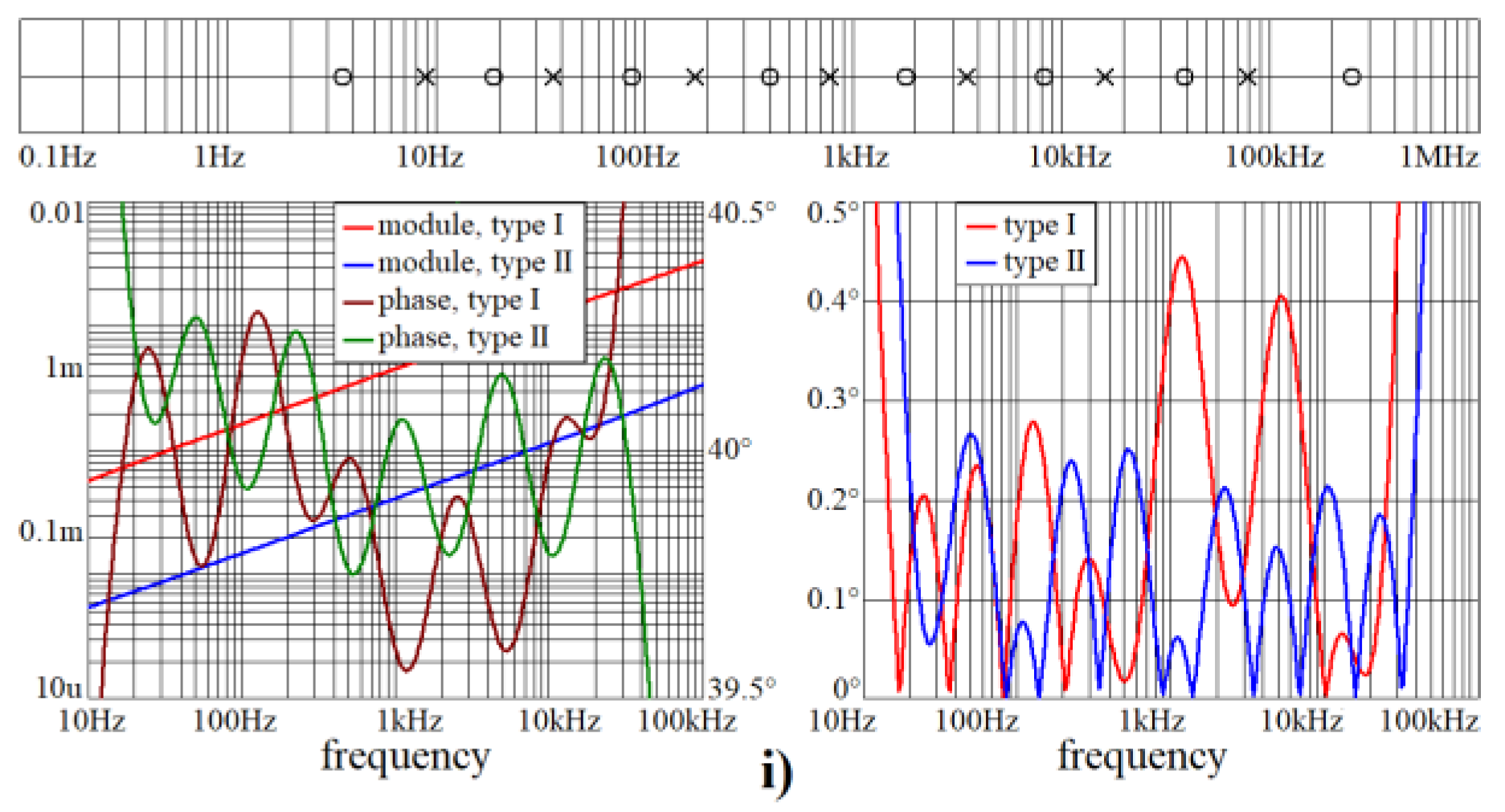
Figure 2.
Polar plots of the complex admittance functions for individual RC approximants of CPE, fully passive ladder realizations based on
Figure 1a dedicated for audio signal processing, infrasound frequencies (
red), active audio range (
green), and ultrasound frequencies (
blue).
Figure 2.
Polar plots of the complex admittance functions for individual RC approximants of CPE, fully passive ladder realizations based on
Figure 1a dedicated for audio signal processing, infrasound frequencies (
red), active audio range (
green), and ultrasound frequencies (
blue).
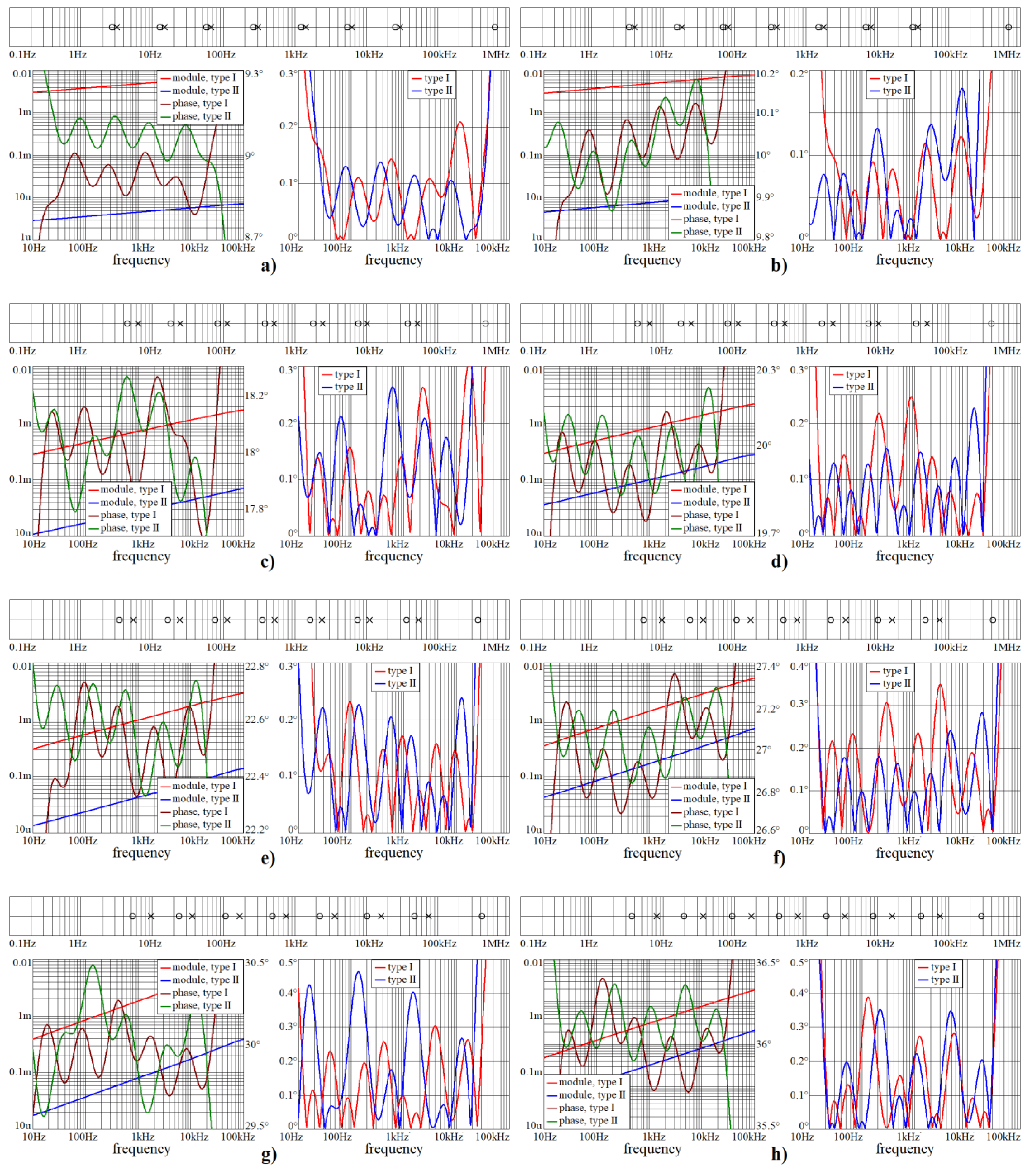
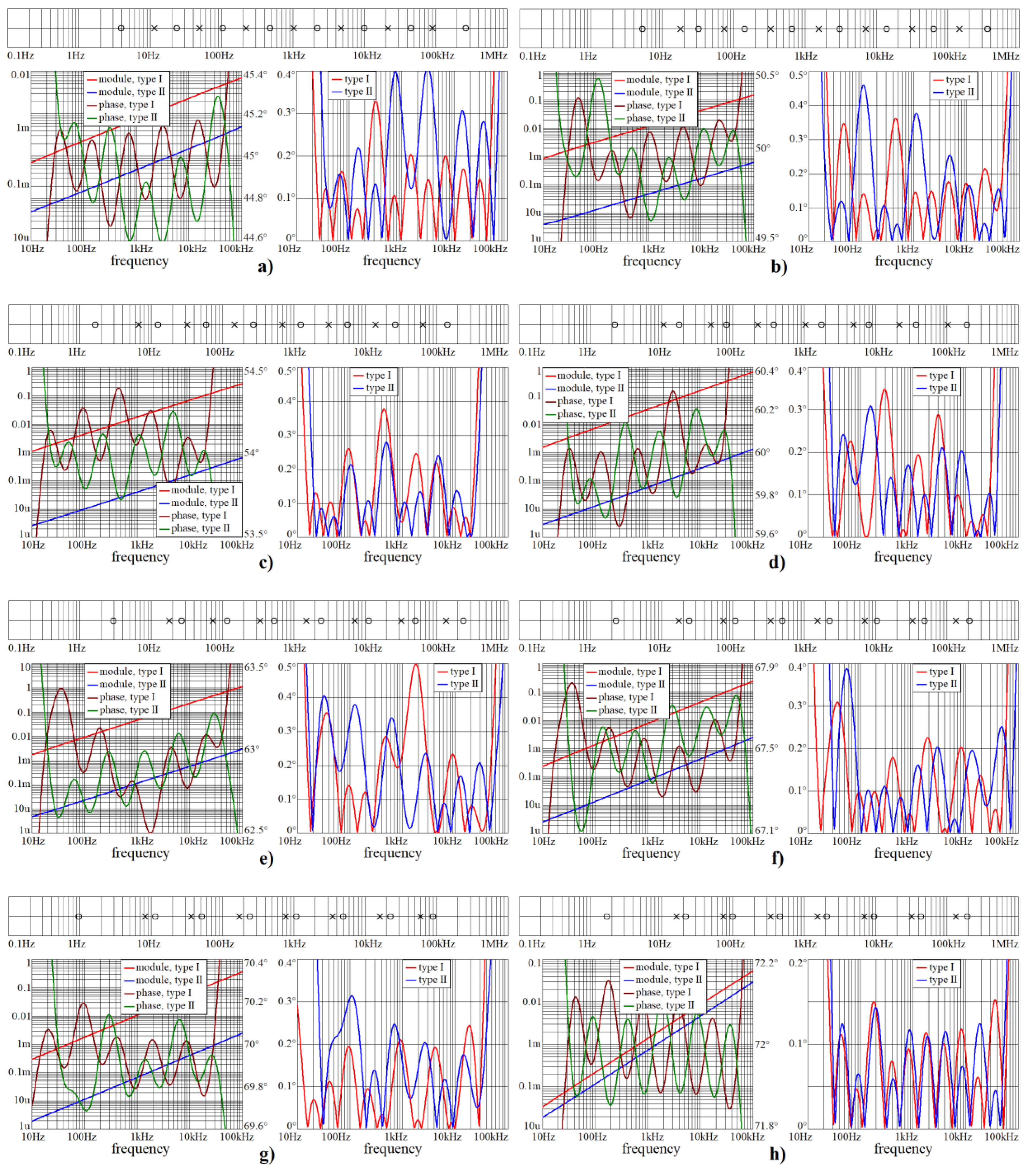
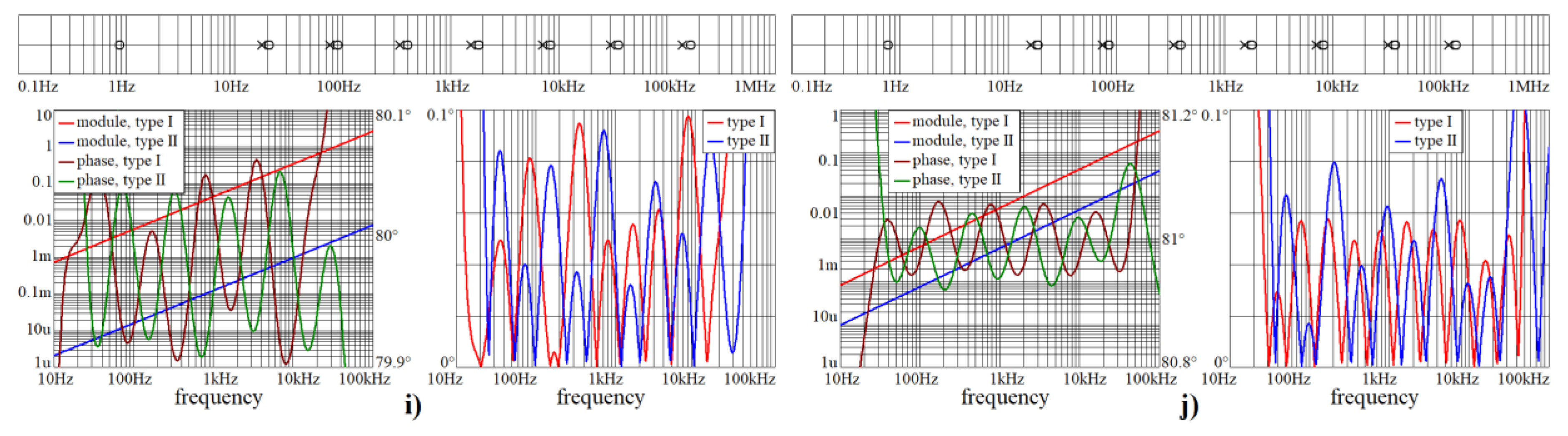
Figure 3.
Numerical verification of designed audio CPEs for orders considered in this paper: (a) α = 1/10, (b) α = 1/9, (c) α = 1/5, (d) α = 2/9, (e) α = 1/4, (f) α = 3/10, (g) α = 1/3, (h) α = 2/5, (i) α = 4/9.
Figure 3.
Numerical verification of designed audio CPEs for orders considered in this paper: (a) α = 1/10, (b) α = 1/9, (c) α = 1/5, (d) α = 2/9, (e) α = 1/4, (f) α = 3/10, (g) α = 1/3, (h) α = 2/5, (i) α = 4/9.
Figure 4.
Numerical validation of designed audio CPEs (continuation of previous figure): (a) α = 1/2, (b) α = 5/9, (c) α = 3/5, (d) α = 2/3, (e) α = 7/10, (f) α = 3/4, (g) α = 7/9, (h) α = 4/5, (i) α = 8/9, (j) α = 9/10.
Figure 4.
Numerical validation of designed audio CPEs (continuation of previous figure): (a) α = 1/2, (b) α = 5/9, (c) α = 3/5, (d) α = 2/3, (e) α = 7/10, (f) α = 3/4, (g) α = 7/9, (h) α = 4/5, (i) α = 8/9, (j) α = 9/10.
Figure 5.
Experimental printed circuit board (PCB) of the fully passive ladder CPE with seven series-parallel RC sections and the so-called three-quarter capacitor (
upper photos). Modular realization of active CPEs in the sense of
Figure 1i, zeroes and poles tunable using variable resistors, and a fragment with four cells (
lower photo).
Figure 5.
Experimental printed circuit board (PCB) of the fully passive ladder CPE with seven series-parallel RC sections and the so-called three-quarter capacitor (
upper photos). Modular realization of active CPEs in the sense of
Figure 1i, zeroes and poles tunable using variable resistors, and a fragment with four cells (
lower photo).
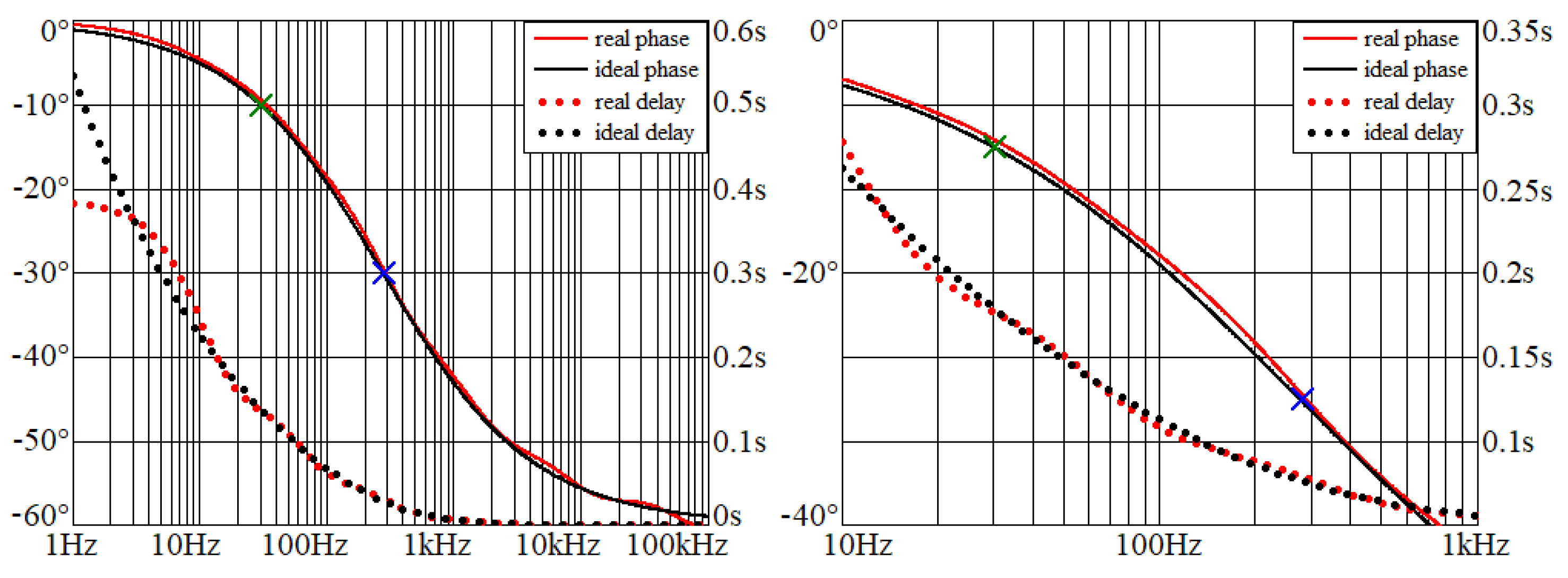
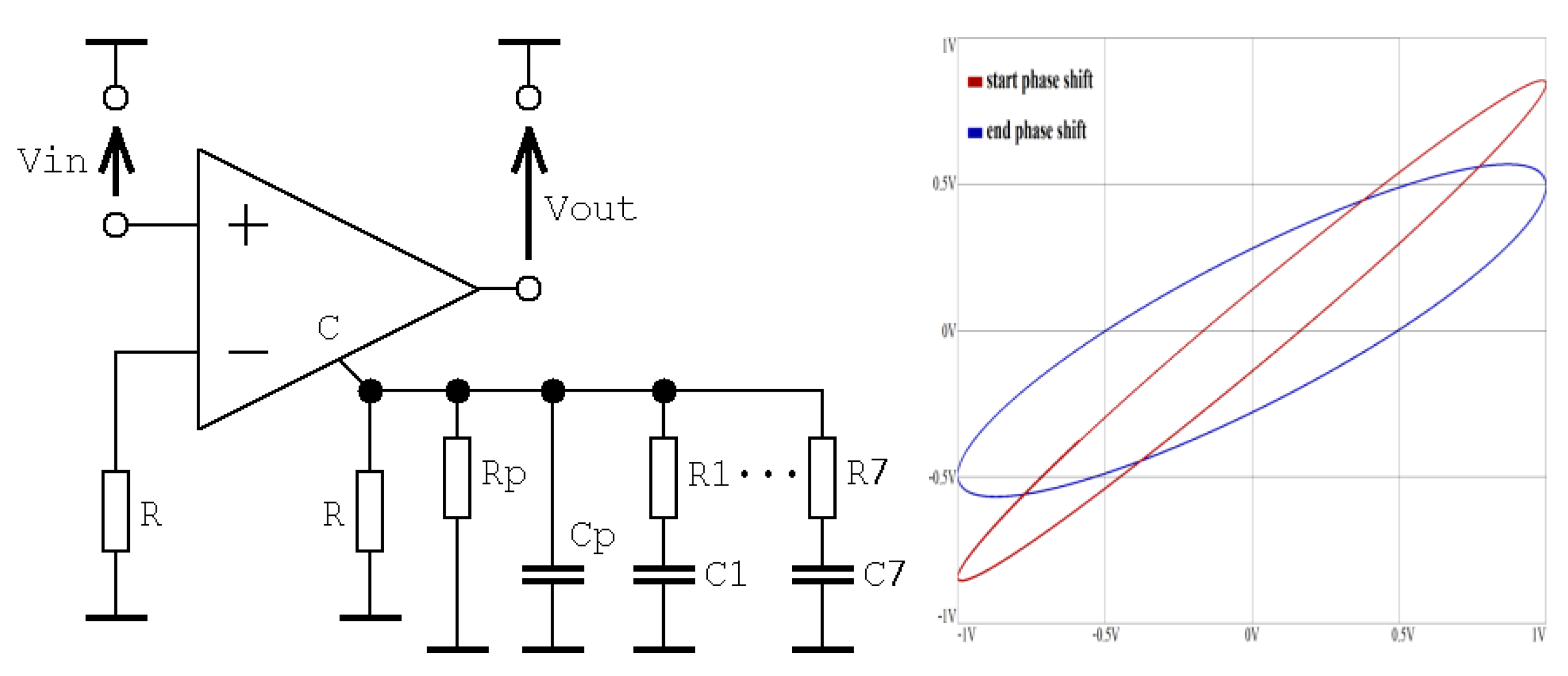
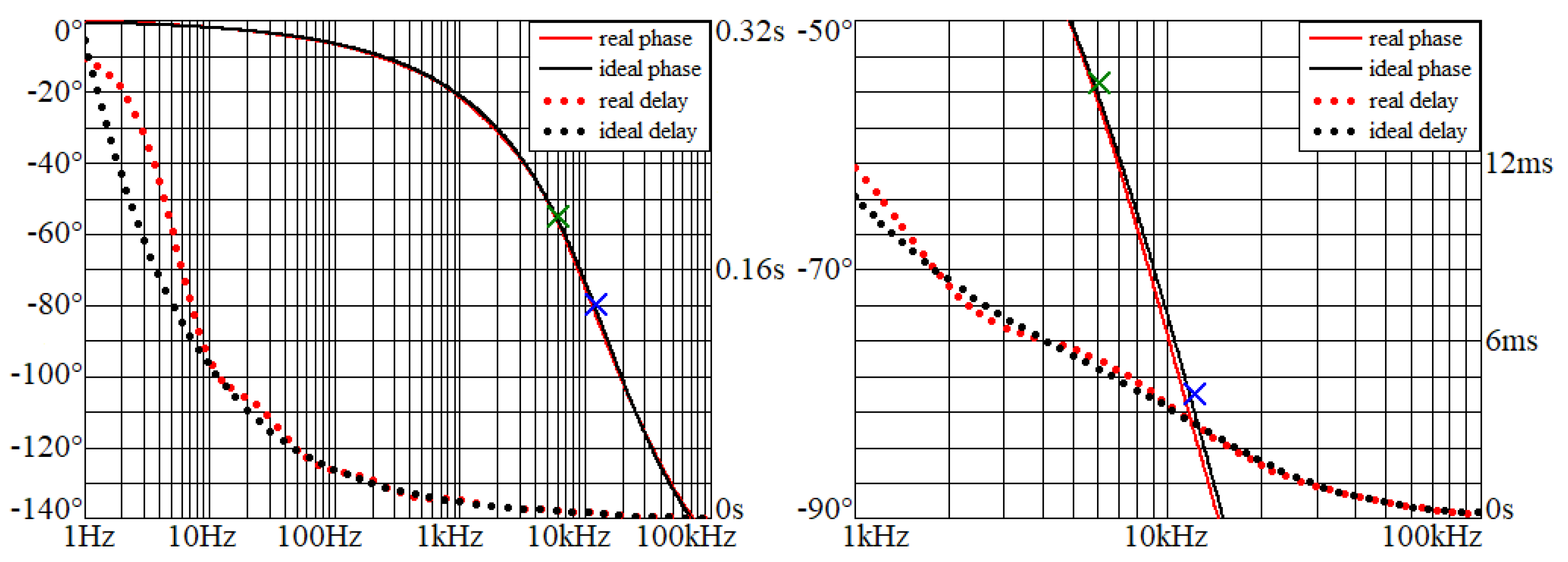
Figure 6.
Phase frequency responses and group delays of Example I: arbitrary non-asymptotical phase shifter over entire acoustic range (left graph) and magnified area as specified by task (right plot).
Figure 6.
Phase frequency responses and group delays of Example I: arbitrary non-asymptotical phase shifter over entire acoustic range (left graph) and magnified area as specified by task (right plot).
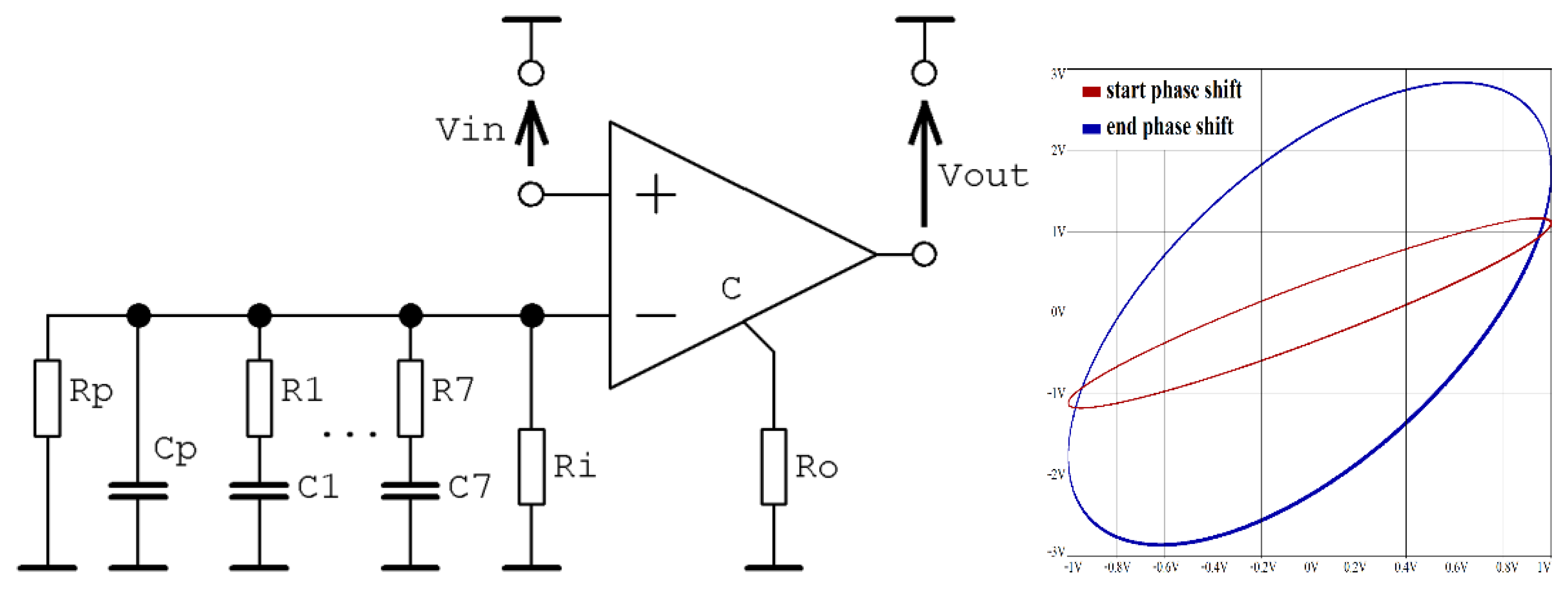
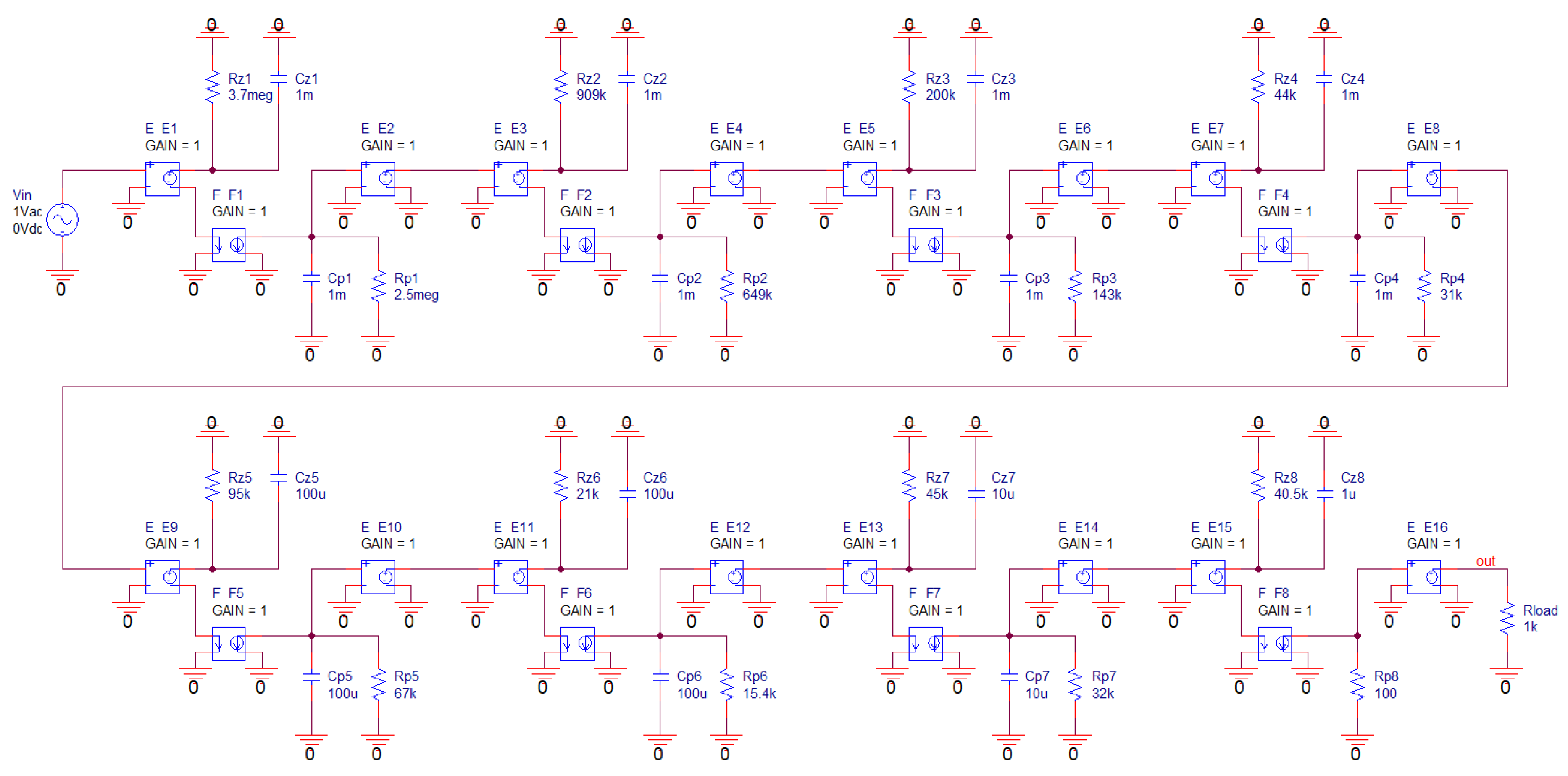
Figure 7.
Circuit realization of Case I phase shifter (left picture), Orcad Pspice time domain circuit simulation, and processed harmonic signals with amplitude 1V in plane projection (right plot).
Figure 7.
Circuit realization of Case I phase shifter (left picture), Orcad Pspice time domain circuit simulation, and processed harmonic signals with amplitude 1V in plane projection (right plot).
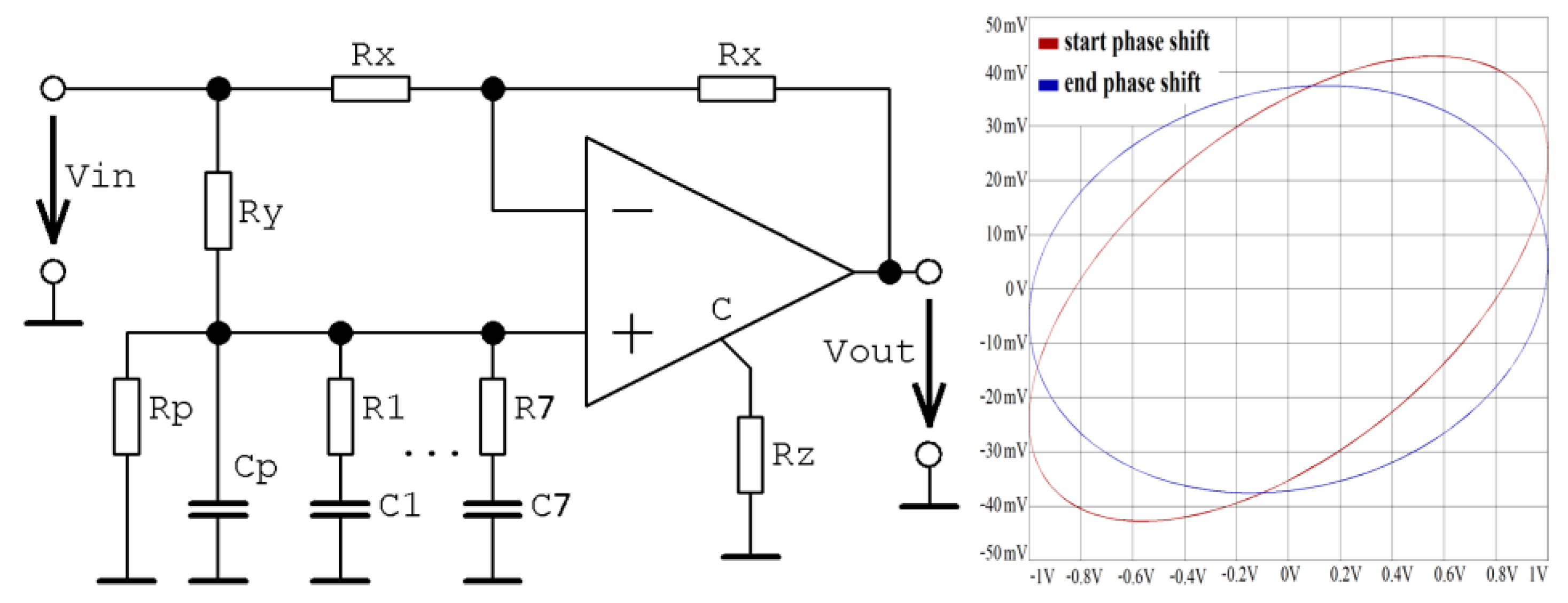
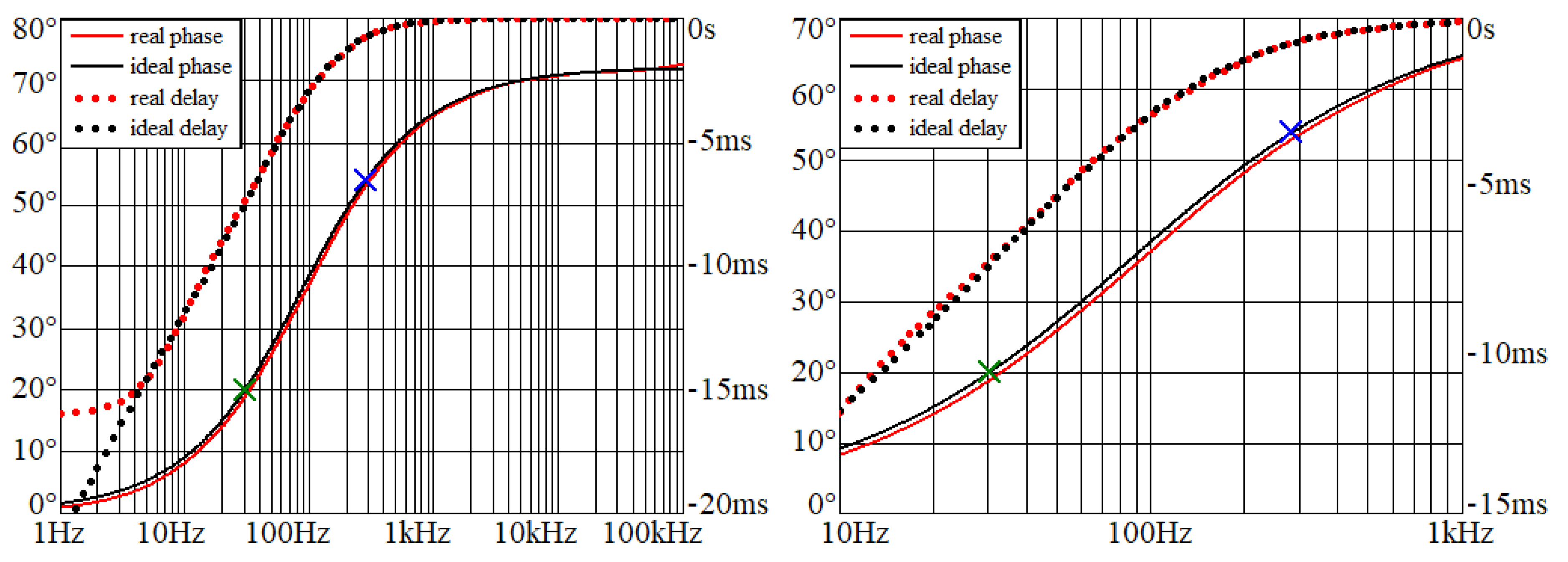
Figure 8.
Phase frequency responses and group delays of Example II: arbitrary non-asymptotical phase shifter over entire acoustic range (left graph) and magnified area of interest (right plot).
Figure 8.
Phase frequency responses and group delays of Example II: arbitrary non-asymptotical phase shifter over entire acoustic range (left graph) and magnified area of interest (right plot).
Figure 9.
Circuit realization of Example II: phase shifter (left schematic), Orcad Pspice time domain circuit simulation processed harmonic signals with amplitude 1V in plane projection (right plot).
Figure 9.
Circuit realization of Example II: phase shifter (left schematic), Orcad Pspice time domain circuit simulation processed harmonic signals with amplitude 1V in plane projection (right plot).
Figure 10.
Circuit realization of Case III: phase shifter, arbitrary non-asymptotical phase shifter over entire acoustic range (left graph) and magnified area of interest (right plot).
Figure 10.
Circuit realization of Case III: phase shifter, arbitrary non-asymptotical phase shifter over entire acoustic range (left graph) and magnified area of interest (right plot).
Figure 11.
Circuit realization of Case III: phase shifter (left schematic), Orcad Pspice time domain circuit simulation and processed harmonic signals with amplitude 1V in plane projection (right plot).
Figure 11.
Circuit realization of Case III: phase shifter (left schematic), Orcad Pspice time domain circuit simulation and processed harmonic signals with amplitude 1V in plane projection (right plot).
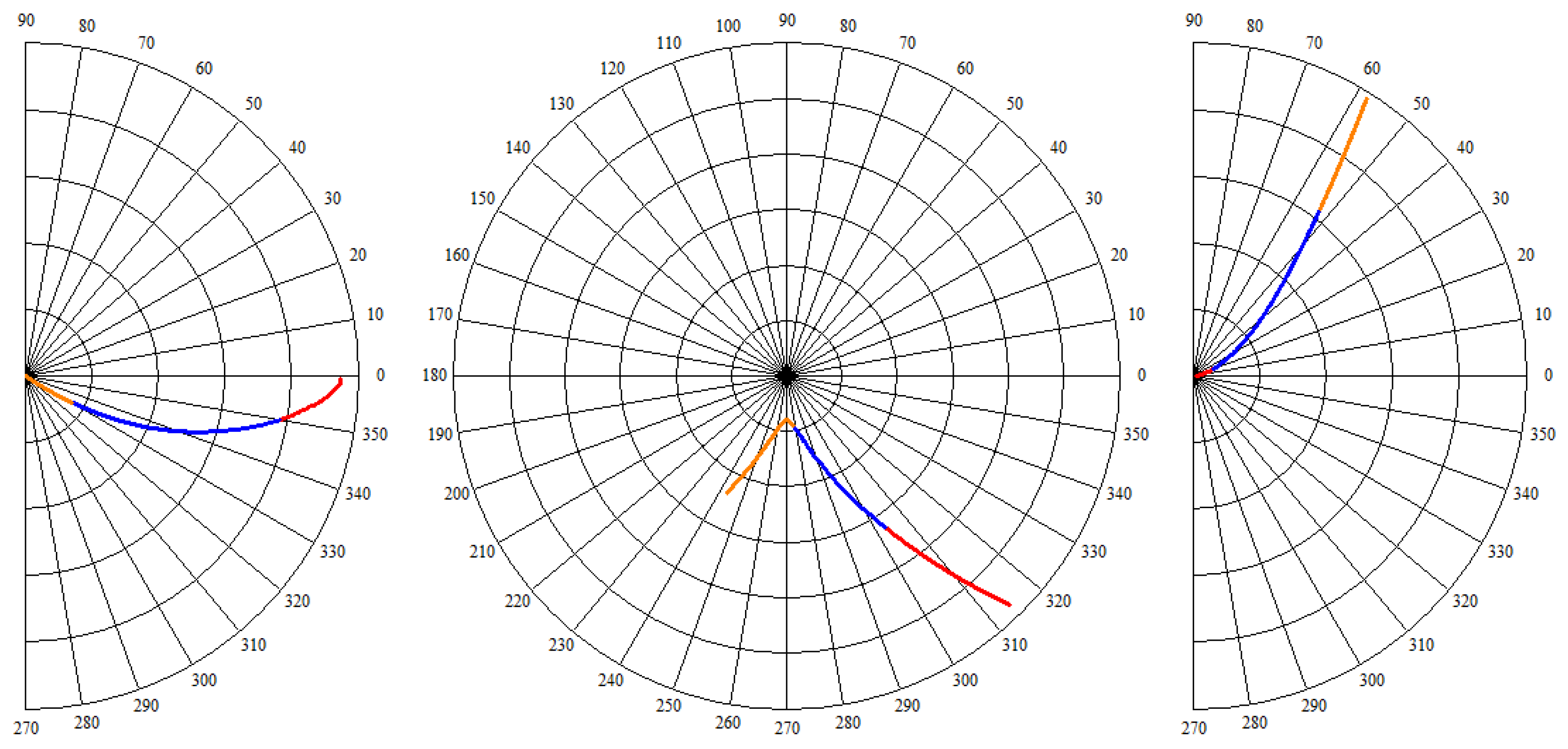
Figure 12.
Polar plots associated with phase shifters: Case I (left), Case II (middle), and Type III (right). Lower frequencies (red), active phase shift (blue), and higher frequencies (orange).
Figure 12.
Polar plots associated with phase shifters: Case I (left), Case II (middle), and Type III (right). Lower frequencies (red), active phase shift (blue), and higher frequencies (orange).
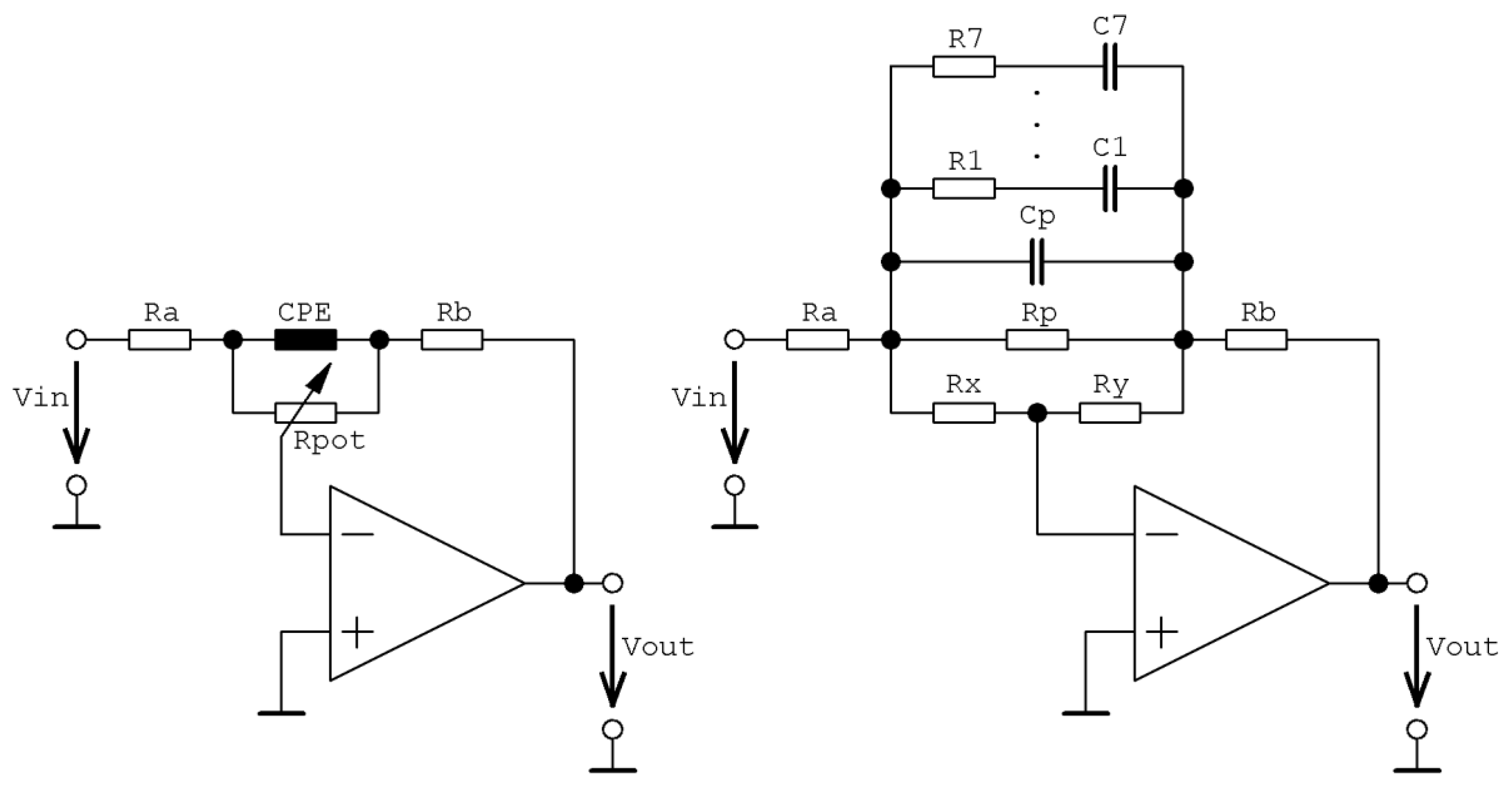
Figure 13.
Circuit realization of the bass-corrector with CPEs (left schematic), decomposition of CPEs and potentiometer introduced to clarify the design formulae (right picture).
Figure 13.
Circuit realization of the bass-corrector with CPEs (left schematic), decomposition of CPEs and potentiometer introduced to clarify the design formulae (right picture).
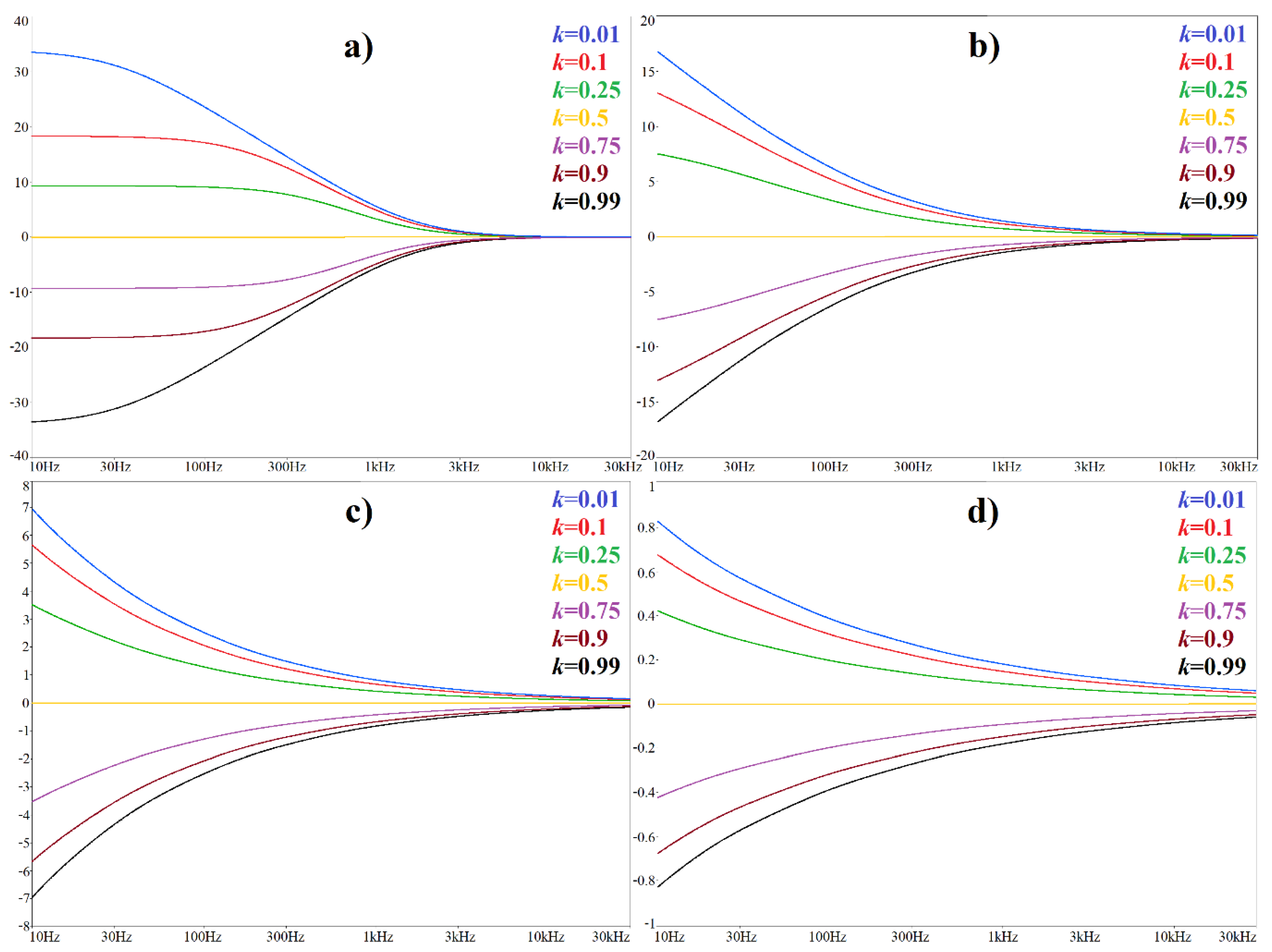
Figure 14.
Module frequency responses in dB of proposed bass-corrector with (a) a standard capacitor, (b) a CPE with a math order α = 2/3, (c) CPE with a math order α = 1/2, (d) CPE with a math order α = 1/3.
Figure 14.
Module frequency responses in dB of proposed bass-corrector with (a) a standard capacitor, (b) a CPE with a math order α = 2/3, (c) CPE with a math order α = 1/2, (d) CPE with a math order α = 1/3.
Figure 15.
Two-port CPEs implemented by general bilinear filtering sections with controlled sources: voltage-controlled voltage-source E and current-controlled current-source F.
Figure 15.
Two-port CPEs implemented by general bilinear filtering sections with controlled sources: voltage-controlled voltage-source E and current-controlled current-source F.
Figure 16.
Orcad Pspice circuit simulation of two-port CPE with phase shift between output and input voltage 20° in frequency domain: (a) phase response, (b) module response, and in time domain: (c) signal frequency 100 μHz, (d) signal frequency 100mHz, input (blue), and output (red) voltage.
Figure 16.
Orcad Pspice circuit simulation of two-port CPE with phase shift between output and input voltage 20° in frequency domain: (a) phase response, (b) module response, and in time domain: (c) signal frequency 100 μHz, (d) signal frequency 100mHz, input (blue), and output (red) voltage.
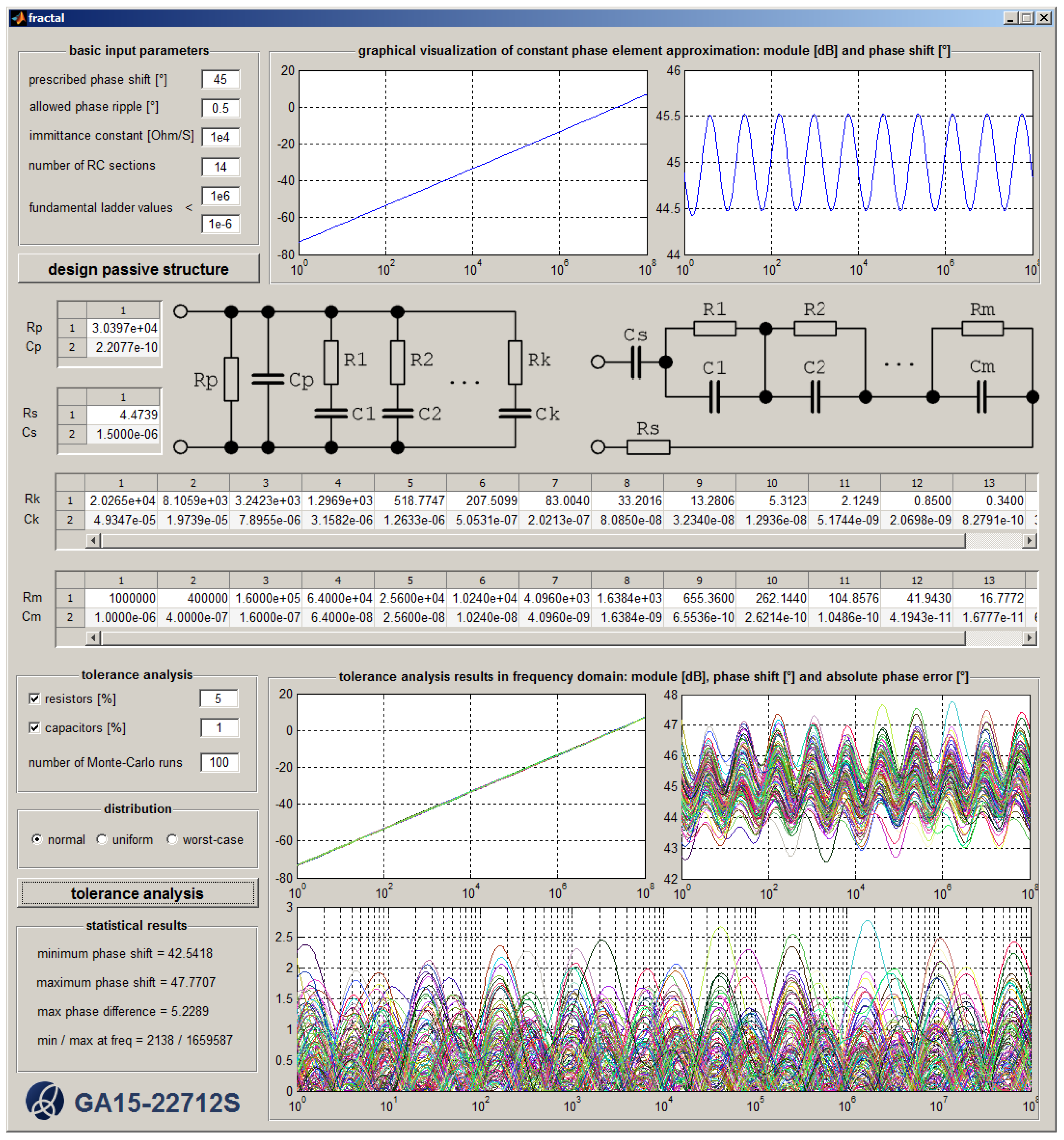
Figure 17.
Graphical user interface created in a Matlab environment that allows for fast design of passive CPE approximants (half-capacitor example implemented by using 14 RC sections for very small phase error, namely less than 0.5°) and performing fundamental tolerance analysis of derived RC structures.
Figure 17.
Graphical user interface created in a Matlab environment that allows for fast design of passive CPE approximants (half-capacitor example implemented by using 14 RC sections for very small phase error, namely less than 0.5°) and performing fundamental tolerance analysis of derived RC structures.
Table 1.
Designed CPEs for audio frequency bands summarized in a comprehensive list.
Table 1.
Designed CPEs for audio frequency bands summarized in a comprehensive list.
| CPE Order | Phase Shift [°] | Phase Error | Table with Values |
|---|
| 1a | 1b | 1a | 1b |
|---|
| 1/10 | 9 | 0.21 | 0.14 | 2 | 3 |
| 1/9 | 10 | 0.13 | 0.18 | 4 | 5 |
| 1/5 | 18 | 0.06 | 0.08 | 6 | 7 |
| 2/9 | 20 | 0.25 | 0.23 | 8 | 9 |
| 1/4 | 22.5 | 0.24 | 0.24 | 10 | 11 |
| 3/10 | 27 | 0.35 | 0.28 | 12 | 13 |
| 1/3 | 30 | 0.3 | 0.46 | 14 | 15 |
| 2/5 | 36 | 0.39 | 0.35 | 16 | 17 |
| 4/9 | 40 | 0.45 | 0.27 | 18 | 19 |
| 1/2 | 45 | 0.33 | 0.4 | 20 | 21 |
| 5/9 | 50 | 0.36 | 0.46 | 22 | 23 |
| 3/5 | 54 | 0.38 | 0.28 | 24 | 25 |
| 2/3 | 60 | 0.35 | 0.31 | 26 | 27 |
| 7/10 | 63 | 0.5 | 0.4 | 28 | 29 |
| 3/4 | 67.5 | 0.31 | 0.38 | 30 | 31 |
| 7/9 | 70 | 0.25 | 0.32 | 32 | 33 |
| 4/5 | 72 | 0.15 | 0.14 | 34 | 35 |
| 8/9 | 80 | 0.1 | 0.1 | 36 | 37 |
| 9/10 | 81 | 0.06 | 0.08 | 38 | 39 |
Table 2.
CPE with math order α = 1/10; fully passive RC series-parallel topology of fractal capacitor.
Table 2.
CPE with math order α = 1/10; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 409 Ω | 2.5 kΩ | 2.1 kΩ | 1840 Ω | 1.6 kΩ | 1.35 kΩ | 1.2 kΩ | 1 kΩ |
| 390 Ω ‖ | 1.5 kΩ ∠ | 2 kΩ ‖ | 1.8 kΩ ∠ | 1.5 kΩ ∠ | 1.2 kΩ ∠ | 1.2 kΩ | 1 kΩ |
| 18 Ω | 1 kΩ | 2 kΩ | 39 Ω | 100 Ω | 150 Ω | | |
| 1.8 nF | 20 μF | 5.1 μF | 1.3 μF | 330 nF | 83.7 nF | 21.3 nF | 5.4 nF |
| 1.8 nF | 10 μF ‖ | 3.9 μF ‖ | 1.2 μF ‖ | 330 nF | 56 nF ‖ | 18 nF ‖ | 3.3 nF ‖ |
| | 10 μF | 2.2 μF | 100 nF | | 27 nF | 3.3 nF | 2.2 nF |
Table 3.
CPE with math order α = 1/10; fully passive RC parallel-series topology of fractal capacitor.
Table 3.
CPE with math order α = 1/10; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 120 kΩ | 50 kΩ | 43 kΩ | 37 kΩ | 31.7 kΩ | 27 kΩ | 24 kΩ | 20 kΩ |
| 120 kΩ | 100 kΩ ‖ | 39 kΩ ∠ | 33 kΩ ∠ | 27 kΩ ∠ | 27 kΩ | 47 kΩ ‖ | 10 kΩ ∠ |
| | 100 kΩ | 3.9 kΩ | 3.3 kΩ | 4.7 kΩ | | 47 kΩ | 10 kΩ |
| 580 nF | 200 nF | 50.8 nF | 12.9 nF | 3.3 nF | 834 pF | 212 pF | 54 pF |
| 560 nF ‖ | 100 nF ‖ | 47 nF ‖ | 10 nF ‖ | 3.3 nF | 820 pF ‖ | 180 pF ‖ | 39 pF ‖ |
| 22 nF | 100 nF | 3.9 nF | 2.7 nF | | 15 pF | 33 pF | 15 pF |
Table 4.
CPE with math order α = 1/9; fully passive RC series-parallel topology of fractal capacitor.
Table 4.
CPE with math order α = 1/9; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 430 Ω | 2300 Ω | 1940 Ω | 1640 Ω | 1380 Ω | 1170 Ω | 987 Ω | 833 Ω |
| 330 Ω ∠ | 2.2 kΩ ∠ | 1.8 kΩ ∠ | 1.5 kΩ ∠ | 1.2 kΩ ∠ | 1 kΩ ∠ | 1 kΩ | 820 Ω |
| 100 Ω | 100 Ω | 150 Ω | 150 Ω | 180 Ω | 180 Ω | | |
| 1.8 nF | 17.4 μF | 4.5 μF | 1.2 μF | 300 nF | 77.6 nF | 20 nF | 5.2 nF |
| 1.8 nF | 15 μF ‖ | 3.9 μF ‖ | 1.2 μF | 150 nF ‖ | 56 nF ‖ | 10 nF ‖ | 3.3 nF ‖ |
| | 2.2 μF | 560 nF | | 150 nF | 22 nF | 10 nF | 1.8 nF |
Table 5.
CPE with math order α = 1/9; fully passive RC parallel-series topology of fractal capacitor.
Table 5.
CPE with math order α = 1/9; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 78 kΩ | 40 kΩ | 33.8 kΩ | 28.5 kΩ | 24.2 kΩ | 20.3 kΩ | 17.2 kΩ | 16 kΩ |
| 56 kΩ ∠ | 39 kΩ ∠ | 33 kΩ | 27 kΩ ‖ | 22 kΩ ∠ | 10 kΩ ∠ | 15 kΩ ∠ | 15 kΩ ∠ |
| 22 kΩ | 1 kΩ | | 1.5 kΩ | 2.2 kΩ | 10 kΩ | 2.2 kΩ | 1 kΩ |
| 2.7 μF | 1 μF | 258 nF | 68 nF | 17 nF | 4.5 nF | 1.1 nF | 330 pF |
| 2.7 μF | 1 μF | 150 nF ‖ | 68 nF | 10 nF ‖ | 3.3 nF ‖ | 1 nF ‖ | 330 pF |
| | | 100 nF | | 6.8 nF | 1.2 nF | 100 pF | |
Table 6.
CPE with math order α = 1/5; fully passive RC series-parallel topology of fractal capacitor.
Table 6.
CPE with math order α = 1/5; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 5 kΩ | 14 kΩ | 10.3 kΩ | 7.6 kΩ | 5.6 kΩ | 4.1 kΩ | 3.1 kΩ | 2.2 kΩ |
| 10 kΩ ‖ | 39 kΩ ‖ | 33 kΩ ‖ | 15 kΩ ‖ | 5.6 kΩ | 3.9 kΩ ∠ | 15 kΩ ‖ | 2.2 kΩ |
| 10 kΩ | 22 kΩ | 15 kΩ | 15 kΩ | | 220 Ω | 3.9 kΩ | |
| 600 pF | 1.8 μF | 634 nF | 188 nF | 56 nF | 16 nF | 5 nF | 1.4 nF |
| 1.2 nF ∠ | 1.8 μF | 10 μF ‖ | 150 nF ‖ | 56 nF | 15 nF ‖ | 10 nF ∠ | 2.7 nF ∠ |
| 1.2 nF | | 680 nF | 39 nF | | 1 nF | 10 nF | 2.7 nF |
Table 7.
CPE with math order α = 1/5; fully passive RC parallel-series topology of fractal capacitor.
Table 7.
CPE with math order α = 1/5; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 13 kΩ | 30 kΩ | 22 kΩ | 16 kΩ | 12 kΩ | 8.9 kΩ | 6.5 kΩ | 5 kΩ |
| 12 kΩ ∠ | 15 kΩ ∠ | 22 kΩ | 15 kΩ ∠ | 12 kΩ | 8.2 kΩ ∠ | 5.6 kΩ ∠ | 10 kΩ ‖ |
| 1 kΩ | 15 kΩ | | 1 kΩ | | 6.8 kΩ | 1 kΩ | 10 kΩ |
| 2.4 μF | 1 μF | 300 nF | 87 nF | 26 nF | 7.7 nF | 2.2 nF | 680 pF |
| 2.2 μF ‖ | 1 μF | 150 nF ‖ | 82 nF ‖ | 22 nF ‖ | 6.8 nF ‖ | 2.2 nF | 680 pF |
| 220 nF | | 150 nF | 4.7 nF | 3.9 nF | 1 nF | | |
Table 8.
CPE with math order α = 2/9; fully passive RC series-parallel topology of fractal capacitor.
Table 8.
CPE with math order α = 2/9; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 5 kΩ | 12.5 kΩ | 8.9 kΩ | 6.4 kΩ | 4.6 kΩ | 3.2 kΩ | 2.4 kΩ | 1.6 kΩ |
| 10 kΩ ‖ | 12 kΩ ∠ | 8.6 kΩ ∠ | 120 kΩ ‖ | 27 kΩ ‖ | 18 kΩ ‖ | 2.2 kΩ ∠ | 1.5 kΩ ∠ |
| 10 kΩ | 470 Ω | 330 Ω | 6.8 kΩ | 5.6 kΩ | 3.9 kΩ | 220 Ω | 100 Ω |
| 900 pF | 2 μF | 732 nF | 224 nF | 69 nF | 21 nF | 6.4 nF | 2 nF |
| 1.8 nF ∠ | 1 μF ‖ | 6.8 μF ∠ | 220 nF ‖ | 68 nF ‖ | 10 nF ‖ | 5.6 nF ‖ | 1 nF ‖ |
| 1.8 nF | 1 μF | 820 nF | 3.9 nF | 1 nF | 10 nF | 820 pF | 1 nF |
Table 9.
CPE with math order α = 2/9; fully passive RC parallel-series topology of fractal capacitor.
Table 9.
CPE with math order α = 2/9; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 3.4 kΩ | 10 kΩ | 7.1 kΩ | 5.1 kΩ | 3.6 kΩ | 2.6 kΩ | 1.8 kΩ | 1.2 kΩ |
| 3.3 kΩ ∠ | 10 kΩ | 6.8 kΩ ∠ | 4.7 kΩ ∠ | 3.3 kΩ ∠ | 2.2 kΩ ∠ | 1.8 kΩ | 1.2 kΩ |
| 100 Ω | | 330 Ω | 390 Ω | 330 Ω | 390 Ω | | |
| 6.8 μF | 3 μF | 918 nF | 281 nF | 86 nF | 26 nF | 8 nF | 3.9 nF |
| 6.8 μF | 1.5 μF ‖ | 820 nF ‖ | 270 nF ‖ | 82 nF ‖ | 680 nF ∠ | 6.8 nF ‖ | 3.9 nF |
| | 1.5 μF | 100 nF | 10 nF | 3.9 nF | 27 nF | 1.2 nF | |
Table 10.
CPE with math order α = 1/4; fully passive RC series-parallel topology of fractal capacitor.
Table 10.
CPE with math order α = 1/4; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 5.2 kΩ | 11 kΩ | 7.5 kΩ | 5.1 kΩ | 3.5 kΩ | 2.4 kΩ | 1.6 kΩ | 1.1 kΩ |
| 68 kΩ ‖ | 10 kΩ ∠ | 15 kΩ ‖ | 3.9 kΩ ∠ | 3.3 kΩ ∠ | 2.2 kΩ ∠ | 1.6 kΩ | 1 kΩ ∠ |
| 5.6 kΩ | 1 kΩ | 15 kΩ | 1.2 kΩ | 220 Ω | 220 Ω | | 100 Ω |
| 1.33 nF | 2.7 μF | 873 nF | 279 nF | 89 nF | 28 nF | 9 nF | 2.7 nF |
| 1 nF ‖ | 2.7 μF | 860 nF ‖ | 270 nF ‖ | 86 nF ‖ | 27 nF ‖ | 18 nF ∠ | 2.7 nF |
| 330 pF | | 12 pF | 10 nF | 3.3 nF | 1 nF | 18 nF | |
Table 11.
CPE with math order α = 1/4; fully passive RC parallel-series topology of fractal capacitor.
Table 11.
CPE with math order α = 1/4; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 6.6 kΩ | 30 kΩ | 20.5 kΩ | 14 kΩ | 9.6 kΩ | 6.5 kΩ | 4.5 kΩ | 3 kΩ |
| 5.6 kΩ ∠ | 15 kΩ ∠ | 15 kΩ ∠ | 10 kΩ ∠ | 220 kΩ ‖ | 150 kΩ ‖ | 3.3 kΩ ∠ | 1.5 kΩ ∠ |
| 1 kΩ | 15 kΩ | 5.6 kΩ | 3.9 kΩ | 10 kΩ | 6.8 kΩ | 1.2 kΩ | 1.5 kΩ |
| 2.1 μF | 1 μF | 319 nF | 102 nF | 33 nF | 10.4 nF | 3.3 nF | 1.3 nF |
| 2.2 μF | 1 μF | 1.8 μF ∠ | 100 nF ‖ | 33 nF | 10 nF ‖ | 3.3 nF | 1.2 nF ‖ |
| | | 390 nF | 2.2 nF | | 3.9 nF | | 100 pF |
Table 12.
CPE with math order α = 3/10; fully passive RC series-parallel topology of fractal capacitor.
Table 12.
CPE with math order α = 3/10; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 4.5 kΩ | 7.3 kΩ | 4.9 kΩ | 3.1 kΩ | 2 kΩ | 1.2 kΩ | 786 Ω | 500 Ω |
| 100 kΩ ‖ | 6.8 kΩ ∠ | 3.9 kΩ ∠ | 2.7 kΩ ∠ | 1 kΩ ∠ | 1 kΩ ∠ | 18 kΩ ‖ | 1 kΩ ‖ |
| 4.7 kΩ | 470 Ω | 1 kΩ | 390 Ω | 1 kΩ | 220 Ω | 820 Ω | 1 kΩ |
| 2.3 nF | 2.3 μF | 893 nF | 308 nF | 106 nF | 37 nF | 12.6 nF | 4.3 nF |
| 2.2 nF ‖ | 2.2 μF ‖ | 8.2 μF ‖ | 4.7 μF ∠ | 100 nF ‖ | 33 nF ‖ | 10 nF ‖ | 3.3 nF ‖ |
| 1 nF | 100 nF | 1 μF | 330 nF | 5.6 nF | 3.9 nF | 2.7 nF | 1 nF |
Table 13.
CPE with math order α = 3/10; fully passive RC parallel-series topology of fractal capacitor.
Table 13.
CPE with math order α = 3/10; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 1.1 kΩ | 10 kΩ | 6.3 kΩ | 4 kΩ | 2.5 kΩ | 1.6 kΩ | 1 kΩ | 650 Ω |
| 1 kΩ ∠ | 10 kΩ | 82 kΩ ∠ | 3.9 kΩ ∠ | 1.5 kΩ ∠ | 1.6 kΩ | 1 kΩ | 470 Ω ∠ |
| 100 Ω | | 6.8 kΩ | 100 Ω | 1 kΩ | | | 180 Ω |
| 3.9 μF | 2 μF | 689 nF | 237 nF | 82 nF | 28 nF | 10 nF | 3.9 nF |
| 3.9 μF | 1 μF ‖ | 680 nF ‖ | 220 nF ‖ | 82 nF | 27 nF ‖ | 10 nF | 3.9 nF |
| | 1 μF | 10 nF | 18 nF | | 1 nF | | |
Table 14.
CPE with math order α = 1/3; fully passive RC series-parallel topology of fractal capacitor.
Table 14.
CPE with math order α = 1/3; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 5.2 kΩ | 7.2 kΩ | 4.5 kΩ | 2.7 kΩ | 1.6 kΩ | 1 kΩ | 600 Ω | 370 Ω |
| 82 kΩ ‖ | 6.8 kΩ ∠ | 3.3 kΩ ∠ | 2.7 kΩ | 1.5 kΩ ∠ | 1 kΩ | 1.2 kΩ ‖ | 330 Ω ‖ |
| 5.6 kΩ | 390 Ω | 1.2 kΩ | | 100 Ω | | 1.2 kΩ | 39 Ω |
| 5.1 nF | 4 μF | 1.5 μF | 535 nF | 190 nF | 68 nF | 25 nF | 9 nF |
| 3.9 nF ‖ | 3.9 μF ‖ | 1.5 μF | 470 nF ‖ | 180 nF ‖ | 68 nF | 22 nF ‖ | 18 nF ∠ |
| 1.2 nF | 100 nF | | 68 nF | 10 nF | | 3.3 nF | 18 nF |
Table 15.
CPE with math order α = 1/3; fully passive RC parallel-series topology of fractal capacitor.
Table 15.
CPE with math order α = 1/3; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 2.2 kΩ | 30 kΩ | 18 kΩ | 11 kΩ | 6.6 kΩ | 3.9 kΩ | 2.4 kΩ | 1.4 kΩ |
| 2.2 kΩ | 15 kΩ ∠ | 18 kΩ | 10 kΩ ∠ | 5.6 kΩ ∠ | 3.9 kΩ | 2.2 kΩ ∠ | 1.2 kΩ ∠ |
| | 15 kΩ | | 1 kΩ | 1 kΩ | | 1.2 kΩ | 220 Ω |
| 1.8 μF | 1 μF | 350 nF | 133 nF | 48 nF | 17 nF | 6.3 nF | 2.7 nF |
| 1.8 μF | 1 μF | 330 nF ‖ | 100 nF ‖ | 47 nF ‖ | 15 nF ‖ | 82 nF ∠ | 2.7 nF |
| | | 22 nF | 33 nF | 1 nF | 2.2 nF | 6.8 nF | |
Table 16.
CPE with math order α = 2/5; fully passive RC series-parallel topology of fractal capacitor.
Table 16.
CPE with math order α = 2/5; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 4.2 kΩ | 4.8 kΩ | 2.6 kΩ | 1.4 kΩ | 779 Ω | 424 Ω | 231 Ω | 125 Ω |
| 2.7 kΩ ‖ | 4.7 kΩ ∠ | 2.2 kΩ ∠ | 1.2 kΩ ∠ | 680 Ω ∠ | 390 Ω ∠ | 220 Ω ∠ | 22 kΩ ‖ |
| 1.5 kΩ | 100 Ω | 390 Ω | 220 Ω | 100 Ω | 33 Ω | 10 Ω | 150 Ω |
| 11.5 nF | 4.1 μF | 1.7 μF | 665 nF | 267 nF | 107 nF | 43 nF | 17 nF |
| 10 nF ‖ | 3.9 μF ‖ | 1.5 μF ‖ | 1.5 μF ∠ | 220 nF ‖ | 100 nF ‖ | 39 nF ‖ | 15 nF ‖ |
| 1.5 nF | 220 nF | 220 nF | 1.2 μF | 47 nF | 6. 8 nF | 3.9 nF | 2.2 nF |
Table 17.
CPE with math order α = 2/5; fully passive RC parallel-series topology of fractal capacitor.
Table 17.
CPE with math order α = 2/5; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 310 Ω | 10 kΩ | 5.4 kΩ | 3 kΩ | 1.6 kΩ | 875 Ω | 476 Ω | 250 Ω |
| 270 Ω ∠ | 10 kΩ | 150 kΩ ‖ | 1.5 kΩ ∠ | 1.5 kΩ ∠ | 820 Ω ∠ | 470 Ω ∠ | 3.3 kΩ ∠ |
| 39 Ω | | 5.6 kΩ | 1.5 kΩ | 100 Ω | 56 Ω | 5.6 Ω | 270 Ω |
| 3 μF | 2 μF | 802 nF | 322 nF | 129 nF | 52 nF | 21 nF | 9.4 nF |
| 1.5 μF ‖ | 1 μF ‖ | 33 μF ∠ | 220 nF ‖ | 120 nF ‖ | 39 nF ‖ | 22 nF | 8.2 nF ‖ |
| 1.5 μF | 1 μF | 820 nF | 100 nF | 10 nF | 12 nF | | 1.2 nF |
Table 18.
CPE with math order α = 4/9; fully passive RC series-parallel topology of fractal capacitor.
Table 18.
CPE with math order α = 4/9; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 3.9 kΩ | 3.9 kΩ | 2 kΩ | 1 kΩ | 526 Ω | 267 Ω | 136 Ω | 68 Ω |
| 3.9 kΩ | 3.9 kΩ | 1 kΩ ∠ | 1 kΩ | 470 Ω ∠ | 220 Ω ∠ | 120 Ω ∠ | 68 Ω |
| | | 1 kΩ | | 56 Ω | 47 Ω | 15 Ω | |
| 24 nF | 4.6 μF | 2.2 μF | 921 nF | 395 nF | 170 nF | 73 nF | 30 nF |
| 22 nF ‖ | 3.9 μF ‖ | 2.2 μF | 820 nF ‖ | 390 nF ‖ | 150 nF ‖ | 68 nF ‖ | 15 nF ‖ |
| 2.2 nF | 680 nF | | 100 nF | 4.7 nF | 22 nF | 4.7 nF | 15 nF |
Table 19.
CPE with math order α = 4/9; fully passive RC parallel-series topology of fractal capacitor.
Table 19.
CPE with math order α = 4/9; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 178 Ω | 10 kΩ | 5.1 kΩ | 2.6 kΩ | 1.3 kΩ | 668 Ω | 339 Ω | 173 Ω |
| 150 Ω ∠ | 10 kΩ | 4.7 kΩ ∠ | 2.2 kΩ ∠ | 1.2 kΩ ∠ | 39 kΩ ‖ | 270 Ω ∠ | 150 Ω ∠ |
| 27 Ω | | 390 Ω | 390 Ω | 100 Ω | 680 Ω | 68 Ω | 22 Ω |
| 2.7 μF | 2 μF | 858 nF | 369 nF | 158 nF | 68 nF | 29 nF | 14 nF |
| 2.7 μF | 1 μF ‖ | 820 nF ‖ | 330 nF ‖ | 150 nF ‖ | 68 nF | 22 nF ‖ | 12 nF ‖ |
| | 1 μF | 39 nF | 39 nF | 8.2 nF | | 6.8 nF | 2.2 nF |
Table 20.
CPE with math order α = 1/2; fully passive RC series-parallel topology of fractal capacitor.
Table 20.
CPE with math order α = 1/2; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 3.2 kΩ | 2.7 kΩ | 1.3 kΩ | 604 Ω | 282 Ω | 132 Ω | 62 Ω | 31 Ω |
| 1.5 kΩ ‖ | 2.7 kΩ | 1.2 kΩ ‖ | 560 Ω ∠ | 270 Ω ∠ | 120 Ω ∠ | 39 Ω ∠ | 15 Ω ∠ |
| 1.8 kΩ | | 100 Ω | 47 Ω | 12 Ω | 12 Ω | 22 Ω | 15 Ω |
| 49 nF | 5.2 μF | 2.5 μF | 1.2 μF | 552 nF | 258 nF | 120 nF | 57 nF |
| 47 nF ‖ | 3.9 μF ‖ | 1.5 μF ‖ | 1.2 μF | 470 nF ‖ | 220 nF ‖ | 120 nF | 47 nF ‖ |
| 2.2 nF | 1.2 μF | 1 μF | | 82 nF | 39 nF | | 10 nF |
Table 21.
CPE with math order α = 1/2; fully passive RC parallel-series topology of fractal capacitor.
Table 21.
CPE with math order α = 1/2; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 92 Ω | 10 kΩ | 4.7 kΩ | 2.2 kΩ | 1 kΩ | 476 Ω | 222 Ω | 104 Ω |
| 180 Ω ‖ | 10 kΩ | 4.7 kΩ | 2.2 kΩ | 1 kΩ | 470 Ω ∠ | 220 Ω | 100 Ω ∠ |
| 180 Ω | | | | | 5.6 Ω | | 3.9 Ω |
| 1.7 μF | 1.6 μF | 700 nF | 327 nF | 153 nF | 71 nF | 33 nF | 18 nF |
| 1.5 μF ‖ | 1.5 μF ‖ | 680 nF ‖ | 270 nF ‖ | 150 nF ‖ | 68 nF ‖ | 33 nF | 18 nF |
| 2.2 μF | 100 nF | 22 nF | 56 nF | 3.3 nF | 3.3 nF | | |
Table 22.
CPE with math order α = 5/9; fully passive RC series-parallel topology of fractal capacitor.
Table 22.
CPE with math order α = 5/9; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 2.3 kΩ | 1.8 kΩ | 757 Ω | 325 Ω | 139 Ω | 60 Ω | 26 Ω | 11 Ω |
| 2.2 kΩ ∠ | 1.8 kΩ | 10 kΩ ‖ | 270 Ω ∠ | 100 Ω ∠ | 120 Ω ‖ | 15 Ω ∠ | 10 Ω ∠ |
| 100 Ω | | 820 Ω | 56 Ω | 39 Ω | 120 Ω | 10 Ω | 1 Ω |
| 100 nF | 5 μF | 2.9 μF | 1.5 μF | 745 nF | 379 nF | 193 nF | 100 nF |
| 100 nF | 10 μF ∠ | 2.7 μF ‖ | 1.5 μF | 8.2 μF ∠ | 330 nF ‖ | 180 nF ‖ | 100 nF |
| | 10 μF | 220 nF | | 820 nF | 47 nF | 12 nF | |
Table 23.
CPE with math order α = 5/9; fully passive RC parallel-series topology of fractal capacitor.
Table 23.
CPE with math order α = 5/9; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 470 Ω | 100 kΩ | 43 kΩ | 18 kΩ | 7.9 kΩ | 3.4 kΩ | 1.5 kΩ | 625 Ω |
| 470 Ω | 100 kΩ | 33 kΩ ∠ | 18 kΩ | 6.8 kΩ ∠ | 3.3 kΩ ∠ | 1.5 kΩ | 560 Ω ∠ |
| | | 10 kΩ | | 1 kΩ | 1 kΩ | | 68 Ω |
| 103 nF | 90 nF | 51 nF | 26 nF | 13 nF | 6.7 nF | 3.4 nF | 1.7 nF |
| 100 nF ‖ | 180 nF ∠ | 39 nF ‖ | 22 nF ‖ | 12 nF ‖ | 6.8 nF | 3.3 nF ‖ | 1.5 nF ‖ |
| 3.3 nF | 180 nF | 12 nF | 3.9 nF | 1 nF | | 1 nF | 220 pF |
Table 24.
CPE with math order α = 3/5; fully passive RC series-parallel topology of fractal capacitor.
Table 24.
CPE with math order α = 3/5; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 3.9 kΩ | 2.4 kΩ | 966 Ω | 388 Ω | 156 Ω | 62 Ω | 25 Ω | 10 Ω |
| 3.9 kΩ | 2.2 kΩ ∠ | 27 kΩ ‖ | 390 Ω | 100 Ω ∠ | 39 Ω ∠ | 15 Ω ∠ | 10 Ω |
| | 220 Ω | 1 kΩ | | 56 Ω | 22 Ω | 10 Ω | |
| 285 nF | 10 μF | 5.2 μF | 2.8 μF | 1.5 μF | 836 nF | 455 nF | 247 nF |
| 270 nF ‖ | 10 μF | 3.9 μF ‖ | 2.7 μF ‖ | 1.5 μF | 820 nF ‖ | 390 nF ‖ | 220 nF ∠ |
| 15 nF | | 1.2 μF | 100 nF | | 15 nF | 68 nF | 27 nF |
Table 25.
CPE with math order α = 3/5; fully passive RC parallel-series topology of fractal capacitor.
Table 25.
CPE with math order α = 3/5; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 642 Ω | 230 kΩ | 92 kΩ | 37 kΩ | 15 kΩ | 6 kΩ | 2.4 kΩ | 958 Ω |
| 12 kΩ ‖ | 220 kΩ ∠ | 82 kΩ ∠ | 33 kΩ ∠ | 15 kΩ | 12 kΩ ‖ | 2.2 kΩ ∠ | 22 kΩ ‖ |
| 680 Ω | 10 kΩ | 10 kΩ | 3.9 kΩ | | 12 kΩ | 220 Ω | 1 kΩ |
| 86 nF | 100 nF | 54 nF | 30 nF | 16 nF | 8.8 nF | 4.8 nF | 2.6 nF |
| 86 nF | 100 nF | 39 nF ‖ | 15 nF ‖ | 10 nF ‖ | 68 nF ∠ | 4.7 nF ‖ | 2.2 nF ‖ |
| | | 15 nF | 15 nF | 1 nF | 10 nF | 1 nF | 390 pF |
Table 26.
CPE with math order α = 2/3; fully passive RC series-parallel topology of fractal capacitor.
Table 26.
CPE with math order α = 2/3; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 2.6 kΩ | 1.5 kΩ | 533 Ω | 193 Ω | 70 Ω | 25 Ω | 9.2 Ω | 3.3 Ω |
| 2.2 kΩ ∠ | 1.5 kΩ | 1.5 kΩ ‖ | 180 Ω ∠ | 68 Ω ∠ | 15 Ω ∠ | 8.2 Ω ∠ | 3.3 Ω |
| 390 Ω | | 820 Ω | 12 Ω | 2.2 Ω | 10 Ω | 1 Ω | |
| 710 nF | 10 μF | 6.1 μF | 3.7 μF | 2.2 μF | 1.3 μF | 806 nF | 470 nF |
| 560 nF ‖ | 10 μF | 3.9 μF ‖ | 3.3 μF ‖ | 2.2 μF | 1.2 μF ‖ | 470 nF ‖ | 470 nF |
| 150 nF | | 2.2 μF | 390 nF | | 100 nF | 330 nF | |
Table 27.
CPE with math order α = 2/3; fully passive RC parallel-series topology of fractal capacitor.
Table 27.
CPE with math order α = 2/3; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 200 Ω | 150 kΩ | 54 kΩ | 20 kΩ | 7.1 kΩ | 2.6 kΩ | 938 Ω | 310 Ω |
| 100 Ω ∠ | 150 kΩ | 47 kΩ ∠ | 10 kΩ ∠ | 5.6 kΩ ∠ | 2.2 kΩ ∠ | 820 Ω ∠ | 270 Ω ∠ |
| 100 Ω | | 6.8 kΩ | 10 kΩ | 1.5 kΩ | 390 Ω | 120 Ω | 39 Ω |
| 69 nF | 100 nF | 60 nF | 36.3 nF | 22 nF | 13 nF | 7.9 nF | 4.7 nF |
| 68 nF ‖ | 100 nF | 120 nF ∠ | 33 nF ‖ | 22 nF | 12 nF ‖ | 4.7 nF ‖ | 4.7 nF |
| 1 nF | | 120 nF | 3.3 nF | | 1 nF | 3.3 nF | |
Table 28.
CPE with math order α = 7/10; fully passive RC series-parallel topology of fractal capacitor.
Table 28.
CPE with math order α = 7/10; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 1.9 kΩ | 1 kΩ | 342 Ω | 118 Ω | 41 Ω | 14 Ω | 5 Ω | 1.8 Ω |
| 1.8 kΩ ∠ | 1 kΩ | 330 Ω ∠ | 100 Ω ∠ | 82 Ω ‖ | 10 Ω ∠ | 10 Ω ‖ | 1.8 Ω |
| 100 Ω | | 12 Ω | 18 Ω | 82 Ω | 3.9 Ω | 10 Ω | |
| 3.15 μF | 9 μF | 6.4 μF | 4 μF | 2.6 μF | 1.6 μF | 1 μF | 650 nF |
| 1 μF ‖ | 18 μF ∠ | 18 μF ∠ | 3.9 μF ‖ | 2.2 μF ‖ | 1.5 μF ‖ | 1 μF | 470 nF ‖ |
| 100 nF | 18 μF | 10 μF | 100 nF | 390 nF | 100 nF | | 150 nF |
Table 29.
CPE with math order α = 7/10; fully passive RC parallel-series topology of fractal capacitor.
Table 29.
CPE with math order α = 7/10; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 82 Ω | 92 kΩ | 34.5 kΩ | 12 kΩ | 4.1 kΩ | 1.4 kΩ | 485 Ω | 167 Ω |
| 82 Ω | 82 kΩ ∠ | 33 kΩ ∠ | 12 kΩ | 3.9 kΩ ∠ | 1.2 kΩ ∠ | 470 Ω ∠ | 150 Ω ∠ |
| | 10 kΩ | 1.5 kΩ | | 220 Ω | 220 Ω | 15 Ω | 18 Ω |
| 120 nF | 200 nF | 126 nF | 80 nF | 50 nF | 32 nF | 20 nF | 13 nF |
| 120 nF | 100 nF ‖ | 100 nF ‖ | 68 nF ‖ | 100 nF ∠ | 18 nF ‖ | 10 nF ‖ | 12 nF ‖ |
| | 100 nF | 27 nF | 12 nF | 100 nF | 15 nF | 10 nF | 1 nF |
Table 30.
CPE with math order α = 3/4; fully passive RC series-parallel topology of fractal capacitor.
Table 30.
CPE with math order α = 3/4; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 18 kΩ | 8.4 kΩ | 2.66 kΩ | 850 Ω | 271 Ω | 86.6 Ω | 27.7 Ω | 10 Ω |
| 18 kΩ | 8.2 kΩ ∠ | 2.2 kΩ ‖ | 820 Ω ∠ | 270 Ω | 82 Ω ∠ | 27 Ω | 10 Ω |
| | 220 Ω | 470 Ω | 33 Ω | | 4.7 Ω | | |
| 260 nF | 1.1 μF | 820 nF | 560 nF | 383 nF | 262 nF | 179 nF | 120 nF |
| 220 nF ‖ | 1 μF ‖ | 820 nF | 560 nF | 1.2 μF ∠ | 220 nF ‖ | 180 nF | 120 nF |
| 39 nF | 100 nF | | | 560 nF | 39 nF | | |
Table 31.
CPE with math order α = 3/4; fully passive RC parallel-series topology of fractal capacitor.
Table 31.
CPE with math order α = 3/4; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 50 Ω | 85.3 kΩ | 32 kΩ | 10 kΩ | 3.3 kΩ | 1 kΩ | 332 Ω | 100 Ω |
| 100 Ω ‖ | 82 kΩ ∠ | 33 kΩ | 10 kΩ | 3.3 kΩ | 1 kΩ | 330 Ω ∠ | 100 Ω |
| 100 Ω | 3.3 kΩ | | | | | 2.2 Ω | |
| 47 nF | 95 nF | 68 nF | 47 nF | 31 nF | 22 nF | 15 nF | 10 nF |
| 47 nF | 82 nF ‖ | 68 nF | 47 nF | 27 nF ‖ | 22 nF | 15 nF | 10 nF |
| | 12 nF | | | 3.9 nF | | | |
Table 32.
CPE with math order α = 7/9; fully passive RC series-parallel topology of fractal capacitor.
Table 32.
CPE with math order α = 7/9; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 30 kΩ | 13 kΩ | 4 kΩ | 1.2 kΩ | 374 Ω | 115 Ω | 35 Ω | 13.3 Ω |
| 15 kΩ ∠ | 12 kΩ ∠ | 3.9 kΩ ‖ | 1.2 kΩ | 330 Ω ∠ | 100 Ω ∠ | 33 Ω ∠ | 10 Ω ∠ |
| 15 kΩ | 1 kΩ | 100 Ω | | 47 Ω | 15 Ω | 2.2 Ω | 3.3 Ω |
| 500 nF | 1.5 μF | 1.1 μF | 779 nF | 556 nF | 396 nF | 283 nF | 200 nF |
| 1 μF ∠ | 1.5 μF | 1 μF ‖ | 560 nF ‖ | 330 nF ‖ | 330 nF ‖ | 270 nF ‖ | 100 nF ‖ |
| 1 μF | | 100 nF | 220 nF | 220 nF | 68 nF | 12 nF | 100 nF |
Table 33.
CPE with math order α = 7/9; fully passive RC parallel-series topology of fractal capacitor.
Table 33.
CPE with math order α = 7/9; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 72 Ω | 220 kΩ | 61 kΩ | 20 kΩ | 5.8 kΩ | 1.8 kΩ | 537 Ω | 165 Ω |
| 68 Ω ∠ | 220 kΩ | 33 kΩ ∠ | 10 kΩ ∠ | 5.6 kΩ ∠ | 1.8 kΩ | 470 Ω ∠ | 150 Ω ∠ |
| 3.9 Ω | | 27 kΩ | 10 kΩ | 2.2 kΩ | | 68 Ω | 15 Ω |
| 42 nF | 100 nF | 71 nF | 51 nF | 36 nF | 25.8 nF | 18.4 nF | 13 nF |
| 39 nF ‖ | 100 nF | 68 nF ‖ | 47 nF ‖ | 33 nF ‖ | 22 nF ‖ | 18 nF ‖ | 10 nF ‖ |
| 330 pF | | 3.3 nF | 3.9 nF | 3.3 nF | 3.9 nF | 390 pF | 3.3 nF |
Table 34.
CPE with math order α = 4/5; fully passive RC series-parallel topology of fractal capacitor.
Table 34.
CPE with math order α = 4/5; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 170 kΩ | 71 kΩ | 21 kΩ | 6.2 kΩ | 1.84 kΩ | 543 Ω | 161 Ω | 48 Ω |
| 3.3 MΩ ‖ | 56 kΩ ∠ | 470 kΩ ‖ | 5.6 kΩ ∠ | 1.5 kΩ ∠ | 390 Ω ∠ | 150 Ω ∠ | 33 Ω ∠ |
| 180 kΩ | 15 kΩ | 22 kΩ | 560 Ω | 330 Ω | 150 Ω | 10 Ω | 15 Ω |
| 62 nF | 141 nF | 104 nF | 77 nF | 57 nF | 42 nF | 31 nF | 25 nF |
| 47 nF ‖ | 120 nF ‖ | 100 nF ‖ | 330 nF ∠ | 330 nF ∠ | 390 nF ∠ | 470 nF ∠ | 100 nF ∠ |
| 15 nF | 22 nF | 3.9 nF | 100 nF | 68 nF | 47 nF | 33 nF | 33 nF |
Table 35.
CPE with math order α = 4/5; fully passive RC parallel-series topology of fractal capacitor.
Table 35.
CPE with math order α = 4/5; fully passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 4.2 Ω | 12.3 kΩ | 4.4 kΩ | 1.3 kΩ | 388 Ω | 114 Ω | 34 Ω | 10 Ω |
| 2.7 Ω ∠ | 12 kΩ ∠ | 2.2 kΩ ∠ | 10 kΩ ‖ | 330 Ω ∠ | 100 Ω ∠ | 33 Ω | 10 Ω |
| 1.5 Ω | 330 Ω | 2.2 kΩ | 1.5 kΩ | 56 Ω | 15 Ω | | |
| 356 nF | 1 μF | 738 nF | 544 nF | 401 nF | 296 nF | 218 nF | 161 nF |
| 330 nF ‖ | 1 μF | 560 nF ‖ | 390 nF ‖ | 390 nF ‖ | 1.2 μF ∠ | 120 nF ‖ | 150 nF ‖ |
| 27 nF | | 180 nF | 150 nF | 10 nF | 390 nF | 100 nF | 10 nF |
Table 36.
CPE with math order α = 8/9; fully passive RC series-parallel topology of fractal capacitor.
Table 36.
CPE with math order α = 8/9; fully passive RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 15.7 kΩ | 5 kΩ | 1.4 kΩ | 366 Ω | 94.6 Ω | 24.4 Ω | 6.8 Ω | 1.7 Ω |
| 15 kΩ ∠ | 10 kΩ ‖ | 1 kΩ ∠ | 5.6 kΩ ∠ | 82 Ω ∠ | 22 Ω ∠ | 6.8 Ω | 1.8 Ω |
| 680 Ω | 10 kΩ | 390 Ω | 390 Ω | 12 Ω | 2.2 Ω | | |
| 3.6 μF | 1.8 μF | 1.5 μF | 1.3 μF | 1.1 μF | 927 nF | 783 nF | 680 nF |
| 3.3 μF ‖ | 1.8 μF | 1.5 μF | 1.2 μF ‖ | 1 μF ‖ | 820 nF ∠ | 680 nF ‖ | 680 nF |
| 330 nF | | | 100 nF | 100 nF | 100 nF | 100 nF | |
Table 37.
CPE with order α = 8/9; fully passive ladder RC parallel-series topology of fractal capacitor.
Table 37.
CPE with order α = 8/9; fully passive ladder RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 10.4 Ω | 79 kΩ | 26 kΩ | 6.7 kΩ | 1730 Ω | 446 Ω | 115 Ω | 30 Ω |
| 8.2 Ω ∠ | 68 kΩ ∠ | 22 kΩ ∠ | 3.3 kΩ ∠ | 1.5 kΩ ∠ | 390 Ω ∠ | 100 Ω ∠ | 15 Ω ∠ |
| 2.2 Ω | 10 Ω | 3.9 kΩ | 3.3 kΩ | 220 Ω | 56 Ω | 15 Ω | 15 Ω |
| 37 nF | 200 nF | 170 nF | 142.6 nF | 120 nF | 102 nF | 86 nF | 72 nF |
| 33 nF ‖ | 100 nF ‖ | 150 nF ‖ | 120 nF ‖ | 120 nF | 100 nF ‖ | 82 nF ‖ | 68 nF ‖ |
| 3.9 nF | 100 nF | 22 nF | 22 nF | | 2.2 nF | 3.9 nF | 3.9 nF |
Table 38.
CPE with order α = 9/10; passive ladder RC series-parallel topology of fractal capacitor.
Table 38.
CPE with order α = 9/10; passive ladder RC series-parallel topology of fractal capacitor.
| Rp/Cp | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 156 kΩ | 53 kΩ | 13.5 kΩ | 3.44 kΩ | 873 Ω | 222 Ω | 56 Ω | 18 Ω |
| 150 kΩ ∠ | 1 MΩ ‖ | 12 kΩ ∠ | 3.3 kΩ ∠ | 860 Ω ∠ | 680 Ω ‖ | 56 Ω | 18 Ω |
| 5.6 kΩ | 56 kΩ | 1.5 kΩ | 180 Ω | 12 Ω | 330 Ω | | |
| 458 nF | 188 nF | 161 nF | 138 nF | 119 nF | 102 nF | 88 nF | 75 nF |
| 390 nF ‖ | 180 nF ‖ | 150 nF ‖ | 120 nF ‖ | 560 nF ∠ | 100 nF ‖ | 330 nF ∠ | 150 nF ∠ |
| 68 nF | 8.6 nF | 10 nF | 18 nF | 150 nF | 2.2 nF | 120 nF | 150 nF |
Table 39.
CPE with math order α = 9/10; passive RC parallel-series topology of fractal capacitor.
Table 39.
CPE with math order α = 9/10; passive RC parallel-series topology of fractal capacitor.
| Rs/Cs | R1/C1 | R2/C2 | R3/C3 | R4/C4 | R5/C5 | R6/C6 | R7/C7 |
|---|
| 1.3 Ω | 12 kΩ | 3.8 kΩ | 968 Ω | 246 Ω | 62 Ω | 16 Ω | 4 Ω |
| 1.2 Ω | 12 kΩ | 12 kΩ ‖ | 33 kΩ ‖ | 330 Ω ‖ | 220 Ω ‖ | 15 Ω ∠ | 15 Ω ‖ |
| | | 5.6 kΩ | 1 kΩ | 1 kΩ | 86 Ω | 1 Ω | 5.6 Ω |
| 165 nF | 1 μF | 859 nF | 738 nF | 633 nF | 544 nF | 467 nF | 401 nF |
| 150 nF ‖ | 1 μF | 860 nF | 680 nF ‖ | 560 nF ‖ | 2.7 μF ∠ | 1.5 μF ∠ | 330 nF ‖ |
| 15 nF | | | 56 nF | 68 nF | 680 nF | 680 nF | 68 nF |