A Tweak-Cube Color Image Encryption Scheme Jointly Manipulated by Chaos and Hyper-Chaos
Abstract
:Featured Application
Abstract
1. Introduction
2. Preliminaries
2.1. The Logistic-Fraction Hybrid Chaotic Map
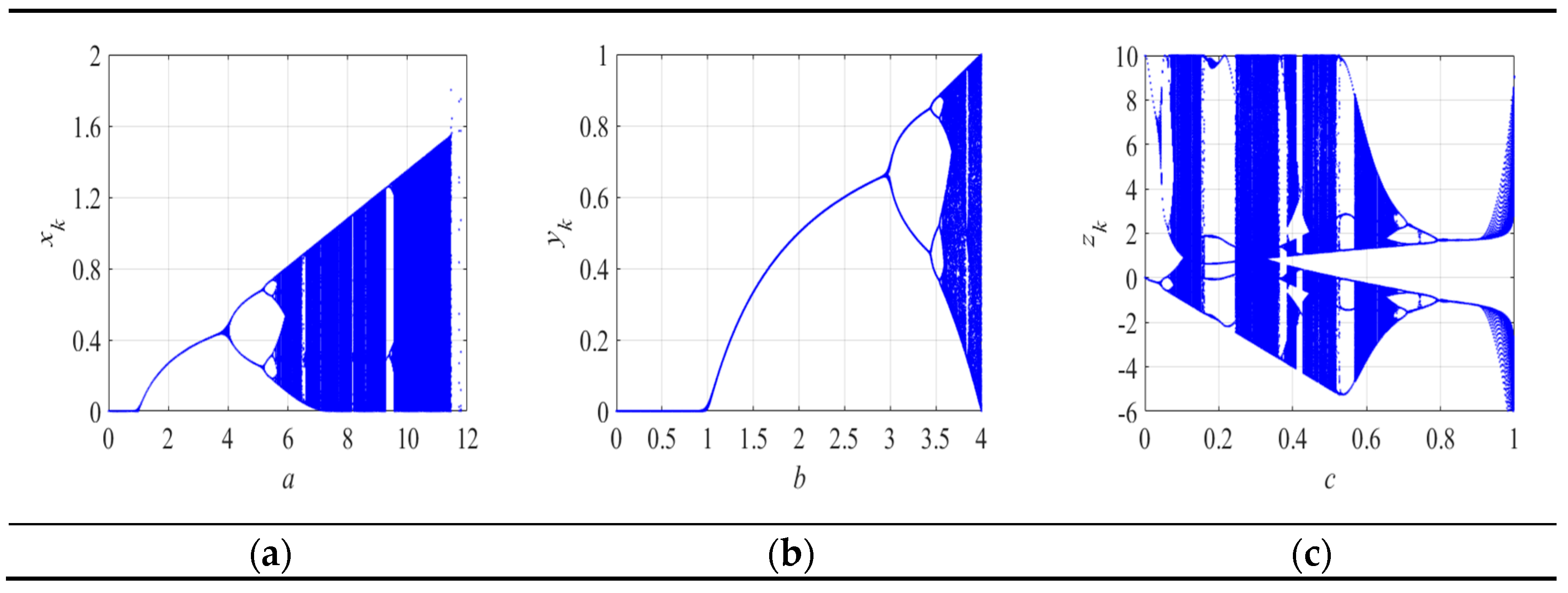
2.1.1. Bifurcation Graph
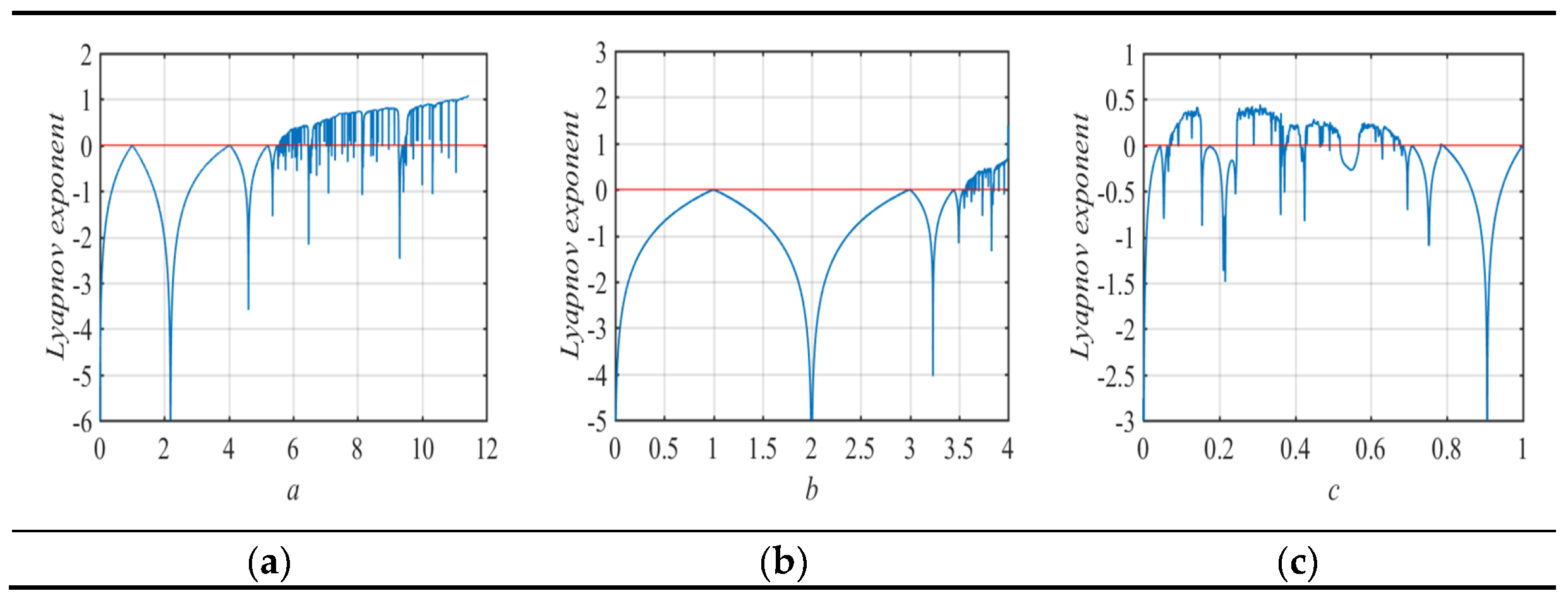
2.1.2. Lyapunov Exponent
2.1.3. Approximate Entropy
2.1.4. NIST Test
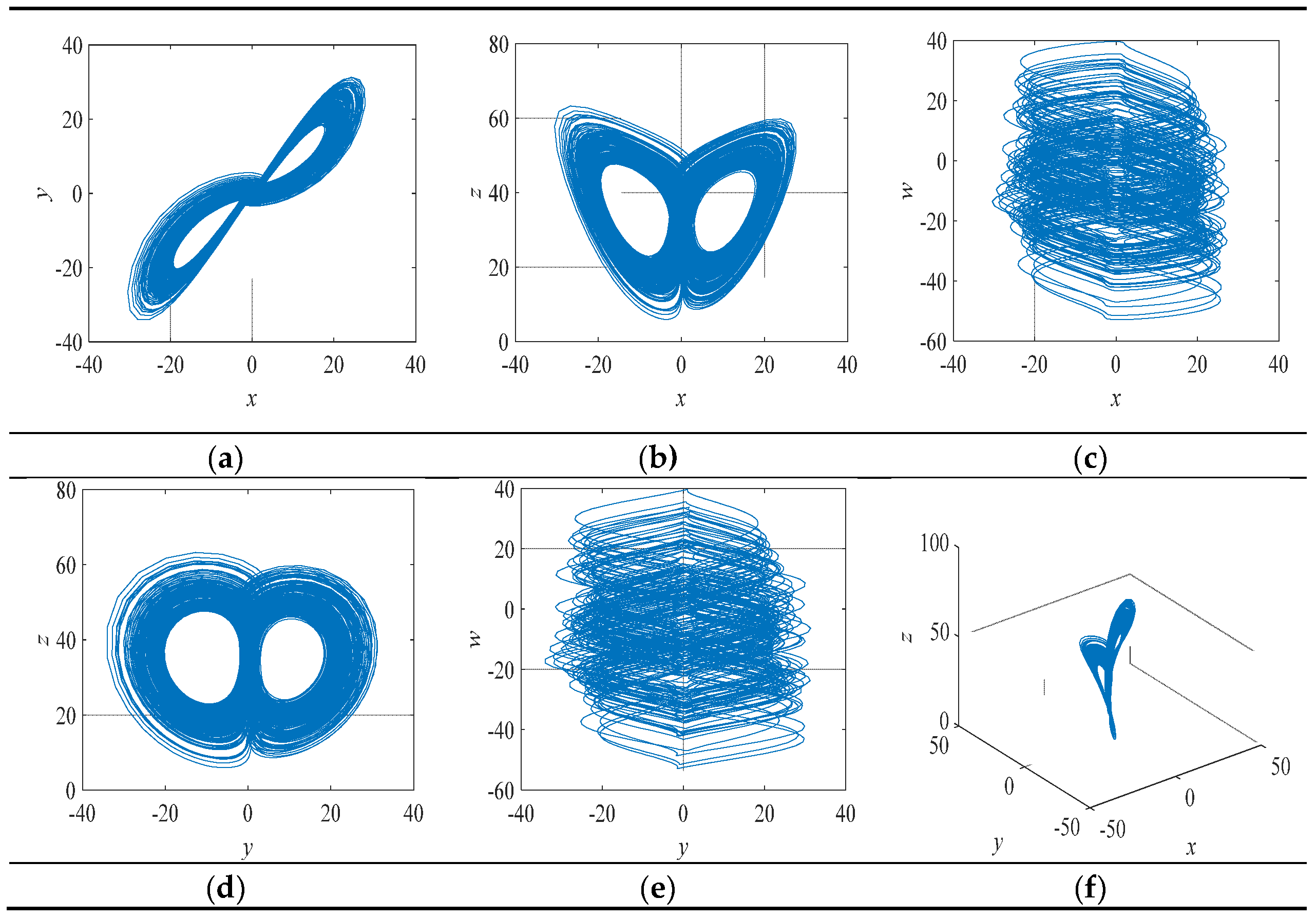
2.2. Hyperchaotic System
3. The Proposed Image Cryptosystem
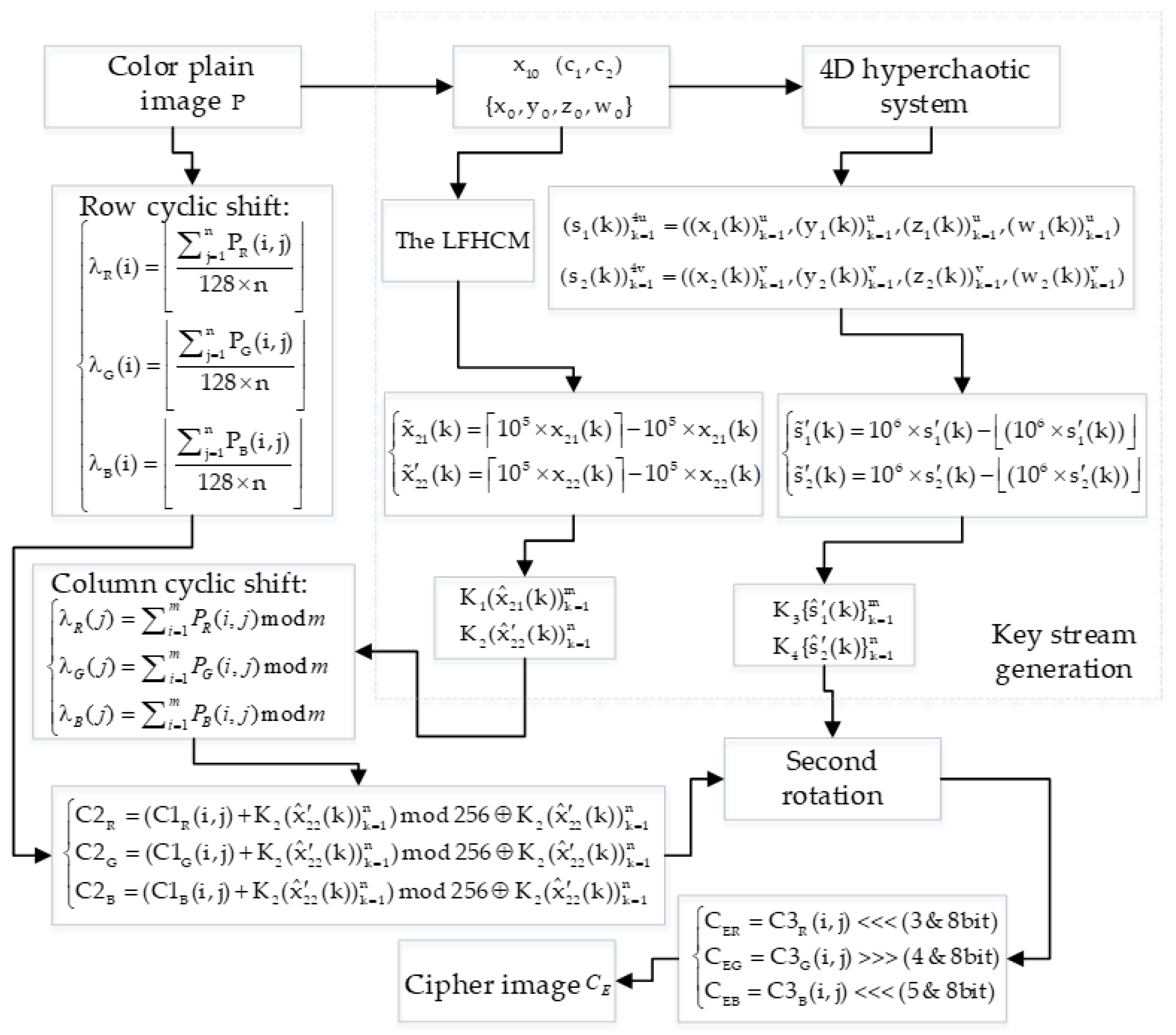
3.1. Key Stream Generation
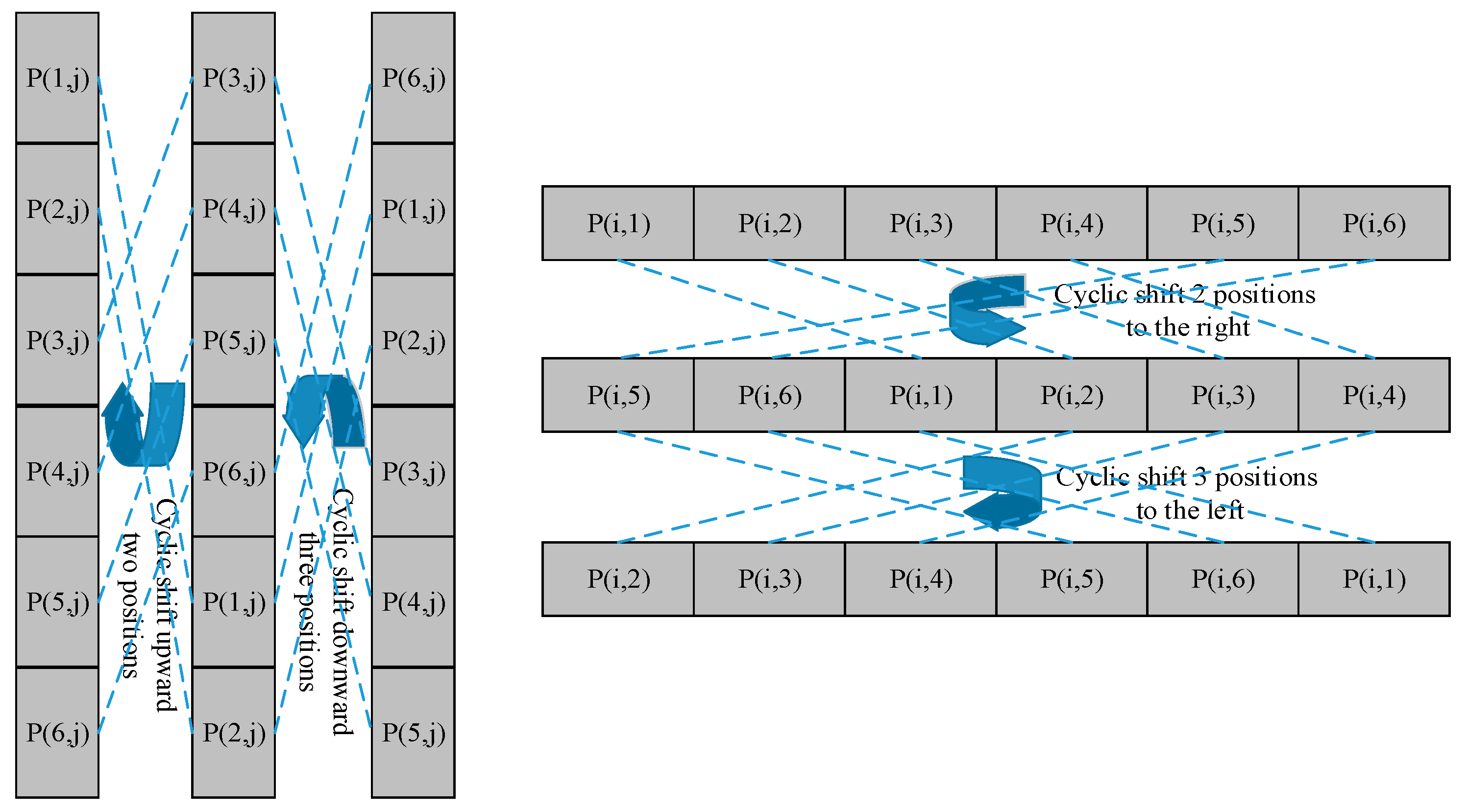
3.2. Encryption Scheme
3.3. Decryption Scheme
4. Experimental Results
5. Performance Analysis
5.1. Key Space
5.2. Key Sensitivity Analysis
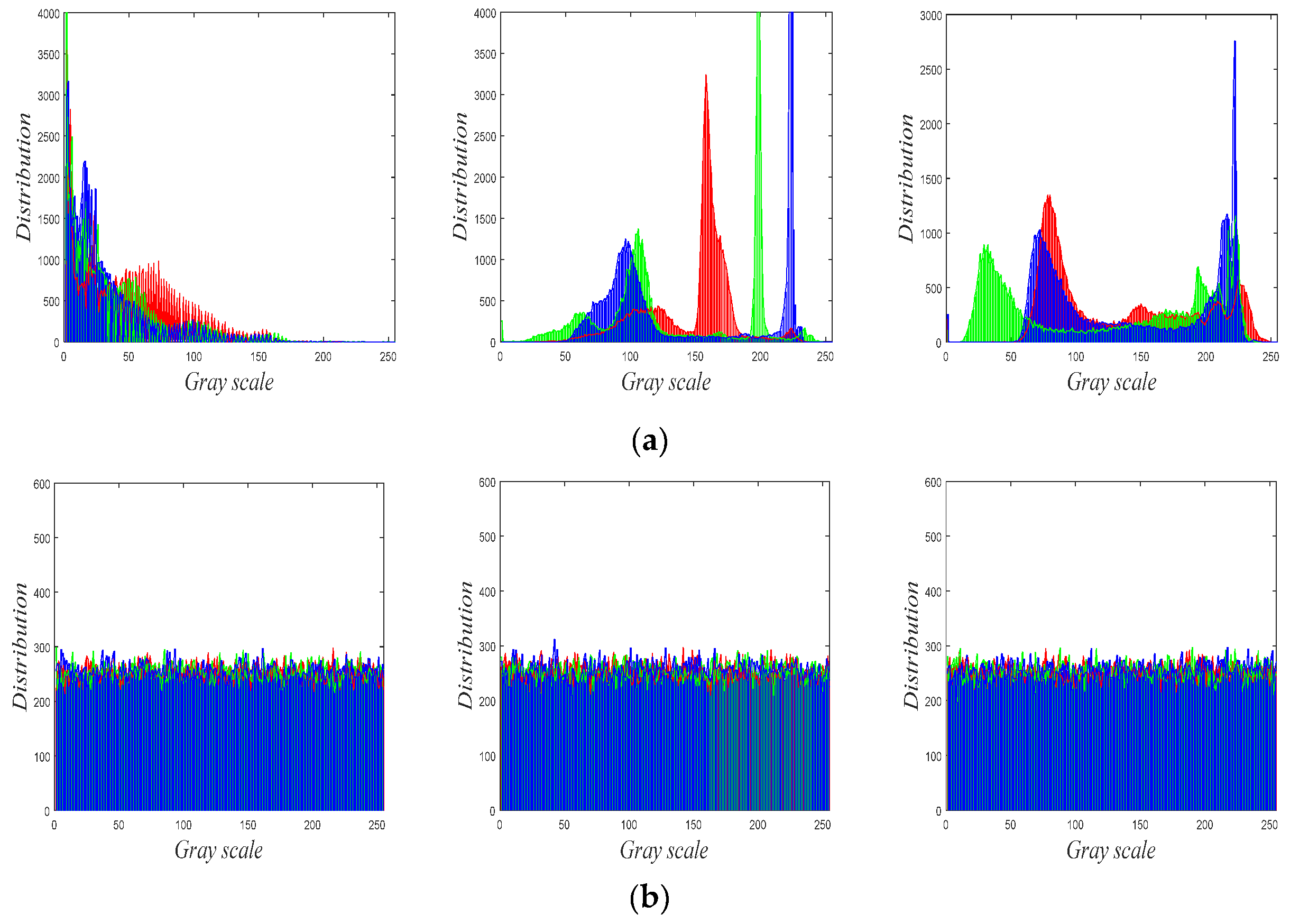
5.3. Histogram Analysis
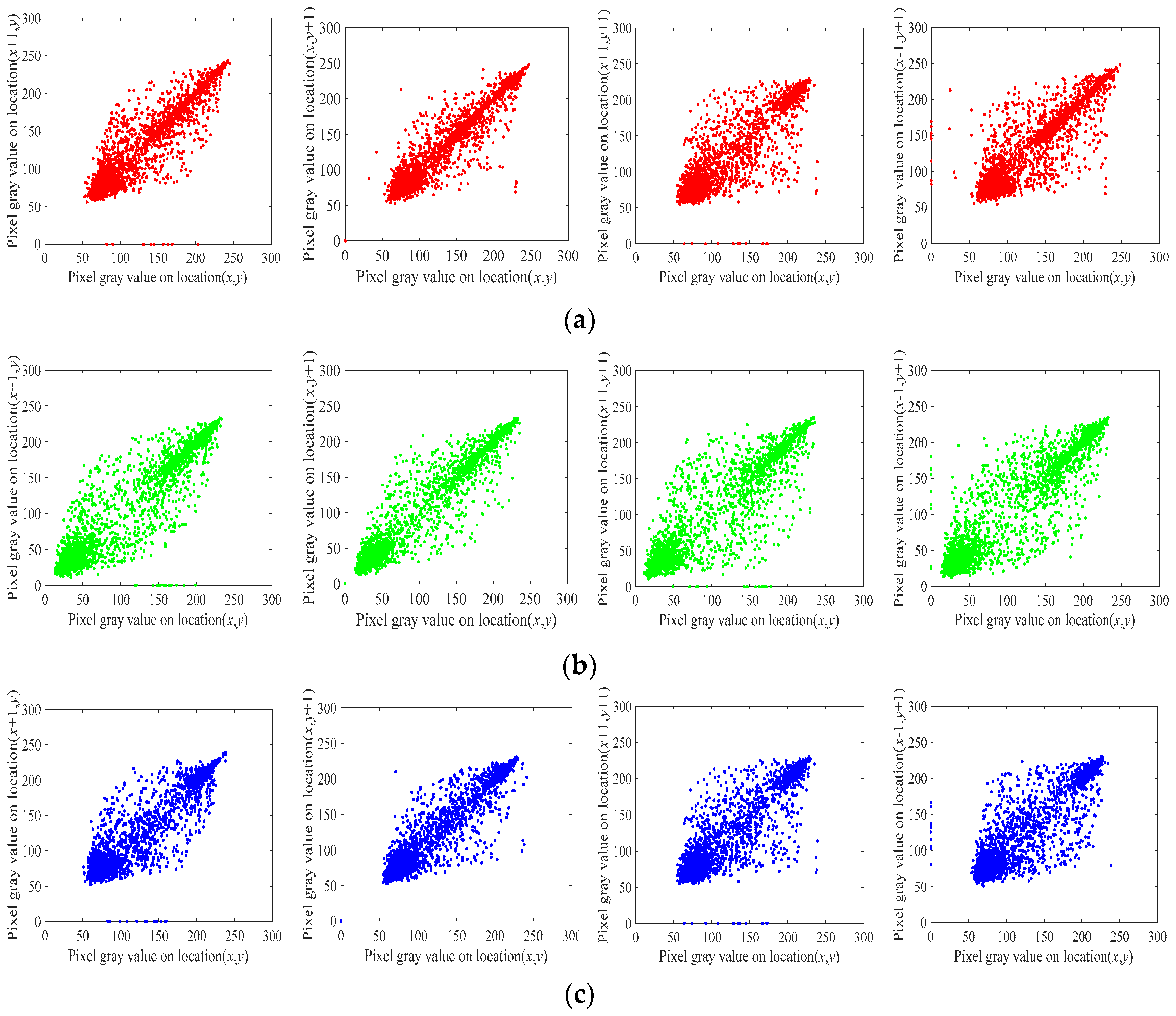
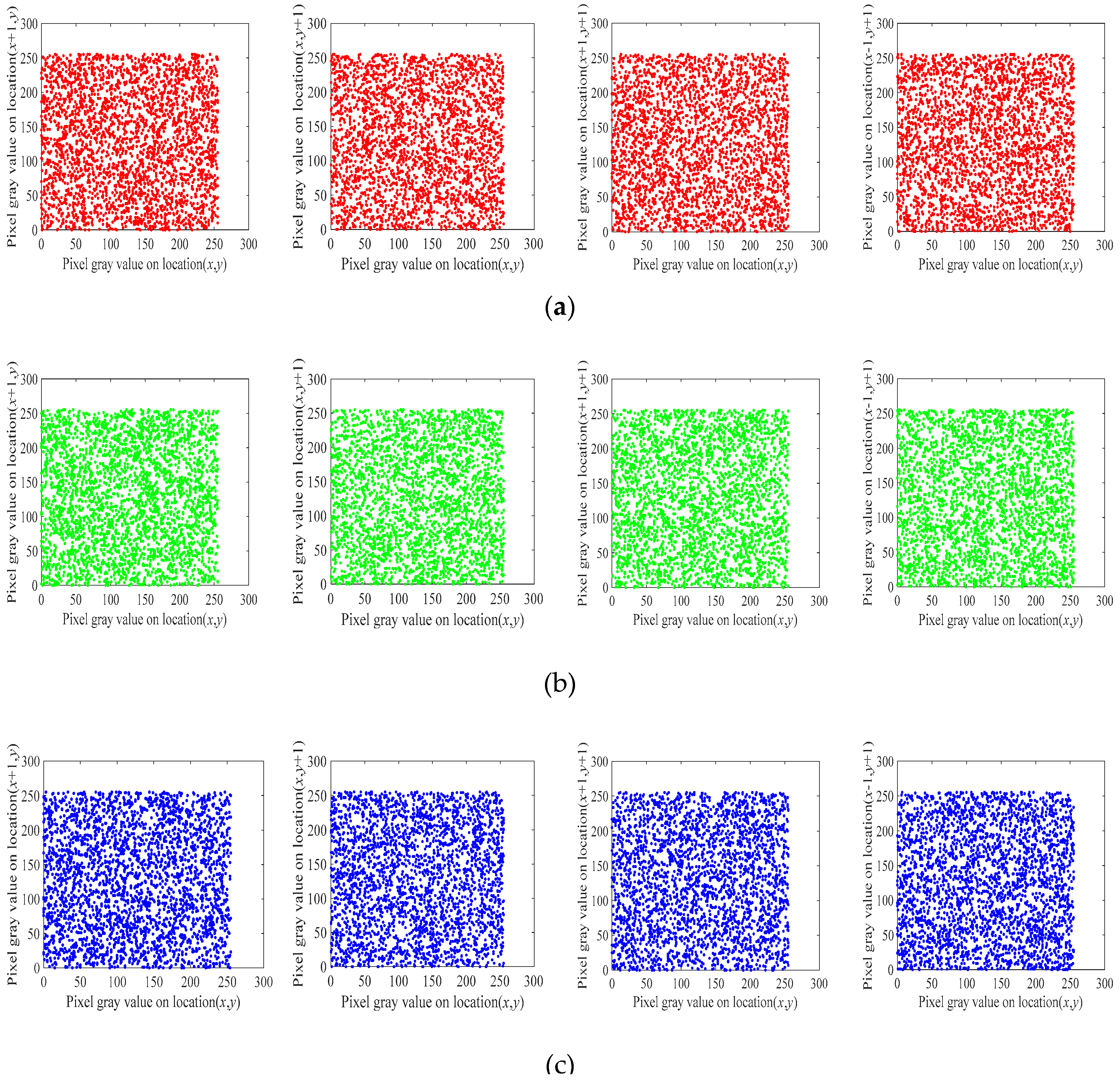
5.4. Correlation Analysis
5.5. Information Entropy Analysis
5.6. Noise Attacks Analysis
5.7. Data Loss Attack
5.8. Differential Attack Analysis
5.9. Time and Computational Complexity Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, X.; Kan, H.; Kurths, J. A new color image encryption scheme based on DNA sequences and multiple improved 1D chaotic maps. Appl. Soft Comput. 2015, 37, 24–39. [Google Scholar] [CrossRef]
- Li, C.; Luo, G.; Ke, Q.; Li, C. An image encryption scheme based on chaotic tent map. Nonlinear Dyn. 2017, 87, 127–133. [Google Scholar] [CrossRef]
- Ye, G.; Chen, P.; Huang, X.; Mei, Q. An efficient pixel-level chaotic image encryption algorithm. Nonlinear Dyn. 2018, 94, 1–12. [Google Scholar] [CrossRef]
- Kaur, M.; Kumar, V. Efficient image encryption method based on improved Lorenz chaotic system. Electron. Lett. 2018, 54, 562–564. [Google Scholar] [CrossRef]
- Wang, X.; Çavuşoğlu, Ü.; Kacar, S.; Akgul, A.; Pham, V.-T.; Jafari, S.; Alsaadi, E.F.; Nguyen, Q.X. S-Box Based Image Encryption Application Using a Chaotic System without Equilibrium. Appl. Sci. 2019, 9, 781. [Google Scholar] [CrossRef]
- Zhou, N.; Li, H.; Di, W.; Pan, S.; Zhou, Z. Image compression and encryption scheme based on 2D compressive sensing and fractional Mellin transform. Opt. Commun. 2015, 343, 10–21. [Google Scholar] [CrossRef]
- Liu, X.; Mei, W.; Du, H. Optical image encryption based on compressive sensing and chaos in the fractional Fourier domain. J. Mod. Opt. 2014, 61, 1570–1577. [Google Scholar] [CrossRef]
- Ye, G. A block image encryption algorithm based on wave transmission and chaotic systems. Nonlinear Dyn. 2014, 75, 417–427. [Google Scholar] [CrossRef]
- Chai, X.L.; Zhu, C.J.; Yang, K.; Gao, Y.L. Block Image Encryption Scheme Based on Wave Transmission and Hyperchaotic Financial System. J. Chin. Comput. Syst. 2016, 37, 1329–1333. [Google Scholar]
- Guesmi, R.; Farah, M.A.B.; Kachouri, A.; Samet, M. A novel chaos-based image encryption using DNA sequence operation and Secure Hash Algorithm SHA-2. Nonlinear Dyn. 2016, 83, 1–14. [Google Scholar] [CrossRef]
- Guesmi, R.; Farah, M.A.B.; Kachouri, A.; Samet, M. Hash key-based image encryption using crossover operator and chaos. Multimed. Tools Appl. 2016, 75, 4753–4769. [Google Scholar] [CrossRef]
- Yong, Z. The image encryption algorithm based on chaos and DNA computing. Multimed. Tools Appl. 2018, 77, 21589–21615. [Google Scholar]
- Chai, X.; Chen, Y.; Broyde, L. A novel chaos-based image encryption algorithm using DNA sequence operations. Opt. Lasers Eng. 2017, 88, 197–213. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.L. A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems. Nonlinear Dyn. 2016, 83, 333–346. [Google Scholar] [CrossRef]
- Chen, J.X.; Zhu, Z.L.; Chong, F.; Zhang, L.B.; Zhang, Y. An efficient image encryption scheme using lookup table-based confusion and diffusion. Nonlinear Dyn. 2015, 81, 1151–1166. [Google Scholar] [CrossRef]
- Kumar, M.; Iqbal, A.; Kumar, P. A new RGB image encryption algorithm based on DNA encoding and elliptic curve Diffie-Hellman cryptography. Signal Process. 2016, 125, 187–202. [Google Scholar] [CrossRef]
- Pareek, N.K.; Patidar, V.; Sud, K.K. Image encryption using chaotic logistic map. Image Vis. Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Singh, N.; Sinha, A. Optical image encryption using Hartley transform and logistic map. Opt. Commun. 2009, 282, 1104–1109. [Google Scholar] [CrossRef]
- Wang, X.; Lin, T.; Xue, Q. A novel colour image encryption algorithm based on chaos. Signal Process. 2012, 92, 1101–1108. [Google Scholar] [CrossRef]
- Yue, W.; Yang, G.; Jin, H.; Noonan, J.P. Image encryption using the two-dimensional logistic chaotic map. J. Electron. Imaging 2012, 21, 3014. [Google Scholar]
- Zhou, Y.; Long, B.; Chen, C.L.P. A new 1D chaotic system for image encryption. Signal Process. 2014, 97, 172–182. [Google Scholar] [CrossRef]
- Hua, Z.; Zhou, Y.; Pun, C.M.; Chen, C.L.P. 2D Sine Logistic modulation map for image encryption. Inf. Sci. 2015, 297, 80–94. [Google Scholar] [CrossRef]
- Pak, C.; Huang, L. A new color image encryption using combination of the 1D chaotic map. Signal Process. 2017, 138, 129–137. [Google Scholar] [CrossRef]
- Hanis, S.; Amutha, R. A fast double-keyed authenticated image encryption scheme using an improved chaotic map and a butterfly-like structure. Nonlinear Dyn. 2019, 95, 421–432. [Google Scholar] [CrossRef]
- Lu, J.A.; Wu, X.; Lü, J.; Kang, L. A new discrete chaotic system with rational fraction and its dynamical behaviors. Chaos Solitons Fractals 2004, 22, 311–319. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, G.; Zhu, C. A Secure and Fast Image Encryption Scheme Based on Double Chaotic S-Boxes. Entropy 2019, 21, 790. [Google Scholar] [CrossRef]
- Pincus, S. Approximate entropy (ApEn) as a complexity measure. Chaos 1995, 5, 110–117. [Google Scholar] [CrossRef]
- He, J.; Cai, J. Design of a New Chaotic System Based on Van Der Pol Oscillator and Its Encryption Application. Mathematics 2019, 7, 743. [Google Scholar] [CrossRef]
- Guangzhou and China. A new hyperchaotic system and its adaptive tracking control. Acta Phys. Sin. 2012, 61, 273–335. [Google Scholar]
- Wang, X.Y.; Li, P.; Zhang, Y.Q.; Liu, L.Y.; Zhang, H.; Wang, X. A novel color image encryption scheme using DNA permutation based on the Lorenz system. Multimed. Tools Appl. 2018, 77, 6243–6265. [Google Scholar] [CrossRef]
- Sun, S. A novel hyperchaotic image encryption scheme based on DNA encoding, pixel-level scrambling and bit-level scrambling. IEEE Photonics J. 2018, 10. [Google Scholar] [CrossRef]
- Enayatifar, R.; Sadaei, H.J.; Abdullah, A.H.; Lee, M.; Isnin, I.F. A novel chaotic based image encryption using a hybrid model of deoxyribonucleic acid and cellular automata. Opt. Lasers Eng. 2015, 71, 33–41. [Google Scholar] [CrossRef]
- Xie, Y.; Yu, J.; Guo, S.; Ding, Q.; Wang, E. Image Encryption Scheme with Compressed Sensing Based on New Three-Dimensional Chaotic System. Entropy 2019, 21, 819. [Google Scholar] [CrossRef]
- Cicek, I.; Pusane, A.E.; Dundar, G. A novel design method for discrete time chaos based true random number generators. Integr. VLSI J. 2014, 47, 38–47. [Google Scholar] [CrossRef]
- Liu, H.; Kadir, A.; Sun, X. Chaos-based fast color image encryption scheme with true random number keys from environmental noise. IET Image Process. 2017, 11, 324–332. [Google Scholar] [CrossRef]
- Parvaz, R.; Zarebnia, M. A combination chaotic system and application in color image encryption. Opt. Laser Technol. 2018, 101, 30–41. [Google Scholar] [CrossRef] [Green Version]
- Niyat, A.Y.; Moattar, M.H.; Torshiz, M.N. Color image encryption based on hybrid hyper-chaotic system and cellular automata. Opt. Lasers Eng. 2017, 90, 225–237. [Google Scholar] [CrossRef]
- Liu, H.; Kadir, A. Asymmetric color image encryption scheme using 2D discrete-time map. Signal Process. 2015, 113, 104–112. [Google Scholar] [CrossRef]
- Wang, L.; Song, H.; Ping, L. A novel hybrid color image encryption algorithm using two complex chaotic systems. Opt. Lasers Eng. 2016, 77, 118–125. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, B.; Hu, Y.; Ran, Y. A Novel Color Image Encryption Scheme Using Rectangular Transform-Enhanced Chaotic Tent Maps. IEEE Access 2017, 5, 6429–6436. [Google Scholar]
- Wu, Y. NPCR and UACI Randomness Tests for Image Encryption. Cyber J. J. Sel. Areas Telecommun. 2011, 1, 31–38. [Google Scholar]
- Wang, X.; Zhao, Y.; Zhang, H.; Guo, K. A novel color image encryption scheme using alternate chaotic mapping structure. Opt. Lasers Eng. 2016, 82, 79–86. [Google Scholar] [CrossRef]
- Suri, S.; Vijay, R. A synchronous intertwining logistic map-DNA approach for color image encryption. J. Ambient Intell. Humaniz. Comput. 2019, 10, 2277–2290. [Google Scholar] [CrossRef]
- Xu, L.; Li, Z.; Li, J.; Hua, W. A novel bit-level image encryption algorithm based on chaotic maps. Opt. Lasers Eng. 2016, 78, 17–25. [Google Scholar] [CrossRef]




| Chaotic Maps | Chaotic Regions |
|---|---|
| The LFHCM | |
| The Logistic map | |
| The Fraction map | |
| Modified logistic map in [24] | |
| Sine-Tent systemin [26] |
| Chaotic Maps | Thresholds | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.02 | 0.04 | 0.06 | 0.08 | 0.10 | 0.12 | 0.14 | 0.16 | 0.18 | 0.20 | 0.22 | 0.24 | 0.26 | |
| The LFHCM | 0.36 | 0.55 | 0.66 | 0.71 | 0.75 | 0.76 | 0.81 | 0.82 | 0.84 | 0.85 | 0.84 | 0.86 | 0.85 |
| The Logistic map | 0.35 | 0.47 | 0.53 | 0.53 | 0.55 | 0.56 | 0.57 | 0.59 | 0.27 | 0.56 | 0.54 | 0.53 | 0.54 |
| The Fraction map | 0.15 | 0.23 | 0.28 | 0.33 | 0.37 | 0.38 | 0.41 | 0.42 | 0.45 | 0.47 | 0.46 | 0.47 | 0.46 |
| Statistical Tests | P-Value | Result |
|---|---|---|
| Frequency | 0.3699 | Pass |
| Block frequency | 0.7872 | Pass |
| Cumulative sums | 0.6584 | Pass |
| Runs | 0.2645 | Pass |
| Longest run | 0.6385 | Pass |
| Rank | 0.2022 | Pass |
| Fast fourier transform | 0.3492 | Pass |
| Non-overlapping template | 0.6286 | Pass |
| Overlapping template | 0.5575 | Pass |
| Universal | 0.6917 | Pass |
| Approximate entropy | 0.5434 | Pass |
| Random excursions | 0.5753 | Pass |
| Random excursions variant | 0.5349 | Pass |
| Linear complexity | 0.4639 | Pass |
| Serial | 0.3972 | Pass |
| Modified Key | Difference Rate (%) | ||
|---|---|---|---|
| Couple | House | Tree | |
| 99.6155 | 99.5880 | 99.5931 | |
| 99.6094 | 99.6190 | 99.6089 | |
| 99.6043 | 99.6002 | 99.6007 | |
| 99.6190 | 99.6237 | 99.6038 | |
| 99.6038 | 99.6165 | 99.6185 | |
| 99.5956 | 99.6185 | 99.6048 | |
| 99.6140 | 99.5946 | 99.6063 | |
| Plain Image | Cipher Image | |||||
|---|---|---|---|---|---|---|
| R | G | B | R | G | B | |
| Couple | 2.1036 × 105 | 3.3786 × 105 | 2.8964 × 105 | 247.6016 | 234.6563 | 249.8984 |
| House | 2.5858 × 105 | 2.9916 × 105 | 3.9404 × 105 | 274.3672 | 277.3203 | 286.9922 |
| Tree | 8.1371 × 104 | 5.7009 × 104 | 1.2982 × 104 | 254.0859 | 244.8125 | 264.3594 |
| Lena | 2.4628 × 105 | 1.1766 × 105 | 3.4033 × 105 | 257.1094 | 261.9063 | 202.1699 |
| Peppers | 5.4984 × 104 | 7.2077 × 104 | 1.1435 × 105 | 279.4395 | 268.0254 | 273.2910 |
| Airplane | 1.6115 × 105 | 1.5940 × 105 | 2.6505 × 105 | 234.2305 | 283.9785 | 243.3086 |
| Lena in [30] | - | - | - | 231.6144 | 248.36505 | 254.4806 |
| Pepper in [30] | - | - | - | 266.1728 | 273.2120 | 252.6552 |
| Airplane in [30] | - | - | - | 275.2378 | 271.7001 | 228.2813 |
| Image | Plain Image | |||
|---|---|---|---|---|
| Horizontal | Vertical | Main-Diagonal | Back-Diagonal | |
| Couple | 0.9566 | 0.9566 | 0.9566 | 0.9566 |
| House | 0.9348 | 0.9693 | 0.9163 | 0.9588 |
| Tree | 0.9298 | 0.9542 | 0.9071 | 0.9047 |
| Lena | 0.9872 | 0.9756 | 0.9633 | 0.9709 |
| Peppers | 0.9466 | 0.9452 | 0.9100 | 0.9186 |
| Baboon | 0.8847 | 0.9099 | 0.8251 | 0.8120 |
| Image | Plain Image | |||
|---|---|---|---|---|
| Horizontal | Vertical | Main-Diagonal | Back-Diagonal | |
| Couple | 0.0024 | 0.0018 | −0.0017 | 0.0027 |
| House | 0.0002 | −0.0004 | −0.0016 | 0.0008 |
| Tree | 0.0001 | −0.0007 | 0.0015 | 0.0013 |
| Lena | −0.0009 | 0.0008 | 0.0021 | 0.0004 |
| Peppers | 0.0019 | −0.0010 | −0.0008 | 0.0021 |
| Baboon | −0.0003 | −0.0028 | −0.0001 | −0.0013 |
| Lena in [14] | 0.0056 | 0.0065 | −0.0073 | - |
| Lena in [31] | −0.0068 | −0.0054 | 0.0010 | - |
| Lena in [32] | 0.0059 | −0.0042 | 0.0180 | - |
| Lena in [33] | 0.0033 | 0.0027 | 0.0014 | - |
| Peppers in [34] | −0.0047 | −0.0024 | −0.0028 | - |
| Peppers in [35] | 0.0002 | 0.0022 | 0.0010 | - |
| Baboon in [35] | 0.0004 | −0.0047 | 0.0001 | - |
| Image | Plain Image | Cipher Image | ||||
|---|---|---|---|---|---|---|
| R | G | B | R | G | B | |
| Couple | 6.2499 | 5.9642 | 5.9309 | 7.9973 | 7.9974 | 7.9973 |
| House | 6.4311 | 6.5389 | 6.2320 | 7.9970 | 7.9973 | 7.9967 |
| Tree | 7.2104 | 7.4136 | 6.9207 | 7.9972 | 7.9973 | 7.9971 |
| Lena | 7.2682 | 7.5901 | 6.9951 | 7.9993 | 7.9993 | 7.9994 |
| Peppers | 7.3319 | 7.5242 | 7.0793 | 7.9992 | 7.9993 | 7.9992 |
| Baboon | 7.7067 | 7.4744 | 7.7522 | 7.9992 | 7.9994 | 7.9993 |
| Lena in [35] | - | - | - | 7.9872 | 7.9875 | 7.9869 |
| Lena in [36] | - | - | - | 7.9970 | 7.9972 | 7.9970 |
| Lena in [37] | - | - | - | 7.9972 | 7.9973 | 7.9972 |
| Peppers in [35] | - | - | - | 7.9869 | 7.9880 | 7.9884 |
| Peppers in [37] | - | - | - | 7.9971 | 7.9975 | 7.9974 |
| Baboon in [35] | - | - | - | 7.9876 | 7.9879 | 7.9876 |
| Baboon in [37] | - | - | - | 7.9972 | 7.9972 | 7.9972 |
| Size | NPCR (%) | UACI (%) | ||||
|---|---|---|---|---|---|---|
| 99.5693 | 99.5527 | 99.5341 | (33.2824,33.6447) | (33.2255,33.7061) | (33.1594,33.7677) | |
| Image | Calculated NPCR (%) | Theoretical NPCR (%) | ||||
|---|---|---|---|---|---|---|
| R | G | B | ||||
| Couple | 99.5956 | 99.6124 | 99.6185 | Passed | Passed | Passed |
| House | 99.6017 | 99.6268 | 99.5956 | Passed | Passed | Passed |
| Tree | 99.6094 | 99.6096 | 99.6129 | Passed | Passed | Passed |
| Lena | 99.6037 | 99.6128 | 99.5995 | Passed | Passed | Passed |
| Peppers | 99.5904 | 99.6246 | 99.6033 | Passed | Passed | Passed |
| Baboon | 99.5921 | 99.6109 | 99.6170 | Passed | Passed | Passed |
| Lena in [35] | 99.6357 | 99.6416 | 99.6224 | - | - | - |
| Lena in [37] | 99.6505 | 99.6444 | 99.6627 | - | - | - |
| Lena in [42] | 99.6300 | 99.5900 | 99.6700 | - | - | - |
| Lena in [43] | 99.6445 | 99.6353 | 99.6429 | - | - | - |
| Peppers in [35] | 99.5693 | 99.6435 | 99.6171 | - | - | - |
| Peppers in [37] | 99.6357 | 99.6158 | 99.6247 | - | - | - |
| Baboon in [35] | 99.6563 | 99.6428 | 99.6493 | - | - | - |
| Baboon in [37] | 99.6536 | 99.6078 | 99.6520 | - | - | - |
| Baboon in [43] | 99.6461 | 99.6628 | 99.6277 | - | - | - |
| Image | Calculated UACI (%) | Theoretical UACI (%) | ||||
|---|---|---|---|---|---|---|
| R | G | B | ||||
| Couple | 33.5911 | 33.4298 | 33.4019 | Passed | Passed | Passed |
| House | 33.5739 | 33.4600 | 33.4721 | Passed | Passed | Passed |
| Tree | 33.4029 | 33.4018 | 33.4793 | Passed | Passed | Passed |
| Lena | 33.5056 | 33.4533 | 33.4719 | Passed | Passed | Passed |
| Peppers | 33.4634 | 33.5485 | 33.4818 | Passed | Passed | Passed |
| Baboon | 33.5139 | 33.4682 | 33.5363 | Passed | Passed | Passed |
| Lena in [35] | 33.5839 | 33.3954 | 33.4687 | - | - | - |
| Lena in [37] | 33.4462 | 33.4131 | 33.4399 | - | - | - |
| Lena in [42] | 33.4300 | 33.3900 | 33.5100 | - | - | - |
| Lena in [43] | 33.1147 | 30.5298 | 27.7471 | - | - | - |
| Peppers in [35] | 33.4317 | 33.5392 | 33.6326 | - | - | - |
| Peppers in [37] | 33.4570 | 33.4705 | 33.4423 | - | - | - |
| Baboon in [35] | 33.3687 | 33.5956 | 33.4528 | - | - | - |
| Baboon in [37] | 33.4753 | 33.5090 | 33.4176 | - | - | - |
| Baboon in [43] | 29.8421 | 28.1446 | 30.7024 | - | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.-L.; Wang, S.-M.; Xiang, J.-H. A Tweak-Cube Color Image Encryption Scheme Jointly Manipulated by Chaos and Hyper-Chaos. Appl. Sci. 2019, 9, 4854. https://doi.org/10.3390/app9224854
Huang L-L, Wang S-M, Xiang J-H. A Tweak-Cube Color Image Encryption Scheme Jointly Manipulated by Chaos and Hyper-Chaos. Applied Sciences. 2019; 9(22):4854. https://doi.org/10.3390/app9224854
Chicago/Turabian StyleHuang, Li-Lian, Shi-Ming Wang, and Jian-Hong Xiang. 2019. "A Tweak-Cube Color Image Encryption Scheme Jointly Manipulated by Chaos and Hyper-Chaos" Applied Sciences 9, no. 22: 4854. https://doi.org/10.3390/app9224854
APA StyleHuang, L.-L., Wang, S.-M., & Xiang, J.-H. (2019). A Tweak-Cube Color Image Encryption Scheme Jointly Manipulated by Chaos and Hyper-Chaos. Applied Sciences, 9(22), 4854. https://doi.org/10.3390/app9224854