Linear Response in Topological Materials
Abstract
1. Background and Introduction
2. Linear Response Theory
3. Anomalous Hall Effect in Ferromagnetic Topological Materials
4. Anomalous Hall Effect in Antiferromagnetic Topological Semimetals
5. Anomalous Hall Effect in Thin Films
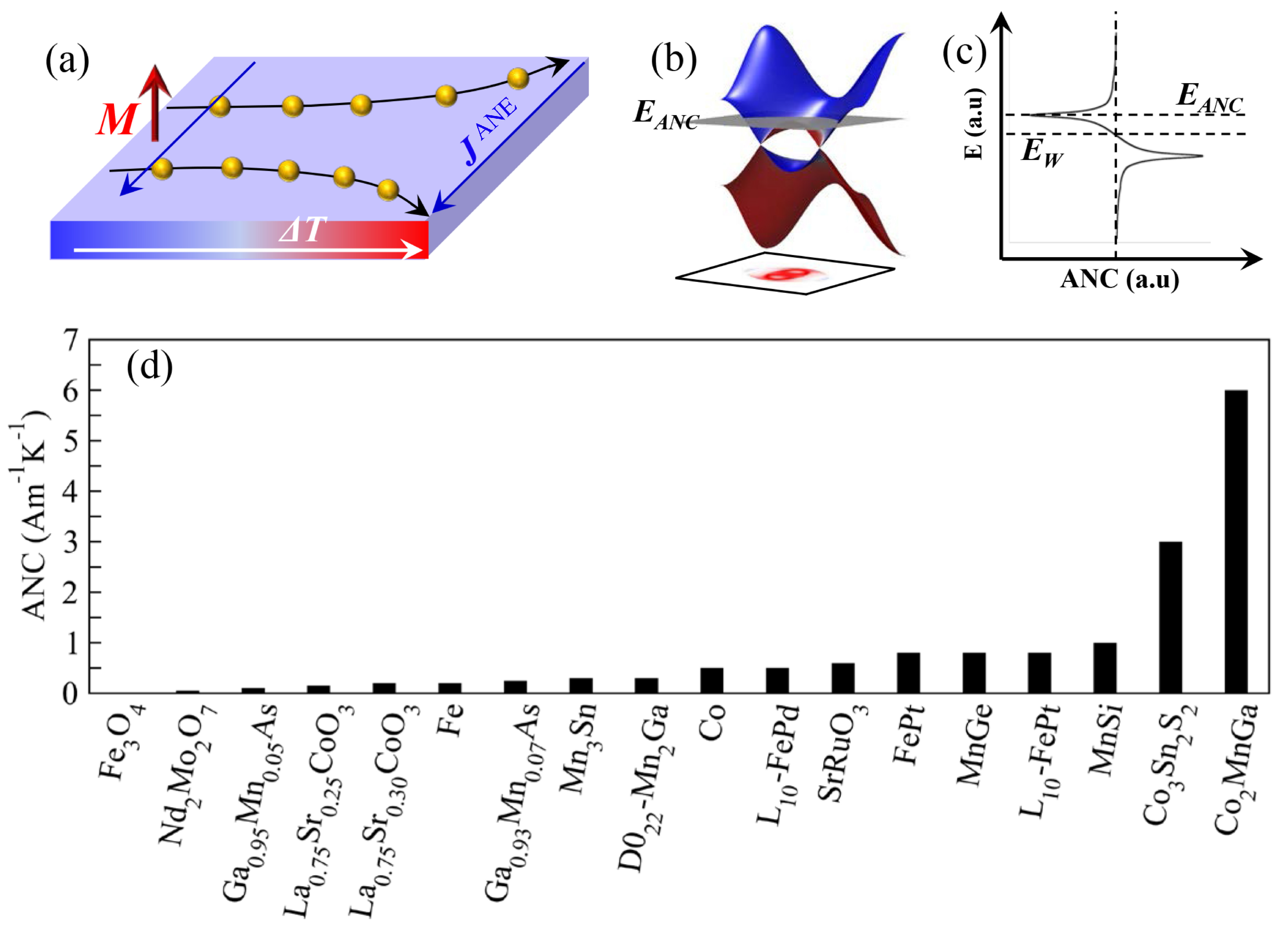
6. Anomalous Nernst Effect in Topological Semimetals
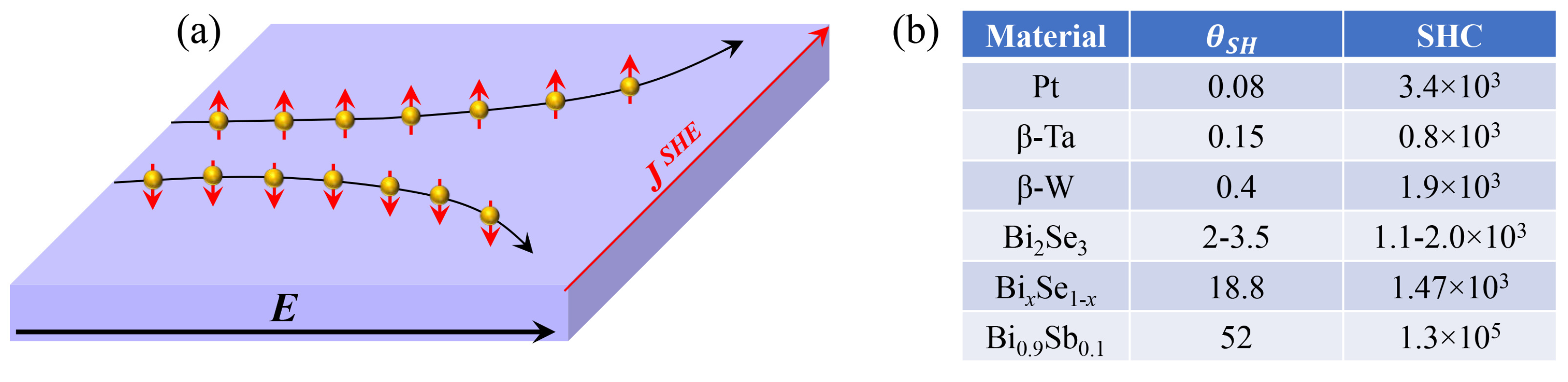
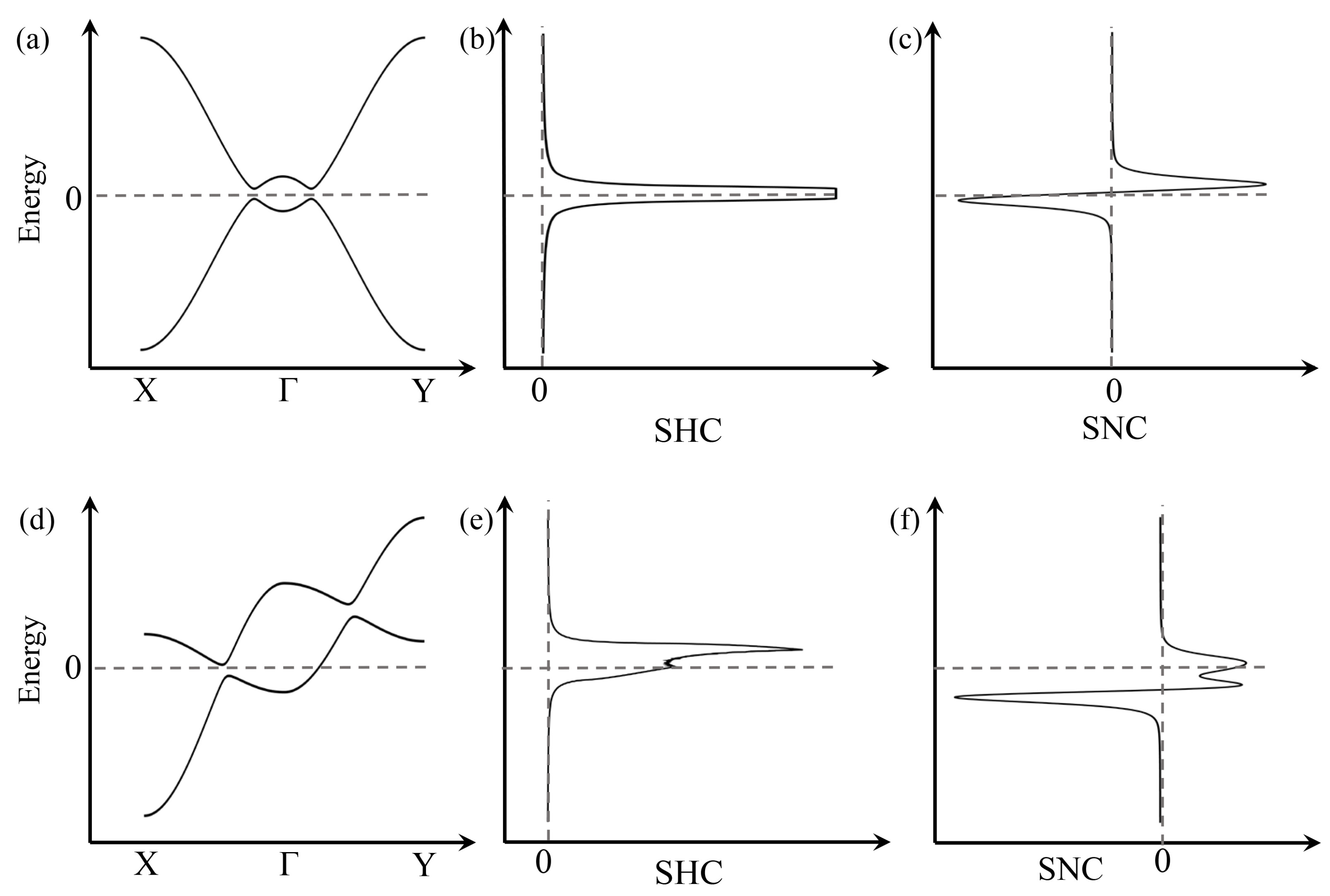
7. Spin Hall Effect in Topological Materials
8. Spin Nernst Effect in Topological Materials
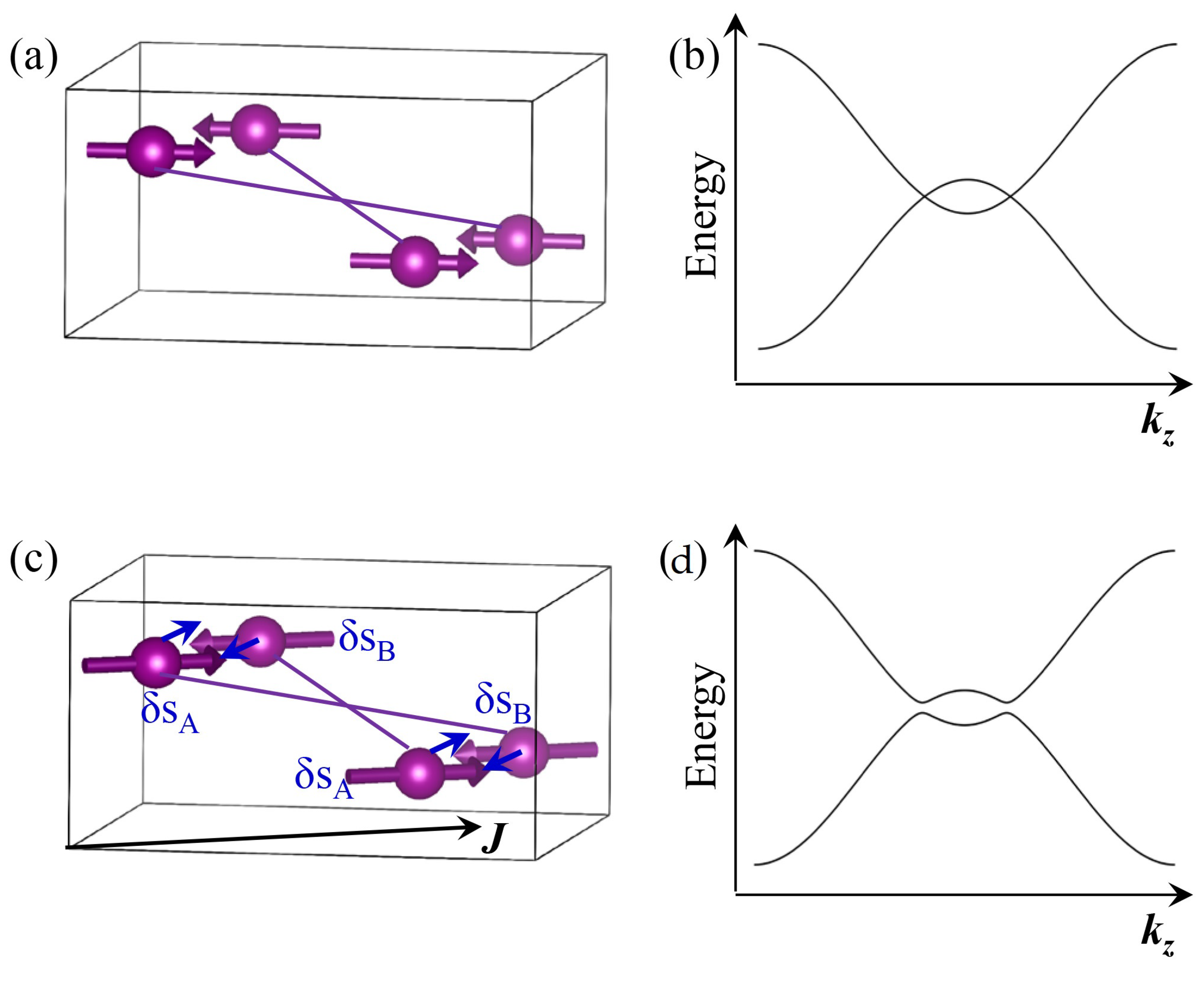
9. Spin–Orbit Torque in Magnetic Semimetals
10. Summary
Author Contributions
Conflicts of Interest
References
- Kane, C.L.; Mele, E.J. Z2 Topological Order and the Quantum Spin Hall Effect. Phys. Rev. Lett. 2005, 95, 146802. [Google Scholar] [CrossRef] [PubMed]
- Kane, C.L.; Mele, E.J. Quantum Spin Hall Effect in Graphene. Phy. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef] [PubMed]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef] [PubMed]
- König, M.; Wiedmann, S.; Brüne, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.L.; Zhang, S.C. Quantum spin Hall insulator state in HgTe quantum wells. Science 2007, 318, 766–770. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Kane, C.L.; Mele, E.J. Topological insulators in three dimensions. Phys. Rev. Lett. 2007, 98, 106803. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y.S.; Cava, R.J.; Hasan, M.Z. A topological Dirac insulator in a quantum spin Hall phase. Nature 2008, 452, 970. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
- Chiu, C.K.; Teo, J.C.; Schnyder, A.P.; Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 2016, 88, 035005. [Google Scholar] [CrossRef]
- Po, H.C.; Vishwanath, A.; Watanabe, H. Symmetry-based indicators of band topology in the 230 space groups. Nat. Commun. 2017, 8, 50. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.; Zhang, T.; Fang, Z.; Fang, C. Quantitative mappings between symmetry and topology in solids. Nat. Commun. 2018, 9, 3530. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.; Zhang, T.; Fang, C. Diagnosis for Nonmagnetic Topological Semimetals in the Absence of Spin-Orbital Coupling. Phys. Rev. X 2018, 8, 031069. [Google Scholar] [CrossRef]
- Kitaev, A. Periodic table for topological insulators and superconductors. AIP Conf. Proc. 2009, 1134, 22–30. [Google Scholar]
- Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 2011, 106, 106802. [Google Scholar] [CrossRef] [PubMed]
- Wan, X.G.; Turner, A.M.; Vishwanath, A.; Savrasov, S.Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 2011, 83, 205101. [Google Scholar] [CrossRef]
- Burkov, A.A.; Balents, L. Weyl Semimetal in a Topological Insulator Multilayer. Phys. Rev. Lett. 2011, 107, 127205. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Sun, Y.; Chen, X.Q.; Franchini, C.; Xu, G.; Weng, H.; Dai, X.; Fang, Z. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 2012, 85, 195320. [Google Scholar] [CrossRef]
- Hsieh, T.H.; Lin, H.; Liu, J.; Duan, W.; Bansil, A.; Fu, L. Topological crystalline insulators in the SnTe material class. Nat. Commun. 2012, 3, 982. [Google Scholar] [CrossRef] [PubMed]
- Young, S.M.; Zaheer, S.; Teo, J.C.Y.; Kane, C.L.; Mele, E.J.; Rappe, A.M. Dirac Semimetal in Three Dimensions. Phys. Rev. Lett. 2012, 108, 140405. [Google Scholar] [CrossRef] [PubMed]
- Ando, Y.; Fu, L. Topological crystalline insulators and topological superconductors: From concepts to materials. Annu. Rev. Condens. Matter Phys. 2015, 6, 361–381. [Google Scholar] [CrossRef]
- Weng, H.; Fang, C.; Fang, Z.; Bernevig, B.A.; Dai, X. Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides. Phys. Rev. X 2015, 5, 011029. [Google Scholar] [CrossRef]
- Huang, S.M.; Xu, S.Y.; Belopolski, I.; Lee, C.C.; Chang, G.; Wang, B.; Alidoust, N.; Bian, G.; Neupane, M.; Zhang, C.; et al. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 2015, 6, 7373. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sankar, R.; Chang, G.; Zhujun, Y.; Lee, C.C.; et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 349, 613. [Google Scholar] [CrossRef] [PubMed]
- Lv, B.Q.; Weng, H.M.; Fu, B.B.; Wang, X.P.; Miao, H.; Ma, J.; Richard, P.; Huang, X.C.; Zhao, L.X.; Chen, G.F.; et al. Experimental Discovery of Weyl Semimetal TaAs. Phys. Rev. X 2015, 5, 031013. [Google Scholar] [CrossRef]
- Bradlyn, B.; Cano, J.; Wang, Z.; Vergniory, M.; Felser, C.; Cava, R.; Bernevig, B.A. Beyond Dirac and Weyl fermions: Unconventional quasiparticles in conventional crystals. Science 2016, 353, 5037. [Google Scholar] [CrossRef] [PubMed]
- Belopolski, I.; Sanchez, D.S.; Ishida, Y.; Pan, X.; Yu, P.; Xu, S.Y.; Chang, G.; Chang, T.R.; Zheng, H.; Alidoust, N.; et al. Discovery of a new type of topological Weyl fermion semimetal state in MoxW1-xTe2. Nat. Commun. 2016, 7, 13643. [Google Scholar] [CrossRef] [PubMed]
- Chang, G.; Xu, S.Y.; Zheng, H.; Singh, B.; Hsu, C.H.; Bian, G.; Alidoust, N.; Belopolski, I.; Sanchez, D.S.; Zhang, S.; et al. Room-temperature magnetic topological Weyl fermion and nodal line semimetal states in half-metallic Heusler Co2TiX (X=Si, Ge, or Sn). Sci. Rep. 2016, 6, 38839. [Google Scholar] [CrossRef] [PubMed]
- Chang, G.; Xu, S.Y.; Sanchez, D.S.; Huang, S.M.; Lee, C.C.; Chang, T.R.; Bian, G.; Zheng, H.; Belopolski, I.; Alidoust, N.; et al. A strongly robust type II Weyl fermion semimetal state in Ta3S2. Sci. Adv. 2016, 2, e1600295. [Google Scholar] [CrossRef] [PubMed]
- Bradlyn, B.; Elcoro, L.; Cano, J.; Vergniory, M.; Wang, Z.; Felser, C.; Aroyo, M.; Bernevig, B.A. Topological quantum chemistry. Nature 2017, 547, 298. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Chang, G.; Huang, S.M.; Guo, C.; Zhang, X.; Zhang, S.; Yin, J.; Xu, S.Y.; Belopolski, I.; Alidoust, N.; et al. Mirror Protected Dirac Fermions on a Weyl Semimetal NbP Surface. Phys. Rev. Lett. 2017, 119, 196403. [Google Scholar] [CrossRef] [PubMed]
- Fei, F.; Bo, X.; Wang, R.; Wu, B.; Jiang, J.; Fu, D.; Gao, M.; Zheng, H.; Chen, Y.; Wang, X.; et al. Nontrivial Berry phase and type-II Dirac transport in the layered material PdTe2. Phys. Rev. B 2017, 96, 041201. [Google Scholar] [CrossRef]
- Xu, S.Y.; Alidoust, N.; Chang, G.; Lu, H.; Singh, B.; Belopolski, I.; Sanchez, D.S.; Zhang, X.; Bian, G.; Zheng, H.; et al. Discovery of Lorentz-violating type II Weyl fermions in LaAlGe. Sci. Adv. 2017, 3. [Google Scholar] [CrossRef] [PubMed]
- Armitage, N.; Mele, E.; Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Schindler, F.; Cook, A.M.; Vergniory, M.G.; Wang, Z.; Parkin, S.S.; Bernevig, B.A.; Neupert, T. Higher-order topological insulators. Sci. Adv. 2018, 4, 0346. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Jiang, Y.; Song, Z.; Huang, H.; He, Y.; Fang, Z.; Weng, H.; Fang, C. Catalogue of topological electronic materials. Nature 2019, 566, 475. [Google Scholar] [CrossRef] [PubMed]
- Tang, F.; Po, H.C.; Vishwanath, A.; Wan, X. Comprehensive search for topological materials using symmetry indicators. Nature 2019, 566, 486. [Google Scholar] [CrossRef] [PubMed]
- Vergniory, M.; Elcoro, L.; Felser, C.; Regnault, N.; Bernevig, B.A.; Wang, Z. A complete catalogue of high-quality topological materials. Nature 2019, 566, 480. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Jia, J.F. Topological superconductivity in a Bi2Te3/NbSe2 heterostructure: A review. Chin. Phys. B 2019, 28, 067403. [Google Scholar] [CrossRef]
- Crépieux, A.; Bruno, P. Theory of the anomalous Hall effect from the Kubo formula and the Dirac equation. Phys. Rev. B 2001, 64, 014416. [Google Scholar] [CrossRef]
- Nolting, W. Fundamentals of Many-Body Physics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics (Saunders College, Philadelphia, 1976); Saunders College Publishing: Saunders College, PA, USA, 1976. [Google Scholar]
- Xiao, D.; Chang, M.C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2010, 82, 1959–2007. [Google Scholar] [CrossRef]
- Nagaosa, N.; Sinova, J.; Onoda, S.; MacDonald, A.H.; Ong, N.P. AnomalousHalleffe. Rev. Mod. Phys. 2010, 82, 1539. [Google Scholar] [CrossRef]
- Hall, E. On a new action of the magnet on electric currents. Am. J. Sci. 1879, 2, 287–292. [Google Scholar] [CrossRef]
- Karplus, R.; Luttinger, J. Hall effect in ferromagnetics. Phys. Rev. 1954, 95, 1154. [Google Scholar] [CrossRef]
- Chang, M.C.; Niu, Q. Berry phase, hyperorbits, and the Hofstadter spectrum: Semiclassical dynamics in magnetic Bloch bands. Phys. Rev. B 1996, 53, 7010. [Google Scholar] [CrossRef] [PubMed]
- Haldane, F. Berry curvature on the Fermi surface: Anomalous Hall effect as a topological Fermi-liquid property. Phys. Rev. Lett. 2004, 93, 206602. [Google Scholar] [CrossRef] [PubMed]
- Haldane, F.D.M. Model for a Quantum Hall Eff’ect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly”. Phys. Rev. Lett. 1988, 61, 2015. [Google Scholar] [CrossRef] [PubMed]
- Halperin, B.I. Quantized Hall conductance, current-carrying edge states, and the existence of extended states in a two-dimensional disordered potential. Phys. Rev. B 1982, 25, 2185. [Google Scholar] [CrossRef]
- Yu, R.; Zhang, W.; Zhang, H.J.; Zhang, S.C.; Dai, X.; Fang, Z. Quantized Anomalous Hall Effect in Magnetic Topological Insulators. Science 2010, 329, 61. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.Z.; Zhang, J.; Feng, X.; Shen, J.; Zhang, Z.; Guo, M.; Kang, L.; Ou, Y.; Wei, P.W.; Wang, L.L.; et al. Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator. Science 2013, 340, 167. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.X.; Zhang, S.C.; Qi, X.L. The quantum anomalous Hall effect: Theory and experiment. Annu. Rev. Condens. Matter Phys. 2016, 7, 301–321. [Google Scholar] [CrossRef]
- Burkov, A.A.; Hook, M.D.; Balents, L. Topological nodal semimetals. Phys. Rev. B 2011, 84, 235126. [Google Scholar] [CrossRef]
- Zyuzin, A.; Wu, S.; Burkov, A. Weyl semimetal with broken time reversal and inversion symmetries. Phys. Rev. B 2012, 85, 165110. [Google Scholar] [CrossRef]
- Lu, H.Z.; Zhang, S.B.Z.; Shen, S.Q. High-field magnetoconductivity of topological semimetals with short-range potential. Phy. Rev. B 2015, 92, 045203. [Google Scholar] [CrossRef]
- Kübler, J.; Felser, C. Berry curvature and the anomalous Hall effect in Heusler compounds. Phys. Rev. B 2012, 85, 012405. [Google Scholar] [CrossRef]
- Manna, K.; Muechler, L.; Kao, T.H.; Stinshoff, R.; Zhang, Y.; Gooth, J.; Kumar, N.; Kreiner, G.; Koepernik, K.; Car, R.; et al. From colossal to zero: controlling the anomalous Hall effect in magnetic Heusler compounds via Berry curvature design. Phys. Rev. X 2018, 8, 041045. [Google Scholar] [CrossRef]
- Wang, Q.; Xu, Y.; Lou, R.; Liu, Z.; Li, M.; Huang, Y.; Shen, D.; Weng, H.; Wang, S.; Lei, H. Large intrinsic anomalous Hall effect in half-metallic ferromagnet Co3Sn2S2 with magnetic Weyl fermions. Nat. Commun. 2018, 9, 3681. [Google Scholar] [CrossRef] [PubMed]
- Liu, E.; Sun, Y.; Kumar, N.; Muechler, L.; Sun, A.; Jiao, L.; Yang, S.Y.; Liu, D.; Liang, A.; Xu, Q.; et al. Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal. Nat. Phys. 2018, 14, 1125. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Seo, J.; Lee, E.; Ko, K.T.; Kim, B.; Jang, B.G.; Ok, J.M.; Lee, J.; Jo, Y.J.; Kang, W.; et al. Large anomalous Hall current induced by topological nodal lines in a ferromagnetic van der Waals semimetal. Nat. Mater. 2018, 17, 794. [Google Scholar] [CrossRef] [PubMed]
- Shindou, R.; Nagaosa, N. Orbital ferromagnetism and anomalous Hall effect in antiferromagnets on the distorted fcc lattice. Phys. Rev. Lett. 2001, 87, 116801. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Niu, Q.; MacDonald, A.H. Anomalous Hall effect arising from noncollinear antiferromagnetism. Phys. Rev. Lett. 2014, 112, 017205. [Google Scholar] [CrossRef] [PubMed]
- Kübler, J.; Felser, C. Non-collinear antiferromagnets and the anomalous Hall effect. EPL (Europhys. Lett.) 2014, 108, 67001. [Google Scholar] [CrossRef]
- Nakatsuji, S.; Kiyohara, N.; Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 2015, 527, 212. [Google Scholar] [CrossRef] [PubMed]
- Nayak, A.K.; Fischer, J.E.; Sun, Y.; Yan, B.; Karel, J.; Komarek, A.C.; Shekhar, C.; Kumar, N.; Schnelle, W.; Ku bler, J.; et al. Large anomalous Hall effect driven by a nonvanishing Berry curvature in the noncolinear antiferromagnet Mn3Ge. Sci. Adv. 2016, 2, e1501870. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Sun, Y.; Yang, H.; Železnỳ, J.; Parkin, S.P.; Felser, C.; Yan, B. Strong anisotropic anomalous Hall effect and spin Hall effect in the chiral antiferromagnetic compounds Mn3X (X = Ge, Sn, Ga, Ir, Rh, and Pt). Phys. Rev. B 2017, 95, 075128. [Google Scholar] [CrossRef]
- Yang, H.; Sun, Y.; Zhang, Y.; Shi, W.J.; Parkin, S.S.; Yan, B. Topological Weyl semimetals in the chiral antiferromagnetic materials Mn3Ge and Mn3Sn. New J. Phys. 2017, 19, 015008. [Google Scholar] [CrossRef]
- Kuroda, K.; Tomita, T.; Suzuki, M.T.; Bareille, C.; Nugroho, A.; Goswami, P.; Ochi, M.; Ikhlas, M.; Nakayama, M.; Akebi, S.; et al. Evidence for magnetic Weyl fermions in a correlated metal. Nat. Mater. 2017, 16, 1090. [Google Scholar] [CrossRef] [PubMed]
- Shi, W.; Muechler, L.; Manna, K.; Zhang, Y.; Koepernik, K.; Car, R.; Van Den Brink, J.; Felser, C.; Sun, Y. Prediction of a magnetic Weyl semimetal without spin-orbit coupling and strong anomalous Hall effect in the Heusler compensated ferrimagnet Ti2MnAl. Phys. Rev. B 2018, 97, 060406. [Google Scholar] [CrossRef]
- Markou, A.; Kriegner, D.; Gayles, J.; Zhang, L.; Chen, Y.C.; Ernst, B.; Lai, Y.H.; Schnelle, W.; Chu, Y.H.; Sun, Y.; et al. Thickness dependence of the anomalous Hall effect in thin films of the topological semimetal Co2MnGa. Phys. Rev. B 2019, 100, 054422. [Google Scholar] [CrossRef]
- Dulal, R.P.; Dahal, B.R.; Forbes, A.; Bhattarai, N.; Pegg, I.L.; Philip, J. Weak localization and small anomalous Hall conductivity in ferromagnetic Weyl semimetal Co2TiGe. Sci. Rep. 2019, 9, 3342. [Google Scholar] [CrossRef] [PubMed]
- Ernst, B.; Sahoo, R.; Sun, Y.; Nayak, J.; Müchler, L.; Nayak, A.K.; Kumar, N.; Gayles, J.; Markou, A.; Fecher, G.H.; et al. Anomalous Hall effect and the role of Berry curvature in Co2TiSn Heusler films. Phys. Rev. B 2019, 100, 054445. [Google Scholar] [CrossRef]
- Xu, G.; Weng, H.; Wang, Z.; Dai, X.; Fang, Z. Chern Semimetal and the Quantized Anomalous Hall Effect in HgCr2Se4. Phys. Rev. Lett. 2011, 107, 186806. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.E.; Hankiewicz, E.M.; Culcer, D. Quantum transport in Weyl semimetal thin films in the presence of spin-orbit coupled impurities. Phys. Rev. B 2017, 96, 045307. [Google Scholar] [CrossRef]
- Muechler, L.; Liu, E.; Xu, Q.; Felser, C.; Sun, Y. Realization of quantum anomalous Hall effect from a magnetic Weyl semimetal. arXiv 2017, arXiv:1712.08115. [Google Scholar]
- Bauer, G.E.; Saitoh, E.; Van Wees, B.J. Spin caloritronics. Nat. Mater. 2012, 11, 391. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.L.; Watauchi, S.; Miller, V.; Cava, R.J.; Ong, N.P. Anomalous Hall Heat Current and Nernst Effect in the CuCr2Se4-xBrx Ferromagnet. Phys. Rev. Lett. 2004, 93, 226601. [Google Scholar] [CrossRef] [PubMed]
- Xiao, D.; Yao, Y.; Fang, Z.; Niu, Q. Berry-phase effect in anomalous thermoelectric transport. Phys. Rev. Lett. 2006, 97, 026603. [Google Scholar] [CrossRef] [PubMed]
- Sakai, A.; Mizuta, Y.P.; Nugroho, A.A.; Sihombing, R.; Koretsune, T.; Suzuki, M.T.; Takemori, N.; Ishii, R.; Nishio-Hamane, D.; Arita, R.; et al. Giant anomalous Nernst effect and quantum-critical scaling in a ferromagnetic semimetal. Nat. Phys. 2018, 14, 1119. [Google Scholar] [CrossRef]
- Guin, S.N.; Manna, K.; Noky, J.; Watzman, S.J.; Fu, C.; Kumar, N.; Schnelle, W.; Shekhar, C.; Sun, Y.; Gooth, J.; et al. Anomalous Nernst effect beyond the magnetization scaling relation in the ferromagnetic Heusler compound Co2MnGa. NPG Asia Mater. 2019, 11, 16. [Google Scholar] [CrossRef]
- Guin, S.N.; Vir, P.; Zhang, Y.; Kumar, N.; Watzman, S.J.; Fu, C.; Liu, E.; Manna, K.; Schnelle, W.; Gooth, J.; et al. Zero-Field Nernst Effect in a Ferromagnetic Kagome-Lattice Weyl-Semimetal Co3Sn2S2. Adv. Mater. 2019, 2019, 1806622. [Google Scholar] [CrossRef] [PubMed]
- Hirokane, Y.; Tomioka, Y.; Imai, Y.; Maeda, A.; Onose, Y. Longitudinal and transverse thermoelectric transport in MnSi. Phys. Rev. B 2016, 93. [Google Scholar] [CrossRef]
- Miyasato, T.; Abe, N.; Fujii, T.; Asamitsu, A.; Onoda, S.; Onose, Y.; Nagaosa, N.; Tokura, Y. Crossover behavior of the anomalous hall effect and anomalous nernst effect in itinerant ferromagnets. Phys. Rev. Lett. 2007, 99. [Google Scholar] [CrossRef] [PubMed]
- Ikhlas, M.; Tomita, T.; Koretsune, T.; Suzuki, M.T.; Nishio-Hamane, D.; Arita, R.; Otani, Y.; Nakatsuji, S. Large anomalous Nernst effect at room temperature in a chiral antiferromagnet. Nat. Phys. 2017, 13, 1085. [Google Scholar] [CrossRef]
- Li, X.; Xu, L.; Ding, L.; Wang, J.; Shen, M.; Lu, X.; Zhu, Z.; Behnia, K. Anomalous Nernst and Righi-Leduc Effects in Mn3Sn: Berry Curvature and Entropy Flow. Phys. Rev. Lett. 2017, 119. [Google Scholar] [CrossRef] [PubMed]
- Hanasaki, N.; Sano, K.; Onose, Y.; Ohtsuka, T.; Iguchi, S.; Kezsmarki, I.; Miyasaka, S.; Onoda, S.; Nagaosa, N.; Tokura, Y. Anomalous nernst effects in pyrochlore molybdates with spin chirality. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef] [PubMed]
- Pu, Y.; Chiba, D.; Matsukura, F.; Ohno, H.; Shi, J. Mott relation for anomalous Hall and Nernst effects in Ga1-xMnxAs ferromagnetic semiconductors. Phys. Rev. Lett. 2008, 101. [Google Scholar] [CrossRef] [PubMed]
- Ramos, R.; Aguirre, M.H.; Anadon, A.; Blasco, J.; Lucas, I.; Uchida, K.; Algarabel, P.A.; Morellon, L.; Saitoh, E.; Ibarra, M.R. Anomalous Nernst effect of Fe3O4 single crystal. Phys. Rev. B 2014, 90. [Google Scholar] [CrossRef]
- Weischenberg, J.; Freimuth, F.; Bluegel, S.; Mokrousov, Y. Scattering-independent anomalous Nernst effect in ferromagnets. Phys. Rev. B 2013, 87. [Google Scholar] [CrossRef]
- Noky, J.; Gooth, J.; Felser, C.; Sun, Y. Characterization of topological band structures away from the Fermi level by the anomalous Nernst effect. Phys. Rev. B 2018, 98, 241106. [Google Scholar] [CrossRef]
- D’yakonov, M.; Perel, V. Possibility of orienting electron spins with current. Sov. J. Exp. Theor. Phys. Lett. 1971, 13, 467. [Google Scholar]
- Hirsch, J. Spin hall effect. Phys. Rev. Lett. 1999, 83, 1834. [Google Scholar] [CrossRef]
- Kato, Y.K.; Myers, R.C.; Gossard, A.C.; Awschalom, D.D. Observation of the spin Hall effect in semiconductors. Science 2004, 306, 1910–1913. [Google Scholar] [CrossRef] [PubMed]
- Sinova, J.; Valenzuela, S.O.; Wunderlich, J.; Back, C.; Jungwirth, T. Spin hall effects. Rev. Mod. Phys. 2015, 87, 1213. [Google Scholar] [CrossRef]
- Murakami, S.; Nagaosa, N.; Zhang, S.C. Dissipationless Quantum Spin Current at Room Temperature. Science 2003, 301, 1348. [Google Scholar] [CrossRef] [PubMed]
- Sinova, J.; Culcer, D.; Niu, Q.; Sinitsyn, N.; Jungwirth, T.; MacDonald, A.H. Universal intrinsic spin Hall effect. Phys. Rev. Lett. 2004, 92, 126603. [Google Scholar] [CrossRef] [PubMed]
- Bernevig, B.A.; Zhang, S.C. Intrinsic Spin Hall Effect in the Two-Dimensional Hole Gas. Phys. Rev. Lett. 2005, 95, 016801. [Google Scholar] [CrossRef] [PubMed]
- Wunderlich, J.; Kaestner, B.; Sinova, J.; Jungwirth, T. Experimental Observation of the Spin-Hall Effect in a Two-Dimensional Spin-Orbit Coupled Semiconductor System. Phy. Rev. Lett. 2005, 94, 047204. [Google Scholar] [CrossRef] [PubMed]
- Day, C. Two Groups Observe the Spin Hall Effect in Semiconductors. Phys. Today 2005, 58, 17. [Google Scholar] [CrossRef]
- Liu, L.; Pai, C.F.; Li, Y.; Tseng, H.W.; Ralph, D.C.; Buhrman, R.A. Spin-Torque Switching with the Giant Spin Hall Effect of Tantalum. Science 2012, 336, 555–558. [Google Scholar] [CrossRef] [PubMed]
- Pai, C.F.; Liu, L.; Li, Y.; Tseng, H.W.; Ralph, D.C.; Buhrman, R.A. Spin transfer torque devices utilizing the giant spin Hall effect of tungsten. Appl. Phys. Lett. 2012, 101. [Google Scholar] [CrossRef]
- Liu, C.; Lee, Y.; Kondo, T.; Mun, E.D.; Caudle, M.; Harmon, B.N.; Bud’ko, S.L.; Canfield, P.C.; Kaminski, A. Metallic surface electronic state in half-Heusler compounds RPtBi (R = Lu, Dy, Gd). Phys. Rev. B 2011, 83, 205133. [Google Scholar] [CrossRef]
- Mellnik, A.; Lee, J.; Richardella, A.; Grab, J.; Mintun, P.; Fischer, M.H.; Vaezi, A.; Manchon, A.; Kim, E.A.; Samarth, N.; et al. Spin-transfer torque generated by a topological insulator. Nature 2014, 511, 449. [Google Scholar] [CrossRef] [PubMed]
- Mahendra, D.; Grassi, R.; Chen, J.Y.; Jamali, M.; Hickey, D.R.; Zhang, D.; Zhao, Z.; Li, H.; Quarterman, P.; Lv, Y.; et al. Room-temperature high spin orbit torque due to quantum confinement in sputtered BixSe(1-x) films. Nat. Mater. 2018, 17, 800. [Google Scholar]
- Khang, N.H.D.; Ueda, Y.; Hai, P.N. A conductive topological insulator with large spin Hall effect for ultralow power spin–orbit torque switching. Nat. Mater. 2018, 17, 808–813. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, T.; Kontani, H.; Naito, M.; Naito, T.; Hirashima, D.S.; Yamada, K.; Inoue, J. Intrinsic spin Hall effect and orbital Hall effect in 4d and 5d transition metals. Phys. Rev. B 2008, 77, 165117. [Google Scholar] [CrossRef]
- Hoffmann, A. Advances in Magnetics: Spin Hall Effects in Metals. IEEE Trans. Magn. 2013, 49, 5172. [Google Scholar] [CrossRef]
- Kimura, T.; Otani, Y.; Sato, T.; Takahashi, S.; Maekawa, S. Room-Temperature Reversible Spin Hall Effect. Phys. Rev. Lett. 2007, 98, 156601. [Google Scholar] [CrossRef] [PubMed]
- Saitoh, E.; Ueda, M.; Miyajima, H.; Tatara, G. Conversion of spin current into charge current at room temperature: Inverse spin-Hall effect. Appl. Phys. Lett. 2006, 88, 182509. [Google Scholar] [CrossRef]
- Fan, Y.; Upadhyaya, P.; Kou, X.; Lang, M.; Takei, S.; Wang, Z.; Tang, J.; He, L.; Chang, L.T.; Montazeri, M.; et al. Magnetization switching through giant spin–orbit torque in a magnetically doped topological insulator heterostructure. Nat. Mater. 2014, 13, 699. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Xu, Q.; Koepernik, K.; Zelezny, J.; Jungwirth, T.; Felser, C.; van den Brink, J.; Sun, Y.S. Spin-orbitronic materials with record spin-charge conversion from high-throughput ab initio calculations. arXiv 2019, arXiv:1909.09605. [Google Scholar]
- Meyer, S.; Chen, Y.T.; Wimmer, S.; Althammer, M.; Wimmer, T.; Schlitz, R.; Geprags, S.; Huebl, H.; Ködderitzsch, D.; Ebert, H.; et al. Observation of the spin Nernst effect. Nat. Mater. 2017, 16, 977. [Google Scholar] [CrossRef] [PubMed]
- Sheng, P.; Sakuraba, Y.; Lau, Y.C.; Takahashi, S.; Mitani, S.; Hayashi, M. The spin Nernst effect in tungsten. Sci. Adv. 2017, 3, e1701503. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.J.; Jeon, C.Y.; Choi, J.G.; Lee, J.W.; Surabhi, S.; Jeong, J.R.; Lee, K.J.; Park, B.G. Observation of transverse spin Nernst magnetoresistance induced by thermal spin current in ferromagnet/non-magnet bilayers. Nat. Commun. 2017, 8, 1400. [Google Scholar] [CrossRef] [PubMed]
- Manchon, A.; Zhang, S. Theory of spin torque due to spin-orbit coupling. Phys. Rev. B 2009, 79, 094422. [Google Scholar] [CrossRef]
- Garate, I.; MacDonald, A.H. Influence of a transport current on magnetic anisotropy in gyrotropic ferromagnets. Phys. Rev. B 2009, 80, 134403. [Google Scholar] [CrossRef]
- Chernyshov, A.; Overby, M.; Liu, X.; Furdyna, J.K.; Lyanda-Geller, Y.; Rokhinson, L.P. Evidence for reversible control of magnetization in a ferromagnetic material by means of spin orbit magnetic field. Nat. Phys. 2009, 5, 656. [Google Scholar] [CrossRef]
- Kurebayashi, H.; Sinova, J.; Fang, D.; Irvine, A.; Skinner, T.; Wunderlich, J.; Novák, V.; Campion, R.; Gallagher, B.; Vehstedt, E.; et al. An antidamping spin orbit torque originating from the Berry curvature. Nat. Nanotechnol. 2014, 9, 211. [Google Scholar] [CrossRef] [PubMed]
- Miron, I.M.; Gaudin, G.; Auffret, S.; Rodmacq, B.; Schuhl, A.; Pizzini, S.; Vogel, J.; Gambardella, P. Current-driven spin torque induced by the Rashba effect in a ferromagnetic metal layer. Nat. Mater. 2010, 9, 230. [Google Scholar] [CrossRef] [PubMed]
- Miron, I.M.; Garello, K.; Gaudin, G.; Zermatten, P.J.; Costache, M.V.; Auffret, S.; Bandiera, S.; Rodmacq, B.; Schuhl, A.; Gambardella, P. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 2011, 476, 189. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Lee, O.; Gudmundsen, T.; Ralph, D.; Buhrman, R. Current-induced switching of perpendicularly magnetized magnetic layers using spin torque from the spin Hall effect. Phys. Rev. Lett. 2012, 109, 096602. [Google Scholar] [CrossRef] [PubMed]
- Pi, U.H.; Kim, K.W.; Bae, J.Y.; Lee, S.C.; Cho, Y.J.; Kim, K.S.; Seo, S. Tilting of the spin orientation induced by Rashba effect in ferromagnetic metal layer. Appl. Phys. Lett. 2010, 97. [Google Scholar] [CrossRef]
- Kim, J.; Sinha, J.; Hayashi, M.; Yamanouchi, M.; Fukami, S.; Suzuki, T.; Mitani, S.; Ohno, H. Layer thickness dependence of the current-induced effective field vector in Ta vertical bar CoFeB vertical bar MgO. Nat. Mater. 2013, 12, 240–245. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, T.; Fukami, S.; Ishiwata, N.; Yamanouchi, M.; Ikeda, S.; Kasai, N.; Ohno, H. Current-induced effective field in perpendicularly magnetized Ta/CoFeB/MgO wire. Appl. Phys. Lett. 2011, 98. [Google Scholar] [CrossRef]
- Gomonay, E.V.; Loktev, V.M. Spintronics of antiferromagnetic systems. Low Temp. Phys. 2014, 40, 17–35. [Google Scholar] [CrossRef]
- MacDonald, A.H.; Tsoi, M. Antiferromagnetic metal spintronics. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 3098–3114. [Google Scholar] [CrossRef] [PubMed]
- Jungwirth, T.; Marti, X.; Wadley, P.; Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotechnol. 2016, 11, 231–241. [Google Scholar] [CrossRef] [PubMed]
- Zelezny, J.; Gao, H.; Vyborny, K.; Zemen, J.; Masek, J.; Manchon, A.; Wunderlich, J.; Sinova, J.; Jungwirth, T. Relativistic Neel-Order Fields Induced by Electrical Current in Antiferromagnets. Phys. Rev. Lett. 2014, 113. [Google Scholar] [CrossRef] [PubMed]
- Wadley, P.; Howells, B.; Zelezny, J.; Andrews, C.; Hills, V.; Campion, R.P.; Novak, V.; Olejnik, K.; Maccherozzi, F.; Dhesi, S.S.; et al. Electrical switching of an antiferromagnet. Science 2016, 351, 587–590. [Google Scholar] [CrossRef] [PubMed]
- Tang, P.; Zhou, Q.; Xu, G.; Zhang, S.C. Dirac fermions in an antiferromagnetic semimetal. Nat. Phys. 2016. [Google Scholar] [CrossRef]
- Smejkal, L.; Zelezny, J.; Sinova, J.; Jungwirth, T. Electric Control of Dirac Quasiparticles by Spin-Orbit Torque in an Antiferromagnet. Phys. Rev. Lett. 2017, 118. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noky, J.; Sun, Y. Linear Response in Topological Materials. Appl. Sci. 2019, 9, 4832. https://doi.org/10.3390/app9224832
Noky J, Sun Y. Linear Response in Topological Materials. Applied Sciences. 2019; 9(22):4832. https://doi.org/10.3390/app9224832
Chicago/Turabian StyleNoky, Jonathan, and Yan Sun. 2019. "Linear Response in Topological Materials" Applied Sciences 9, no. 22: 4832. https://doi.org/10.3390/app9224832
APA StyleNoky, J., & Sun, Y. (2019). Linear Response in Topological Materials. Applied Sciences, 9(22), 4832. https://doi.org/10.3390/app9224832



