A High-Accuracy Model Average Ensemble of Convolutional Neural Networks for Classification of Cloud Image Patches on Small Datasets
Abstract
1. Introduction
2. Methodology
2.1. CNN Model Design
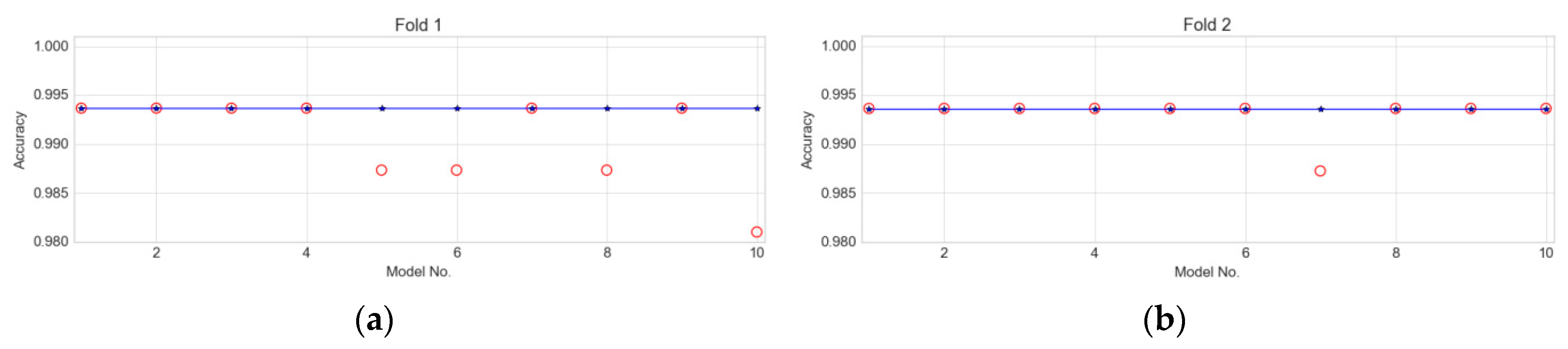
2.2. Model Average Ensemble of CNN
2.3. Model Regularization
2.3.1. L2 Weight Regularization
2.3.2. Data Augmentation
3. Experiments
3.1. SWIMCAT Dataset
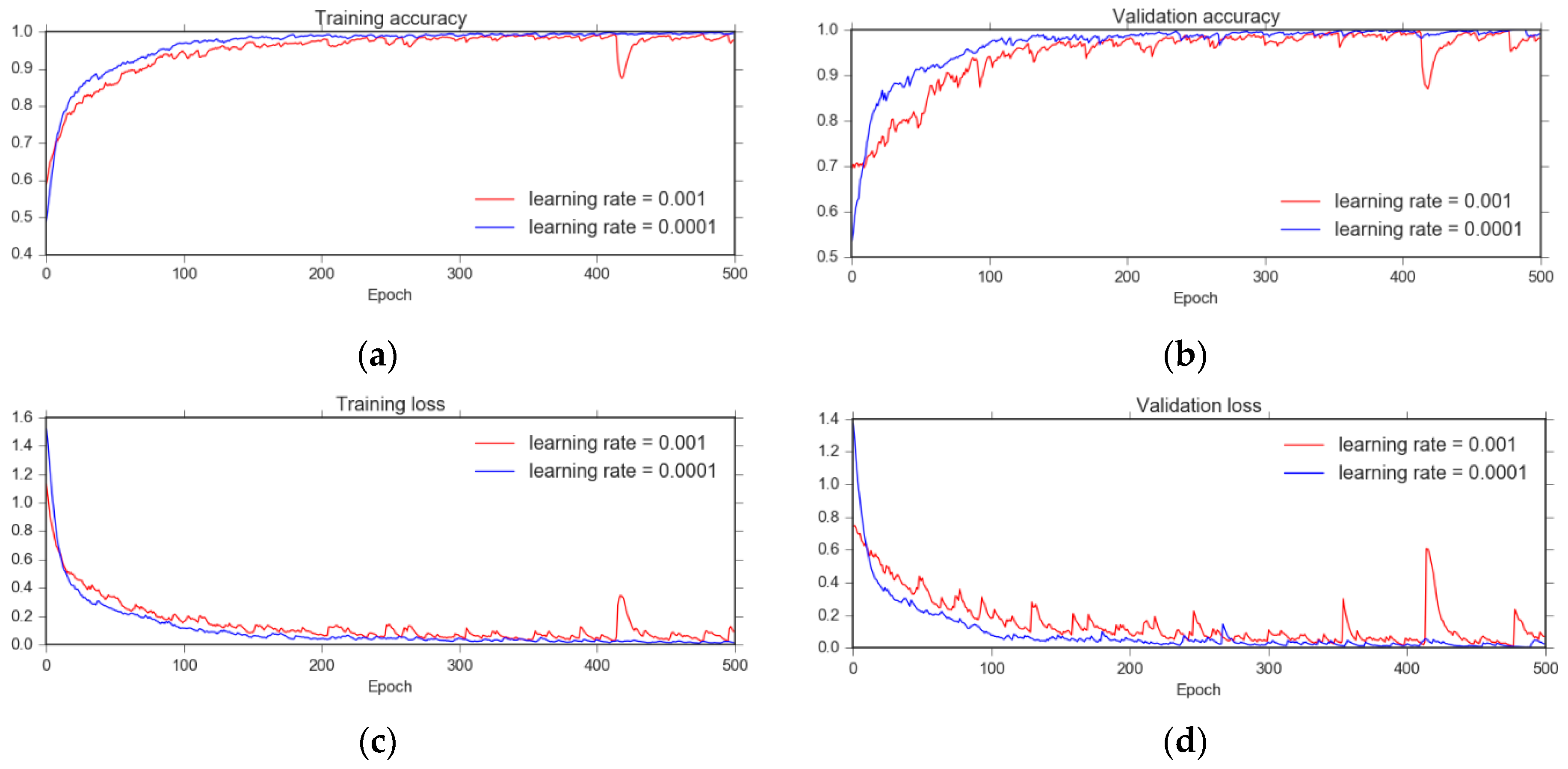
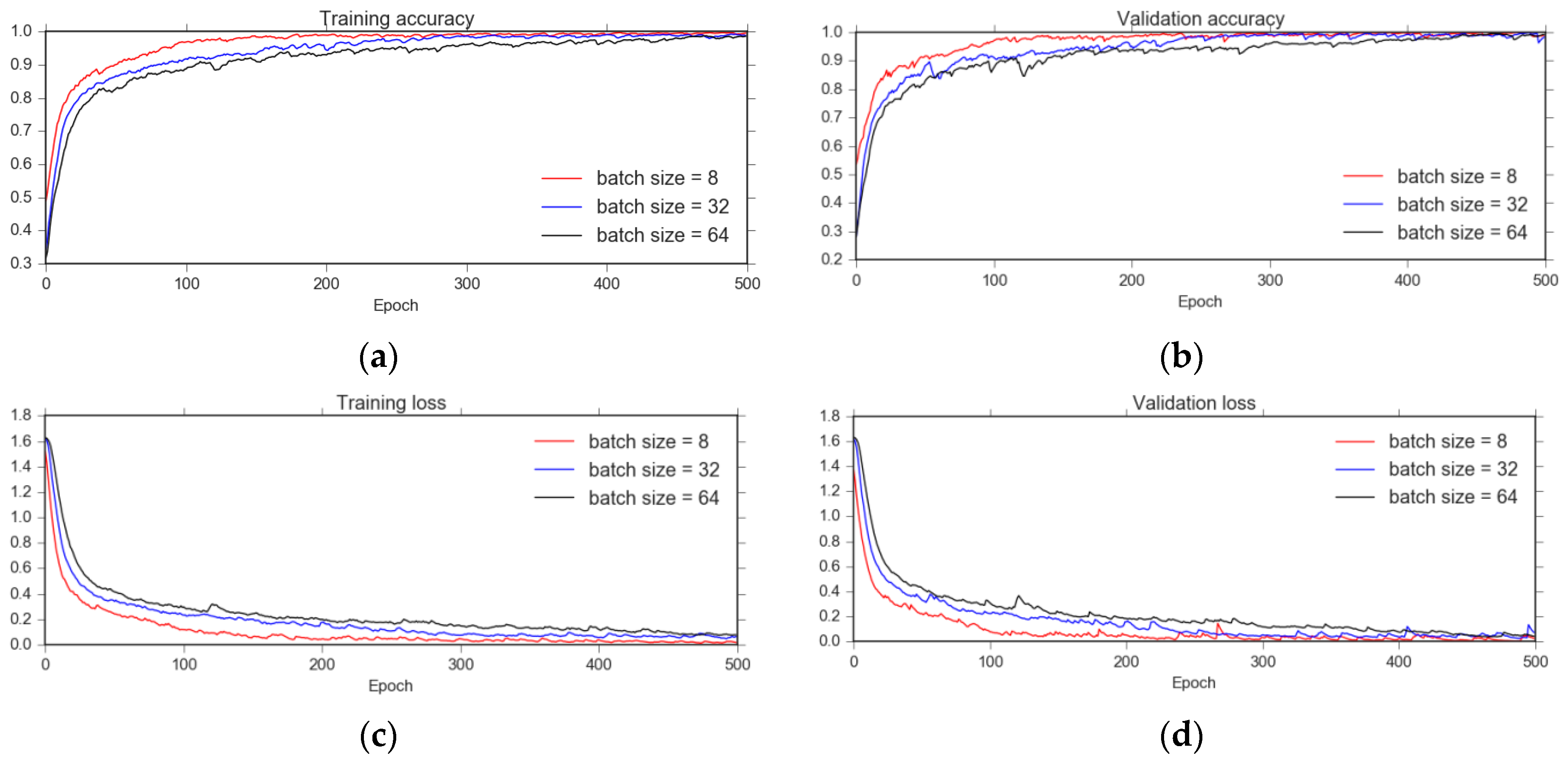
3.2. Experimental Configuration
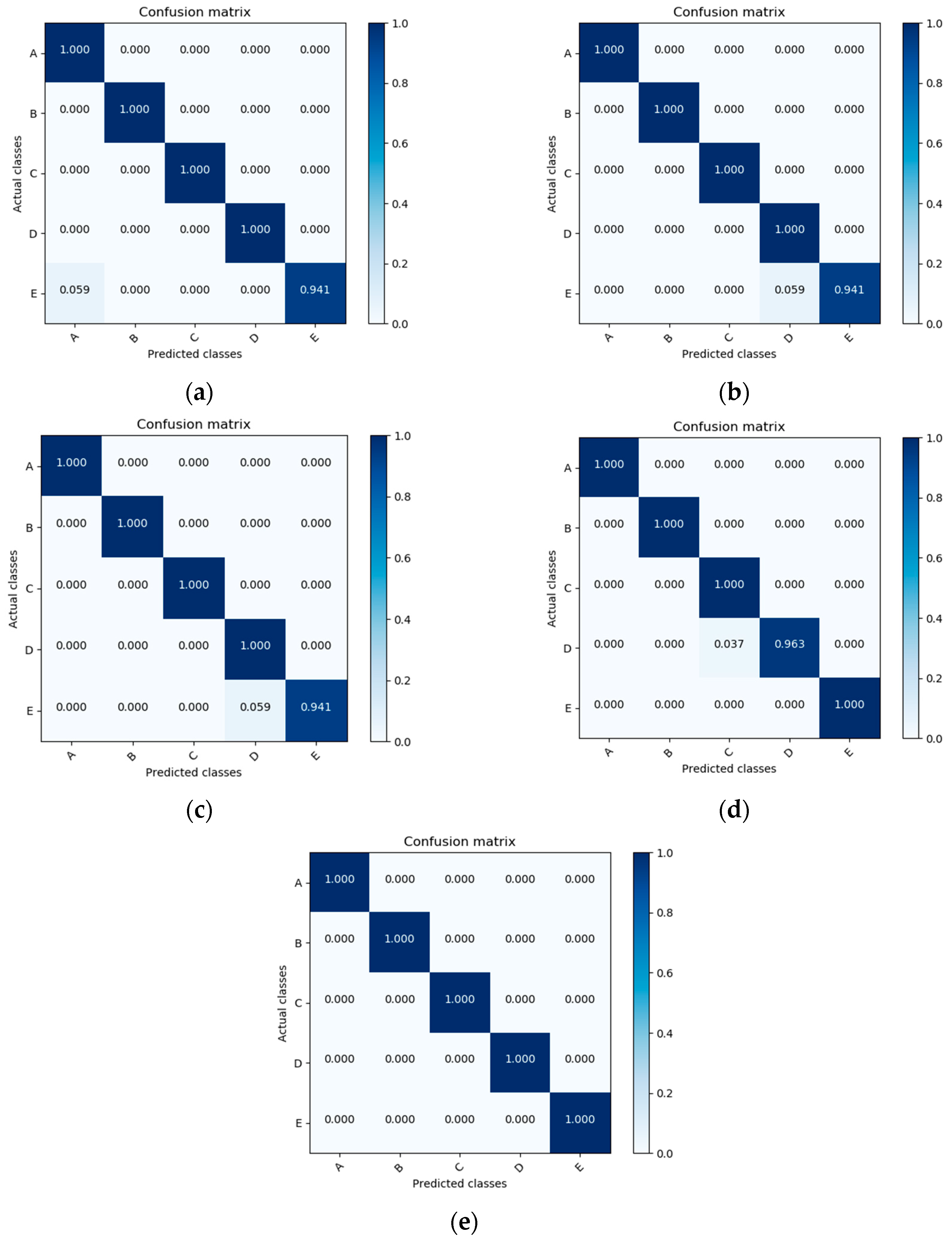
3.3. K-Fold Cross-Validation
3.4. Performance Metrics
3.5. Network Visualization
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Abbreviations | Meaning |
| Adam | Adaptive moment estimation |
| CNN | Convolutional neural networks |
| SVM | Support Vector Machine |
| SWIMCAT | Singapore Whole-sky Imaging CATegories |
| SPD | Symmetric Positive Define |
| WAHRSIS | Wide Angle High-Resolution Sky Imaging System |
References
- Naud, C.M.; Booth, J.F.; Del Genio, A. The relationship between boundary layer stability and cloud cover in the post-cold frontal region. J. Clim. 2016, 29, 8129–8149. [Google Scholar] [CrossRef] [PubMed]
- Cui, F.; Ju, R.R.; Ding, Y.Y.; Ding, H.; Cheng, X. Prediction of regional global horizontal irradiance combining ground-based cloud observation and numerical weather prediction. Adv. Mater. Res. 2015, 1073, 388–394. [Google Scholar] [CrossRef]
- Liu, Y.; Key, J.R.; Wang, X. The influence of changes in cloud cover on recent surface temperature trends in the arctic. J. Clim. 2008, 21, 705–715. [Google Scholar] [CrossRef]
- Hartmann, D.L.; Ockert-Bell, M.E.; Michelsen, M.L. The effect of cloud type on earth’s energy balance: Global analysis. J. Clim. 1992, 5, 1281–1304. [Google Scholar] [CrossRef]
- Yuan, F.; Lee, Y.H.; Meng, Y.S. Comparison of radio-sounding profiles for cloud attenuation analysis in the tropical region. In Proceedings of the IEEE Antennas and Propagation Society International Symposium (APSURSI), Memphis, TN, USA, 6–11 July 2014. [Google Scholar] [CrossRef]
- Pagès, D.; Calbò, J.; Long, C.; González, J.; Badosa, J. Comparison of several ground-based cloud detection techniques. In Proceedings of the European Geophysical Society XXVII General Assembly, Nice, France, 21–26 April 2002. [Google Scholar]
- Hu, J.; Chen, Z.; Yang, M.; Zhang, R.; Cui, Y. A multiscale fusion convolutional neural network for Plant Leaf Recognition. IEEE Signal Process. Lett. 2018, 25, 853–857. [Google Scholar] [CrossRef]
- Wu, X.; Zhan, C.; Lai, Y.K.; Cheng, M.M.; Yang, J. IP102: A large-scale benchmark dataset for insect pest recognition. In Proceeding of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Singh, M.; Glennen, M. Automated ground-based cloud recognition. Pattern Anal. Appl. 2005, 8, 258–271. [Google Scholar] [CrossRef]
- Calbó, J.; Sabburg, J. Feature extraction from whole-sky ground-based images for cloud-type recognition. J. Atmos. Ocean. Technol. 2008, 25, 3–14. [Google Scholar] [CrossRef]
- Heinle, A.; Macke, A.; Srivastav, A. Automatic cloud classification of whole sky images. Atmos. Meas. Tech. 2010, 3, 557–567. [Google Scholar] [CrossRef]
- Liu, S.; Wang, C.; Xiao, B.; Zhang, Z.; Shao, Y. Illumination-invariant completed LTP descriptor for cloud classification. In Proceedings of the 5th International Congress on Image and Signal Processing, Chongqing, China, 16–18 October 2012. [Google Scholar] [CrossRef]
- Liu, L.; Sun, X.J.; Chen, F.; Zhao, S.J.; Gao, T.C. Cloud classification based on structure features on infrared images. J. Atmos. Ocean. Technol. 2011, 28, 410–497. [Google Scholar] [CrossRef]
- Liu, S.; Wang, C.; Xiao, B.; Zhang, Z.; Shao, Y. Salient local binary pattern for ground-based cloud classification. Acta Meteorol. Sin. 2013, 27, 211–220. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Z.; Mei, X. Ground-based cloud classification using weighted local binary patterns. J. Appl. Remote Sens. 2015, 9, 905062. [Google Scholar] [CrossRef]
- Dev, S.; Lee, Y.H.; Winkler, S. Categorization of cloud image patches using an improved texton-based approach. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015. [Google Scholar]
- Gan, J.R.; Lu, W.T.; Li, Q.Y.; Zhang, Z.; Yang, J.; Ma, Y.; Yao, W. Cloud type classification of total-sky images using duplex norm-bounded sparse coding. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3360–3372. [Google Scholar] [CrossRef]
- Luo, Q.X.; Meng, Y.; Liu, L.; Zhao, X.F.; Zhou, Z.M. Cloud classification of ground-based infrared images combining manifold and texture features. Atmos. Meas. Technol. 2018, 11, 5351–5361. [Google Scholar] [CrossRef]
- Luo, Q.X.; Zhou, Z.M.; Meng, Y.; Li, Q.; Li, M.Y. Ground-based cloud-type recognition using manifold kernel sparse coding and dictionary learning. Adv. Meteorol. 2018, 2018, 9684206. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, C.Z.; Wang, C.H.; Xiao, B.H. Ground-based cloud classification by learning stable local binary patterns. Atmos. Res. 2018, 207, 74–89. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the Neural Information Processing Systems Conference, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Ye, L.; Cao, Z.; Xiao, Y. Ground-based cloud image categorization using deep convolutional features. In Proceedings of the IEEE International Conference on Image Processing, Quèbec City, QC, Canada, 27–30 September 2015; pp. 4808–4812. [Google Scholar]
- Ye, L.; Cao, Z.; Xiao, Y.; Li, W. DeepCloud: Ground-Based Cloud Image Categorization Using Deep Convolutional Features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5729–5740. [Google Scholar] [CrossRef]
- Shi, C.; Wang, C.; Wang, Y.; Xiao, B. Deep convolutional activations-based features for ground-based classification. IEEE Geosci. Remote Sens. Lett. 2017, 14, 816–820. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, D.H.; Liu, S.; Xiao, B.H.; Cao, X.Z. Multi-view ground-based cloud recognition by transferring deep visual information. Appl. Sci. 2018, 8, 748. [Google Scholar] [CrossRef]
- Phung, V.H.; Rhee, E.J. A Deep Learning Approach for Classification of Cloud Image Patches on Small Datasets. J. Inf. Commun. Converg. Eng. 2018, 16, 173–178. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, P.; Zhang, F.; Song, Q. CloudNet: Ground-based cloud classification with deep convolutional neural network. Geophys. Res. Lett. 2018, 45, 8665–8672. [Google Scholar] [CrossRef]
- Fukushima, K. Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biol. Cybern. 1980, 36, 193–202. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- ImageNet Large Scale Visual Recognition Competition (ILSVRC). Available online: http://www.image-net.org/challenges/LSVRC/ (accessed on 10 October 2019).
- Deng, J.; Dong, W.; Socher, R.; Li, L.; Li, K.; Li, F.F. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR’09), Miami Beach, FL, USA, 20–25 June 2009. [Google Scholar]
- Hertel, L.; Barth, E.; Käster, T.; Martinetz, T. Deep convolutional neural networks as generic feature extractors, In Proceeding of the 2015 International Joint Conference on Neural Networks, Killarney, Ireland, 12–16 July 2015.
- CS231n Convolutional Neural Networks for Visual Recognition. Available online: http://cs231n.github.io/convolutional-networks/ (accessed on 10 October 2019).
- Srivastava, N.; Hinton, G.E.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Hansen, L.K.; Salamon, P. Neural Network Ensembles. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 993–1001. [Google Scholar] [CrossRef]
- Krogh, A.; Vedelsby, J. Neural network ensembles, cross validation, and active learning. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1995; pp. 231–238. [Google Scholar]
- Dev, S.; Savoy, F.M.; Lee, Y.H.; Winkler, S. WAHRSIS: A low-cost, high-resolution whole sky imager with ner-infrared capabilities. In Proceedings of the SPIE—The International Society for Optical Engineering, Baltimore, MD, USA, 5–9 May 2014; Volume 9071. [Google Scholar] [CrossRef]
- Keras. Available online: https://keras.io/ (accessed on 10 October 2019).
- Tensorflow. Available online: https://www.tensorflow.org/ (accessed on 10 October 2019).
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the ICLR, Vancouver Convention Center, Vancouver, BC, Canada, 7–9 May 2015; pp. 1–15. [Google Scholar]
- F1 Score. Available online: https://en.wikipedia.org/wiki/F1_score (accessed on 10 October 2019).
- Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Tallón-Ballesteros, A.J.; Riquelme, J.C. Data mining methods applied to a digital forensics task for supervised machine learning. In Computational Intelligence in Digital Forensics: Forensic Investigation and Applications, 1st ed.; Muda, A.K., Choo, Y.H., Abraham, A., Srihari, S.N., Eds.; Springer: Cham, Switzerland, 2014; Volume 555, pp. 413–428. [Google Scholar]
- Hastie, T.; Friedman, J.; Tibshirani, R. Ensemble Learning. In The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009; pp. 605–624. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
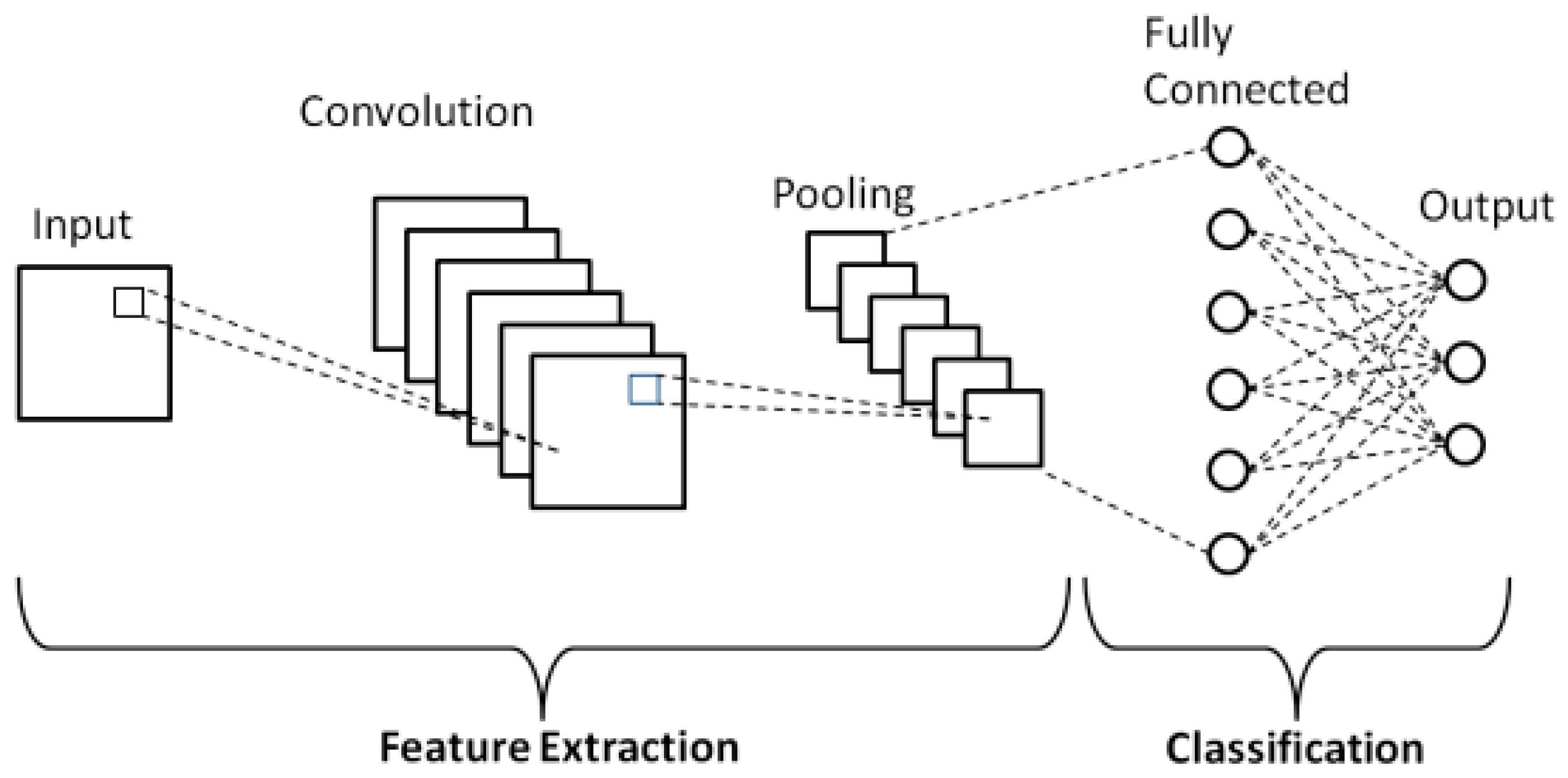
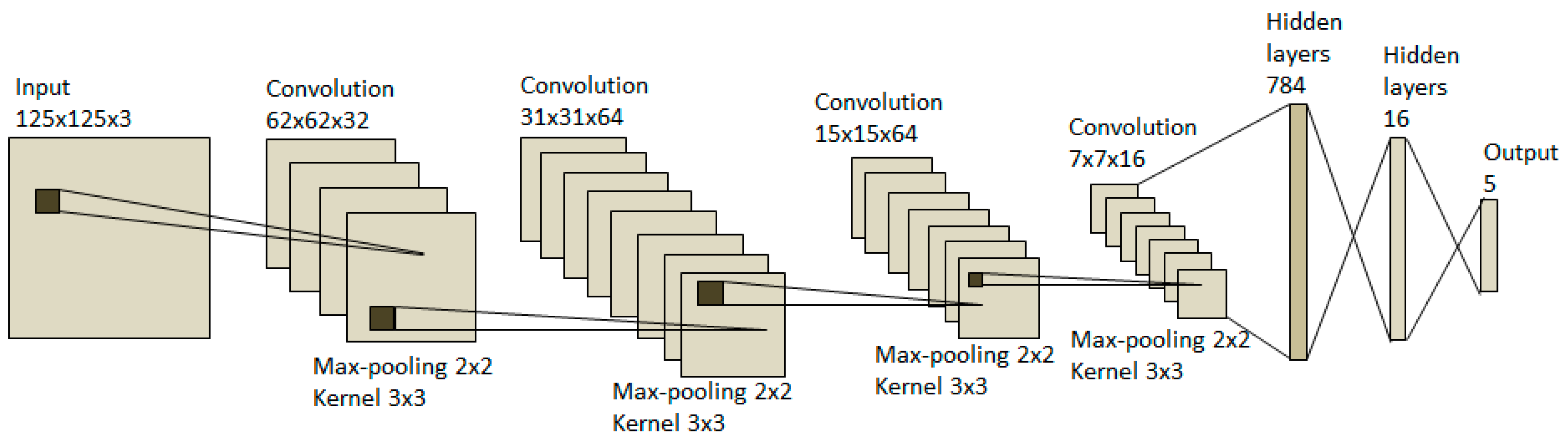
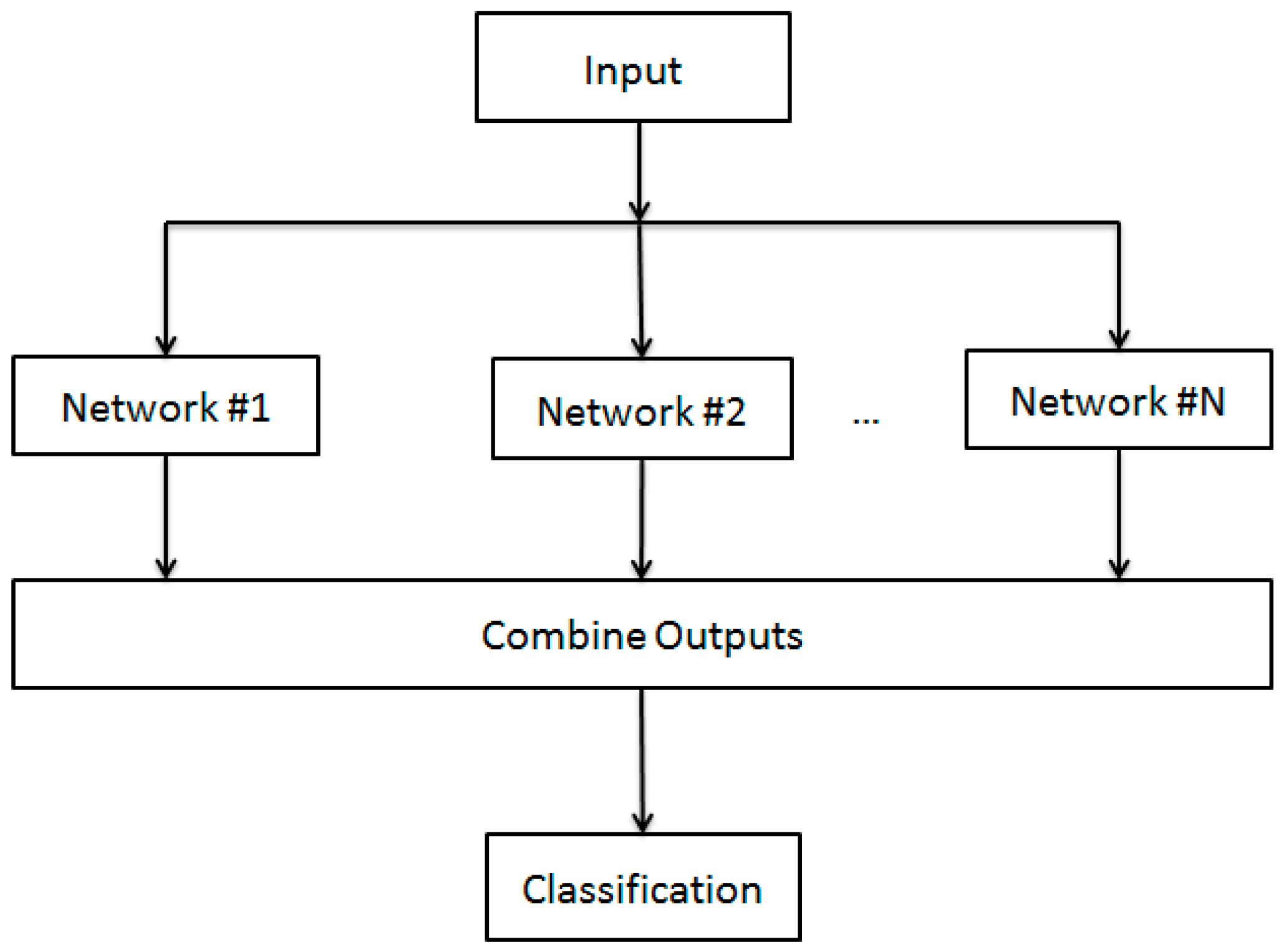



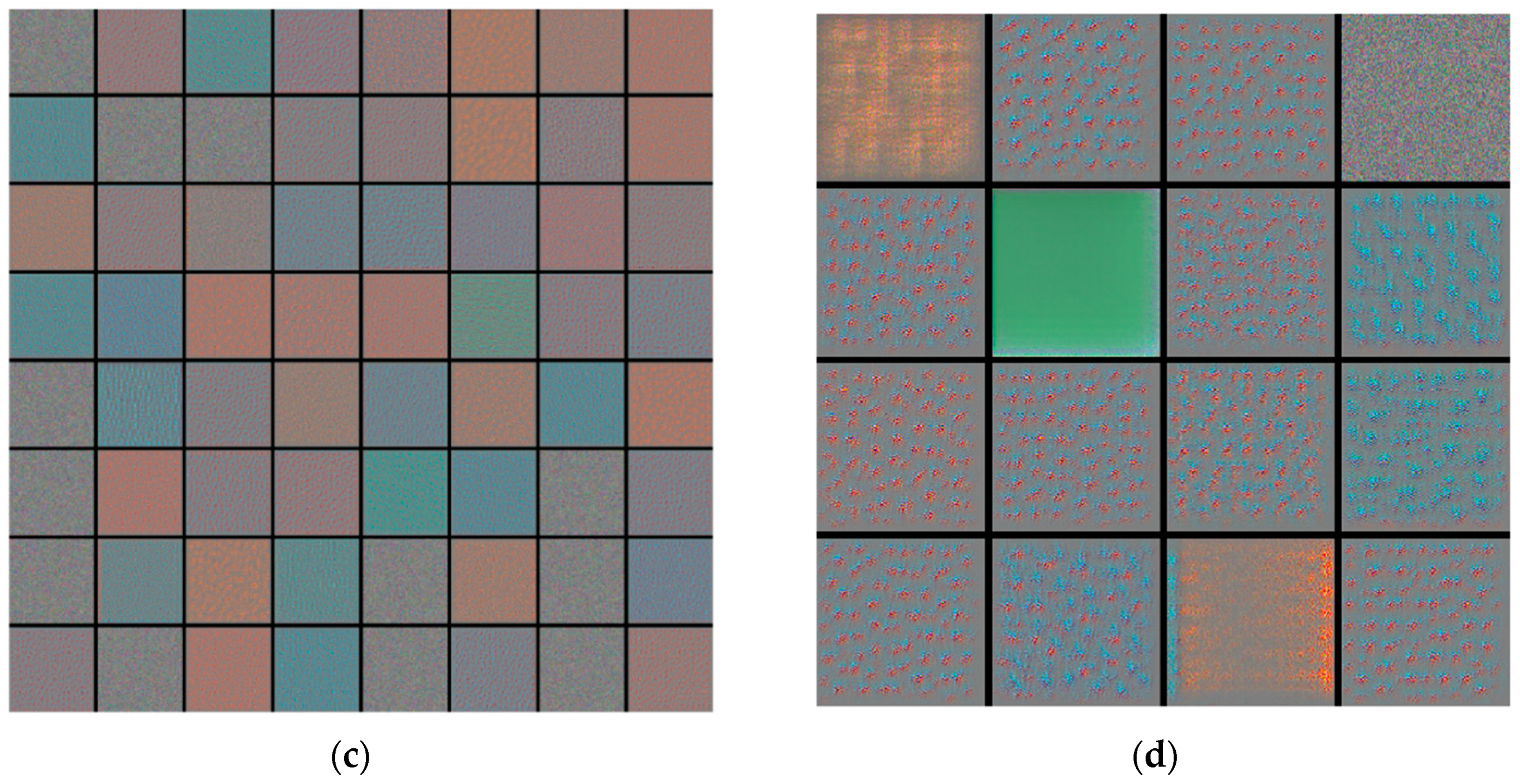
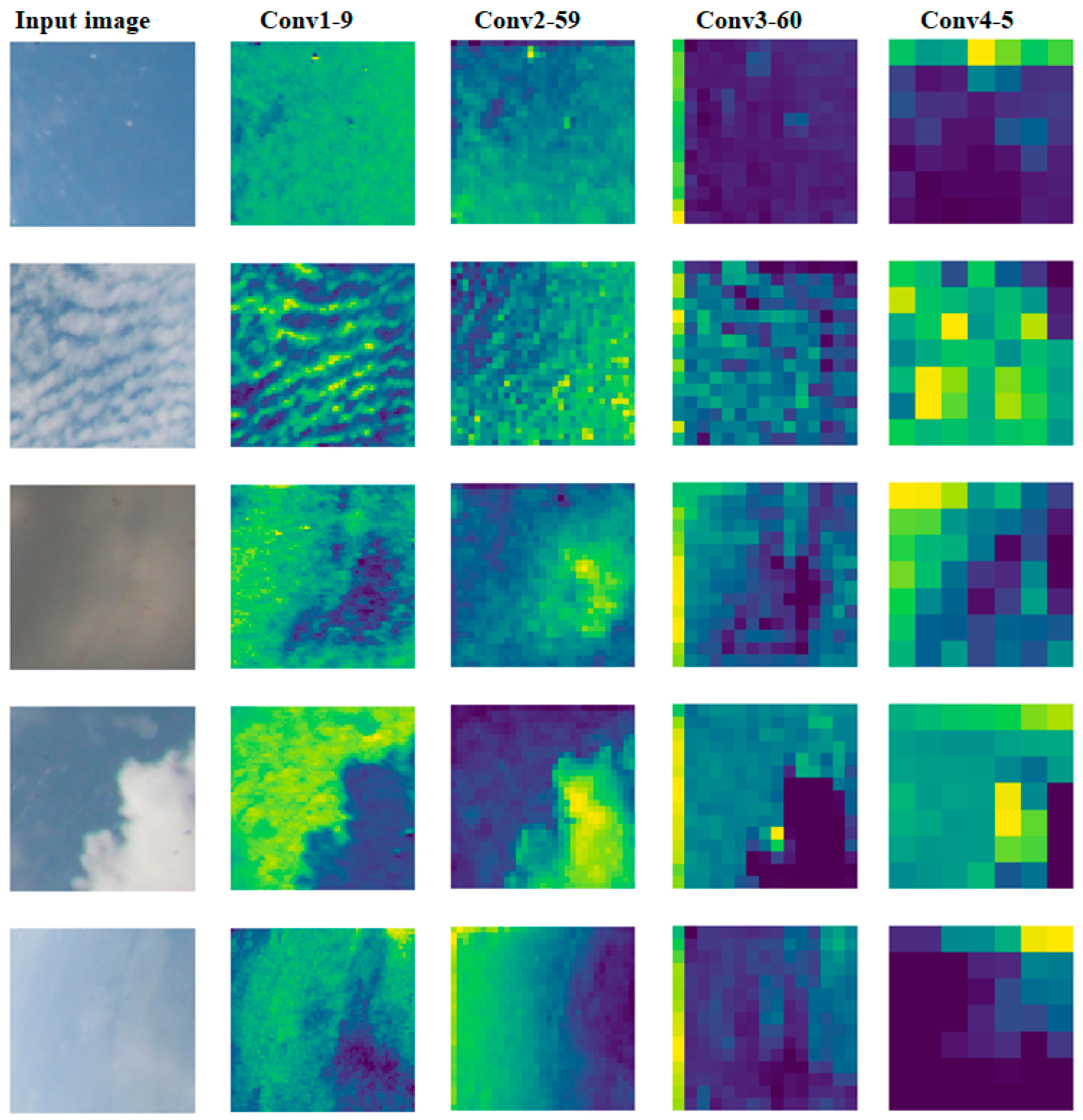

| No. | Layer | Output Size | Filter Size | Stride Size | Dropout |
|---|---|---|---|---|---|
| 1. | Input | 125 × 125 × 3 | - | - | - |
| 2. | Convolution 1 | 125 × 125 × 32 | 3 × 3 | - | - |
| 3. | Relu | 125 × 125 × 32 | - | - | - |
| 4. | Max pooling | 62 × 62 × 32 | - | 2 × 2 | - |
| 5. | Convolution 2 | 62 × 62 × 64 | 3 × 3 | - | - |
| 6. | Relu | 62 × 62 × 64 | - | - | - |
| 7. | Max pooling | 31 × 31 × 64 | - | 2 × 2 | - |
| 8. | Convolution 3 | 31 × 31 × 64 | 3 × 3 | - | - |
| 9. | Relu | 31 × 31 × 64 | - | - | - |
| 10. | Max pooling | 15 × 15 × 64 | - | 2 × 2 | - |
| 11. | Convolution 4 | 15 × 15 × 16 | 3 × 3 | - | - |
| 12. | Relu | 15 × 15 × 16 | - | - | - |
| 13. | Max pooling | 7 × 7 × 16 | - | 2 × 2 | - |
| 14. | Flatten | 1 × 1 × 784 | - | - | - |
| 15. | Fully connected | 1 × 1 × 784 | - | - | - |
| 16. | Relu | 1 × 1 × 784 | - | - | - |
| 17. | Dropout | 1 × 1 × 784 | - | - | 0.25 |
| 18. | Fully connected | 1 × 1 × 64 | - | - | - |
| 19. | Relu | 1 × 1 × 64 | - | - | - |
| 20. | Dropout | 1 × 1 × 64 | - | - | 0.5 |
| 21. | Fully connected | 1 × 1 × 5 | - | - | - |
| 22. | Softmax | 1 × 1 × 5 | - | - | - |
| No. | Augmentation | Parameter |
|---|---|---|
| 23. | Rotation | 40° |
| 24. | Width shift | 20% |
| 25. | Height shift | 20% |
| 26. | Shear | 20% |
| 27. | Zoom | 20% |
| 28. | Horizontal flip | Yes |
| 29. | Vertical flip | Yes |
| No. | Class | Type | Number of Image |
|---|---|---|---|
| 1. | A | Clear Sky | 224 |
| 2. | B | Patterned clouds | 89 |
| 3. | C | Thick dark clouds | 251 |
| 4. | D | Thick white clouds | 135 |
| 5. | E | Veil clouds | 85 |
| No. | Fold | Accuracy | F1 Score | Cohen’s Kappa |
|---|---|---|---|---|
| 1. | Fold 1 | 0.994 | 0.992 | 0.992 |
| 2. | Fold 2 | 0.994 | 0.990 | 0.992 |
| 3. | Fold 3 | 0.994 | 0.990 | 0.992 |
| 4. | Fold 4 | 0.994 | 0.994 | 0.992 |
| 5. | Fold 5 | 1.000 | 1.000 | 1.000 |
| 6. | Average | 0.995 | 0.993 | 0.993 |
| No. | Method | Accuracy | F1 Score | Cohen’s Kappa |
|---|---|---|---|---|
| 1. | Wang et al. [20] | 0.911 | 0.897 | 0.888 |
| 2. | Dev et al. [16] | 0.951 | 0.953 | 0.939 |
| 3. | Luo et al. [19] | 0.983 | 0.984 | 0.979 |
| 4. | Phung and Rhee [26] | 0.986 | 0.982 | 0.982 |
| 5. | Zhang et al. [27] | 0.986 | 0.987 | 0.983 |
| 6. | Shi et al. [24] | 0.987 | - | - |
| 7. | Proposed method | 0.995 | 0.993 | 0.993 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phung, V.H.; Rhee, E.J. A High-Accuracy Model Average Ensemble of Convolutional Neural Networks for Classification of Cloud Image Patches on Small Datasets. Appl. Sci. 2019, 9, 4500. https://doi.org/10.3390/app9214500
Phung VH, Rhee EJ. A High-Accuracy Model Average Ensemble of Convolutional Neural Networks for Classification of Cloud Image Patches on Small Datasets. Applied Sciences. 2019; 9(21):4500. https://doi.org/10.3390/app9214500
Chicago/Turabian StylePhung, Van Hiep, and Eun Joo Rhee. 2019. "A High-Accuracy Model Average Ensemble of Convolutional Neural Networks for Classification of Cloud Image Patches on Small Datasets" Applied Sciences 9, no. 21: 4500. https://doi.org/10.3390/app9214500
APA StylePhung, V. H., & Rhee, E. J. (2019). A High-Accuracy Model Average Ensemble of Convolutional Neural Networks for Classification of Cloud Image Patches on Small Datasets. Applied Sciences, 9(21), 4500. https://doi.org/10.3390/app9214500





