Comparison of CS-Based Channel Estimation for Millimeter Wave Massive MIMO Systems
Abstract
1. Introduction
- In this paper, with a unified massive MIMO framework, we compare the NMSE performance among three categories of algorithms, which is affected by the received SNR, the number of resolvable paths and pilot symbols, angular quantization error, hardware impairments and computational complexity. Through comprehensive comparison, the characteristics and application conditions of each algorithm are revealed and the factors that affect the estimated error and computational complexity are also presented.
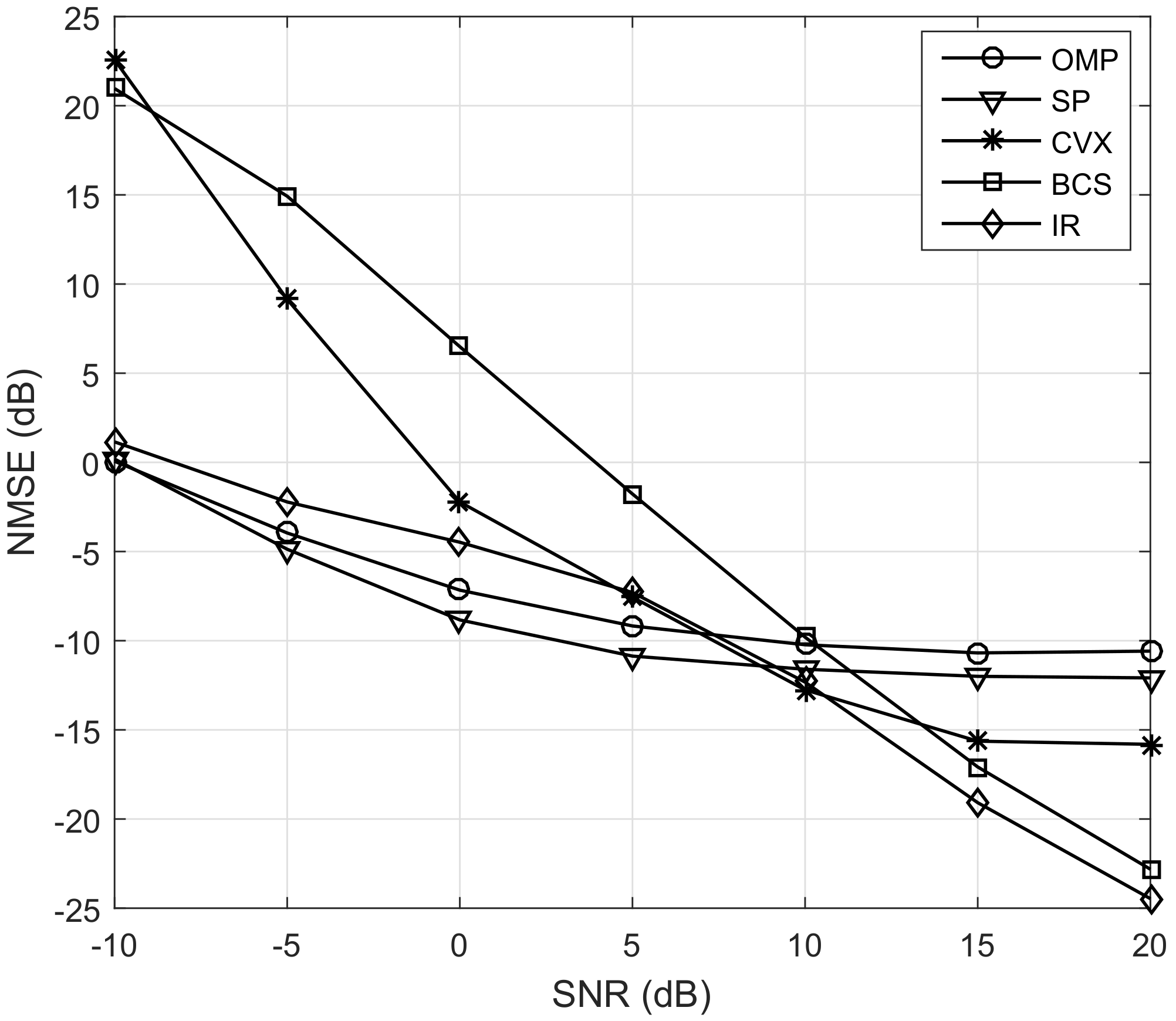
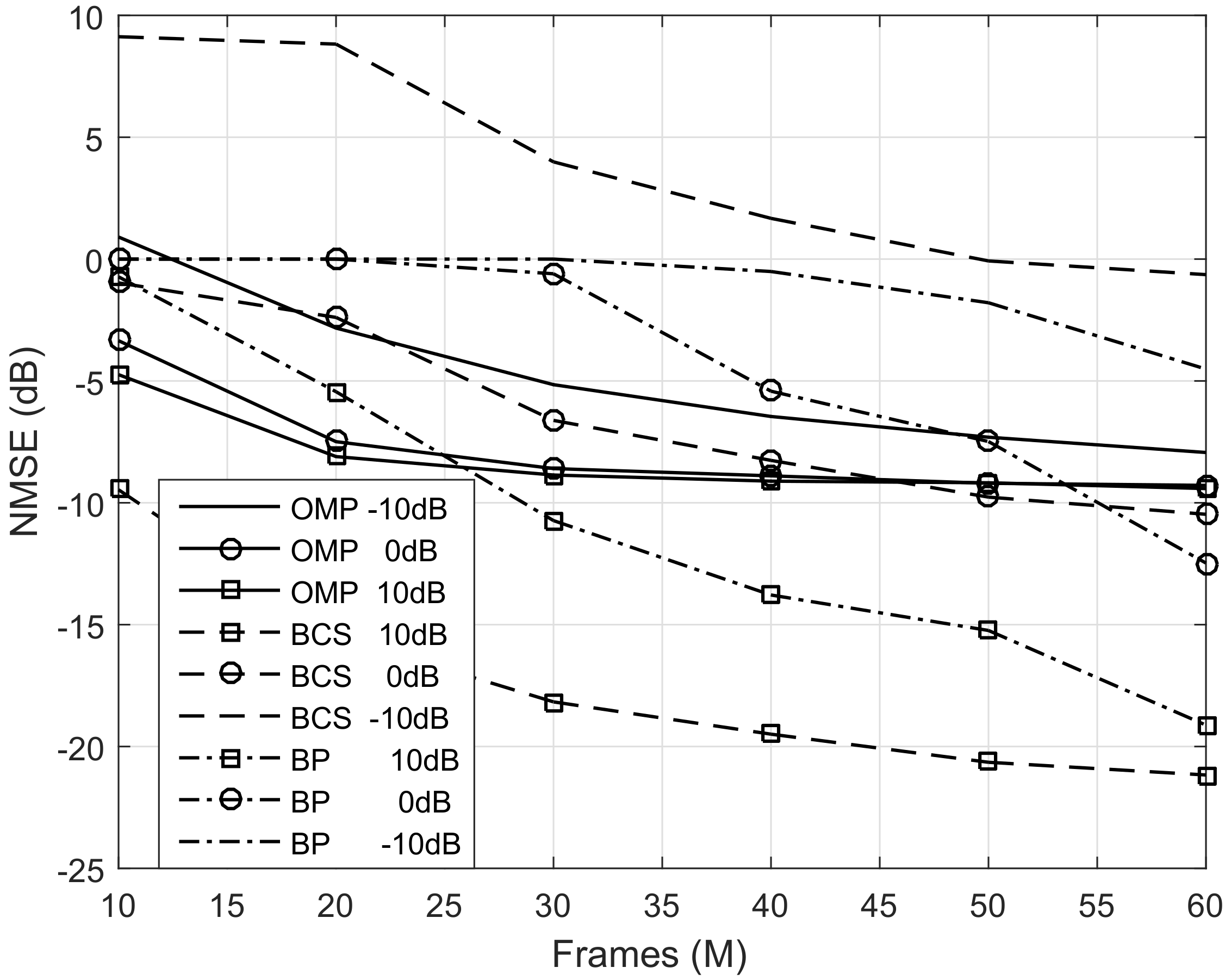
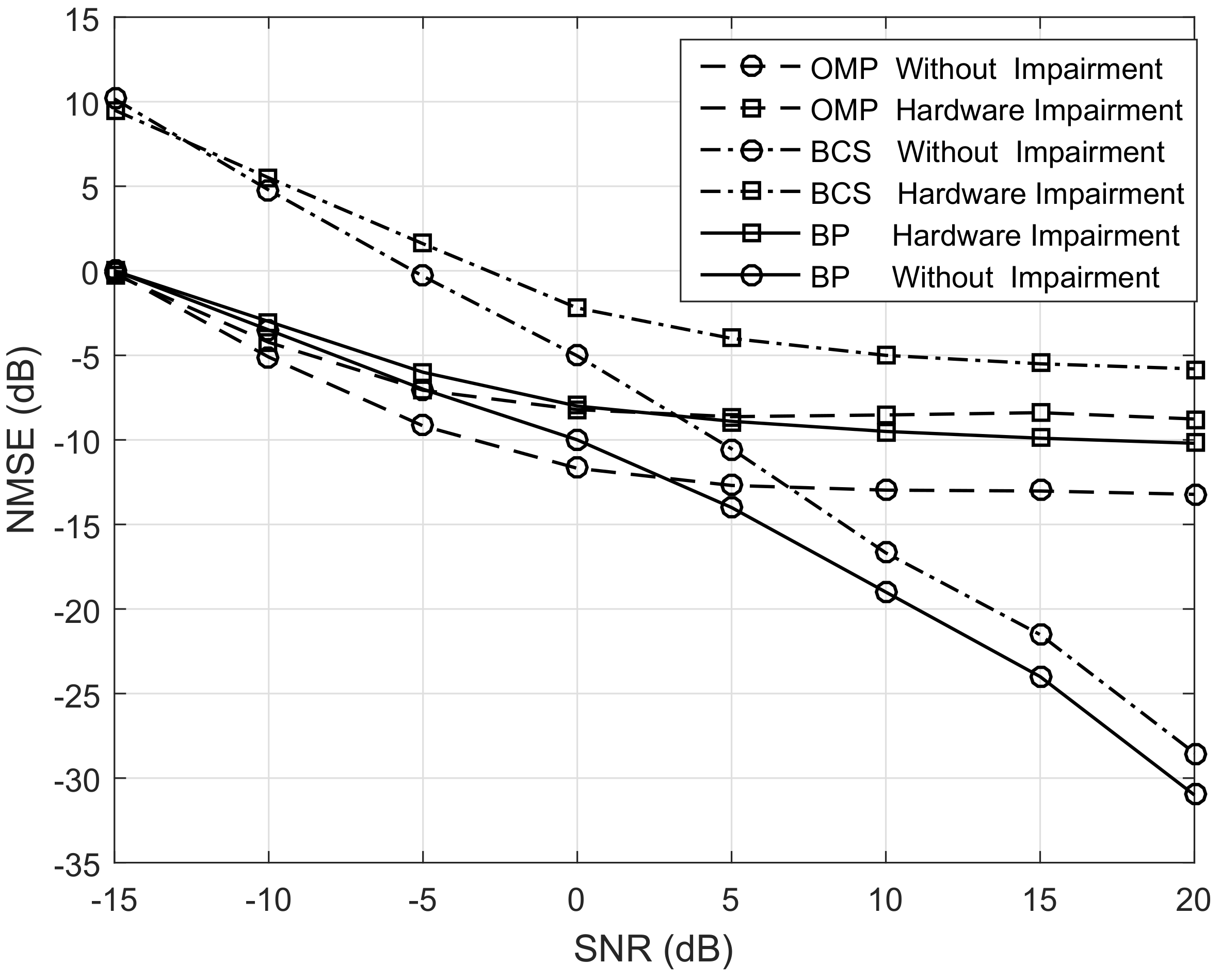
- Through theoretical analysis and simulation results, we show that convex relation algorithms achieve the best estimation accuracy at the high SNR range and it is mainly affected by the received SNR and transmitter’s hardware impairments. At the low SNR range, greedy iteration algorithms outperform others and the estimated accuracy is then limited by the angle quantization error. Furthermore, a tradeoff between the estimated error and complexity is achieved in Bayesian inference algorithms, although its estimated error is sensitive to the number of available pilot symbols.
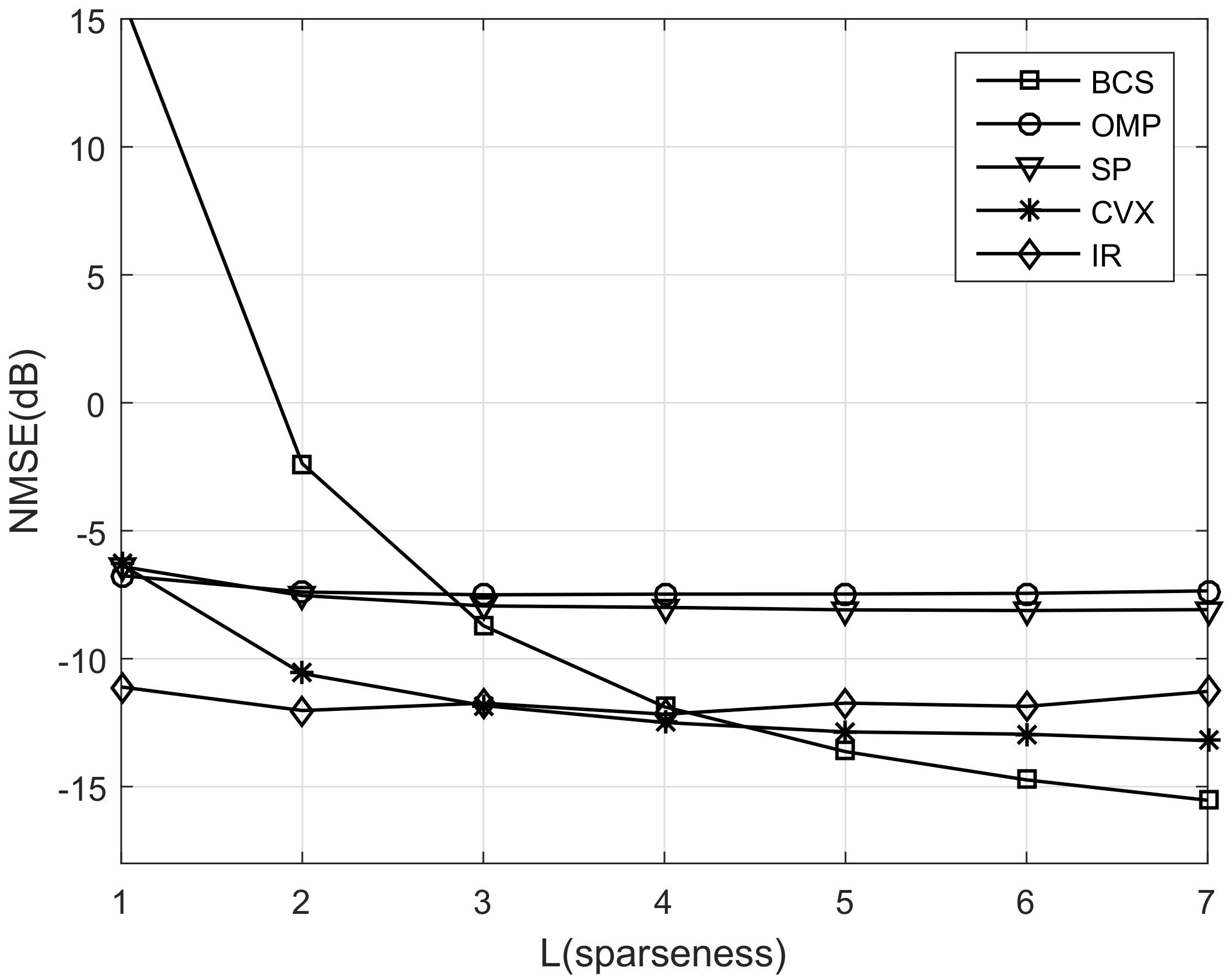
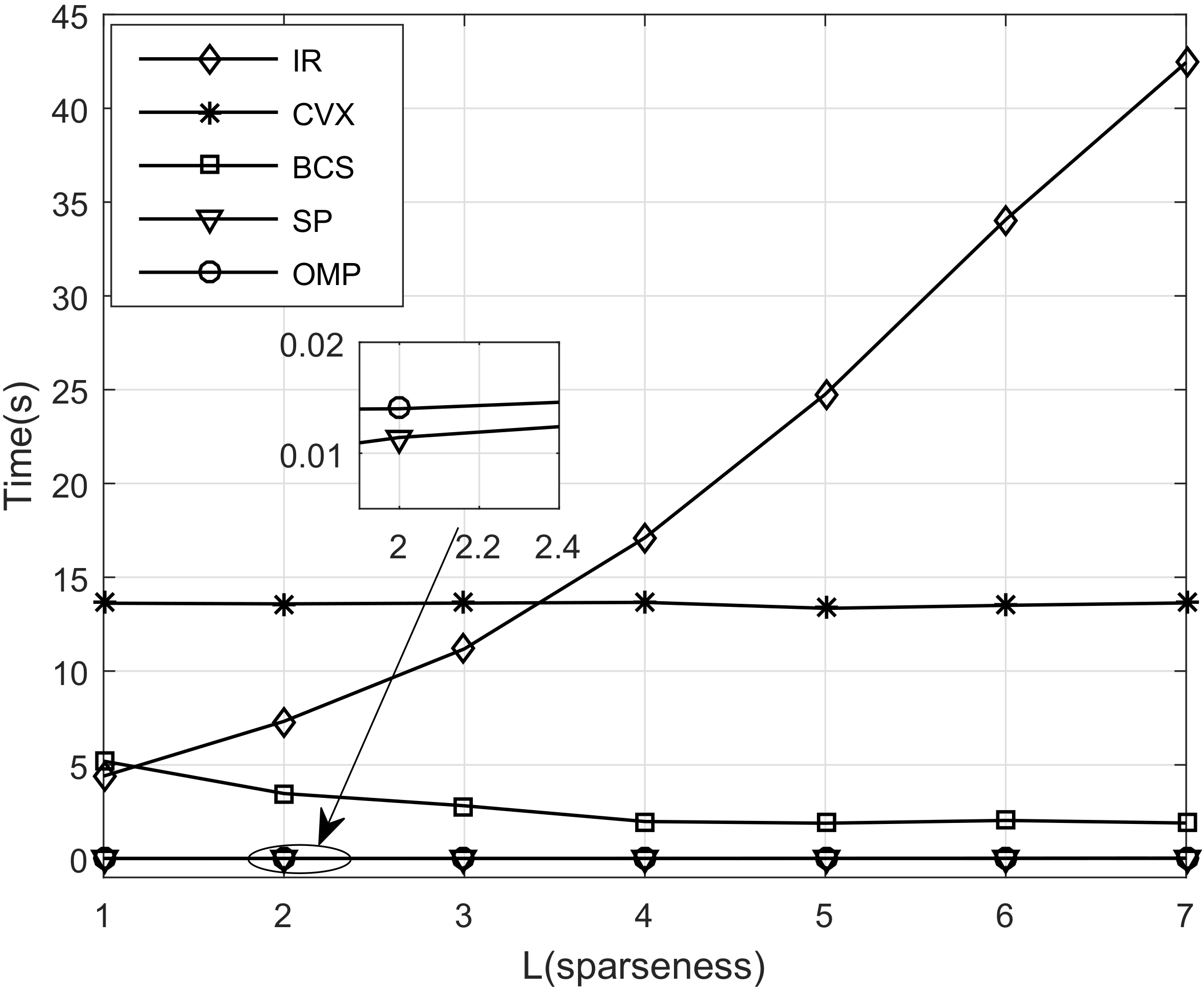
- We also analyze the overall computational complexities of three categories of algorithms and visually represent them by the running time. Through illustrating the runtime of different algorithms versus the sparseness, we show that the computational complexity in the convex relaxation algorithm is the highest, and it even squarely increases with the sparseness in the gradient descent-based convex algorithm, while that in greedy iteration algorithms is minimum and grows linearly with the sparseness. In contrast to them, the computational complexities of Bayesian inference algorithm decreases as the sparseness increases.
2. System Model
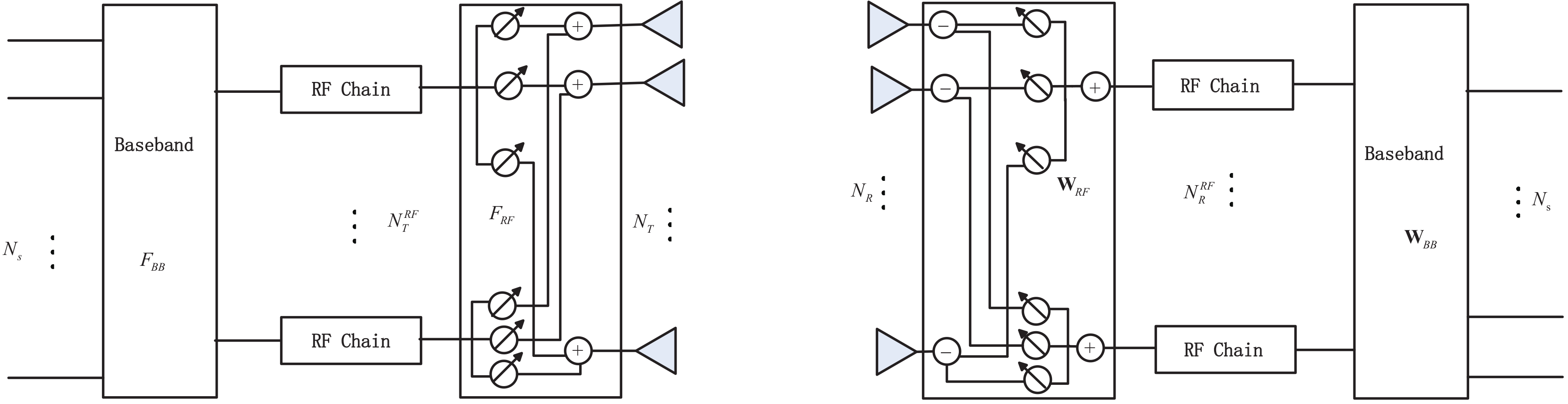
2.1. System Model
2.2. Channel Model
3. Formulation of the Channel Estimation Problem via Compressed Sensing
4. A Comparison of Sparse Signal Recovery Algorithms
4.1. Convex Relaxation Algorithms
4.2. Greedy Iterative Algorithms
4.3. Bayesian Inference Algorithms
5. Simulation Results
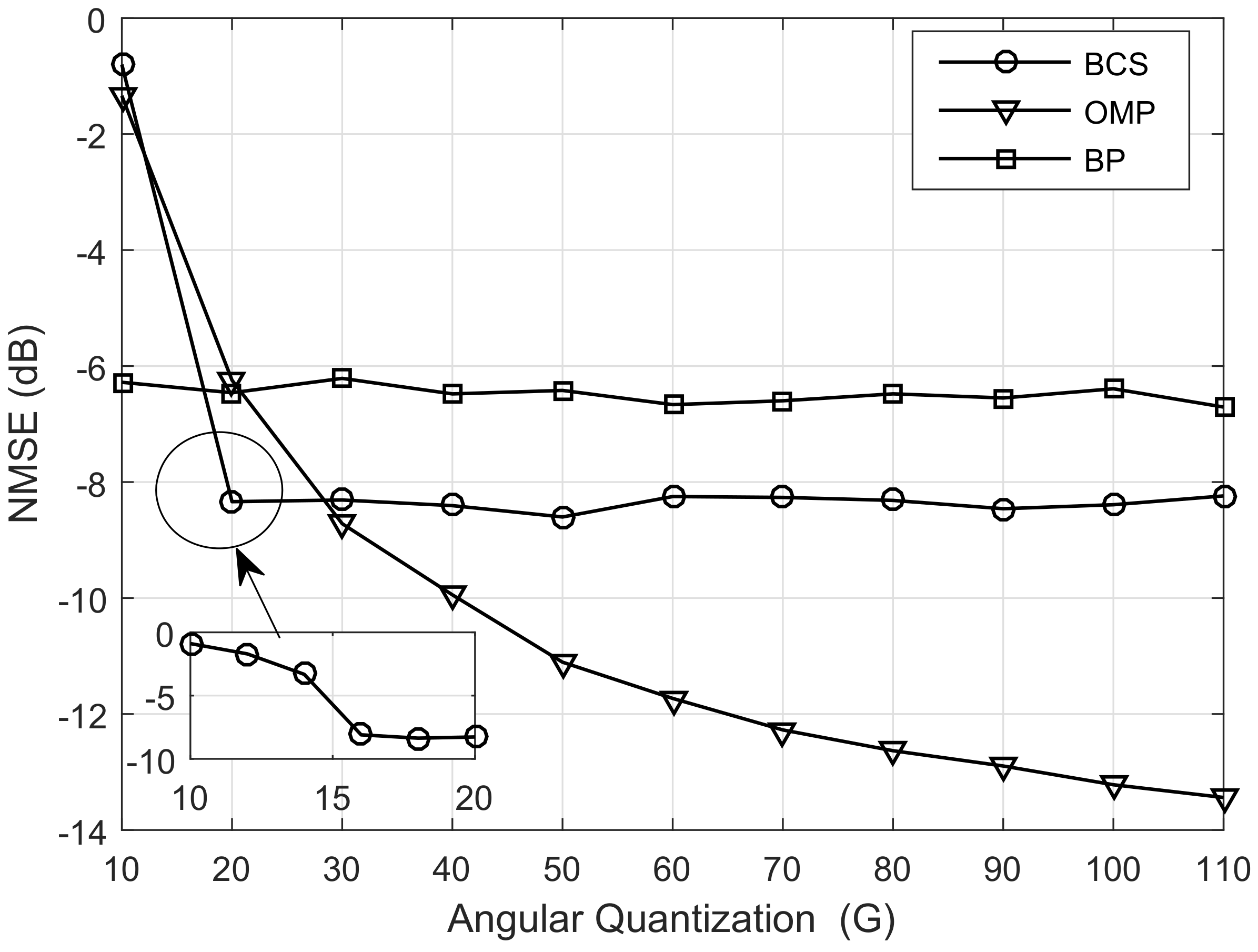
5.1. Comprehensive Comparison of Estimation Quality
5.2. Computation Complexity versus Sparseness
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xiao, M.; Mumtaz, S.; Huang, Y.; Dai, L.; Li, Y. Millimeter Wave Communications for Future Mobile Networks. IEEE J. Sel. Areas Commun. 2017, 35, 1909–1935. [Google Scholar] [CrossRef]
- Yang, L.; Zeng, Y.; Zhang, R. Channel Estimation for Millimeter Wave MIMO Communications with Lens Antenna Arrays. IEEE Trans. Veh. Technol. 2018, 67, 3239–3251. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Mi, D.; Wang, Z. Mmwave massive MIMO-based Wireless Backhaul for the 5G Ultra-Dense Network. IEEE Wirel. Commun. 2015, 22, 13–21. [Google Scholar] [CrossRef]
- Chen, J.; Yin, X.; Cai, X.; Wang, S. Measurement-based Massive MIMO Channel Modeling for Outdoor LoS and NLoS Environments. IEEE Access 2017, 5, 2126–2140. [Google Scholar] [CrossRef]
- Lin, X.; Wu, S.; Jiang, C.; Kuang, L.; Yan, J.; Hanzo, L. Estimation of Broadband Multiuser Millimeter Wave Massive MIMO-OFDM Channels by Exploiting Their Sparse Structure. IEEE Trans. Wirel. Commun. 2018, 17, 3959–3973. [Google Scholar] [CrossRef]
- Mezghani, A.; Swindlehurst, A. Blind Estimation of Sparse Broadband Massive MIOM Channels with Ideal and One-Bit ADCs. IEEE Trans. Signal Process. 2017, 66, 2972–2983. [Google Scholar] [CrossRef]
- Zhang, J.; Yuan, X.; Zhang, Y. Blind Signal Detection in Massive MIMO: Exploiting the Channel Sparsity. IEEE Trans. Commun. 2018, 66, 700–712. [Google Scholar] [CrossRef]
- Ma, J.; Ping, L. Data-aided Channel Estimation in Large Antenna Systems. IEEE Trans. Signal Process. 2014, 62, 3111–3124. [Google Scholar]
- Hu, C.; Dai, L.; Mir, T.; Gao, Z.; Fang, J. Super-resolution Channel Estimation for mmWave Massive MIMO with Hybrid Precoding. IEEE Trans. Veh. Technol. 2017, 67, 8954–8958. [Google Scholar] [CrossRef]
- Li, X.; Fang, J.; Li, H.; Wang, P. Millimeter Wave Channel Estimation via Exploiting Joint Sparse and Low-Rank Structures. IEEE Trans. Wirel. Commun. 2018, 17, 1123–1133. [Google Scholar] [CrossRef]
- Tsai, C.-R.; Liu, Y.-H.; Wu, A.-Y. Efficient Compressive Channel Estimation for Millimeter Wave Large-Scale Antenna Systems. IEEE Trans. Signal Process. 2018, 66, 2414–2428. [Google Scholar]
- Kiran, V.; Ahmed, A.; Nuria, G.P.; Robert, J.; Heath, W. Chnanel Estimation for Hybrid Architecture-based Wideband Millimeter Wave System. IEEE J. Sel. Areas Commun. 2017, 35, 1996–2009. [Google Scholar]
- Wen, C.K.; Jin, S.; Wong, K.K.; Chen, J.C.; Ting, P. Channel Estimation for Massive MIMO Using Gaussian Mixture Bayesian Learning. IEEE Trans. Wirel. Commun. 2015, 14, 1356–1368. [Google Scholar] [CrossRef]
- Wu, Y.; Gu, Y.; Wang, Z. Channel Estimation for mmWave MIMO with Transmitter Hardware Impairments. IEEE Commun. Lett. 2017, 22, 320–323. [Google Scholar] [CrossRef]
- Xiong, Y.; Wei, N.; Zhang, Z.; Li, B.; Chen, Y. Channel Estimation and IQ Imbalance Compensation for Uplink Massive MIMO Systems with Low-Resolution ADCs. IEEE Access 2017, 5, 6372–6388. [Google Scholar] [CrossRef]
- Wang, Y.F.; Lee, J.H. A Simple Phase Noise Suppression Scheme for Massive MIMO Uplink Systems. IEEE Trans. Veh. Technol. 2017, 66, 4769–4780. [Google Scholar] [CrossRef]
- Hojatian, H.; Omidi, M.J.; Saeedi-Sourck, H.; Farhang, A. Joint CFO and Channel Estimation in OFDM-based Massive MIMO Systems. In Proceedings of the International Symposium on Telecommunications, Chania, Greece, 4–6 October 2016; pp. 343–348. [Google Scholar]
- Bjrnson, E.; Hoydis, J.; Kountouris, M.; Debbah, M. Massive MIMO Systems with Non-Ideal Hardware: Energy Efficiency, Estimation, and Capacity Limits. IEEE Trans. Inf. Theory 2013, 60, 7112–7139. [Google Scholar] [CrossRef]
- Studer, C.; Wenk, M.; Burg, A. MIMO Transmission with Residual Transmit-RF Impairments. In Proceedings of the International ITG Workshop on Smart Antennas, Berlin, Germany, 16–18 February 2009; pp. 189–196. [Google Scholar]
- Bajwa, W.U.; Haupt, J.; Sayeed, A.M.; Nowak, R. Compressed Channel Sensing: A New Approach to Estimating Sparse Multipath Channels. Proc. IEEE 2010, 98, 1058–1076. [Google Scholar] [CrossRef]
- Heath, R.W.; Gonz lez-Prelcic, N.; Rangan, S.; Roh, W.; Sayeed, A.M. An Overview of Signal Processing Techniques for Millimeter Wave MIMO Systems. IEEE J. Sel. Top. Signal Process. 2017, 10, 436–453. [Google Scholar] [CrossRef]
- Zhang, J.; Dai, L.; Li, X.; Liu, Y.; Hanzo, L. On Low-Resolution ADCs in Practical 5G Millimeter Wave Massive MIMO Systems. IEEE Commun. Mag. 2018, 56, 2–8. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, D.; Wang, J.; You, X. Channel Estimation for Massive MIMO-OFDM Systems by Tracking the Joint Angle-Delay Subspace. IEEE Access 2016, 4, 10166–10179. [Google Scholar] [CrossRef]
- Alkhateeb, A.; Ayach, O.E.; Leus, G.; Heath, R.W. Channel Estimation and Hybrid Precoding for Millimeter Wave Cellular Systems. IEEE J. Sel. Top. Signal Process. 2014, 8, 831–846. [Google Scholar] [CrossRef]
- Junho, L.; Gye-Tae, G.; Yong, L. Chnanel Estimation via Orthogonal Matching Pursuit for Hybrid MIMO Systems in Millimeter Wave Communications. IEEE Trans. Commun. 2016, 64, 2370–2386. [Google Scholar]
- Ren, X.; Chen, W.; Tao, M. Position-based Compressed Channel Estimation and Pilot Design for High-Mobility OFDM Systems. IEEE Trans. Veh. Technol. 2015, 64, 1918–1929. [Google Scholar] [CrossRef]
- Nguyen, S.L.H.; Ghrayeb, A. Compressive Sensing-based Channel Estimation for Massive Multiuser MIMO Systems. In Proceedings of the IEEE Wireless Communications and Networking Conference, Shanghai, China, 7–10 April 2013; pp. 2890–2895. [Google Scholar]
- Ji, S.; Xue, Y.; Carin, L. Bayesian Compressive Sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Chen, C.Y.; Wu, W.R. Joint AoD, AoA, and Channel Estimation for MIMO-OFDM Systems. IEEE Trans. Veh. Technol. 2018, 67, 5806–5820. [Google Scholar] [CrossRef]
- Carlin, M.; Rocca, P.; Oliveri, G.; Viani, F. Directions-of-Arrival Estimation Through Bayesian Compressive Sensing Strategies. IEEE Trans. Antennas Propag. 2013, 61, 3828–3838. [Google Scholar] [CrossRef]
- Rocca, P.; Hannan, M.A.; Salucci, M.; Massa, A. Single-Snapshot DoA Estimation in Array Antennas with Mutual Coupling through a Multi-Scaling Bayesian Compressive Sensing Strategy. IEEE Trans. Antennas Propag. 2017, 65, 3203–3213. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, X.; Yang, W.; Cai, Y.; Guan, X. Comparison of CS-Based Channel Estimation for Millimeter Wave Massive MIMO Systems. Appl. Sci. 2019, 9, 4346. https://doi.org/10.3390/app9204346
Lu X, Yang W, Cai Y, Guan X. Comparison of CS-Based Channel Estimation for Millimeter Wave Massive MIMO Systems. Applied Sciences. 2019; 9(20):4346. https://doi.org/10.3390/app9204346
Chicago/Turabian StyleLu, Xingbo, Weiwei Yang, Yueming Cai, and Xinrong Guan. 2019. "Comparison of CS-Based Channel Estimation for Millimeter Wave Massive MIMO Systems" Applied Sciences 9, no. 20: 4346. https://doi.org/10.3390/app9204346
APA StyleLu, X., Yang, W., Cai, Y., & Guan, X. (2019). Comparison of CS-Based Channel Estimation for Millimeter Wave Massive MIMO Systems. Applied Sciences, 9(20), 4346. https://doi.org/10.3390/app9204346





